2. 哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001
2. Fundamental Science on Nuclear Safety and Simulation Technology Laboratory, Harbin Engineering University, Harbin 150001, China
为缓解急剧增长的能源需求及减小对环境污染,核能的和平利用受到越来越多的关注。作为一个复杂的大系统,核动力装置包含各种结构、系统及组件(SSCs),当这些设备及过程出现故障时,可能严重威胁到系统的可靠性。据统计,核电厂的运行和维护成本占总发电成本的60%~70%[1]。同时工程实践表明,当发生故障时,操作人员的误操作和误诊可能会造成灾难性后果[2]。因此,向操作员提供有效的运行信息不仅能合理降低运行维护成本,而且可以提高核动力装置的安全性。近年来,基于数据驱动的故障诊断技术蓬勃发展[3-4],同时为降低误操作率,研究人员也越来越意识到故障程度评估的重要性。魏玮等[5]将堆芯损伤评价导则应用于冷却剂丧失事故的损伤程度评估,作为评价损伤程度的可靠方法。Peng等[2]提出基于马氏距离的故障程度评估方法,结果验证了该方法的有效性。Liu等[6]将Elman神经网络用于故障程度估计,并验证了该方法为操作员提供综合信息的可靠性。
本文考虑到需要从大量的监测信号中挖掘故障程度信息,采用最小二乘-支持向量机(least square support vector machine, LSSVM)来提取参数间约束关系及故障程度规律,并采用粒子群优化(particle swarm optimization, PSO)算法来搜寻最优超参数,提高故障程度评估精度,降低计算量,为操作员决策及干预提供良好基础。
1 破口故障程度评估 1.1 最小二乘-支持向量机支持向量机(support vector machine, SVM)是Vapnik基于统计学习提出的高效机器学习方法[7],借助结构风险最小化原则,有效抑制了过拟合现象,解决神经网络训练时间长、结果随机性等缺陷,适用于复杂非线性建模问题[8]。为了挖掘系统级运行参数的约束关系,本文将LSSVM用于故障程度评估。LSSVM是由Suykens等[9]提出的一种SVM改进方法,借助与样本集的结构风险最小化原则建立回归模型,综合考虑模型复杂度项及拟合误差项:
| $ \left\{\begin{array}{l} \min J(\boldsymbol{\omega}, \boldsymbol{e})=\frac{1}{2}\|\boldsymbol{\omega}\|^{2}+\frac{1}{2} c \sum\limits_{i=1}^{l} e_{i}^{2} \\ \text { s. t. } \boldsymbol{y}_{i}=\boldsymbol{\omega}^{\mathrm{T}} \varphi\left(\boldsymbol{x}_{i}\right)+b+\boldsymbol{e}_{i}, i=1, 2, \cdots, l \end{array}\right. $ | (1) |
式中:误差变量ei表示模型对样本集的回归误差。训练样本集S={(xi, yi), i=1, 2, …, l},xi∈Rn是输入数据,yi∈Rn是输出数据;φ(·)表示xi从原始空间Rn到高维特征空间H的非线性映射;J是损失函数;权值向量ω∈H;偏置项b∈R;c是惩罚因子。LS-SVM采用等式约束条件,求解的是线性方程组,提高了计算速度和精度[10]。式(1)对应的Lagrange函数为:
| $ L(\boldsymbol{\omega}, b, \boldsymbol{e}, \boldsymbol{a})=J(\boldsymbol{\omega}, \boldsymbol{e})-\sum\limits_{i=1}^{l} \alpha_{i}\left[\boldsymbol{\omega}^{\mathrm{T}} \varphi\left(\boldsymbol{x}_{i}\right)+b+\boldsymbol{e}_{i}-\boldsymbol{y}_{i}\right] $ | (2) |
式中:拉格朗日乘子αi∈R,α=[α1 α2 … αl]T∈Rl;e=[e1 e2 … el]T∈Rl。对式(2)进行优化得:
| $ \left\{\begin{array}{l} \frac{\partial L}{\partial \omega}=0 \Rightarrow \boldsymbol{\omega}=\sum\limits_{i=1}^{l} \alpha_{i} \varphi\left(\boldsymbol{x}_{i}\right) \\ \frac{\partial L}{\partial b}=0 \Rightarrow \sum\limits_{i=1}^{l} \alpha_{i}=0 \\ \frac{\partial L}{\partial e_{i}}=0 \Rightarrow \alpha_{i}=\gamma e_{i}, i=1, 2, \cdots, l \\ \frac{\partial L}{\partial \alpha_{i}}=0 \Rightarrow \boldsymbol{\omega}^{\mathrm{T}} \varphi\left(\boldsymbol{x}_{i}\right)+b+e_{i}-\boldsymbol{y}_{i}=0, i=1, 2, \cdots, l \end{array}\right. $ | (3) |
消除变量ω、e,可以得到矩阵方程:
| $ \left[\begin{array}{cc} 0 & \boldsymbol{e}_{n}^{\mathrm{T}} \\ \boldsymbol{e}_{n} & \mathit{\boldsymbol{ \boldsymbol{\varOmega}}}+\boldsymbol{\gamma}^{-1} \boldsymbol{e}_{n} \end{array}\right]\left[\begin{array}{l} b \\ \boldsymbol{\alpha} \end{array}\right]=\left[\begin{array}{l} 0 \\ \boldsymbol{y} \end{array}\right] $ | (4) |
式中: en=[1 1 … 1]T, α=[α1 α2 … αl]T, y=[y1 y2 … yl]T,核函数Ω为对称矩阵:
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega}}}=\left[\mathit{\boldsymbol{ \boldsymbol{\varOmega}}}_{i j}\right]_{l \times l}, \mathit{\boldsymbol{ \boldsymbol{\varOmega}}}_{i j}=\boldsymbol{\varphi}^{\mathrm{T}}\left(x_{j}\right) \boldsymbol{\varphi}\left(x_{i}\right)=\boldsymbol{K}\left(x_{j}, x_{i}\right) $ | (5) |
由于惩罚因子c及核函数参数σ2对回归精度影响较大,因此必须对超参数Θ=(c, σ2)进行优化。然而核动力装置参数众多,一般的共轭梯度法在高精度需求下,需要较多训练样本,而共轭梯度的求解需要进行矩阵逆运算以及较大内存空间,从而导致计算低效[11],因此本文使用PSO算法以提高计算效率。
1.2 粒子群优化PSO是由Kennedy等[12]基于人工生命和演化计算理论提出,用于求解优化问题。在PSO中,“粒子”代表搜索空间中的潜在解,具有初始速度和位置,由适应度函数决定适应值[13]。粒子速度和位置更新由适应度和粒子个体极值pbesti, j(t)及种群全局极值gbesti, j(t)决定:
| $ \begin{gathered} v_{i, j}(t+1)=\omega v_{i, j}(t)+c_{1} R_{1}\left[\text { pbest }_{i, j}(t)-x_{i, j}(t)\right]+ \\ c_{2} R_{2}\left[\text { gbest }_{j}(t)-x_{i, j}(t)\right] \end{gathered} $ | (6) |
| $ x_{i, j}(t+1)=x_{i, j}(t)+v_{i, j}(t+1) $ | (7) |
式中:i=1, 2, …, N为粒子;j=1, 2, …, D为搜索维度;t为迭代次数;vi, j(t)及xi, j(t)为第i个粒子在j维的速度及位置,惯性权重ω∈[0, 1];加速系数c1、c2∈[0, 2]调节认知及种群组分影响;R1、R2为均匀分布随机数;pbesti, j(t)为粒子历史最优位置;gbesti, j(t)为总群体历史最优位置。
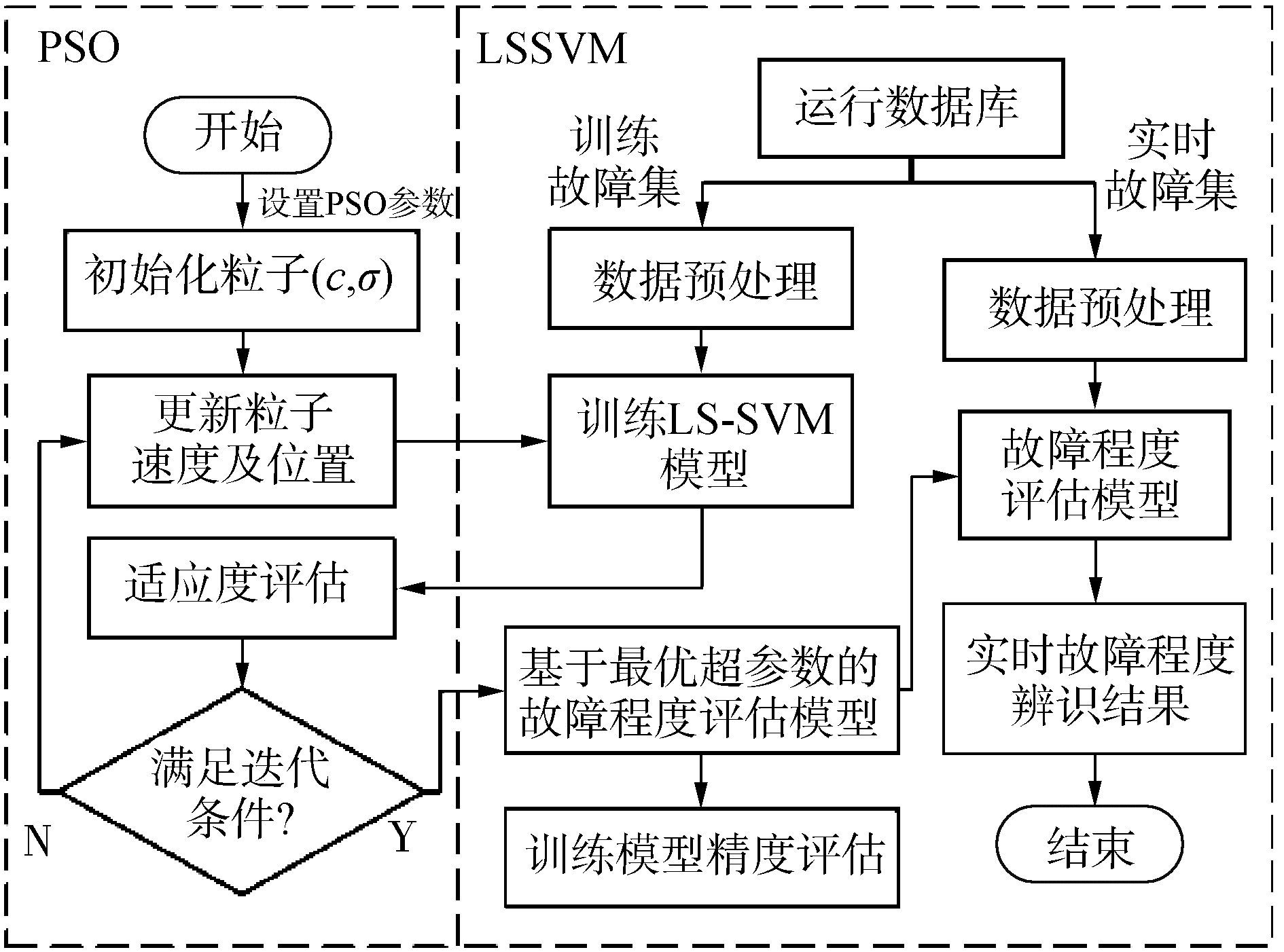
1.3 基于PSO-LSSVM的故障程度评估方法针对核动力装置的特点,本文提出的故障程度评估流程如图 1所示,主要包括基于PSO的超参数寻优以及程度评估阶段2个阶段:1)针对储存在运行数据库的各种采集信号,经过数据处理后,运用PSO方法在参数空间进行全局寻优,实现对回归模型的参数优化;2)基于LSSVM与样本集的结构风险最小化原则来建立程度评估模型,提取运行数据参数间的约束关系及故障程度规律。对于特定故障的PSO-LSSVM模型,输入实时故障运行数据即可判断此时的严重程度。提出的优化程度评估方法综合了智能寻优及数据驱动方法,充分发挥各方法的优势,提高了模型回归精度,并且避免了基于模型的故障程度回归方法的缺陷,比如模型误差、计算效率低、耦合响应慢等。
|
Download:
|
| 图 1 基于PSO-LSSVM的核动力装置故障程度评估流程 Fig. 1 Failures severity assessment process of NPPs based on PSO-LSSVM | |
为了验证提出方法的可靠性,本文应用PCTRAN来模拟运行工况[14],通过插入6类各12种程度的故障,得到94个参数时间序列。其中故障程度通过键入程度百分比设置,根据PCTRAN故障程度定义,破口类事故程度为破口与总截面积比值,甩负荷事故程度为负荷与满功率比值。通过剔除与故障程度无关数据,最终得到64个有效参数数据。同时在之前故障诊断研究工作中[15],基于Pearson相关系数计算验证了64个参数与故障均呈现一定相关性,包括安全壳压力、地坑水位、稳压器水位、回路过冷度、上冲流量等参数,从而保证了故障程度评估的效率。
在6种故障的程度估计模型建立中,训练时将各自故障程度分别为5%、10%、15%、20%、25%、30%、35%、40%、45%及50%的数据作为训练集,测试集选为12%及22%的数据,数据细节如表 1所示。采集数据从故障插入开始截取,每秒采集一个数据,得到的时间序列是插入瞬态事故后的变化及系统自动化补偿的结果。模型训练时,输入数据为同一时刻64个参数的归一化向量,输出则为此刻的故障程度值,如50%程度的破口类事故表示此时破口面积达到了总面积的50%,因此得到的模型则反映了参数间相对关系与故障程度的实时对应规律。需要指出的是,当甩负荷故障程度超过25%后,由于故障较为剧烈导致停堆,无法获取完整的参数运行曲线,且运行曲线重叠在一起,不利于回归模型的学习,因此甩负荷故障的训练集仅取5%~25%的故障程度数据。
| 表 1 故障程度评估的数据细节 Table 1 Data details of failure severity assessment |
为提高模型回归精度,在训练及测试时采用最大差分方法进行归一化:
| $ x^{*}(t)=\frac{x(t)-x_{\min }(t)}{x_{\max }(t)-x_{\min }(t)} $ | (8) |
式中:x*(t)为归一化后的t时刻的各参数值x(t);xmin(t)、xmax(t)分别为t时刻的最小、最大参数值。经过无量纲化的运行数据能够保留与故障程度有关信息,并且加速模型的收敛。
为了全面评价模型回归性能,采用平均绝对百分误差RMAPE及相关系数R2评估模型精度:
| $ R_{\mathrm{MAPE}}=\frac{1}{N} \sum\limits_{i=1}^{N}\left|\frac{y_{i}-\hat{y}_{i}}{y_{i}}\right| \times 100 $ | (9) |
| $ R^{2}=1-\sum\limits_{i=1}^{N}\left(y_{i}-\hat{y}_{i}\right)^{2} / \sum\limits_{i=1}^{N}\left(y_{i}-\bar{y}_{i}\right)^{2} $ | (10) |
式中:yi及
本文对PSO-LSSVM故障程度评估方法各方面进行对比测试,包括采用不同核函数对比测试、应用不同回归算法对比测试以及对PSO-LSSVM抗噪性能进行分析,同时各种测试分别独立运行20次取平均值,从而充分验证本文提出的方法应用于核动力装置系统级故障程度评估的可靠性。
2.2.1 核函数选择分别采用基于线性、多项式以及径向基核函数的PSO-LSSVM模型进行程度评估,其他参数一致。将6种故障的各程度训练数据输入至LSSVM回归器中进行学习,同时采用基于PSO算法对惩罚系数及核函数参数进行多目标寻优。设置的PSO种群大小设为200,学习因子设置为1.49,最大迭代次数为600,惯性权重初始为1,粒子初始速度为[0, 1]的随机数,适应度函数为:
| $ f=\frac{1}{m} \sum\limits_{i=1}^{m}\left[g\left(x_{i}\right)-y_{i}\right]^{2} $ | (11) |
式中:g(xi)为第i个训练样本的预测值;yi为训练样本的实际值;m为训练集样本数。
图 2所示为测试结果对比,由图 2中的平均绝对百分误差RMAPE曲线可知,线性核函数方法误差普遍较高,多项式核函数误差虽然在故障1、2下接近于0,但在其他故障下却导致较大的偏差,而RBF核函数得到误差最小。相关系数对比也表明了基于RBF核函数的回归值与真实值最为接近,因此本文的PSO-LSSVM模型采用RBF核函数。同时不同核函数的最优超参数及评价结果细节如表 2所示。

|
Download:
|
| 图 2 不同核函数程度评估的测试RMAPE与R2结果 Fig. 2 RMAPE and R2 of severity evaluation with different kernel function | |
| 表 2 不同核函数的LSSVM故障程度评估细节 Table 2 Details of LSSVM failure severity evaluation with different kernel functions |
为验证基于PSO-LSSVM方法应用于故障程度评估有效性,本文选用PSO-SVM以及LSSVM方法进行对比测试。在PSO-LSSVM算法设置中,基于核函数选择对比测试结果,选择RBF核函数,优化的参数设置与其保持一致,同时优化的适应度评价准则如式(11)所示。在PSO-SVM算法中,同样应用PSO方法优化SVM超参数,优化参数与本文一致。最终得到6种故障下各方法的RMAPE结果对比,分别如图 3所示。在结果展示中,将故障程度为22%的误差曲线连接在12%之后,图中虚线表示2种测试故障程度的分界线。

|
Download:
|
| 图 3 6种故障下程度评估RMAPE曲线 Fig. 3 RMAPE curves for the severity evaluation of six faults | |
由图 3可以看出,PSO-SVM算法误差普遍较大,尤其是在故障运行末期,随着时间的运行,程度回归效果逐渐变差;经典LSSVM算法在运行期间均有不同幅度的误差,这是由于未能优化超参数导致模型的泛化能力较弱。在图 3中,对比算法的误差曲线均有不同程度的峰值或谷值,表示该算法在此时刻具有较大的误差,对于测试样本的辨识精度较低。而PSO-LSSVM模型的误差最小,其回归精度较高,尤其在故障5中,训练数据的减小使得误差曲线在初期有较大波动,但是随后迅速降低到最小值。综上所述,本文的算法在多种系统级故障中表现出良好的程度评估性能,具有较好的可靠性。
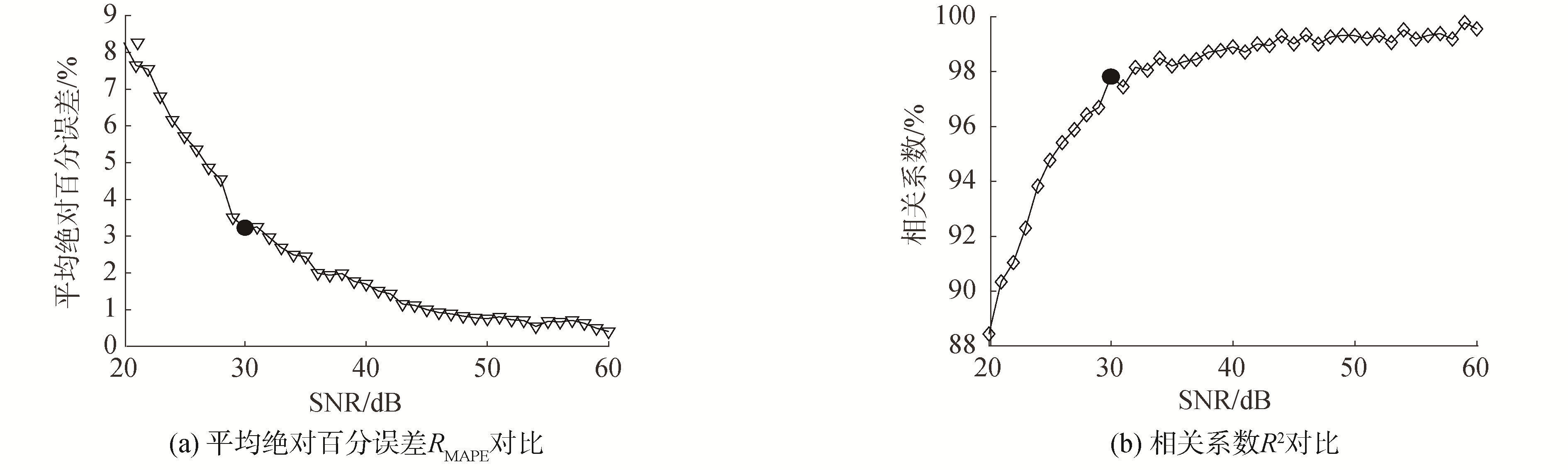
2.2.3 抗噪性能测试由于核动力装置复杂的运行环境,实际传感器测得信号不可避免带有各种噪声及其他干扰,不利于的故障程度的识别。因此,本研究还对PSO-LSSVM方法的抗噪性能进行测试,以验证该方法对系统级故障程度评估的有效性。针对上述获取的研究数据,分别将运行数据加入不确定性最大的白噪声,使其SNR分别为20~60 dB。将加噪的训练数据分别输入至PSO-LSSVM模型中,并应用对应信噪比的测试数据进行验证,从而得到了不同信噪比下6种故障的平均回归评价,如图 4所示。
|
Download:
|
| 图 4 不同信噪比下程度评估的测试RMAPE与R2结果 Fig. 4 The RMAPE and R2 of severity evaluation under different SNR | |
从图 4的RMAPE曲线可知,当信号SNR为20 dB,测试得到的程度评估精度也低于9%。随着信噪比的增加,即噪声的减少,PSO-LSSVM模型回归误差逐渐降低,当信噪比为30 dB时,误差为3%左右,如图中黑点所示,随后逐渐收敛到0。由R2曲线可知,当信噪比大于30 dB时,相关系数均在97%以上,表明评估结果十分接近实际故障程度。而在核动力装置中,一般监测信号夹杂的噪声较少,即使振动信号信噪比也在30 dB以上[16]。因此在核动力装置运行环境下,基于PSO-LSSVM的故障程度评估方法能取得较高的精度,具有稳定的抗噪性能。
3 结论1) LSSVM方法可从多维监测信号中有效挖掘故障程度信息,将模型训练转化为求解线性方程组问题,相对SVM具有更快的收敛速度。
2) 基于PSO方法能够建立最优故障程度评估模型,提高建模效率的同时保证了评估的精度。
3) 在核动力装置运行环境下,该方法能够表现出较强的抗噪稳定性,从而保证核动力装置的安全运行。
本文仅对PCTran软件的数据进行了案例测试,后续将会考虑仿真机数据中更多故障工况的验证,以完善算法的测试工作。
| [1] |
COBLE J B, RAMUHALLI P, BOND L J, et al. Prognostics and health management in nuclear power plants: a review of technologies and applications[M]. Richland: Pacific Northwest National Laboratory, 2012: 30.
(  0) 0)
|
| [2] |
PENG Minjun, WANG Hang, CHEN Shanshan, et al. An intelligent hybrid methodology of on-line system-level fault diagnosis for nuclear power plant[J]. Nuclear engineering and technology, 2018, 50(3): 396-410. DOI:10.1016/j.net.2017.11.014 (  0) 0)
|
| [3] |
HWANG I, KIM S, KIM Y, et al. A survey of fault detection, isolation, and reconfiguration methods[J]. IEEE transactions on control systems technology, 2010, 18(3): 636-653. DOI:10.1109/TCST.2009.2026285 (  0) 0)
|
| [4] |
MA Jianping, JIANG Jin. Applications of fault detection and diagnosis methods in nuclear power plants: a review[J]. Progress in nuclear energy, 2011, 53(3): 255-266. DOI:10.1016/j.pnucene.2010.12.001 (  0) 0)
|
| [5] |
魏玮, 周志伟. 中国百万千瓦级核电站严重事故下堆芯损伤评价[J]. 原子能科学技术, 2011, 45(3): 302-306. WEI Wei, ZHOU Zhiwei. Core damage assessment for Chinese 1000 MWe NPP under severe accident conditions[J]. Atomic energy science and technology, 2011, 45(3): 302-306. (  0) 0)
|
| [6] |
LIU Yongkuo, ABIODUN A, WEN Zhibin, et al. A cascade intelligent fault diagnostic technique for nuclear power plants[J]. Journal of nuclear science and technology, 2018, 55(3): 254-266. DOI:10.1080/00223131.2017.1394228 (  0) 0)
|
| [7] |
VAPNIK V N. The nature of statistical learning theory[M]. New York: Springer, 1995: 138-146.
(  0) 0)
|
| [8] |
KISI O, PARMAR K S. Application of least square support vector machine and multivariate adaptive regression spline models in long term prediction of river water pollution[J]. Journal of hydrology, 2016, 534: 104-112. DOI:10.1016/j.jhydrol.2015.12.014 (  0) 0)
|
| [9] |
SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural processing letters, 1999, 9(3): 293-300. DOI:10.1023/A:1018628609742 (  0) 0)
|
| [10] |
DENG Wu, YAO Rui, ZHAO Huimin, et al. A novel intelligent diagnosis method using optimal LS-SVM with improved PSO algorithm[J]. Soft computing, 2019, 23(7): 2445-2462. DOI:10.1007/s00500-017-2940-9 (  0) 0)
|
| [11] |
NOORI M, HASSANI H, JAVAHERIAN A, et al. Automatic fault detection in seismic data using Gaussian process regression[J]. Journal of applied geophysics, 2019, 163: 117-131. DOI:10.1016/j.jappgeo.2019.02.018 (  0) 0)
|
| [12] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of ICNN'95-International Conference on Neural Networks. Perth, 1995: 1942-1948.
(  0) 0)
|
| [13] |
FANG Debin, ZHANG Xiaoling, YU Qian, et al. A novel method for carbon dioxide emission forecasting based on improved Gaussian processes regression[J]. Journal of cleaner production, 2018, 173: 143-150. DOI:10.1016/j.jclepro.2017.05.102 (  0) 0)
|
| [14] |
CHENG Y H, SHIH C, CHIANG S C, et al. Introducing PCTRAN as an evaluation tool for nuclear power plant emergency responses[J]. Annals of nuclear energy, 2012, 40(1): 122-129. DOI:10.1016/j.anucene.2011.10.016 (  0) 0)
|
| [15] |
PENG Binsen, XIA Hong, LIU Yongkuo, et al. Research on intelligent fault diagnosis method for nuclear power plant based on correlation analysis and deep belief network[J]. Progress in nuclear energy, 2018, 108: 419-427. DOI:10.1016/j.pnucene.2018.06.003 (  0) 0)
|
| [16] |
YANG Bo, XIA Hong, ANNOR-NYARKO M, et al. Application of total variation denoising in nuclear power plant signal pre-processing[J]. Annals of nuclear energy, 2020, 135: 106981. DOI:10.1016/j.anucene.2019.106981 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


