2. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001;
3. 西藏大学 工学院, 西藏 拉萨 850000;
4. 中国电子科技集团公司第五十四研究所, 河北 石家庄 050081
2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China;
3. College of Engineering, Tibet University, Lhasa 850000, China;
4. The 54th Research Institute of China Electronics Technology Group Corporation, Shijiazhuang 050081, China
浅海低频海洋信道具有稳定的干涉结构,其中包含了许多环境参数和目标运动信息,目标运动速度参数的获取是海洋目标检测、估计和定位的重要环节。对于单水听器被动测距而言,互谱法是估计目标径向运动速度常采用的方法。
文献[1-4]都是采用互谱测速,利用得到的径向速度信息进一步处理得到目标距离。这种方法无需声场先验信息,宽容性较高,有较高的发展应用潜力。另外,目标绝对速度参数是表征目标运动的一个物理量,也是被动声呐目标识别的重要特征之一。运动目标的速度估计在被动声呐信号处理中占据重要作用。
Rakotonarivo等[1]提出了单水听器互谱测速的基本原理与测量方法,并以此给出了2种目标距离的被动估计算法。在此基础上王鹏等[2]将其算法拓展应用到水平阵的被动目标互谱测速并且进行了随机相位扰动补偿,可以在更低的信噪比情况下进行互谱测速。邵云生等[3]利用水平线阵获得波束域信号,对不同时刻波束域声场的互相关信号进行频谱分析估计运动目标速度值,并且进行了基于声速扰动统计量的随机相位扰动补偿,可以在相对较低信噪比情况下获得运动目标径向速度值。王超等[4]则将文献3的相位补偿方法改进到单水听器互谱测速中,以此来获得更好的处理结果。
以上文献可以看到互谱测速的发展其实都是对传统互谱测速的原理进行一些补偿或者应用范围的拓展,并没有对互谱测速的原理算法进行更深的探究和拓展。
而本文进一步从原理上拓展了互谱的变化规律,根据目标接近最近通过点过程中,其线谱信号互谱的变化规律,提出了时频互谱测速算法,能够在更高的信噪比增益条件下,利用WVD变换测量目标的绝对速度。
1 时频互谱获得目标速度的基本原理根据浅海声场简正波表达式,将海洋波导看作是距离无关的水平分层环境,只考虑声速和密度随深度z的变化,将声源视为点源,可以得到一般情况下,由连续谱和离散谱组成的声场表达式[5]:
| $ p\left( {r, z} \right) = \frac{{\rm{i}}}{{\rho ({z_s})\sqrt {8{\rm{ \mathsf{ π} }}r} }}{{\rm{e}}^{ - i\pi /4}}\sum\limits_{m = 1}^\infty {{\psi _m}({z_s}){\psi _m}\left( z \right)} \frac{{{{\rm{e}}^{i{k_{rm}}r}}}}{{{k_{rm}}}} - {\smallint _{{C_{EJP}}}} $ | (1) |
式中:krm表示本征值;ψm(z)表示本征函数;∫CEJP表示连续谱成分;ρ(zs)表示声源处的密度。
离散成分表示为海水中传播的简正波部分,而连续成分表示主要在海底传播的侧面波部分。当声波远距离传播时,侧面波的贡献可以忽略不计。
将式(1)简化得到:
| $ p\left( {r, z} \right) = \sum\limits_{m = 1}^M {{A_m}\exp \left( {{\rm{i}}{k_{rm}}r + {\rm{i}}\left( {{\varphi _0} + {\varphi _{{\rm{noise}}}}\left( t \right) + \varphi \left( r \right)} \right)} \right)} $ |
其中:
| $ \left\{ \begin{array}{l} {A_m} = \sqrt {\frac{1}{{8\pi {k_m}r}}} {C_m}\exp \left( { - {\rm{i \mathsf{ π} /4}}} \right)\\ {C_m} = {\psi _m}\left( z \right){\psi _m}\left( {{z_s}} \right) \end{array} \right. $ | (2) |
式中: φ0表示初始相位;φnoise(t)是杂波和噪声引起的相位起伏分量,声速剖面存在声速扰动时,存在随距离变化的相位扰动φ(r),该相位扰动由于声速在距离上的扰动引起,会对简正波波数产生影响,并且可通过声速剖面的一阶、二阶统计量进行相对补偿。
假定目标做匀速直线运动,在t1、t2 2个时刻处目标与水听器相隔的距离分别为r1、r2。则其声压信号可以分别表示为:
| $ \begin{array}{l} p\left( {{t_1}, f} \right) = \sum\limits_n {{A_n}\exp \left( {{\rm{i}}{k_{rm}}{r_1} + {\rm{i}}\left( \varphi \right)} \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_n {{A_n}\exp \left( {{\rm{i}}{k_{rm}}\left( {r - \frac{{\Delta r}}{2}} \right) + {\rm{i}}\left( \varphi \right)} \right)} \\ p\left( {{t_2}, f} \right) = \sum\limits_n {{A_n}\exp \left( {{\rm{i}}{k_{rm}}{r_2} + {\rm{i}}\left( \varphi \right)} \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_n {{A_n}\exp \left( {{\rm{i}}{k_{rm}}\left( {r - \frac{{\Delta r}}{2}} \right) + {\rm{i}}\left( \varphi \right)} \right)} \end{array} $ | (3) |
将式(3)进行声压信号的互谱可以得到:
| $ \begin{array}{l} {I_c}\left( {\Delta t, f} \right) = p\left( {{t_1}, f} \right) \cdot \left( {{t_2}, f} \right) \approx \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{m, n} {{A_m}{A_n}^ * {{\rm{e}}^{ - {\rm{j}}\Delta {k_{mn}}\bar r}}{{\rm{e}}^{{\rm{j}}{{\bar k}_r} \cdot \Delta r}}} \end{array} $ | (4) |
式中:r=(r1+r2)/2;Δr=r2-r1,Δt=t2-t1为2个时刻之间的时间间隔;Δkmn=krm-krn表示第n阶模态的水平波数与第m阶模态的水平波数差,kr=2πf/cp,cp表示平均相速度,因此kr可以表示为平均水平波数,vr表示目标的径向运动速度,则在时间间隔内目标的距离变化为Δr。
因此,可以将式(4)进一步整理化简,对于目标在Δt的时间间隔内,从t1时刻运动到t2时刻,目标与水听器之间的距离由r变为r+Δr,可以得到:
| $ \begin{array}{l} {I_c}\left( {\Delta t, f} \right) = {\rm{Re}}\left[ {p\left( {r + \Delta r} \right){p^ * }\left( r \right)} \right] \approx \\ \;\;\;\;\;\;\;\;\;\;\;I\left( {r + \frac{{\Delta r}}{2}} \right)\cos \left( {\frac{{2\pi f}}{{{c_p}}} \cdot \Delta r} \right) \end{array} $ | (5) |
式(5)中I(r+Δr/2)与coskrΔr的变化相比被认为是缓慢变化的,在Δr≪r时可以将第1项视为常量。
式(5)可以看出,互谱随着Δr的变化规律而变化,通过探究Δr与目标速度的关系即可实现目标径向速度的估计。
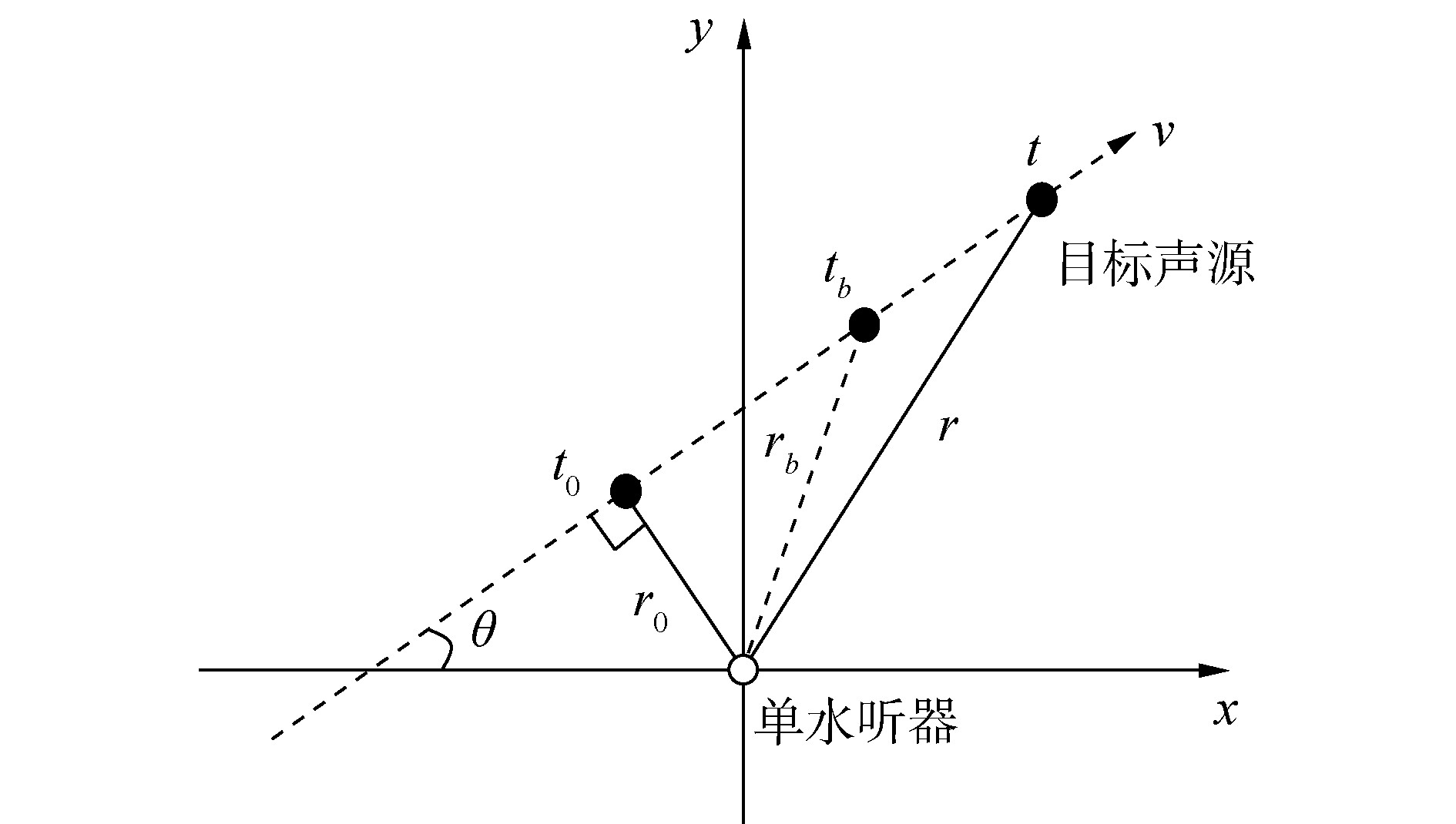
对于匀速直线运动的目标,其绝对速度为一定值,如下图所示,目标做匀速直线运动,航向角恒定为θ,目标运动过程中与水听器的最近距离定义为r0,通过最近距离处的时刻定义为t0,对于任意时刻t目标距离水听器距离r,目标的绝对速度为v,以水听器为坐标原点。
|
Download:
|
| 图 1 目标运动 Fig. 1 Target movement trend | |
而当目标远离最近通过点时,即径向速度没有迅速变化时,则在时间间隔内目标的距离变化为:Δr=vr·Δt。
| $ \begin{array}{l} {I_c}\left( {\Delta t, f} \right) = {\rm{Re}}\left[ {p\left( {r + \Delta r} \right){p^ * }\left( r \right)} \right] \approx \\ \;\;\;\;\;\;\;\;\;\;\;I\left( {r + \frac{{\Delta r}}{2}} \right)\cos \left( {\frac{{2\pi f}}{{{c_p}}} \cdot {v_r} \cdot \Delta r} \right) \end{array} $ | (6) |
对于Δr可以进一步简化为:
| $ \Delta r = \sqrt {r_0^2 + {{\left( {v\left( {t - {t_0}} \right)} \right)}^2}} $ | (7) |
假定最近通过时刻设为初始t=0时刻,并进行泰勒展开取其前2项可以得到:
| $ \Delta r = {v^2} \cdot {t^2}/2{r_0} $ | (8) |
将式(8)代入到式(5)可以得到:
| $ \begin{array}{l} {I_c}\left( {\Delta t, f} \right) = {\rm{Re}}\left[ {p\left( {r + \Delta r} \right){p^ * }\left( r \right)} \right] \approx \\ \;\;\;\;\;\;\;\;\;\;\;I\left( {r + \frac{{\Delta r}}{2}} \right)\cos \left( {\frac{{2\pi f}}{{{c_p}}} \cdot {v^2} \cdot {t^2}/2{r_0}} \right) \end{array} $ | (9) |
因此对于接近最近通过点的互谱呈现线性调频信号的形式,因此可以通过时频分析方法提取相关参数,得到目标的v2/r0。
式(6)的处理方法已在文献[1]中叙述,本文主要讨论式(9),对于接近最近通过点处目标的线谱进行互谱计算,获得其呈现线性调频信号的形式,可以通过时频分析方法提取其目标的v2/r0。对干涉条纹进行Hough变换[6-9]估计目标的v/r0[6],利用估计目标的v2/r0和v/r0就可以进一步计算目标的绝对速度和最近通过距离,而目标任意时刻的距离也可以根据式(7)来进行估计。
而如果干涉条纹不清晰,可以通过互谱结合时频分析,并将其计算结果代入到式(6)进一步计算此时刻的径向速度,结合目标运动几何关系:
| $ {v_r} = \frac{{{v^2}}}{{{r_0}}}\left( {t - {t_0}} \right)\frac{1}{{\sqrt {1 + {{\left( {\frac{v}{{{r_0}}}\left( {t - {t_0}} \right)} \right)}^2}} }} $ | (10) |
也可以得到目标的绝对速度和最近通过距离。
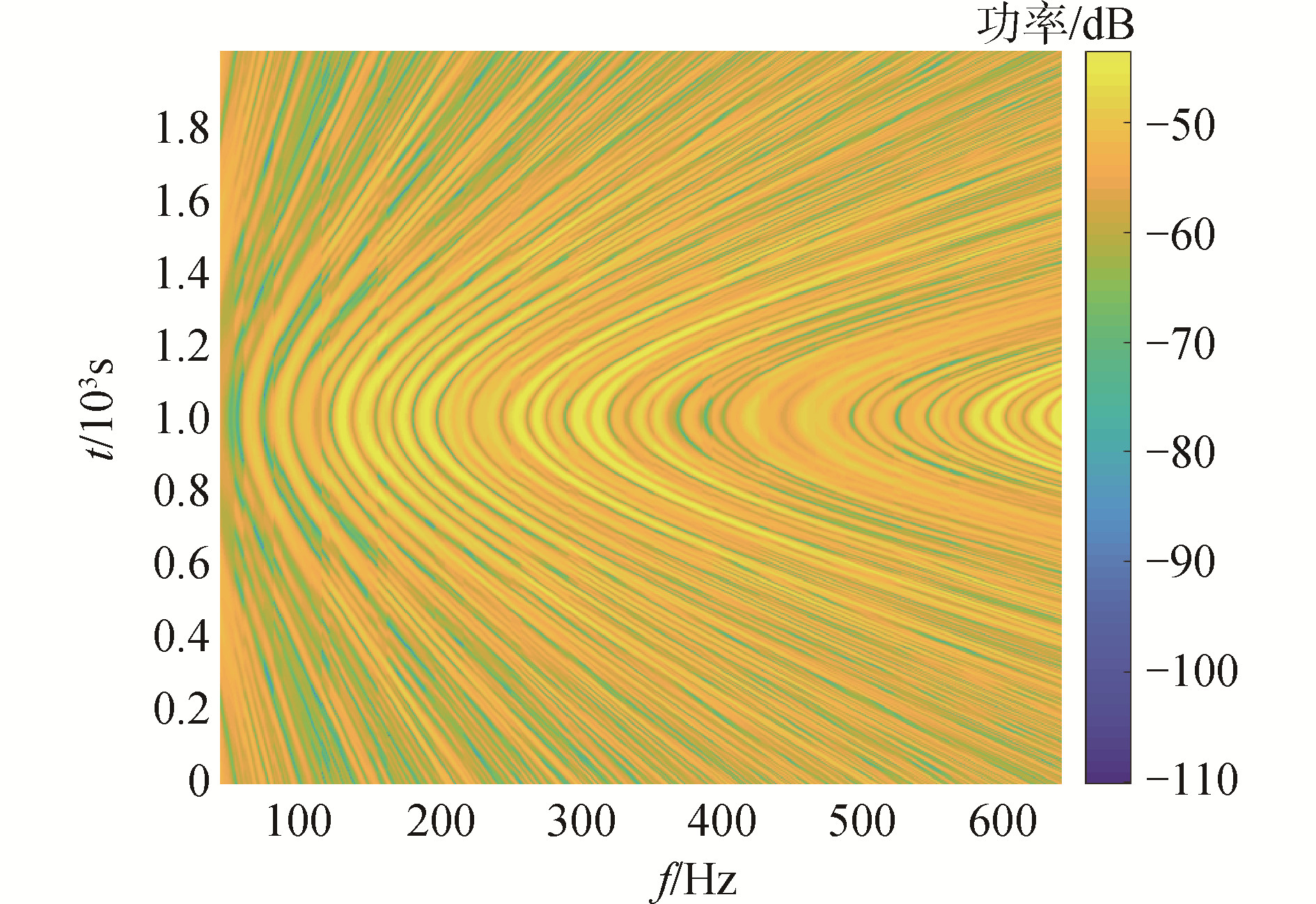
2 仿真数据处理仿真条件:海深200m,在海水中声速为1 500m/s,密度为1 g/cm3,海底声速为1 800m/s,密度为1.8 g/cm3,点源位于水下4m,水听器位于水下30m,声源频率范围为40~640 Hz,目标以2.5m/s的速度航行,与接收水听器的最近通过距离为708m,首先利用Kraken仿真模型得到目标运动LOFAR图。
|
Download:
|
| 图 2 运动目标LOFAR Fig. 2 LOFAR map of moving target | |
采取其49 Hz处的频谱信息,在1 000s~1 400s处进行互谱得到目标互谱图如图 3所示。
|
Download:
|
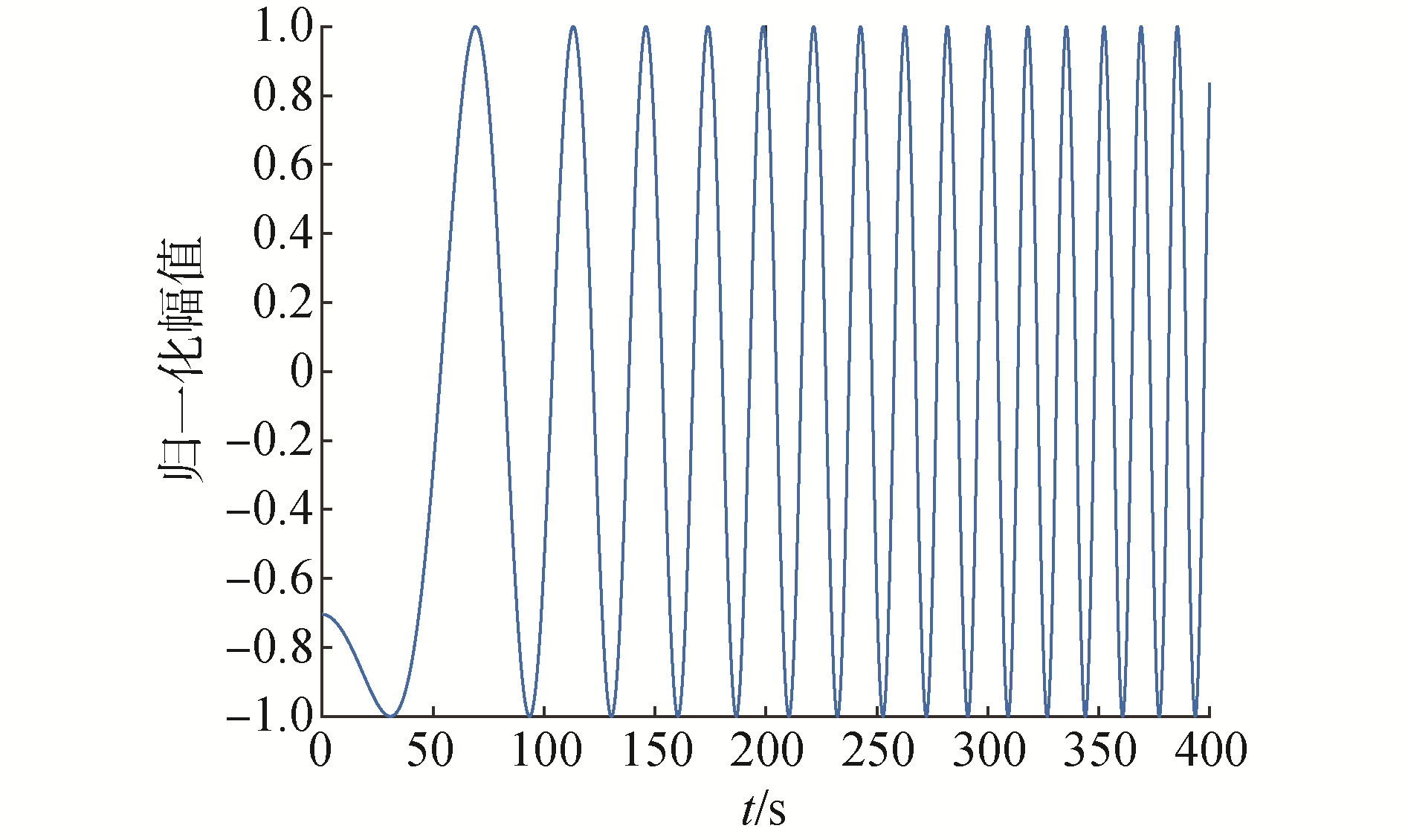
| 图 3 运动目标互谱 Fig. 3 Cross spectrum of moving target | |
从图 3中可以看到目标最近通过距离处的线谱互谱运算得结果呈现线性调频信号变化,正如式(9)所示,对图 3的计算结果进行WVD变换[10-13]得到广义时频图如下所示:
|
Download:
|
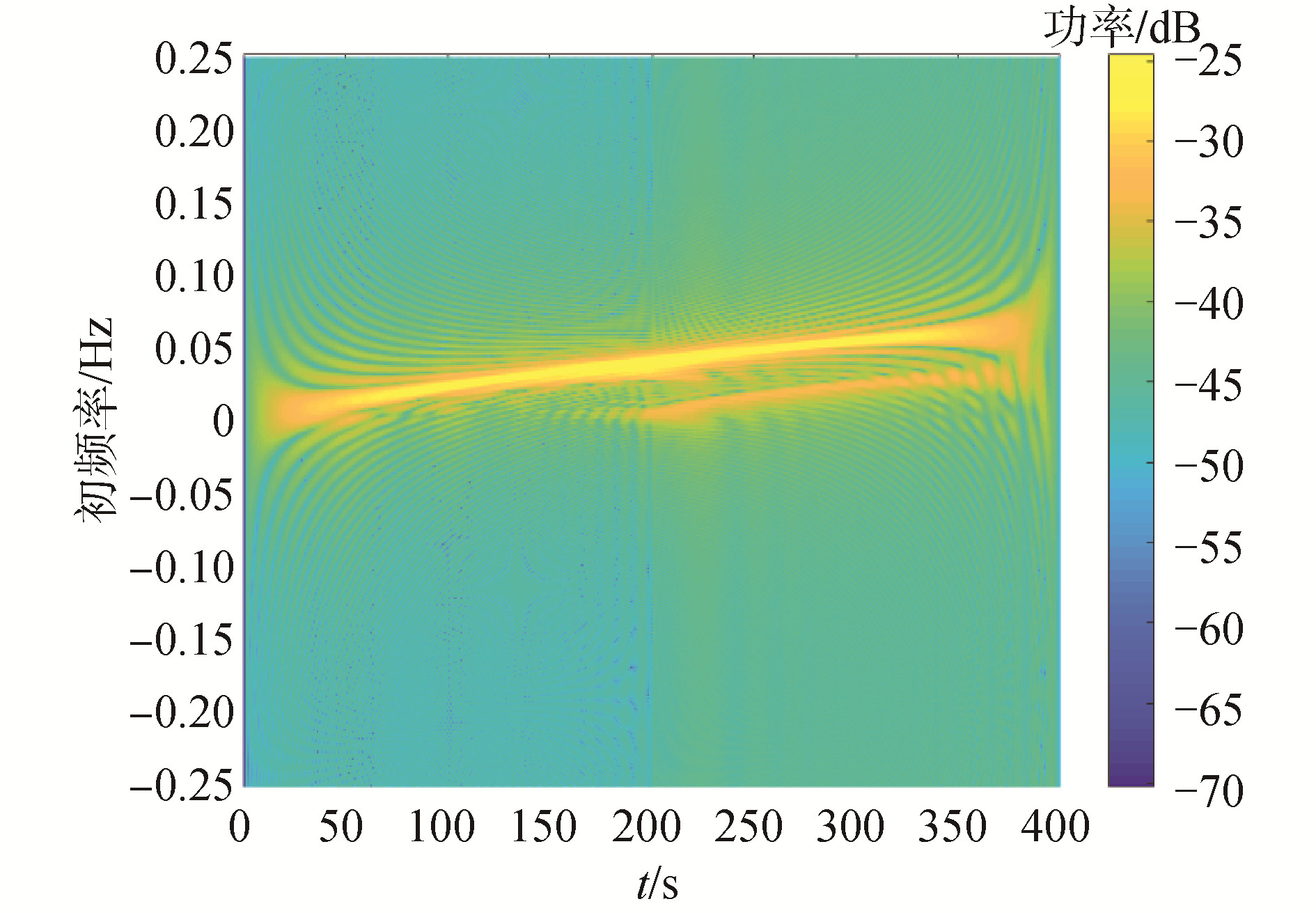
| 图 4 目标互谱的WVD变换 Fig. 4 WVD transformation of target cross spectrum | |
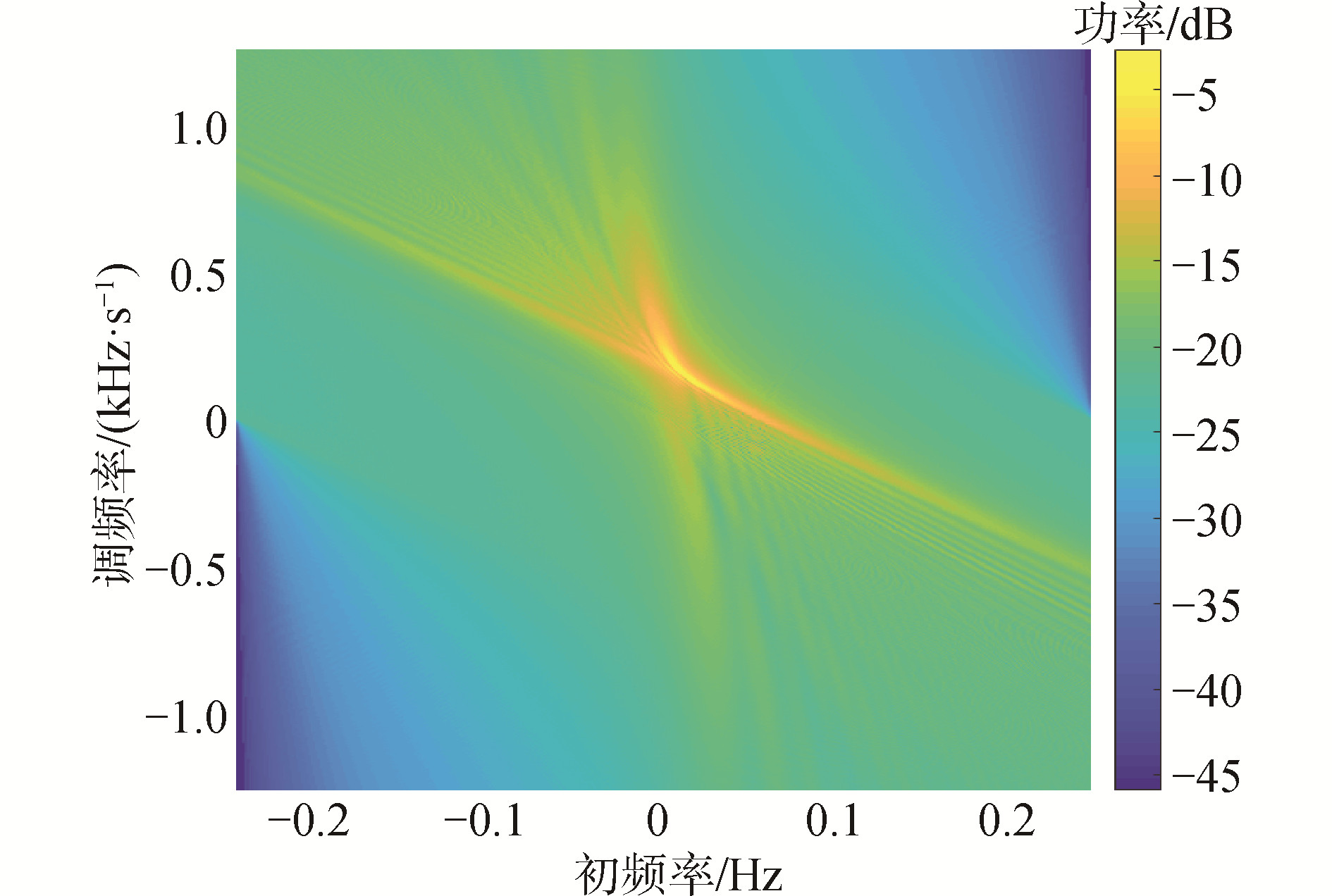
方法1 利用图 5搜寻到的峰值点代入式(9)计算目标的v2/r0估计值为0.0085,将图 2进行Hough变换得到v/r0为0.0034,进一步可以得到目标的绝对速度估计值为2.51m/s,最近通过距离为735m。绝对速度的估计误差为0.4%,最近通过距离的误差为2.4%。采用此算法可以得到较为理想的绝对速度和距离的估计结果。
|
Download:
|
| 图 5 目标互谱的R-WVD变换 Fig. 5 R-WVD transformation of target cross spectrum | |
方法2 如果只有线谱信息,将v2/r0估计值结合式(10),得到v/r0为0.0036,估计的绝对速度为2.36m/s,最近通过距离为655m,绝对速度的估计误差为5.6%,最近通过距离的误差为7.4%。
以上为仿真计算得出的结果可以验证2种算法的有效性,由于方法2只利用线谱信息,所以误差较大。
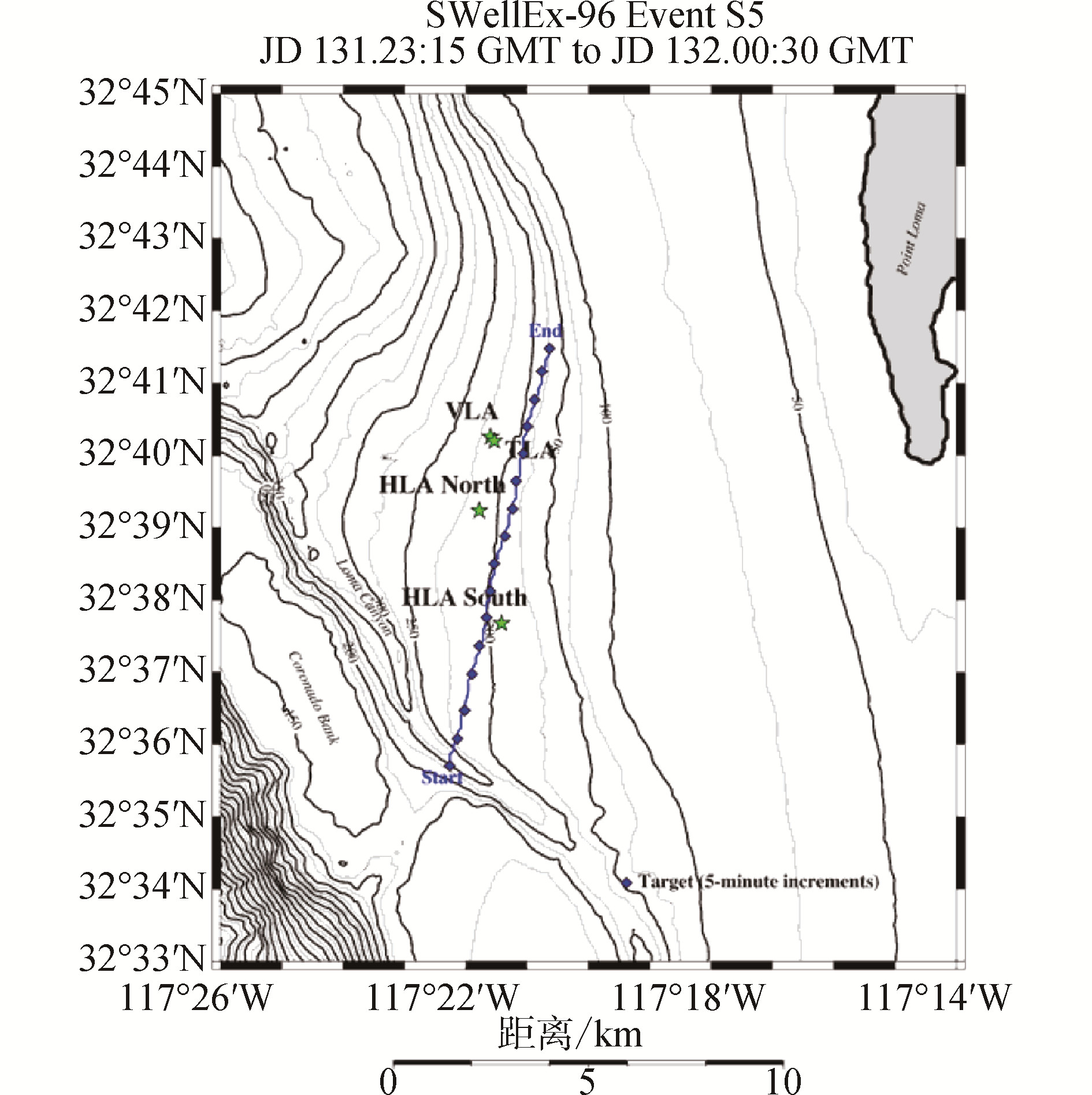
3 SWellEx-96海上试验数据处理 3.1 试验概况SWellEx-96试验[14]是加利福尼亚大学Scripps海洋研究院于1996年5月10日-1996年5月18日,距离加利福尼亚圣地亚哥附近的洛马角的尖端约12 km进行的声学试验。声源为拖曳式声源,发射信号为50~400 Hz的线谱或有一定带宽的信号。SWellEx-96试验中部署的声学传感器包括:垂直线阵VLA,倾斜的线阵TLA,安装在海底的2个水平阵列HLA,分为北部和南部HLA。数据主要为S5、S59两组。
S5中,声源拖曳在一条等深线上,整个试验过程没有大的干扰物出现。声源拖曳船从所有基阵的南侧以5 kn(2.5m/s)的速度向北行驶,大部分声源拖曳海区的深度为180~220m,另一半试验的声源是沿180m等深线进行拖曳的。
有深(J-15)、浅(J-13)2个声源,深的声源拖曳深度大约54m,它发射49~400 Hz多条线谱。浅声源的拖曳深度大约9m,它发射109~385 Hz的9个频率,编号为C-109-9S。
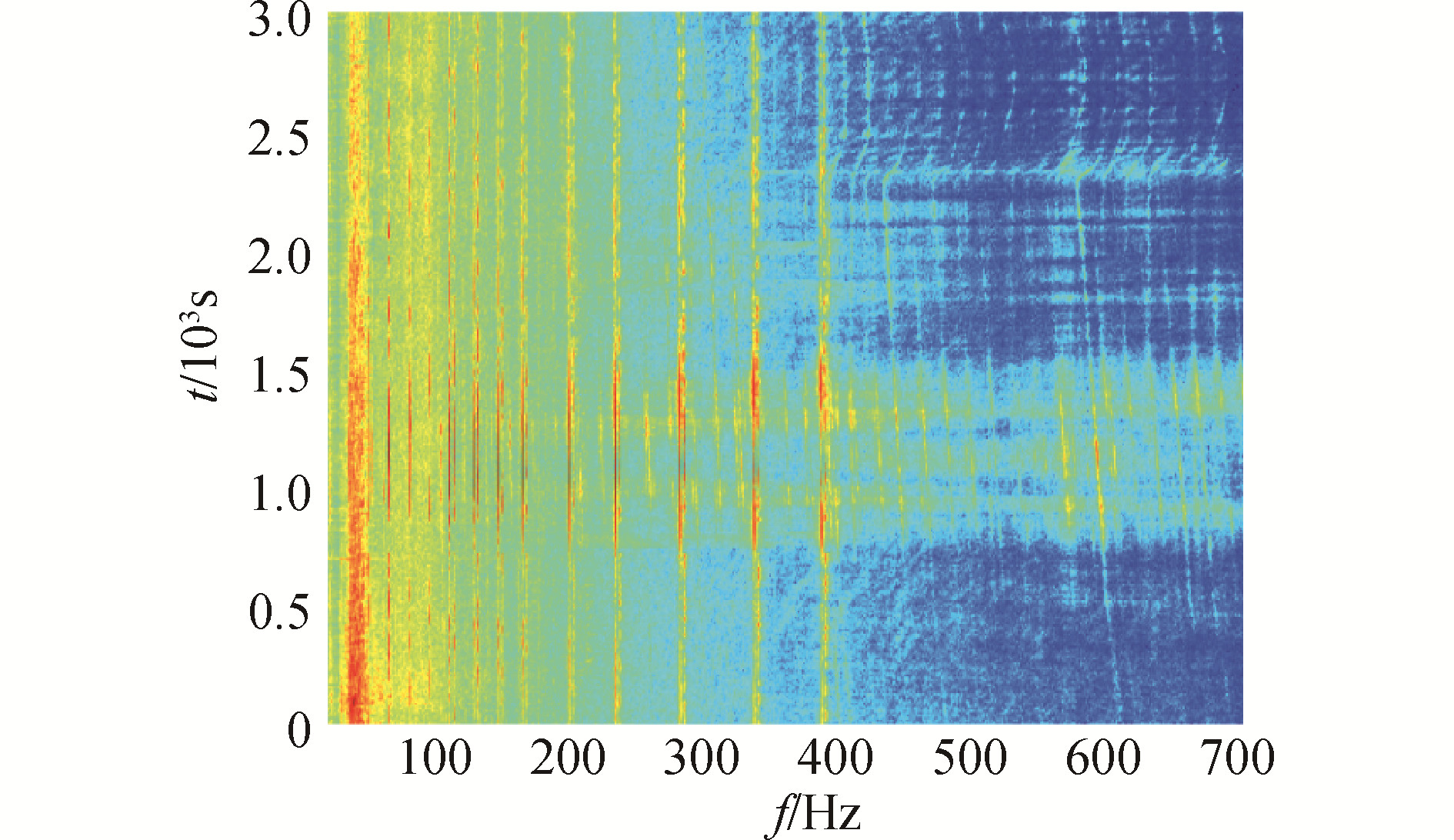
3.2 试验数据处理如图 6所示,为S5实验的HLA North阵列的接收数据进行分析,目标距离阵的最近通过距离708m,图 7为某接收阵元的声压信号进行短时傅里叶变换得到的目标LOFAR图。
|
Download:
|
| 图 6 试验布置 Fig. 6 Test layout | |
|
Download:
|
| 图 7 接收阵元LOFAR Fig. 7 LOFAR of receiving element | |
采取其49 Hz处的频谱信息,在1 200s~1 600s处进行互谱得到目标互谱图如图 8所示。

|
Download:
|
| 图 8 线谱49 Hz运动目标互谱 Fig. 8 Moving target cross spectrum of 49 Hz line spectrum | |
|
Download:
|
| 图 9 目标互谱的WVD变换 Fig. 9 WVD transformation of target cross spectrum | |
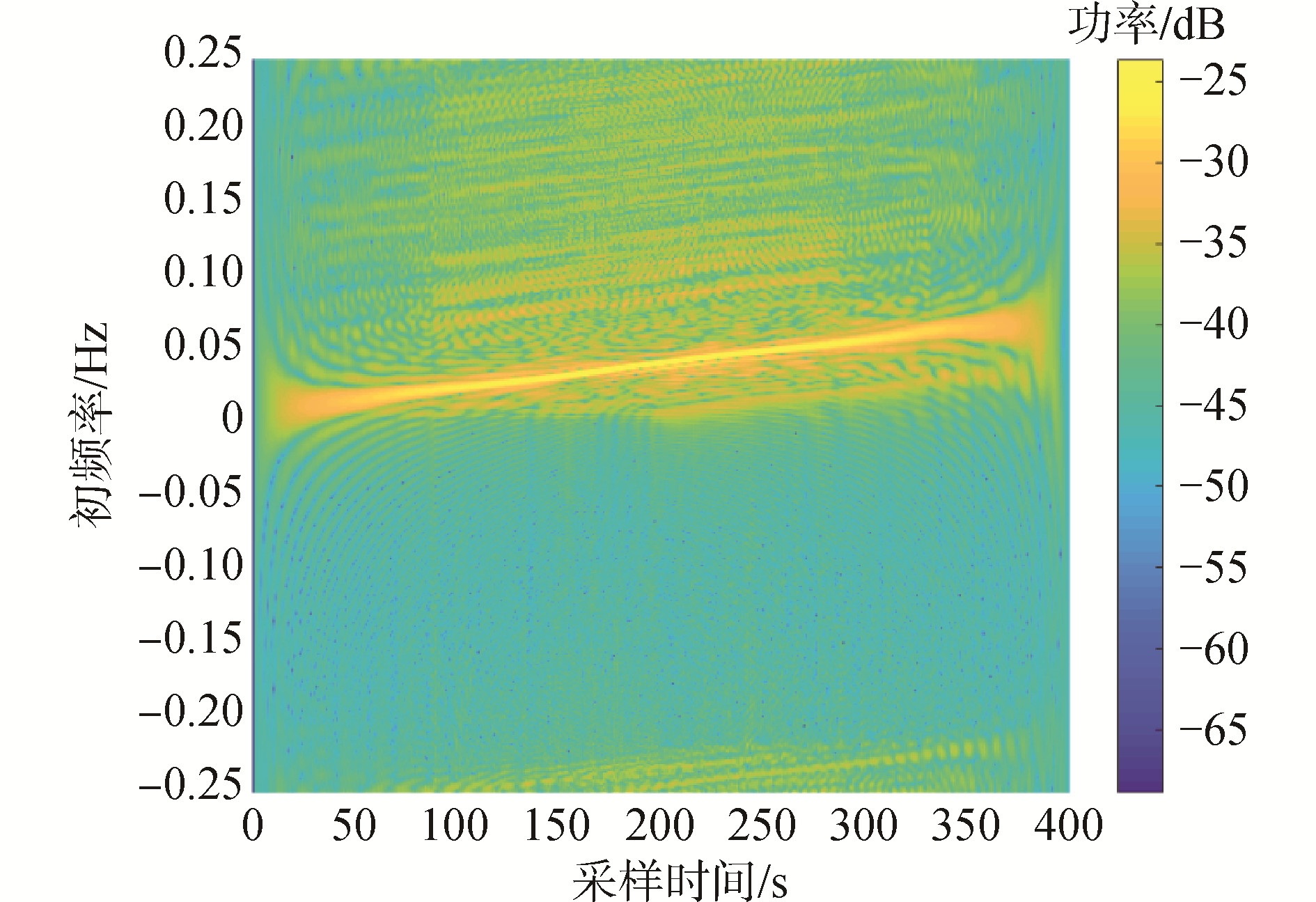
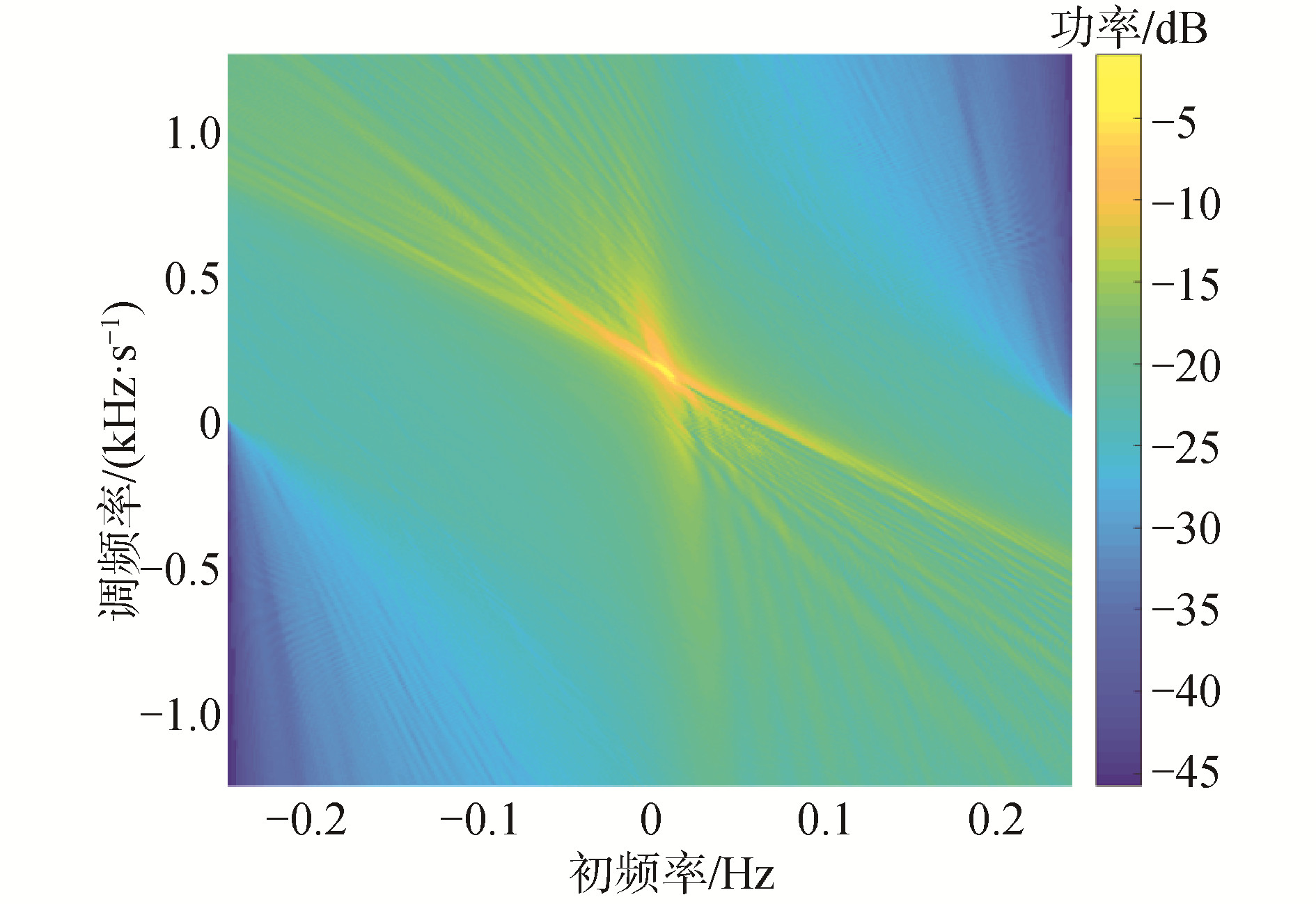
通过图 10可以获得调频率为0.000151,代入到式(9)计算目标的v2/r0估计值为0.00927,将图 9与式(6)联立可得300s时目标径向速度为1.84m/s,将其代入式(10)计算v/r0为0.0037,进一步可以计算目标的绝对速度估计值为2.5m/s,最近通过距离为675m。估计的绝对速度和最近通过距离误差都在10%以内。并且对比常规互谱的输出信噪比,由于时频互谱可以无视径向速度的变化,因此可以一次处理更长的接收信号,所以可以获得更高的信噪比增益。
|
Download:
|
| 图 10 目标互谱的R-WVD变换 Fig. 10 R-WVD transformation of target cross spectrum | |
通过时频互谱得到的输出信噪比由于其积分时间更长,所以获得的输出信噪比增益更大[15-16],在各向同性白噪声背景中,其积分时间长度与增益的关系如下式所示:
| $ G = 5\lg T $ | (11) |
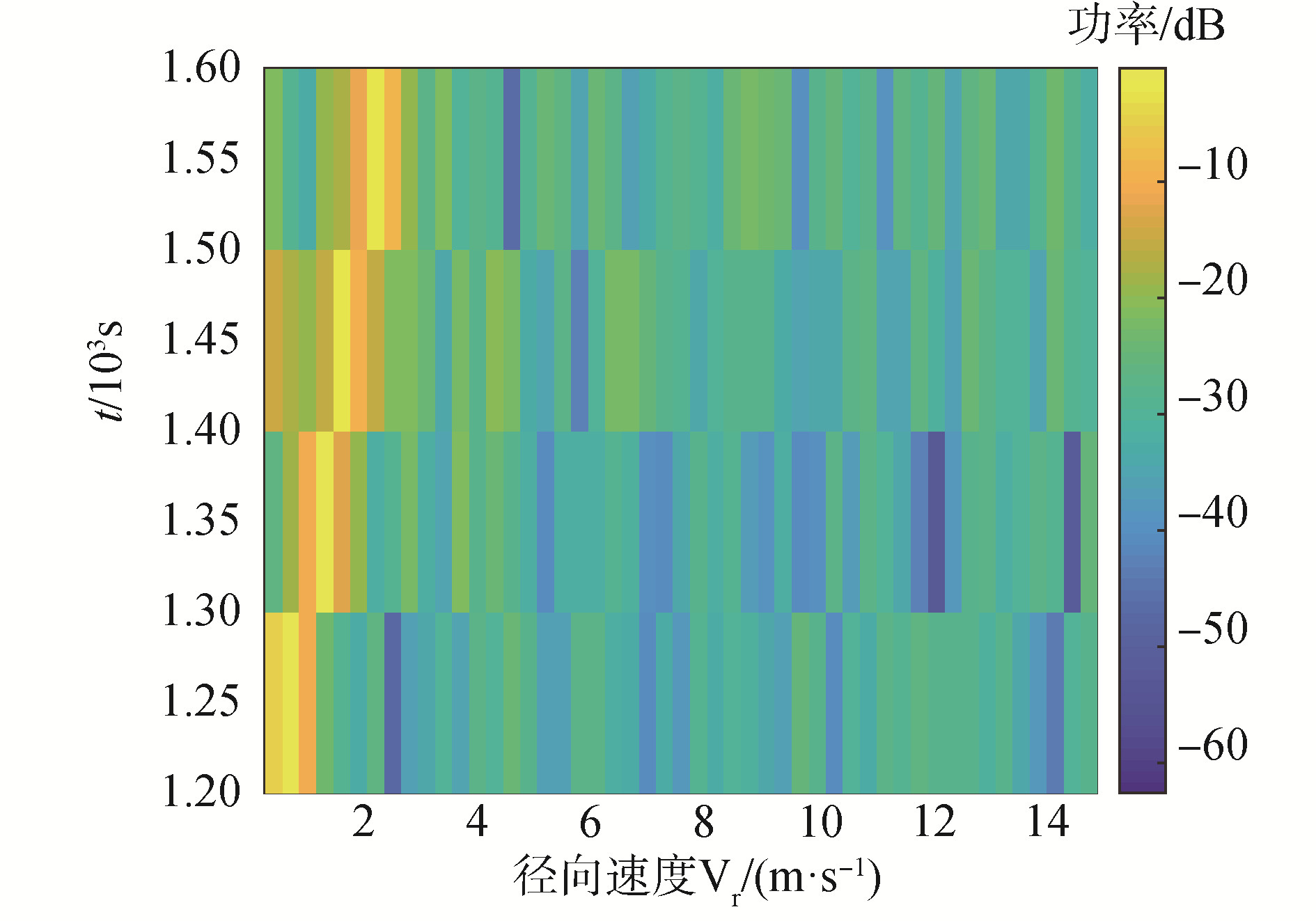
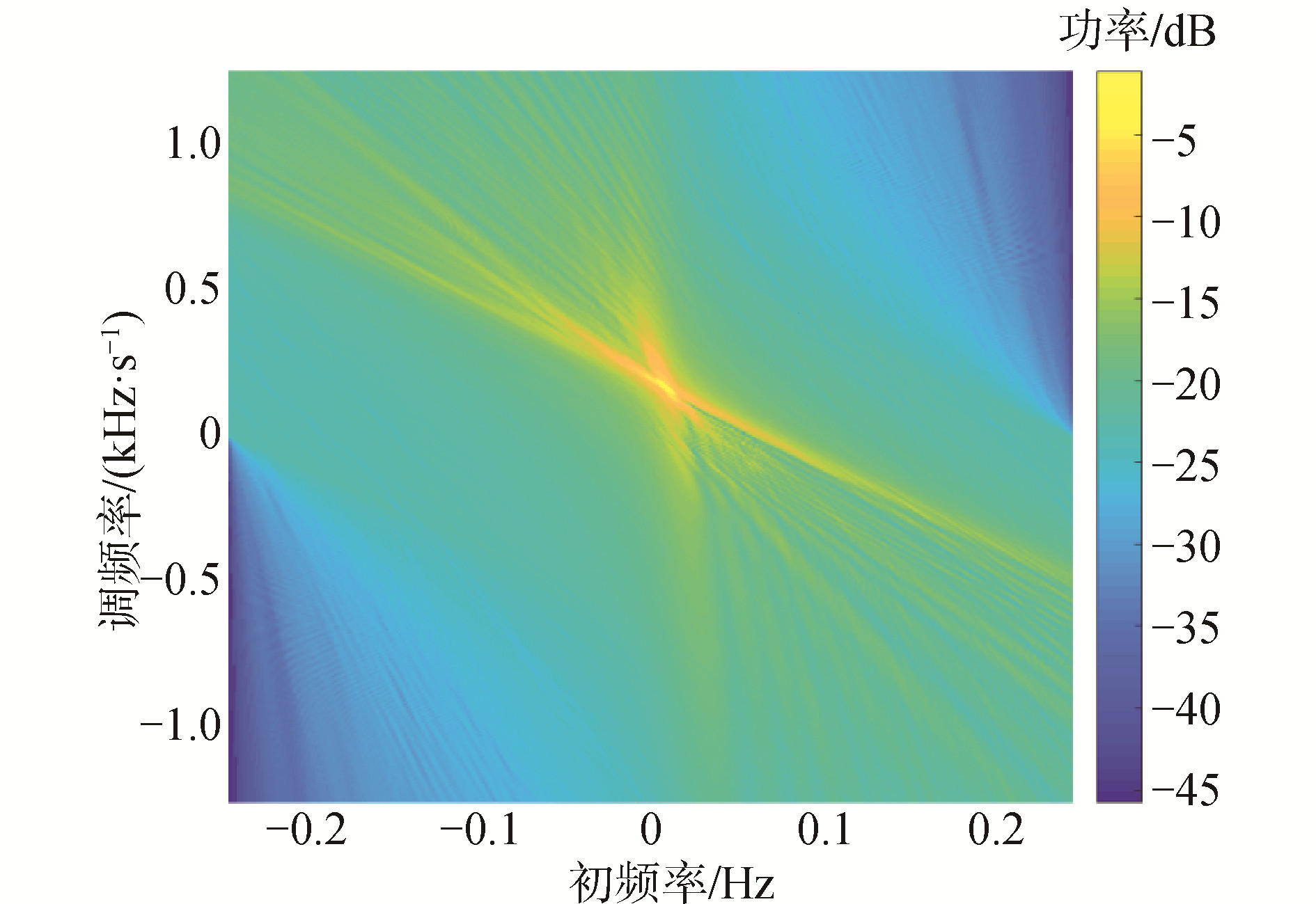
通过图 11与图 12对比可以得到,图 12的输出干扰更小,图 11是每100 s进行一次传统互谱测速得到的目标径向速度估计图,图 12是用本文提出的算法,由于不受径向速度变化的限制,所以可以将所有采样点一次处理,图 12的时间积分长度是图 11的4倍,通过计算得到图 11平均输出信噪比比图 12的输出信噪比低2 dB,其理论值为5lg4≈3.01 dB,可以得到通过本文的算法可以得到更高的信噪比增益。
|
Download:
|
| 图 11 常规互谱目标速度估计 Fig. 11 Target velocity estimation of classic cross-spectrum | |
|
Download:
|
| 图 12 时频互谱目标速度估计 Fig. 12 Target velocity estimation of time-frequency cross-spectrum | |
由上述对开源海试数据的分析研究可见,本文所提出的时频互谱算法是有效的,其试验数据处理结果与试验理论值之间的误差在10%以内,并且用时频互谱法的输出信噪比更高。
4 结论1) 对于水下目标辐射的低频线谱可采用互谱法进行被动速度估计。相对于传统互谱估计的目标径向速度,本文提出的时频互谱法可以直接估计目标的绝对速度。
2) 时频互谱法在提高信噪比增益的同时也降低了估计误差,补充和拓展了传统的互谱算法。
| [1] |
RAKOTONARIVO S T, KUPERMAN W A. Model-independent range localization of a moving source in shallow water[J]. The journal of the acoustical society of America, 2012, 132(4): 2218-2223. DOI:10.1121/1.4748795 (  0) 0)
|
| [2] |
王鹏, 郑胜家, 黄勇, 等. 浅海运动目标波束域波导不变量测距方法研究[J]. 声学学报, 2015, 40(6): 789-798. WANG Peng, ZHENG Shengjia, HUANG Yong, et al. Range estimation based on waveguide invariant using beam intensity striations for moving target in shallow water[J]. Acta acustica, 2015, 40(6): 789-798. (  0) 0)
|
| [3] |
邵云生, 王朋, 黄勇, 等. 浅海随机相位起伏声场中速度估计的互谱分析方法[J]. 应用声学, 2015, 34(6): 501-508. SHAO Yunsheng, WANG Peng, HUANG Yong, et al. Velocity estimation by cross-spectral analysis in a random shallow water channel[J]. Journal of applied acoustics, 2015, 34(6): 501-508. (  0) 0)
|
| [4] |
王超, 周武. 一种被动目标运动速度估计方法[C]//中国声学学会水声学分会2019年学术会议论文集. 南京, 2019: 181-183. WANG Chao, ZHOU Wu. A way of estimation of passive target speed[C]//2019 Academic Conference of the Hydroacoustics Branch of the Acoustic Society of China. Nanjing, 2019: 181-183. (  0) 0)
|
| [5] |
宋雪晶. 基于声场干涉结构的水声目标被动定位技术[D]. 哈尔滨: 哈尔滨工程大学, 2017. SONG Xuejing. Underwater acoustic target passive localization techniques based on acoustic field interference structure[D]. Harbin: Harbin Engineering University, 2017. (  0) 0)
|
| [6] |
秦川, 姜可宇. 一种改进的基于Radon变换的多目标轨迹提取方法[C]//中国声学学会水声学分会2019年学术会议论文集. 南京, 2019: 361-363. QIN Chuan, JIANG Keyu. An improved method to extract multi-target tracks based on Radon transform[C]//2019 Academic Conference of the Hydroacoustics Branch of the Acoustic Society of China. Nanjing, 2019: 361-363. (  0) 0)
|
| [7] |
DJEKOUNE A O, MESSAOUDI K, AMARA K. Incremental circle hough transform: An improved method for circle detection[J]. Optik, 2017, 133: 17-31. DOI:10.1016/j.ijleo.2016.12.064 (  0) 0)
|
| [8] |
BARINOVA O, LEMPITSKY V, KHOLI P. On detection of multiple object instances using Hough transforms[J]. IEEE transactions on pattern analysis and machine intelligence, 2012, 34(9): 1773-1784. DOI:10.1109/TPAMI.2012.79 (  0) 0)
|
| [9] |
MUKHOPADHYAY P, CHAUDHURI B B. A survey of Hough Transform[J]. Pattern recognition, 2015, 48(3): 993-1010. DOI:10.1016/j.patcog.2014.08.027 (  0) 0)
|
| [10] |
陶冶, 杨喜娟. 线性调频信号的检测与调制参数估值[J]. 通信技术, 2019, 52(7): 1569-1573. TAO Ye, YANG Xijuan. Detection of linear FM signal and modulation parameter estimation[J]. Communications technology, 2019, 52(7): 1569-1573. DOI:10.3969/j.issn.1002-0802.2019.07.004 (  0) 0)
|
| [11] |
XU Xiaodi, LIU Jinzhao, WANG Weidong, et al. An Improved time and frequency analysis method combined with WVD and EEMD[C]//2nd International Workshop on Structural Health Monitoring for Railway System. Qingdao, 2018.
(  0) 0)
|
| [12] |
HOSSEINI S M, MOHSENI R. Interception FMCW radar using Wigner-Ville distribution (WVD)[J]. Majlesi journal of telecommunication devices, 2014, 2(4): 153-159. (  0) 0)
|
| [13] |
WU Yushuang, LI Xiukun. Elimination of cross-terms in the Wigner-Ville distribution of multi-component LFM signals[J]. IET signal processing, 2017, 11(6): 657-662. DOI:10.1049/iet-spr.2016.0358 (  0) 0)
|
| [14] |
BACHMAN R T, SCHEY P W, BOOTH N O, et al. Geoacoustic databases for matched-field processing: Preliminary results in shallow water off San Diego, California[J]. The journal of the acoustical society of America, 1998, 99(4): 2077-2085. (  0) 0)
|
| [15] |
黄益旺. 海洋环境噪声空间相关特性建模综述[J]. 应用声学, 2019, 38(4): 729-733. HUANG Yiwang. Review of the spatial correlation modeling of ocean ambient noise[J]. Journal of applied acoustics, 2019, 38(4): 729-733. (  0) 0)
|
| [16] |
杨学猛, 刘彦森, 蒋行海. 浅海目标辐射噪声矢量场特性实验研究[J]. 装备环境工程, 2010, 7(4): 42-44. YANG Xuemeng, LIU Yansen, JIANG Xinghai. Experimental research on vector field characteristic of radiated noise originated from target in shallow sea[J]. Equipment environmental engineering, 2010, 7(4): 42-44. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


