2. 上海海事大学 海洋科学与工程学院, 上海 201306
2. College of Ocean Science and Engineering, Shanghai Maritime University, Shanghai 201306, China
三体船是公认的高性能船舶之一,因其2个侧体与主船体共享1个甲板及上层建筑,具有较大的甲板面积和良好的横摇稳定性。目前三体船的水动力性能研究主要集中在阻力[1-3]和耐波性能[4-6],而操纵性能对于高速三体船在高速航行中的危险规避和航行安全又极为重要,又由于三体船比传统船型较宽,随着技术的成熟和实船建造数量的增多,它的机动性、回转性能和航向的纠偏能力研究和预报越来越紧迫。同时,国际海事组织[7-9]对船舶的操纵能力提出了更严格的要求,有必要对三体船操纵性做深入研究和特性预报分析,以指导后续的研究和实船设计。
目前,船舶操纵性能预报方法主要有数值方法和试验方法。然而,试验方法由于场地和设备成本高昂、试验过程复杂,以及操纵运动中模型周围流场无法观测等原因,同时随着数值方法和计算机能力的不断发展,人们开始越来越多的采用数值方法代替试验方法进行船舶操纵性能研究。自20世纪初船舶操纵运动方程[10]和船舶运动数学模型[11-15]的提出,数值方法开始在船舶操纵性研究中得到发展。平野等[16]提出了一种考虑横倾运动的大横倾船舶回转运动的数值模拟方法。文献[17-19]采用势流方法对三体船型操纵运动进行了仿真计算。张豪[20]采用STAR-CCM+软件对三体船斜拖运动和旋臂运动进行了数值模拟,对不同侧体布局的三体船回转运动进行了预报及研究。郭海鹏等[21-22]使用STAR-CCM+对ONR Tumblehome船模型的回转、静态漂移和横倾试验进行了数值模拟,并基于四自由度MMG模型预报了该船型在静水中的回转和Z形操纵运动。文献[23-24]利用STAR-CCM+软件分别对KCS集装箱船和KVLCC2油轮的约束模型试验进行了数值模拟,并基于操纵运动数学模型预报了船舶的回转和Z形操纵运动。
综上所述,当前三体船操纵运动数值预报方法还是以势流方法为主,同时船舶操纵运动的数值预报研究通常采用三自由度或四自由度的运动数学模型,但这对于三体船的操纵性预报而言却忽略了航行姿态对预报结果的影响,而这可能导致预报结果和实际情况存在较大偏差,因此有必要开展六自由度的三体船操纵运动的精确预报。本文将考虑航态的影响,研究不同航速及片体布局的三体船在静水中水平面内的操纵运动。基于开源CFD求解器OpenFOAM,利用六自由度MMG模型,对三体船在静水中的回转和Z形的操纵运动进行了数值模拟。为了验证数值方法的有效性,以某三体船型A为例进行了数值模拟并与试验结果进行对比。利用验证后的理论方法对另一三体船型B在不同傅汝德数和片体布局下的操纵运动进行了预报。
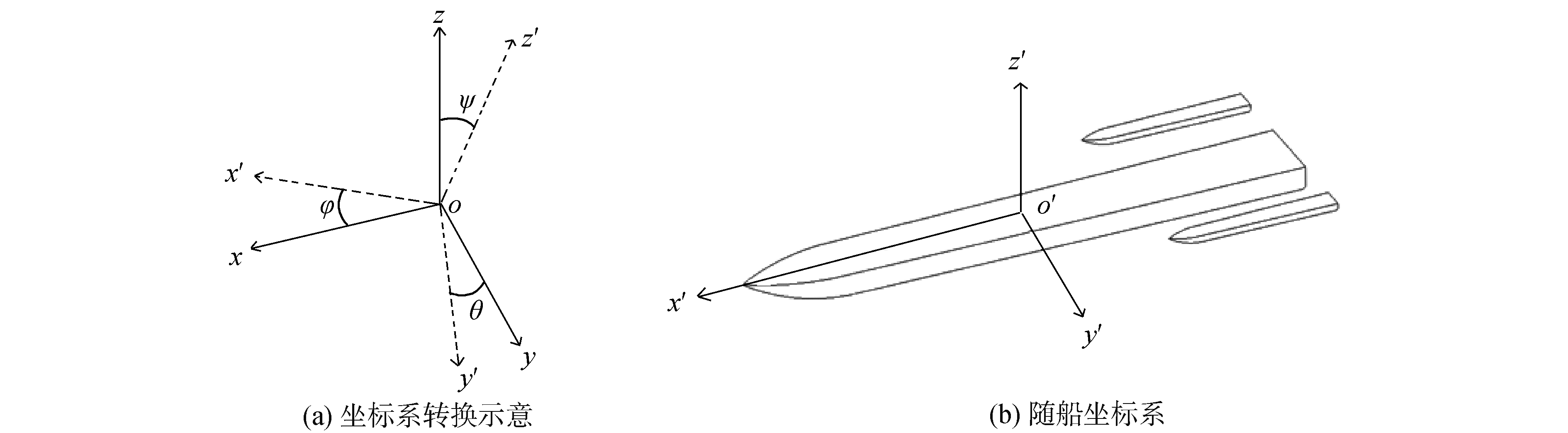
1 六自由度操纵运动模拟数学模型及方法 1.1 坐标系本文采用如图 1所示的2种右手坐标系来描述六自由度船舶操纵运动:1)大地坐标系oxyz,oxy平面固定在静水表面,z轴垂直于静水面向上;2)随船坐标系o′x′y′z′,坐标原点o′固定在船舶重心,x′轴指向船艏,y′轴指向左舷,z′轴向上。计算开始时,2个坐标系是对齐的。船体在大地坐标系中的平移位移表示为η=(x, y, z),转向角用欧拉角表示为σ=(φ, θ, ψ)。船体运动在局部坐标系中的速度矢量为V=(ux′, vy′, wz′),ux′、vy′、wz′分别为x′、y′、z′轴方向的速度分量,加速度为
| $ \mathit{\boldsymbol{\dot \eta }} = {\mathit{\boldsymbol{J}}_1} \cdot \mathit{\boldsymbol{V}} $ | (1) |
| $ \mathit{\boldsymbol{\dot \sigma }} = {\mathit{\boldsymbol{J}}_2} \cdot \mathit{\boldsymbol{r}} $ | (2) |
|
Download:
|
| 图 1 操纵运动坐标系 Fig. 1 The sketch of the co-ordinate system for maneuver | |
其中,
| $ \mathit{\boldsymbol{J}} _{1}=\left[\begin{array}{ccc} \cos \theta \cos \psi & \sin \varphi \sin \theta \cos \psi-\cos \varphi \sin \psi & \cos \varphi \sin \theta \cos \psi+\sin \varphi \sin \psi \\ \cos \theta \sin \psi & \sin \varphi \sin \theta \sin \psi+\cos \varphi \cos \psi & \cos \varphi \sin \theta \sin \psi-\sin \varphi \cos \psi \\ -\sin \theta & \sin \varphi \cos \theta & \cos \varphi \cos \theta \end{array}\right] $ |
| $ \mathit{\boldsymbol{J}}_{2}=\left[\begin{array}{ccc} 1 & \sin \varphi \tan \theta & \cos \varphi \tan \theta \\ 0 & \cos \varphi & -\sin \varphi \\ 0 & \sin \varphi / \cos \theta & \cos \varphi / \cos \theta \end{array}\right] $ |
本文计算域流场求解的控制方程用三维不可压缩非定常雷诺平均N-S(URANS)方程表示:
| $ \nabla \cdot \mathit{\boldsymbol{U}} = 0 $ | (3) |
| $ \begin{gathered} \frac{\partial(\rho \boldsymbol{U})}{\partial t}+\nabla \cdot\left[\rho\left(\boldsymbol{U}-\boldsymbol{U}_{g}\right) \boldsymbol{U}\right]= \\ \quad-\nabla \cdot p_{d}-\boldsymbol{g} \cdot x \nabla \cdot \rho+\nabla \cdot \\ \left(\mu_{\mathrm{eff}} \nabla \cdot \boldsymbol{U}\right)+(\nabla \cdot \boldsymbol{U}) \cdot \nabla \mu_{\mathrm{eff}}+f_{\sigma}+f_{s} \end{gathered} $ | (4) |
式中:
湍流模型采用SST k-ω模型[25]。自由面求解采用带有人工可压缩项的流体体积函数(volume of fluid,vof)方法[26],仅在空气与水的交界面处保持连续和非零,体积输运用平流函数表示为:
| $\frac{\partial \alpha}{\partial t}+\nabla \cdot\left[\left(\boldsymbol{U}-\boldsymbol{U_{g}}\right) \alpha\right]+\nabla \cdot\left[\boldsymbol{U_{r}} \alpha(1-\alpha)\right]=0 $ | (5) |
式中:Ur为用于压缩界面的速度场,Ur=min{cα|U|, max(|Uf|)};cα为压缩系数,取默认值1;α为欧拉两相流的体积分数,代表液体部分所占体积百分比,在空气中,α=0;水中α=1;在水平面0 < α < 1。
两相流的混合密度ρ和粘度μ可以用体积分数α表示为:
| $ \left\{ \begin{array}{l} \rho = {\rho _{{\rm{water}}}}\alpha + {\rho _{{\rm{air}}}}\left( {1 - \alpha } \right)\\ \mu = {\mu _{{\rm{water}}}}\alpha + {\mu _{{\rm{air}}}}\left( {1 - \alpha } \right) \end{array} \right. $ | (6) |
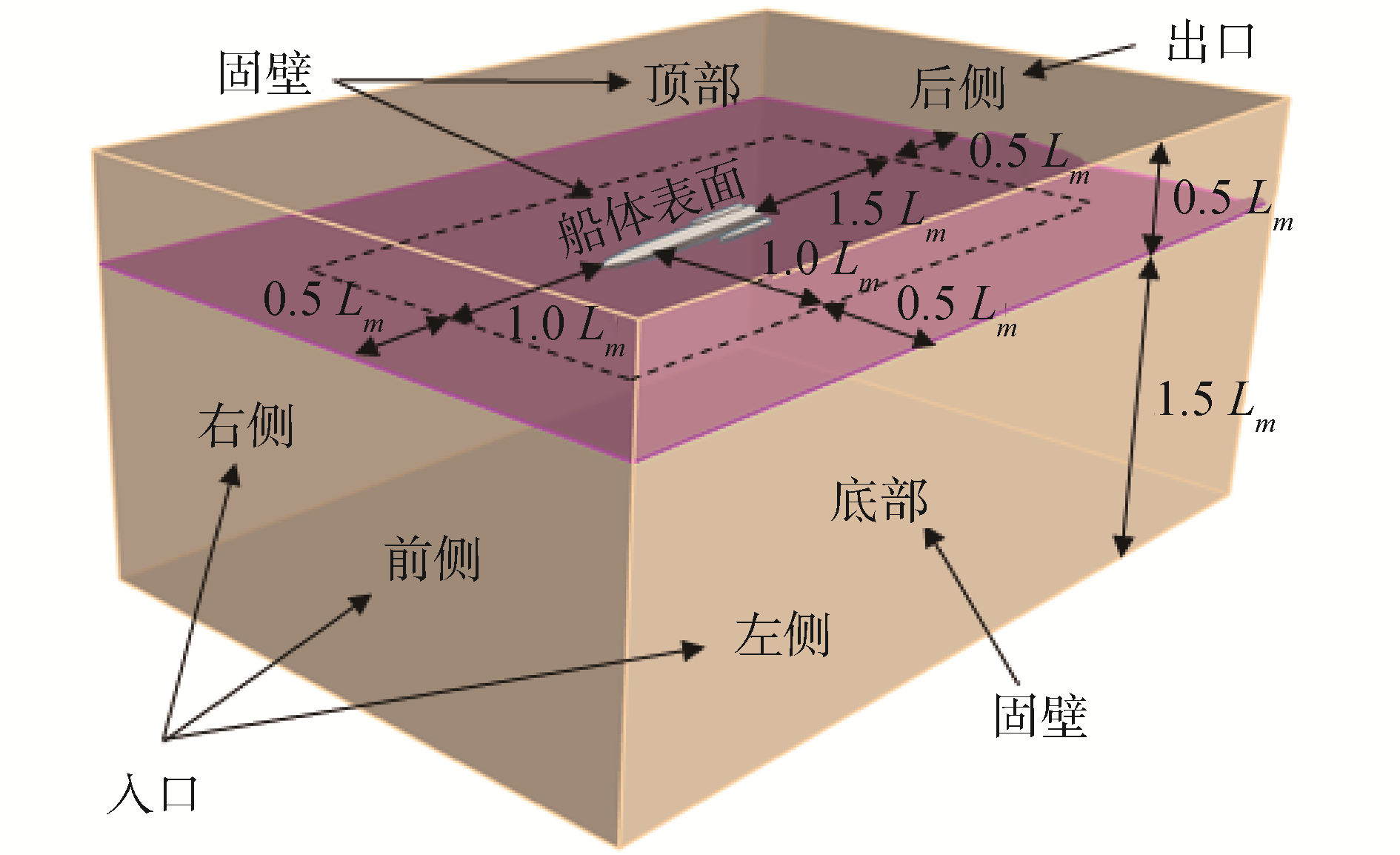
本文的耦合离散方程采用PIMPLE算法求解,计算域尺寸和边界条件如图 2所示,计算域总长度为4.5Lm,宽度为3Lm,水深为1.5Lm,自由面以上高度为0.5Lm,Lm为主体水线长。边界条件:船体表面、计算域底部和顶部设置为固壁边界条件,计算域后部设置为压力出口,其他计算域外面的3个位置设置为速度入口。在2个侧面、出口和入口处,各设置了0.5Lm的人工数值阻尼消波区,来降低数值震荡,由于模拟的是静水条件下的回转和Z形运动,因此在入口处的速度设置为0,出口处的压力梯度设置为0,以确保不会发生回流。由于本文中的模拟没有风,所以对于α < 0的部分,初始速度设置为0。
|
Download:
|
| 图 2 计算域和边界条件 Fig. 2 Diagram of domain size and boundaries | |
本文中的三体船由喷水推进器提供推进力,同时通过改变喷水推进器的喷口方向实现三体船的转向,即没有舵,因此采用六自由度MMG模型建立的操纵运动模型可表示为:
| $ \left\{\begin{array}{l} m\left(\dot{u}_{x^{\prime}}-v_{y^{\prime}} r_{z^{\prime}}+w_{z^{\prime}} r_{y^{\prime}}\right)=F_{H x^{\prime}}+F_{P x^{\prime}} \\ m\left(\dot{v}_{y^{\prime}}-w_{z^{\prime}} r_{x^{\prime}}+u_{x^{\prime}} r_{z^{\prime}}\right)=F_{H y^{\prime}}+F_{P y^{\prime}} \\ m\left(\dot{w}_{z^{\prime}}-u_{x^{\prime}} r_{y^{\prime}}+v_{y^{\prime}} r_{x^{\prime}}\right)=F_{H z^{\prime}}+F_{P z^{\prime}} \\ I_{x^{\prime}} r_{x^{\prime}}+\left(I_{z^{\prime}}-I_{y^{\prime}}\right) r_{y^{\prime}} r_{z^{\prime}}=M_{H x^{\prime}}+M_{P x^{\prime}} \\ I_{y^{\prime}} r_{y^{\prime}}+\left(I_{x^{\prime}}-I_{z^{\prime}}\right) r_{x^{\prime}} r_{z^{\prime}}=M_{H y^{\prime}}+M_{P y^{\prime}} \\ I_{z^{\prime}} r_{z^{\prime}}+\mid\left(I_{y^{\prime}}-I_{x^{\prime}}\right) r_{x^{\prime}} r_{y^{\prime}}=M_{H z ^{\prime}}+M_{P z^{\prime}} \end{array}\right. $ | (7) |
式中:m为船舶质量;(Ix′, Iy′, Iz′)为船在局部坐标系下的惯性矩;(FHx′, FHy′, FHz′)和(MHx′, MHy′, MHz′)分别为船在局部坐标系下产生的水动力和力矩;(FPx′, FPy′, FPz′)和(MPx′, MPy′, MPz′)则分别为喷水推进器在局部坐标系下产生的力和力矩。操纵运动的力和力矩是通过喷水推进器喷口转动实现的,所以没有舵的力和力矩项。本文没有模拟实际的喷水推进器,力和力矩是通过经验公式计算[27-29],忽略速度损失对喷水推进器效率的影响。
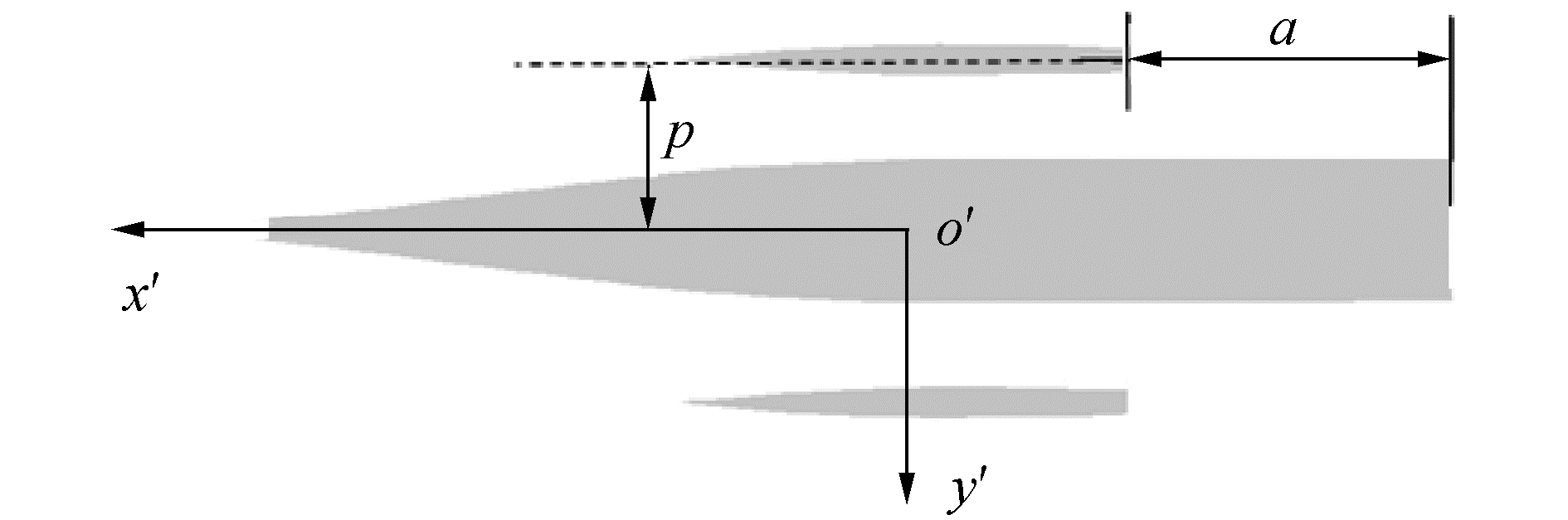
2 三体船操纵运动计算模型及算例 2.1 三体船操纵运动计算模型本文选取三体船型A作为方法验证模型,将模型A的模拟结果与试验结果进行对比,从而验证数值方法的有效性。船型A的三体船喷水推进自航模型试验在一个6 m多深,试验直径600 m的人工湖上进行,试验模型水线长6 m。数值方法得到验证后,选取另一艘与船型A相似的三体船型B,通过在不同傅汝德数和侧体布局下,对六自由度的三体船回转和Z形运动进行了数值模拟,以研究航速和侧体布局对三体船操纵性能的影响。文中三体船模型的主体和侧体主要参数如表 1所示,表中Ls为侧体水线长,三体船船体布局示意图如图 3所示。
| 表 1 模型主尺度 Table 1 Principal particulars of models |
|
Download:
|
| 图 3 三体船船体及布局 Fig. 3 Schematic diagram of hull and layout of trimaran | |
数值计算中,所有域网格均通过snappyHexMesh生成,以背景网格为基础,对船体表面周围区域进行二次网格细化,以确保船舶运动的兴波的传播足够平滑。船体表面采用棱柱层网格,从而精确求解流场,无量纲化的壁面到第一层网格的距离y+取25。网格示意图如图 4所示,计算网格总数量为143万。

|
Download:
|
| 图 4 计算域网格 Fig. 4 Sketch of mesh of domain | |
为了验证数值方法的有效性,本文分别对三体船型A的回转和Z形运动进行了由喷水推进器推进的三体船自航模型试验和数值模拟,试验和模拟工况选取2种不同的侧体位置,主侧体横向间距p=d1/Lm=0.10,主侧体纵向间距a=d2/Lm=0,0.23,操舵角δ=25°,船舶初始航速Fn=0.35,合计4个工况,进而将试验结果和数值模拟结果进行比较。
三体船型A的自航模型试验利用差分GPS对模型运动轨迹进行监测,利用光纤陀螺对垂荡幅值、横摇角、俯仰角和航向角进行监测,所有试验在一个6 m多深,试验直径600 m的人工湖上进行,三体船型A试验模型如图 5所示。

|
Download:
|
| 图 5 三体船型A试验模型 Fig. 5 Sketch of the trimaran A test model | |
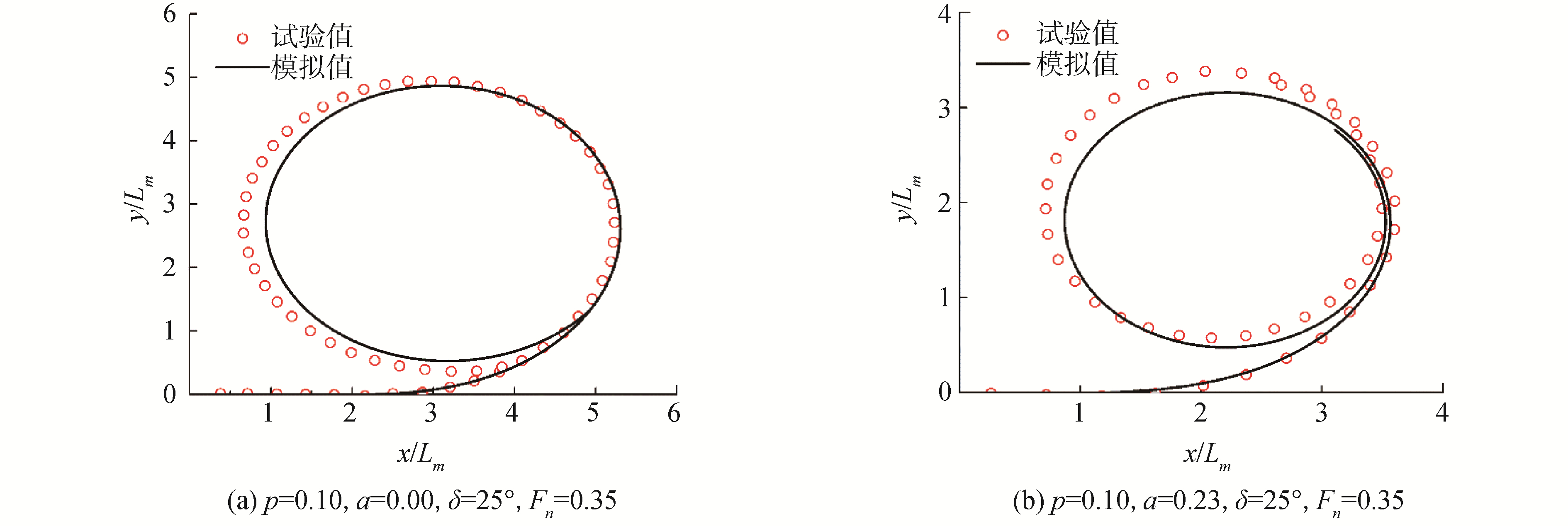
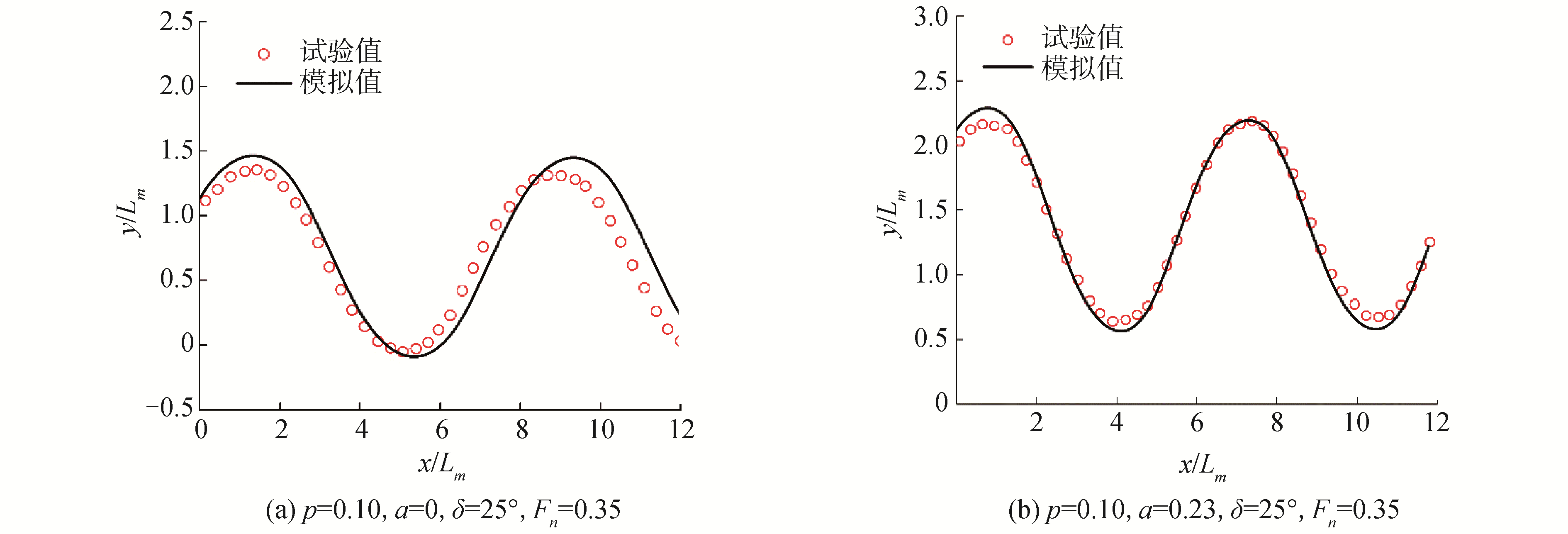
三体船型A六自由度操纵运动数值模拟的所有算例都基于一台Xeon E5-2650V4集群计算机进行,采用10个进程并行计算,每个算例执行50 s。图 6~9所示为数值预报的三体船型A的六自由度回转和Z形运动的模拟值和试验值对比。可以看出2种不同侧体布局的回转和Z形操纵运动的数值模拟结果与试验结果吻合较好,但是回转圈轨迹直径模拟结果比试验结果小6%左右,Z形操纵运动的运动周期模拟结果略大于试验值,这主要是由于数值模拟中推进器的力和力矩是通过经验公式获得,其结果和试验中的喷水推进器产生的力和力矩有所不同。同时,可以看到在Z形操纵运动时三体船发生了明显的横倾。因此,可以证明本文提出的三体船操纵运动的数值模拟方法的有效性和正确性,该方法可以很好地模拟三体船静水中的操纵运动。
|
Download:
|
| 图 6 回转圈轨迹对比 Fig. 6 Comparison of turning circle trajectories | |
|
Download:
|
| 图 7 Z形操纵运动轨迹对比 Fig. 7 Comparison of zigzag maneuvering trajectories | |

|
Download:
|
| 图 8 Z形操纵运动艏向角/舵角时历曲线对比 Fig. 8 Comparison of zigzag maneuvering heading/rudder angle time curves | |

|
Download:
|
| 图 9 Z形操纵运动横倾角时历曲线对比 Fig. 9 Comparison of zigzag maneuvering roll angle time curves | |
利用上文经过验证的数值模拟方法,对三体船型B,在3种侧体布局(p=0.10, a=0;p=0.15, a=0;p=0.10, a=0)和3种航速(Fn=0.24, 0.35, 0.47)下操舵角为25°时的六自由度回转和Z形操纵运动进行了数值模拟,探讨了不同航速和侧体布局对三体船操纵性能的影响。图 10所示为三体船型B数值预报的静水中回转运动在不同侧体布局和航速下的运动轨迹对比图。从图中可以看出,相较于侧体位置p=0.10, a=0,侧体横向间距增大,回转直径增大25%~29%;侧体纵向位置前移,回转直径减小35%左右,但在高航速Fn为0.47时,回转直径反而增大10%。相同侧体布局不同航速间比较时,航速Fn由0.24到0.35,各侧体布局的回转直径增加8%~14%,当在高航速Fn为0.47时,相比于Fn为0.24时的回转直径并不是简单的增加,当侧体位于艉部,即a=0时,回转直径减小7%左右,当侧体前移,即a=0.30时,回转直径则增加60%。

|
Download:
|
| 图 10 回转圈轨迹对比 Fig. 10 Comparison of turning circle trajectories | |
以上结果说明,三体船回转运动的回转直径受到航速和侧体布局变化的影响明显,但并不是单调的增加或减小,而是存在明显的波动变化。侧体横向间距增大,回转直径增大,回转性能降低。在低速段Fn低于0.35时,回转直径随航速增大而增大,随侧体纵向位置前移而减小,在高速段则由于主侧体间的兴波干扰和波形位置的改变导致回转性能发生改变,回转直径在侧体靠近船中时反而增大,此时相对低速时的回转直径也不再是单调增加。
图 11所示为三体船型B数值预报的静水中Z形运动在不同侧体布局和航速下的艏向角/舵角时历曲线对比图。从图中可以看出,相较于侧体位置p=0.10, a=0,侧体横向间距增大,初转期、超越时间和周期都随之增大,增大幅度达29%~66%,超越角在Fn为0.24时变化不大,在0.35时增大32%,在0.47时则减小9%;侧体纵向位置前移,超越角则明显增大,且航速越低,增大幅度越明显,航速Fn由0.24到0.47,超越角分别增大了78%、57%和20%。相同侧体布局不同航速间比较时,随着航速增大,初转期、超越时间和周期承减小趋势,超越角则是除了侧体位置p=0.15, a=0,其他位置也均呈减小趋势。

|
Download:
|
| 图 11 Z形操纵运动艏向角/舵角时历曲线对比 Fig. 11 Comparison of zigzag maneuvering heading/rudder angle time curves | |
以上结果说明,三体船Z形运动的主要参数受航速和侧体布局的影响明显,但和回转运动一样并非是单一变化。侧体横向间距增大,初转期、超越时间和周期显著增大,超越角则在不同航速下有不同的变化,航向改变性能降低。侧体纵向位置前移,超越角明显增大。
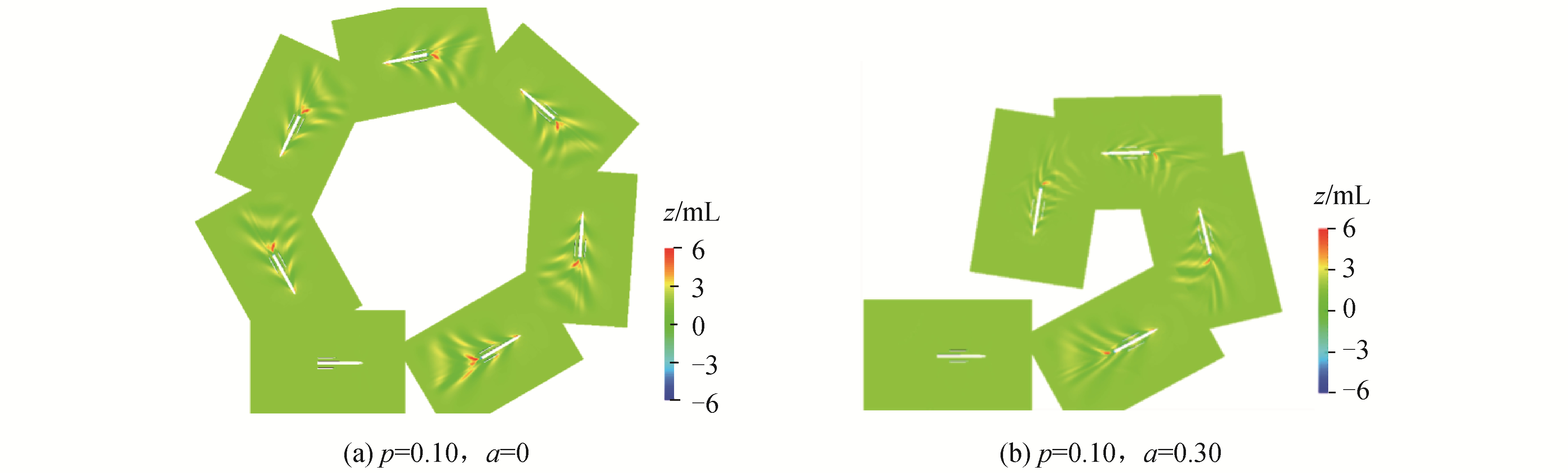
图 12和图 13所示为三体船型B在静水中回转和Z形操纵运动过程中,自由面兴波仿真结果图,分别对应侧体位置p=0.10, a=0和位置p=0.10, a=0.30,航速Fn=0.35的仿真结果。从图中可以看出,在回转和Z形操纵运动时,三体船船艏兴波会延伸到侧体位置,这种变化在航速发生变化时也同时存在,航速和侧体位置的变化会导致侧体遭遇的艏部兴波波形和干扰情况发生变化,这也是三体船回转和Z形操纵运动受到航速和侧体布局变化的影响明显,但并不是单调的增加或减小,而是存在明显的波动变化的主要原因之一。同时三体船两侧波面存在的高度差导致的船体两侧压力分布不均,也使得三体船操纵性能发生变化。
|
Download:
|
| 图 12 回转运动仿真波形 Fig. 12 Waveform of turning motion simulation | |

|
Download:
|
| 图 13 z形操纵运动仿真波形图 Fig. 13 Waveform of zigzag maneuvering motion simulation | |
1) 三体船操纵性能受航速和侧体布局变化的影响明显,但这种影响并不是单调变化,而是存在明显波动的变化。这种变化是由于三体船航行过程中侧体遭遇的艏部兴波波形和干扰会受到航速和侧体布局变化的影响,同时三体船两侧波面高度差导致的压力分布不均的原因。
2) 对于回转性能,侧体横向间距增大,回转直径增大,回转性能降低。在低速段Fn低于0.35时,随侧体纵向位置前移而减小,回转性能增加,在高速段时回转直径在侧体靠近船中时增大,回转性能降低。
3) 对于航向改变性能,侧体横向间距增大,初转期、超越时间和周期显著增大,航向改变性能降低。侧体纵向位置前移,超越角明显增大,航向改变性能降低。
由于当前数值模拟中推进器的力和力矩是通过经验公式获得,其结果和试验中的喷水推进器产生的力和力矩有所不同,这也导致了目前的数值预报存在一定的误差,将来的工作将基于更为精确的模拟方法进行三体船操纵性数值模拟研究,获得更高精度的数值预报模拟。同时,对三体船操纵性能受到的航速和侧体布局变化的复杂影响,从流场和优化方法角度进行更系统的研究。
| [1] |
MIZINE I, AMROMIN E, CROOK L, et al. High-speed trimaran drag: numerical analysis and model tests[J]. Journal of ship research, 2004, 48(3): 248-259. DOI:10.5957/jsr.2004.48.3.248 (  0) 0)
|
| [2] |
邓锐, 黄德波, 周广利. 三体船阻力的数值计算研究[J]. 哈尔滨工程大学学报, 2008, 29(7): 673-676. DENG Rui, HUANG Debo, ZHOU Guangli. Numerical calculation of resistance of trimarans[J]. Journal of Harbin Engineering University, 2008, 29(7): 673-676. DOI:10.3969/j.issn.1006-7043.2008.07.006 (  0) 0)
|
| [3] |
周广利, 艾子涛, 邓锐, 等. 高速三体船的阻力预报方法研究[J]. 船舶力学, 2016, 20(7): 805-815. ZHOU Guangli, AI Zitao, DENG Rui, et al. Resistance prediction method research of high speed trimaran[J]. Journal of ship mechanics, 2016, 20(7): 805-815. DOI:10.3969/j.issn.1007-7294.2016.07.003 (  0) 0)
|
| [4] |
HEBBLEWHITE K, SAHOO P K, DOCTORS L J. A case study: theoretical and experimental analysis of motion characteristics of a trimaran hull form[J]. Ships and offshore structures, 2007, 2(2): 149-156. DOI:10.1080/17445300701430242 (  0) 0)
|
| [5] |
马山, 段文洋, 王冰, 等. 三体船在斜浪规则波中运动响应预报方法研究[J]. 水动力学研究与进展A辑, 2012, 27(2): 224-230. MA Shan, DUAN Wenyang, WANG Bing, et al. Prediction of ship motions of trimaran in oblique regular wave[J]. Chinese journal of hydrodynamics series A, 2012, 27(2): 224-230. DOI:10.3969/j.issn1000-4874.2012.02.015 (  0) 0)
|
| [6] |
WANG S M, MA S, DUAN W Y. Seakeeping optimization of trimaran outrigger layout based on NSGA-Ⅱ[J]. Applied ocean research, 2018, 78: 110-122. DOI:10.1016/j.apor.2018.06.010 (  0) 0)
|
| [7] |
IMO. Interim standards for ship manoeuvrability[S]. IMO Resolution A. 751(18): 1993.
(  0) 0)
|
| [8] |
IMO. Explanatory notes to the interim standards for ship manoeuvrability[S]. IMO Circular MSC/Circ 644, 1994.
(  0) 0)
|
| [9] |
IMO. Standards for ship manoeuvrability[S]. IMO Resolution MSC. 137(76): 2002.
(  0) 0)
|
| [10] |
DAVIDSON K S M, SCHIFF L. Turning and course keeping qualities of ships[R]. Jersey City: Society of Naval Architects and Marine Engineers, 1946.
(  0) 0)
|
| [11] |
ABKOWITZ M A. Lectures on ship hydrodynamics——steering and manoeuvrability[R]. Lyngby, Denmark: Hydro-Og Laboratorium, 1964.
(  0) 0)
|
| [12] |
OGAWA A, KOYAMA T, KIJIMA K. MMG report-I, on the mathematical model of ship manoeuvring[J]. Bull Soc naval archit Jpn, 1977, 575: 22-28. (  0) 0)
|
| [13] |
OGAWA A, KASAI H. On the mathematical model of manoeuvring motion of ships[J]. International shipbuilding progress, 1978, 25(292): 306-319. DOI:10.3233/ISP-1978-2529202 (  0) 0)
|
| [14] |
小濑邦治, 操縦運動の数学モデルの具体化[R]. 日本造船学会, 1978. KOSE Kuniji. Realization of mathematical model of manoeuvring motions[R]. Naval architecture society of Japan, 1978. (  0) 0)
|
| [15] |
小瀬邦治, 佐伯敏朗. 操縦運動の新しい数学モデルについて[C]//日本造船学会論文集, 1979(146): 229-236. KOSE Kuniji, SAEKI Toshiro. On a new mathematical model of manoeuvring motions of a ship[C]//Proceedings of the Naval Architecture Society of Japan, 1979(146): 229-236. (  0) 0)
|
| [16] |
HIRANO M, TAKASHINA J. A calculation of ship turning motion taking coupling effect due to heel into consideration[J]. Journal of the West Japan society of naval architects, 1980. (  0) 0)
|
| [17] |
卢晓平, 姚迪, 王波. 三体船操纵性计算与特性分析[J]. 海军工程大学学报, 2009, 21(1): 47-53. LU Xiaoping, YAO Di, WANG Bo. Trimaran maneuverability prediction and its feature analysis[J]. Journal of naval university of engineering, 2009, 21(1): 47-53. (  0) 0)
|
| [18] |
詹金林, 卢晓平, 李光磊. 三体船操纵性水动力的势流理论计算[J]. 哈尔滨工程大学学报, 2012, 33(5): 642-647. Zhan Jinlin, Lu Xiaoping, Li Guanglei. Calculation of trimaran's maneuverability hydrodynamics by the potential flow theory[J]. Journal of Harbin Engineering University, 2012, 33(5): 642-647. DOI:10.3969/j.issn.1006-7043.201106049 (  0) 0)
|
| [19] |
詹金林, 黄汛, 张源, 等. 三体船旋转水动力的势流计算与分析[J]. 海军工程大学学报, 2017, 29(5): 58-61, 66. ZHAN Jinlin, HUANG Xun, ZHANG Yuan, et al. Potential flow calculation and analysis of rotary hydrodynamics for trimaran[J]. Journal of naval university of engineering, 2017, 29(5): 58-61, 66. (  0) 0)
|
| [20] |
张豪. 三体船操纵性能理论预报方法及性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2014. ZHANG H. The research about theoretical method and prediction of maneuverability of trimaran[D]. Harbin: Harbin Engineering University, 2014. (  0) 0)
|
| [21] |
GUO Haipeng, ZOU Zaojian. System-based investigation on 4-DOF ship maneuvering with hydrodynamic derivatives determined by RANS simulation of captive model tests[J]. Applied ocean research, 2017, 68: 11-25. DOI:10.1016/j.apor.2017.08.006 (  0) 0)
|
| [22] |
LIU Yi, ZOU Lu, ZOU Zaojian, et al. Predictions of ship maneuverability based on virtual captive model tests[J]. Engineering applications of computational fluid mechanics, 2018, 12(1): 334-353. DOI:10.1080/19942060.2018.1439773 (  0) 0)
|
| [23] |
BALAGOPALAN A, TIWARI K, RAMEESHA T V, et al. Manoeuvring prediction of a container ship using the numerical PMM test and experimental validation using the free running model test[J]. Ships and offshore structures, 2020, 15(8): 852-865. DOI:10.1080/17445302.2019.1688921 (  0) 0)
|
| [24] |
DAI Kun, LI Yunbo. Manoeuvring prediction of KVLCC2 with hydrodynamic derivatives generated by a virtual captive model test[J]. Polish maritime research, 2019, 26(4): 16-26. DOI:10.2478/pomr-2019-0062 (  0) 0)
|
| [25] |
MENTER F R, KUNTZ M, LANGTRY R. Ten years of industrial experience with the SST turbulence model[J]. Turbulence heat and mass transfer, 2003, 4(1): 625-632. (  0) 0)
|
| [26] |
BERBEROVIĆ E, VAN HINSBERG N P, JAKIRLIĆ S, et al. Drop impact onto a liquid layer of finite thickness: dynamics of the cavity evolution[J]. Physical review E, statistical, nonlinear, and soft matter physics, 2009, 79(3): 036306. DOI:10.1103/PhysRevE.79.036306 (  0) 0)
|
| [27] |
YASUKAWA H, HIRATA N, KOSE K. Influence of outrigger position on the performaces of a high speed trimaran (3rd Report: Maneuverability)[J]. Journal of the Japan society of naval architects and ocean engineers, 2005, 2: 197-203. DOI:10.2534/jjasnaoe.2.197 (  0) 0)
|
| [28] |
JAVANMARDI M, JAHANBAKHSH E, SEIF M, et al. Hydrodynamic analysis of trimaran vessels[J]. Polish maritime research, 2008, 15(1): 11-18. DOI:10.2478/v10012-007-0046-5 (  0) 0)
|
| [29] |
KATAYAMA T, TANIGUCHI T, FUJII H, et al. Development of maneuvering simulation method for high speed craft using hydrodynamic forces obtained from model tests[C]//Proceedings of the 10th International Conference on Fast Sea Transportation FAST 2009. Athens, Greece, 2009.
(  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


