2. 西北工业大学 无人水下运载技术重点实验室, 陕西 西安 710072
2. Key Laboratory for Unmanned Underwater Vehicle, Northwestern Polytechnical University, Xi'an 710072, China
现今复杂产品的设计通常涉及多目标、多学科等计算耗时的仿真分析过程,使得产品设计优化过程异常复杂。传统的基于仿真分析优化方法往往需要调用数以千计的真实分析模型来处理复杂工程问题,耗费大量计算资源。而元模型能够在复杂产品设计优化过程中替代真实分析模型,极大地降低计算量,被广泛应用于工程设计优化领域[1]。目前,广泛使用的元模型包括:多项式响应面(polynomial response surfaces,PRS)、径向基函数(radial basis functions,RBF)、克里金(Kriging,KRG)等。对于不同特性优化问题,上述元模型拥有各自优势和不足,在诸如精度、效率、鲁棒性等方面表现各异[2]。Goel等[3]提出了基于广义均方根误差的权重因子计算方法,通过测试函数验证了混合元模型在预测精度和鲁棒性方面均优于所选单一元模型。Acar等[4]通过最小化混合元模型的最大绝对误差来获得权重因子。黄焕军等[5]使用混合元模型拟合车身正面碰撞、侧面碰撞和白车身模态分析等多种响应,建立针对安全性的车身结构多学科优化模型。上述研究表明混合元模型拥有选取的多个元模型的优点,能够同时获取更多关于未知优化问题的信息,有效降低单一元模型出错率,鲁棒性更强。
尽管各类基于元模型优化方法提高了优化效率,但仍无法高效求解复杂工程优化问题。空间探索方法能够识别包含全局最优点的潜在区域,极大缓解计算压力。周仕明等[6]提出一种基于元模型和聚类算法的设计空间分割与减缩优化方法。龙腾等[7]提出一种基于信赖域动态径向基函数优化策略。Younis等[8]利用空间探索和单峰区域消除(space exploration and unimodal region elimination,SEUMRE)策略加快寻优进程。Gu等[9]提出一种基于多个元模型自适应建模优化方法(hybrid and adaptive metamodeling,HAM),通过确定有效的设计子空间,加快优化收敛速度。
本文针对混合元模型和空间探索方法的特点,提出了混合元模型自适应空间探索优化方法(hybrid metamodels based adaptive space exploration optimization method,HMASEO)。HMASEO方法能够在迭代过程中自适应提高混合元模型在有效设计子空间内的近似精度,通过逐步减小探索区域以较快的速度收敛到全局最优解。最后,将HMASEO方法成功应用于翼身融合水下滑翔机(blended wing body underwater glider,BWBUG)外形设计优化实例中,验证其有效性和优越性。
1 混合元模型混合元模型由多个元模型线性加权组合而成,其数学表达式为:
| $ \left\{\begin{array}{l} \tilde{y}_{e}=\sum\limits_{i=1}^{m_{s}} w_{i} \tilde{y}_{i}(\boldsymbol{x}) \\ \sum\limits_{i=1}^{m_{s}} w_{i}=1 \end{array}\right. $ | (1) |
式中:x为设计变量;ms表示元模型数量;
混合元模型预测精度很大程度上由权重因子决定,权重因子的选择需满足2个基本原则:1) 能够反映元模型近似精度;2) 能够避免元模型在样本稀疏区域糟糕表现。Goel等[3]根据上述原则,采用预测均方根误差计算权重因子:
| $ \left\{\begin{array}{l} w_{i}=w_{i}^{*} / \sum\limits_{j=1}^{m_{s}} w_{j}^{*} \\ w_{i}^{*}=\left(E_{i}+\alpha \bar{E}\right)^{\beta} \\ \bar{E}=\frac{1}{m_{s}} \sum\limits_{i=1}^{m_{s}} E_{i} \end{array} \quad \alpha<1, \beta<0\right. $ | (2) |
式中:Ei为选用的第i个元模型的预测均方根误差;E表示所有元模型的预测均方根误差的平均值。参数α和β分别控制平均和单一元模型的重要程度。其中,参数α值越小,参数β负值越大,则最佳元模型分配到权重因子越大;参数α值越大,参数β负值越小,则元模型平均重要程度越高。Goel等[3]研究发现参数α和β分别取0.05和-1时,构建的混合元模型预测精度较高。Acar等[4]认为固定参数值降低了权重因子选择的灵活性,无法适应不同特性工程问题,建议将参数α和β作为设计变量进行优化。受文献[3-4]启发,本文提出一种基于预测均方根误差权重因子优化方法,通过求解如下优化问题获得权重因子:
| $ \left\{\begin{array}{l} \text {Find }\ \ \alpha, \beta \\ \min\ \ E_{e}=\sqrt{\frac{1}{N} \sum\limits_{k=1}^{N}\left(y\left(\boldsymbol{x}_{k}\right)-\sum\limits_{i=1}^{m_{s}} w_{i} \cdot \tilde{y}(-k)_{i}\left(\boldsymbol{x}_{k}\right)\right)^{2}} \\ \ \ \ \ \ \ \ \ \ \ w_{i}=w_{i}^{*} / \sum\limits_{j=1}^{m_{s}} w_{j}^{*} \\ \ \ \ \ \ \ \ \ \ \ w_{i}^{*}=\left(E_{i}+\alpha \bar{E}\right)^{\beta} \\ \ \ \ \ \ \ \ \ \ \ \bar{E} =\frac{1}{m_{s}} \sum\limits_{i=1}^{m_{s}} E_{i} \\ \ \ \ \ \ \ \ \ \ \ E_{i} =\sqrt{\frac{1}{N} \sum\limits_{k=1}^{N}\left(y\left(\boldsymbol{x}_{k}\right)-\tilde{y}(-k)_{i}\left(\boldsymbol{x}_{k}\right)\right)^{2}} \\ \text { s.t. } \ \ E_{i}+\alpha \bar{E}>0, \alpha<1, \beta<0 \end{array}\right. $ | (3) |
式中:Ee表示混合元模型的预测均方根误差;N为训练样本点数量;y(xk)为第k个训练样本点xk处真实响应值;
自适应空间探索方法利用迭代过程中已有的“昂贵”样本点确定2个有效的设计子空间“S1”和“S2”。然后在S1和S2内进行空间探索,并通过补充新样本点自适应更新。设计子空间S1往往包含更多的局部最优点,而S2则更专注于探索关键区域。
2.1 S1空间探索方法按照所有样本点对应的真实目标函数值进行排序,选择目标函数值较小的前M1个样本点(M1取值为“昂贵”样本点数量一半)。然后使用模糊C均值聚类算法[6](fuzzy C-means,FCM)计算得到设计子空间S1,具体计算公式为:
| $ \left\{\begin{array}{l} \boldsymbol{S}_{S_{1}}^{\operatorname{top}M_{1}} \Leftarrow\left[\begin{array}{ccccc} X_{1}^{\mathrm{Rank} 1} & X_{2}^{\mathrm{Rankl}} & \cdots & X_{n}^{\text {Rank1 }} & Y^{\text {Rank} 1} \\ X_{1}^{\text {Rank} 2} & X_{2}^{\text {Rank2 }} & \cdots & X_{n}^{\text {Rank} 2} & Y^{\text {Rank2 }} \\ \vdots & \vdots & & \vdots & \\ X_{1}^{\text {Rank} M_{1}} & X_{2}^{\text {Rank} M_{1}} & \cdots & X_{n}^{\text {Rank} M_{1}} & Y^{\text {Rank} M_{1}} \end{array}\right]\\ \boldsymbol{S}_{S_{1}}^{\text {top}M_{1}} \stackrel{\text { FCM }}{\Rightarrow}\left[\boldsymbol{S}_{\text {fcm1 }}^{\text {top} Q_{1}}, \quad \boldsymbol{S}_{\text {fcm2 }}^{\text {top} Q_{2}}\right]\\ c=2 \end{array}\right. $ | (4) |
式中:SS1topM1表示选用的真实目标函数值较小的前M1个“昂贵”样本点集; n为设计变量; XRanki和YRanki分别表示函数值较小的第i个样本点的设计变量值和对应的真实目标函数值; c为聚类中心数,本文c取2; Sfcm1topQ1和Sfcm2topQ2分别表示在2聚类集内的数量为Q1和Q2“昂贵”样本点集。计算2个聚类集内所有“昂贵”样本点的真实目标函数值,包含最小值的聚类集将被确定为最优聚类集。设计子空间S1将由最优聚类集内所有样本点在每个维度上的最大和最小坐标值计算得到。
采用多起点序列二次规划算法(multi-start SQP,MS-SQP)在设计子空间S1内对混合元模型进行全局寻优,获得数量为MS近似响应面全局最优点,根据预测响应值的大小从中选择所需数量的新样本点。MS取值满足:
| $ \left\{\begin{array}{ll} M_{S}=20, & m<50 \\ M_{S}=30, & 50 \leqslant m<100 \\ M_{S}=50, & m \geqslant 100 \end{array}\right. $ | (5) |
式中m表示样本点数据库中“昂贵”样本点数量。
2.2 S2空间探索方法选用真实目标函数值较小的前M2个“昂贵”样本点,设计子空间S2计算公式为:
| $ \left\{\begin{array}{l} \boldsymbol{S}_{S_{2}}^{\operatorname{top}M_{2}} \Leftarrow\left[\begin{array}{ccccc} X_{2}^{\mathrm{Rank} 1} & X_{2}^{\mathrm{Rankl}} & \cdots & X_{n}^{\text {Rank1 }} & Y^{\text {Rank} 1} \\ X_{2}^{\text {Rank} 2} & X_{2}^{\text {Rank2 }} & \cdots & X_{n}^{\text {Rank} 2} & Y^{\text {Rank2 }} \\ \vdots & \vdots & & \vdots & \\ X_{2}^{\text {Rank}M_{2}} & X_{2}^{\text {Rank}M_{2}} & \cdots & X_{n}^{\text {Rank} M_{2}} & Y^{\text {Rank} M_{2}} \end{array}\right]\\ \mathrm{LB}_{j}=\min \left[\begin{array}{llll} X_{j}^{\text {Rank1 }} & X_{j}^{\text {Rank2 }} & \cdots & X_{j}^{\text {Rank}M_{2}} \end{array}\right]^{\mathrm{T}}\\ \mathrm{UB}_{j}=\max \left[\begin{array}{llll} X_{j}^{\mathrm{Rank} 1} & X_{j}^{\mathrm{Rank} 2} & \cdots & X_{j}^{\mathrm{Rank} M_{2}} \end{array}\right]^{\mathrm{T}}\\ \boldsymbol{S}_{2 j}=\left[\begin{array}{ll} \mathrm{LB}_{j} & \mathrm{UB}_{j} \end{array}\right]^{\mathrm{T}}, \quad j=1,2, \cdots, n \end{array}\right. $ | (6) |
式中:SS2topM2表示选用的真实目标函数值较小的前M2个“昂贵”样本点集,本文M2设为8;UBj和LBj分别表示S2在第j维的上下边界值。在迭代过程中,设计子空间S2将随着获取样本信息的增多而逐步向实际全局最优点潜在区域移动、收缩或扩大。相比设计子空间S1,设计子空间S2是一个更小的立方体空间。
本文提出一种混合自适应有效样本方法(hybrid and adaptive promising sampling,HAPS)在设计子空间S2内确定新增样本点。HAPS方法操作步骤如下:
1) 提取样本点数据库中的所有“昂贵”样本点,分别构造元模型PRS、RBF和KRG。为便于描述,分别使用
2) 基于3种元模型分别构造4种不同混合元模型。为便于描述,
3) 在探索区域内产生数量为GN“便宜”样本点,记为XH1, XH2, …, XHGN。本文GN设为10 000。
4) 分别使用元模型
5) 选择预测响应值较小的前Gn个“便宜”样本点,分别记为XHP1, XHP2, …, XHPGn;XHR1, XHR2, …, XHRGn;XHK1, XHK2, …, XHKGn。本文Gn设为100。
6) 分别将“便宜”样本点XHP1, XHP2, …, XHPGn;XHR1, XHR2, …, XHRGn;XHK1, XHK2, …, XHKGn保存到样本集A-
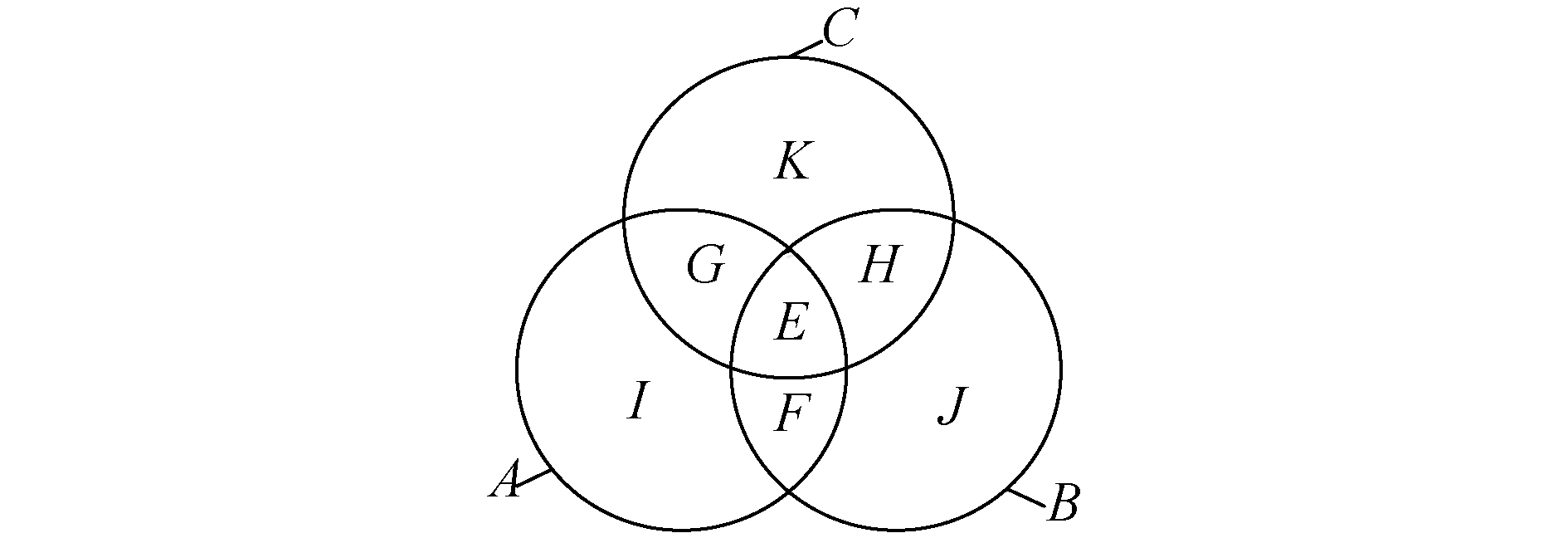
7) 确定同时出现在任意2个样本集或3个样本集中的样本点,3个样本集A、B、C将被划分为7个样本子集E~K(如图 1所示):
| $ \left\{\begin{array}{l} E=A \cap B \cap C \\ F=A \cap B-E \\ G=A \cap C-E \\ H=B \cap C-E \\ I=A-(E+F+G) \\ J=B-(E+F+H) \\ K=C-(E+G+H) \end{array}\right. $ | (7) |
|
Download:
|
| 图 1 样本子集E~K Fig. 1 Sample subsets E~K | |
8) 在所有样本子集E~K中选取数量为Num_new有效样本点,各子集分配到的样本点数量Snewi由如下公式决定:
| $ \left\{\begin{array}{l} \text { Snew}_{i}=\text { round }\left(\text { Num_new } \times \lambda_{i}\right), \\ \lambda_{i}=\frac{r_{i} \times l_{i}}{3 \times G_{n}}, i=1,2, \cdots, 7 \end{array}\right. $ | (8) |
式中:i表示各样本子集E~K序号,round表示对结果进行四舍五入。λi为反映不同样本子集重要性的权系数,由各样本子集本身重要性指数li和包含的样本点数量ri共同决定。本文将li取为样本子集涉及的元模型数量,即l1=3,l2-4=2,l5-7=1。
9) 采用相对应的混合元模型
在探索过程中,S1和S2可能出现不包含实际全局最优解情况。为了避免HMASEO方法陷入局部最优,同样采用HAPS方法在初始全局空间(original global space,OGS)内进行探索。HMASEO方法每隔3次迭代依次在OGS、S1和S2空间内进行探索,确定新增样本点,自适应更新混合元模型和设计子空间S1和S2。
3 HMASEO方法本文提出的HMASEO方法联合混合元模型和自适应空间探索方法,流程见图 2,步骤如下:

|
Download:
|
| 图 2 各测试函数优化结果箱线 Fig. 2 Boxplot on optimization results for all test functions | |
1) 建立真实分析模型,确定设计变量和设计空间,初始化HMASEO方法参数,令迭代参数k=1。
2) 使用增强随机进化算法[10](enhanced stochastic evolutionary,ESE)在整个设计空间内生成8个初始样本点,同时调用真实分析模型计算响应值。将设计样本点及其所对应的真实模型响应值保存到样本点数据库中。
3) 提取样本点数据库中的所有样本点及其所对应的真实模型响应值,分别构造单一元模型PRS、RBF和KRG。
4) 求解式(3)中的优化问题,计算得到优化权重因子,构造混合元模型。参数α和β初始值分别设为0.05和-1。
5) 判断迭代数k是否满足公式Rem(k, 3)=2, 如果满足,则计算设计子空间S1;否则,转入步骤7)。Rem表示计算余数。
6) 采用MS-SQP算法在设计子空间S1内产生3个有效样本点,转入步骤10)。
7) 判断迭代数k是否满足公式Rem(k, 3)=0, 如果满足,则计算设计子空间S2;否则,转入步骤9)。
8) 采用HAPS方法在设计子空间S2内产生3个有效样本点,转入步骤10)。
9) 采用HAPS方法在初始全局空间OGS内产生3个有效样本点。
10) 将获得的有效样本点和样本点数据库中已有样本点进行比较,满足式(9)的有效样本点将被剔除。保存剩余新样本点及其所对应的真实模型响应值到样本点数据库中。
| $ \left\{\begin{array}{l} d\left(\boldsymbol{x}_{p}, \boldsymbol{x}_{e}\right)<\eta \cdot \max _{i=1}^{n}\left(\mathrm{Ub}_{i}-\mathrm{Lb}_{i}\right) \\ d=\max _{i=1}^{n}\left(\left|x_{p}^{i}-x_{e}^{i}\right|\right) \end{array}\right. $ | (9) |
式中:d表示有效样本点xp和数据库中样本点xe在任意维度上的最大距离,Ubi和Lbi分别表示整个设计空间在第i维上的上下边界值。η为距离控制系数,较大的η值会使优化算法错失重要的新样本点,而较小的η值则会产生多余的新样本点,浪费计算资源,本文η值取0.000 1。
11) 重复步骤3~10,直到满足终止准则,终止准则数学表达式为:
| $ \left\{\begin{array}{l} \left|\bar{F}_{i+1}-\bar{F}_{i}\right| \leqslant \varepsilon \\ \bar{F}_{i}=\sum\nolimits_{j=1}^{5} f_{j} / 5 \end{array} \quad \text { 或者 } \mathrm{NFE}>300\right. $ | (10) |
式中:fj是第j个最小函数值;Fi是第i次迭代获得的5个最小函数值平均值;ε用于判断是否满足收敛,由研究人员自行设定。上述收敛准则采用迭代过程中5个最小真实响应值的平均值是否改进作为判断依据,有效避免优化方法陷入早熟陷阱。本文假设真实最优解未知,采用的收敛准则适用于处理实际工程应用。NFE表示复杂仿真分析模型调用次数(number of function evaluations,NFE)。当NFE大于阈值300时,当前最优结果将作为获得的最终优化结果。
4 测试结果与分析 4.1 标准优化函数选用8个经典标准优化函数来测试HMASEO方法的性能,同时选取2种经典的基于元模型优化方法HAM和SEUMRE进行比较分析。
1) Six-hump Camel-Back函数(SC),n=2
| $ \begin{aligned} f(x)=& 4 x_{1}^{2}-2.1 x_{1}^{4}+x_{1}^{6} / 3+x_{1} x_{2}-4 x_{2}^{2}+4 x_{2}^{4}, \\ & x \in[-2,2], f_{\min }=-1.031\ 6 \end{aligned} $ | (11) |
2) Goldstein and Price函数(GP),n=2
| $ \begin{gathered} f(x)=\left[1+\left(x_{1}+x_{2}+1\right)^{2}\left(19-14 x_{1}+3 x_{1}^{2}-\right.\right. \\ \left.\left.14 x_{2}+6 x_{1} x_{2}+3 x_{2}^{2}\right)\right] \times\left[30+\left(2 x_{1}-3 x_{2}\right)^{2} \times\right. \\ \left.\left(18-32 x_{1}+12 x_{1}^{2}+48 x_{2}-36 x_{1} x_{2}+27 x_{2}^{2}\right)\right] ,\\ x \in[-2,2], f_{\min }=3 \end{gathered} $ | (12) |
3) Branin函数(BR),n=2
| $ \begin{gathered} f(x)=\left(x_{2}-\frac{5.1}{4 {\rm{ \mathsf{ π} }}^{2}} x_{1}^{2}+\frac{5}{{\rm{ \mathsf{ π} }}} x_{1}-6\right)^{2}+ \\ 10\left(1-\frac{1}{8 {\rm{ \mathsf{ π} }}}\right) \cos x_{1}+10, \\ x_{1} \in[-5,10], x_{2} \in[0,15], f_{\min }=0.397\ 9 \end{gathered} $ | (13) |
4) Trid 6函数(TR6),n=6
| $ \begin{aligned} f(x) &=\sum\limits_{i=1}^{n}\left(x_{i}-1\right)^{2}-\sum\limits_{i=2}^{n} x_{i} x_{i-1}, \\ x & \in[-36,36], f_{\min }=-50 \end{aligned} $ | (14) |
5) Trid 10函数(TR10),n=10
| $ \begin{gathered} f(x)=\sum\limits_{i=1}^{n}\left(x_{i}-1\right)^{2}-\sum\limits_{i=2}^{n} x_{i} x_{i-1}, \\ x \in[-100,100], f_{\min }=-210 \end{gathered} $ | (15) |
6) Sphere函数(SP12),n=12
| $ \begin{gathered} f(x)=\sum\limits_{i=1}^{n} x_{i}^{2},\\ x \in[-5.12,5.12], f_{\min }=0 \end{gathered} $ | (16) |
7) Sum Squares函数(SF15),n=15
| $ \begin{gathered} f(x)=\sum\limits_{i=1}^{n} i x_{i}^{2}, \\ x \in[-10,10], f_{\min }=0 \end{gathered} $ | (17) |
8) A Function of 16 Variables函数(F16),n=16
| $ \begin{array}{l} \ \ \ \ \ \ f(x)=\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} \alpha_{i j}\left(x_{i}^{2}+x_{i}+1\right)\left(x_{j}^{2}+x_{j}+1\right), \\ i=1,2, \cdots, n, x \in[-1,1], f_{\min }=25.875\ 0 \end{array} $ | (18) |
式中αij取值参考文献[9]。
本文选用的8个标准优化函数从低维到高维,具有不同函数特性,能够代表不同特征工程设计优化问题。对于每个测试函数,分别用3种优化方法连续运行10次以减小随机误差影响,避免获得不具代表性的优化结果。在测试过程中,3种优化方法SEUMRE、HAM和HMASEO的收敛参数ε分别设为0.01、0.01和0.001。在实际工程应用中,优化时间基本上取决于调用真实分析模型的次数NFE。因此,对于工程优化方法来说,尽可能减少调用高精度分析模型的次数是一个非常重要评价指标,本文采用NFE来表征优化效率。另外,收敛全局最优解fopt也将用于反映优化精度和鲁棒性。3种优化方法精度和效率测试结果对比如表 1和表 2所示。
| 表 1 优化精度测试结果对比 Table 1 Comparison results on optimization accuracy |
| 表 2 优化效率测试结果对比 Table 2 Comparison results on optimization efficiency |
分析表 1优化精度测试结果可知,在实际最优解未知的情况下,HMASEO方法能够成功捕捉到所有测试函数的理想优化解(与真实最优解相差在1%以内),除SC和GP函数外优化精度均好于比较方法HAM和SEUMRE。而对于SC和GP函数,HMASEO方法获得的优化结果与实际全局最优解也非常接近,相差在1%以内。HAM方法在SC和GP函数中获得的fopt平均值最接近实际全局最优解,但在高维函数TR10、SF15和F16中,分别有数次无法获得收敛优化解(Shan等[11]将设计变量n≥10定义为高维问题)。同样地,SEUMRE方法在高维函数TR10、SP12、SF15和F16中无法获得令人满意的优化解。测试结果表明HMASEO方法不仅具有较高优化精度,而且具备处理高维优化问题能力,而HAM和SEUMRE方法无法在有限计算资源内获得令人满意的全局优化解。
分析表 2优化效率测试结果可知,HMASEO方法在其中6个测试函数中均能以最小计算资源获得理想优化解,仅在SC和GP函数中所需NFE多于SEUMRE方法。以TR6函数为例,HMASEO方法平均只需要调用真实分析模型95.1次,比HAM方法平均少101.2次,比SEUMRE方法少105.2次。另外,HAM和SEUMRE方法在2个函数TR10和SF15中完全不能捕捉到全局最优解,同时在F16函数中分别有4、1次无法得到收敛优化解。HMASEO方法采用自适应空间探索方法,能够有效减少真实分析模型调用次数,减轻计算压力,优化效率明显高于比较方法HAM和SEUMRE。
为了更加直观展现HMASEO方法在鲁棒性方面优势,采用箱线图对各测试函数优化结果进行统计分析,如图 2所示。箱线图矩形内部的横线表示中位数,矩形上下两端分别对应数据的上、下四分位数,矩形端外的2条线段分别对应数据的上、下四分位距,这2条线段表示异常值截断处,异常值截断处之外的点为异常值,用+表示。异常值通常与其他统计结果相差较大,表示可靠性较低。分析图中矩形盒长度和中位线可以看出,HMASEO方法在所有测试函数中均表现稳定,具有很强鲁棒性。而比较方法HAM和SEUMRE表现糟糕,优化结果分布分散,鲁棒性较弱。再来分析图中异常值,发现3种方法在不同测试函数中均存在异常值,其中HMASEO方法在SC、GP、BR、F16函数中存在异常值。事实上,HMASEO方法对于所有测试函数都能获得理想优化解,因此异常值在选取的测试函数中并不能很好地表征鲁棒性。HMASEO方法在寻优过程中同时调用3种典型元模型,可以很好地利用各模型优点,有效规避每个模型本身不足之处,形成组合保险机制,相比其他优化方法更加稳健高效。
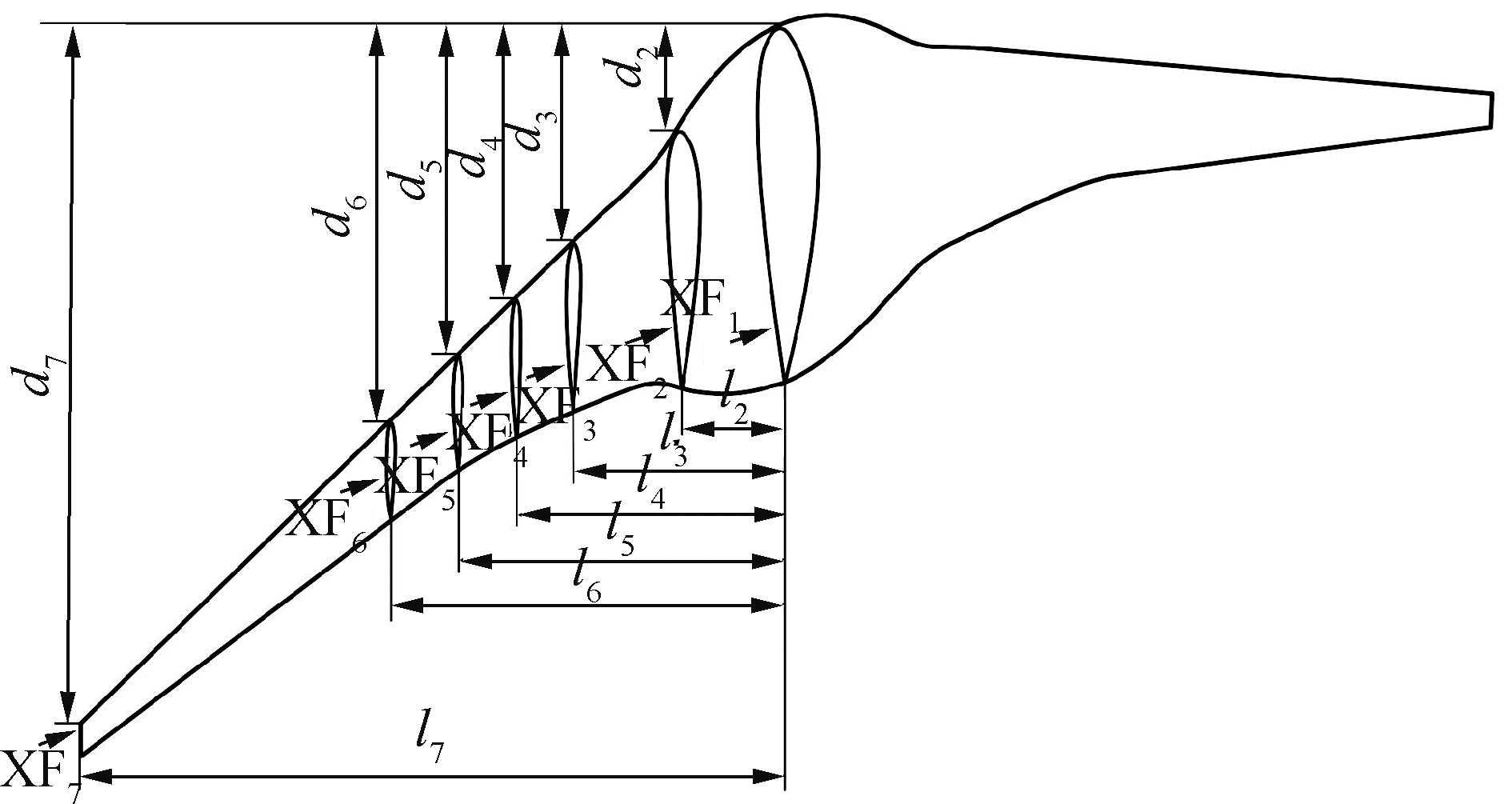
4.2 翼身融合水下滑翔机外形设计优化实例翼身融合水下滑翔机外形采用翼身融合技术,使得整体沿翼展方向各截面均为翼型,可视为由一系列不同截面翼型组成滑翔机,如图 3所示。BWBUG外形设计优化是一个极其复杂的系统工程问题,不仅设计周期长,研制成本高,而且优化模型复杂。参考文献[12],本文在保持BWBUG总体外形轮廓不变前提下,以升阻比最大为优化目标,选择了7个关键位置处的站位翼型在攻角α=7°、速度v=1 m/s工况下进行优化,然后将优化翼型代替初始翼型,最后使用Unigraphics NX (UG) 软件利用优化翼型重新生成BWBUG优化外形。图 4给出了7个站位翼型的位置示意图,图中l1~l7和d1~d7分别表示站位翼型与中心截面翼型前缘的水平和垂直距离。7个站位翼型基本信息如表 3所示。

|
Download:
|
| 图 3 初始BWBUG外形设计 Fig. 3 Initial BWBUG shape design | |
|
Download:
|
| 图 4 站位翼型展向位置 Fig. 4 Illustration of the key airfoils′ positions | |
| 表 3 站位翼型基本信息 Table 3 Basic information on key airfoils |
采用4阶形状类别函数变换方法[13](class function/shape function transformation,CST)构建得到站位翼型的参数化模型,并保证优化BWBUG外形仍为上下对称。每个站位翼型的优化设计变量数为5,因此BWBUG外形设计优化问题总共包含35个设计参数。站位翼型优化问题定义为:
| $ \left\{\begin{array}{ll} \min & f(X)=-L / D \\ \text { s.t. } & g_{1}(X)=t_{\text {ini }}-t_{\text {opt }} \leqslant 0 \\ & g_{2}(X)=s_{\text {ini }}-s_{\text {opt }} \leqslant 0 \\ & x_{i}^{l}<x_{i}<x_{i}^{u}, i \in 1,2, \cdots, 5 \end{array}\right. $ | (19) |
式中:L和D分别表示翼型升力和阻力;tini、topt、sini、sopt分别表示优化前后翼型的最大相对厚度和横截面积;xil和xiu分别表示设计参数的最小和最大取值,表 4给出了各站位翼型对应的设计变量取值范围。约束函数g1和g2能够确保优化翼型的最大相对厚度和横截面积都不小于初始翼型,很好地平衡了BWBUG优化外形的有效容积和水动力性能[14]。使用HMASEO方法对BWBUG外形设计优化问题进行求解,并与HAM和SEUMRE方法进行比较。站位翼型XF1~XF2和XF3~XF7的收敛判定参数ε分别设为0.5和0.01。
| 表 4 站位翼型设计变量取值范围 Table 4 Design ranges for key airfoils |
站位翼型优化结果如表 5所示,3种优化方法SEUMRE、HAM和HMASEO获得的BWBUG优化外形的升阻比均大于初始外形,分别提高了19.00%、23.19%和24.32%。而HMASEO方法优化得到的BWBUG外形升阻比为14.26,高于比较方法HAM和SEUMRE。同时,HMASEO方法优化过程中调用的真实分析模型次数NFE仅为426次,相比HAM和SEUMRE方法分别减少了235次和88次,HMASEO方法所需的计算资源最少。另外,HAM方法得到的优化外形的排水体积最大,相比初始设计提高了3.03%,而SEUMRE、HMASEO方法分别提高了1.52%和2.65%。排水体积的增大能够使BWBUG获得更大的有效容积,携带更多的仪器设备,拓宽其任务范围。
| 表 5 BWBUG外形设计优化结果对比 Table 5 Comparison results for BWBUG shape design optimization |
分析上述结果可以发现,当BWBUG外形选用水动力性能更优的站位翼型时,滑翔机整体外形的升阻比将得到同步提高。另外,相比HAM和SEUMRE方法,本文提出的HMASEO方法不仅极大地降低了计算资源,同时提高了BWBUG外形的流体动力性能和有效容积,具有较强的工程实用性和有效性。
5 结论1) 自适应空间探索方法打破了传统优化方法依赖经验给定设计空间的局限,通过自适应更新设计子空间,逐步提高混合元模型在最优解附近的近似精度,最后引导优化快速收敛到全局最优解。
2) 采用8个标准优化函数和翼身融合水下滑翔机外形设计优化实例对HMASEO方法的性能进行测试,并与HAM和SEUMRE方法进行比较分析,结果表明HMASEO方法在全局收敛性、优化效率和鲁棒性方面具有一定的优越性,尤其是针对高维优化问题。
HMASEO方法在处理高维工程问题时还有待进一步研究与提高。在未来研究中,考虑引入维度降低策略,发展针对高维优化问题的自适应空间探索方法。
| [1] |
LIU Haitao, ONG Y S, CAI Jianfei. A survey of adaptive sampling for global metamodeling in support of simulation-based complex engineering design[J]. Structural and multidisciplinary optimization, 2018, 57(1): 393-416. DOI:10.1007/s00158-017-1739-8 (  0) 0)
|
| [2] |
YE Pengcheng, PAN Guang. Global optimization method using adaptive and parallel ensemble of surrogates for engineering design optimization[J]. Optimization, 2017, 66(7): 1135-1155. DOI:10.1080/02331934.2016.1266627 (  0) 0)
|
| [3] |
GOEL T, HAFTKA R T, SHYY W, et al. Ensemble of surrogates[J]. Structural and multidisciplinary optimization, 2007, 33(3): 199-216. DOI:10.1007/s00158-006-0051-9 (  0) 0)
|
| [4] |
ACAR E, RAIS-ROHANI M. Ensemble of metamodels with optimized weight factors[J]. Structural and multidisciplinary optimization, 2009, 37(3): 279-294. DOI:10.1007/s00158-008-0230-y (  0) 0)
|
| [5] |
黄焕军, 张博文, 吴光强, 等. 基于组合代理模型的车身多学科设计优化[J]. 汽车工程, 2016, 38(9): 1107-1113. HUANG Huanjun, ZHANG Bowen, WU Guangqiang, et al. Multidisciplinary design optimization of vehicle body based on ensemble surrogates[J]. Automotive engineering, 2016, 38(9): 1107-1113. DOI:10.3969/j.issn.1000-680X.2016.09.011 (  0) 0)
|
| [6] |
周仕明, 李道奎, 唐国金. 基于元模型与聚类算法的设计空间减缩策略及工程应用[J]. 计算力学学报, 2012, 29(2): 242-248. ZHOU Shiming, LI Daokui, TANG Guojin. Design space reduction based on the metamodeling and clustering method[J]. Chinese journal of computational mechanics, 2012, 29(2): 242-248. (  0) 0)
|
| [7] |
龙腾, 郭晓松, 彭磊, 等. 基于信赖域的动态径向基函数代理模型优化策略[J]. 机械工程学报, 2014, 50(7): 184-190. LONG Teng, GUO Xiaosong, PENG Lei, et al. Optimization strategy using dynamic radial basis function metamodel based on trust region[J]. Journal of mechanical engineering, 2014, 50(7): 184-190. (  0) 0)
|
| [8] |
YOUNIS A, DONG Zuomin. Metamodelling and search using space exploration and unimodal region elimination for design optimization[J]. Engineering optimization, 2010, 42(6): 517-533. DOI:10.1080/03052150903325540 (  0) 0)
|
| [9] |
GU J, LI G Y, DONG Zuomin. Hybrid and adaptive meta-model-based global optimization[J]. Engineering optimization, 2012, 44(1): 87-104. DOI:10.1080/0305215X.2011.564768 (  0) 0)
|
| [10] |
JIN Ruichen, CHEN Wei, SUDJIANTO A. An efficient algorithm for constructing optimal design of computer experiments[J]. Journal of statistical planning and inference, 2005, 134(1): 268-287. DOI:10.1016/j.jspi.2004.02.014 (  0) 0)
|
| [11] |
SHAN Songqing, WANG G G. Survey of modeling and optimization strategies to solve high-dimensional design problems with computationally-expensive black-box functions[J]. Structural and multidisciplinary optimization, 2010, 41(2): 219-241. DOI:10.1007/s00158-009-0420-2 (  0) 0)
|
| [12] |
孙龙. 新型水下滑翔机翼型优化设计及水动力性能研究[D]. 西安: 西北工业大学, 2016: 50-70. SUN Long. Optimization design of new underwater glider airfoil and research on hydrodynamic performance[D]. Xi'an: Northwestern Polytechnical University, 2016: 50-70. (  0) 0)
|
| [13] |
ZHANG Yu, HAN Zhonghua, ZHANG Keshi, et al. Variable-fidelity expected improvement method for efficient global optimization of expensive functions[J]. Structural and multidisciplinary optimization, 2018, 58(4): 1431-1451. DOI:10.1007/s00158-018-1971-x (  0) 0)
|
| [14] |
DONG Huachao, LI Chengshan, SONG Baowei, et al. Multi-surrogate-based Differential Evolution with multi-start exploration (MDEME) for computationally expensive optimization[J]. Advances in engineering software, 2018, 123: 62-76. DOI:10.1016/j.advengsoft.2018.06.001 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


