反舰导弹通过侵彻至舰船内部并爆炸来对舰船造成毁伤[1-2]。舰船典型结构为空间板架结构,板架结构中纵骨与横梁相互交错,以提高船体结构强度。板架结构板厚较小,板格部分较容易被导弹穿透,而纵骨与横梁等型材会显著影响导弹的受力和姿态,对导弹的侵彻起到抵挡作用[3]。开展板架结构与反舰导弹的高速侵彻耦合动力学问题研究,对预测反舰导弹在侵彻舰船板架结构时的弹道特性及板架结构毁伤有重要的意义。对于反舰导弹侵彻能力的考核与评估常常采用舰船陆地靶标侵彻试验。舰船多采用高强度特种钢制造,钢材价格昂贵,如仍采用特种钢制作舰船靶标,则造价过高,使得试验成本过高。因此,有必要开发采用普通钢替代特种钢的舰船靶标设计技术。目前国内对于普通钢代替特种钢的材料等效方法,主要采用强度等效方法。对于平板而言,此种方法保证原型与模型的板厚与屈服强度的乘积相等。此方法虽在工程中得到了一些应用,但尚有缺陷,通过此方法计算出的等效板厚偏大。且此方法缺乏理论证明,不能保证侵彻毁伤效应的相似性。此外,加筋板侵彻与侵彻平板靶板的动力学响应存在差异,板架结构加强筋的存在会影响弹体的弹道特性。在传统的舰船靶标的设计方法中,依据质量等效法将舰船板架等效为一定厚度的光板结构,将此作为舰船实际板架结构的等效设计方法[4]。这种模拟造成的不合理性主要有2个方面:1)舰船空间板架结构对反舰导弹侵彻最大的影响为战斗部侵彻时攻角的改变[5-10],加强筋对弹体姿态角改变影响很大,而平板等效方法难以保证侵彻弹体姿态角改变相似性;2)侵彻舰船实际板架结构的毁伤模式与半无限厚靶板穿甲机理和毁伤模式不同。弹体侵彻光板结构会造成板架连接处塑性大变形和靶板破口的毁伤模式[11]; 弹体侵彻舰船板架结构会造成板架中心区域大变形,进而产生板架的拉伸断裂。由于不同结构产生不同的毁伤模式造成弹体弹道姿态和剩余速度的不相似特性。
本文基于塑性动力学理论[12],推导了金属板架结构侵彻毁伤模式相似的材料等效板厚的计算公式,给出了侵彻靶标后破口与塑性区范围大小的预估公式,并将理论与数值计算结果进行了验证。
1 靶标材料等效方法在实际靶标设计过程中,为了更好地反应舰船实际的结构特性,往往使用制造实际舰船的特种钢材作为靶标的主要材料。对比普通钢材,特种钢材具有更特殊的加工工艺,但是在加工安装过程中存在着较大的不便性。同时特种钢材较高的生产成本以及稀缺的货源都为一系列考核战斗部的试验带来了高昂的成本与不便。为了节约试验成本,通常采用等效靶标设计方法,设计出与实际船体毁伤模式与毁伤效果相似的等效靶标,常用的等效方法包括基于强度的等效方法与基于剩余速度的等效方法。
1.1 已有材料等效方法国内外针对普通钢材代替船用特种合金钢材的材料等效方法,一般采取基于材料屈服强度和基于弹体剩余速度的2种材料等效的方法分别为:
| $ \sigma_{m} h_{m}=\sigma_{s} h_{s} $ | (1) |
| $ \sigma_{m}^{0.5} h_{m}^{0.7}=\sigma_{s}^{0.5} h_{s}^{0.7} $ | (2) |
式中:σs为原型靶板材料屈服强度;σm为模型靶板材料屈服强度;hs为原型靶板厚度;hm为模型靶板厚度。
针对加筋板等效光板靶板,上述2种等效方法存在局限性,无法保证侵彻后靶板毁伤结果的相似性和弹体姿态的相似性。因此,研究新的弹体侵彻舰船板架结构的等效设计方法具有重要意义。
1.2 舰船板架结构的材料等效设计方法对侵彻板架结构的理论模型进行简化:1)将舰船板架结构等效为平板结构;2)四边框架为刚性固定;3)舰船板架结构无刚体运动;4)假设结构材料均为理想刚塑性材料。
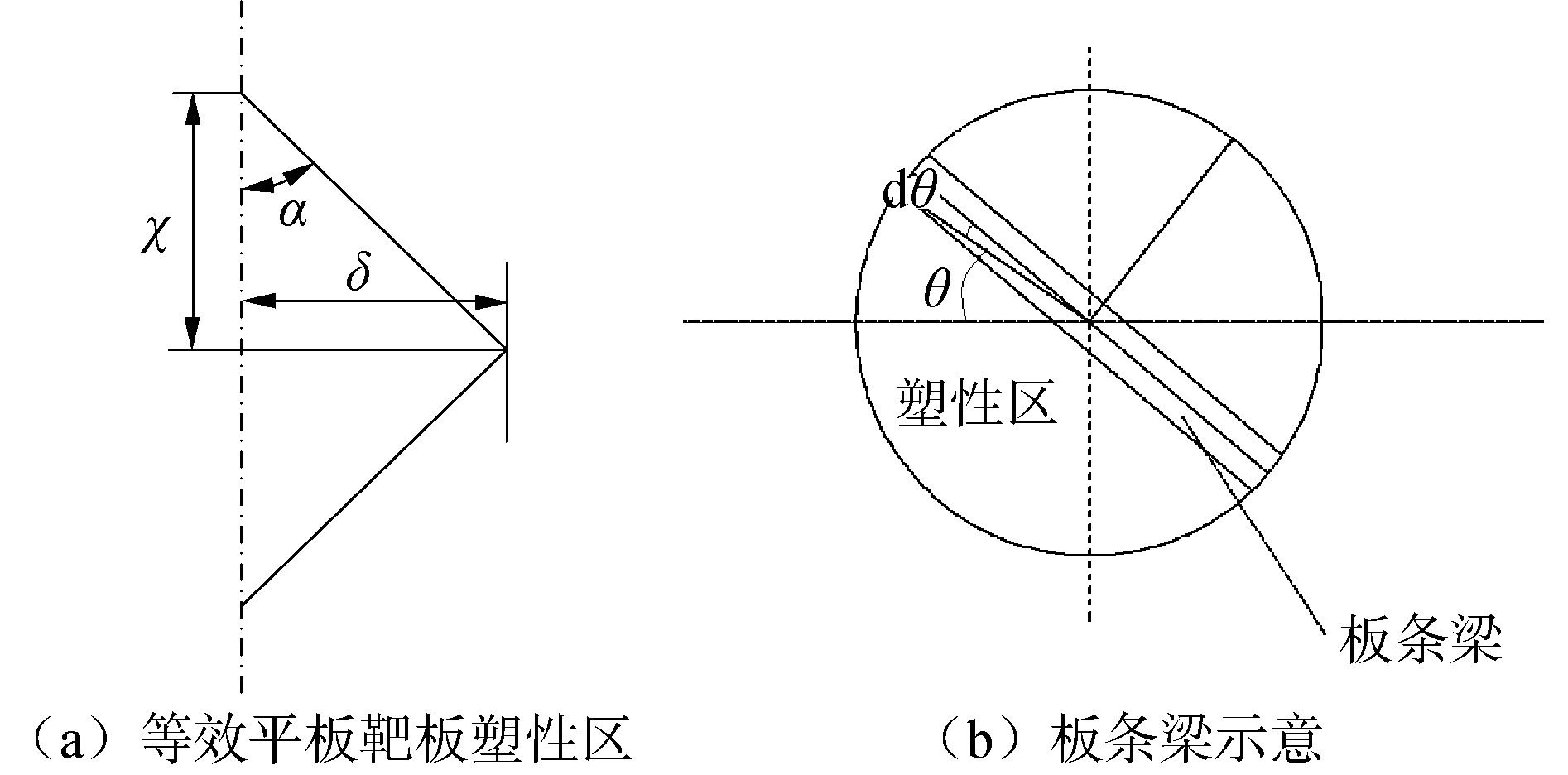
χ为侵彻靶板过程中任意时刻t板的塑性区半径,δ为靶板中心的塑性变形若靶板塑性大变形且只有只受中面力作用时,将靶板塑性区域划分为多条板条梁,塑性区与板条梁示意如图 1所示。每条板条梁对弹体头部作用力为dFD为:
| $ \mathrm{d} F_{D}=-2 \sigma_{m} \mathrm{~d} A \sin \alpha $ | (3) |
|
Download:
|
| 图 1 等效平板靶板塑性区与板条梁 Fig. 1 Equivalent target board plastic zone and slab beam diagram | |
式中:σm为模型靶板材料屈服强度;dA为靶板发生塑性流动时板条梁横截面面积;α为靶板靶面产生的塑性变形与靶板水平方向的夹角。
由文献[9]体积守恒可知:
| $ \mathrm{d} A=\mathrm{d} A_{0} \frac{\chi}{\sqrt{\chi^{2}+\delta^{2}}} $ | (4) |
| $ \sin \alpha=\frac{\delta}{\sqrt{\chi^{2}+\delta^{2}}} $ | (5) |
式中dA0为板条梁在未发生塑性变形时横截面面积:
| $ \mathrm{d} A_{0}=h_{m} \chi \mathrm{d} \theta $ | (6) |
式中hm为平板靶板厚度。
将式(4)和式(5)代入式(3)得:
| $ \mathrm{d} F_{D}=-\frac{2 \sigma_{m} \mathrm{~d} A_{0} \chi \delta}{\chi^{2}+\delta^{2}} $ | (7) |
将式(6)代入式(7),并在[0 π]对θ积分,可得:
| $ \int_{0}^{{\rm{ \mathsf{ π} }}} F_{D}=\int_{0}^{{\rm{ \mathsf{ π} }}} \mathrm{d} F_{D}=-\frac{2 {\rm{ \mathsf{ π} }} \sigma_{m} h_{m} \chi^{2} \delta}{\chi^{2}+\delta^{2}} $ | (8) |
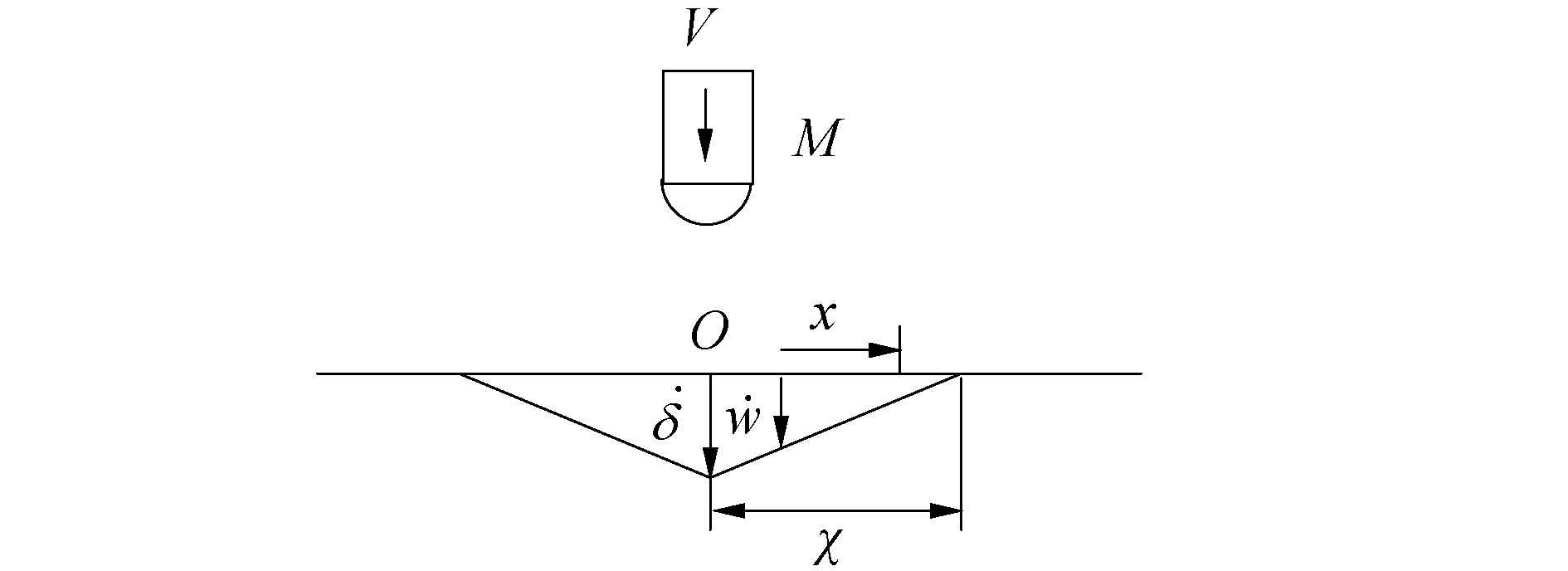
由式(8)可知弹体受力是随时间变化的函数。弹体侵彻靶板时塑性区域半径χ如图 2所示,其中V为弹体初速度;M为弹体质量。
|
Download:
|
| 图 2 侵彻时塑性区速度场 Fig. 2 Schema of plastic zone for missile penetration | |
靶板的横向速度场可以表示为[12]:
| $ \left\{\begin{array}{lc} \dot{w}=\dot{\delta}\left(1-\frac{x}{\chi}\right), & 0 \leqslant x \leqslant \chi \\ \dot{w}=0, & x>\chi \end{array}\right. $ | (9) |
式中
随着靶板塑性区域半径的扩大,在dx长度方向产生的惯性力dFm为:
| $ \mathrm{d} F_{m}=2 {\rm{ \mathsf{ π} }} x \mathrm{d} x \cdot \rho h_{m} \cdot \ddot{w}(x, t) $ | (10) |
式中ρ为靶板密度。
当塑性区半径为χ时,靶板横向惯性力Fm为:
| $ F_{m}=2 {\rm{ \mathsf{ π} }} \rho h_{m}\left(\frac{\ddot{\delta} \chi^{2}}{6}+\frac{1}{3} \dot{\delta} \dot{\chi} \chi\right) $ | (11) |
对于任意时刻t,靶板塑性区在横向上平衡的条件为:
| $ M \ddot{\delta}+\frac{{\rm{ \mathsf{ π} }} \rho h_{m}}{3}\left(\ddot{\delta} \chi^{2}+2 \dot{\delta} \dot{\chi} \chi\right)=0 $ | (12) |
将式(11)代入式(12),可得:
| $ M \ddot{\delta}+\frac{{\rm{ \mathsf{ π} }} \rho h_{m}}{3}\left(\ddot{\delta} \chi^{2}+2 \dot{\delta} \dot{\chi} \chi\right)=0 $ | (13) |
注意到:
| $ M \ddot{\delta}+\frac{{\rm{ \mathsf{ π} }} \rho h_{m}}{3} \frac{\mathrm{d}\left(\dot{\delta} \chi^{2}\right)}{\mathrm{d} t}=0 $ | (14) |
对式(14)t进行积分,令初始条件t=0时,弹体初速度为V,靶板不动,则有:
| $ M(\dot{\delta}(t)-\dot{\delta}(0))+\frac{{\rm{ \mathsf{ π} }} \rho h_{m}}{3}\left[\dot{\delta}(t) \chi^{2}(t)-\dot{\delta}(0) \chi^{2}(0)\right]=0 $ | (15) |
代入初始条件可得:
| $ M V=\left(M+\frac{{\rm{ \mathsf{ π} }} \rho h_{m}}{3} \chi^{2}\right) \dot{\delta} $ | (16) |
针对弹体运动,由动量定理可得:
| $ \frac{1}{2} M \dot{\delta}^{2}-\frac{1}{2} M V^{2}=\int_{0}^{\delta} F_{D} \mathrm{~d} \delta $ | (17) |
将式(8)和式(16)代入式(17)可得:
| $ \begin{gathered} \frac{1}{2} M V^{2}\left[\left(\frac{M}{M+\frac{{\rm{ \mathsf{ π} }} \rho h_{m}}{3} \chi^{2}}\right)^{2}-1\right]= \\ -{\rm{ \mathsf{ π} }} \sigma_{m} h_{m} \chi^{2} \ln \left(1+\frac{\delta^{2}}{\chi^{2}}\right) \end{gathered} $ | (18) |
通常
| $ \ln \left(1+\frac{\delta^{2}}{\chi^{2}}\right) \approx \frac{\delta^{2}}{\chi^{2}} $ | (19) |
经整理式(18)变为:
| $ \chi^{2}=\frac{3 M}{{\rm{ \mathsf{ π} }} \rho h_{m}}\left(\frac{1}{\sqrt{1-\frac{2 {\rm{ \mathsf{ π} }} \sigma_{m} h_{m}}{M V^{2}} \delta^{2}}}-1\right) $ | (20) |
若
| $ \chi \approx \sqrt{\frac{3 \sigma_{m}}{\rho V^{2}}} \delta $ | (21) |
由文献[10],靶标塑性区中心横向塑性位移的最大值wf为:
| $ \frac{w_{f}}{h_{\mathrm{m}}}=\sqrt{\frac{3 \gamma_{\mathrm{m}} \varOmega_{\mathrm{m}}\left(1+6 \gamma_{\mathrm{m}}\right)}{{\rm{ \mathsf{ π} }}\left(1+3 \gamma_{\mathrm{m}}\right)^{2}}+1}-1 $ | (22) |
式中:
当随着靶板中心横向塑性位移的增加,即δ>wf时,由于中面力作用会造成靶板拉伸断裂。对于靶板板架结构可得:
| $ \frac{{\rm{ \mathsf{ π} }}\left(1+3 \gamma_{m}\right)^{2}}{3 \gamma_{m} \varOmega_{m}\left(1+6 \gamma_{m}\right)}<<1 $ | (23) |
则式(23)可近似表示为:
| $ \begin{aligned} \frac{w_{f}}{h_{m}}=& \sqrt{\frac{3 \gamma_{m} \varOmega_{m}\left(1+6 y_{m}\right)}{{\rm{ \mathsf{ π} }}\left(1+3 \gamma_{m}\right)^{2}}} \sqrt{\left[1+\frac{{\rm{ \mathsf{ π} }}\left(1+3 \gamma_{m}\right)^{2}}{3 \gamma_{m} \varOmega_{m}\left(1+6 y_{m}\right)}\right]}-1 \approx \\ & \sqrt{\frac{3 \gamma_{m} \varOmega_{m}\left(1+6 \gamma_{m}\right)}{{\rm{ \mathsf{ π} }}\left(1+3 \gamma_{m}\right)^{2}}}-1=\\ & \sqrt{\frac{3 \gamma_{m} \varOmega_{m}}{{\rm{ \mathsf{ π} }}}} \sqrt{1+\frac{9 \gamma_{m}^{2}}{\left(1+3 \gamma_{m}\right)^{2}}}-1 \end{aligned} $ | (24) |
又因为γm>1,则式(24)可近似为:
| $ \frac{w_{f}}{h_{m}}=\sqrt{\frac{3 \gamma_{\mathrm{m}} \varOmega_{\mathrm{m}}}{{\rm{ \mathsf{ π} }}}}-1=\frac{M V}{r h_{m}^{2} {\rm{ \mathsf{ π} }}} \sqrt{\frac{3}{2 \rho \sigma_{m}}}-1 $ | (25) |
由式(21)可知:
| $ r=\sqrt{\frac{3 \sigma_{m}}{\rho V^{2}}} w_{f} $ |
将靶板最大塑性区半径r代入式(25),可得:
| $ \frac{w_{f}}{h_{m}}+1=\frac{M V^{2}}{\sqrt{2} {\rm{ \mathsf{ π} }} h_{m}^{2} w_{f} \sigma_{m}} $ | (26) |
同理可得:
| $ \left\{\begin{array}{l} \frac{W_{f}}{h_{s}}+1=\frac{M V^{2}}{\sqrt{2} {\rm{ \mathsf{ π} }} h_{s}^{2} W_{f} \sigma_{s}} \\ R=\sqrt{\frac{3 \sigma_{s}}{\rho V^{2}}} W_{f} \end{array}\right. $ | (27) |
式中:Wf为横向塑性极限位移值;hs为等效模型平板板厚;σs为材料屈服极限;R为塑性区区域半径。
在本文中,板架结构与靶板之间满足几何相似条件,且几何缩比为1,按照经典相似理论可得:
| $ \frac{W_{f}}{h_{s}}=\frac{w_{f}}{h_{m}} $ | (28) |
即:
| $ h_{m}^{3} {\sigma}_{m}=h_{s}^{3} {\sigma}_{s} $ | (29) |
由式(29)可以求出靶板的等效厚度hm为:
| $ h_{m}=\left(\frac{\sigma_{s}}{\sigma_{m}}\right)^{\frac{1}{3}} h_{s} $ | (30) |
根据前文材料等效设计方法与实船板架结构毁伤结果相似的等效靶标,设计方法为:
1) 针对弹体和板架结构的具体情况,确定弹体重量M、速度V以及弹体板架结构的几何尺寸和材料;
2) 将原型板架结构采用极限弯矩方法等效为光板结构;其中极限弯矩为:
| $ M_{0}=\sigma_{m}\left(S_{1}+S_{2}\right) $ | (31) |
式中:M0为梁的极限弯矩;S1为中性轴以上的面积对中性轴静矩;S2为中性轴以下的面积对中性轴静矩;
3) 根据式(30),将原型材料平板厚度等效为替代平板材料等效厚度;
4) 根据梁极限弯矩计算式(31)将材料等效厚度平板转化为等效材料的板架结构。本文的舰船结构统计规律是指板架结构的具体参数应该符合的统计规律,包括靶板板厚和加强筋型材尺寸等。文献[12]针对我国主流驱逐舰进行了板架结构参数统计,并给出了板厚和型材尺寸的统计规律。在本文的等效设计方法中,需要保证等效板架结构符合舰船结构统计规律,以避免不切实际的等效板架结构设计。
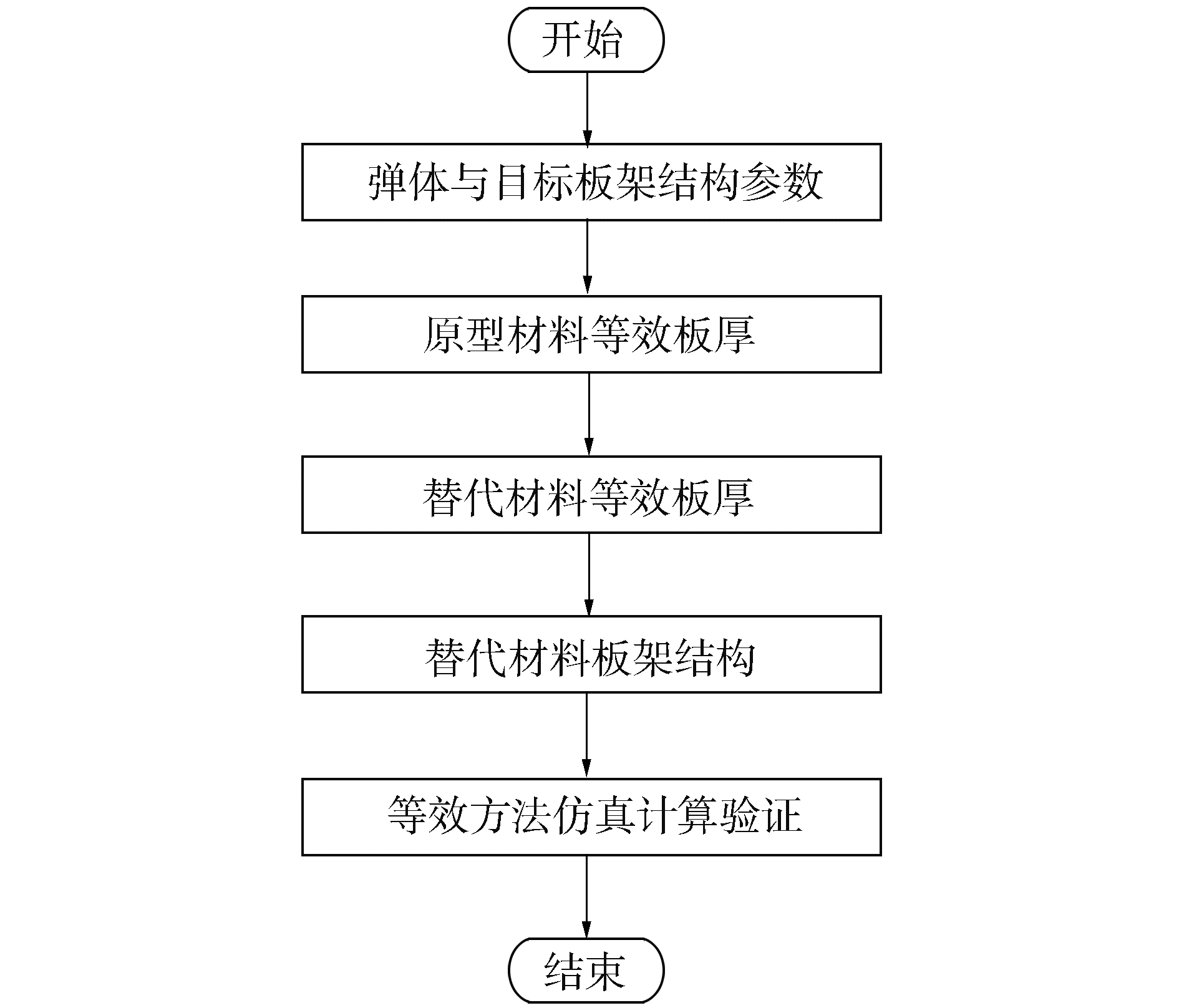
等效靶标设计的流程图如图 3所示。
|
Download:
|
| 图 3 等效靶标设计流程 Fig. 3 Equivalent target design flow chart | |
针对不同靶板侵彻后毁伤效果和弹体剩余速度与靶板塑性区区域数值仿真计算结果进行分析。对前文的2种材料等效方法与本文研究的材料等效方法进行对比。
文中对某7 000吨级舰船甲板建立数值仿真模型进行分析。2种靶板材料参数[13-15]如表 1。其中,硬化模量和应变率强化系数C、p为后文数值计算中所需要的参数。后文计算中,靶板材料采用动塑性材料本构模型,应变率强化效应用CS模型进行考虑:
| $ \sigma_{0}^{\prime}=\sigma_{0}\left[1+\left(\frac{\dot{\varepsilon}}{C}\right)^{1 / p}\right] $ | (32) |
| 表 1 材料参数表 Table 1 Material parameter table |
式中:σ′0为动态屈服应力;
本文针对重量为250 kg反舰导弹,长度1 200 mm,弹径240 mm,其中弹头曲率半径为576 mm,选取板架结构长宽尺寸均为4 m。
在研究弹体高速侵彻靶板问题时,采用LS-Dyna有限元软件的Lagrange算法;数值计算准确与否,与靶板材料以及破坏准则的选取相关。根据实际材料失效情况,选取材料模型和参数,本文中靶板材料采用PLASTIC-KINEMATIC模式[16-17]。采用LS-Dyna有限元软件,通过Lagrange算法,对弹体-靶板侵彻模型有限元模型建立;靶板的边界条件设定为四周刚性固定,材料选用船用921A钢,等效靶材为Q235钢。根据过往经验弹体侵彻金属薄板时,弹体自身几乎不发生塑性变形,因此将弹体材料设置为刚体,弹-靶有限元模型如图 4所示。

|
Download:
|
| 图 4 弹-靶有限元模型 Fig. 4 Finite element model of projectile-target | |
选取的921A钢材料靶标舰船板架结构尺寸如表 2所示。
| 表 2 材料参数表 Table 2 Material parameter table |
材料为921A板架结构加强筋通过极限弯矩方法等效平板厚度为16 mm的数值如表 3所示。
| 表 3 等效平板板厚表 Table 3 Equivalent plate thickness meter |
联立方程(28)求解参数σs为681 MPa、ρ为7 850 kg/m、V为750 m/s、hs为0.071 6 m、M为250 kg。Wf=0.770 7 m与R=0.524 2 m。对方程(30)进行求解,得到等效板厚hm。
计算所得板厚如表 4所示。为了进一步与其他材料等效方法对比,根据式(1)和(2)等效方法对等效板厚进行计算,并将计算结果列入表 4中。
| 表 4 等效板厚表 Table 4 Equivalent plate thickness meter |
根据式(31)将等效材料的平板板厚转化为等效材料的加筋板板架结构,板架结构等效尺寸如表 5所示。
| 表 5 等效加筋板结构尺寸表 Table 5 Equivalent plate thickness meter |
本文针对靶标等效性的研究分别从战斗部的弹道特性等效和靶标的毁伤等效2方面进行[6]。战斗部的弹道特性分析主要分为战斗部的剩余速度、着角与攻角的分析,靶板毁伤分析为靶板毁伤模式与塑性区区域范围分析。
战斗部在实际侵彻舰船甲板的过程中,弹体有一定的姿态角,弹体速度方向与靶板法线之间的夹角称为弹体着角φ,弹体轴线与弹体速度方向之间的角度称为弹体攻角β。本文中,在不同工况下对不同等效方法设计出的靶标进行侵彻计算,分析侵彻结束后靶标的毁伤情况、战斗部的剩余速度以及战斗部的姿态。选取的着角为0°~40°,选取的攻角为-6°~10°。通常情况当着角大于50°时,战斗部侵彻靶板时会发生跳弹现象,此时认为战斗部侵彻失败。
2.3.1 弹体侵彻后弹体剩余速度分析当弹体以750 m/s的初速度垂直入射时,对原型结构、本文等效设计方法设计板架结构、基于材料屈服强度等效和弹体剩余速度2种等效方法设计靶标的侵彻后弹体剩余速度的影响进行对比分析,侵彻结束后战斗部的剩余速度统计数据如表 6所示。
| 表 6 侵彻结束后战斗部的剩余速度统计表 Table 6 Statistical table of remaining velocity of warhead after penetration |
由上表可以看出:本文提出的材料等效靶标设计方法,侵彻后弹体剩余速度与原型板架结构误差为1.24%,优于其他2种材料等效设计方法。
2.3.2 弹体侵彻后靶板破口大小分析当弹体以750 m/s的初速度垂直入射时,对原型结构、本文等效设计方法设计板架结构、基于材料屈服强度等效和弹体剩余速度2种等效方法设计靶标的侵彻后的破口形状和破口大小的影响进行对比分析。弹体侵彻靶板后破口形状如图 5所示。

|
Download:
|
| 图 5 破口形状 Fig. 5 Penetration breakthrough shape map | |
通过AUTOCAD软件对破口的大小测量后的结果如表 7。
| 表 7 靶板破口大小统计表 Table 7 Break diameter statistics table |
通过表 7可得:剩余速度材料等效设计方法误差与本文材料等效设计方法破口大小与原型板架误差均为3.7%,且上述3种等效设计方法设计破口形状均为圆形。
2.3.3 侵彻结束后靶标塑性区尺寸比对当弹体以750 m/s的初速度垂直入射时,对原型结构、本文等效设计方法设计板架结构、基于材料屈服强度等效和弹体剩余速度2种等效方法设计靶标的侵彻后的塑性区区域半径进行对比分析。结果如表 8所示。
| 表 8 靶板塑性区区域大小统计表 Table 8 Statistical table of plastic zone range |
通过表 8可得:本文提出的材料等效靶标设计方法塑性区与原型板架结构误差为4.3%,而另外2种方法误差较大。
3 结论1) 基于塑性动力学原理,对战斗部侵彻舰船板架结构的塑性动力学响应进行推导,得到靶板塑性区区域半径大小与靶板最大位移的计算公式。
2) 以板架结构侵彻毁伤相似为准则,推导出了板架结构材料等效板厚计算公式。同时提出了具有侵彻毁伤相似的等效板架结构设计方法,并通过数值方法验证了等效方法的正确性,为后续的舰船靶标设计相关研究提供了参考。
| [1] |
朱平云, 胥辉旗, 曲晖. 反舰导弹突防技术[M]. 北京: 兵器工业出版社, 2015: 24-25. ZHU Pingyun, XU Huiqi, QU Hui. Anti-ship missile penetration technology[M]. Beijing: Ordnance Industry Press, 2015: 24-25. (  0) 0)
|
| [2] |
于文满, 何顺禄, 关世义. 舰艇毁伤图鉴[M]. 北京: 国防工业出版社, 1991. YU Wenman, HE Shunlu, GUAN Shiyi. Ship damage illustrated book[M]. Beijing: National Defense Industry Press, 1991. (  0) 0)
|
| [3] |
朱锡, 张振华, 梅志远, 等. 舰船结构毁伤力学[M]. 北京: 国防工业出版社, 2013: 37-43. ZHU Xi, ZHANG Zhenhua, MEI Zhiyuan, et al. Damage mechanics of warship structure subjected to explosion[M]. Beijing: National Defense Industry Press, 2013: 37-43. (  0) 0)
|
| [4] |
甘宏伟, 陈威, 李吉峰, 等. 加筋板架结构与均质靶板等效关系的数值分析[J]. 四川兵工学报, 2010, 31(11): 20-22. GAN Hongwei, CHEN Wei, LI Jifeng, et al. Numerical analysis of equivalent relationship between stiffened plate frame structure and homogeneous target plate[J]. Acta armamentarii, 2010, 31(11): 20-22. (  0) 0)
|
| [5] |
毕广剑, 尹建平, 王志军, 等. 穿甲弹头部结构在侵彻钢板时的跳弹研究[C]//OSEC首届兵器工程大会论文集. 重庆, 中国, 2017: 266-269. BI Guangjian, YIN Jianping, WANG Zhijun, et al. Research on ricochet of armor-piercing projectile head structure when penetrating steel plate[C]//Proceedings of OSEC First Ordnance Engineering Conference. Chongqing, China, 2017: 266-269. (  0) 0)
|
| [6] |
吴普磊, 李鹏飞, 董平, 等. 攻角对弹体斜侵彻多层混凝土靶弹道偏转影响的数值模拟及试验验证[J]. 火炸药学报, 2018, 41(2): 202-207. WU Pulei, LI Pengfei, DONG Ping, et al. Numerical simulation and experimental verification on the influence of angle of attack on ballistic deflection of oblique penetrating multi-layer concrete targets for projectile[J]. Chinese journal of explosives & propellants, 2018, 41(2): 202-207. (  0) 0)
|
| [7] |
段卓平. 半穿甲弹丸对加筋靶板侵彻的终点弹道的实验和理论研究[J]. 爆炸与冲击, 2005, 25(6): 547-552. DUAN Zhuoping. The experimental and theoretical research for end-point trajectory of warhead penetrating ribbings structural target[J]. Explosion and shock waves, 2005, 25(6): 547-552. DOI:10.3321/j.issn:1001-1455.2005.06.011 (  0) 0)
|
| [8] |
BETH R A. Penetration of projectiles in concrete, PB48189[R]. Ballistic Research Laboratory, 1941.
(  0) 0)
|
| [9] |
于辉, 徐峰. 船体加筋板与均质板结构对反舰导弹战斗部穿甲性能影响的对比分析[J]. 广东造船, 2019, 38(4): 27-30. YU Hui, XU Feng. Comparative analysis on armor piercing performance between stiffened plate and homogeneous plate for warhead[J]. Guangdong shipbuilding, 2019, 38(4): 27-30. DOI:10.3969/j.issn.2095-6622.2019.04.008 (  0) 0)
|
| [10] |
姚熊亮, 吴子奇, 王治, 徐振桓. 战斗部对舰船靶标侵彻毁伤效能研究[J]. 哈尔滨工程大学学报, 2019, 40(1): 141-145. YAO Xiongliang, WU Ziqi, Wang zhi, XU Zhenhuan. Study on damage effectiveness of warhead on ship target[J]. Journal of Harbin Engineering University, 2019, 40(1): 141-145. (  0) 0)
|
| [11] |
诺曼·琼斯. 结构冲击[M]. 许骏, 蒋平, 译. 2版. 北京: 国防工业出版社, 2018: 18-46. JONES N. Structural impact[M]. Xu Jun, Jiang Ping, trans. 2nd ed. Beijing: National Defense Industry Press, 2018: 18-46. (  0) 0)
|
| [12] |
杨桂通. 塑性动力学[M]. 3版. 北京: 高等教育出版社, 2012: 147-177. YANG Guitong. Plastic dynamics[M]. 3rd ed. Beijing: Higher Education Press, 2012: 147-177. (  0) 0)
|
| [13] |
吴子奇. 弹目结合的反舰导弹对目标舰船靶标侵彻毁伤研究[D]. 哈尔滨: 哈尔滨工程大学, 2019. WU Ziqi. Study on damage effectiveness of warhead on ship target[D]. Harbin: Harbin Engineering University, 2019. (  0) 0)
|
| [14] |
PONCELET J V. Cours de mecanique industrielle[M]. Paris, 1835.
(  0) 0)
|
| [15] |
吴子奇, 徐振桓, 王志凯, 等. 基于典型舰船结构特征的陆地靶标设计方案[J]. 中国舰船研究, 2018, 13(3): 125-130. WU Ziqi, XU Zhenhuan, WANG Zhikai, et al. Land target design scheme based on typical ship structure features[J]. Chinese journal of ship research, 2018, 13(3): 125-130. (  0) 0)
|
| [16] |
ROSENBERG Z, KOSITSKI R. The hole diameter in metallic plates impacted by hypervelocity projectiles[J]. International journal of impact engineering, 2017, 102: 147-155. (  0) 0)
|
| [17] |
MASRI R. Ballistically equivalent aluminium targets and the effect of hole slenderness ratio on ductile plate perforation[J]. International journal of impact engineering, 2015, 80: 45-55. DOI:10.1016/j.ijimpeng.2015.01.003 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


