2. 海洋信息获取与安全工信部重点实验室(哈尔滨工程大学), 黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001
2. Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Harbin 150001, China;
3. College of Underwater Acoustic Engineering Harbin Engineering University, Harbin 150001, China
在主动声呐的目标识别系统设计中,目标特征的提取以及技术的选择通常是处于水中回波数据采集和识别判决2个环节之间[1-2]。因此,目标回波特征的提取结果关乎声呐识别系统的好坏。根据水下声传播理论和目标回波的物理特性,汤渭霖[3]提出了水下目标回波的亮点模型,该模型将具有复杂形状目标的回波看成各子目标回波信号的干涉叠加,每个子目标回波即一个亮点。亮点的特征通常与目标的姿态、表面形状、尺度有较大关系,研究如何有效精确提取目标回波亮点的方法,就成为了提高声呐识别能力的关键环节[4]。STFT和WVD时频分析方法是提取目标回波亮点的常用技术[5-7]。STFT的基本思想是借助滑动窗函数将信号分成许多的时间间隔,用傅里叶变换获得信号的局部频谱。由于窗函数的固有结构,限制了STFT的时频分辨能力,最终导致STFT时频域图像“模糊”。利用长短时组合窗函数来提高STFT的时频聚集性,依然受Heisenberg不确定性原理制约[8]。WVD达到了不确定性原理下界,对单分量信号具有最佳分辨率。但是,对于多分量信号,由于二次型时频分布的本质,WVD时频可读性较差[9]。本文根据STFT的特性,提出了一种改进方法进行目标亮点特征提取。通过分析变换原理,建立STFT的卷积模型,并结合图像去模糊理论,提高STFT时频分辨能力同时抑制噪声背景,为目标亮点提取和识别提供保障。
1 水中目标亮点提取方法 1.1 目标回波多亮点模型在水下进行目标回波数据采集时,由于不同目标的形状、姿态、尺度各异,目标产生的散射声波常常可以由几个较强信号的叠加表示,每一个信号分量即一个目标亮点。不同目标具有不同的亮点组合形式。
假设发射信号波形为:
| $ {p_0}\left( t \right) = a\left( t \right){{\rm{e}}^{{\rm{j}}wt}} $ | (1) |
式中:a(t)为信号包络; w为信号载频。
那么对于具有单一亮点特征(如单一刚性球体)的目标,其回波具有:
| ${p_1}\left( t \right) = \frac{{{{\rm{e}}^{{\rm{j}}kr}}}}{r}A{p_0}\left( {t - \tau } \right){{\rm{e}}^{{\rm{j}}\varphi }} $ | (2) |
式中:A为该亮点的幅度响应因子; τ为该亮点的时延,由声波的行程差决定; φ为该亮点的相位响应因子。这3个参数可以表征目标的特性,但是由于水下环境复杂,φ往往不易测量,而A和τ的测量稳定,常被选为识别目标的特征参数。
同理,复杂结构的目标回波具有多亮点特征,其回波为多个亮点的叠加形式:
| $ {p_2}\left( t \right) = \frac{{{{\rm{e}}^{{\rm{j}}kr}}}}{r}\sum\limits_{i = 1}^N {{A_i}{p_0}(t - {\tau _i}){{\rm{e}}^{{\rm{j}}{\varphi _i}}}} $ | (3) |
式中N为目标亮点的数量。
因此,如何通过有效的手段确定目标亮点的个数,进而求得各个亮点的特征参数,是决定识别系统识别成败的关键。
1.2 短时傅里叶变换若目标回波为p(t),其STFT幅度谱定义为:
| $ {\rm{STFT}}\left( {t, w} \right) = \left| {\int {p\left( \tau \right){g^*}\left( {\tau - t} \right){e^{ - {\rm{j}}w\tau }}{\rm{d}}\tau } } \right| $ | (4) |
式中:g(t)为窗函数,具有时域对称结构。
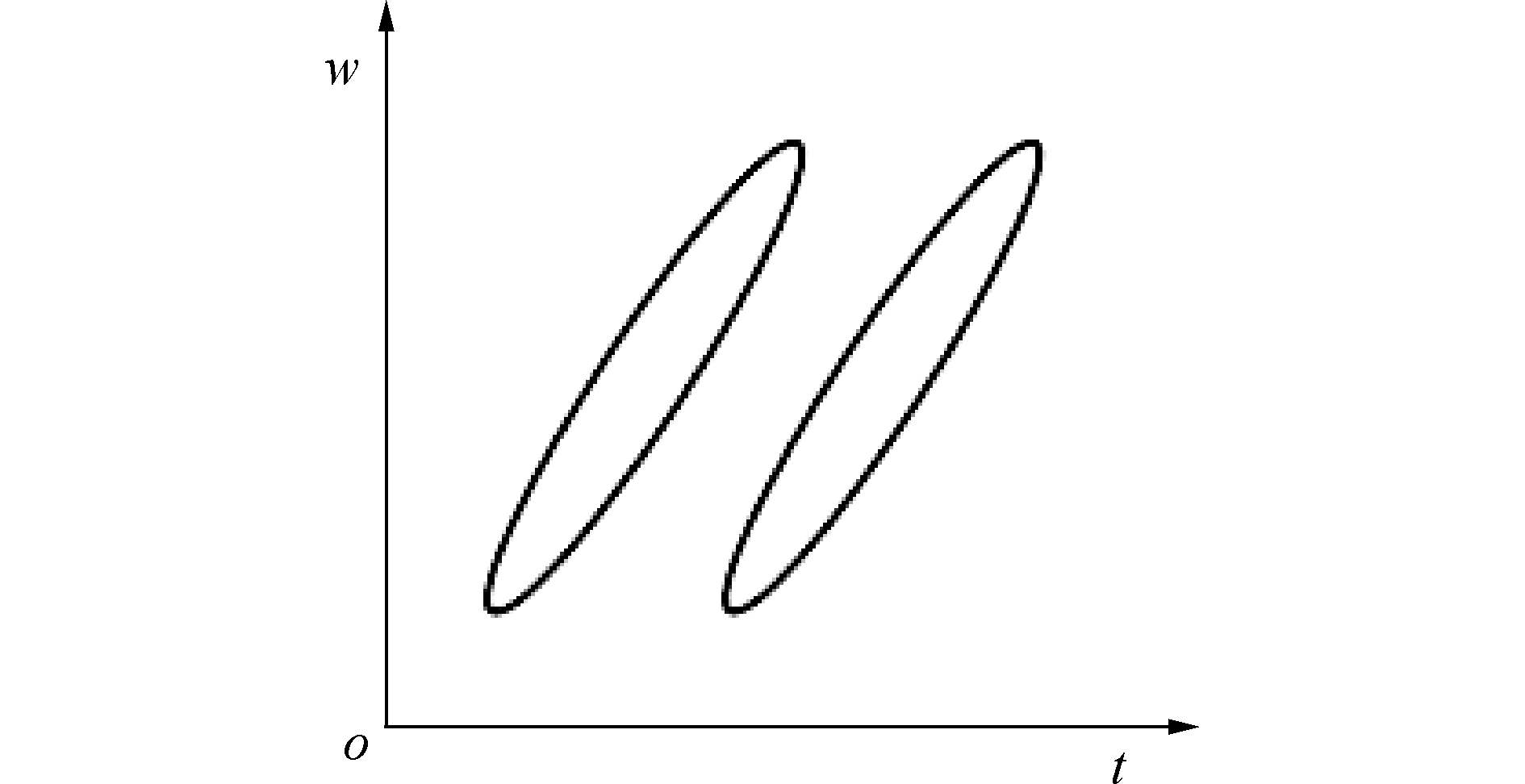
以LFM脉冲信号为例,当接收目标回波含有2个亮点时,经过短时傅里叶变换处理后的幅度谱示意如图 1所示。
|
Download:
|
| 图 1 目标回波中含有2个亮点的幅度谱 Fig. 1 The sketch of STFT of target echo with two highlight | |
窗函数对STFT的时频定位功能有着重要的影响:窗函数的时间宽度愈短,则获取“局部频谱”时所需要的分析时间愈短,STFT的频率分辨能力愈低;反之,窗函数的时间宽度愈长,STFT的频率分辨能力愈高,但同时将远离分析时刻的信号纳入到分析窗口中,导致STFT的时间分辨能力降低。
因此,对于给定的窗函数,短时傅里叶变换的时间分辨能力与频率分辨能力是不可调和的,通过短时傅里叶变换获取的幅度谱是模糊的,如何提高短时傅里叶变换的时频分辨能力是获取目标回波亮点特征的重要问题。
1.3 去模糊方法(RLSTFT)根据1.2节的分析,提出了一种新的方法RLSTFT来提高STFT的时频定位能力。
在一个短时窗长度内的目标回波的傅里叶变换后的频谱为STFT(w),而信号实际的频谱为RLSTFT(w),图像的模型可以表示为:
| $ {\rm{STFT}}(w) = {\rm{RLSTFT}}(w) \otimes H(w) + n(w) $ | (5) |
| $ {\rm{RLSTFT}}(w) = \sum\limits_{i = 1}^N {{A_i}\delta (w - {w_i})} $ | (6) |
| $ H(w) = \left| {\int {g\left( t \right){{\rm{e}}^{ - {\rm{j}}wt}}{\rm{d}}t} } \right| $ | (7) |
式中:*表示卷积运算; n为噪声。
以矩形窗函数为例:
| $ \left\{ \begin{array}{l} g\left( t \right) = u\left( {t + \frac{T}{2}} \right) - u\left( {t - \frac{T}{2}} \right)\\ H(w) = \left| {\frac{{{\rm{sin}}({\rm{ \mathsf{ π} }}w)}}{{{\rm{ \mathsf{ π} }}w}}} \right| \end{array} \right. $ | (8) |
从本质上来说,短时傅里叶变换是建立在窗函数的基础上求得的。因此,提高短时傅里叶变换的时频分辨能力必须解决点散射函数造成的图像“模糊”。Richardson和Lucy以及其他学者曾提出通过迭代算法进行图像去模糊[10-15]。去模糊理论被广泛的应用于工业、天文及物理领域[16-18]。本文求解信号真实的时频分布幅度谱的步骤可表示为:
| ${\rm{RLSTF}}{{\rm{T}}_{k + 1}} = \left[ {H \oplus \frac{{{\rm{STFT}}}}{{H \otimes {\rm{RLSTF}}{{\rm{T}}_k}}}} \right]{\rm{RLSTF}}{{\rm{T}}_k} $ | (9) |
式中:
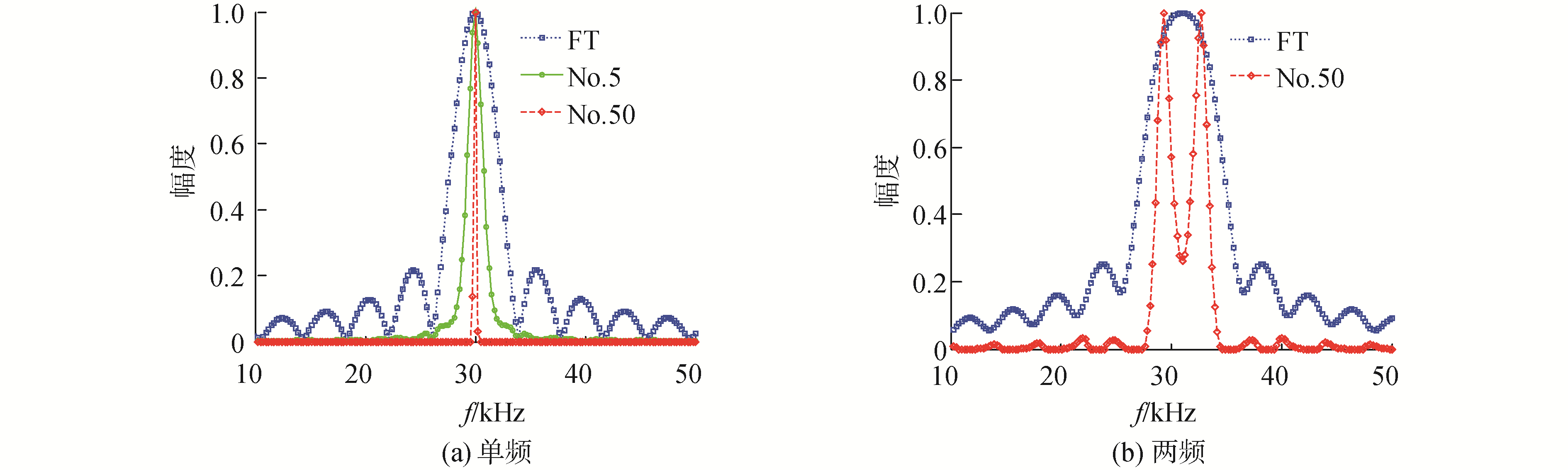
分析参数:CW信号频率30 kHz,采样频率1 MHz,矩形窗长度256点,FFT长度4 096点。
在分析窗内的结果如图 2(a)所示。随着迭代次数的增加,“频谱泄露”得到了有效的抑制,当次数为50次时,频谱近似为一个冲激函数。图 2(b)展示了在一个分析窗内具有2个频率的信号的频谱,常规FFT受旁瓣干扰,导致无法分辨出2个频谱,RLSTFT能够抑制旁瓣,在不增加FFT点数的情况下,具有更高的频率分辨能力。
|
Download:
|
| 图 2 短时窗内信号频谱 Fig. 2 The spectrum for CW signal in a short time window | |
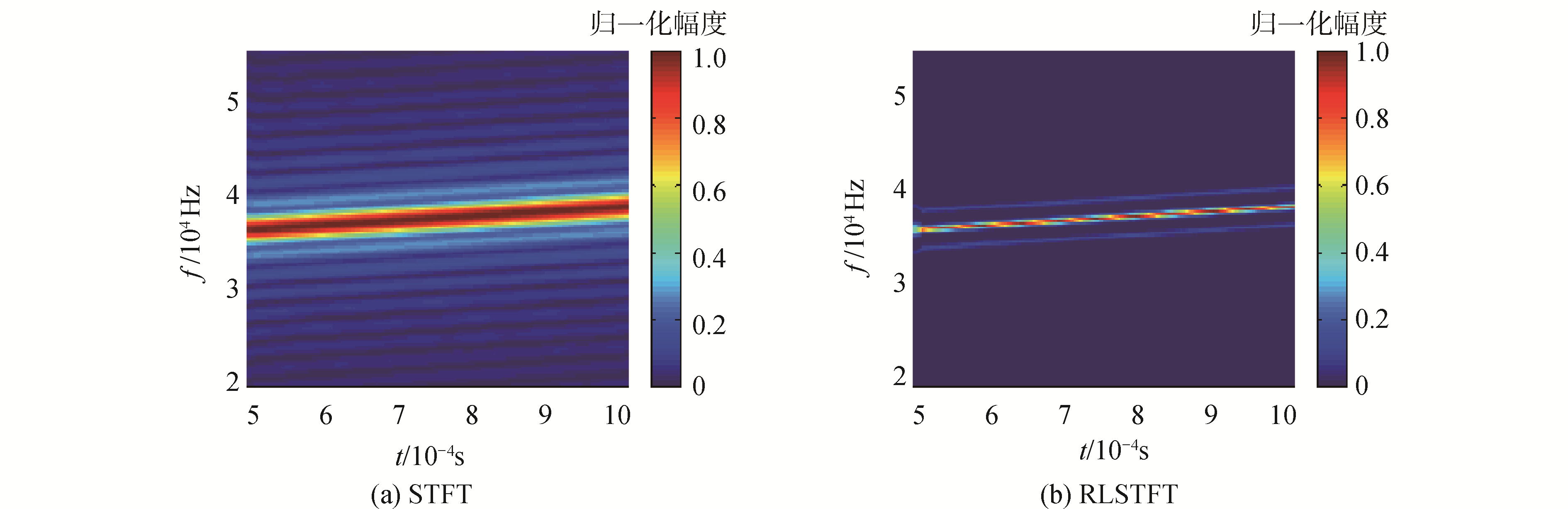
分析参数:LFM信号调谐频率35~40 kHz,采样频率1 MHz,矩形窗长度256点,FFT长度4 096点。结果如图 3所示,其中RLSTFT迭代次数为50次。
|
Download:
|
| 图 3 LFM信号的时频分布幅度谱 Fig. 3 The amplitude spectrum for LFM signal base on time-frequency analysis | |
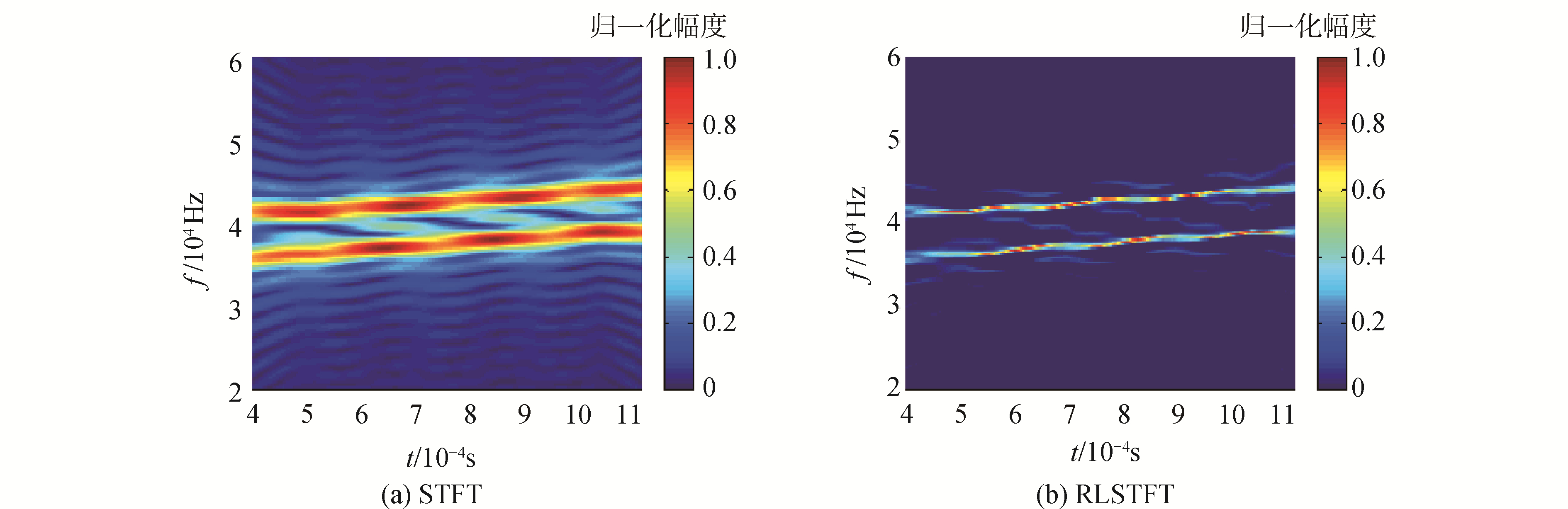
图 4展示了2个LFM信号的时频分布幅度谱,调谐频率分别为35~40 kHz和40~45 kHz,幅度谱中的旁瓣得到了抑制。
|
Download:
|
| 图 4 2个LFM信号的时频分布幅度谱 Fig. 4 The amplitude spectrum for two LFM signal base on time-frequency analysis | |
根据2.1节的比较可知,RLSTFT比FFT具有更优良的频率分辨能力。本节将具体研究RLSTFT在不同频率间隔Δf下的分辨能力。我们对不同频率间隔的信号进行频谱分析,FFT点数N=4 096,采样频率fs=1 MHz,FFT固有分辨率为244 Hz,两频点间隔Δf从24.4 kHz(为固有分辨率的100倍)逐渐减小到0 Hz,结果如图 5所示。图 5(a)显示的是FFT的结果,图 5(b)和5(c)分别展示了迭代次数为5和50次的结果。

|
Download:
|
| 图 5 不同频率间隔条件下的频率分辨性能 Fig. 5 The results of spectrum analysis in frequency spacing | |
分析参数:参数与2.2节一致,时域信噪比分别为0 dB和-10 dB,仿真结果如图 6所示。可以发现,RLSTFT能够提升频率分辨能力的同时有效抑制了噪声背景,有利于目标回波亮点的检测。

|
Download:
|
| 图 6 不同强度白噪声背景下的处理结果 Fig. 6 The results of time-frequency analysis in noise | |
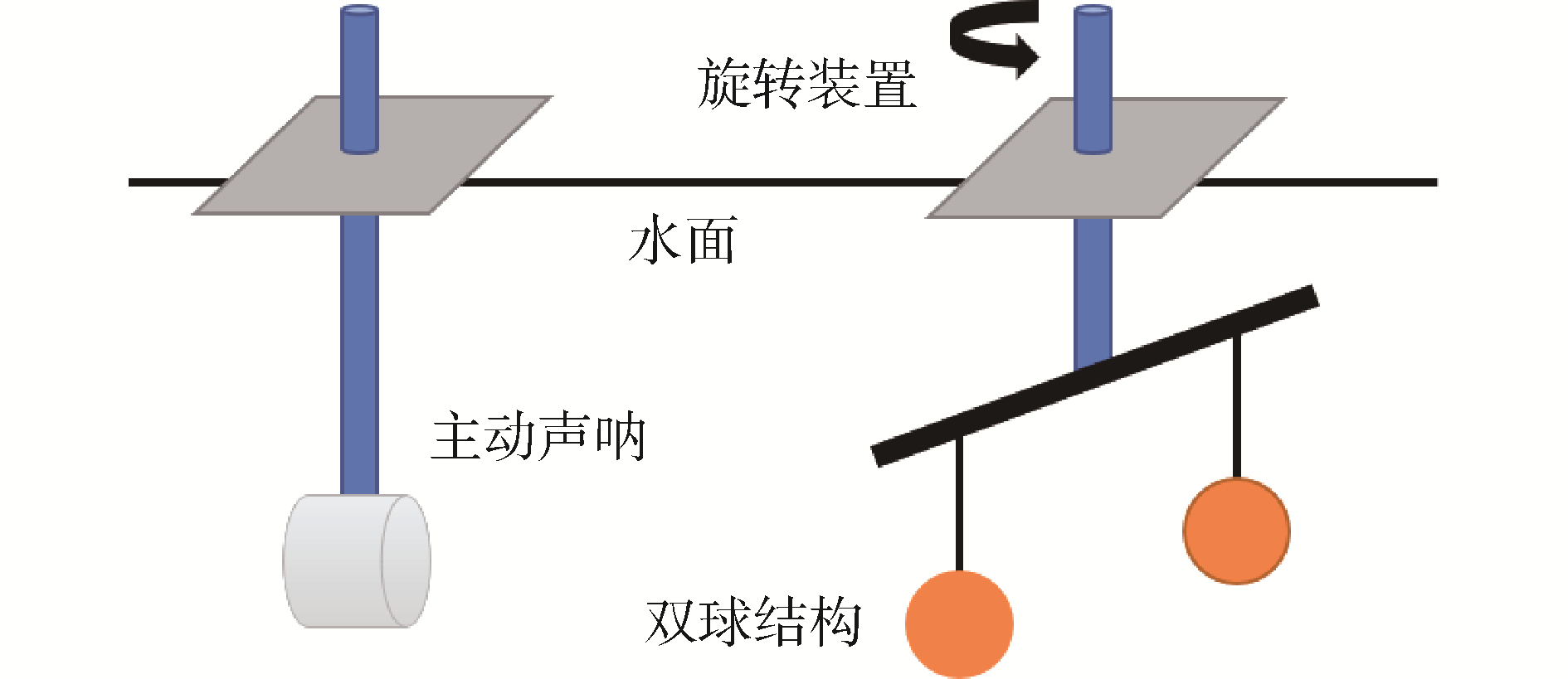
在松花江水域进行目标回波的采集工作,图 7是测量试验简图。被测水中目标是由2个具有钢制外壳的空心球体组成的结构,两球直径为均为0.1 m,间距为0.8 m。声呐距离目标结构几何中心4.5 m,发射信号为LFM脉冲信号,频率为35~40 kHz,采样频率为1 MHz,脉冲周期为20 ms,填充宽度0.5 ms(500点)。
|
Download:
|
| 图 7 目标回波测试简图 Fig. 7 Schematic diagram of experimental arrangements | |
|
Download:
|
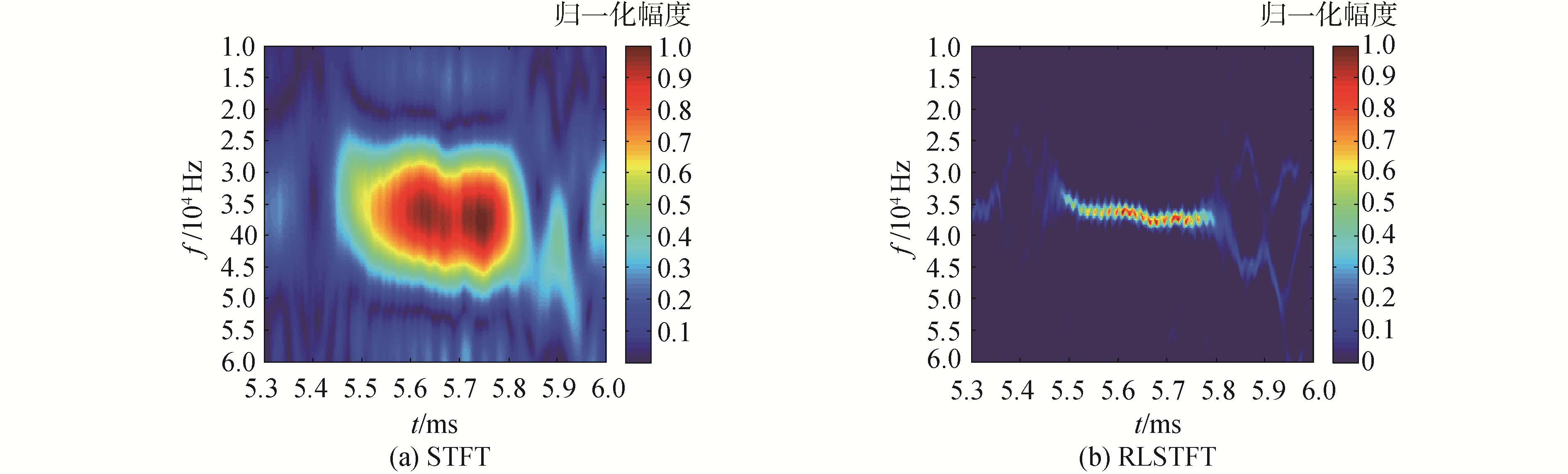
| 图 8 单球试验结果 Fig. 8 The results of time-frequency analysis using one ball | |
在松花江水首先进行了水下单球目标的回波亮点提取,窗函数为64点矩形窗,FFT点数为4 096点,RLSTFT迭代次数为50次。目标回波的时频幅度谱显示RLSTFT频率分辨能力远远优于STFT。
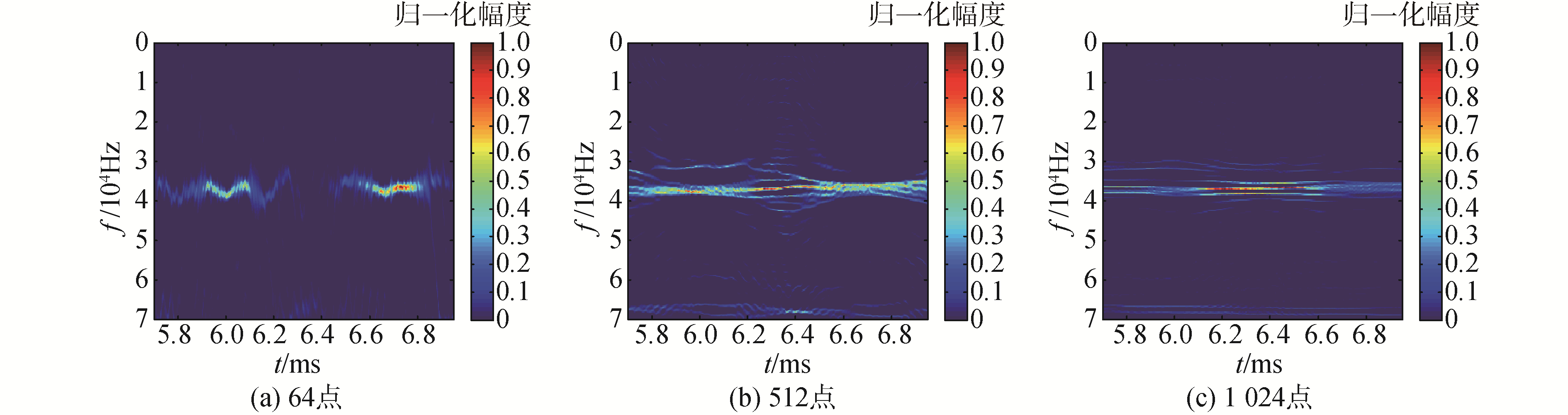
3.3 双球目标亮点测量试验双球目标试验相对于单球试验添加了窗函数长度对试验的影响,分别设置矩形窗函数长度为64,512和1 024点,STFT以及RLSTFT的处理结果如图 9和图 10所示。

|
Download:
|
| 图 9 双球STFT试验结果 Fig. 9 The results of STFT using two balls | |
|
Download:
|
| 图 10 双球RLSTFT试验结果 Fig. 10 The results of RLSTFT using two balls | |
对比图 9,随着窗函数长度的增加,STFT的频率分辨能力在增加,但是其时间分辨能力下降。特别是在窗长度为1 024(大于双球回波时间差)时,STFT无法分辨2个目标。对比图 9(c)和图 10(a),在STFT的窗函数长度是RLSTFT的16倍时,STFT的时间分辨力已经无法满足2个目标亮点分辨要求。而RLSTFT在保证时间分辨能力的前提下,其频率分辨能力依然优于STFT。
4 结论1) 继承了STFT的特性,抑制带外能量泄漏;
2) 与STFT相比具有更高的时频定位能力,同时有效降低噪声背景,分辨多亮点目标回波。计算机仿真对比了在不同信噪比、不同信号类型下RLSTFT与STFT的估计性能,证明了RLSTFT的优越性。松花江实验验证了RLSTFT算法能够获得更加清晰的时频分布,具有更好的时频分辨能力。
| [1] |
辛光红, 杨波. 基于声呐图像处理的船用水下目标识别技术研究[J]. 舰船科学技术, 2018, 40(4): 115-117. XIN Guanghong, YANG Bo. Research on underwater target recognition technology based on sonar image processing[J]. Ship science and technology, 2018, 40(4): 115-117. (  0) 0)
|
| [2] |
宋波. 水下目标识别技术的发展分析[J]. 舰船电子工程, 2014, 34(4): 168-173. SONG Bo. Development analysis of the underwater target recognition technology[J]. Ship electronic engineering, 2014, 34(4): 168-173. (  0) 0)
|
| [3] |
汤渭霖. 声呐目标回波的亮点模型[J]. 声学学报, 1994, 19(2): 92-100. TANG Weilin. Highlight model of echoes from sonar targets[J]. Acta acustica, 1994, 19(2): 92-100. (  0) 0)
|
| [4] |
陈云飞, 李桂娟, 王振山, 等. 水中目标回波亮点统计特征研究[J]. 物理学报, 2013, 62(8): 084302. CHEN Yunfei, LI Guijuan, WANG Zhenshan, et al. Statistical feature of underwater target echo highlight[J]. Acta physica sinica, 2013, 62(8): 084302. (  0) 0)
|
| [5] |
朱广平, 王飞, 孙辉. 时频域滤波沉底目标亮点特征提取方法研究[J]. 哈尔滨工程大学学报, 2015, 36(5): 616-622. ZHU Guangping, WANG Fei, SUN Hui. Extraction method of highlight features of a bottom target based on time-frequency dominant filtering[J]. Journal of Harbin Engineering University, 2015, 36(5): 616-622. (  0) 0)
|
| [6] |
张光普, 梁国龙, 范展, 等. 瞬时相关积分法及其在线谱检测中的应用[J]. 兵工学报, 2011, 32(1): 69-73. ZHANG Guangpu, LIANG Guolong, FAN Zhan, et al. Instantaneous correlation integral algorithm and application in the detection of the line spectrum[J]. Acta armamentarii, 2011, 32(1): 69-73. (  0) 0)
|
| [7] |
李秀坤, 杨阳, 孟祥夏. 水下目标回波与混响的时频形态特征域盲分离[J]. 声学学报, 2017, 42(2): 169-177. LI Xiukun, YANG Yang, MENG Xiangxia. Morphological characteristics separation of underwater target echo and reverberation in time and frequency domain[J]. Acta acustica, 2017, 42(2): 169-177. (  0) 0)
|
| [8] |
肖瑛, 冯长建. 组合窗函数的短时傅里叶变换时频表示方法[J]. 探测与控制学报, 2010, 32(3): 43-47. XIAO Ying, FENG Changjian. A time-frequency representation method of STFT with combining window functions[J]. Journal of detection & control, 2010, 32(3): 43-47. (  0) 0)
|
| [9] |
汪伟, 谢皓臣, 梁光明, 等. 加窗离散傅里叶变换性能分析和比对[J]. 现代电子技术, 2012, 35(3): 115-118. WANG Wei, XIE Haochen, LIANG Guangmin, et al. Performance analysis and comparison of windowed discrete Fourier transform[J]. Modern electronics technique, 2012, 35(3): 115-118. (  0) 0)
|
| [10] |
闻毅. Lucy-Richardson算法在模糊图像复原中的应用[J]. 智能计算机与应用, 2015, 5(1): 95-97. WEN Yi. Application of lucy-richardson algorithm in the fuzzy image restoration[J]. Intelligent computer and applications, 2015, 5(1): 95-97. (  0) 0)
|
| [11] |
RICHARDSON W H. Bayesian-based iterative method of image restoration[J]. Journal of the optical society of America, 1972, 62(1): 55-59. DOI:10.1364/JOSA.62.000055 (  0) 0)
|
| [12] |
王志伟, 缪磊磊, 吴晨健. 噪声自适应射影运动Richardson-Lucy去模糊算法研究[J]. 电脑知识与技术, 2017, 13(31): 192-195. WANG Zhiwei, MIAO Leilei, WU Chenjian. Noise adaptive projective motion richardson-lucy deblurring algorithm research[J]. Computer knowledge and technology, 2017, 13(31): 192-195. (  0) 0)
|
| [13] |
LUCY L B. An iterative technique for the rectification of observed distributions[J]. Astronomical journal, 1974, 79: 745-754. DOI:10.1086/111605 (  0) 0)
|
| [14] |
赵博, 张文生, 丁欢. 基于Richardson-Lucy的图像去模糊新算法[J]. 计算机工程与应用, 2011, 47(34): 1-4, 77. ZHAO Bo, ZHANG Wensheng, DING Huan. Novel image deblurring algorithm based on Richardson-Lucy[J]. Computer engineering and applications, 2011, 47(34): 1-4, 77. (  0) 0)
|
| [15] |
BIGGS D S C, ANDREWS M. Acceleration of iterative image restoration algorithms[J]. Applied optics, 1997, 36(8): 1766-1775. DOI:10.1364/AO.36.001766 (  0) 0)
|
| [16] |
朱非甲, 金鹏. 面向工业检测的图像快速去直线运动模糊方法[J]. 哈尔滨工业大学学报, 2018, 50(9): 123-129. ZHU Feijia, JIN Peng. Fast moving line motion de-blurring for image detection of industrial inspection[J]. Journal of Harbin Institute of Technology, 2018, 50(9): 123-129. (  0) 0)
|
| [17] |
SOUZA E S, SILVANI M I, ALMEIDA G L, et al. Determination of a neutron beam divergence after the rocking curve concept using Richardson-Lucy's unfolding algorithm[J]. Nuclear instruments and methods in physics research section A:accelerators, spectrometers, detectors and associated equipment, 2018, 908: 172-181. DOI:10.1016/j.nima.2018.08.055 (  0) 0)
|
| [18] |
INGARAMO M, YORK A G, HOOGENDOORN E, et al. Richardson-Lucy deconvolution as a general tool for combining images with complementary strengths[J]. Chemphyschem, 2014, 15(4): 794-800. DOI:10.1002/cphc.201300831 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


