随着雷达体制的不断发展，电子侦察面临的电磁环境越来越复杂，传统的信道化数字接收机正面临着各种问题，如采样数据量过大，跨信道信号的处理等，增加了后续信号处理的难度^[1]。压缩采样理论的提出为上述问题提供了解决方法^[2-3]。文献[4]提出的调制宽带转换器结构可对频域稀疏的多带信号进行压缩采样，并提出了该结构下的信号重构方案。文献[5]将调制宽带转换器结构扩展到离散数字域构建了基于调制宽带转换器的压缩采样数字接收机，该接收机可以灵活解决跨信道信号问题，且经过压缩采样获得的数据量远少于传统的信道化数字接收机。由于调制宽带转换器结构不会提高各支路的信噪比，因此传统的载频恢复算法，如正交匹配追踪(orthogonal matching pursuit，OMP)算法，需要的运算量过大，且低信噪比下恢复效果差。为解决上述问题，文献[6]提出基于阵列结构的调制宽带转换器结构，并提出了该结构下的载频和到达角(direction of arrival, DOA)联合恢复算法，且证明了该结构具有更好的抗噪声性能。文献[7]提出一种基于参考阵元的均匀阵列调制宽带转换器结构，并利于相关性检验的方法完成多信号的载频和DOA估计；然而所提出的结构较为复杂，且提出的算法依旧是以重构算法为基础，需要的运算量较大。文献[8]提出了基于均匀阵列结构的压缩采样数字接收机，在该结构中利用循环移位的伪随机序列来构造特殊的通道间相位差，并直接利用压缩采样数据完成了载频和DOA估计。所提出的方法低信噪比下估计性能较差，为了提高精度必须要增加阵元数，提高了系统的复杂度。稀疏阵列可以利用较少的阵元获得较大的阵列孔径，不仅可以提高测向性能，还可以降低天线的建造成本^[9-12]。文献[13]中提出了一种基于稀疏阵列的接收机结构，可以利用压缩信号数据得到载频和DOA的估计。本文根据稀疏阵列布阵灵活，可以有效减小阵列冗余度的优点，提出了压缩采样稀疏阵列结构，降低了接收系统复杂度，并提出利用多重信号分类算法(multiple signal classification, MUSIC)直接处理压缩采样数据完成载频和DOA的联合估计，减少了后续处理的数据量和处理速率，更易于硬件实现。

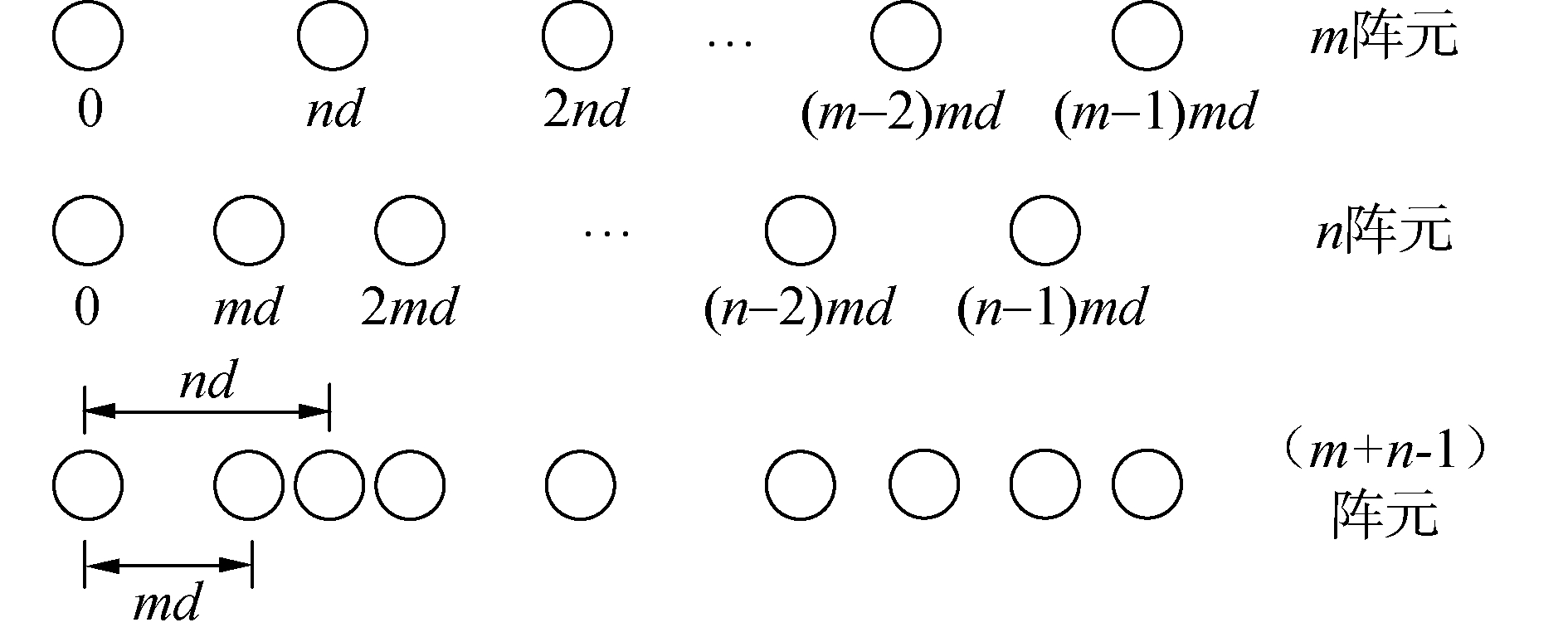
1 系统结构和原理 1.1 稀疏阵列接收信号模型

稀疏阵列有2种特殊的形式，即互质阵列和嵌套阵列。其中互质阵列是由2个不同间距的均匀阵列穿插组合而成，互质阵列结构如图 1所示。

假设其中一个含有m个阵元，阵元间距为nd；另一个含有n个阵元，阵元间距为md，m和n为2个互质的数，且m < n。可以得到2个子阵阵元位置分别表示为D₁={ind, i=0, 1, …, m－1}和D₂={jmd, j=0, 1, …, n－1}。对应虚拟阵元位置为：D_CA={±(in－jm)d, 0≤i≤m－1, 0≤j≤n－1}。

因此得到互质阵列下的导向矢量表示为：

$ \mathit{\boldsymbol{a}}(\theta ) = {\left[ {\begin{array}{*{20}{c}} 1&{{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi md}}{\lambda }{\rm{sin}}{\kern 1pt} {\kern 1pt} \theta }}}&{{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi nd}}{\lambda }{\rm{sin}}{\kern 1pt} {\kern 1pt} \theta }}}& \ldots &{{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi (m - 1)nd}}{\lambda }{\rm{sin}}\theta }}} \end{array}} \right]^{\rm{T}}} $

(1)

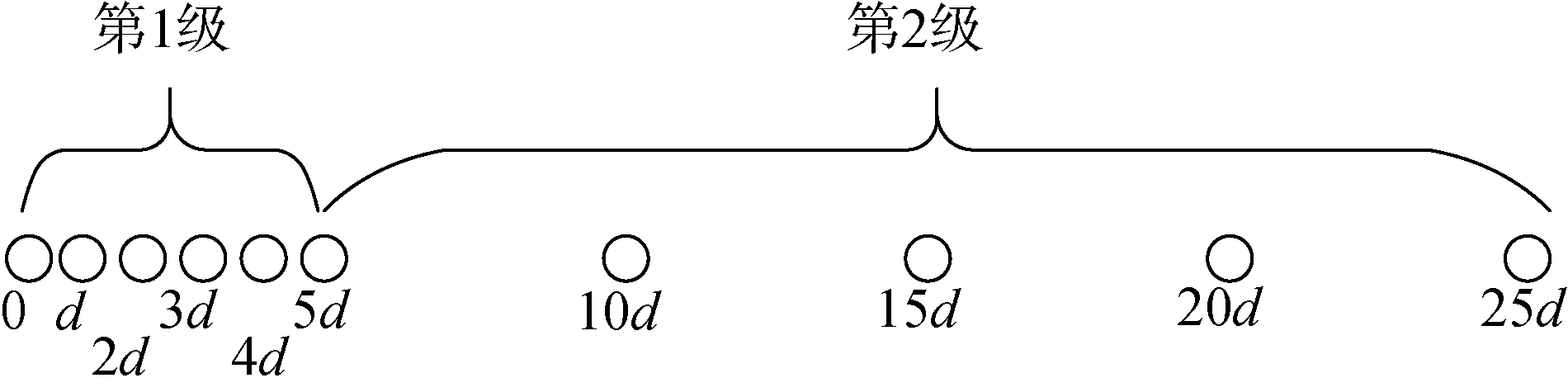
嵌套阵列种类较多，本文只介绍二级嵌套阵列。二级嵌套阵列与互质阵列类似，都是由2个子阵组合而成，其结构如图 2所示。

假设一级子阵含有L₁个阵元，阵元间距为d₁；二级子阵含有L₂个阵元，阵元间距为d₂=(L₁+1)d₁，则一级子阵的阵元位置可以表示为D₁={l₁d₁, l₁=0, 1, …, L₁－1}，二级子阵的阵元位置为D₂={l₂L₁d₁, l₂=1, 2, …, L₂}，对应虚拟阵元位置为：D_NA={nd₁, n=－L, －L+1, …, L－1, L, L=L₂(L₁+1)－1}。

二级嵌套阵列的导向矢量表示为：

$ \begin{array}{l} \mathit{\boldsymbol{a}}(\theta ) = \left[ {\begin{array}{*{20}{l}} 1&{{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi {d_1}}}{\lambda }{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }}}& \cdots &{{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi \left( {{L_1} - 1} \right){d_1}}}{\lambda }{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }}} \end{array}} \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left. {\begin{array}{*{20}{c}} {{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi {L_1}{d_1}}}{\lambda }{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }}}& \cdots &{{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi {L_2}{L_1}{d_1}}}{\lambda }{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }}} \end{array}} \right]^{\rm{T}}} \end{array} $

(2)

由式(1)、(2)可知，互质阵列和嵌套阵列阵元摆放位置不同，由于相同阵元数下，嵌套阵列的虚拟阵元为无孔满阵，因此其性能优于互质阵列。

假设稀疏阵列阵元位置设置为D=[d₁, d₂, …, d_M]d，其中d_i∈Z, i=1, 2, …, M，阵元最小间距d为波长λ的一半。在电子侦察环境中，在绝大多数情况下电子侦察接收机处理的信号情况为单个到达的信号，因此考虑只有1个信号入射到M个阵元的稀疏阵列上，假设入射信号s[n]为复数离散信号，入射角度为θ，因此信号接收模型可以表示为：

$ x[n] = As[n] + \eta [n],n = 1,2, \cdots $

(3)

式中：阵列流形为A=[a(θ)]，导向矢量为a(θ)，为方便后续公式推导，将导向矢量表示为$\mathit{\boldsymbol{a}}\left( \theta \right) = {[{\alpha _1}\left( \theta \right),{\alpha _2}\left( \theta \right), \ldots ,{\alpha _M}\left( \theta \right)]^{\rm{T}}}$；s[n]为远场窄带信号；$ \mathit{\boldsymbol{\eta }}\left[ n \right] = [{\eta _1}n],{\eta _2}\left[ n \right], \ldots ,{\eta _M}{\left[ n \right]^{\rm{T}}}$为均值是0、方差是σ²的独立同分布的高斯白噪声。

1.2 提出的接收机原理

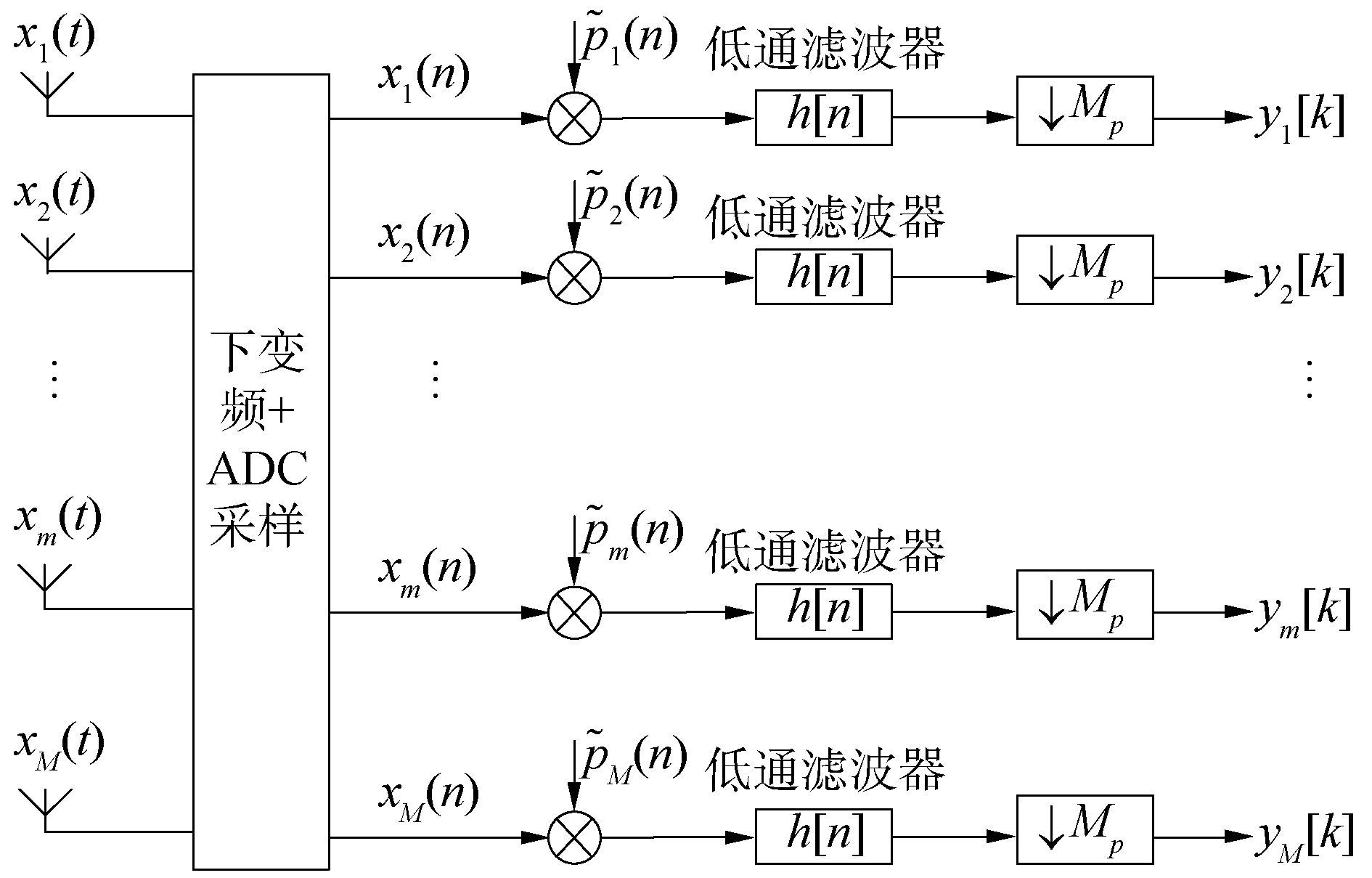
基于稀疏阵列的压缩采样数字接收机结构如图 3所示。在原型压缩采样数字接收机结构前添置稀疏阵列天线，使每个天线对应接收机的一路通道。根据调制宽带转换器原理，接收信号首先经过周期性伪随机序列混频，再经过低通滤波器滤波和降采样操作最终得到压缩采样数据。

选择第m路通道进行说明，伪随机序列$ {{\widetilde{p}}_{m}}\left[ n \right]$选择值为±1的伯努利序列，周期为T_p，每个周期包含M_p为T_pf_NYQ个元素，其中f_NYQ为奈奎斯特采样速率，本结构中同ADC采样率，则$ {{\widetilde{p}}_{m}}\left[ n \right]$可以表示为：

$ {\tilde p_m}[n] = \frac{1}{{{M_p}}}\sum\limits_{l = 0}^{{M_p} - 1} {{P_m}} (l){{\rm{e}}^{{\rm{j}}\frac{{2\pi }}{{{M_p}}}nl}} $

(4)

式中：l为子带索引值；0≤l≤M_p－1表示子带索引；P_m(l)为$ {{\widetilde{p}}_{m}}\left[ n \right]$的离散傅里叶变换系数。

根据式(3)，第m路接收信号可以表示为：

$ {x_m}[n] = {\alpha _m}s[n] + {\eta _m}[n] $

(5)

由伪随机序列的混频特性可知，接收信号经过混频后，频谱将被划分为M_p个子带，每个子带带宽f_p为f_NYQ/M_p。定义混频速率为f_p，保证f_p大于信号带宽避免产生边缘效应，则混频后的信号$ {{\widetilde{x}}_{m}}\left[ n \right]={{x}_{m}}\left[ n \right]{{\widetilde{p}}_{m}}\left[ n \right]$的离散傅里叶变换为：

$ \begin{array}{*{20}{l}} {{{\tilde X}_m}({{\rm{e}}^{{\rm{j}}2\pi f{T_{{\rm{NYQ}}}}}}) = \sum\limits_{n = 0}^{ + \infty } {{x_m}} [n] \cdot {{\tilde p}_m}[n]{{\rm{e}}^{ - {\rm{j}}2\pi fn{T_{{\rm{NYQ}}}}}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{{M_p}}}\sum\limits_{l = 0}^{{M_p} - 1} {{P_m}} (l){X_m}({{\rm{e}}^{{\rm{j}}2\pi {T_{{\rm{NYQ}}}}(f - l{f_p})}})} \end{array} $

(6)

式中X_m(e^{j2πT_NYQ(f－lfp)})是接收信号x_m[n]的离散傅里叶变换。之后混频信号经过截止频率为f_p/2的理想滤波器h[n]进行滤波并以速率f_s=f_p进行采样，可以得到最终的压缩采样数据，可以表示为：

$ \begin{array}{*{20}{l}} {{y_m}[k] = {{\{ ({x_m}[n] \cdot {{\tilde p}_m}[n]) * h[n]\} }_{ \downarrow {M_p}}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left\{ {\frac{1}{{{M_p}}}\sum\limits_{l = 0}^{{M_p} - 1} {{P_m}} (l){{\rm{e}}^{{\rm{j}}\frac{{2\pi }}{{{M_p}}}nl}}{x_m}[n]} \right\}}_{ \downarrow {M_p}}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{l = 0}^{{M_p} - 1} {P_m^\prime } (l){a_m}(\theta )\bar s[k] + {{\bar \eta }_m}[k]} \end{array} $

(7)

式中{·}_↓Mp表示降采样操作；P′_m(l)=P_m(l)/M_p；s[k]是信号经过降采样后得到的压缩采样数据；η_m[k]为噪声的压缩采样数据。根据文献[5]中的分析，该接收机不会提高通道信噪比。

根据式(7)，第m路输出的离散傅里叶形式为：

$ \begin{array}{*{20}{l}} {{Y_m}({{\rm{e}}^{{\rm{j}}2\pi f{T_s}}}) = \sum\limits_{k = 0}^{ + \infty } {{y_m}} [k]{{\rm{e}}^{ - {\rm{j}}2\pi fk{T_s}}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{l = 0}^{{M_p} - 1} {{\alpha _m}} (\theta )P_m^\prime (l)S({{\rm{e}}^{{\rm{j}}2\pi {T_{NYQ}}(f - l{f_p})}}) + {N_m}({{\rm{e}}^{{\rm{j}}2\pi f{T_s}}})} \end{array} $

(8)

其中$ f\in {{F}_{s}}, {{F}_{s}}\underline{\underline{\Delta }}[0, {{f}_{p}}]$。

与文献[5]中的原型压缩采样数字接收机输出相对比发现，所提出的基于稀疏阵列的压缩采样数字接收机保留了原型接收机的优点，即可以解决跨信道问题和减少采样数据量。由于设计的每个子带的带宽大于信号的带宽，因此信号的真实载频只存在于某一未知子带l′(0≤l′≤M_p－1)中，即信号能量集中于子带l′，忽略其他子带，第m路输出为：

$ \begin{array}{l} \begin{array}{*{20}{l}} {{y_m}[k] = {{\{ ({x_m}[n] \cdot {{\tilde p}_m}[n]) * h[n]\} }_{ \downarrow {M_p}}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left\{ {\frac{1}{{{M_p}}}{P_m}({l^\prime }){{\rm{e}}^{{\rm{j}}\frac{{2\pi }}{{{M_p}}}n{l^\prime }}}{x_m}[n]} \right\}}_{ \downarrow {M_p}}} = } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P_m^\prime ({l^\prime }){a_m}(\theta )\bar s[k] + {{\bar \eta }_m}[k] \end{array} $

(9)

从式(9)可以看出，信号经过混频后丢失了真实的载频，且接收机第m路和第m－1路通道间存在未知的相位差${{{P}'}_{m}}\left( {{l}'} \right){{a}_{m}}\left( \theta \right)/{{{P}'}_{m-1}}\left( {{l}'} \right){{a}_{m-1}}\left( \theta \right) $，利用传统方法直接对接收机输出进行处理将无法得到信号真实频率和真实DOA。

2 载频和到达角联合估计算法

本节介绍如何利用MUSIC算法实现载频和DOA联合估计。根据式(9)可以得到整个系统的输出：

$ \mathit{\boldsymbol{y}}[k] = \mathit{\boldsymbol{P}} \cdot \mathit{\boldsymbol{A}}\bar s[k] + \mathit{\boldsymbol{\eta }}[k] $

(10)

其中$ \mathit{\boldsymbol{P}} = {[{P'_1}\left( {l\prime } \right),{P'_2}\left( {l\prime } \right), \ldots ,{P'_M}\left( {l\prime } \right)]^{\rm{T}}}$，当混频序列被确定时，矩阵P通过对混频序列做离散傅里叶变换获得；A为阵列流形矩阵；$ \mathit{\boldsymbol{\eta }}\left[ k \right] = {\left[ {[{{\bar \eta }_1}k], {{\bar \eta }_2}\left[ k \right], \ldots , {{\bar \eta }_M}\left[ k \right]} \right]^{\rm{T}}}$为压缩噪声矩阵；·表示Hadamard积。

对比式(3)，式(10)可视为是压缩采样数据的阵列接收模型，定义压缩采样数据的阵列流形为${\mathit{\boldsymbol{A}}_{cs}} = \mathit{\boldsymbol{P}} \cdot \mathit{\boldsymbol{A}} = \left[ {{\mathit{\boldsymbol{a}}_{cs}}\left( {\theta , l\prime } \right)} \right] $。通过式(10)可以得到压缩采样数据的协方差矩阵为：

$ {\mathit{\boldsymbol{R}}_y} = {\rm{E}}\{ \mathit{\boldsymbol{y}}{\mathit{\boldsymbol{y}}^{\rm{H}}}\} = {\mathit{\boldsymbol{A}}_{cs}}{\mathit{\boldsymbol{R}}_s}\mathit{\boldsymbol{A}}_{cs}^{\rm{H}} + {\sigma ^2}/{M_p}\mathit{\boldsymbol{I}} $

(11)

式中：E{·}表示求期望操作；R_s=E{ss^H}。由于实际采样的快拍数有限，因此式(11)可以表示为：

$ {\mathit{\boldsymbol{R}}_y} = \frac{1}{K}\sum\limits_{m = 0}^{K - 1} \mathit{\boldsymbol{y}} [k]{\mathit{\boldsymbol{y}}^{\rm{H}}}[k] $

(12)

式中K表示压缩采样数据的快拍数。

对R_y进行特征值分解可以得到空间谱估计为：

$ {P_{{\rm{ MUSIC }}}}(\theta ,{l^\prime }) = \frac{1}{{\mathit{\boldsymbol{a}}_{cs}^{\rm{H}}(\theta ,{l^\prime }){\mathit{\boldsymbol{U}}_N}\mathit{\boldsymbol{U}}_N^{\rm{H}}{\mathit{\boldsymbol{a}}_{cs}}(\theta ,{l^\prime })}} $

(13)

式中U_N表示由最小特征值对应的特征矢量张成的阵列压缩采样噪声子空间。

压缩采样数据丢失了真实频率，对压缩采样数据进行快速傅里叶(fast Fourier transformation，FFT)运算^[14]，求得信号的基带频率f_b，再根据混频特性可知信号真实频率f_c和基带频率的关系：

$ {f_c} = {f_p}{l^\prime } + {f_b} $

(14)

对式(13)所得空间谱，分别对子带索引l′和角度θ进行遍历，可得到载频和DOA联合估计：

$ (\theta ,{f_c}) = {\rm{ar}}{{\rm{g}}_{(f,\theta )}}{\rm{min}}{\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{a}}_{cs}^{\rm{H}}(\theta ,{f_c}){\mathit{\boldsymbol{U}}_N}\mathit{\boldsymbol{U}}_N^{\rm{H}}{\mathit{\boldsymbol{a}}_{cs}}(\theta ,{f_c}) $

(15)

由于各通道输出的基带频率相同，可利用所有通道的输出，即利用所有通道的压缩采样数据来进行基带频率估计，以此获得更高的频率估计精度。

3 载频和到达角联合估计仿真实验

假设单个信号入射到阵元数M为10的嵌套阵列上，2个子阵个数分别为L₁=5, L₂=5，阵元位置D=[1, 2, 3, 4, 5, 6, 12, 18, 24, 30]d, 阵元最小间距d为λ/2。奈奎斯特采样率f_NYQ为1.2 GHz；混频序列采用值为±1的伯努利序列，每个周期元素个数M_p为100，则每个子带带宽f_p=f_s/M_p为12 MHz；理想滤波器截至频率为f_p/2，降采样速率f_s=f_p=12 MHz。

仿真实验1：入射信号频率f_c=800 MHz，入射角θ为5°，信噪比为20 dB，经过压缩后信号快拍数C为200；阵列结构选择嵌套阵列，阵元个数M为10，2个子阵个数分别为L₁为5, L₂为5，阵元位置D为[1, 2, 3, 4, 5, 6, 12, 18, 24, 30]d, 阵元最小间距d为λ/2。图 4所示为压缩采样数据的MUSIC谱。

从图中可以得知，谱峰位置处的横纵坐标即为载频和DOA的估计值，因此通过搜索谱峰的方法获得载频和DOA估计。该图也证明了所提出的载频和DOA联合估计算法的正确性。

利用均方根误差(root mean squared error，RMSE)计算算法抗噪声性能。均方根误差为：

$ {E_{{\rm{RMSE}}}} = \sqrt {\frac{1}{N}\sum\limits_{n = 1}^N {{{(\alpha _n^\prime - \alpha )}^2}} } $

(16)

式中：N为蒙特卡洛独立实验的次数；α′_n为算法求得的估计值；α为实际值。

仿真实验2：由前面的分析可知，实际频率估计的性能受2个因素的影响，即FFT算法求得的基带频率和MUSIC谱峰搜索求得的子带索引。因此，本实验分别对压缩采样数据的基带频率估计和MUSIC谱峰搜索得到子带索引估计进行实验。

假设入射信号为载频随机、角度随机的远场窄带信号，载频范围为f_c∈(700 MHz, 1 000 MHz)，精度为1 MHz，入射角度范围θ∈(－30°, 30°)，精度为0.1°；分别在不同压缩采样快拍数进行实验。

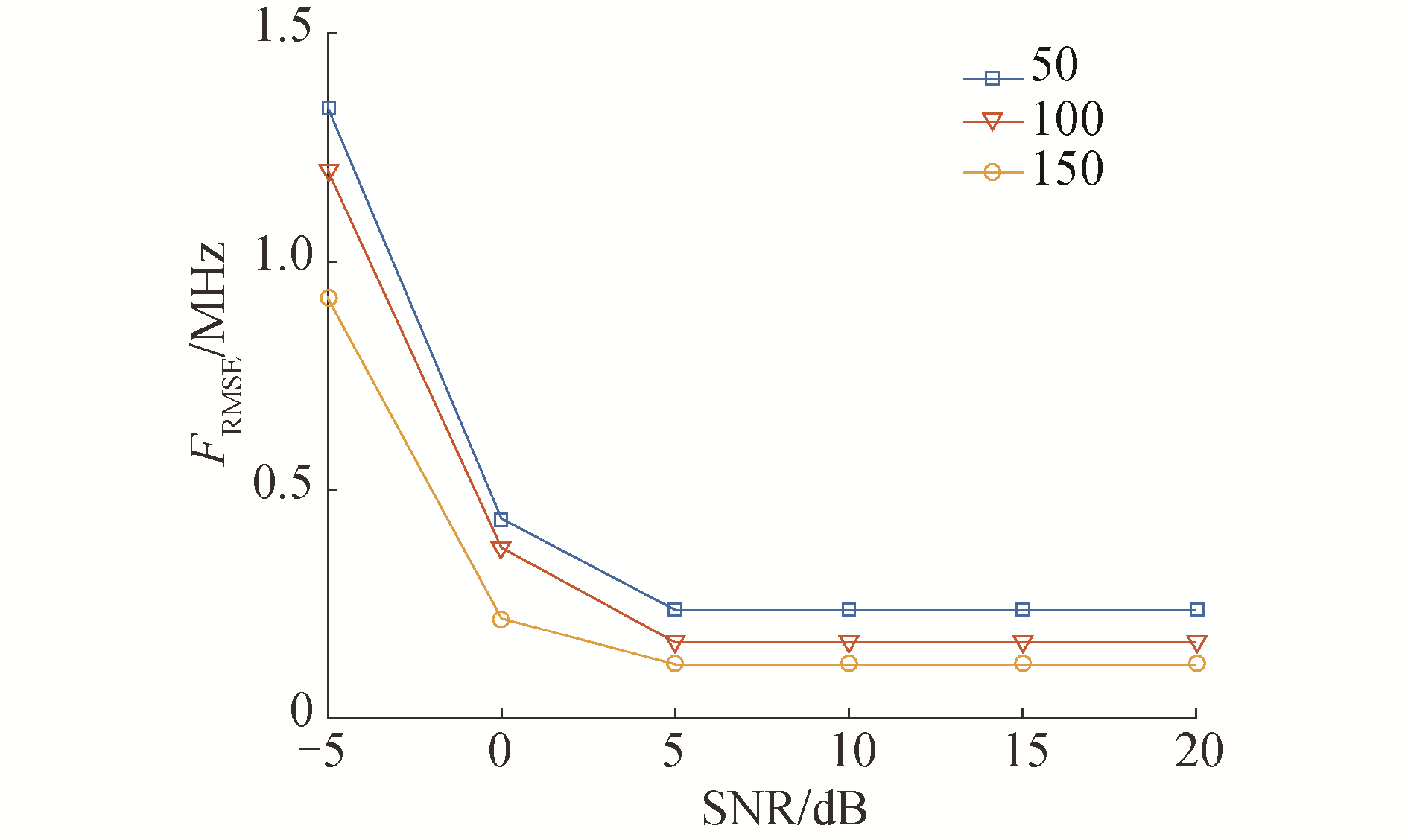
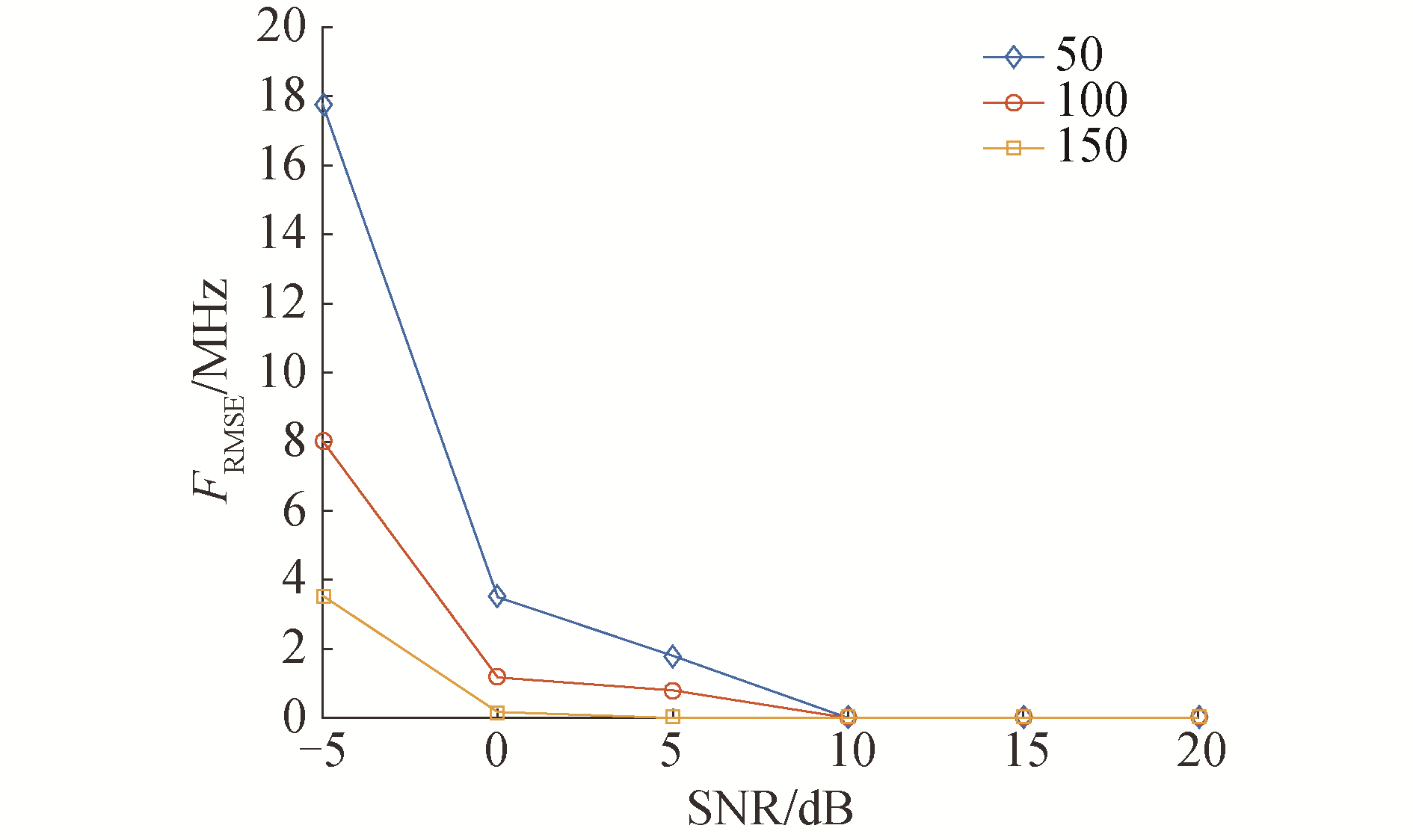
图 5为在嵌套阵列条件下的基带频率估计的RMSE值H_RMSE随信噪比变化曲线。图 6为在嵌套阵列条件下的子带估计的RMSE值L_RMSE随信噪比变化曲线。嵌套阵列的设置为L₁=5, L₂=5, 阵元位置为D=[1, 2, 3, 4, 5, 6, 12, 18, 24, 30]d，信噪比变化范围-5~20 dB，变化步长为5 dB，每个信噪比条件下蒙特卡洛实验次数N=1 000。基带频率估计的RMSE值随信噪比变化而降低，由于实验时FFT点数为压缩信号的快拍数，因此快拍数越大，FFT精度越高。由图 6结果可知，子带估计的RMSE随信噪比提升而降低，且当快拍数增加时，子带估计精度更高。因此在低信噪比下，子带估计RMSE值较大，即对信号原始载频估计值造成较大误差。当信噪比大于10 dB，且快拍数大于50时，子带索引的RMSE值达到0，此时对信号的原始载频估计值主要取决于基带频率的估计值。

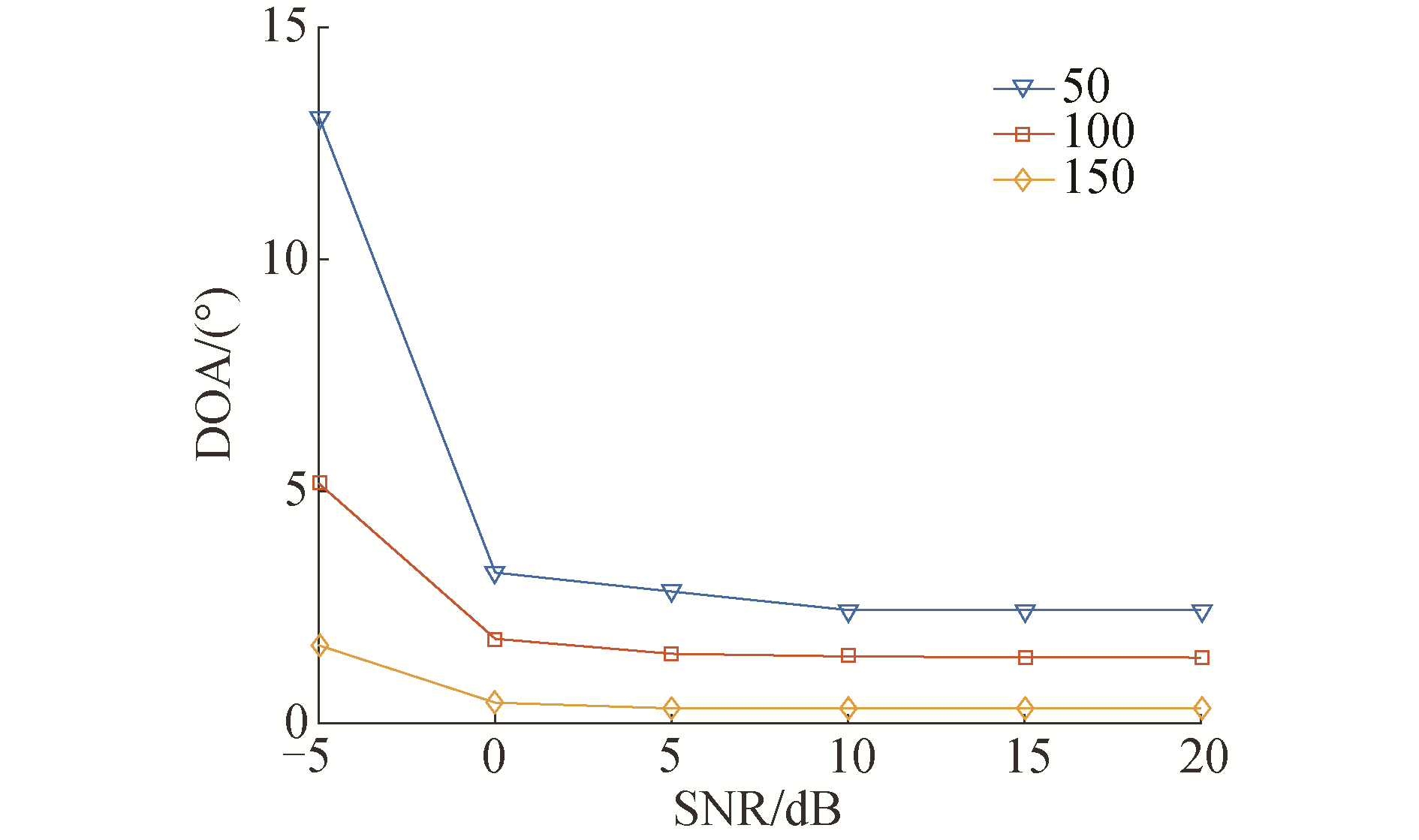
仿真实验3：在实验条件与实验2相同的条件下，图 7为嵌套阵列条件下的DOA估计的RMSE值D_RMSE随信噪比变化曲线。从图中可以看出DOA估计的RMSE值随信噪比提高而减小，且快拍数较多时，DOA估计值更为精确。

4 结论

1) 本文提出的压缩采样稀疏阵列结构，为压缩采样数字接收机的应用提供了思路。仿真实验证明了所提出结构和算法的正确性。

2) 从实验结果可以看出，在阵元数为10的情况下，系统在信噪比大于10 dB时的参数估计误差最小，但此信噪比对实际应用来说仍然较高。

增加快拍数可以有效提高估计精度，但却会增加算法的运算量，从而增加硬件实现难度。因此未来将进一步研究降低系统复杂度、提升算法信噪比的新结构和新算法。