2. 上海交通大学 高新船舶与深海开发装备协同创新中心, 上海 200240;
3. 上海交通大学 船舶海洋与建筑工程学院, 上海 200240
2. Collaboration Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai Jiao Tong University, Shanghai 200240, China;
3. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
超材料指的是人为设计的新奇材料,具有自然界中普通材料不具备的物理性质,其宏观特性很大程度上取决于内部微结构(胞元或功能基元)构造而非母材本身的性质。超材料在近年来受到广泛关注,众多学者对其进行了一系列研究[1-5]。负刚度超材料是其中重要的一个类别,其在变形时力与位移变化的方向相反[6-9]。Qiu等[10]提出了预成型余弦曲梁,该梁在中点受集中力时发生屈曲而产生负刚度效应。Correa等[11]结合选择性激光烧结技术,设计了一种负刚度蜂窝超材料,可用于抗冲击吸能。Restrepo等[12]引入相变概念,研究了多层负刚度超材料结构的多稳态效应,指出其力-位移关系的迟滞特性,Shan等[13]利用弹性倾斜直梁屈曲的负刚度效应提出了一种负刚度超材料,并通过实验验证了其具备多稳态、最大屈曲力阈值、抗冲击防护能力等多种特性。大多数工程材料在承受单轴拉伸时横截面会发生收缩,承受压缩时横向膨胀,而负泊松比超材料恰好与之相反。后者通常表现出低相对密度、高阻尼、吸声、隔热等物理特性,对航空航天、半导体器件、光学元件、精密仪器以及建筑材料等领域具有重要意义[14-18]。Hewage等[19]设计了一种同时展现负刚度和负泊松比特性的超材料,由带接头的六边形部件组成,部件之间利用弹簧、PMI泡沫、磁铁对或屈曲梁装配连接,不适合一体化成型,对材料尺度有要求。如果可以得到一体化的负刚度负泊松比胞元,结合增材制造即可实现从微观到宏观不同尺度的双负超材料设计,目前这方面的研究还比较少。
本文设计了一种一体化成型负刚度负泊松比效应超材料,其胞元由倾斜放置的余弦形曲梁与其支撑框架组成,胞元垂向受压时内部微曲梁发生屈曲并产生横向位移。介绍了该超材料的胞元结构与宏观变形特性,基于局部对称性对胞元准静态大变形过程进行了分析,探讨几何参数对其刚度和泊松比特性的影响,研究了该超材料结构在冲击载荷作用下的力学行为。
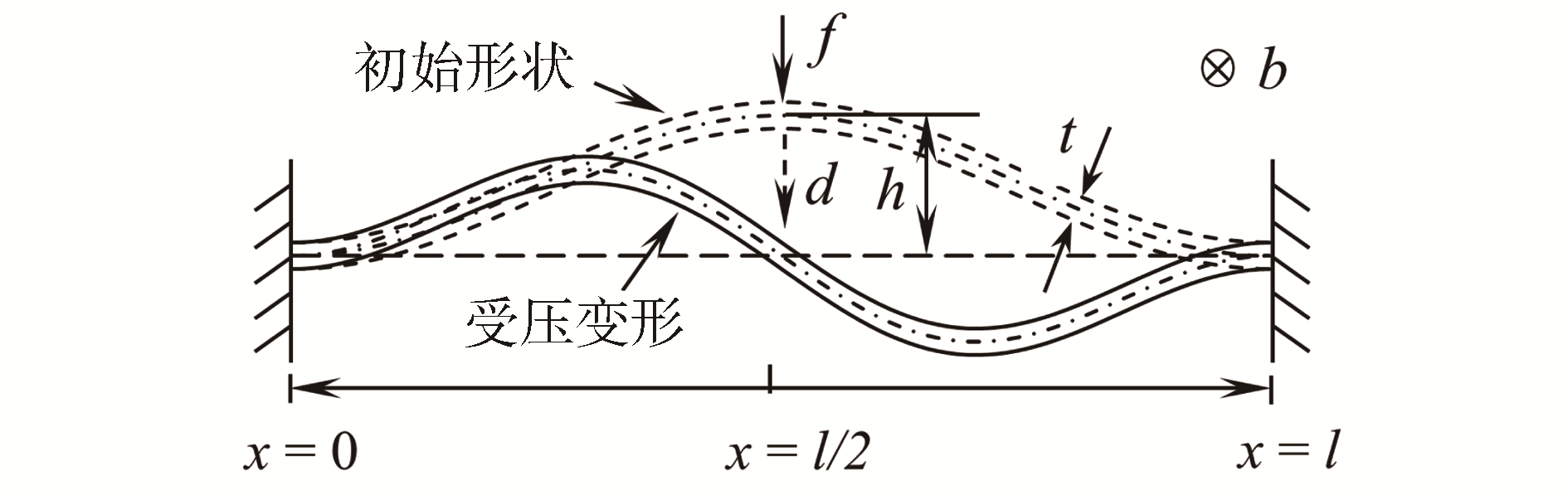
1 负刚度负泊松比超材料设计图 1所示为余弦形曲梁,其参数包括梁两约束端的距离l、梁截面厚度t、梁截面宽度b和梁轴线中点距两端点连线的距离h等,初始构为:
| $ w(x) = h/2 \cdot [1 - \cos (2{\rm{ \mathsf{ π} }}x/l)] $ | (1) |
|
Download:
|
| 图 1 跨中受压的余弦形曲梁 Fig. 1 Schematic diagram of prefabricated cosine beam under lateral force at midpoint | |
梁中点受到垂直向下的力f作用时,梁产生跃越屈曲而表现为负刚度。中心点垂向位移d和f的关系、变形过程及力学特性已由Qiu等[10]给出。Ren等[20]在此基础上设计了具有多向负刚度特性的周期性超材料。
本文将双向负刚度超材料在平面内旋转,使原胞元的对角线平行于水平轴,得到如图 2所示的另一种负刚度周期性超材料。该超材料可以看作由矩形胞元周期排布形成,每个胞元含4组倾斜对置的余弦形曲梁及其支撑框架,框架刚度远大于曲梁。为增强横向刚度,在框架水平两端点间额外增加了连接梁。垂向受压时,倾斜曲梁发生跃越屈曲,垂向刚度存在小于零的情况,又因为在水平方向表现为收缩变形,所以该材料也具有负泊松比特性。泊松比为:
| $ {N_{YX}} = - \frac{{{\varepsilon _X}}}{{{\varepsilon _Y}}}, {N_{XY}} = - \frac{{{\varepsilon _Y}}}{{{\varepsilon _X}}} $ | (2) |

|
Download:
|
| 图 2 负刚度负泊松比超材料及其胞元 Fig. 2 A metamaterial displaying negative stiffness and negative Poisson's ratio and its unit cell | |
式中:εX为超材料横向应变;εY为垂向应变。
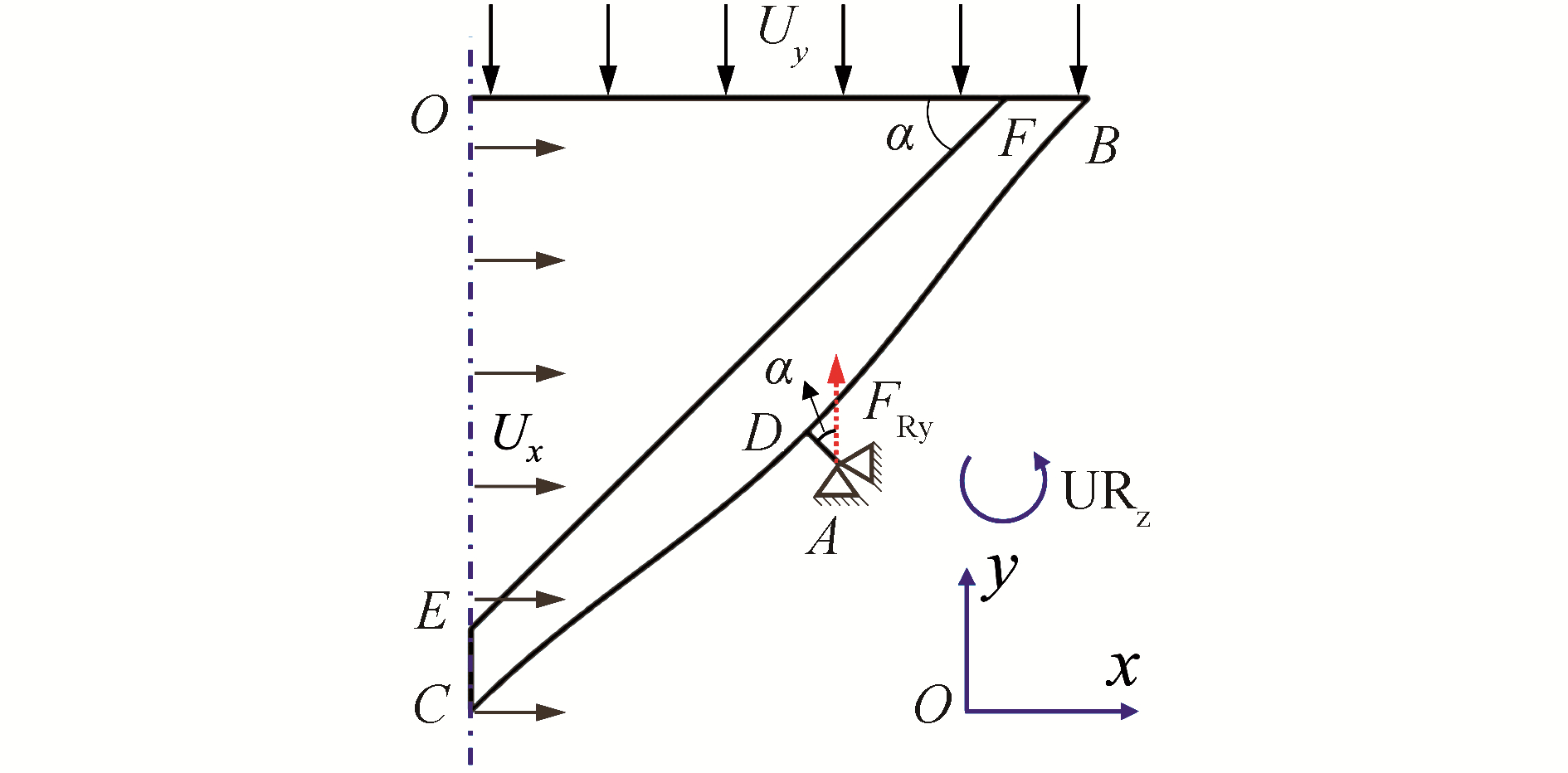
2 双负超材料的胞元静力学特性 2.1 双负超材料胞元的泊松比与等效弹性模量根据对称性,图 2中胞元静力学性能(泊松比与等效弹性模量)可通过研究仅含一条曲梁的1/8胞元模型得到,如图 3。其中,BDC段为曲梁,其余为支撑结构。可变参数为曲梁的厚度t以及与水平轴的夹角α。下文中,计算结果下标为大写字母(如X、Y)对应胞元坐标系,见图 2,下标为小写字母(如x、y)对应1/8模型局部坐标系,见图 3。
|
Download:
|
| 图 3 负刚度负泊松比超材料胞元的1/8模型 Fig. 3 The 1/8 model of the NSNPR metamaterial unit cell | |
在短梁A端点设置简支边界条件,对OFB段施加垂直向下的强制位移Uy,可得OEC对称面的水平位移Ux及压缩过程中支座上的反力FRy。由于几何大变形的存在,水平位移及垂向支反力与垂向位移的关系均呈强非线性,因此引入增量泊松比:
| $ {\nu _{YX}} = - \frac{{{\rm{d}}{\varepsilon _X}}}{{{\rm{d}}{\varepsilon _Y}}} = - \frac{{{\rm{d}}\left( {\ln \left( {W/{W_0}} \right)} \right)}}{{{\rm{d}}\left( {\ln \left( {H/{H_0}} \right)} \right)}} = - \frac{H}{W} \cdot \frac{{{\rm{d}}W}}{{{\rm{d}}H}} $ | (3) |
增量等效弹性模量:
| $ \begin{array}{*{20}{r}} {{E_Y} = \frac{{{\rm{d}}{\sigma _Y}}}{{{\rm{d}}{\varepsilon _Y}}} = \frac{{{\rm{d}}\left( {{F_Y}/Ar} \right)}}{{d\left( {\ln \left( {H/{H_0}} \right)} \right)}} = }\\ {\frac{H}{{b{W^2}}}\left( {W\frac{{{\rm{d}}{F_Y}}}{{{\rm{d}}H}} - {F_Y}\frac{{{\rm{d}}W}}{{{\rm{d}}H}}} \right)} \end{array} $ | (4) |
式中:H、H0=4|yA|分别是胞元的实际高度与初始高度;W、W0=4|xA|分别是胞元的实际宽度与初始宽度;FY为胞元上的垂向力,如图 2,Ar=Wb为胞元受压面积,如图 1。
| $ \left\{ {\begin{array}{*{20}{l}} {H = {H_0} + 4{U_y}}\\ {W = {W_0} - 4{U_x}}\\ {{F_Y} = - 2{F_{Ry}}} \end{array}} \right. $ | (5) |
和
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{d}}H = 4{\rm{d}}{U_y}}\\ {{\rm{d}}W = - 4{\rm{d}}{U_x}}\\ {{\rm{d}}{F_Y} = - 2{\rm{d}}{F_{Ry}}} \end{array}} \right. $ | (6) |
代入式(3)、(4)中得增量泊松比与增量等效弹性模量。
根据图 2中的位置关系,每层胞元允许的最大垂向压缩距离为:
| $ \left| {{U_{Y\max }}} \right| = 2 \times \left( {\left| {{y_{\rm{A}}}} \right| - \left| {{y_{\rm{C}}} - {y_{\rm{A}}}} \right|} \right) = 4\left( {{l_{{\rm{AD}}}} + h} \right)\cos \alpha $ | (7) |
则每条曲梁(图 3)允许的最大垂向压缩距离为:
| $ \left| {{U_{y\max }}} \right| = \left( {{l_{{\rm{AD}}}} + h} \right)\cos \alpha $ | (8) |
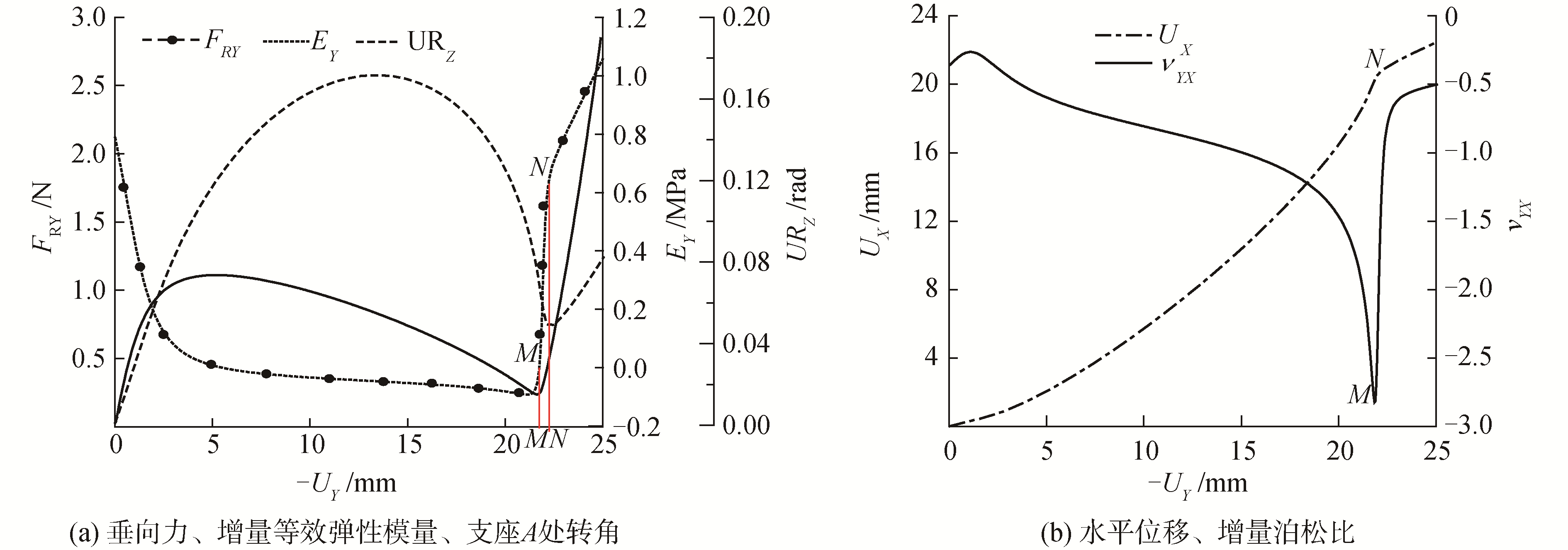
式(8)即为OFB梁段强制位移的最大值。利用数值分析得到的Ux-Uy、FRy-Uy关系,即可按式(3)~(6)计算胞元增量泊松比与增量等效弹性模量。以参数l=90 mm、h=4 mm、t=1 mm、b=1 mm、α =45°时为例,材料选取聚乳酸(PLA,弹性模量为3 283 MPa、泊松比0.38、密度1 210 kg/m3),其计算结果如图 4所示。
从图 4(a)可以看出,随着压缩增加,垂向支反力变化趋势与正置曲梁的一致,均可划分为正刚度段、负刚度段和强化段。变形过程中,增量等效弹性模量与垂向支反力曲线的斜率呈正相关,例如支反力取到极大值时,增量等效弹性模量降到零;当垂向位移达到M时,增量等效弹性模量等于零,支反力取到极小值。在强化段,增量等效弹性模量曲线上存在一个角点(横坐标为N),在该点处支座A处转角取极小值,转动方向发生改变,因此影响了梁的整体刚度。由图 4(b),水平方向变形始终表现为收缩(UX>0),且收缩得越来越快(曲线斜率越来越大),曲线到达角点N后则变得缓和。增量泊松比始终小于零,极小值点在横坐标为M时取到,即在该点单位垂向压缩引起的横向收缩最大,之后随着曲梁进入强化阶段,增量泊松比绝对值将迅速减小。
|
Download:
|
| 图 4 胞元垂向受压静力学特性与垂向位移的关系 Fig. 4 The relations between static properties of the vertically-compressed metamaterial cell and the vertical displacement | |
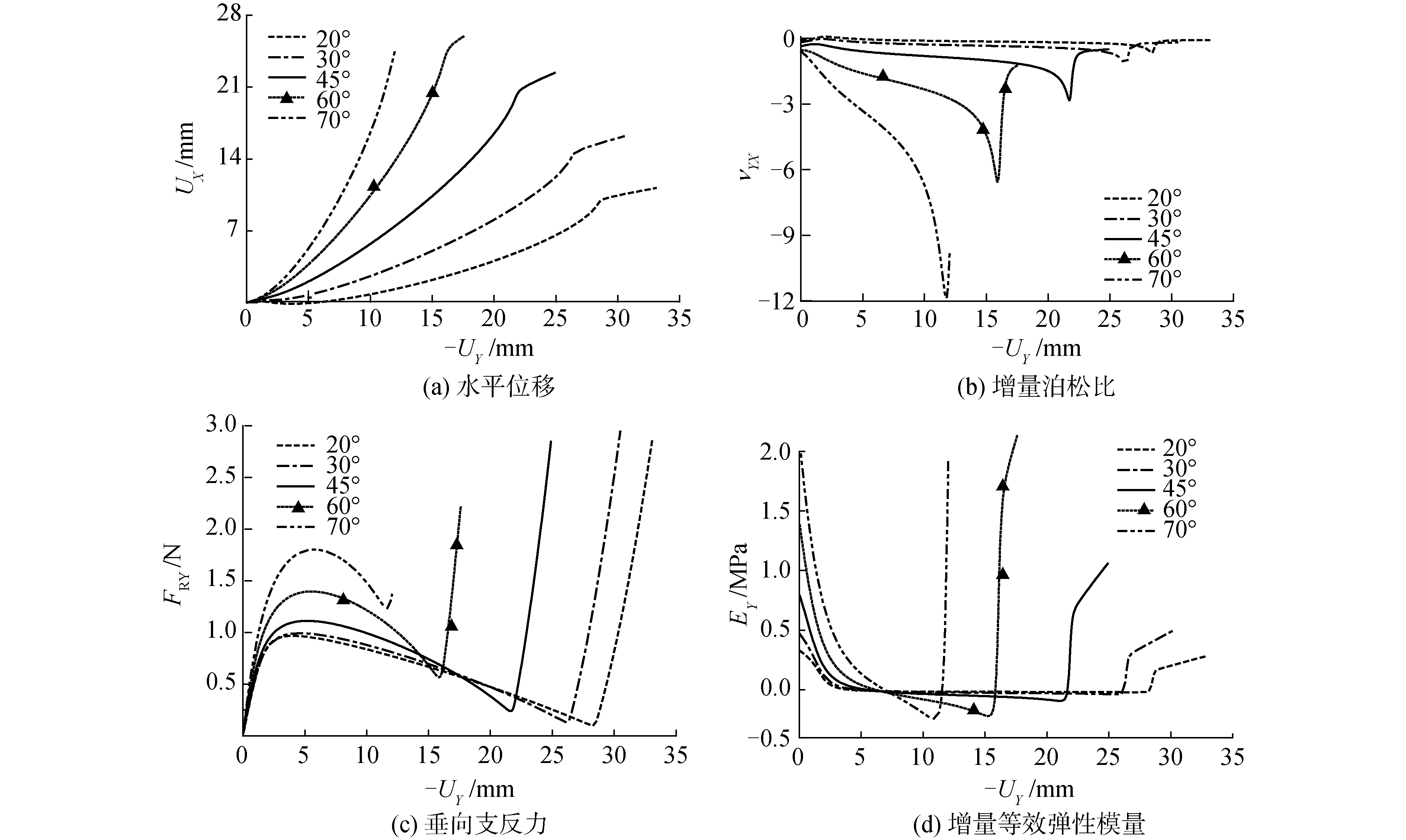
保持曲梁的跨长l、拱高h、厚度t不变,通过修改与水平轴的夹角α,研究其对负刚度负泊松比超材料胞元力学特性的影响,α的取值分别为20°、30°、45°、60°和70°。得到一系列的水平位移、增量泊松比、垂向支反力及增量等效弹性模量,转换得到胞元对应结果,如图 5所示。
|
Download:
|
| 图 5 不同夹角α的胞元垂向受压时的影响 Fig. 5 The effections of the metamaterial cell with different angle α | |
由图 5可知,保持其他条件不变时,允许的最大垂向位移随α的增大而减小,水平方向最大收缩则逐渐增大,但角度增大到一定程度后(如α =70°),水平位移曲线的第2段不再出现。这是因为此时支座A处的转动方向不发生第2次改变,对应图 4中横坐标N点之后的部分不再出现。对于增量泊松比,夹角α越大,其绝对值越大,即横向的收缩越明显,不同角度下其随垂向位移的变化趋势一致。由图中的支反力曲线可知,夹角α越大,初始刚度越大,屈曲临界力也越大,垂向位移的负刚度段也越短。对于增量等效弹性模量,随着夹角α的增大,正刚度段、负刚度段和强化段3个部分的绝对值均增加,正负刚度均加强。
2.3 胞元中曲梁的厚度对其静力学特性的影响仅通过修改曲梁的厚度t来改变曲梁自身刚度,研究其对负刚度负泊松比超材料胞元力学特性的影响,t的取值分别为0.6、0.8、1.0、1.2和1.4 mm。得到一系列的水平位移、增量泊松比、垂向支反力及增量等效弹性模量,转换得到胞元对应结果,如图 6所示。

|
Download:
|
| 图 6 不同曲梁厚度t的胞元垂向受压时的影响 Fig. 6 The effections of the metamaterial cell with different thickness | |
从图 6可以看出,保持其他条件不变时,改变梁的厚度,对于水平位移的影响不大,同样对于增量泊松比,也仅影响峰值(绝对值)区域,随着厚度增加,增量泊松比最大值(绝对值)减小。同时,垂向支反力和增量等效弹性模量(绝对值)均呈现为增大的趋势。此外,增大梁的厚度导致关键点位置M点和N点(见图 4)均提前。因此改变梁厚度可以在垂向和水平位移量(即超材料的宏观变形)保持不变的情况下,有效地调整其刚度特性。
2.4 胞元完全压缩时负泊松比效应计算胞元中倾斜梁在垂向压缩达到最大时OEC对称面的水平位移,可得完全受压胞元泊松比(初始胞元间隙被占满,如图 2):
| $ {\nu _{YX - {\rm{ ult }}}} = - \frac{{{U_{x\max }}}}{{\left| {{U_{{{y\max }}}}} \right|}} $ | (9) |
式中:Uxmax表示垂向压缩达到最大时OEC对称面水平位移。给出不同夹角α和曲梁厚度t下的泊松比计算结果,如图 7所示。
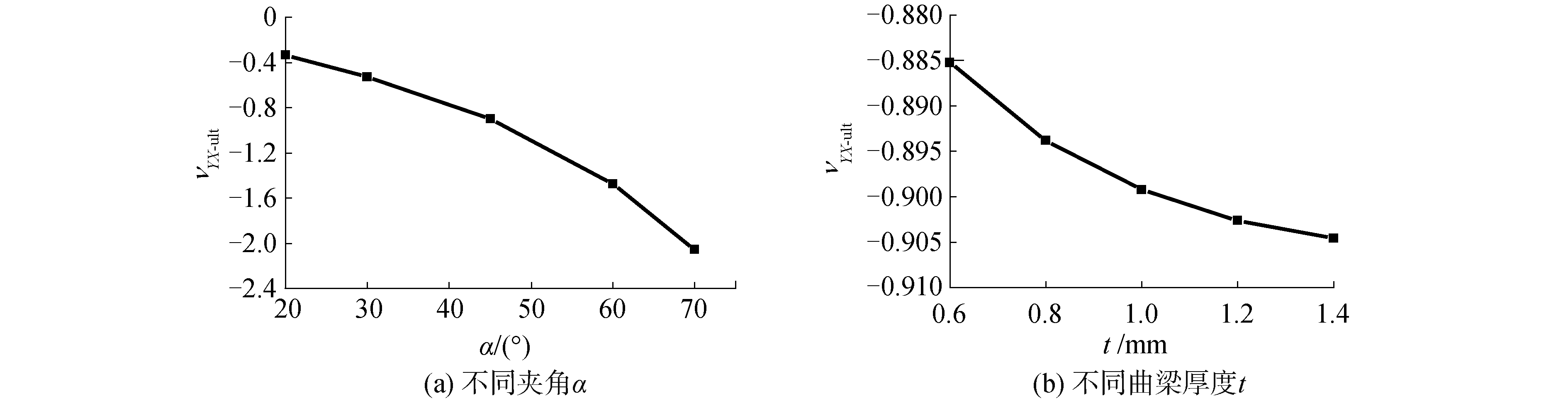
|
Download:
|
| 图 7 不同几何参数的胞元垂向完全压缩泊松比 Fig. 7 Ultimate Poisson's ratio of the fully-compressed cell with different geometric parameters | |
由图 7可以看出,夹角α和厚度t的增加均导致泊松比减小。但夹角对于泊松比的影响更为明显,在所给的参数范围内,泊松比变化范围超过1.5;而改变厚度时泊松比变化范围仅约为0.02,且后一条曲线向上凹,继续增加厚度对减小泊松比的作用将变弱。这是因为对于后者来说,结构的基本构型保持不变,仅改变曲梁厚度不足以对泊松比产生很大影响。
3 负刚度负泊松比超材料抗冲击性能 3.1 抗冲击模型与边界条件以5层4列胞元构成的超材料平面结构为例,采用显式动力学方法研究其抗冲击性能。结构底部固定,上方跌落一质量为10 kg的刚性方形重物,重物水平位移与面内转动自由度被约束,但允许其在垂向自由反弹。设置重物在撞击结构前的初速度分别为80、160、240、320、400、480 mm/s,确保输入能量在结构的承载范围内(碰撞后结构内部不会发生胞元间碰撞或穿透),计算其在碰撞过程中的位移、速度、加速度响应。
3.2 几何参数对于特性的影响以参数l=90 mm、h=4 mm、b=10 mm为参考模型,通过修改胞元内曲梁与水平轴的夹角α与曲梁的厚度t,分别研究两者对双负超材料结构抗冲击性能的影响,α的取值分别为20°、30°、45°、60°和70°,t的取值分别为0.6、0.8、1.0、1.2和1.4 mm。选取2个物理量作为抗冲击性能指标,分别为碰撞后与碰撞前重物动能之比(如图 8)和垂向最大变形与初始高度之比(如图 9)。

|
Download:
|
| 图 8 重物与不同几何参数的超材料结构碰撞后动能与初始动能之比 Fig. 8 The ratio of the mass's kinetic energy after impact with metamaterial structures to its initial kinetic energy | |

|
Download:
|
| 图 9 不同几何参数的超材料结构碰撞后最大垂向变形与初始高度之比 Fig. 9 The ratio of the metamaterial structure's maximal vertical deformation to its initial height | |
如图 8所示,夹角α的改变对于动能比-冲击速度曲线的趋势影响不大,动能比在低速冲击时比较大且随冲击速度变化很小,而随着冲击速度的增加,动能比逐渐减小,这一趋势约从v0=240 mm/s处开始较为显著。对(α =20°,v0=480 mm/s),动能比减小到了约0.58。改变斜梁的厚度t,动能比-冲击速度曲线的趋势则产生变化。t增大时,曲线后端依次升高,高速区域的动能比大幅增加,超材料结构刚度变大,吸能效应减弱。
从图 9可以看出,随着冲击速度的增加,最大垂向变形与初始高度之比逐渐增加,更多的胞元参与变形。在同一冲击速度时,夹角α越大,变形比越小;厚度t越大,变形比越小。相比α,斜梁厚度t对变形比的影响更为显著,当t=0.6 mm、v0=480 mm/s时,变形比高达0.163。
4 结论1) 该双负超材料的负刚度负泊松比效应可分别采用增量等效弹性模量和增量泊松比评价。胞元内倾斜微曲梁与水平轴夹角决定了该超材料的几何构型,对泊松比影响较大;胞元内微曲梁厚度则可以有效调节该超材料刚度,对其抗冲击性能影响更大。
2) 该负刚度负泊松比超材料为一体成型的周期性多孔材料,便于实现,且对于几何参数敏感,具有较强的可设计性。该超材料组成的结构兼顾大变形,具备较好的抗冲击吸能性,且因其不产生塑性变形的特点而可重复使用。
| [1] |
XIE Yimin, YANG Xiaoying, SHEN Jianhu, et al. Designing orthotropic materials for negative or zero compressibility[J]. International journal of solids and structures, 2014, 51(23/24): 4038-4051. (  0) 0)
|
| [2] |
XU Hang, FARAG A, PASINI D. Routes to program thermal expansion in three-dimensional lattice metamaterials built from tetrahedral building blocks[J]. Journal of the mechanics and physics of solids, 2018, 117: 54-87. DOI:10.1016/j.jmps.2018.04.012 (  0) 0)
|
| [3] |
于相龙, 周济. 力学超材料的构筑及其超常新功能[J]. 中国材料进展, 2019, 38(1): 14-21. YU Xianglong, ZHOU Ji. Mechanical metamaterials:architected materials and unexplored properties[J]. Materials China, 2019, 38(1): 14-21. (  0) 0)
|
| [4] |
YU Xianglong, ZHOU Ji, LIANG Haiyi, et al. Mechanical metamaterials associated with stiffness, rigidity and compressibility:a brief review[J]. Progress in materials science, 2018, 94: 114-173. DOI:10.1016/j.pmatsci.2017.12.003 (  0) 0)
|
| [5] |
温卓群, 王鹏飞, 张雁, 等. 面向大尺度结构的力学超材料减振技术[J]. 航空学报, 2018, 39(S1): 155-159. WEN Zhuoqun, WANG Pengfei, ZHANG Yan. Vibration reduction technology of mechanical metamaterials presented to large scale structures[J]. Acta aeronautica et astronautica sinica, 2018, 39(S1): 155-159. (  0) 0)
|
| [6] |
WANG Y C, LAKES R S. Extreme thermal expansion, piezoelectricity, and other coupled field properties in composites with a negative stiffness phase[J]. Journal of applied physics, 2001, 90(12): 6458-6465. DOI:10.1063/1.1413947 (  0) 0)
|
| [7] |
CORREA D M, KLATT T, CORTES S, et al. Negative stiffness honeycombs for recoverable shock isolation[J]. Rapid prototyping journal, 2015, 21(2): 193-200. DOI:10.1108/RPJ-12-2014-0182 (  0) 0)
|
| [8] |
FRENZEL T, FINDEISEN C, KADIC M, et al. Tailored buckling microlattices as reusable light-weight shock absorbers[J]. Advanced materials, 2016, 28(28): 5865-5870. DOI:10.1002/adma.201600610 (  0) 0)
|
| [9] |
GOLDSBERRY B M, HABERMAN M R. Negative stiffness honeycombs as tunable elastic metamaterials[J]. Journal of applied physics, 2018, 123(9): 091711. DOI:10.1063/1.5011400 (  0) 0)
|
| [10] |
QIU Jiu, LANG J H, SLOCUM A H. A curved-beam bistable mechanism[J]. Journal of microelectromechanical systems, 2004, 13(2): 137-146. DOI:10.1109/JMEMS.2004.825308 (  0) 0)
|
| [11] |
CORREA D M, KLATT T, CORTES S, et al. Negative stiffness honeycombs for recoverable shock isolation[J]. Rapid prototyping journal, 2015, 21(2): 193-200. DOI:10.1108/RPJ-12-2014-0182 (  0) 0)
|
| [12] |
RESTREPO D, MANKAME N D, ZAVATTIERI P D. Phase transforming cellular materials[J]. Extreme mechanics letters, 2015, 4: 52-60. DOI:10.1016/j.eml.2015.08.001 (  0) 0)
|
| [13] |
SHAN Sicong, KANG S H, RANEY J R, et al. Multistable architected materials for trapping elastic strain energy[J]. Advanced materials, 2015, 27(29): 4296-4301. DOI:10.1002/adma.201501708 (  0) 0)
|
| [14] |
于靖军, 谢岩, 裴旭. 负泊松比超材料研究进展[J]. 机械工程学报, 2018, 54(13): 1-14. YU Jingjun, XIE Yan, PEI Xu. State-of-art of metamaterials with negative poisson's ratio[J]. Journal of mechanical engineering, 2018, 54(13): 1-14. (  0) 0)
|
| [15] |
LI Yang, HARRYSSON O, WEST H, et al. Mechanical properties of 3D re-entrant honeycomb auxetic structures realized via additive manufacturing[J]. International journal of solids and structures, 2015, 69-70: 475-490. DOI:10.1016/j.ijsolstr.2015.05.005 (  0) 0)
|
| [16] |
任鑫, 张相玉, 谢亿民. 负泊松比材料和结构的研究进展[J]. 力学学报, 2019, 51(3): 656-687. REN Xin, ZHANG Xiangyu, XIE Yimin. Research progress in auxetic materials and structures[J]. Chinese journal of theoretical and applied mechanics, 2019, 51(3): 656-687. (  0) 0)
|
| [17] |
GRIMA J N, MANICARO E, ATTARD D. Auxetic behaviour from connected different-sized squares and rectangles[J]. Proceedings of the royal society A:mathematical, physical and engineering sciences, 2011, 467(2126): 439-458. DOI:10.1098/rspa.2010.0171 (  0) 0)
|
| [18] |
EBRAHIMI H, MOUSANEZHAD D, NAYEB-HASHEMI H, et al. 3D cellular metamaterials with planar anti-chiral topology[J]. Materials & design, 2018, 145: 226-231. (  0) 0)
|
| [19] |
HEWAGE T A M, ALDERSON K L, ALDERSON A, et al. Double-negative mechanical metamaterials displaying simultaneous negative stiffness and negative poisson's ratio properties[J]. Advanced materials, 2016, 28(46): 10323-10332. DOI:10.1002/adma.201603959 (  0) 0)
|
| [20] |
REN Chenhui, YANG Deqing, QIN Haoxing. Mechanical performance of multidirectional buckling-based negative stiffness metamaterials:an analytical and numerical study[J]. Materials, 2018, 11(7): 1078. DOI:10.3390/ma11071078 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


