海洋立管是深海资源开发设备所不可或缺的基础结构,其结构强度与使用寿命等问题一直备受关注,而涡激振动(vortex-induced vibration,VIV)则是导致这种圆柱结构遭受疲劳损伤的一个主要原因。VIV是一种复杂的现象,具有非线性、自激和自限制等典型特征,人们尝试使用多种方式对这一现象进行了丰富的研究。到目前为止VIV的研究大多侧重于将刚性圆柱作为研究对象,Williamson[1]以及Gabbai[2]对此方面研究进展进行了全面的总结。细长柔性圆柱的涡激振动特性与刚性圆柱相比有很大的不同,其不再是单一模态的振动形式,而表现为多模态的振动特性[3],对其振动响应的预测格外困难。VIV预报模型可以分为计算流体力学(computational fluid dynamics,CFD)模型和经验模型2类。CFD方法方面,文献[4-8]分别采用直接数值模拟(direct numerical simulation,DNS)、雷诺平均(Reynolds-averaged navier-stokes equations,RANS)、大涡模拟(large eddy simulation,LES)和离散涡方法(discrete vortex method,DVM),分析了大长径比柔性圆柱的涡激振动现象。经验模型中基于频域方法的一些商业软件已经普遍应用于实际工程之中,如Shear7[9]和VIVANA[10]等。但频域方法无法考虑复杂的边界条件效应,相较之下,时域预报方法能够适用于更广泛的对象及工况[11]。时域方法中被讨论最多的是尾流振子模型,Harden等[12]最早提出了尾流振子的概念,Facchinetti等[13]利用尾流振子模型研究了细长线缆的涡激振动响应,并与数值模拟和实验数据进行了比较。随着计算机技术不断提高,CFD方法在VIV研究方面取得了很大进步,但其计算精度依赖于网格质量,且柔性圆柱长径比较大,需要更多的计算资源。经验模型的预报过于依赖经验系数的选取,而目前柔性圆柱经验模型选取的流体力系数主要来源于刚性圆柱实验,导致预报结果与实验结果存在一定差异[14]。而人工神经网络作为一种拥有优秀的非线性逼近性能的数据处理模型[15],能够有效规避以上问题。在涡激振动相关领域内,已经有研究学者开始利用人工神经网络解决复杂的科研难题。Wong等[16]通过神经网络以及Shear7计算得出的数据,建立了海洋立管VIV疲劳损伤的预报模型。Wu等[17]在以往实验数据的基础上,构建了可以计算VIVACE(一种利用VIV获取潮流能的装置)升力和功率的神经网络模型。林海花[18]利用BP神经网络,以雷诺数,Keulegan-Carpenter数和粗糙度参数为输入变量,计算了结构物涡激振动的阻尼系数和惯性力系数。虽然目前已经有学者采用神经网络模型分析计算了海洋结构物VIV的疲劳损伤以及流体力系数等特性,但利用此方法直接针对VIV响应进行预报的研究还有待进一步展开。本文以柔性圆柱涡激振动的实验数据作为依托,应用BP(error back propagation)神经网络,建立了柔性圆柱VIV在横流向及顺流向上的响应预报模型。
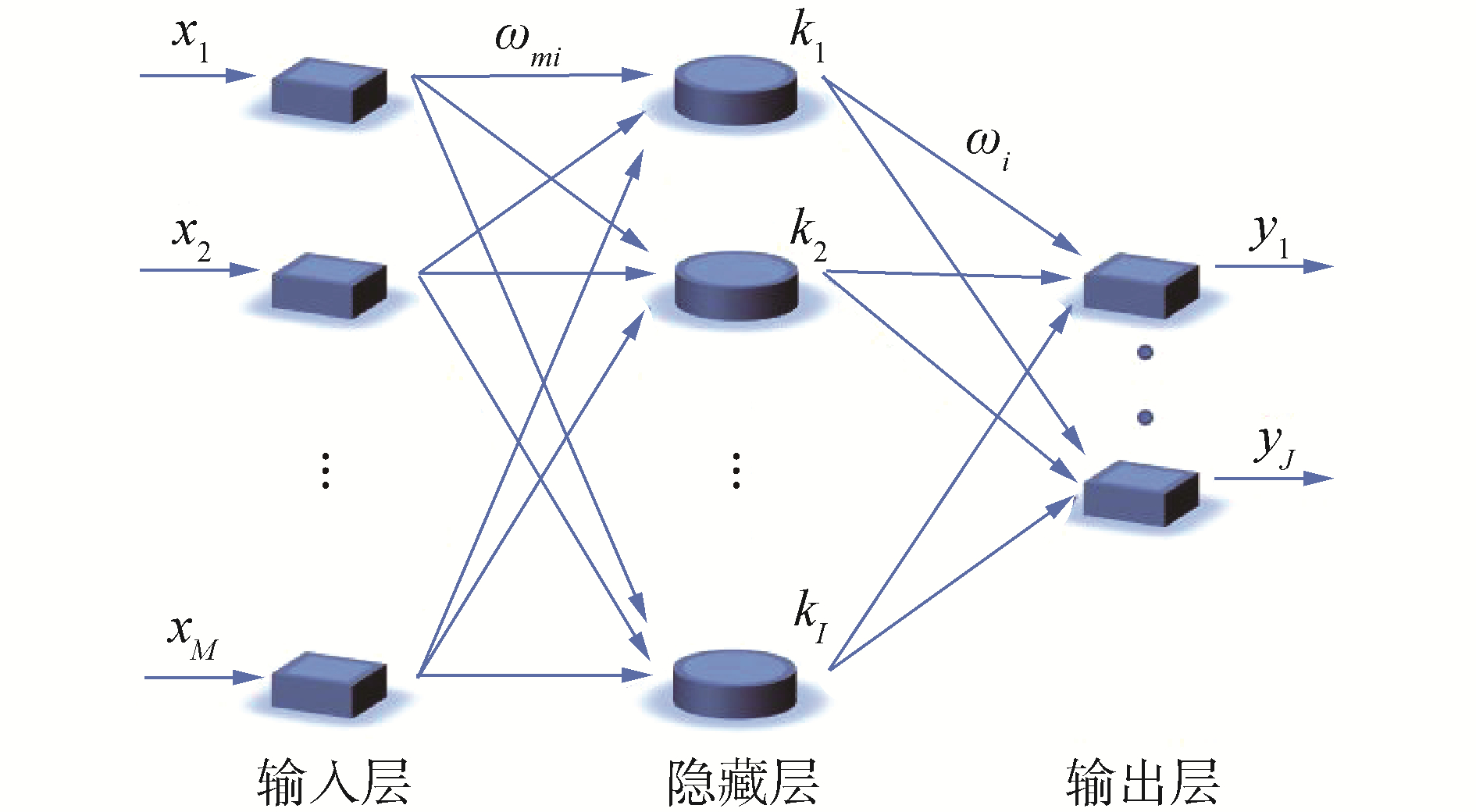
1 BP神经网络及预报模型BP神经网络是神经网络中最常用的一种,它是具有多层结构的前向神经网络,学习过程运用了误差反向传播法。此类神经网络一般包含一个输入层,一个输出层和若干个隐藏层,图 1所示的是只包含单个隐藏层的简单的3网络结构。BP神经网络具有以下特点:网络的结构是多层的,每个神经元都与相邻层的全部神经元相连接,处于同一层的各神经元之间没有连接;传递函数一般选用具有可微特性的Sigmoid函数或着线性函数;样本数据正向传播,即从输入层经过隐藏层传向输出层,而在对权值进行训练时,则恰好相反,从输出层经过隐藏层到输入层,沿着减少误差的方向修正神经元之间连接的权值[15]。
|
Download:
|
| 图 1 BP神经网络结构 Fig. 1 BP neural network structure | |
本文利用BP神经网络,分别构建了可以预报柔性圆柱VIV的横流向及顺流向位移和频率响应的4个模型。位移预报模型中输入数据为轴向力、流速和圆柱上的空间位置,输出数据为位移均方根,即输入层有3个节点,输出层只包含1个神经元;频率预报模型中输入数据只有轴向力和流速,输出数据为主控频率,即输入层含2个节点,输出层也只有1个神经元。
BP神经网络可以包含1至多个隐藏层,但由于可以通过适当增加神经元节点数来实现任意非线性映射,因此,多数问题都可以被只含有一个隐藏层的BP神经网络解决。本文中输入层和输出层节点数均较少,且数据样本规模不大,单个隐藏层即可满足需求。层与层之间通过权值ω连接,同一层之间的神经元无连接。
除隐藏层层数外,还需确定隐藏层节点数,隐藏层节点数关乎神经网络模型的训练速度和精准度。一般较多的节点数可以为神经网络带来更好的性能,但可能导致训练时间过长。通过经验公式确定隐藏层节点数[15]:
| $ \sum\limits_{n = 0}^M {C_I^n} > h $ | (1) |
式中:h为样本数;I为隐藏层神经元个数;M为输入层节点数。
位移预报模型中设置20个隐藏层节点,频率预报模型中设置15个隐藏层节点,既满足式(1)要求,可得到较好的预报效果,也不会致使训练时间过长。
神经元在输入信号作用下产生输出信号的规律由神经元传递函数给出。BP神经网络要求传递函数必须是可微的,一般采用Sigmoid函数作为隐藏层的传递函数,线性函数作为输出层的传递函数。本问题中,隐藏层采用BP神经网络常用的Sigmoid函数。但输出层如果使用一般的线性函数,会导致输出结果数值分布范围过大,甚至出现负数情况。因此,输出层传递函数同样使用Sigmoid函数,将输出结果限制在可控范围之内。基本的Sigmoid函数为:
| $ f(x) = \frac{1}{{1 + {{\rm{e}}^{ - x}}}} $ | (2) |
确定了输入输出层节点数、隐藏层层数、隐藏层节点数和传递函数等信息后,即可调用样本数据,开始BP神经网络的学习。以图 1中的BP神经网络为例,隐藏层中第i个神经元的输入为:
| $ {u_i} = \sum\limits_{m = 1}^M {{\omega _{mi}}} {x_m} $ | (3) |
设f(·)为Sigmoid函数,该神经元的输出为:
| $ {k_i} = f({u_i}) $ | (4) |
定义输出层的传递函数为g(·),输出层的第j个神经元的输入和输出分别为:
| $ {{v_j} = \sum\limits_{i = 1}^I {{\omega _{ij}}} {k_i}} $ | (5) |
| $ {{y_j} = g({v_j})} $ | (6) |
若该输出层神经元的期望输出为dj,采用均方误差的形式表示误差,则此神经网络的误差为:
| $ e = \frac{1}{J}\sum\limits_{j = 1}^J {{{({d_j} - {y_j})}^2}} $ | (7) |
在BP神经网络的学习过程中,误差信号反向传播,权值根据误差从后向前逐层进行修正,首先调整隐藏层与输出层之间的误差ωij。采用梯度下降法,先计算误差对ωij的偏导:
| $ \frac{{\partial e}}{{\partial {\omega _{ij}}}} = \frac{{\partial e}}{{\partial {y_j}}} \cdot \frac{{\partial {y_j}}}{{\partial {v_j}}} \cdot \frac{{\partial {v_j}}}{{\partial {\omega _{ij}}}} = - \frac{2}{J}({d_j} - {y_j}) \cdot {g^\prime }({v_j}) \cdot {k_i} $ | (8) |
定义BP神经网络的学习效率为η,修正后的权值为:
| $ \omega _{ij}^\prime = {\omega _{ij}} - \eta \cdot \frac{{\partial e}}{{\partial {\omega _{ij}}}} $ | (9) |
使用同样的方法修正输入层与隐藏层之间的权值ωmi:
| $ {\frac{{\partial e}}{{\partial {\omega _{mi}}}} = \left( {\sum\limits_{j = 1}^J {\frac{{\partial e}}{{\partial {y_j}}}} \cdot \frac{{\partial {y_j}}}{{\partial {v_j}}} \cdot \frac{{\partial {v_j}}}{{\partial {k_i}}}} \right) \cdot \frac{{\partial {k_i}}}{{\partial {u_i}}} \cdot \frac{{\partial {u_i}}}{{\partial {x_m}}}} $ | (10) |
| $ {\omega _{mi}^\prime = {\omega _{mi}} - \eta \cdot \frac{{\partial e}}{{\partial {\omega _{mi}}}}} $ | (11) |
至此,已经进行了一次权值的修正。再输入下一个样本,循环上述过程,直至误差大小低于目标要求或循环次数达到上限,便完成了该BP神经网络的学习过程,构建出了所需的预报模型。
1.2 数据样本构建BP神经网络预报模型的数据样本来源于柔性圆柱VIV的室内模型实验[19]。圆柱模型长5.6 m,外径0.016 m,长径比为350,质量比为1.90。流速变化范围为0.05~1.00 m/s,间隔0.05 m/s。轴向力大小可通过张紧器进行调整,取其中轴向力为277、368、460、551 N的实验数据作为构建预报模型的样本。
实验直接获得的数据为圆柱振动应变信息,通过位移重构和傅里叶变换等数据处理方式,将其转换为所需的位移和频率信息。构建BP神经网络预报模型所使用的位移数据为上述4个轴向力,0.05~1.00 m/s的流速范围内20个流速下,柔性圆柱上均布的21个点的横流向和顺流向位移均方根,2个方向各包含1 680个样本;频率数据为与位移数据相同的轴向力和流速下,该圆柱的横流向和顺流向主控频率,2个方向各包含80个样本。数据样本中输入变量的具体数值如表 1所示。
| 表 1 输入数据的具体数值 Table 1 Value of input data |
为验证所构建出的BP神经网络预报模型的准确性,在1 680个位移数据样本中随机选取出30个作为测试集,80个频率数据样本中随机选10个作测试集,其余样本作为训练集,用于神经网络的训练。
2 预报结果使用Matlab软件构建BP神经网络,利用训练集中的数据样本完成神经网络的训练过程,得到预报模型。输入测试集中的输入数据,得到预报模型的预测结果,将其与测试集的真实数据进行对比,以决定系数作为评判预报模型是否精确的标准,决定系数R2为:
| $ {R^2} = \frac{{\sum {{{({{\hat y}_j} - \bar y)}^2}} }}{{\sum {{{({y_j} - \bar y)}^2}} }} $ | (12) |
式中:j为BP神经网络的预测值;yj为真实值;y为真实值的平均值;R2的数值范围为0~1,表示预测值和真实值之间的相关程度,模型的R2值越接近1,代表其预测效果越好。
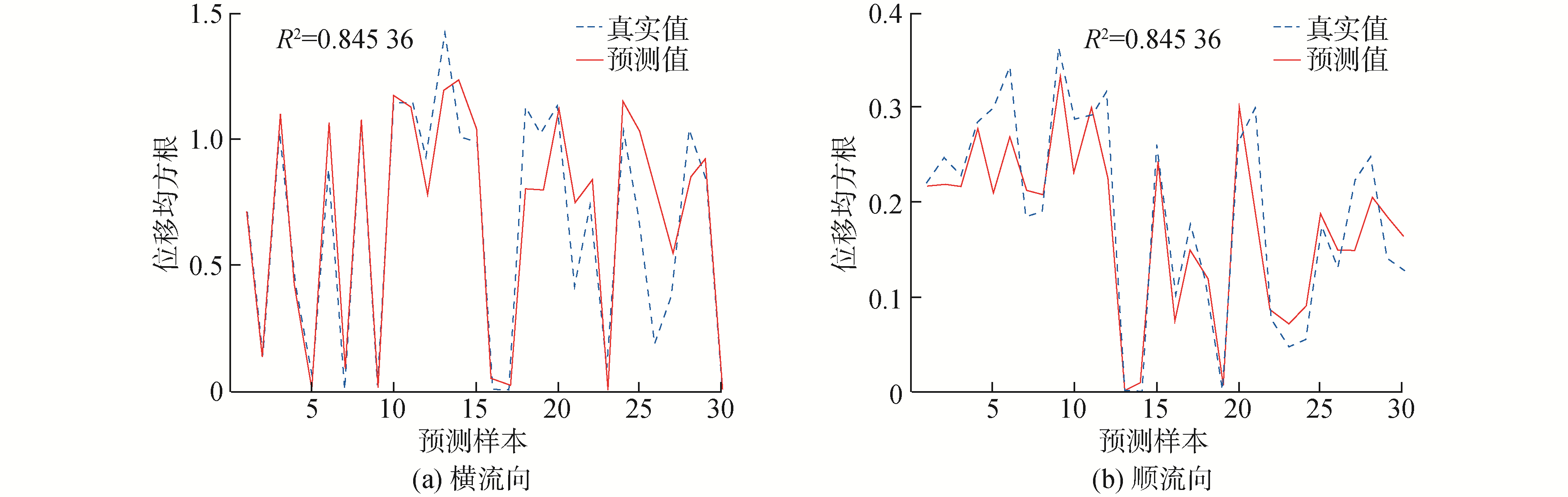
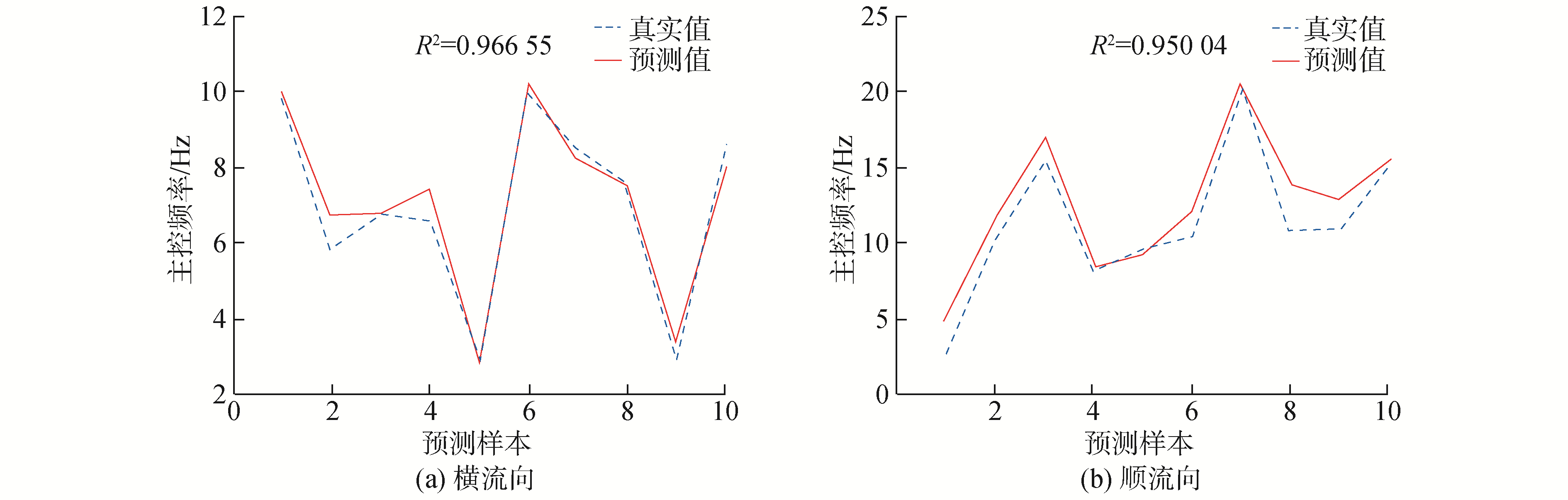
图 2和图 3分别给出了位移模型和频率模型的预测值与测试集中的实验数据的对比结果。可以看到大部分样本点的预测值与真实值都很接近,且无论横流向还是顺流向,位移预报模型的决定系数R2都可达到0.8以上,频率模型的R2甚至超过0.9。表明通过BP神经网络构建出的这两种预报模型都具有出色的预测能力。
|
Download:
|
| 图 2 位移模型预测值与真实值对比 Fig. 2 Comparison of predicted values of displacement models with real values | |
|
Download:
|
| 图 3 频率模型预测值与真实值对比 Fig. 3 Comparison of predicted values of frequency models with real values | |
频率预报模型的整体精准度高于位移模型,原因在于位移预报模型的输入数据包含3个变量,而频率模型中只包含2个输入变量。虽然位移样本量多于频率样本,但1 680个样本还不足以弥补变量数目差距造成的影响。且由于位移均方根随变量的变化较主控频率更加剧烈,造成位移预报结果对比中某些点预测值与真实值差距较大,较为明显为横流向第26个测试集样本点,预测值超过真实值2倍以上。但此情况属于个例,对整体预测无较大影响,而且可通过增加样本量来提高预报精准度。
位移模型可以实现在模型实验的轴向力和流速范围内,预报该柔性圆柱上任意位置的横流向和顺流向位移均方根。图 4所示为选取圆柱中点位置,由位移模型得到的横流向及顺流向位移均方根随轴向力和流速变化的三维图像。与位移模型类似,频率模型能够对该范围内圆柱的主控频率进行预测,预报结果如图 5中2个方向的主控频率随变量变化的三维图所示。

|
Download:
|
| 图 4 位移模型在圆柱中点处的预报结果 Fig. 4 Prediction results of displacement models at the midpoint of the cylinder | |

|
Download:
|
| 图 5 频率模型预报结果 Fig. 5 Prediction results of frequency models | |
图 4中可以看出,横流向位移均方根在0.05~0.4 m/s流速范围内,随流速增大先上升后下降,变化速度较快,有明显锁频现象。当流速大于0.4 m/s时,位移均方根再次出现上升和下降,但起伏较小。顺流向位移均方根随流速变化与横流向相似,但峰值较小,最大不超过0.3,且整体后移,在流速超过0.8 m/s后出现第3次上涨。位移均方根随轴向力变化时,不论横流向和顺流向都在轴向力为400 N左右出现下降,这可能是由于实验数据中只涉及了4个轴向力,数据样本过少所造成的。
图 5中的主控频率预报结果显示,横流向和顺流向主控频率都随流速增大而增大,数值上,顺流向主控频率大概是横流向的2倍左右。轴向力方向除了一些位置主控频率有小幅波动,其他位置无明显规律性变化。
位移模型和频率模型的预报结果整体不论在趋势还是数值大小上都与实际相符,且图 2、图 3中的对比结果中的决定系数也达到了很高的水准,足以证明采用BP神经网络所构建出的VIV响应预报模型拥有较高的可信度。
3 结论1) 以柔性圆柱涡激振动实验数据为基础,分别建立了预报柔性圆柱VIV在横流向和顺流向上的位移及频率响应的4个BP神经网络模型。
2) 预报模型可以实现在轴向力为277~551 N,流速为0.05~1.00 m/s,预测该柔性圆柱发生涡激振动时,任意点位置的横流向和顺流向位移均方根大小,以及2个方向的主控频率。
3) BP神经网络模型的构建只需要提供数据样本,而不深究VIV的力学机理,具有高度自学习和自适应的能力,相比常见的预报方法具有一定优势。
4) 位移预报模型的决定系数R2超过0.8,频率预报模型的R2更可以达到0.9以上;且位移均方根和主控频率的预报结果在随变量的变化趋势和数值上整体与实际相符,证明模型具备优秀的预测性能。
由于本文建立BP神经网络模型所使用的数据样本存在一定的局限性,涉及的变量仅有轴向力、流速及空间位置,因此该模型仅可对实验圆柱进行预报,还无法预测如质量比、圆柱直径等因素对VIV响应的影响。但此研究内容为柔性圆柱涡激振动的响应预报提供了一种新的思路,利用BP神经网络的研究还处于探索阶段,进一步引入更多变量并扩大变量范围,使用完备的数据样本后,可得到具备普适性的预报模型。
| [1] |
WILLIAMSON C H K, GOVARDHAN R. A brief review of recent results in vortex-induced vibrations[J]. Journal of wind engineering and industrial aerodynamics, 2008, 96(6/7): 713-735. (  0) 0)
|
| [2] |
GABBAI R D, BENAROYA H. An overview of modeling and experiments of vortex-induced vibration of circular cylinders[J]. Journal of sound and vibration, 2005, 282(3/5): 575-616. (  0) 0)
|
| [3] |
万德成, 端木玉. 深海细长柔性立管涡激振动数值分析方法研究进展[J]. 力学季刊, 2017, 38(2): 179-196. WAN Decheng, DUAN Muyu. A recent review of numerical studies on vortex-induced vibrations of long slender flexible risers in deep sea[J]. Chinese quarterly of mechanics, 2017, 38(2): 179-196. (  0) 0)
|
| [4] |
LUCOR D, IMAS L, KARNIADAKIS G E. Vortex dislocations and force distribution of long flexible cylinders subjected to sheared flows[J]. Journal of fluids and structures, 2001, 15(3/4): 641-650. (  0) 0)
|
| [5] |
HUANG K, CHEN H C, CHEN C R. Time-domain simulation of riser VIV in sheared current[C]//The International Conference on Offshore Mechanics and Arctic Engineering. San Diego, 2007: 911-920.
(  0) 0)
|
| [6] |
HUANG K, CHEN H C, CHEN C R. Flexible catenary riser VIV simulation in uniform current[C]//Proceedings of the 20th International Offshore and Polar Engineering Conference. Beijing, 2010: 1129-1135.
(  0) 0)
|
| [7] |
KAMBLE C. 3D VIV fatigue analysis using CFD simulation for long marine risers[C]//Proceedings of the 26th International Ocean and Polar Engineering Conference. Rhodes, 2016.
(  0) 0)
|
| [8] |
YAMAMOTO C T, MENEGHINI J R, SALTARA F, et al. Numerical simulations of vortex-induced vibration on flexible cylinders[J]. Journal of fluids and structures, 2004, 19(4): 467-489. (  0) 0)
|
| [9] |
VANDIVER J K, LI Li. SHEAR7 V4.4 program theoretical manual[M]. Cambridge: Massachusetts Institute of Technology, 2005.
(  0) 0)
|
| [10] |
LARSEN C M, LIE H, PASSANO E, et al. VIVANA-theory manual (version 3.7)[M]. Trondheim: Norwegian Marine Technology Research Institute, 2009.
(  0) 0)
|
| [11] |
袁昱超, 薛鸿祥, 唐文勇. 振荡流下柔性立管涡激振动时域响应研究[J]. 振动与冲击, 2018, 37(13): 56-64, 91. YUAN Yuchao, XUE Hongxiang, TANG Wenyong. Vortex-induced vibration time domain responses of flexible risers under oscillatory flows[J]. Journal of vibration and shock, 2018, 37(13): 56-64, 91. (  0) 0)
|
| [12] |
HARTLEN R T, CURRIE I G. Lift-oscillator model of vortex-induced vibration[J]. Journal of the engineering Mechanics, 1970, 96(5): 577-591. (  0) 0)
|
| [13] |
FACCHINETTI M L, DE LANGRE E, BIOLLEY F. Vortex-induced travelling waves along a cable[J]. European journal of mechanics-B/Fluids, 2004, 23(1): 199-208. DOI:10.1016/j.euromechflu.2003.04.004 (  0) 0)
|
| [14] |
徐万海, 马烨璇, 张书海, 等. 柔性圆柱涡激振动流体力系数识别方法[J]. 中国海洋平台, 2019, 34(1): 1-8, 15. XU Wanhai, MA Yexuan, ZHANG Shuhai, et al. Identification methods for hydrodynamic coefficients of flexible cylinder subjected to vortex-induced vibration[J]. China offshore platform, 2019, 34(1): 1-8, 15. (  0) 0)
|
| [15] |
陈明. MATLAB神经网络原理与实例精解[M]. 北京: 清华大学出版社, 2013: 4-165. CHEN Ming. Principles and examples of MATLAB neural network[M]. Beijing: Tsinghua University Press, 2013: 4-165. (  0) 0)
|
| [16] |
WONG E W C, KIM D K. A simplified method to predict fatigue damage of TTR subjected to short-term VIV using artificial neural network[J]. Advances in engineering software, 2018, 126: 100-109. DOI:10.1016/j.advengsoft.2018.09.011 (  0) 0)
|
| [17] |
WU Wenhua, SUN Hai, LV Baicheng, et al. Modelling of a hydrokinetic energy converter for flow-induced vibration based on experimental data[J]. Ocean engineering, 2018, 155: 392-410. (  0) 0)
|
| [18] |
林海花.隔水管涡激动力响应及疲劳损伤可靠性分析[D].大连: 大连理工大学, 2008. LI Haihua. Analysis of VIV dynamic response and fatigue damage reliability for marine riser[D]. Dalian: Dalian University of Technology, 2008. (  0) 0)
|
| [19] |
马烨璇.柔性圆柱涡激振动的水动力学系数识别[D].天津: 天津大学, 2017. MA Yexuan. Identification of hydrodynamic coefficients for a flexible cylinder undergoing vortex-induced vibration[D]. Tianjin: Tianjin University, 2017. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


