2. 福建省船舶与海洋工程重点实验室, 福建 厦门 361021;
3. 哈尔滨工程大学 动力与能源工程学院, 黑龙江 哈尔滨 150001
2. Fujian Provincial Key Laboratory of Naval Architecture and Ocean Engineering, Xiamen 361021, China;
3. College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China
双原动机动力装置是由2种型式或不同功率的推进装置组成, 通常情况下, 在低速工况下工作时, 由其中一台原动机单独工作;而在高速直至全工况时, 由另一台高功率的原动机单独工作或两个原动机共同在线工作。双原动机驱动负荷的动力装置比较适宜于负荷变化范围大的动力系统。如大型工程机械, 舰船推进等, 也可以用于移动应急电站, 以提高供电的可靠性[1-2]。自动同步离合器作为双原动机动力装置中的常用的传动部件, 其性能直接影响着系统的整体性能, 自动同步离合器在接入过程前期, 要求阻尼油腔无阻尼力或者产生较小的阻尼力, 这样有利于提高切换过程的机动性能。在自动同步离合器的接入过程中, 中间传动部件处于零阻尼状态, 角加速度为正值, 中间传动部件与动力输出部件之间就会产生过大的转速差进而在二者之间产生剧烈的结合碰撞, 在接入运动的后期, 即后5 mm, 液压阻尼油腔产生较大的阻尼力, 有效的缓解了中间传动部件与动力输出部件之间的结合碰撞力, 从而避免损坏离合器;另一方面, 对处于脱离运动状态的自动同步离合器来说, 为防止很小的转速差就产生脱开运动, 在脱开动作的前段, 液压阻尼油腔产生的驻退阻尼可以防止离合器产生频繁的脱开和接入动作, 现有的条件下, 通过人工更换阻尼螺栓这个配件可以调整阻尼力的大小[3-6]。
本文在双原动机(以柴油机和燃气轮机双原动机为例)及传动部件的仿真平台上通过改变柴油机的控制规律(调速器的PID控制参数), 在恒阻尼条件下就改变工作模式切换过程的时间参数进行可行性分析, 并结合实验结果进行比较研究。
1 原动机数学模型增压中冷柴油机的数学模型由以下6个部分组成[7]:
1) 柴油机本体模型为:
| $ T\frac{{{\rm{d}}\varphi }}{{{\rm{d}}t}} + k\varphi = q + {\theta _1}\rho - {\theta _2}{\alpha _n} $ | (1) |
式中:q为供油量波动系数;φ为柴油机曲轴角速度波动系数;ρ为增压压力变化;αn为耗能参数;k为系统结构系数;T为加速时间;θ1为增压压力增益;θ2为负荷装置调整增益。
2) 增压器数学模型为:
| $ {T_K}\frac{{{\rm{d}}{\varphi _K}}}{{{\rm{d}}t}} + {K_K}{\varphi _K} = \xi + {\theta _q}q - {\theta _\rho }\rho $ | (2) |
式中:ξ为无量纲的涡轮入口压力变化;θq和θρ为无量纲放大系数, 表示循环供油量和增压压力的波动对涡轮增压器的影响参数;φK为无量纲的增压器转子角速度改变;TK为速度调整时间;KK为涡轮增压器的自平衡因子。
3) 柴油机进气数学模型描述为:
| $ {k_B}\rho = {\varphi _K} - {\theta _B}\varphi $ | (3) |
式中:kB为进气管自平衡无量纲因子;θB为发动机曲轴角速度无量纲增益。
4) 柴油机排气单元数学模型为:
| $ {k_r}\xi = \varphi + {\theta _r}\rho - {\theta _G}q $ | (4) |
式中:kr为排气管自平衡无量纲系数;θr为增压压力放大系数;θG为循环供油量增益。
5) 供油系统数学模型为:
| $ {k_q}q = x $ | (5) |
式中:x为无量纲的曲轴角速度变化;kq为供油位置参数。
综合上述部件模型得到二阶线性非齐次微分方程:
| $ {a_1}\frac{{{{\rm{d}}^2}\phi }}{{{\rm{d}}{t^2}}} + {a_2}\frac{{{\rm{d}}\phi }}{{{\rm{d}}t}} + {a_3}\phi = {a_r}\frac{{{\rm{d}}x}}{{{\rm{d}}t}} + {a_5}x - {a_6}\frac{{{\rm{d}}{\alpha _n}}}{{{\rm{d}}t}} - {a_7}{\alpha _n} $ | (6) |
式中系数由柴油机及增压器的静态特性来确定。在Matlab/Simulink环境中得到柴油机的数学模型[8-9]。模型表达了柴油机及增压器各部件仿真模块的连接以及相互之间的参数联系。
6) 调速器数学模型描述为:转速测量值和设定值形成的转速差信号作为比例积分微分调节器的输入参数, 经功率放大模块驱动执行单元为:
| $ {G_2}(s) = {K_p}\left( {1 + \frac{1}{{{T_i}s}} + {T_d}s} \right) $ | (7) |
式中:Kp为增益;Ti为积分环节时间参数;Td为微分环节时间参数。
电磁驱动机构是执行单元主要组成部分, 其作用是用来把控制器控制的输出信号线性变换为油门位置。其工作原理是驱动机构和弹簧弹力的力学平衡, 执行器单元的数学模型经拉普拉斯变换后表示为:
| $ {G_A}(s) = \frac{1}{{1 + {b_1}s + {b_2}{s^2} + {b_3}{s^3}}} $ | (8) |
式中b1、b2、b3为结构参数。
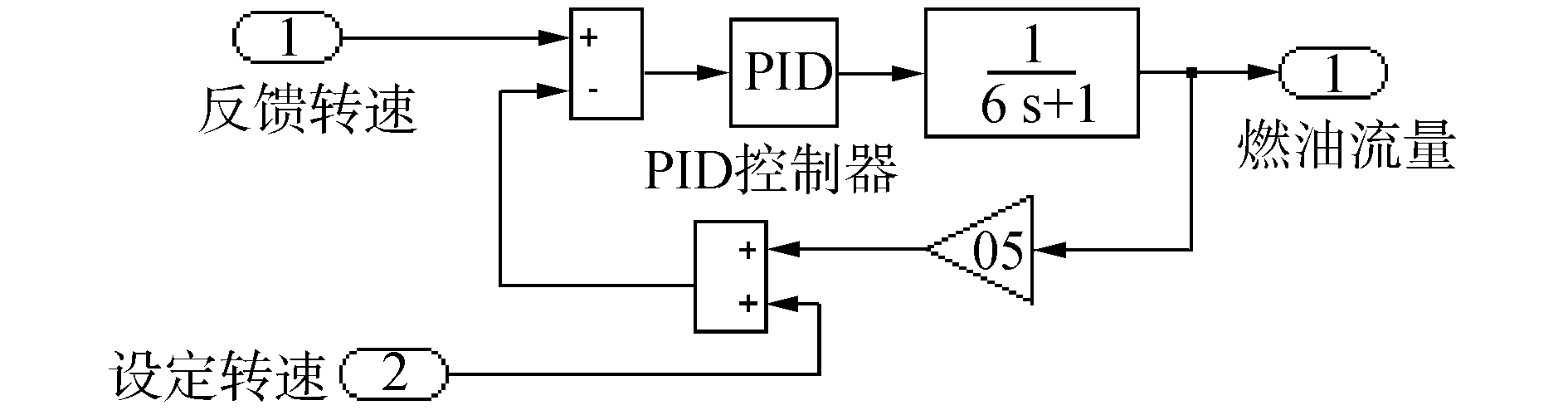
调速器的仿真模型如图 1所示, 模型中调速器根据转速差及负荷修正, 通过PID算法来控制齿杆的位置, 从而控制油门的大小。图中设定转速和初始转速由控制单元产生。
|
Download:
|
| 图 1 电子调速器仿真模型 Fig. 1 Simulation model of electronic governor | |
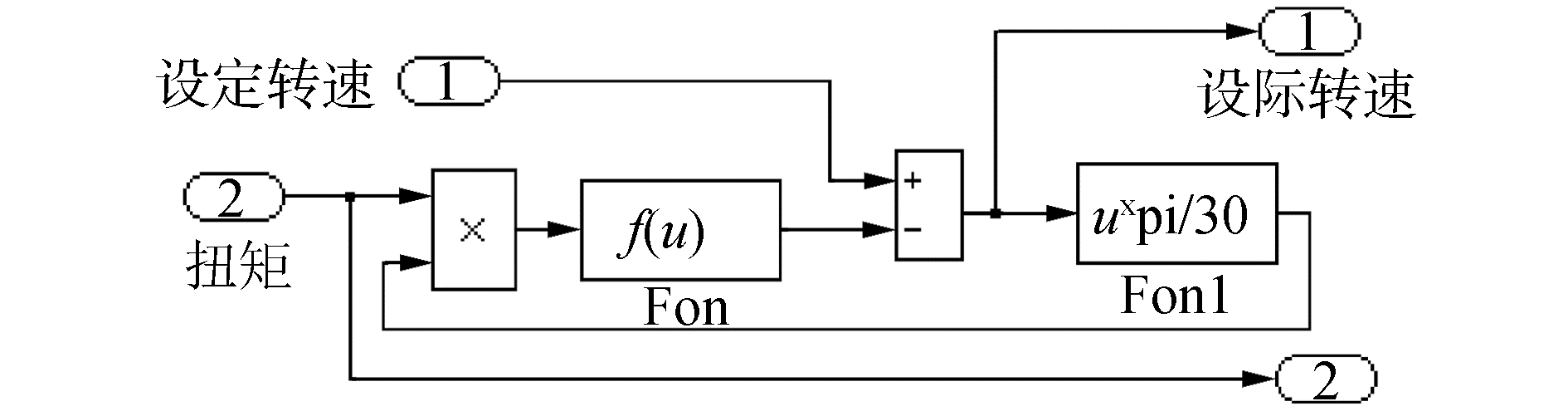
由于联合动力装置实验台燃气轮机采用的是定转速调节系统, 被调量只有1个, 即燃油流量Gf。鉴于该燃机的特点, 转速的调节范围小, 在额定负荷下, 变速齿轮箱输出转速为1 500 r/min。经多次实验得出燃机具有4%的静态下垂特性。通过对燃气轮机转速调节器的改造, 使燃气轮机机可以在小范围内调速。对于调节后的燃机转速和功率的关系, 可以认为是线性的, 尤其在驱动模式转换过程中, 燃机在较低负荷的运行状态更是如此。其静态下垂特性可表示为:
| $ {n_g} = {n_{g0}} - 60{N_g}/220.5 $ | (9) |
式中:ng、ng0分别为加负荷后转速和无负荷时转速;Ng为功率。
切换过程距离燃机运行的危险边界较远, 因此考虑其功率、转速的动态变化过程, 对其他如压气机出口温度和压力、涡轮排气温度等在仿真中不作计算。建立燃气轮机转速控制模型, 如图 2所示。
|
Download:
|
| 图 2 燃气轮机转速控制模型 Fig. 2 Gas turbine speed control model | |
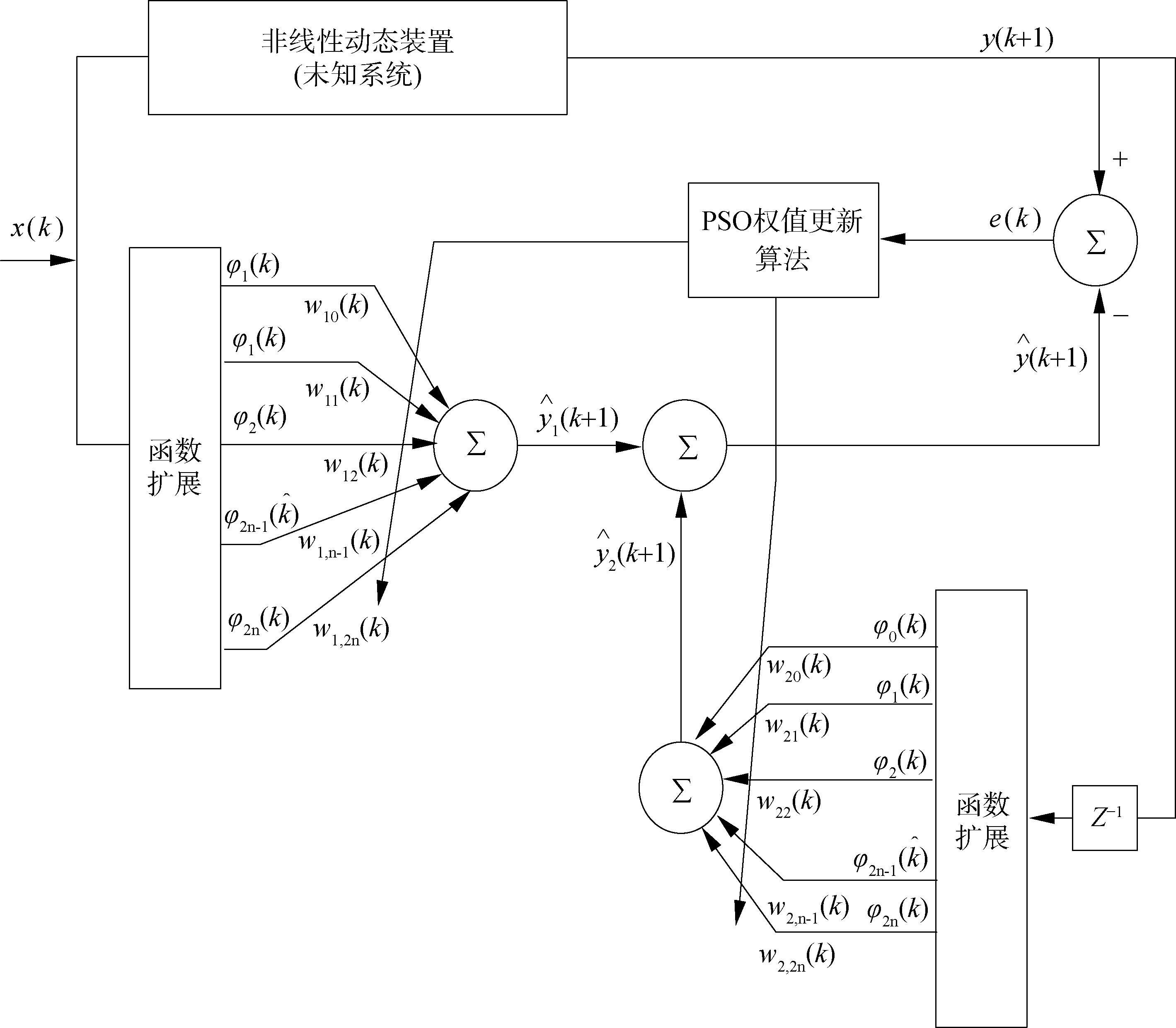
自动同步离合器仿真模型中, 输入参数为主动部件转速, 从动部件的转速以及主动部件的力矩, 输出则为发动机转速信号和自动同步离合器状态参数。当主动部件和从动输出部件之间的转速差大于一定值时自动同步离合器接入, 反之自动同步离合器脱开。离合器的完全接入或脱开之间存在一个滞后环节, 同时, 模型中对离合器的负载扭矩区间作了限值, 设计的扭矩峰值为工作值的1.1倍, 最小扭矩工作值的0.9倍, 这2个参数可以调整[10-12]。为了简化辨识模型和减少运算工作量, 本文基于函数链神经网络(functional link artificial neural networks, FLANN)和粒子群优化算法(particle swarm optimization, PSO), 构建一种非线性动态系统自适应辨识方法, 辨识过程中, 具有三角函数特征的神经网络用来逼近系统, 而粒子群算法主要用于训练, 获得与函数神经网络中各个三角函数相对应的权值, 以达到系统辨识的目的。非线性动态装置自适应辨识模型如文献[13]所示[13]。
系统辨识的模型在(k+1)时刻的输出为:
| $ \hat y(k + 1) = g[x(k)] + f[y(k)] $ | (10) |
式中:f和g分别表示函数神经网络结构的前馈和反馈部分, 其权值由粒子群算法来获取, 输入x(k)经非线性扩展为:
| $ \mathit{\boldsymbol{\varphi }}(k) = {[{\varphi _0}(k),{\varphi _1}(k),{\varphi _2}(k), \cdots ,{\varphi _{2n - 1}}(k),{\varphi _{2n}}(k)]^{\rm{T}}} $ | (11) |
其中:
| $ \left\{ {\begin{array}{*{20}{l}} {{\varphi _0}(k) = 1}\\ {{\varphi _1}(k) = {\rm{sin}}(\pi x(k))}\\ {{\varphi _2}(k) = {\rm{cos}}(\pi x(k))}\\ \vdots \\ {{\varphi _{2n - 1}}(k) = {\rm{sin}}(n\pi x(k))}\\ {{\varphi _{2n}}(k) = {\rm{cos}}(n\pi x(k))} \end{array}} \right. $ | (12) |
由此可看出, 扩展后三角函数有n项, 还有1项(首项)为单位输入, 由此可得到输入向量含有(2n+1)个分量。设式(11)和式(12)中在第k时刻输入向量的权值为:
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{W}}_1}(k) = [{w_{10}}(k),{w_{11}}(k),{w_{12}}(k), \cdots ,}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {w_{1,2n - 1}}(k),{w_{1,2n}}(k){]^{\rm{T}}}} \end{array} $ | (13) |
式(10)中第1部分的输出估计值为:
| $ {\hat y_1}(k + 1) = {\mathit{\boldsymbol{\varphi }}^{\rm{T}}}(k){\mathit{\boldsymbol{W}}_1}(k) $ | (14) |
式(10)中第2部分输出估计值也由式(12)得到:
| $ {\hat y_2}(k + 1) = {\mathit{\boldsymbol{\varphi }}^{\rm{T}}}(k){\mathit{\boldsymbol{W}}_2}(k) $ | (15) |
其中:
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{W}}_2}(k) = [{w_{20}}(k),{w_{21}}(k),{w_{22}}(k), \cdots ,}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {w_{2,2n - 1}}(k),{w_{2,2n}}(k){]^{\rm{T}}}} \end{array} $ | (16) |
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\varphi }}(k) = [{\varphi _0}(k),{\varphi _1}(k),{\varphi _2}(k), \cdots ,}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{2n - 1}}(k),{\varphi _{2n}}(k){]^{\rm{T}}}} \end{array} $ | (17) |
即:
| $ \left\{ {\begin{array}{*{20}{l}} {{\varphi _0}(k) = 1}\\ {{\varphi _1}(k) = {\rm{sin}}(\pi y(k))}\\ {{\varphi _2}(k) = {\rm{cos}}(\pi y(k))}\\ \vdots \\ {{\varphi _{2n - 1}}(k) = {\rm{sin}}(n\pi y(k))}\\ {{\varphi _{2n}}(k) = {\rm{cos}}(n\pi y(k))} \end{array}} \right. $ | (18) |
图 3所示模型的输出估计值为:
|
Download:
|
| 图 3 非线性动态装置自适应模型 Fig. 3 Adaptive model of nonlinear dynamic device | |
| $ \hat y(k + 1) = {\hat y_1}(k + 1) + {\hat y_2}(k + 1) $ | (19) |
粒子群算法是一种基于种群的随机优化技术[14], 在优化求解的时候, 首先寻求空间内随机初始化粒子, 每个粒子都有自己的位置和速度参数, 同时含有与被优化函数相关的适应值。在迭代过程中通过参数匹配的程序来实现自我更新, 并评价新的适应函数值, 适应函数值可由下式计算得到:
| $ E{\rm{ }} = \frac{{\mathop \sum \limits_{k = 1}^K {{[y(k) - \hat y(k)]}^2}}}{K} $ | (20) |
式中:K为输入样本个数;
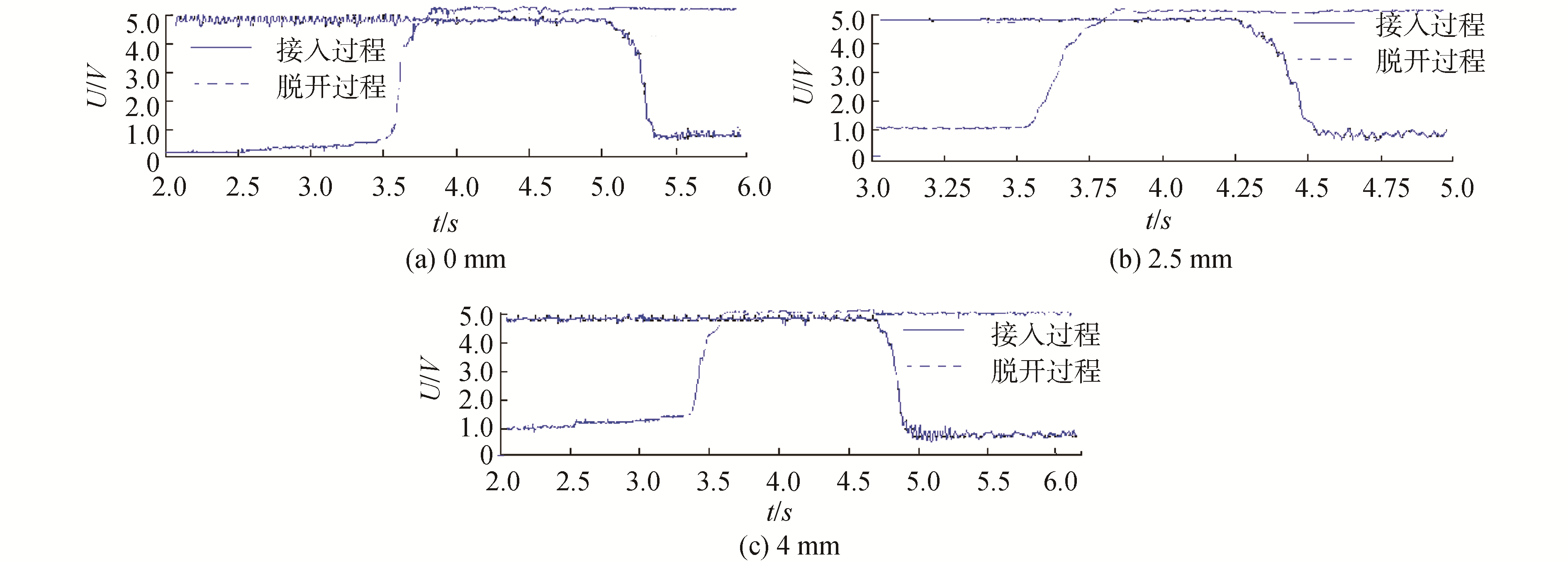
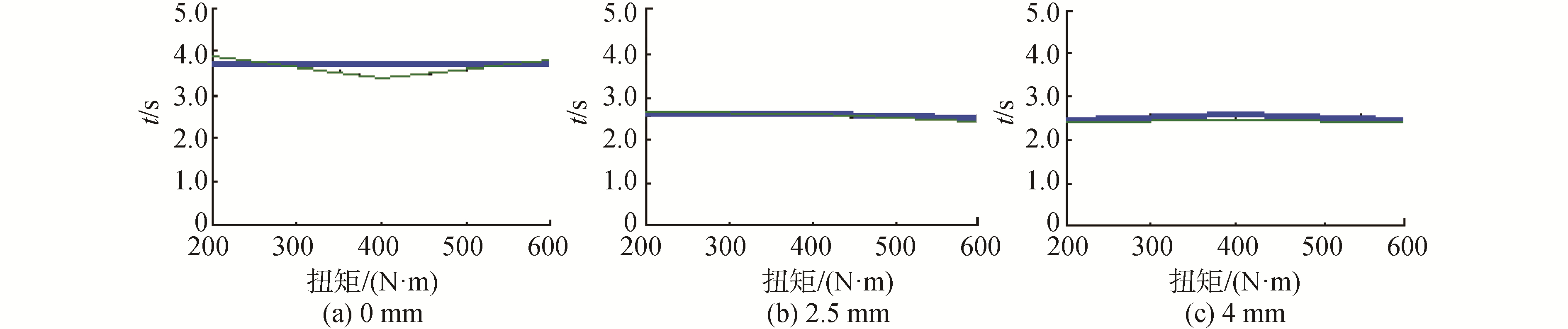
柴油机和燃气轮机携带各自的自动同步离合器通过传动系统与电涡流测功器相联接, 为减少自动同步离合器的结合碰撞带来的实验风险, 电涡流测功器把负荷设置在较低的区间。部分实验结果如图 4所示, 该实验结果是在200 N·m负荷不同阻尼孔0、2.5以及4 mm阻尼孔条件下获取的。
|
Download:
|
| 图 4 动力切换实验在200 N·m负荷不同阻尼孔条件下的时间参数 Fig. 4 Time parameters of power switching experiment with different damper hole condition under load 200 N·m | |
图 4中3组数据分别显示了200 N·m负荷不同阻尼孔条件下的时间参数, 每组数据有2部分。上部分显示动力由燃气轮机到柴油机切换柴油机端自动同步离合器接入过程曲线;下部分显示动力由燃气轮机到柴油机切换燃气轮机端自动同步离合器脱开过程曲线。接入时间的试验结果分别为0.37、0.29和0.26 s。
自动同步离合器的配件中准备了3种阻尼螺栓即0、2.5以及4 mm这3种规格, 仿真计算中模型采用0 mm的阻尼螺栓, 在200 N·m负荷条件下调节柴油机的控制器即图 1电子调速器模型的PID控制模块的参数(用调节方程描述, 记为调节方程1, 调节方程2, 调节方程3)图 5分别显示出了相同工况在3种不同调节方程控制下的切换时间参数中的接入时间。柴油机端分别为0.38、0.28和0.26 s(经过四舍五入得到), 与实验结果基本吻合。
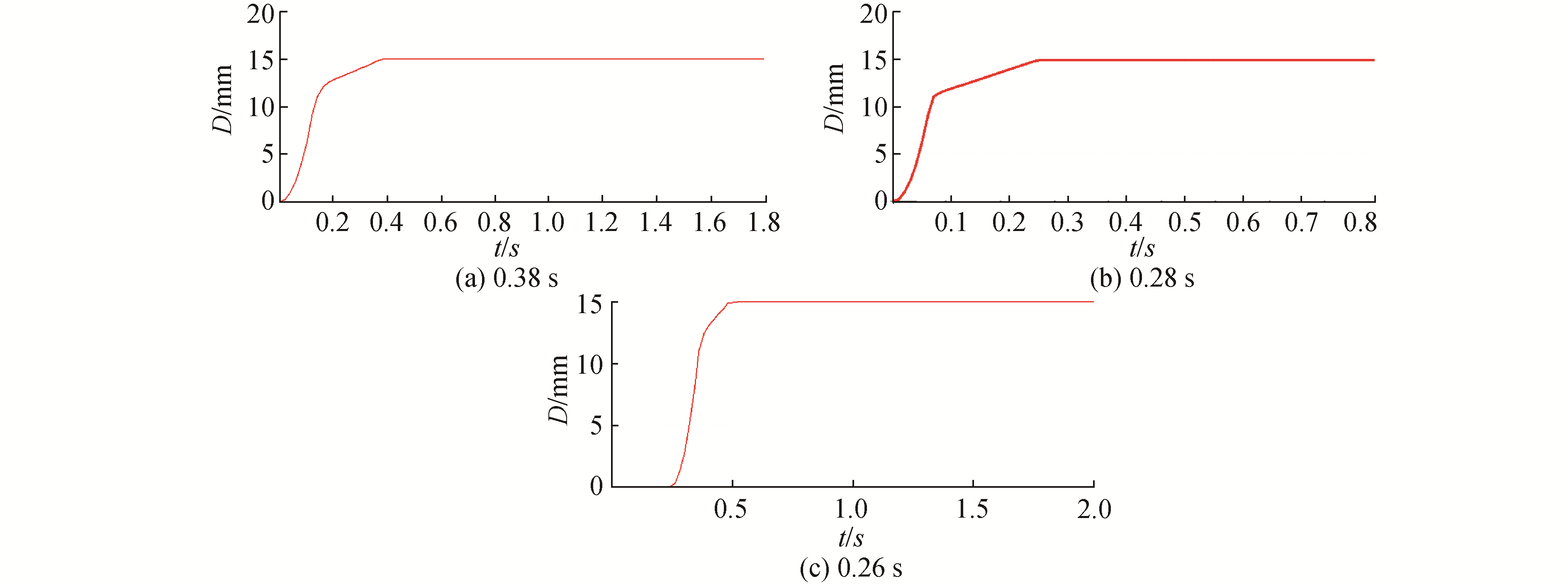
|
Download:
|
| 图 5 不同调节方程控制作用下的接入时间 Fig. 5 Meshing time controlled by different governing equations | |
从仿真结果可以看出, 以负荷200 N·m负荷为例, 为了免除了更换阻尼螺栓的工作, 2.5和4 mm阻尼孔条件下的接入时间, 可以通过改变调节方程在0 mm阻尼孔条件下获取。同时有理由推断在系统稳定以及传动系统强度能承受接入碰撞力的前提下, 接入时间可以在相应的时间段内连续可控。大量的实验结果显示阻尼孔从0~4 mm在高负荷下, 接入时间的改变非常微小。如图 6所示分别显示了0、2.5以及4 mm阻尼孔条件下接入时间随负荷的改变情况。
|
Download:
|
| 图 6 动力切换实验中接入时间随负荷的变化 Fig. 6 Change of meshing time with load in power switching experiment | |
实验中的阻尼改变是有限的, 在模型平台上通过连续的仿真发现当阻尼孔大于3.4 mm(接近)时高负荷下接入时间基本不发生改变。高负荷大阻尼孔的条件下自动同步离合器的阻尼油腔呈现较强的滞后性, 其本质和定量关系值得作深入的研究。动力切换发生的环境大部分在低负荷下[14-18]。
4 结论1) 建立了原动机的模型, 考虑传动系统特别是自动同步离合器的时滞性和非线性, 基于FLANN-PSO实现了传动装置非线性动态系统辨识, 为系统仿真提供了研究基础。
2) 通过控制程序修改控制参数比更换传动系统的实体部件更方便快捷。论证了恒阻尼控制的可行性, 同时对高负荷下的系统滞后特性进行了初步分析, 为该类型动力装置传动系统的设计提供了参考。
不足之处在于, 未能通过实验获得各种工况状态下的切换过程的时间参数, 更好的完成仿真结论的实验验证。可以通过实验结果进一步修正控制参数, 以实现不同状态下切换动作的参数自动在线识别以及控制参数的自主设定。
| [1] |
吴少华, 孙绍增, 李争起. 水平浓缩煤粉燃烧器关键技术的试验研究[J]. 动力工程, 1999, 19(2): 15-20. WU Shaohua, SUN Shaozeng, LI Zhengqi. Industrial experimental study of the key technique of horizo-ntal bias combustion burners[J]. Power Engineering, 1999, 19(2): 15-20. (  0) 0)
|
| [2] |
蒋德松, 谢春玲, 孙聿峰. 一种基于联合动力装置的船舶电力推进原动机模块[J]. 热能动力工程, 2003, 18(3): 248-251. JIANG Desong, XIE Chunling, SUN Yufeng. A com-bined power plant-based prime-mover module for m-arine electric propulsion[J]. Journal of Engineering for Thermal Energy and Power, 2003, 18(3): 248-251. DOI:10.3969/j.issn.1001-2060.2003.03.008 (  0) 0)
|
| [3] |
王敏.燃燃联合动力装置特性的仿真研究[D].哈尔滨: 哈尔滨工程大学, 2007. WANG Min. The simulation study on the dynamic behavior of COGAG power plant[D]. Harbin: Harbin Engineering University, 2007. (  0) 0)
|
| [4] |
孙佰仲.油页岩及半焦混合燃烧特性理论与试验研究[D].保定: 华北电力大学能源动力与机械工程学院, 2008. SUN Baizhong. Theory and experimental investigationon combustion characteristics of oil shale and semi-coke blends[D]. Baoding: North China Electric Power University, 2008. (  0) 0)
|
| [5] |
姚黎明.船舶柴-燃联合主动力推进装置及其控制系统的建模与仿真研究[D].大连: 大连理工大学, 2008. YAO Liming. The study of modeling and simulation for marine main combined power plant of diesel or gas turbine and its control system[D]. Dalian: Dalian University of Technology, 2008. (  0) 0)
|
| [6] |
董喆渊.联合动力装置动力学仿真分析与研究[D].上海: 上海交通大学, 2009. DONG Zheyuan. Dynamic Simulation Analysis and Research of Combined Power Plant[D]. Shanghai: Sh-anghai Jiaotong University, 2008. (  0) 0)
|
| [7] |
滕万庆.柴油机数字式电子调速系统智能控制技术研究[D].哈尔滨: 哈尔滨工程大学, 1997. TENG Wanqing. Research on intelligent control tec-hnology of digital electronic speed regulation syste-m for diesel engine[D]. Harbin: Harbin Engineering University, 1997. (  0) 0)
|
| [8] |
曹安港.柴-燃联合动力并车系统冲击及频响特性仿真分析[D].哈尔滨: 哈尔滨工程大学, 2014. CAO Angang. Impact and frequency simulation analy-sis of combined diesel and gas power jiont system[D].Harbin: Harbin Engineering University, 2014. (  0) 0)
|
| [9] |
田颖, 孙聿峰, 卢青春. 基于Matlab的自动同步离合器建模与仿真[J]. 清华大学学报(自然科学版), 2004, 44(2): 255-257. TIAN Ying, SUN Yufeng, LU Qingchun. Simulation of synchronous-self-shifting clutches based on Matlab[J]. Journal of Tsinghua University(science and technology), 2004, 44(2): 255-257. DOI:10.3321/j.issn:1000-0054.2004.02.032 (  0) 0)
|
| [10] |
吴启泉.大型燃气轮机试验系统建模与仿真研究[D].镇江: 江苏科技大学, 2013. WU Qiquan. The modeling study and simulation of the large gas turbine's test system[D]. Zhenjiang: Jiangsu University of Science and Technology, 2013. (  0) 0)
|
| [11] |
JIANG Desong. The study on dynamic parameters of CODOG in the mode switching process[Z]. Beijing: 2008 IEEE/ASME International Conference on Mechatronics and Embedded Systems and Applications, MESA 2008, 2008.
(  0) 0)
|
| [12] |
JIANG Desong. The controller design for ship wet compression and experimental study[Z]. Chengdu: 2010 Asia-Pacific Power and Energy Engineering Conference, 2010.
(  0) 0)
|
| [13] |
王荣杰, 朱昱. 基于FLANN的非线性动态系统辨识[J]. 集美大学学报(自然科学版), 2011, 16(2): 128-133. WANG Rongjie, ZHU Yu. Nonlinear dynamic systemidentification based on FLANN[J]. Journal of Jimei University(natural science), 2011, 16(2): 128-133. DOI:10.3969/j.issn.1007-7405.2011.02.010 (  0) 0)
|
| [14] |
陈虹丽, 王子元, 赵凯岐. 船舶燃机电机混合动力控制方法[J]. 海军航空工程学院学报, 2016, 31(1): 63-66. CHEN Hongli, WANG Ziyuan, ZHAO Kaiqi. Hybrid power control method of ship burning gas turbine and motor[J]. Journal of Naval Aeronautical and Astronautical University, 2016, 31(1): 63-66. (  0) 0)
|
| [15] |
Clevenger Mark. CODOG system to power Navy's new X-Craft[J]. Diesel and Gas Turbine Worldwide, 2013, 35(4): 48. (  0) 0)
|
| [16] |
JIANG Desong, WANG Rongjie. Research on intelligent ultrasonic thickness measurement system applied to large area of hull[J]. High Technology Letters, 2017, 23(1): 77-83. (  0) 0)
|
| [17] |
GUO Jianghua, LU Jinhui, Hou Xinguang. Building of marine power equipment model based on wavelet neural network[J]. Journal of Wuhan University of Technology (transportation science and engineering), 2008, 32(5): 929-932. (  0) 0)
|
| [18] |
CHEN Yutao, ZENG Fanming, CHEN Guojun. Model of parallel running controller and analysis of characteristics of marine CODAD propulsion plant based on single governor method[J]. Journal of Wuhan University of Technology (transportation science and engineering), 2008, 32(6): 1039-1047. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


