2. 中国工程物理研究院 化工材料研究所, 四川 绵阳 621000
2. Institute of Chemical Materials, China Academy of Engineering Physics, Mianyang 621000, China
随着机械臂越来越多的应用于装配、手术[1]、协作等任务,对机械臂的末端定位精度有着越来越高的要求。目前,机械臂末端的位置和姿态无法直接进行测量,通常使用机械臂的运动学模型和关节参数间接计算得到。但是由于制造公差、磨损、传输误差、安装位置、环境变化等因素的影响,实际的运动学参数与其名义值之间存在偏差,若仍使用运动学参数的名义值计算末端位姿,将会降低机械臂末端位姿的定位精度。所以,为了提高机器人的绝对定位精度,必须对机器人运动学参数进行有效的标定,这也一直是机器人学研究领域的难点之一。
学者针对运动学参数标定问题已经开展了许多研究工作。通常基于建立的运动学误差模型,使用高精度的测量仪器,如坐标测量机[2]、激光跟踪干涉仪[3]、伸缩式球杆仪[4],测量真实的末端位姿,然后用于标定运动学参数。虽然这类方法标定精度高,但是测量仪器非常昂贵且标定过程十分复杂,并且对安装调试和测量过程的技术要求较高。基于视觉的标定方法[5-8]成本低且易于使用,相机通常固定在机械臂末端或工作环境中的某一位置,用于测量机械臂末端的实际位姿,然后根据测量的位姿完成机械臂几何结构参数的标定。在这些方法中,相机作为一种测量工具测量实际的末端位姿,相机视野和相机参数误差对运动学参数的标定结果有很大影响。
为了避免测量设备对标定结果的影响,Bennett等[9]提出了运动约束方法,通过在机械臂末端添加约束条件构建封闭运动链,利用关节角数据及闭环运动学方程辨识运动学参数。Yin等[10]利用安装在机械臂末端的相机和激光传感器构建点约束,只利用关节角数据完成标定;Joubair等[11]利用距离约束和球面约束大幅提高了六自由度机械臂的定位精度;Shi等[12]通过采样针到达采样盒中的多个点,利用采样盒与机器人的几何约束关系进行运动学参数标定,但是需要在机械臂末端安装一个特殊设计的采样针。
为了避免使用昂贵的高精度仪器及特定的标定设备,本文提出一种基于相机光轴虚拟约束的机械臂运动学参数标定方法,相机不用于测量末端位姿,而是提供光轴作为虚拟约束,降低了相机参数及视野对运动学参数标定结果的影响,使用关节角数据即可完成标定。
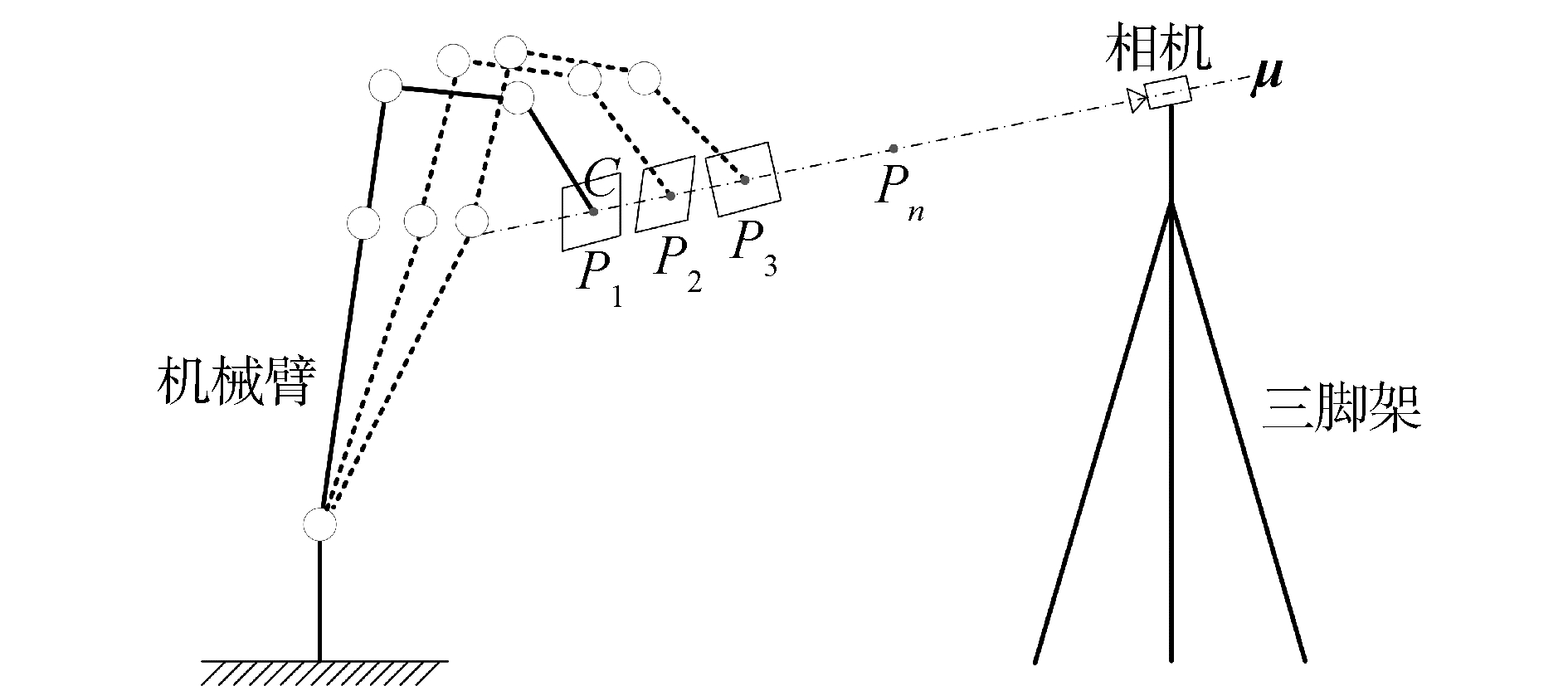
1 基于相机光轴虚拟约束的标定方法本文提出的基于光轴虚拟约束的标定系统包括一台待标定机械臂和一台安装在工作环境中的相机,如图 1所示。为了降低相机畸变对标定结果的影响,根据镜头的畸变原理,在镜头光轴中心附近几乎没有畸变。因此将相机的光轴向量μ作为虚拟直线约束,选定机械臂末端标定板的一个固定位置C作为特征点,使用视觉控制方法控制机械臂,使特征点C依次到达光轴上的多个位置P1,P2,…,Pn。
|
Download:
|
| 图 1 基于光轴虚拟约束的标定方法 Fig. 1 The calibration method based on virtual constraint of optical axis | |
此标定方法的具体步骤可分为3步:
1) 建立运动学误差模型:使用改进的Denavit-hartenberg方法建立机械臂的运动学模型,在此基础上建立基于直线虚拟约束的误差模型,描述对齐误差与运动学参数误差之间的关系,其中对齐误差是指机械臂末端在各位置点处名义位置横向分量的差;
2) 对齐误差矩阵计算:使用基于图像的视觉控制方法控制机械臂,使末端标定板上的特征点在合理误差范围内依次到达相机光轴上的多个位置点,记录机械臂位于每个位置点处的关节角,根据正运动学模型计算特征点在机械臂基坐标系下的对齐误差矩阵;
3) 运动学参数标定:根据运动学误差模型及计算的对齐误差矩阵,使用迭代最小二乘法估计运动学参数误差向量。
2 机械臂运动学误差模型 2.1 运动学模型串联机械臂的运动学模型是指末端执行器的位姿和基座之间的关系。用于标定的运动学模型需要满足:1)完备性:模型参数必须足够用于描述实际运动学模型与其名义值的偏差;2)参数最少化:模型中不包括多余的参数;3)连续性:机械臂末端的微小变化会导致运动学参数的微小变化[13]。
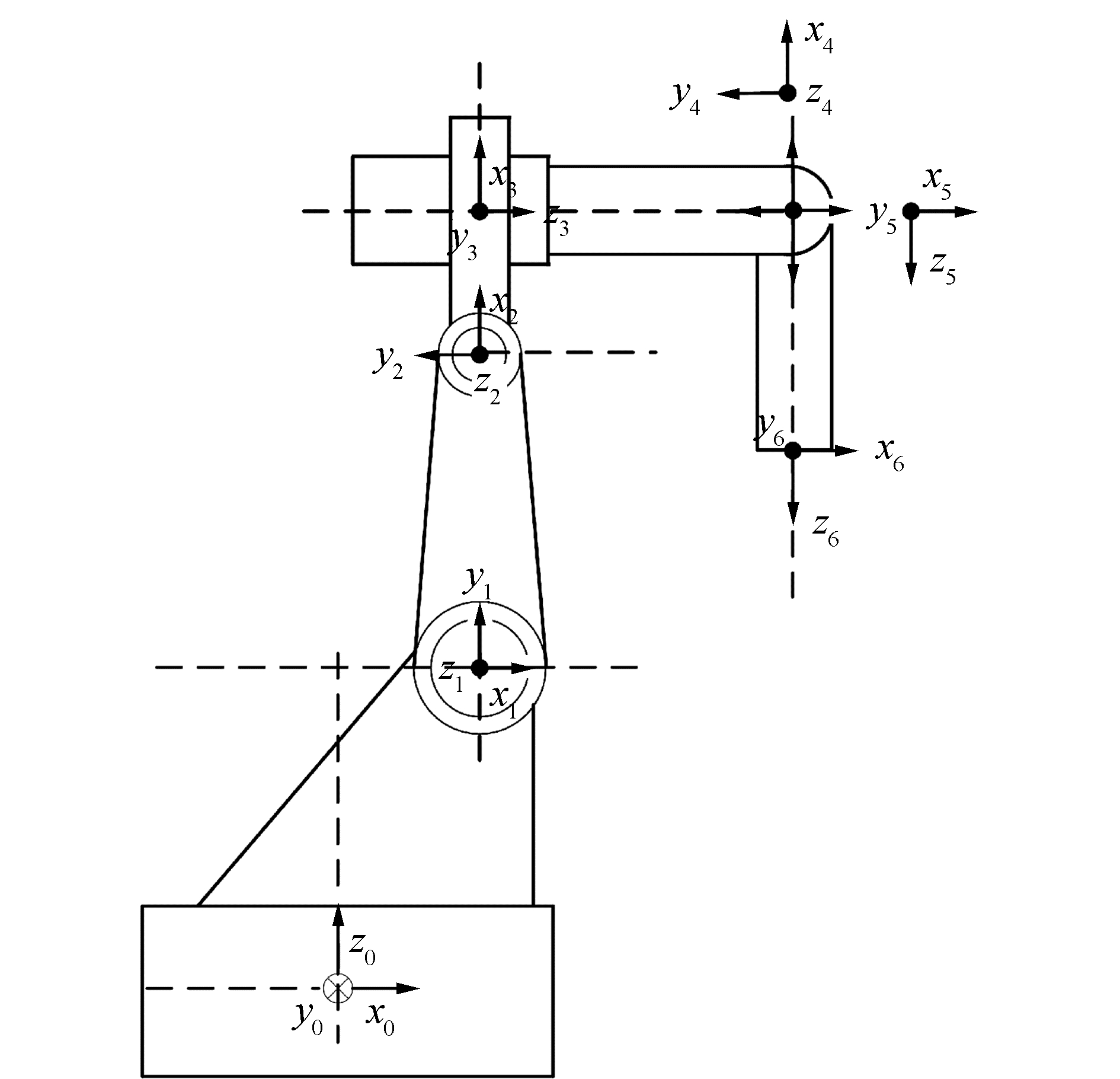
通常使用DH模型描述机械臂的运动学,但是当机械臂的相邻连杆近似平行时,基于DH模型建立的机械臂误差模型不连续,标定时可能产生较大误差。改进的DH模型[14]避免了复杂的模型转换,建模过程简便,解决了DH模型不连续的问题。本文采用改进的DH模型对Reinovo-6R工业机械臂进行运动学建模,其连杆坐标系如图 2所示。
|
Download:
|
| 图 2 Reinovo机械臂连杆坐标系 Fig. 2 Reinovo robot with link frames | |
六自由度机械臂的变换矩阵为:
| $ {}^0{\mathit{\boldsymbol{T}}_6} = {}^0{\mathit{\boldsymbol{T}}_1}{}^1{\mathit{\boldsymbol{T}}_2} \cdots {}^5{\mathit{\boldsymbol{T}}_6} = \prod\limits_{i = 1}^6 {{}^{i - 1}{\mathit{\boldsymbol{T}}_i}} $ | (1) |
式中:i-1Ti为第i-1个坐标系与第i个坐标系之间的变换矩阵。针对Reinovo机械臂的构型,对不同的关节轴使用不同的方法建模,其中关节轴1和关节轴2近似平行,采用改进的DH方法建立运动学模型,变换矩阵1T2为:
| $ \begin{array}{*{20}{c}} {{}^1{\mathit{\boldsymbol{T}}_2} = }\\ {\left[ {\begin{array}{*{20}{c}} {{c_{{\theta _2}}}{c_{{\beta _2}}} - {s_{{\theta _2}}}{s_{{\alpha _2}}}{s_{{\beta _2}}}}&{ - {s_{{\theta _2}}}{c_{{\alpha _2}}}}&{{c_{{\theta _2}}}{s_{{\beta _2}}} + {s_{{\theta _2}}}{s_{{\alpha _2}}}{s_{{\beta _2}}}}&{{\alpha _2}{c_{{\theta _2}}}}\\ {{s_{{\theta _2}}}{c_{{\beta _2}}} + {c_{{\theta _2}}}{s_{{\alpha _2}}}{s_{{\beta _2}}}}&{{c_{{\theta _2}}}{c_{{\alpha _2}}}}&{{s_{{\theta _2}}}{s_{{\beta _2}}} - {c_{{\theta _2}}}{s_{{\alpha _2}}}{c_{{\beta _2}}}}&{{\alpha _2}{s_{{\theta _2}}}}\\ { - {c_{{\alpha _2}}}{s_{{\beta _2}}}}&{{s_{{\alpha _2}}}}&{{c_{{\alpha _2}}}{c_{{\beta _2}}}}&0\\ 0&0&0&1 \end{array}} \right]} \end{array} $ | (2) |
其他关节轴采用标准的DH方法建模,变换矩阵为:
| $ {}^{i - 1}{\mathit{\boldsymbol{T}}_i} = \left[ {\begin{array}{*{20}{c}} {{\rm{c}}{\theta _i}}&{ - {\rm{s}}{\theta _i}{\rm{c}}{\alpha _i}}&{{\rm{s}}{\theta _i}{\rm{s}}{\alpha _i}}&{{a_i}{\rm{c}}{\theta _i}}\\ {{\rm{s}}{\theta _i}}&{{\rm{c}}{\theta _i}{\rm{c}}{\alpha _i}}&{ - {\rm{c}}{\theta _i}{\rm{s}}{\alpha _i}}&{{a_i}{\rm{s}}{\theta _i}}\\ 0&{{\rm{s}}{\alpha _i}}&{{\rm{c}}{\alpha _i}}&{{d_i}}\\ 0&0&0&0 \end{array}} \right] $ | (3) |
式中:ai、di、αi、θi、βi为第i(i=1, 2,…, 6)个连杆的运动学参数,分别为连杆长度、连杆偏距、连杆转角、关节角及平行关节轴的连杆转角。连杆2由参数a2、α2、θ2、β2描述,其他连杆由参数ai、di、αi、θi描述,各运动学参数的名义值见表 1。
| 表 1 Reinovo机械臂运动学参数名义值 Table 1 The nominal kinematic parameters of Reinovo robot |
Reinovo机械臂的每个连杆由4个运动学参数进行描述,共24个参数,令连杆参数向量为:
| $ \mathit{\boldsymbol{\varphi }} = {\left[ {\mathit{\boldsymbol{\varphi }}_1^{\rm{T}},\mathit{\boldsymbol{\varphi }}_2^{\rm{T}}, \cdots ,\mathit{\boldsymbol{\varphi }}_6^{\rm{T}}} \right]^{\rm{T}}},\mathit{\boldsymbol{\varphi }} \in {{\bf{R}}^{4{\rm{N}}}} $ | (4) |
连杆参数名义值φ′i与实际的参数φi存在偏差,假设第i个连杆参数误差为Δφi,则:
| $ {\mathit{\boldsymbol{\varphi }}_i} = {{\mathit{\boldsymbol{\varphi '}}}_i} + \Delta {\mathit{\boldsymbol{\varphi }}_i} $ | (5) |
实际的变换矩阵i-1Ti为:
| $ {}^{i - 1}{\mathit{\boldsymbol{T}}_i} = {}^{i - 1}{{\mathit{\boldsymbol{T'}}}_i}\left( {{{\mathit{\boldsymbol{\varphi '}}}_i} + \Delta {\mathit{\boldsymbol{\varphi }}_i}} \right) = {}^{i - 1}{{\mathit{\boldsymbol{T'}}}_i} + \Delta {}^{i - 1}{\mathit{\boldsymbol{T}}_i} $ | (6) |
式中:i-1T′i为变换矩阵i-1Ti的名义值;Δi-1Ti为变换矩阵的误差矩阵。
机械臂的实际运动学模型为:
| $ {}^0{\mathit{\boldsymbol{T}}_6} = {}^0{{\mathit{\boldsymbol{T'}}}_6} + \Delta {}^0{\mathit{\boldsymbol{T}}_6} = \prod\limits_{i = 1}^6 {\left( {{}^{i - 1}{{\mathit{\boldsymbol{T'}}}_i} + \Delta {}^{i - 1}{\mathit{\boldsymbol{T}}_i}} \right)} $ | (7) |
式中:0T6为基座到末端执行器的实际变换矩阵;0T′6为其名义值;Δ0T6为变换矩阵误差。忽略包含两个以上误差矩阵相乘的无穷小量,则:
| $ {}^0{\mathit{\boldsymbol{T}}_6} = \prod\limits_{i = 1}^6 {\left( {{}^{i - 1}{{\mathit{\boldsymbol{T'}}}_i}} \right)} + \sum\limits_{i = 1}^6 {\left( {\prod\limits_{j = 1}^{i - 1} {{}^{j - 1}{{\mathit{\boldsymbol{T'}}}_j}} } \right)\Delta {}^{i - 1}{\mathit{\boldsymbol{T}}_i}\left( {\prod\limits_{j = i + 1}^6 {{}^{j - 1}{{\mathit{\boldsymbol{T'}}}_j}} } \right)} $ | (8) |
| $ \Delta {}^0{\mathit{\boldsymbol{T}}_6} = {}^0{{\mathit{\boldsymbol{T'}}}_6}\left[ {\sum\limits_{i = 1}^6 {\mathit{\boldsymbol{U}}_{i + 1}^{ - 1}{\delta ^{i - 1}}{\mathit{\boldsymbol{T}}_i}{\mathit{\boldsymbol{U}}_{i + 1}}} } \right] = {}^0{{\mathit{\boldsymbol{T'}}}_6}\left[ {\begin{array}{*{20}{c}} {\Delta {P_{\rm{e}}}}\\ {\Delta {R_{\rm{e}}}} \end{array}} \right] $ | (9) |
| $ {\mathit{\boldsymbol{U}}_{i + 1}} = \prod\limits_{j = i + 1}^6 {{}^{j - 1}{{\mathit{\boldsymbol{T'}}}_j}} $ | (10) |
式中:
根据式(9)、(10)得到误差向量
| $ \left[ {\begin{array}{*{20}{c}} {\Delta {P_{\rm{e}}}}\\ {\Delta {R_{\rm{e}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{J_{{P_e},\varphi }}}\\ {{J_{R,\varphi }}} \end{array}} \right]\Delta {\varphi _{\theta = {\theta _m}}} $ | (11) |
相机光轴是指通过镜头中心与镜面垂直的直线,本文将相机光轴作为虚拟直线约束。在机械臂末端的标定板上选取一个特征点,控制机械臂使特征点运动到光轴上,由于运动学参数的实际值与名义值存在误差,基于机械臂的正运动学,使用运动学参数的名义值计算的特征点位置偏离光轴向量,利用对齐误差即可估计得到真实的运动学参数。
条光轴约束向量为μk,设特征点在光轴上的第i个实际位置为
| $ \mathit{\boldsymbol{P'}}_e^{\left( {i,k} \right)} - \mathit{\boldsymbol{P}}_e^{\left( {i,k} \right)} = {}^0{{\mathit{\boldsymbol{R'}}}_6} \cdot {\mathit{\boldsymbol{J}}_{p,\varphi }}\left( \theta \right)\left| {_{\theta = \theta _m^{\left( {i,k} \right)}}} \right. \cdot \Delta \varphi $ | (12) |
式中0R′6为机械臂基座到末端的名义姿态变换矩阵。
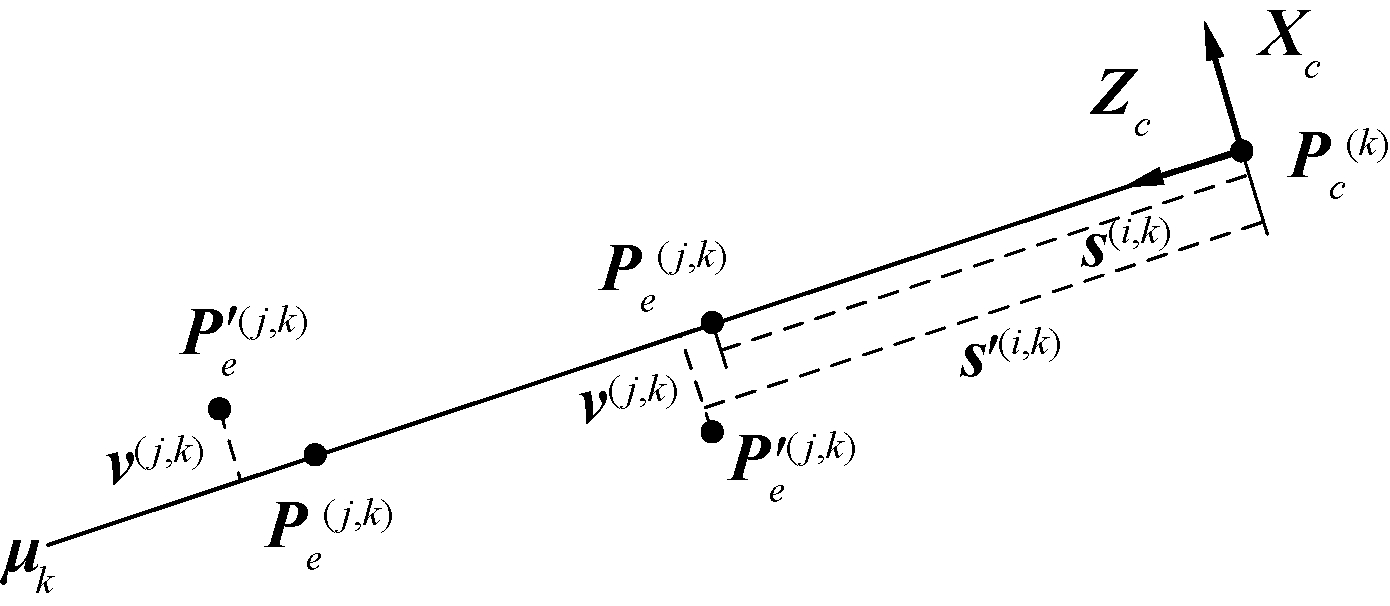
图 3为特征点位置示意图,
| $ \mathit{\boldsymbol{P}}_e^{\left( {i,k} \right)} = {\mathit{\boldsymbol{S}}^{\left( {i,k} \right)}}{\mathit{\boldsymbol{\mu }}_k} + \mathit{\boldsymbol{P}}_c^{\left( k \right)} $ | (13) |
| $ \mathit{\boldsymbol{P'}}_e^{\left( {i,k} \right)} = {{\mathit{\boldsymbol{S'}}}^{\left( {i,k} \right)}}{\mathit{\boldsymbol{\mu }}_k} + {\mathit{\boldsymbol{v}}^{\left( {i,k} \right)}} + \mathit{\boldsymbol{P}}_c^{\left( k \right)} $ | (14) |
|
Download:
|
| 图 3 特征点位置示意 Fig. 3 The schmatic diagram of the feature points poses | |
式中:S(i, k)是点
将式(13)、(14)代入式(12),得到:
| $ \begin{array}{*{20}{c}} {\left( {{\mathit{\boldsymbol{S}}^{\left( {i,k} \right)}} - {{\mathit{\boldsymbol{S'}}}^{\left( {i,k} \right)}}} \right){\mathit{\boldsymbol{\mu }}_k} + {\mathit{\boldsymbol{v}}^{\left( {i,k} \right)}} = }\\ {{}^0{{\mathit{\boldsymbol{R'}}}_6} \cdot {\mathit{\boldsymbol{J}}_{p,\varphi }}\left( \theta \right)\left| {_{\theta = \theta _m^{\left( {i,k} \right)}}} \right. \cdot \Delta \varphi } \end{array} $ | (15) |
定义算子[μk×]为
| $ \left[ {{\mathit{\boldsymbol{\mu }}_k} \times } \right]N = {\mathit{\boldsymbol{\mu }}_k} \times N,\forall N \in {{\bf{R}}^3} $ | (16) |
显然
| $ \left[ {{\mathit{\boldsymbol{\mu }}_k} \times } \right]{\mathit{\boldsymbol{v}}^{\left( {i,k} \right)}} = - \left[ {{\mathit{\boldsymbol{\mu }}_k} \times } \right]{}^0{{\mathit{\boldsymbol{R'}}}_6} \cdot {\mathit{\boldsymbol{J}}_{P,\varphi }}\left( \theta \right)\left| {_{\theta = \theta _m^{\left( {i,k} \right)}}} \right. \cdot \Delta \varphi $ | (17) |
把虚拟约束上2个不同的位置点pe(i, k)和pe(j, k)代入式(17)得到2个方程,2个方程作差
| $ \begin{array}{*{20}{c}} {\left[ {{\mathit{\boldsymbol{\mu }}_k} \times } \right]\left( {{\mathit{\boldsymbol{v}}^{\left( {j,k} \right)}} - {\mathit{\boldsymbol{v}}^{\left( {i,k} \right)}}} \right) = \left[ {{\mathit{\boldsymbol{\mu }}_k} \times } \right]\left[ {{}^0{\mathit{\boldsymbol{R}}_6}\left( \theta \right) \cdot } \right.}\\ {\left. {{\mathit{\boldsymbol{J}}_{P,\varphi }}\left( \theta \right)\left| {_{\theta = \theta _m^{\left( {i,k} \right)}}} \right. - {}^0{\mathit{\boldsymbol{R}}_6}\left( \theta \right) \cdot {\mathit{\boldsymbol{J}}_{P,\varphi }}\left( \theta \right)\left| {_{\theta = \theta _m^{\left( {i,k} \right)}}} \right.} \right] \cdot \Delta \varphi } \end{array} $ | (18) |
定义E(i, j, k)为对齐误差,
| $ {{\mathit{\boldsymbol{\bar E}}}^{\left( {i,j,k} \right)}} = \left[ {{\mathit{\boldsymbol{\mu }}_k} \times } \right]\left( {{\mathit{\boldsymbol{v}}^{\left( {j,k} \right)}} - {\mathit{\boldsymbol{v}}^{\left( {i,k} \right)}}} \right) $ | (19) |
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\bar J}}}^{\left( {i,j,k} \right)}} = \left[ {{\mathit{\boldsymbol{\mu }}_k} \times } \right]\left[ {{}^0{\mathit{\boldsymbol{R}}_6}\left( \theta \right) \cdot {\mathit{\boldsymbol{J}}_{P,\varphi }}\left( \theta \right)\left| {_{\theta = \theta _m^{\left( {j,k} \right)}}} \right. - } \right.}\\ {\left. {{}^0{\mathit{\boldsymbol{R}}_6}\left( \theta \right) \cdot {\mathit{\boldsymbol{J}}_{P,\varphi }}\left( \theta \right)\left| {_{\theta = \theta _m^{\left( {i,k} \right)}}} \right.} \right]} \end{array} $ | (20) |
则式(18)变为
| $ {\mathit{\boldsymbol{E}}^{\left( {i,j,k} \right)}} = {{\mathit{\boldsymbol{\bar J}}}^{\left( {i,j,k} \right)}}\Delta \varphi $ | (21) |
可以看出,(21)与位置点到相机坐标原点pc(k)的垂直距离无关,即无需相机的深度信息,消除了较低的相机深度估计精度的影响。
选择q条光轴进行测量,特征点分别运动到每条光轴上的p个位置点,构建位置对齐误差矩阵E回归矩阵Φ:
| $ \mathit{\boldsymbol{E}} = {\left[ {{\mathit{\boldsymbol{E}}^{{{\left( {1,1,1} \right)}^{\rm{T}}}}}, \cdots ,{\mathit{\boldsymbol{E}}^{{{\left( {1,p,1} \right)}^{\rm{T}}}}}, \cdots ,{\mathit{\boldsymbol{E}}^{{{\left( {1,1,q} \right)}^{\rm{T}}}}}, \cdots ,{\mathit{\boldsymbol{E}}^{{{\left( {1,p,q} \right)}^{\rm{T}}}}}} \right]^{\rm{T}}} $ | (22) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = {\left[ {{{\mathit{\boldsymbol{\bar J}}}^{{{\left( {1,1,1} \right)}^{\rm{T}}}}}, \cdots ,{{\mathit{\boldsymbol{\bar J}}}^{{{\left( {1,p,q} \right)}^{\rm{T}}}}}, \cdots ,{{\mathit{\boldsymbol{\bar J}}}^{{{\left( {1,1,q} \right)}^{\rm{T}}}}}, \cdots ,{{\mathit{\boldsymbol{\bar J}}}^{{{\left( {1,p,q} \right)}^{\rm{T}}}}}} \right]^{\rm{T}}} $ | (23) |
式中:E和Φ满足:
| $ \mathit{\boldsymbol{E}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\Delta \varphi $ | (24) |
式(24)即为求解运动学参数误差向量Δφ的误差模型,其未知参数数量小于方程个数,可以使用估计方法进行解算。
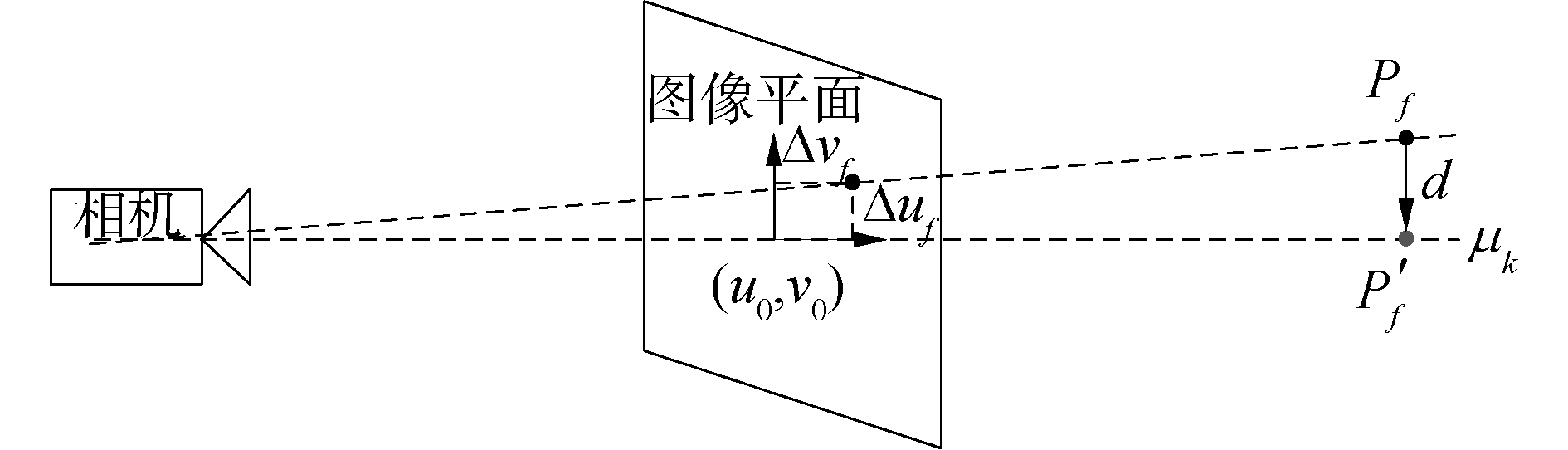
3 基于误差模型的运动学参数标定 3.1 位置对齐误差计算令机械臂末端的标定板完全位于相机的视野中,使用基于图像的视觉控制方法[15]控制机械臂运动,使标定板上的特征点到达光轴上,原理如图 4所示。
|
Download:
|
| 图 4 基于图像的视觉控制方法原理图 Fig. 4 The schematic diagram of visual control method based on image | |
假设特征点当前位置Pf与光轴μk的距离为d,特征点的图像坐标为(uf, vf),光轴中心点的图像坐标为(u0, v0),视觉控制的目的是使pf运动到光轴上的位置点P′f,此时d→0,根据相机的中心投影准则,光轴上的所有位置点均投影到图像平面的图像主点上,此时uf→u0, vf→v0。
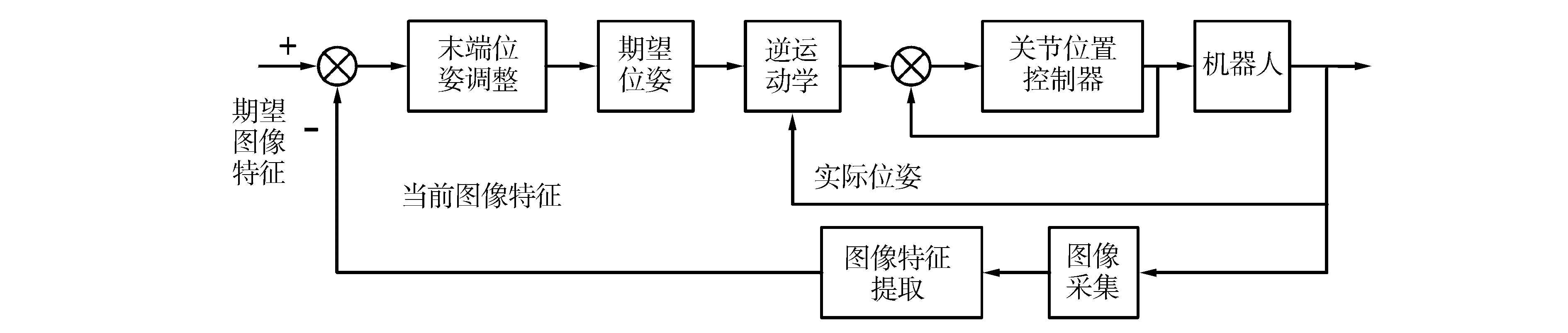
基于图像的视觉控制框图见图 5,由图像特征外环和机械臂位置控制内环组成。图像特征外环的控制目标是使特征点的图像坐标(uf, vf)与光轴中心点的图像坐标(u0, v0)重合,相机采集的当前图像作为视觉反馈,特征点在图像坐标中当前的实际坐标与期望坐标的偏差为(uf-u0, vf-v0),根据末端位姿调整策略将图像坐标偏差转化为机械臂末端在基坐标系下的偏差,实现图像空间偏差到笛卡尔空间偏差的转换。在机械臂控制内环中,根据反馈的机械臂末端位姿偏差计算得到期望位姿,根据逆运动学计算期望关节角,利用机械臂的关节位置控制器控制机械臂运动到期望的位置和姿态。其中在末端位姿调整策略中,图像偏差到笛卡尔空间偏差的转换矩阵为:
| $ \Delta \mathit{\boldsymbol{P}}_f^b = \mathit{\boldsymbol{R}}_c^b\Delta \mathit{\boldsymbol{P}}_f^c = P_c^b\left[ {\begin{array}{*{20}{c}} {\left( {{u_f} - {u_0}} \right){z_f}/{k_x}}\\ {\left( {{v_f} - {v_0}} \right){z_f}/{k_y}}\\ 0 \end{array}} \right] $ | (25) |
|
Download:
|
| 图 5 基于视觉控制的特征点自动对齐框图 Fig. 5 The diagram of the feature point alignment automatically based on visual control | |
式中:ΔPfb为特征点在基坐标系下实际位置与期望位置的偏差;Rcb为相机坐标系到机械臂基坐标系的旋转矩阵;ΔPfc为特征点在相机坐标系下的位置偏差,可根据相机模型计算得到;(u0, v0)可以通过相机标定得到;kx、ky为常系数。
在位置控制内环中,由于存在运动学参数误差,不能根据逆运动学将机械臂运动到期望位置,需要控制机械臂以小增量的方式运动,使特征点逐渐靠近光轴,直至特征点与光轴的距离到达可接受的误差范围。设k为小于1的正常数,机械臂末端的实际运动增量为:
| $ \Delta \mathit{\boldsymbol{P}} = k\Delta \mathit{\boldsymbol{P}}_f^b $ | (26) |
为了得到所有运动学参数的误差,并提高标定的精度,特征点需要依次到达光轴上多个位置,然后根据每个位置点处的关节角,使用正运动学计算特征点在机械臂基坐标系下的名义位置,根据式(19)及(22),得到位置对齐误差矩阵E。
3.2 运动学参数辨识算法根据计算的一条光轴上特征点的名义位置
| $ \frac{{x - {x_0}}}{m} = \frac{{y - {y_0}}}{n} = \frac{z}{1} $ | (27) |
其中,待求参数x0、y0、m、n为:
| $ \left[ {\begin{array}{*{20}{c}} m&{{x_0}}\\ n&{{y_0}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\sum {{x_i}{z_i}} }&{\sum {{x_i}} }\\ {\sum {{y_i}{z_i}} }&{\sum {{y_i}} } \end{array}} \right]{\left[ {\begin{array}{*{20}{c}} {\sum {z_i^2} }&{\sum {{z_i}} }\\ {\sum {{z_i}} }&s \end{array}} \right]^{ - 1}} $ | (28) |
根据回归矩阵Φ和前文计算的测量矩阵E,基于误差模型式(24),使用参数辨识算法即可估计得到运动学参数误差向量Δφ。为了减小光轴向量的估计误差对Δφ求解的影响,使用迭代最小二乘法求解超定方程(24),第t次迭代的估计值
| $ \Delta \hat \varphi \left( t \right) = \left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{{\left( t \right)}^{\rm{T}}}} \right){\left. {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( t \right) + \lambda \left( t \right)I} \right)^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\left( t \right)^{\rm{T}}}\mathit{\boldsymbol{E}}\left( t \right) $ | (29) |
式中:Φ(t)和E(t)分别为每次迭代更新
| $ \lambda \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \lambda \left( t \right)/h,\\ \lambda \left( t \right)h, \end{array}&\begin{array}{l} f\left( {t + 1} \right) > f\left( t \right)\\ f\left( {t + 1} \right) < f\left( t \right) \end{array} \end{array}} \right. $ | (30) |
| $ f\left( t \right) = {\left[ {\mathit{\boldsymbol{E}} - \Delta \varphi \left( t \right)} \right]^{\rm{T}}}\left[ {\mathit{\boldsymbol{E}} - \Delta \varphi \left( t \right)} \right] $ | (31) |
式中:h通常为2~10的常数;λ(0)为0.001~0.1的常数。
4 机械臂标定实验及结果分析基于相机光轴虚拟约束的机器人标定系统由一台Reinovo REbot-V-6R-6500工业机械臂和一台Bumblebee相机组成,如图 6所示,相机安装在工作环境中,使用Sony 1/3″ CCD,其分辨率为1 024×768,焦距为3.8 mm,机械臂末端法兰上固定4×4棋盘格标定板,选择棋盘格的中间角点为特征点,相机标定得到光轴中心点的图像坐标(u0, v0)为(513.56, 403.95)。只要标定板全部在其视野范围内,确定一条光轴的方向后,固定相机即可。

|
Download:
|
| 图 6 实验环境图 Fig. 6 The workcell configuration | |
假设特征点的图像坐标与光轴中心点的图像坐标之差的绝对值小于0.1像素时,认为特征点已经到达相机光轴上。以特征点到达光轴上的某一位置为例,视觉控制前后机械臂在相机视野中的图像分别如图 7和图 8所示。图中两个圆分别以光轴中心点和特征点为圆心,图 7右侧圆的圆心为特征点,左侧圆的圆心为光轴中心点,图 8两圆的圆心基本重合。左侧第一行坐标为当前特征点与光轴中心点图像坐标的差,通过视觉控制方法使图像坐标差由(68.10, -33.76)像素降至(-0.02, -0.06)像素,第二行坐标为当前特征点的图像坐标,特征点通过视觉控制逐渐靠近光轴。

|
Download:
|
| 图 7 视觉控制前相机采集的图像 Fig. 7 The picture taked by camera before visual control | |

|
Download:
|
| 图 8 视觉控制后相机采集的图像 Fig. 8 The picture taked by camera after visual control | |
当特征点与光轴中心点图像坐标的差Δuf与Δvf均小于0.1像素时,认为特征点已到达相机的光轴上。根据相机中CCD的实际尺寸及相机分辨率计算得到0.1像素对应的成像平面的距离为4.654 μm,令特征点距离相机的最大距离为500 mm,根据相机小孔成像原理,计算得到特征点到达光轴直线的最大误差e0为0.087 mm。
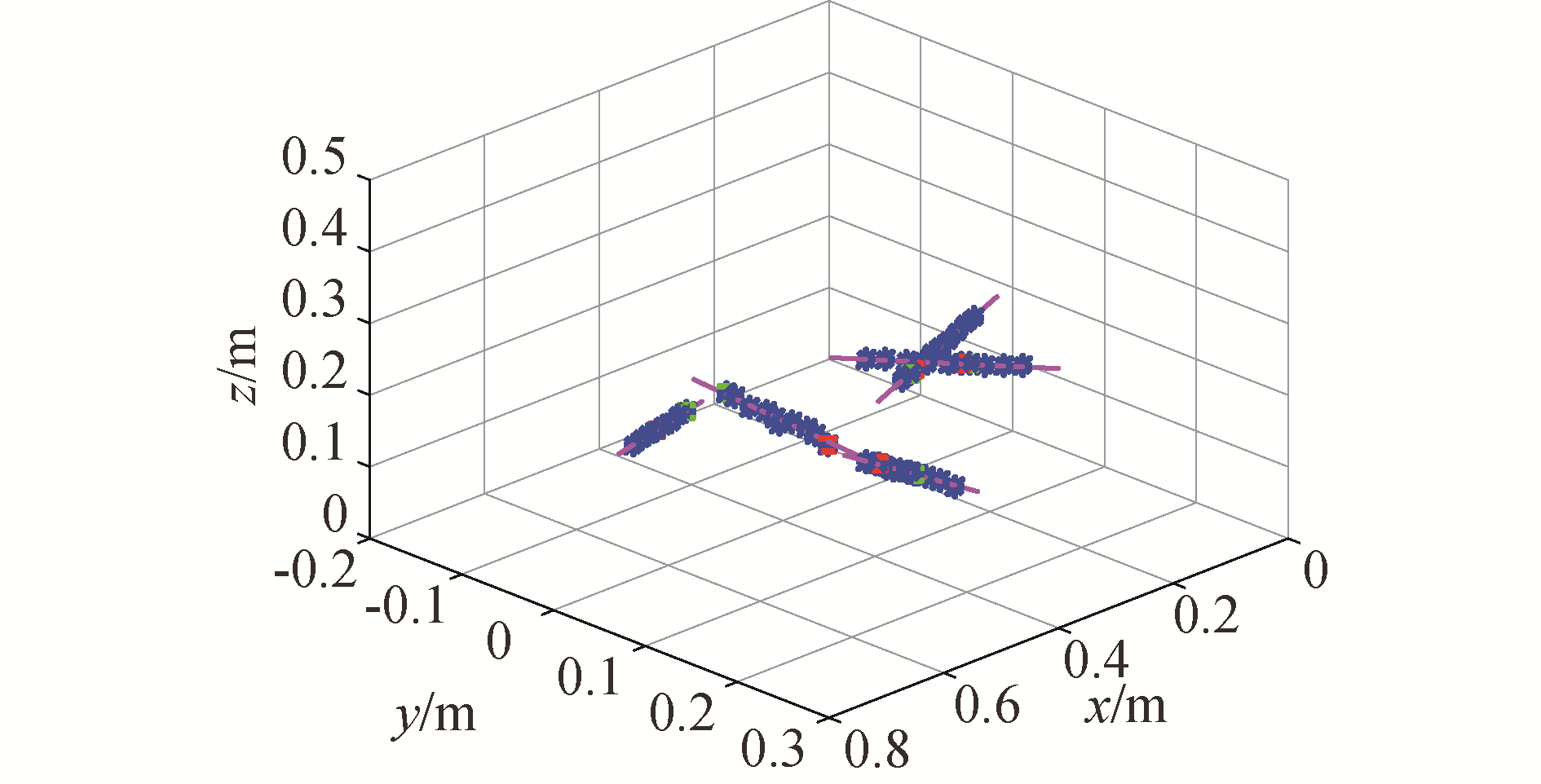
随机选择5条不同方向的光轴,使特征点依次到达每条光轴上的10个不同位置,保存每个位置处机械臂的关节角,根据机械臂正运动学及名义运动学参数可计算机械臂基坐标系下的光轴方向及特征点名义位置如图 9所示。使用迭代最小二乘法进行运动学参数辨识时进行20次迭代,λ(0)=0.01,h=3,标定得到的机械臂的运动学参数误差见表 2。
|
Download:
|
| 图 9 光轴方向及特征点的名义位置 Fig. 9 The directions of optical axes and the nominal positions of feature points | |
| 表 2 Reinovo机械臂运动学参数误差 Table 2 The kinematic parameter errors of Reinovo robot |
分别利用标定前后的运动学参数计算位置对齐误差Δe:
| $ \Delta e = \sqrt {{{\left( {\Delta \mathit{\boldsymbol{x}}} \right)}^2} + {{\left( {\Delta \mathit{\boldsymbol{y}}} \right)}^2} + {{\left( {\Delta \mathit{\boldsymbol{z}}} \right)}^2}} $ | (32) |
式中:Δx、Δy和Δz为向量E(i, j,k)的分量。
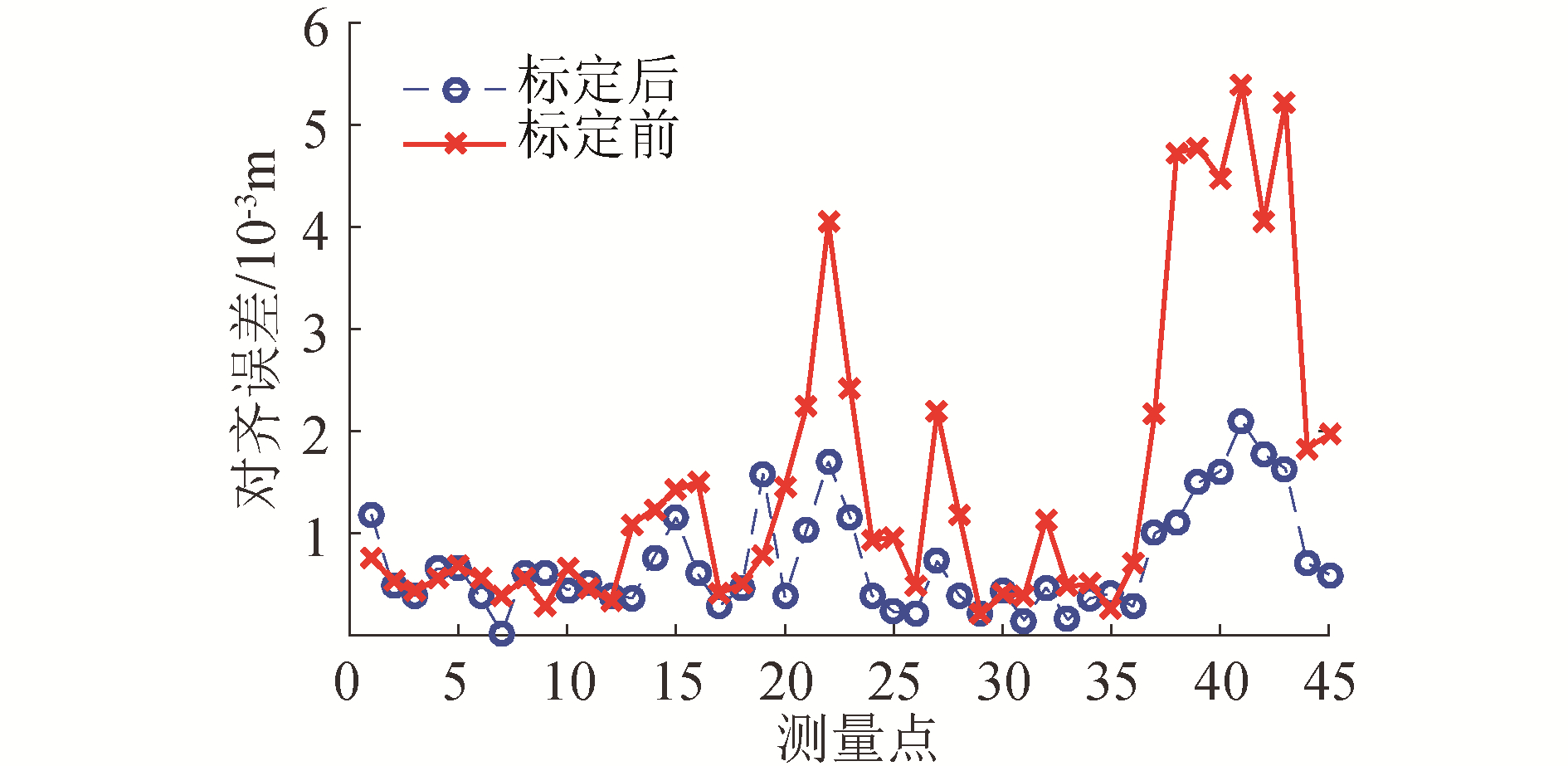
标定前后的对齐误差如图 10所示,5条光轴共45个对齐误差数据,对齐误差越小表明运动学参数越精确,标定后的对齐误差明显比标定前小,且测量点的对齐误差不超过2 mm,标定前的平均对齐误差为1.50 mm,标定后下降到0.72 mm,精度提高了52%。由于随机选取的第1条光轴上特征点的名义位置较精确,标定后的对齐误差下降较小。
|
Download:
|
| 图 10 运动学参数标定前后的对齐误差 Fig. 10 The alignment error before and after calibration of the kinematic parameters | |
1) 本文提出一种利用相机的光轴作为直线约束进行机械臂运动学参数标定的方法。这种方法的优势在于:仅需相机的光轴和机械臂的关节角即可完成运动学参数的标定,无需其他昂贵的高精度仪器及特定的标定设备,成本低且易操作。
2) 建立的基于直线约束的运动学误差模型对较低的相机深度测量精度具有鲁棒性,除了相机光轴中心点的图像坐标,不需要标定其他的相机参数。
3) 使用Reinovo六自由度工业机械臂进行标定实验,标定后机械臂的对齐误差下降了52%,表明本文提出的标定方法可以明显提高机械臂的绝对定位精度,具有很强的实用性。
| [1] |
WANG Weidong, SONG Huajian, YAN Zhiyuan, et al. A universal index and an improved PSO algorithm for optimal pose selection in kinematic calibration of a novel surgical robot[J]. Robotics and computer-integrated manufacturing, 2018, 50: 90-101. DOI:10.1016/j.rcim.2017.09.011 (  0) 0)
|
| [2] |
DRIELS M R, POTTER W S S. Full-pose calibration of a robot manipulator using a coordinate-measuring machine[J]. The international journal of advanced manufacturing technology, 1993, 8(1): 34-41. DOI:10.1007/BF01756635 (  0) 0)
|
| [3] |
PARK I W, LEE B J, CHO S H, et al. Laser-based kinematic calibration of robot manipulator using differential kinematics[J]. IEEE/ASME transactions on mechatronics, 2012, 17(6): 1059-1067. DOI:10.1109/TMECH.2011.2158234 (  0) 0)
|
| [4] |
NUBIOLA A, BONEV I A. Absolute robot calibration with a single telescoping ballbar[J]. Precision engineering, 2014, 38(3): 472-480. DOI:10.1016/j.precisioneng.2014.01.001 (  0) 0)
|
| [5] |
VACO M, ŠEKORANJA B, ŠULIGOJ F, et al. Calibration of an industrial robot using a stereo vision system[J]. Procedia engineering, 2014, 69: 459-463. DOI:10.1016/j.proeng.2014.03.012 (  0) 0)
|
| [6] |
DU Guanglong, ZHANG Ping. Online robot calibration based on vision measurement[J]. Robotics and computer-integrated manufacturing, 2013, 29(6): 484-492. DOI:10.1016/j.rcim.2013.05.003 (  0) 0)
|
| [7] |
ZHANG Xuanchen, SONG Yuntao, YANG Yang, et al. Stereo vision based autonomous robot calibration[J]. Robotics and autonomous systems, 2017, 93: 43-51. DOI:10.1016/j.robot.2017.04.001 (  0) 0)
|
| [8] |
LIU Tao, YIN Shibin, GUO Yin, et al. Rapid global calibration technology for hybrid visual inspection system[J]. Sensors, 2017, 17(6): 1440. DOI:10.3390/s17061440 (  0) 0)
|
| [9] |
BENNETT D J, HOLLERBACH J M. Autonomous calibration of single-loop closed kinematic chains formed by manipulators with passive endpoint constraints[J]. IEEE transactions on robotics and automation, 1991, 7(5): 597-606. DOI:10.1109/70.97871 (  0) 0)
|
| [10] |
YIN Shibin, REN Yongjie, ZHU Jigui, et al. A vision-based self-calibration method for robotic visual inspection systems[J]. Sensors, 2013, 13(12): 16565-16582. DOI:10.3390/s131216565 (  0) 0)
|
| [11] |
JOUBAIR A, BONEV I A. Kinematic calibration of a six-axis serial robot using distance and sphere constraints[J]. The international journal of advanced manufacturing technology, 2015, 77(1/4): 515-523. (  0) 0)
|
| [12] |
SHI Jingfei, ZHANG Hongsheng, LIU Yuan, et al. A self-calibration method for robot based on geometric constraints[C]//Proceedings of 2016 IEEE International Conference on Information and Automation. Ningbo, China, 2016: 1863-1867.
(  0) 0)
|
| [13] |
CHEN Gang, LI Tong, CHU Ming, et al. Review on kinematics calibration technology of serial robots[J]. International journal of precision engineering and manufacturing, 2014, 15(8): 1759-1774. DOI:10.1007/s12541-014-0528-1 (  0) 0)
|
| [14] |
HAYATI S A. Robot arm geometric link parameter estimation[C]//Proceedings of the 22nd IEEE Conference on Decision and Control. San Antonio, TX, USA, 1983: 1477-1483.
(  0) 0)
|
| [15] |
徐德, 谭民, 李原. 机器人视觉测量与控制[M]. 2版. 北京: 国防工业出版社, 2011: 226-230. XU De, TAN Min, LI Yuan. Visual measurement and control for robots[M]. 2nd ed. Beijing: National Defend Industry Press, 2011: 226-230. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


