2. 中国科学院海洋研究所, 山东 青岛 266071;
3. 东北大学 资源与土木工程学院, 辽宁 沈阳 110819
2. Institute of Oceanology, Chinese Academy of Sciences, Qingdao 266071, China;
3. School of Resources and Civil Engineering, Northeastern University, Shenyang 110819, China
全海深潜水器在挑战者深渊作业潜浮过程中会产生重浮力变化[1-3]。人类已有的设计经验不能完全指导全海深智能水下机器人(full ocean depth autonomous underwater vehicle, FOD-AUV)的设计。全海深ARV Nereus的AUV功能只在几十米的浅海水域应用[4-6]。Trieste[7]和Deepsea Challenge及Kaikor[8-9]全海深潜水器的重浮力平衡调整存在人工干预[9-10], 控制精准高效。但由于机构复杂, 不适合全海深水下机器人。Sentry[11]、Remus 6000、Autosub 6000[12]、CR-01/02[10]等的设计深度为6 km[13], 是目前潜深最大的AUV, 对重浮力的变化考虑有限[12]。直接将耐压壳体设计成不同压力状态下的等浮力结构[14-15], 挂载油囊或空气囊[16]可以实现AUV的静力平衡。但是考虑到体积、重量、可靠程度, 难以适用于FOD-AUV。
本文考虑到实际情况, 全海深AUV在设计时精确计算其工作深度(如11 km)的重浮力状态, 采用一次性抛载进行重浮力调整[17], 实现静力平衡。通过分析挑战者深渊深度剖面地球和海洋物理参数, 结合材料和力学知识对潜器重浮力变化定量分析。
1 全海深水下机器人静力学平衡方程海洋航行器依赖水的浮力航行和作业。当环境物理参数变化时, 重浮力会随之产生变化[18]。对于潜器重浮力平衡可能会被打破。
全海深AUV由M个暴露于水中的耐压部件Ci组成, 包含耐压舱、浮力材料、抛载装置(下潜抛载Cd-d、上浮抛载Cd-u)等, 重力与浮力表示为:
| $ {P = g\sum\limits_{i = 1}^{M - 2} {{m_{{{\rm{C}}_i}}}} + g{m_{{{\rm{C}}_{{\rm{d - u}}}}}} + g{m_{{{\rm{C}}_{{\rm{d - d}}}}}}} $ | (1) |
| $ {\varDelta = {\rho _{\rm{w}}}g\sum\limits_{i = 1}^{M - 2} {{V_{{{\rm{C}}_i}}}} + {\rho _{\rm{w}}}g{V_{{{\rm{C}}_{{\rm{d - u}}}}}} + {\rho _{\rm{w}}}g{V_{{{\rm{C}}_{{\rm{d - d}}}}}}} $ | (2) |
式中:g为重力加速度;mCi、mCD-u、mCd-d为耐压部件质量;ρw为海水密度。
分下潜-海底作业-上浮3个阶段描述AUV的静力平衡关系:
1) 下潜。AUV布放入水时搭载全部2组抛载, 此时静力学不平衡, 将在Cd-d的作用下自由下潜, 静力合力表示为:
| $ {\begin{array}{*{20}{l}} {{F_{\rm{d}}} = P - \Delta = (g\sum\limits_{i = 1}^{M - 2} {{m_{{{\rm{C}}_i}}}} + g{m_{{{\rm{C}}_{{\rm{d - u}}}}}})}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({\rho _{\rm{w}}}g\sum\limits_{i = 1}^{M - 2} {{V_{{{\rm{C}}_i}}}} + {\rho _{\rm{w}}}g{V_{{{\rm{C}}_{{\rm{d - u}}}}}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (g{m_{{{\rm{C}}_{{\rm{d - d}}}}}} - {\rho _{\rm{w}}}g{V_{{{\rm{C}}_{{\rm{d - d}}}}}})} \end{array}} $ | (3) |
式中:V为耐压部件体积。
2) 海底作业。抵达设计水深时将Cd-d抛掉, AUV在平衡状态下进行作业:
| $ {P^\prime } = P - g{m_{{{\rm{C}}_{{\rm{d - d}}}}}} = g\sum\limits_{i = 1}^{M - 2} {{m_{{{\rm{C}}_i}}}} + g{m_{{{\rm{C}}_{{\rm{d - u}}}}}} $ | (4) |
| $ \begin{array}{l} {\varDelta ^\prime } = \varDelta - {\rho _{\rm{w}}}g{V_{{{\rm{C}}_{{\rm{d - d}}}}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rho _{\rm{w}}}g\sum\limits_{i = 1}^{M - 2} {{V_{{{\rm{C}}_i}}}} + {\rho _{\rm{w}}}g{V_{{{\rm{C}}_{{\rm{d - u}}}}}} \end{array} $ | (5) |
有P′=Δ′, 即:
| $ \begin{array}{l} g\sum\limits_{i = 1}^{M - 2} {{m_{{{\rm{C}}_i}}}} + g{m_{{{\rm{C}}_{{\rm{d - u}}}}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rho _{\rm{w}}}g\sum\limits_{i = 1}^{M - 2} {{V_{{{\rm{C}}_i}}}} + {\rho _{\rm{w}}}g{V_{{{\rm{C}}_{{\rm{d - u}}}}}} \end{array} $ | (6) |
3) 上浮。作业完毕, 将Cd-u抛掉, 静力学不平衡, AUV将自由上浮。
| $ {F_{\rm{u}}} = {P^{\prime \prime }} - {\varDelta ^{\prime \prime }} = g\sum\limits_{i = 1}^{M - 2} {{m_{{{\rm{C}}_i}}}} - {\rho _{\rm{w}}}g\sum\limits_{i = 1}^{M - 2} {{V_{{{\rm{C}}_i}}}} $ | (7) |
依据式(6), 可得到:
| $ {{F_{\rm{d}}} = g{m_{{{\rm{C}}_{{\rm{d - d}}}}}} - {\rho _{\rm{w}}}g{V_{{{\rm{C}}_{{\rm{d - d}}}}}}} $ | (8) |
| $ {{F_{\rm{u}}} = - (g{m_{{{\rm{C}}_{{\rm{d - u}}}}}} - {\rho _{\rm{w}}}g{V_{{{\rm{C}}_{{\rm{d - u}}}}}})} $ | (9) |
对于式(6), 等式左侧重力的因素g与等式右侧浮力的因素g相同, 可进一步简化为:
| $ {\sum\limits_{i = 1}^{M - 2} {{m_{{{\rm{C}}_i}}}} + {m_{{{\rm{C}}_{{\rm{d - u}}}}}} = {\rho _{\rm{w}}}\sum\limits_{i = 1}^{M - 2} {{V_{{{\rm{C}}_i}}}} + {\rho _{\rm{w}}}{V_{{{\rm{C}}_{{\rm{d - u}}}}}}} $ | (10) |
注意式(10)只在11 km的设计深度成立。全海深AUV在设计深度正常工作的必要条件是:
| $ {{m_{\sum {} }} = {V_{\sum {{\rm{11}}{\kern 1pt} {\kern 1pt} 000} }} \cdot {\rho _{{\rm{W11}}{\kern 1pt} {\kern 1pt} 000}}} $ |
式(8)和(9)同样只在11 km水深时成立, 可以写出潜浮过程中任意水深的静力合力公式:
| $ \begin{array}{l} {F_{\rm{d}}} = P(d) - \varDelta (d) = g(d) \cdot [(\sum\limits_{i = 1}^{M - 2} {{m_{{{\rm{C}}_i}}}} + {m_{{{\rm{C}}_{{\rm{d - u}}}}}}) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rho _{\rm{w}}}(d)(\sum\limits_{i = 1}^{M - 2} {{V_{{{\rm{C}}_i}}}} (d) + {V_{{{\rm{C}}_{{\rm{d - u}}}}}}(d))] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} g(d)[{m_{{{\rm{C}}_{{\rm{d - d}}}}}} - {\rho _{\rm{w}}}(d){V_{{{\rm{C}}_{{\rm{d - d}}}}}}(d)] \end{array} $ | (11) |
| $ \begin{array}{l} {F_{\rm{u}}} = {P^{\prime \prime }}(d) - {\varDelta ^{\prime \prime }}(d) = g(d)[(\sum\limits_{i = 1}^{M - 2} {{m_{{{\rm{C}}_i}}}} + {m_{{{\rm{C}}_{{\rm{d - u}}}}}}) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rho _{\rm{w}}}(d)(\sum\limits_{i = 1}^{M - 2} {{V_{{{\rm{C}}_i}}}} (d) + {V_{{{\rm{C}}_{{\rm{d - u}}}}}}(d))] - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} g(d)[{m_{{{\rm{C}}_{{\rm{d - u}}}}}} - {\rho _{\rm{w}}}(d){V_{{{\rm{C}}_{{\rm{d - u}}}}}}(d)] \end{array} $ | (12) |
重力加速度g(d)、海水密度ρw(d)和部件体积VCd-u(d)构成了合力变化的主要因素, 因此要研究这3个物理量在海水深度剖面的变化规律。
2 重力加速度和重力异常重力场在全球的分布随时间和空间变化[1, 19]。在地表转移时, 重力异常使潜器的总重变化;在设计深度作业重力异常不影响静力平衡状态;潜浮过程中, 重力异常在深度剖面发生变化。
2.1 潜器重量受地球表面位置变化的影响在地球表面, 重力加速度包含2部分:
| $ g = {g_0} + {g^\prime } $ | (13) |
式中:g0为基础值;g′为异常值。
在陆地上, g的计算参考张昆[20]的公式;在海洋上采用公开的DTU13计算海上的异常值[21-22]。
依据以上信息分别计算AUV在哈尔滨工程大学、三亚深海所和马里亚纳海沟海域海水表面的重力加速度。全海深AUV从哈尔滨工程大学转移到中科院深海所, 重力变化-2.18‰;转移至挑战者深渊试验海域, 重力变化-2.79‰。
2.2 深渊剖面的重力异常对重浮力合力的影响对挑战者深渊深度剖面的重力加速的估算依据为NODC公开的海洋剖面观测数据[23]以及布格异常规律。
依据NODC的数据, 在马里亚纳海沟附近水域水下3.8 km时, 重力加速度较水面减小86 mGal, 如果按照比例计算, 在0~11 km垂直剖面, 重力异常值约为-249 mGal。但是, 挑战者深渊呈现两边高中间低的沟壑。依据布格异常的规律:马里亚纳海沟某深度重力异常的值比同深度的海域值小, 因此估计海沟处的真实值小于-249 mGal。重力加速度在0~11 km的分布规律可以描述为:随着水深增加, 重力加速度减小, 并且在入沟之后受海沟两侧的沟崖影响, 减小的速度增加。依据论文[2]中对海沟处的重力异常描述, 估计挑战者深渊11 km处的重力异常值不可能超过-1 000 mGal。全海深AUV在潜浮过程中, 重力异常一般不超过-1 000 mGal且只影响合力(≤980 N), 即重力异常带来的合力变化不超过1 N。
3 挑战者深渊剖面的海水物理特征依据海水状态方程[24-26], 温度T、盐度S和压力P共同决定海水的密度ρ;同时, 海水状态量T-P共同影响AUV排水体积。过去50年间挑战者深渊处的海水状态参数变化, 不足以对全海深AUV的力学计算带来明显影响[3, 27-28]。依据1992年获取于挑战者深渊的公开数据, 临近若干站点气候数据。
1) 温度。水面温度为28.4 ℃, 在4 596 m时温度降为最低值1.46 ℃, 之后温度缓慢上升, 10 860 m的温度为2.45 ℃。
2) 盐度。表层水盐度约为34.5‰, 在130~160 m时盐度达到顶峰, 约为35.1‰;之后, 随着深度增加盐度下降明显, 至410~440 m时盐度达到最低, 约为34.3‰;随后, 盐度随深度增加而缓慢增加, 在深度大于3 km时, 盐度基本恒定, 约为34.7‰。
3) 压强。3 km以深的压强-深度曲线采用二次拟合, 结果表示为:P=2.185 022 8×10-6d2+1.007 621 0 d-4.219 983 1, 残差范数为6.218 1;此时的压力精度水平达到了dbar(1 dbar=0.1 bar, 约1 m水压)级。外推可得11 km水深处的压强为114.950 MPa。
4) 密度。海水密度依据海水状态方程间接获取[29-30]。EOS80海水状态方程适应范围是:温度-2~40 ℃;实用盐度0~42%;海压0~103 MPa。挑战者深渊的温度、盐度均满足条件, 但压强1.134 462 5×103 MPa超过公式的适用范围。由公式判断:在大深度条件(水深超过1 km), 海水密度变化的主要因素是压力的变化, 且二者呈近似线性关系, 尽管水的压缩系数随压力增大而缓慢减小, 但此范围内不会发生突变[31]。因而仍可用该方程近似估算114.950 MPa的海水密度。结果如图 1, 表层海水密度约为1 021.87 kg/m3, 10.8 km时密度为1 074.54 kg/m3。4 km以深的海水密度采用二次拟合:ρ=-4.233 604 8×10-8d2+4.800 0×10-3d+1 027.80, 残差范数为0.412 0;外推得11 km处的海水密度为1 075.06 kg/m3。

|
Download:
|
| 图 1 全海深AUV主要部件随深度变化的体积及浮力变化情况 Fig. 1 Change of volume and buoyancy of several major components with depth | |
潜浮过程中, AUV的排水体积变化分别对应热胀冷缩形变以及静水压力导致的力学形变[32]。考虑到如下因素:1)潜浮速度通常不超过2 m/s, AUV周围海水的状态变化缓慢;2)AUV自身产热较少与海水的相对运动会迅速实现热量交换;3)环境温度的变化不对AUV部件的材料性能产生明显的影响。
提出如下假设:1)AUV各部件的温度与海水环境的温度变化一致, 并且没有滞后;2)各部件在海水压力的作用下变形充分, 不考虑变形的动态过程;3)各部件材料的力学特性, 如弹性模量、泊松比、体积模量等, 在1~30 ℃范围内不随温度变化而发生改变。
依据结构形式的不同, 将部件分为2类[33]:1)各向同性的实心部件Θ。如浮力材、蒙皮、合金框架、抛载等, 其中浮力材是构成AUV质量和体积的最主要部件(质量占比超过40%, 体积占比接近70%)。此类部件的体积变化依据温度、压力的影响下的体积膨胀率和体积弹性模量直接计算;2)耐压壳体结构部件Φ。如玻璃球壳、信标/光源/摄像机等高强合金柱壳/球壳等, 其中玻璃球壳排水量占比约为17%, 是最重要的壳类部件。此类部件的体积变化需首先计算在温度、压力的影响下部件基本尺寸(如球壳的外径)的变化, 再依据体积公式计算体积变化[32-33]。
表 1为主要部件的材料、结构参数以及体积变化量。可以看出:
| 表 1 AUV主要部分部件的基本信息以及体积变化情况 Table 1 Basic parameters and volume changes of important components of AUV |
1) 浮力材作为体积占比最高的部件, 体积变化量也最明显, 其中温度影响较压力影响小1个数量级;2)壳类部件中, 玻璃球壳是体积占比最高的, 同样也是体积变化量最大的, 高于其它小型壳体2个数量级;3)金属实心部件初始体积较小, 同时由于具有较大的体积模量和较小的热胀系数而在单位体积下的变化量较小, 与小型壳类部件的体积变化量同属一个数量级, 二者的体积变化量甚至小于量测或加工误差;4)非金属实心部件(如玻璃球壳保护罩)与金属实心部件属性相反, 其具有较小的体积模量和较大的热胀系数, 单位体积下的变化量高于实心金属部件1~2个数量级。
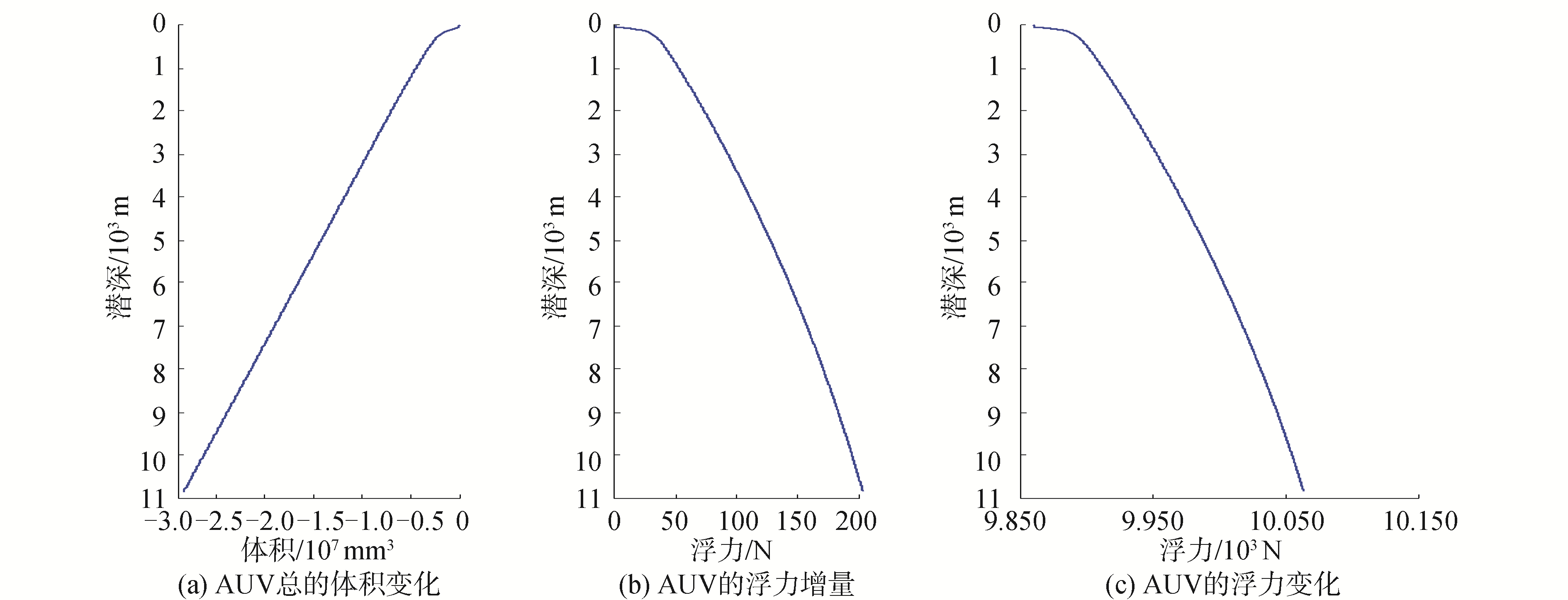
结合密度变化, 可以绘出各部件以及AUV整体在深度剖面的体积和浮力变化曲线。如图 2所示。
|
Download:
|
| 图 2 AUV整体的体积和浮力变化曲线 Fig. 2 Change of volume and buoyancy of the FOD-AUV with depth | |
1) 大深度作业的AUV在设计阶段需要考虑作业海域立体空间的重力加速度、海水密度、海水压力等海洋物理参数变化引起AUV的重量、体积及浮力变化。该结论可对结构材料选取、潜浮运动方式、控制策略等进行指导。
2) 重力加速度的变化往往会被设计者忽略, 但AUV的动力系统往往较其重量小1~2个数量级, 因而全海深水下机器人的设计不能忽略重力异常带来的影响。
3) 文中的数据引用准确和计算方法正确, 其结果可为总体设计以及海上作业提供指导。
| [1] |
BEYER L A, VON HUENE R E, MCCULLOH T H, et al. Measuring gravity on the sea floor in deep water[J]. Journal of geophysical research, 1966, 71(8): 2091-2100. DOI:10.1029/JZ071i008p02091 (  0) 0)
|
| [2] |
FRANCO H, ABBOTT D. Gravity signatures of terrane accretion[J]. Lithos, 1999, 46(1): 5-15. DOI:10.1016/S0024-4937(98)00060-7 (  0) 0)
|
| [3] |
VAN HAREN H, BERNDT C, KLAUCKE I. Ocean mixing in deep-sea trenches:new insights from the Challenger Deep, Mariana Trench[J]. Deep sea research part I:oceanographic research papers, 2017, 129: 1-9. DOI:10.1016/j.dsr.2017.09.003 (  0) 0)
|
| [4] |
WHITCOMB L L, JAKUBA M V, KINSEY J C, et al. Navigation and control of the Nereus hybrid underwater vehicle for global ocean science to 10, 903 m depth: Preliminary results[C]//Proceedings of the 2010 IEEE International Conference on Robotics and Automation. Anchorage, AK, USA, 2010: 594-600.
(  0) 0)
|
| [5] |
BOWEN A D, YOERGER D R, TAYLOR C, et al. The Nereus hybrid underwater robotic vehicle for global ocean science operations to 11000 m depth[C]//Proceedings of the OCEANS 2008. Quebec City, QC, Canada, 2008: 1-10.
(  0) 0)
|
| [6] |
BOWEN A D, YOERGER D R, TAYLOR C, et al. Field trials of the Nereus hybrid underwater robotic vehicle in the challenger deep of the Mariana Trench[C]//Proceedings of the OCEANS 2009. Biloxi, MS, USA, 2009: 1-10.
(  0) 0)
|
| [7] |
PICCARD J, DIETZ R S. Seven miles down:the story of the bathyscaph Trieste[M]. New York: Putnam, 1961.
(  0) 0)
|
| [8] |
WIKIPEDIA. Deepsea challenger[M]. Wikipedia, 2012.
(  0) 0)
|
| [9] |
CAMERON J. http://www.deepseachallenge.com/the-film/synopsis/[M/OL]. (2012-03-26). http://www.deepseachallenge.com/the-film/synopsis/.
(  0) 0)
|
| [10] |
WU Jianguo, LIU Jian, XU Huixi. A variable buoyancy system and a recovery system developed for a deep-sea AUV Qianlong I[C]//Proceedings of the OCEANS 2014-TAIPEI. Taipei, China, 2014: 1-4.
(  0) 0)
|
| [11] |
PONTBRIAND C, FARR N, HANSEN J, et al. Wireless data harvesting using the AUV Sentry and WHOI optical modem[C]//Proceedings of the OCEANS 2015-MTS/IEEE Washington. Washington, 2015: 1-6.
(  0) 0)
|
| [12] |
MCPHAIL S. Autosub6000:a deep diving long range AUV[J]. Journal of bionic engineering, 2009, 6(1): 55-62. DOI:10.1016/S1672-6529(08)60095-5 (  0) 0)
|
| [13] |
HUMPHRIS S E. Vehicles for deep sea exploration[M]//STEELE J H. Encyclopedia of Ocean Sciences. 2nd ed. Oxford: Academic Press, 2009: 255-266.
(  0) 0)
|
| [14] |
ERIKSEN C C, OSSE T J, LIGHT R D, et al. Seaglider:a long-range autonomous underwater vehicle for oceanographic research[J]. IEEE journal of oceanic engineering, 2001, 26(4): 424-436. DOI:10.1109/48.972073 (  0) 0)
|
| [15] |
PHILLIPS A B, BLAKE J I R, BOYD S W, et al. Nature in Engineering for Monitoring the Oceans (NEMO): An isopycnal soft bodied approach for deep diving autonomous underwater vehicles[C]//Proceedings of the 2012 IEEE/OES Autonomous Underwater Vehicles. Southampton, UK, 2012: 1-8.
(  0) 0)
|
| [16] |
FURLONG M E, PAXTON D, STEVENSON P, et al. Autosub long range: a long range deep diving AUV for ocean monitoring[C]//Proceedings of the 2012 IEEE/OES Autonomous Underwater Vehicles. Southampton, UK, 2012: 1-7.
(  0) 0)
|
| [17] |
鲍林.全海深水下机器人多模式抛载技术研究[D].哈尔滨: 哈尔滨工程大学, 2018. BAO Lin. Research on multi-mode emergency ejection system of full-ocean-depth underwater vehicles[D]. Harbin: Harbin Engineering University, 2018. (  0) 0)
|
| [18] |
刘鑫宇, 李一平, 封锡盛. 万米级水下机器人浮力实时测量方法[J]. 机器人, 2018, 40(2): 216-221. LIU Xinyu, LI Yiping, FENG Xisheng. Real-time measurement method of buoyancy of a full-ocean-depth underwater robot[J]. Robot, 2018, 40(2): 216-221. (  0) 0)
|
| [19] |
AMOS J. Gravity satellite yields 'Potato Earth' view[M]. 2011.
(  0) 0)
|
| [20] |
张昆. 新的重力加速度公式研究[J]. 地球物理学进展, 2011, 26(3): 824-828. ZHANG Kun. New gravity acceleration formula research[J]. Progress in geophysics, 2011, 26(3): 824-828. DOI:10.3969/j.issn.1004-2903.2011.03.006 (  0) 0)
|
| [21] |
ANDERSEN O, KNUDSEN P, STENSENG L. The DTU13 MSS (mean sea surface) and MDT (mean dynamic topography) from 20 years of satellite altimetry[M]//JIN Shuanggen, BARZAGHI R. IGFS 2014: Proceedings of the 3rd International Gravity Field Service. Cham: Springer, 2015: 111-121.
(  0) 0)
|
| [22] |
张胜军.利用多源卫星测高资料确定海洋重力异常的研究[D].武汉: 武汉大学, 2016. ZHANG Shengjun. Research on determination of marine gravity anomalies from multi-satellite altimeter data[D]. Wuhan: Wuhan University, 2016. (  0) 0)
|
| [23] |
NODC. Oceanographic data collected during the Submarine Ring of Fire 2006 expedition aboard the R/V MELVILLE along the Mariana Arc in the Philippine Sea from April 18, 2006-May 13, 2006(NODC Accession 0010750)[R]. 2006.
(  0) 0)
|
| [24] |
MILLERO F J, CHEN C T, BRADSHAW A, et al. A new high pressure equation of state for seawater[J]. Deep sea research part A. oceanographic research papers, 1980, 27(3/4): 255-264. (  0) 0)
|
| [25] |
FOFONOFF N P, MILLARD R C. Algorithms for computation of fundamental properties of seawater[J]. UNESCO technical papers in marine science, 1983, 44: 1-53. (  0) 0)
|
| [26] |
冯士筰, 李凤岐, 李少莆. 海洋科学导论[M]. 北京: 高等教育出版社, 1999. FENG Shizuo, LI Fengqi, LI Shaopu. An introduction to marine science[M]. Beijing: Higher Education Press, 1999. (  0) 0)
|
| [27] |
TAIRA K, YANAGIMOTO D, KITAGAWA S. Deep CTD casts in the challenger deep, mariana trench[J]. Journal of oceanography, 2005, 61(3): 447-454. DOI:10.1007/s10872-005-0053-z (  0) 0)
|
| [28] |
TAIRA K. Super-deep CTD measurements in the Izu-Ogasawara trench and a comparison of geostrophic shears with direct measurements[J]. Journal of oceanography, 2006, 62(5): 753-758. DOI:10.1007/s10872-006-0092-0 (  0) 0)
|
| [29] |
NODC. WORLD OCEAN ATLAS 2013 version 2[M]. NODC, 2013.
(  0) 0)
|
| [30] |
NODC. WORLD OCEAN DATABASE 2013[M]. NODC, 2013.
(  0) 0)
|
| [31] |
NAVE C R. Compressibility of liquids[M]. Georga State University, 2001.
(  0) 0)
|
| [32] |
武建国, 徐会希, 刘健, 等. 深海AUV下潜过程浮力变化研究[J]. 机器人, 2014, 36(4): 455-460. WU Jianguo, XU Huixi, LIU Jian, et al. Research on the buoyancy change of deep-sea autonomous underwater vehicle in diving process[J]. Robot, 2014, 36(4): 455-460. (  0) 0)
|
| [33] |
潘彬彬, 崔维成, 叶聪, 等. 蛟龙号载人潜水器无动力潜浮运动分析系统开发[J]. 船舶力学, 2012, 16(1/2): 58-71. PAN Binbin, CUI Weicheng, YE Cong, et al. Development of the unpowered diving and floating prediction system for deep manned submersible "JIAOLONG"[J]. Journal of ship mechanics, 2012, 16(1/2): 58-71. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


