立体匹配作为计算机视觉研究领域的关键技术已被广泛地应用在机器人自主导航、物体识别与跟踪及地理信息系统等领域。Scharstein等[1]人总结了现有的立体匹配算法的理论框架,将基于双目视觉的立体匹配算法分解为匹配代价计算、匹配代价聚合、视差计算及优化和视差细化4个步骤。根据视差计算方法的不同,将立体匹配算法分为基于全局的立体匹配算法和基于局部的立体匹配算法两大类。全局方法通过构造能量函数中数据项、平滑项及遮挡项等系数和的最小值来获得匹配结果,精度较高但效率较低,通常难以满足实际应用的需求[2]。基于局部的立体匹配算法将像素点及其邻域像素点的局部信息作为匹配基元,构造的能量函数只涉及到数据项,计算复杂度低,实时应用效果较好。但是局部算法往往对支撑窗口的大小和形状选择困难。在匹配代价聚合过程中窗口选择太大,虽然视差图整体平滑性较好,但窗口会包含深度不一致的像素,导致视差边界附近的背景区域像素点更倾向于错误地获得前景区域的视差,即产生“前景膨胀”现象,使得视差图轮廓、细节模糊;窗口选择太小,虽然视差不连续区域的匹配精度会得到提高,视差图中的轮廓、细节清晰,但是杂点较多,有破碎感。
局部算法支撑窗口的选择策略中,文献[3]提出了多窗口立体匹配方法,在预先给定的多个窗口中选择最优窗口作为支持窗口,该方法在一定程度上提高了图像中非纹理及视差不连续区域的视差精度,抑制了“前景膨胀”现象。但是由于支撑窗口的形状被限制,缺乏一定的灵活性,很难适应图像结构序列的改变,得到视差边缘也不够清晰。文献[4]提出一种窗口自适应加权立体匹配方法,该方法可以构造有效的代价聚合,减少匹配的歧义性,得到较为精确的视差图,但自适应权值的时间复杂度较高,无法体现局部匹配方法的实时性优势。文献[5]提出一种自适应窗口的立体匹配方法,将待匹配点的匹配代价对周围邻域像素进行传递以提高图像鉴别性,但该方法需要设定窗口的初始骨架,并且对于每一个待匹配点都需要进行色彩阈值和距离阈值的确定,算法效率较低。同时,确定的窗口直接利用胜者全取策略求得匹配点视差,对图像的辐射畸变敏感,鲁棒性较差。针对以上问题,本文提出一种基于像素扩展的自适应窗口立体匹配方法,降低了遮挡和深度不连续区域的误匹配率,具有更好的匹配精度。
1 像素扩展自适应窗口算法 1.1 匹配代价聚合窗口选择在参考图像中待匹配像素点与目标图像中同行极线搜索范围内的每个像素点比较相似程度获得视差结果时,由于单个像素点的匹配代价鉴别性较低,需要将待匹配像素点之间的匹配延伸到周围邻域像素点以提高待匹配像素点的鉴别性。在弱纹理区域,需要较大的窗口来确定当前像素点的精确位置以提高匹配精度;而在深度不连续区域,则需要较小的窗口以保护物体边缘细节等信息。本文提出一种自适应的像素扩展窗口选择方法,假设参考图像中的待匹配点为p(x, y),以待匹配点为基准点,其x方向上的相邻像素点为p(x-1, y)与p(x+1, y)。如果相邻像素灰度差异较小,则希望窗口能够包含这些像素点,以p(x, y)点和其右侧相邻像素点p(x+1, y)为例,像素点灰度差异的判别准则为
| $ \frac{{\sqrt {\left| {{{\left( {{I_{x + 1}}} \right)}^2} - {{\left( {{I_x}} \right)}^2}} \right|} }}{{\max \left\{ {{I_{x + 1}},{I_x}} \right\}}} \le \varepsilon $ | (1) |
式中:Ix为待匹配点p(x, y)的灰度值,Ix+1为p(x+1, y)的灰度值,ε为根据实际需求所选择的预设灰度阈值,0≤ε < 1。为了使max{Ix+1, Ix}不为0,在进行立体匹配前对立体像对中灰度值为0的像素点进行高斯滤波。当待匹配点与其右侧相邻像素点满足式(1)的限制条件时,窗口在以px点为基准在当前行方向向右扩展一个像素,此时窗口的大小为p(x, y)和p(x+1, y)两个像素点,再比较p(x+1, y)点与其右侧相邻像素点p(x+2, y)的灰度值,以此递推来确定窗口右侧边界的最终像素点位置。然而只有一个限制条件会使窗口在灰度平稳过渡区域造成窗口无限选择问题,而且通过设置不同的灰度阈值来避免该情况时往往会导致窗口尺寸较小,不满足实际应用需要,甚至有时还会造成窗口无法选择。为解决上述问题,本文在扩展过程中增加了窗口截断限制条件:
| $ \frac{{\sqrt {\left| {{{\left( {{I_n}} \right)}^2} - {{\left( {{I_x}} \right)}^2}} \right|} }}{{{I_n}}} > \rho $ | (2) |
式中:In为待匹配点p(x, y)向右扩展到的第n个像素点的灰度值,n≠x。ρ为窗口截断灰度阈值,0≤ε < ρ < 1。综上所述,以待匹配点p(x, y)为基准点的x轴方向右侧整体窗口确定准则函数为
| $ \begin{array}{*{20}{c}} {{p_{{\rm{r - final}}}} = }\\ {\left\{ \begin{array}{l} p\left( {x + n + 1,y} \right),\\ \frac{{\sqrt {\left| {{{\left( {{I_{n + 1}}} \right)}^2} - {{\left( {{I_n}} \right)}^2}} \right|} }}{{\max \left\{ {{I_{n + 1}},{I_n}} \right\}}} \le \varepsilon \cap \frac{{\sqrt {\left| {{{\left( {{I_n}} \right)}^2} - {{\left( {{I_x}} \right)}^2}} \right|} }}{{{I_n}}} \le \rho ;\\ p\left( {x + n,y} \right),\\ \frac{{\sqrt {\left| {{{\left( {{I_{n + 1}}} \right)}^2} - {{\left( {{I_n}} \right)}^2}} \right|} }}{{\max \left\{ {{I_{n + 1}},{I_n}} \right\}}} > \varepsilon \cup \frac{{\sqrt {\left| {{{\left( {{I_n}} \right)}^2} - {{\left( {{I_x}} \right)}^2}} \right|} }}{{{I_n}}} > \rho \end{array} \right.} \end{array} $ | (3) |
式中:pr-final表示待匹配点p(x, y)右侧扩展的最终窗口边界像素点,In+1为p(x+n+1, y)点的灰度值。同理以待匹配点p(x, y)为基准点的x轴方向左侧整体窗口确定准则函数为
| $ \begin{array}{*{20}{c}} {{p_{{\rm{l - final}}}} = }\\ {\left\{ \begin{array}{l} p\left( {x - m - 1,y} \right),\\ \frac{{\sqrt {\left| {{{\left( {{I_{ - m - 1}}} \right)}^2} - {{\left( {{I_{ - m}}} \right)}^2}} \right|} }}{{\max \left\{ {{I_{ - m - 1}},{I_{ - m}}} \right\}}} \le \varepsilon \cap \frac{{\sqrt {\left| {{{\left( {{I_{ - m}}} \right)}^2} - {{\left( {{I_x}} \right)}^2}} \right|} }}{{{I_{ - m}}}} \le \rho \\ p\left( {x - m,y} \right),\\ \frac{{\sqrt {\left| {{{\left( {{I_{ - m - 1}}} \right)}^2} - {{\left( {{I_{ - m}}} \right)}^2}} \right|} }}{{\max \left\{ {{I_{ - m - 1}},{I_{ - m}}} \right\}}} > \varepsilon \cup \frac{{\sqrt {\left| {{{\left( {{I_{ - m}}} \right)}^2} - {{\left( {{I_x}} \right)}^2}} \right|} }}{{{I_{ - m}}}} > \rho \end{array} \right.} \end{array} $ | (4) |
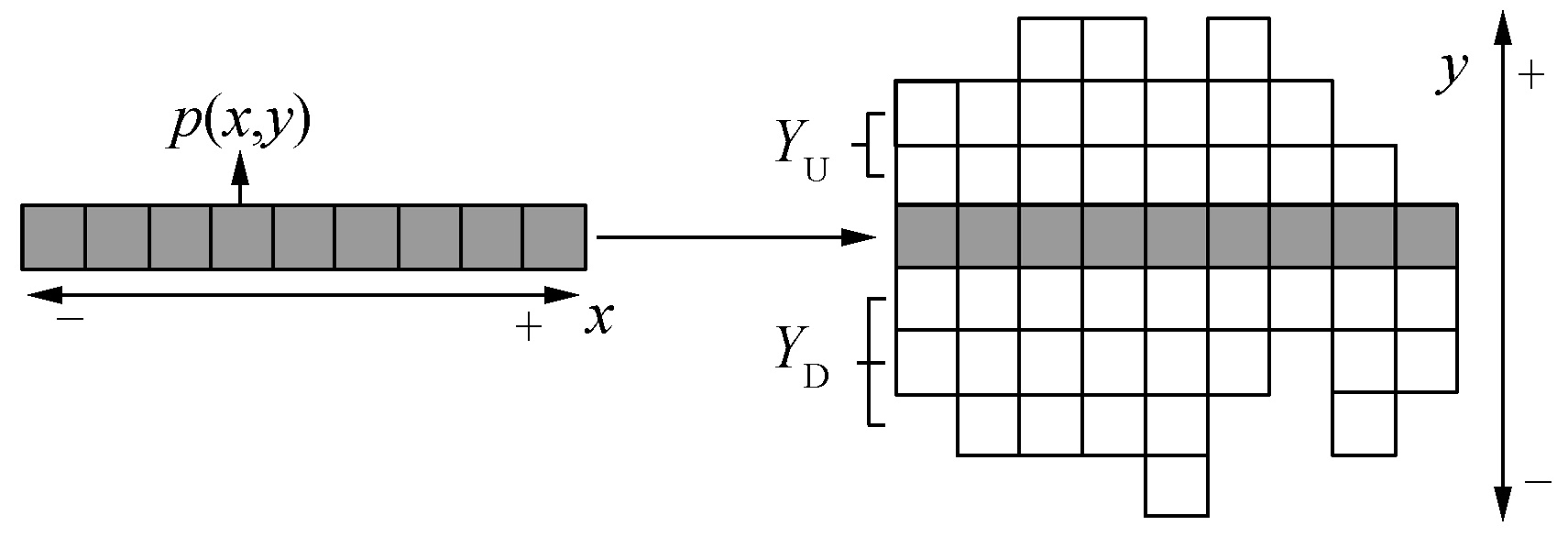
式中:pl-final表示待匹配点p(x, y)左侧扩展的最终窗口边界像素点,I-m为点p(x-m, y)的灰度值,I-m-1为p(x-m-1, y)点的灰度值。至此该支撑窗口沿待匹配点x轴方向的像素扩展已经完成,将基准点所在的x轴定义为窗口中心轴,中心轴确定了支撑窗口的左右边界和中心轴上包含的像素点的数量。为了确定支撑窗口的最终尺寸,需以x轴方向的扩展结果为基准利用上述扩展规则向y方向再进行一次扩展,扩展后所得到的支撑窗口可以表示为W={p(x, y), XL, XR, YU, YD, Z},其中p(x, y)为窗口基准像素点的位置,XL为该基准点与窗口左侧边界像素点间的像素点个数,XR为该基准点与窗口右侧边界像素点间的像素点个数,YU为窗口上沿与窗口中心轴间像素点个数的最大值,YD为窗口下沿与窗口中心轴间像素点个数的最大值,Z表示窗口内像素点的总数。图 1为窗口中心轴沿y方向扩展的示意图。在图 1中p(x, y)为窗口基准点,灰色区域为窗口中心轴,箭头方向为像素扩展方向。在对p(x, y)进行扩展得到窗口中心轴后,以窗口中心轴上每个像素点基准点分别再沿y方向按照同样的准则进行扩展,最后可以得到图 1中右侧的自适应窗口区域来进行后续的匹配代价聚合,其中YU和YD分别为2和3。
|
Download:
|
| 图 1 x轴方向像素点沿y方向扩展示意图 Fig. 1 The y axis direction expansion on x axis pixels | |
令参考图像中通过窗口确定准则获得的待匹配像素点的支撑窗口为Wref、目标图像中搜索范围d内的像素点相应的支撑窗口为Wtar。假设参考图像中的待匹配点p(x, y)对应的在目标图像中以d为搜索范围内点的集合为A={q(x-d, y), q(x-d+1, y), …, q(x+d-1, y), q(x+d, y)},那么支撑窗口Wtar的个数为N=2 d+1。直接利用支撑窗口Wref与Wtar中的每个支撑窗口进行匹配代价聚合并计算得到最终视差结果的时间复杂度往往较高,实际应用中需要在确定支撑窗口的基础上先进行窗口预匹配判定,即对Wref与Wtar先进行模型上的匹配判定,排除搜索范围d内一部分存在歧义的窗口,再对剩余的窗口进行代价聚合与视差计算。根据1.1节提出的窗口确定准则,待匹配点对间具有较高的相似度是它们具有相似窗口形状的充要条件,然而在目标图像的搜索范围内,一些连续的像素点所确定的支撑窗口模型可能是相同的,甚至比真正的匹配像素点更接近参考图像待匹配点的窗口模型。图 2为在预匹配中仅考虑窗口形状所带来的不确定性结果示意。在图 2中,Wref是以a1为待匹配点在参考图像中确定的窗口模型,b1、b2和b3分别为目标图像搜索范围内的连续像素点,其确定的窗口模型Wtar与Wref相同,由于参考图像中的待匹配点只能对应一个目标图像中的像素点,因此只判断像素点所确定的窗口形状不能满足预匹配的需要。

|
Download:
|
| 图 2 窗口形状对窗口预匹配的影响 Fig. 2 The effect of window shape on pre-matching | |
为了解决上述问题,本文提出一种定点窗口重合率的预匹配判定方法。像素点确定的窗口W={p(x, y), XL, XR, YU, YD, Z}可以表示成矩阵W,矩阵的行数和列数均为2n+1,其中n=max{XL, XR, YU, YD} +1。因此这个不规则的支撑窗口可以用一个行列确定的正方形矩阵进行表示,该窗口矩阵中的元素用像素点的赋值表示。首先对像素点进行信息赋值,对于支撑窗口外的像素点赋值为0,窗口内的像素点赋值为1,每个支撑窗口都可以得到相应的信息赋值矩阵。然后对像素点进行位置赋值,将基准点定义为矩阵的相对中心点,其位置赋值为a(0, 0),矩阵中其余元素按照坐标位置关系赋值,获得整个窗口矩阵中所有元素的位置赋值结果,其中窗口矩阵第1行第1列及第2n+1行第2n+1列的元素分别为a(-n, n)和a(n, -n)。
通过窗口矩阵的位置赋值和信息赋值可以得到矩阵中每个像素点的双重赋值表示,即每一个位置赋值都有一个与之对应的信息赋值。令
| $ U = \sum\limits_{i = - n}^n {\sum\limits_{j = - n}^n {\left| {{I_{\left( {i,j} \right)}} - {{I'}_{\left( {i,j} \right)}}} \right|} } $ | (5) |
式中:I(i, j)为参考图像中窗口矩阵,a(i, j)位置点的信息赋值,I′(i, j)为目标图像中窗口矩阵,a(i, j)位置点的信息赋值,U为参考图像窗口矩阵与目标图像窗口矩阵间的歧义性结果,U越小表示待匹配窗口区域的相似程度越高。通过定义一个窗口矩阵歧义性阈值
在进行匹配代价聚合时需要选择相应的相似性测度函数,并对匹配代价进行求解。通常利用像素点的灰度设计相似性测度函数的方法最直接而且常用,包括差绝对值和方法(SAD)[6]、差平方和方法(SSD)[7]以及互相关系数方法(NCC)[8-9]等,其中NCC是相似性测度函数中抗噪声能力和匹配精度较高的方法,同时也是取值范围相对易于控制的方法。
传统的NCC的相似性度量函数为
| $ \begin{array}{*{20}{c}} {{\rm{NCC}}\left( {x,y,D} \right) = }\\ {\frac{{\sum\limits_{i = - n}^n {\sum\limits_{j = - m}^m {{I_{\rm{R}}}\left( {x + i,y + j} \right){I_{\rm{T}}}\left( {x + i + d,y + j} \right)} } }}{{\sqrt {\sum\limits_{i = - n}^n {\sum\limits_{j = - m}^m {I_{\rm{R}}^2\left( {x + i,y + j} \right)} } \sum\limits_{i = - n}^n {\sum\limits_{j = - m}^m {I_{\rm{T}}^2\left( {x + i + d,y + j} \right)} } } }}} \end{array} $ | (6) |
式中:IR(x+i, y+j)为参考图像支撑窗口内像素点p(x+i, y+j)的灰度值,IT(x+i+d, y+j)为目标图像中视差为d的支撑窗口内像素点p(x+i+d, y+j)的灰度值。从式(6)中可以看出,公式的取值范围为-1~1,越大表示越相似。寻找参考图像中的点p(x, y)在目标图像中匹配点的过程就是在搜索窗内找到NCC(x, y,D)为最大值时的d值,该d值对应的像素点即为匹配点。然而在式(6)中参考图像与目标图像通过待匹配点对所得到的支撑窗口是规则的矩形窗口且大小一致,窗口的长和宽分别为2 m+1和2n+1,无法对不规则的自适应窗口进行匹配,为了使基于像素扩展的自适应窗口满足NCC方法的使用条件,需要对目标图像中满足预匹配判定的支撑窗口进行规则化处理。
在窗口预匹配后,目标图像中的剩余支撑窗口与参考图像中的支撑窗口都具有较为相似的窗口模型,窗口间的歧义性较小。为了规则化处理这些窗口,以每个窗口矩阵的相对中心点为基准,根据1.2节确定的窗口矩阵中每个元素的位置赋值及信息赋值,提取这些支撑窗口内位置赋值和信息赋值都相同的像素点,对这些位置和信息相同的像素点进行重新排列得到一个W(1×n)的新窗口,所得的规则化窗口矩阵W(1×n)表示为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{W}}\left( {1 \times n} \right) = }\\ {\left[ {{a_{\left( {i,j} \right)}} \cdots {a_{\left( {i,j + t} \right)}} \cdots {a_{\left( {i + s,j} \right)}} \cdots {a_{\left( {i',j'} \right)}}} \right]} \end{array} $ | (7) |
式中:a(i, j),a(i, j+t),a(i+s, j),a(i′, j′)为组成规则化窗口的像素点位置赋值,其中t>0,s>0,i+s < i′,j+t < j′。这些像素点具体排列方法表述为:1)像素点位置赋值中x坐标较小的像素点重排至规则化窗口的左侧;2)若x坐标值相同,y坐标值较小的像素点排至规则化窗口的左侧。在得到这些大小相同的规则化窗口后,对规则化窗口中各像素点进行灰度互相关系数的计算,计算公式为
| $ \begin{array}{*{20}{c}} {{\rm{NCC}}\left[ {\mathit{\boldsymbol{W}}\left( {1 \times n} \right),D} \right] = }\\ {\frac{{\sum\limits_{i = 1}^n {{I_{\rm{R}}}\left( {x + i,y} \right){I_{\rm{T}}}\left( {x + d + i,y} \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {I_{\rm{R}}^2\left( {x + i,y} \right)} \sum\limits_{i = 1}^n {I_{\rm{T}}^2\left( {x + d + i,y} \right)} } }}} \end{array} $ | (8) |
| $ d = \arg \max {\rm{NCC}}\left[ {\mathit{\boldsymbol{W}}\left( {1 \times n} \right),D} \right] $ | (9) |
式中:IR(x+i, y)为参考图像中规则化窗口内像素点p(x, y+j)的灰度值,IT(x+d+i, y)为目标图像中视差为d的规则化窗口内像素点p(x+d+i, y)的灰度值。式(9)表示NCC[W(1×n),D]取值最大时d的取值,d即为该待匹配像素点的初始视差值。
1.4 初始视差优化利用灰度互相关系数方法,在遇到遮挡情况时,会无法计算出正确的匹配点,从而无法生成准确的视差图。在这类误匹配发生时,会出现以下两个问题:1)在视差图中,误差不会表现为相互分离的点,而是相互连接的区域,如遮挡区域等。2)与上述情况相反,视差图中一些比较稀疏的匹配点,如低分辨率下产生的物体边缘处的少数匹配点,在通过普通滤波器时反而会被当作噪声滤除。为了提高匹配的准确性,有必要对最终视差图生成之前的匹配过程做进一步的匹配有效性校验,以优化匹配结果。
本文在平滑性假设的基础上采用图像分割的方法对误匹配区域的像素点视差进行校正。考虑误匹配区域与真实表面区域的各自特点,确定平滑视差平面的分割标准,对分割后的视差连续平面内的任意一个像素点p都满足:
| $ \left\{ \begin{array}{l} \left| {{d_q} - {d_p}} \right| \le \delta \\ q \in N\left( p \right) \subset S \end{array} \right. $ | (10) |
式中:N(p)为像素点p的邻域,q为N(p)中的一个像素点,S表示视差连续平面的分割区域,dp和dq分别为p和q两个位置处的视差,δ为设定的阈值,表示同一视差连续平面上相邻像素点之间所允许的最大视差偏差,本文取δ=1。对视差连续的分割平面,如果其覆盖的全部像素数为e,那么对于一个给定的阈值k,k表示一个有效平面所应覆盖的最少像素数,k值越大,视差图能被分割出的平面越少。根据图像分辨率的不同,k的取值范围为100~500。
判断e≥k是否成立来确定分割区域是否为有效平面,如果关系式成立,则认为此平面为有效平面,其初始视差值即为最终视差值;否则,认为其为无效平面即为误匹配区域。在这些误匹配区域中遮挡区域占绝大多数,需要重新确定其视差结果。在本文中以左图为参考图像,右图为目标图像,在参考图像中会存在物体左侧部分遮挡,即物体左侧部分区域在目标图像中有显示,而在参考图像中可能存在遮挡而不显示。由于在平滑视差平面进行分割,重新确定的视差结果为
| $ \left\{ \begin{array}{l} {p_m} \in \tilde S\\ {p_{m - 1}} \in S,{p_n} \in S\\ {d_m} = \frac{{{d_n} - {d_{m - 1}}}}{{m - 1 - n}} + {{\bar d}_m} \end{array} \right. $ | (11) |
式中:
本文算法详细描述如下:
1) 将RGB图像进行灰度图像转换,定义目标图像中待匹配点的搜索范围,根据目标图像的尺寸对搜索范围进行相应选择。
2) 分别以参考图像中的待匹配点和目标图像搜索范围内的像素点为基准点进行行列像素灰度扩展。首先通过基准点进行行方向扩展,通过式(3)和式(4)确定窗口的左右边界点。然后对窗口中心轴的每个像素点再进行列方向扩展,得到最终的支撑窗口表示为W={p(x, y), XL, XR, YU, YD, Z}。
3) 根据得到的支撑窗口W确定相应的窗口矩阵W,对窗口矩阵中每个元素进行位置赋值和信息赋值。利用式(5)判定参考图像支撑窗口与目标图像支撑窗口的歧义性,通过设置窗口歧义性阈值
4) 对这些歧义性较小的窗口进行规则化处理,使它们表示成W(1×n)的规则化矩阵形式。通过式(8)、(9)确定待匹配点的初始视差值。通过平滑视差平面的分割确定误匹配区域并对其进行视差重新确定从而得到图像的最终视差结果。
2 Middlebury数据实验结果及分析为了验证本文算法的准确性,本文利用Matlab实现了所提出的算法。实验对象采用Middlebury大学立体视觉数据库提供的第三版的测试数据[10],该数据由15组给出真实视差图的x方向极线矫正立体像对组成,选择其中4组数据进行实验分析,包括Bicycle2、Classroom2、Hoops和Staircase。每张图片的尺寸为750像素×500像素,根据图像尺寸设置视差搜索范围为60像素。对上述图像分别进行实验验证本文算法的准确性,图 3给出了本文算法的实验结果,在遮挡区域的误匹配结果显示为灰色,在非遮挡区域的误匹配结果显示为黑色。

|
Download:
|
| 图 3 本文算法的实验结果 Fig. 3 Experimental results of the proposed algorithm | |
图 4为本文算法与LAMC_DSM算法[7]的最终视差图以及视差误差为2时视差的误匹配结果比较,LAMC_DSM是一种局部自适应多代价的立体匹配算法,其窗口选择模式是基于像素骨架交叉的支撑区域扩展方法。在图 4 a的LAMC_DSM最终视差图中,方块区域作为遮挡较小的深度不连续区域,其视差边界模糊,视差结果具有非常明显的“前景膨胀”现象,造成这些区域的误匹配率明显增加,同时椭圆形区域作为图像中的遮挡区域,其视差结果表现为“尖刺状”,说明遮挡区域获得的视差结果的鲁棒性较差。在图 4(b)的本文算法最终视差图中,非遮挡区域的匹配效果较好,最大程度上限制了方块区域以及其他深度不连续处的“前景膨胀”现象,同时遮挡区域的“尖刺状”效果得到明显改善,物体边缘深度信息的还原度较好。

|
Download:
|
| 图 4 LAMC_DSM算法与本文算法的最终视差图以及视差误差为2时视差的误匹配结果比较 Fig. 4 The experimental results of LAMC_DSM and the proposed algorithm when error is 2 | |
表 1为本文算法对Bicycle2、Classroom2、Hoops和Staircase这4组测试数据全部实验结果的量化表示,并且与近几年基于局部的立体匹配算法实验结果进行对比。这些算法来源于Middlebury视觉网站中目前公布的立体匹配算法的参考列表,根据Middlebury网站提供的定量算法评价参数对比各算法在全图的误匹配率,其中“非遮挡”表示非遮挡区域的误匹配率,“全部”表示图像整体的误匹配率,算法允许的误差为2。
| 表 1 各种算法在Middlebury数据库上的量化对比 Tab.1 quantitative comparison of various algorithms on Middlebury database |
从表 1中可以看出,本文算法在纹理较为丰富以及深度不连续区域较多的Bicycle2和Classroom2图像中匹配准确率较高,同时遮挡区域对算法精确度的影响较小。在纹理丰富并且存在少量倾斜区域的Hoops图像中,本文算法的效果略好于LPU算法。但在存在大量倾斜区域和弱纹理区域的Staircase图像中,本文算法的误匹配率比LPU算法略高,说明本文算法在处理具有大面积平滑区域和倾斜区域图像的方面有待加强,尤其当支撑窗口内同时出现大面积平滑区域和倾斜区域时,匹配效果不理想,还需后续进一步分析和研究针对性的有效方法以提高大面积平滑区域和倾斜区域的匹配准确率。
3 结论1) 利用像素扩展的自适应窗口立体匹配算法,解决立体匹配视差图中的前景膨胀和尖刺状边缘问题。在实验图像Bicycle2、Classroom2、Hoops和Staircase中的非遮挡区域的误匹配率分别为6.81%%、5.35%、16.8%和12.4%。Bicycle2、Classroom2、Hoops和Staircase图像的整体误匹配率分别为9.75%、13.1%、31.0%和24.2%。与文献[11]、文献[12]和文献[14]算法相比算法精度具有大幅度的提高,在视差图的边缘区域精度提升较大。
2) 相对于纹理较为丰富的Bicycle2和Classroom2图像,在存在大量倾斜区域和非纹理区域的Hoops和Staircase图像中,本文算法的误匹配率较高。在平滑和倾斜区域较少的Hoops图像中,非遮挡区域以及图像整体的误匹配率与文献[13]算法相比基本相同,而在平滑和倾斜区域较大的Staircase图像中非遮挡区域和图像整体区域的误匹配率与文献[13]算法相比分别增加了0.8%和2.1%。说明本文算法在处理图像中存在大面积平滑区域和倾斜区域的能力有待提高。当支撑窗口中同时出现大面积平滑区域和倾斜区域时,匹配效果不理想。
| [1] |
SCHARSTEIN D, SZELISKI R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms[J]. International journal of computer vision, 2002, 47(1121-3): 7-42. (  0) 0)
|
| [2] |
祝世平, 杨柳. 基于自适应分水岭的图割的立体匹配算法[J]. 光学学报, 2013, 33(3): 0315004. ZHU Shiping, YANG Liu. Stereo matching algorithm with graph cuts based on adaptive watershed[J]. Acta optica sinica, 2013, 33(3): 0315004. (  0) 0)
|
| [3] |
张敦凤, 张华, 王姮, 等. 改进rank变换的多窗口彩色图像立体匹配算法[J]. 云南大学学报(自然科学版), 2014, 36(3): 347-352. ZHANG Dunfeng, ZHANG Hua, WANG Heng, et al. Multi-window color image stereo matching algorithm based on improved rank transform[J]. Journal of Yunnan University(natural sciences), 2014, 36(3): 347-352. (  0) 0)
|
| [4] |
吴方, 王沛. 一种改进的自适应权重立体匹配算法与校正[J]. 电视技术, 2012, 36(11): 19-23. WU Fang, WANG Pei. Improved adaptive support-weight algorithm and adjustment[J]. Video engineering, 2012, 36(11): 19-23. DOI:10.3969/j.issn.1002-8692.2012.11.006 (  0) 0)
|
| [5] |
祝世平, 李政. 基于改进梯度和自适应窗口的立体匹配算法[J]. 光学学报, 2015, 35(1): 01150003. ZHU Shiping, LI Zheng. A stereo matching algorithm using improved gradient and adaptive window[J]. Acta optica sinica, 2015, 35(1): 01150003. (  0) 0)
|
| [6] |
岳陈平, 孟丽娅. 基于SAD算法的立体匹配的实现[J]. 微型机与应用, 2013, 32(6): 41-43. YUE Chenping, MENG Liya. Implementation of the stereo matching based on SAD algorithm[J]. Microcomputer & its Applications, 2013, 32(6): 41-43. (  0) 0)
|
| [7] |
卢思军, 唐振民, 卢阿丽, 等. 基于色彩相似性的自适应多窗口立体匹配[J]. 系统仿真学报, 2009, 21(8): 2235-2238. Lu Sijun, Tang Zhenmin, Lu Ali, et al. Dense Stereo Matching Based on Recursive Adaptive Size Multi-windowing Using Constraint of Color Similarity[J]. Journal of System Simulation, 2009, 21(8): 2235-2238. (  0) 0)
|
| [8] |
欧阳鑫玉, 张娟娟, 赵楠楠, 等. 基于NCC的改进立体匹配算法[J]. 微型机与应用, 2015, 34(3): 54-57. OUYANG Xinyu, ZHANG Juanjuan, ZHAO Nannan, et al. Improved stereo matching algorithm based on NCC[J]. Microcomputer & its Applications, 2015, 34(3): 54-57. (  0) 0)
|
| [9] |
张华东, 潘晨, 章东平. 基于视觉显著性的区域立体匹配算法[J]. 计算机应用, 2015, 35(12): 3565-3569. ZHANG Huadong, PAN Chen, ZHANG Dongping. Regional stereo matching algorithm based on visual saliency[J]. Journal of Computer Applications, 2015, 35(12): 3565-3569. (  0) 0)
|
| [10] |
SCHARSTEIN D, HIRSCHMULLER H, KITAJIMA Y, et al. High-resolution stereo datasets with subpixel-accurate ground truth[M]. Berlin Heidelberg: Springer, 2014: 31-42.
(  0) 0)
|
| [11] |
STENTOUMIS C, GRAMMATIKOPOULOS L, KALISPERAKIS I, et al. On accurate dense stereo-matching using a local adaptive multi-cost approach[J]. Isprs journal of photogrammetry and remote sensing, 2014, 91: 29-49. DOI:10.1016/j.isprsjprs.2014.02.006 (  0) 0)
|
| [12] |
KOWALCZUK J, PSOTA E T, PEREZ L C. Real-time stereo matching on CUDA using an iterative refinement method for adaptive support-weight correspondences[J]. IEEE transactions on circuits and systems for video technology, 2013, 23(1): 94-104. DOI:10.1109/TCSVT.2012.2203200 (  0) 0)
|
| [13] |
HORNA L, FISHER R B. 3D plane labeling stereo matching with content aware adaptive windows[C]//Procoeedings of the 12th International Conference on Computer Vision Theory and Applications (VISAPP 2017), Edinburgh, 2016: 1-10.
(  0) 0)
|
| [14] |
SINHA S N, SCHARSTEIN D, SZELISKI R. Efficient high-resolution stereo matching using local plane sweeps[C]//Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA: IEEE. 2014: 1582-1589.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


