低检测概率(low probability of detection,LPD)通信技术是提升通信隐蔽性能的主要手段之一[1]。与低截获(low probability of interception,LPI)通信相比,LPD技术在确保信息安全的同时,可进一步从波形层面实现隐蔽,防止频谱暴露,进而使得非合作方难以察觉通信过程的存在。为了实现LPD通信,一般可采取尽量降低信号的功率谱密度或缩短信号暴露时间的方法来实现。前者可以采用扩频技术,后者可以通过短时猝发通信的方式来保障。因此,目前隐蔽通信中,基于直接序列扩频和跳频的短时猝发隐蔽通信技术被广泛采用[2-3]。扩频技术从20世纪70年代起就已在军用通信中得到大规模应用,随着几十年来信号侦测技术的快速发展和大量的针对性研究,对传统隐蔽通信扩频信号的侦测能力不断提升,现在已经有较为成熟的侦测技术(如采用循环谱特征侦测直扩信号)[4-6]。而随着软硬件水平的提高,非合作信号侦测和捕获所需的时间越来越短,若为了隐蔽性进一步降低猝发通信的时间,对合作方而言同步难度和同步开销将成为制约通信性能的主要因素[7]。因此有必要结合通信领域的新技术、新体制,研究新型LPD通信波形和通信方案设计。例如,文献[8]提出将扩频隐蔽通信与OFDM技术结合,文献[9]研究了基于四项加权分数傅里叶变换的隐蔽通信体制。此次方案拟从波形设计的角度,研究一种新型LPD通信波形。随着软件无线电和数字信号处理技术的发展,通信波形不再仅限于正余弦波形,以Chirp波形作为信息载体的新型调制方式在通信中受到了越来越多的关注[10-11]。例如在IEEE 802.15.4 a标准中就将Chirp扩频技术列为物理层技术方案之一。事实上,Chirp波形由于其良好的脉冲压缩特性,在雷达系统中早已被广泛采用,近年来分数阶傅里叶变换等信号处理手段的发展也进一步推动了Chirp波形在通信系统中的应用研究[12-13]。此次方案拟基于Chirp扩频技术构造新型LPD隐蔽通信方案,上述相关研究成果将为此方案的开展提供坚实完善的理论参考体系。此外,Chirp波形还具有易于产生,通信距离远的特点,所需的信号处理理论及相应硬件设备也已经较为成熟。
1 变时宽chirp率调制信号模型 1.1 发送方案已经有研究表明,在复杂的电磁环境中,相较于调幅、调频、调相而言,Chirp率调制(chirp rate modulation, CRM)方式更不易受到信道干扰的扭曲,具有更好的鲁棒性[10-11]。下面以二进制、线性基为例说明其原理。当发送信息bj取0时,发送的Chirp波形为
| $ {{c}_{0}}\left( t \right)=\text{cos}(-\mathsf{ π} k{{t}^{2}}+2\mathsf{ π}{{f}_{0}}t) $ | (1) |
当bj取1时,发送的Chirp波形为
| $ {{c}_{1}}\left( t \right)=\text{cos}(\mathsf{ π} k{{t}^{2}}+2\mathsf{ π}{{f}_{1}}t) $ | (2) |
即这种简化情形下,分别用调频率的正负来代表数据1和0。在这里使用的是实Chirp信号。其基于幅度归一化的时域波形分别如图 1(a)、(b)所示。

|
Download:
|
| 图 1 Chirp率调制时域基本波形 Fig. 1 Chirp rate modulation waveforms | |
根据线性调频信号(Chirp信号)的特点,在时间宽度T内,记信号调频率为k,其扫频频带宽度为B=kT。即线性调频信号为宽带信号,当取较大的时宽带宽积D=TB时,可以认为是一种扩频信号,具有时、频域平坦的功率分布,因而具有隐蔽通信能力。
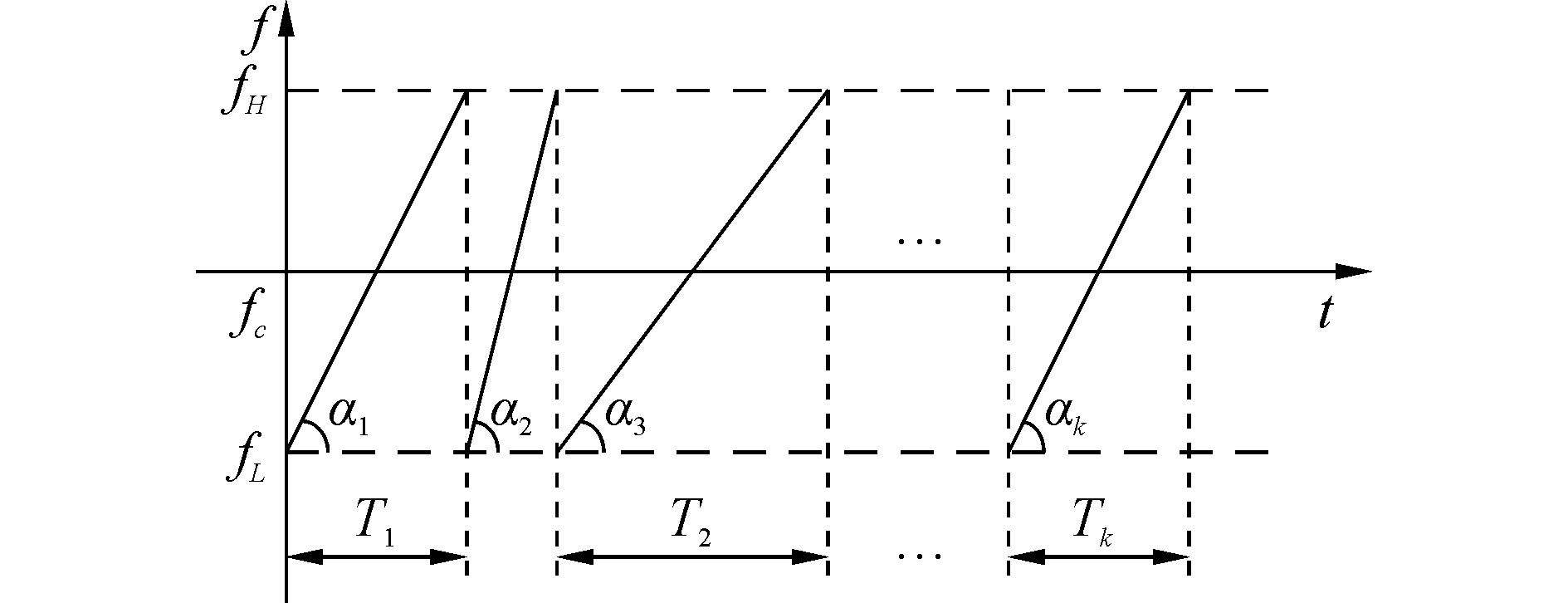
为了提高发送波形的LPD性能,考虑将其由等时宽模式扩展为变时宽模式,即VT-CRM(变时宽Chirp率调制)方式。其原理如图 2所示。此时每符号内信号带宽相同,时间宽度由伪随机序列控制,取K种离散取值,相应地,调频率的绝对值有K种状态,调频率的正负则用于承载信息。由于发送信号的非周期特征,使得其可以抗现有的基于统计特征的信号侦查手段,同时其随机变化的符号周期使得信号即使被检测到,也具有一定的抗信息截获能力。
|
Download:
|
| 图 2 “变时宽”的原理示意图 Fig. 2 Examples of "variable time-width" | |
当采用大时宽带宽积Chirp信号,即TB≫1时,可采用脉冲压缩特性处理Chirp信号以获得扩频增益,从而提升抗干扰性能。脉冲压缩的过程是将Chirp信号通过一个冲击响应也是Chirp信号的匹配滤波器,且两个Chirp信号的调频率互为相反数,输出信号则是一个窄带脉冲信号。基于脉冲压缩特性的相干解调系统框图如图 3所示。

|
Download:
|
| 图 3 相干解调系统框图 Fig. 3 System diagram of coherent demodulator | |
首先假设输入的Chirp调频信号为s(t),则匹配滤波器的时域冲击响应可表示为
| $h\left( t \right)={{s}_{i}}({{t}_{0}}-t), 0<t<{{t}_{o}} $ | (3) |
相应的,匹配滤波器输出为
| $ \begin{align} &{{s}_{o}}\left( t \right)={{s}_{i}}\left( t \right)*h\left( t \right)= \\ &\int_{-\infty }^{+\infty }{{{s}_{i}}\left( t-y \right)\times h\left( y \right)\text{d}\mathit{y}}= \\ &\int_{-\infty }^{+\infty }{{{s}_{i}}\left( t-y \right)\times {{s}_{i}}({{t}_{0}}-y)\text{d}\mathit{y}} \\ \end{align} $ | (4) |
令t0-y=x, t0-t=t1,则
| $ \begin{align} &{{s}_{0}}\left( t \right)=s\int_{-\infty }^{+\infty }{{{s}_{i}}\left( x-{{t}_{1}} \right)\times {{s}_{i}}\left( x \right)\text{d}\mathit{x}}= \\ &\ \ \ \ {{A}^{2}}\int_{-\infty }^{+\infty }{\text{cos}~\left[2\mathsf{ π} ~\left( {{f}_{0}}x+\frac{1}{2}\mu {{x}^{2}}~ \right) \right]\times } \\ &\text{cos}~\left\{ 2\mathsf{ π} \left[{{f}_{0}}(x-{{t}_{1}})+\frac{1}{2}\mu {{(x-{{t}_{1}})}^{2}} \right] \right\}\text{d}\mathit{t} \\ \end{align} $ | (5) |
对两个余弦函数的乘积做积化和差后忽略高频部分(认为其积分很小),则可将式(5)表示为
| $ \begin{align} &{{s}_{0}}\left( t \right)=\frac{1}{2}{{A}^{2}}{{\int }^{+\infty }}_{-\infty }\text{rect}\left( \frac{x}{T} \right)\times \text{rect}\left( \frac{x-{{t}_{1}}}{T} \right)\times \\ &\ \ \ \ \ \ \ \ \text{cos}~\left[2\mathsf{ π} \left( {{f}_{0}}{{t}_{1}}+\mu x{{t}_{1}}-\frac{1}{2}\mu t_{1}^{2} \right)~ \right]\text{d}\mathit{x}= \\ &\frac{{{A}^{2}}T}{2}\times ~\frac{\text{sin}\left[\mathsf{ π} B{{t}_{1}}\left( 1-\frac{\left| {{t}_{1}} \right|}{T} \right) \right]}{\mathsf{ π} B{{t}_{1}}}~\times \text{cos}(2\mathsf{ π} {{f}_{0}}{{t}_{1}})~ \\ \end{align} $ | (6) |
其中|t1|≤T。从式(6)可以看出,Chirp信号通过匹配滤波之后所得波形为sinc函数,当信号完全进入滤波器的时候(t1=0),输出达到最大值A2T/2,且输出相关峰的主瓣宽度为2/B。即随着时宽的增大,其峰值增大;随着带宽的增大,其主瓣宽度减小。因此通过增大时宽带宽积,取得了类似扩频通信解扩过程中信号能量的“聚敛”操作,而干扰则不具有此“聚敛”特性,因此可以通过脉压过程结合滤波实现干扰消除。
2 隐蔽性能分析 2.1 信号各域特征分析 2.1.1 功率密度谱特征图 4为两种信号在无噪条件下的功率密度谱(PSD)特征曲线。由此可见:

|
Download:
|
| 图 4 VT-CRM信号和直扩信号的功率谱特征对比 Fig. 4 PSD of VT-CRM signal and DS signal | |
1) 信号的功率密度谱反映了信号的功率在频域随频率的分布情况;信号的功率密度谱特征含有信号的载波频率、带宽等信息,信号的功率密度谱特征可作为信号截获的参量之一。
2) 在无噪情况下,两种信号均可被有效地截获。
3) VT-CRM信号具有更为平坦的频域能量分布,更易于在低信噪比条件下隐藏于噪声中。
2.1.2 循环谱特征由循环谱的特征分析可以得到信号统计量随时间的变化规律。利用该方法可以从噪声和干扰中识别出LPD信号,根据循环谱的峰值位置,可以进行参数估计。
图 5、6分别给出了BPSK/DS信号和VT-CRM信号的循环谱特征。结合图 5进行分析可得,循环谱特征主要含有信号的周期/速率特征,即

|
Download:
|
| 图 5 BPSK/DS信号循环谱特征 Fig. 5 Cyclic spectrum of BPSK/DS signal | |

|
Download:
|
| 图 6 VT-CRM信号循环谱特征 Fig. 6 Cyclic spectrum of VT-CRM signal | |
1) 由图 5可知:BPSK/DS信号的循环相关特征明显,且f=0截面的循环特征较强(比值1:1)。
2) 由图 6可知:在无噪情况下,VT-CRM信号也具有一定的循环相关特征,但f=0截面的循环特征相对较弱(比值0.125 5:1)。结合其扩频引入的低功率谱密度特征,在存在噪声条件下,f=0截面的弱特征可增大VT-CRM检测的难度。
2.1.3 倒谱特征对信号y(t)的对数功率谱求功率谱就是该信号的倒谱C(τ),C(τ)的表达式为
| $ C\left( \tau \right)=|\text{FFT}\{\text{lg}|\text{FFT}\left[y\left( t \right) \right]{{|}^{2}}\}{{|}^{2}} $ | (7) |
根据式(7)可知,信号y(t)共进行了三次映射,分别为从时域到频域、频域到频域、频域到时域,从而得到C(τ)。整个过程可以视为从时间域t到伪时域τ的变换。
由于在频域内进行了一次非线性变换(即取对数运算),所以在映射回时域时,将C定义为伪时域内的函数。倒谱通常用来分析信号在复杂频谱图上的周期结构,从而对密集泛频信号中的周期成分进行分离和提取。倒谱在分析具有同族谐频、多成分边频等复杂的信号时具有良好的效果。
图 7为两种信号在无噪条件下的倒谱特征曲线。由图可见,倒谱特征主要含有信号的周期/速率特征,即全局图中相邻主峰值之间的时间为基带信息速率的倒数,局部图中相邻次峰值间距为扩频码片周期。

|
Download:
|
| 图 7 倒谱特征 Fig. 7 Cepstrum spectrum | |
由图 7(b)可得:虽然VT-CRM信号也含有倒谱分量,但由于采用变时宽通信方法,其倒谱特征的周期规律不明显。
2.2 信号抗检测、抗截获能力分析在传输速率等通信指标均相同的情况下对比分析BPSK/DS短波通信系统和VT-CRM系统的抗截获能力。
2.2.1 基于循环谱的抗检测能力分析由于信号在循环频率上的特性,循环谱检测时主要看在相应2fc处的峰值,此次检测时采用累积检测法,即每次检测1个码元,检测10次取其平均值画图,观察其循环谱特性。
由图 8(a)、(b)可以看出,信噪比为-9 dB时,直扩信号具有明显的CYC特征,VT-CRM信号仅具有微弱的CYC特征;由图 8(a)、(b)可以看出信噪比为-12 dB时,直扩信号仍具有微弱的CYC特征,而VT-CRM信号不具有CYC特征,无法使用CYC方法检测。

|
Download:
|
| 图 8 不同信噪比下两种信号的CYC曲线 Fig. 8 CYC curves of two signals with different SNR | |
假设非合作方在估计出通信平均时宽的、判决处通信体制为Chirp类通信的前提下对VT-CRM系统进行破译,以衡量VT-CRM通信系统的抗破译能力。经仿真计算,此时所生成的用于恢复信息的本地CRM信号间的归一化互相关值均小于10-2。下面举例说明。
假设已被估计出参数,利用均匀时宽进行接收VT-CRM信号,误码率性能如图 9所示。

|
Download:
|
| 图 9 三种模式下的误码率曲线 Fig. 9 BER of three modes | |
1) 模式1:非合作模式,收端采用时宽均匀,调频斜率变化规律与发端相同,带宽随之变化的Chirp信号进行相干解调。
2) 模式2:非合作模式,收端采用时宽均匀,调频斜率确定,带宽恒定的Chirp信号与接收信号进行相干解调。
3) 模式3:合作模式,VT-CRM通信系统的合作方接收方式。
由图 9可见,在未知带宽-调频率联合捷变参数的情况下,采用两种均时宽相干解调方案误码率为50%。这从通信误码率的角度,证明了VT-CRM通信系统具有较强的抗破译能力。
3 结论本文提出一种新型的隐蔽通信波形设计方案,该方案选用Chirp波形,通过多调频率改变码元时宽,与现有隐蔽通信波形相比,通信体制非周期,增加了波形的随机性;在频域上,该通信信号具有“类噪声”的特性,因此,具有良好的LPD和LPI性能。仿真结果表明,相比较于传统基于直扩的BPSK/DS波形,所设计的新型VT-CRM波形具有如下特征:1)具有频域扩频特性,且频域能量分布较BPSK/DS波形更平坦;2) VT-CRM波形循环谱f=0截面谱峰值明显低于BPSK/DS波形,可有效对抗循环谱检测手段;3)相较于BPSK/DS波形,VT-CRM波形倒谱谱峰无明显周期特征,无法通过倒谱估计其周期/速率信息;4)在抗破译方面,即使VT-CRM波形被截获,由于时宽和调频率的随机变化性,信息也难以被破译。
| [1] |
崔和, 郑珂. 基于直接序列扩频的鱼雷低截获概率信号及检测技术[J]. 鱼雷技术, 2015, 23(3): 187-195. CUI He, ZHENG Ke. Low probability of intercept signal and detection technology for torpedo based on direct sequence spread spectrum[J]. Torpedo technology, 2015, 23(3): 187-195. (  0) 0)
|
| [2] |
BASH B A, GOECKEL D, TOWSLEY D. Covert communication gains from adversary's ignorance of transmission time[J]. IEEE transactions on wireless communications, 2016, 15(12): 8394-8405. DOI:10.1109/TWC.2016.2614502 (  0) 0)
|
| [3] |
MILLS R F, PRESCOTT G E. Waveform design and analysis of frequency hopping LPI networks[C]//Proceedings of Military Communications Conference. San Diego, CA, USA, 1995: 778-782. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=483633
(  0) 0)
|
| [4] |
FAN Haining, GUO Ying, MENG Qingwei. Blind detection and parameter estimation algorithm based on atomic decomposition and information theoretic criterion[C]//Proceedings of International Conference on Networks Security, Wireless Communications and Trusted Computing. Wuhan, Hubei, China, 2009: 509-512. http://ieeexplore.ieee.org/document/4908316/
(  0) 0)
|
| [5] |
余敬东, 郭伟, 李牧. 直接序列扩频通信的循环谱检测和参数估计技术[J]. 电子科技大学学报, 1996(S3): 439-444. YU Jingdong, GUO Wei, LI Mu. Circular spectrum detection and parameter estimation techniques for direct sequence spread spectrum communication[J]. Journal of University of Electronic Science and Technology of China, 1996(S3): 439-444. (  0) 0)
|
| [6] |
雷开洪, 游庆山. 基于循环平稳特性的直扩信号检测与参数估计[J]. 四川大学学报(自然科学版), 2010, 47(1): 44-48. LEI Kaihong, YOU Qingshan. Detect DSSS and estimate its parameters based on cyclic spectrum correlation technology[J]. Journal of Sichuan University (natural science edition), 2010, 47(1): 44-48. DOI:10.3969/j.issn.0490-6756.2010.01.009 (  0) 0)
|
| [7] |
WANG Ligong, WORNELL G W, ZHENG Lizhong. Fundamental limits of communication with low probability of detection[J]. IEEE transactions on information theory, 2016, 62(6): 3493-3503. DOI:10.1109/TIT.2016.2548471 (  0) 0)
|
| [8] |
WANG Shilian, ZHU Jiang, ZHOU Jie. OFDM-based chaotic spread spectrum communications with high bandwidth efficiency[C]//Proceedings of International Conference on Control Engineering and Communication Technology. Liaoning, China, 2012: 940-943. http://dl.acm.org/citation.cfm?id=2473401
(  0) 0)
|
| [9] |
MEI Lin, SHA Xuejun, RAN Qinwen, et al. Research on the application of 4-weighted fractional Fourier transform in communication system[J]. Science China information sciences, 2010, 53(6): 1251-1260. DOI:10.1007/s11432-010-0073-1 (  0) 0)
|
| [10] |
DENG Bing, TAO Ran, CHEN Enqing. ANovel method for binary chirp-rate modulation and demodulation[C]//Proceedings of the 8th International Conference on Signal Processing. Beijing, China, 2006: 1-4. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGAN200611001167.htm
(  0) 0)
|
| [11] |
DENG Bing, TAO Ran, PING Dianfa. Study on chirp-rate modulation and demodulation based on fractional fourier transform[J]. Acta electronica sinica, 2008, 36(6): 1078-1083. (  0) 0)
|
| [12] |
NAMIAS V. The fractional order Fourier transform and its application to quantum mechanics[J]. IMA journal of applied mathematics, 1980, 25(3): 241-265. DOI:10.1093/imamat/25.3.241 (  0) 0)
|
| [13] |
QI Lin, TAO Ran, ZHOU Siyong, et al. Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform[J]. Science in China series F:information sciences, 2004, 47(2): 184-198. DOI:10.1360/02yf0456 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


