2. 寒地农业可再生资源利用技术与装备重点实验室, 哈尔滨 黑龙江 150030;
3. 东北农业大学 理学院, 黑龙江 哈尔滨 150030;
4. 鸟取大学 地域学部, 日本 鸟取 6808552
2. Key Laboratory of technology and equipment for the utilization of agricultural renewable resources in Cold Region, Harbin 150030, China;
3. College of Science, Northeast Agricultural University, Harbin 150030, China;
4. Faculty of Regional Sciences, Tottori University, Tottori 6808552, Japan
在当今能源短缺日渐凸显,环境压力日益增大的大背景下,风能作为一种清洁的可再生能源,正受到世界各国的广泛关注。现代的大部分风力机是研究者们利用航空的空气动力学技术,结合传统的飞机机翼翼型工作原理,针对风力机大气工作环境而设计研发的[1-3]。风力机高效工作具有两个前提:优秀的风资源与高效的风能捕获装置。寒冷地区通常具有更好的风资源,该地区风速更大,空气密度更高,但是该地区环境恶劣,这就为风力机设计提出了更高要求[4]。结冰问题是寒冷地区风力机设计面对的一个典型的挑战,例如我国三北地区的风场冬季常面临降雪结冰、南方高山风电场及沿海风场由于空气中水气含量较高或海浪飞溅形成水雾,造成风力机云雾结冰。结冰后风力机叶片外形发生改变,气动特性受到破坏、载荷分布不均,轻则降低发电效率,重则造成风力机停机甚至发生安全事故[5-7]。
近年来,为研究风力机结冰,研究者们大多借鉴飞机结冰的研究方法,最常用的是CFD数值模拟法与结冰风洞试验法。在数值计算方面,易贤等对二维翼型结冰及风力机结冰进行了计算[8-10],邓晓湖等进行了水平轴风力机叶片翼型结冰的数值模拟[11-12],朱程香等进行了风力机叶片翼型的结冰数值模拟研究[13-14];李岩等对风力机的结冰问题也进行了初步的研究[15-16]。然而风力机叶片做的是旋转运动,而飞机机翼是平动飞行,虽然在风力机叶片气动设计过程中常将其叶片翼型看作平动进行设计,但是在结冰过程中,液滴撞击到风力机叶片并凝结的过程中始终受到旋转的离心力作用,其结冰外形也相应的受到影响。针对风力机旋转叶片结冰的试验研究较计算研究相对很少,国外典型研究有Neil通对小型水平轴风力机结冰进行研究[17],Gillenwater等对结冰状态下的风机性能进行评价[18],Kraj等利用小型冰风洞研究了风力机叶片结冰过程[19],HAN等做过旋转叶片结冰风洞试验,但未能对冰形规律进行系统的分析[20],国内对旋转叶片结冰研究的相关报道较少,国内蒋兴良等对小风力机结冰进行了研究[21-22],李岩等对小型垂直轴风力机结冰进行了研究[23]。
为此,在前期研究的基础上,基于自行开发设计的利用自然低温的结冰风洞试验系统,对绕轴旋转的对称翼型叶片及非对称翼型叶片进行结冰试验研究,在验证试验系统可靠性后,提出了针对不规则冰形的典型特征量的分析方法,并对在不同工况下两种翼型叶片的结冰规律进行分析研究。
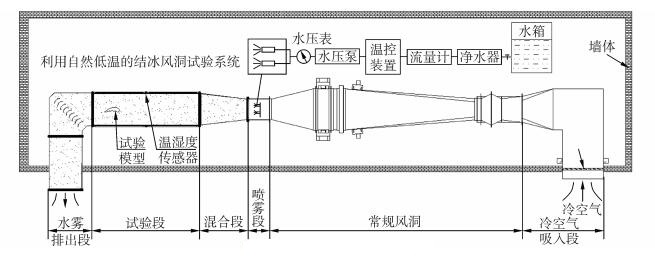
1 试验设备与方法 1.1 试验设备旋转叶片结冰试验所采用的冰风洞试验系统如图 1所示[24],所采用的基础风洞为日本鸟取大学工学部设计制造的开口射流式风洞,试验段截面为0.6 m×0.6 m,风速范围为1~15 m/s。在该风洞的吹出口处安装了水雾喷射系统,在其后设置了喷雾段、混合段和试验段。室外冷空气由冷风段吸入后,在喷雾段与喷雾系统喷出的过冷水滴在混合段充分混合,然后作用于试验段的试验物上结冰。
|
| 图1 结冰风洞试验系统 Figure 1 Experiment system of icing wind tunnel |
系统试验台如图 2所示,调频电机、力矩仪与转轴同轴连接,在转轴端部连接旋转梁,在旋转梁的端部固装试验用叶片模型,其中调频电机与力矩仪安装在气道外部,旋转部分位于气道内部,试验过程中通过高速摄像机 (美国Phantom v5.1,分辨率1 024×1 024像素) 拍摄旋转过程中结冰叶片图像。

|
| 图2 结冰测试试验台 Figure 2 Test station for icing measurement |
旋转叶片结冰试验所用的叶片模型如图 3所示,选用的翼型分别为NACA0018翼型和S809翼型,所采用的材质为实心铝制,叶片弦长c为100 mm。

|
| 图3 叶片模型 Figure 3 Experimental model of blade |
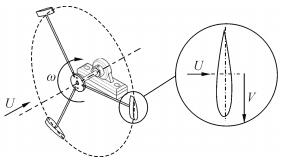
旋转叶片结冰试验运动参数如图 4所示,试验在2015年冬季进行,其中结冰风洞的相关参数标定方法在作者的前期研究中已给出介绍,主要包括试验段温度稳定性验证,试验段截面液态水含量分布标定及过冷水滴直径标定。确定试验条件为:结冰温度,T=-8℃;来流风速,U=4.54 m/s;液态水含量,LWC=0.5 g/m3;过冷水滴平均粒径,MVD=40 μm;绕轴旋转直径,D=0.5 m;选取了两种直径的叶片,分别为NACA0018翼型与S809翼型;选取了两个结冰时间:t=5 min和t=10 min;选取了4个旋转速度ω分别为200、400、600、800 r/min。
|
| 图4 旋转叶片运动参数 Figure 4 Motion parameters of rotating blade |
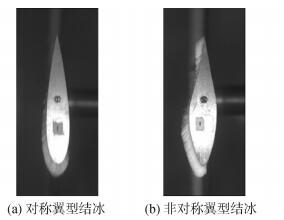
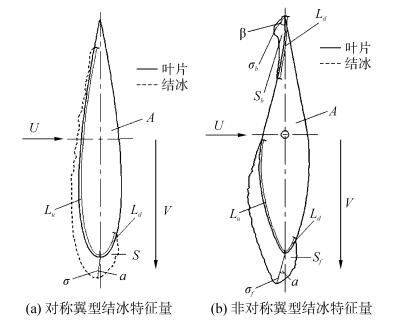
常见的风力机叶片翼型分为对称型与非对称型,其结冰情况存在不同,最典型的区别是非对称翼型在某些工况下其尾缘部分会出现单独结冰,见图 5。对二维翼型的结冰形状进行分析,可提炼出冰形几何特征量。针对本研究中获得的不规则冰形,对于对称翼型的叶片结冰,采用结冰冰形面积S、驻点厚度σ、驻点偏转角α、结冰上极限Lu与结冰下极限Ld,见图 6(a)。对于非对称翼型的叶片结冰,采用前缘结冰面积Sf、驻点厚度σf、驻点偏转角α,结冰上极限Lu、结冰下极限Ld,后缘结冰面积Sb,后缘偏角β,后缘厚度σb及后缘极限Lb,见图 6(b)。
|
| 图5 典型旋转叶片结冰 Figure 5 Typical icing on rotating blade |
|
| 图6 翼型结冰典型特征量 Figure 6 Typical factors of blade icing |
对于不同弦长的叶片,其结冰的特征量就无法相互比较,对其几何特征量进行无量纲化,引入如下无因次参数,对于对称翼型有
无因次结冰面积ηs:
| $ {\eta _s} = \frac{S}{A} $ | (1) |
无因次结冰驻点厚度ησ:
| $ {\eta _\sigma } = \frac{\sigma }{c} $ | (2) |
无因次结冰上极限ηLu:
| $ {\eta _{{L_u}}} = \frac{{{L_u}}}{c} $ | (3) |
无因次结冰下极限ηLd:
| $ {\eta _{{L_d}}} = \frac{{{L_d}}}{c} $ | (4) |
式中:A为翼型的面积,c为翼型的弦长。
对于非对称翼型有:
无因次前缘结冰面积ηSf:
| $ {\eta _{{S_f}}} = \frac{{{S_f}}}{A} $ | (5) |
无因次结冰驻点厚度ησf:
| $ {\eta _{{\sigma _f}}} = \frac{{{\sigma _f}}}{c} $ | (6) |
无因次结冰上极限ηLu:
| $ {\eta _{{L_u}}} = \frac{{{L_u}}}{c} $ | (7) |
无因次结冰下极限ηLd:
| $ {\eta _{{L_d}}} = \frac{{{L_d}}}{c} $ | (8) |
无因次后缘结冰面积ηSb:
| $ {\eta _{{S_b}}} = \frac{{{S_b}}}{A} $ | (9) |
无因次后缘厚度ησb:
| $ {\eta _{{\sigma _b}}} = \frac{{{\sigma _b}}}{c} $ | (10) |
无因次后缘极限ηLb:
| $ {\eta _{{L_b}}} = \frac{{{L_b}}}{c} $ | (11) |
虽然对称翼型和非对称翼型的结冰特征量评价方法存在差异,但是根据其相关性对于相同部位的特征量可共同比较。其非对称翼型无因次总结冰面积ηs可看作无因次前缘结冰面积ηSf与无因次后缘结冰面积ηSb的和,即
| $ {\eta _s} = {\eta _{{S_f}}} + {\eta _{{S_b}}} $ | (12) |
图 7所示为NACA0018铝制叶片在不同转速下结冰时间分别为5 min和10 min的叶片表面结冰分布情况。在相同的工况下,分别用3个叶片进行试验,可知这3个叶片上的结冰分布基本一致,利用本试验系统进行对称翼型旋转叶片的结冰试验具有可重复性。

|
| 图7 NACA0018翼型在不同转速下的结冰分布情况 Figure 7 Distributions of NACA0018 airfoil icing under different rotational speed |
当其他条件相同,转速不同时,叶片表面结冰情况不相同。1) 当转速为200 r/min时,结冰主要集中在迎风面,非迎风面结冰很少,迎风面结冰分布比较均匀,冰层厚度较一致,一直从前缘生长至尾缘。2) 当转速为400 r/min时,迎风面与非迎风面积冰发生变化,对于迎风面结冰仍然从前缘生长至尾缘,但是厚度不再一致,前缘厚度增加,尾缘厚度减小,非迎风面结冰开始向尾缘延伸。3) 当转速为600 r/min时,迎风面已经无法完全覆冰,冰层无法生长到尾缘部分,冰层厚度更加不一致,前缘部分结冰厚度要更大于后缘部分积冰,非迎风面结冰更像后延伸。4) 当转速为800 r/min时,结冰主要集中到了前缘部分,迎风面的结冰延伸距离变短,非迎风面的结冰延伸变长,前缘结冰厚度更厚。综合对比可发现,随着转速的增加,迎风面结冰延伸变短,非迎风面结冰延伸变长,迎风面结冰延伸距离要大于非迎风面结冰延伸距离,迎风面结冰要更加平滑,非迎风面结冰在尾部会急剧收缩。随着转速增加,结冰厚度分布变得不均衡,前缘结冰的厚度增大,后缘结冰厚度减小。
当其他条件相同,结冰时间不同时,叶片表面结冰情况仍满足上述结冰分布规律,所不同的是当叶片结冰时间由5 min增加到10 min时,叶片表面的结冰量增大,厚度增加,结冰在叶片表面的爬伸距离不能看出明显变化。
图 8所示为S809实心铝制叶片在不同转速下结冰时间分别为5 min和10 min的叶片表面结冰分布情况。在相同工况下分别对3个叶片结冰进行试验,可知这3种叶片结冰分布一致,利用本试验系统进行非对称翼型旋转叶片结冰试验具有可重复性。

|
| 图8 S809翼型在不同转速下的结冰分布情况 Figure 8 Distributions of S809 airfoil icing under different rotational speeds |
当其他条件相同,转速不同时,叶片表面结冰情况不同。1) 当转速为200 r/min时,结冰主要集中在迎风面且将其全部覆盖,非迎风面很少,这与NACA0018翼型结冰趋势相同,但是冰层厚度并不一致,其中前缘部分与尾缘部分的结冰厚度要大,中间部分结冰厚度要小。2) 当转速为400 r/min时,结冰不能将迎风面完全覆盖,其中结冰由前缘部分延伸到叶片中部,同时在叶片尾缘部分出现结冰,同时叶片非迎风面结冰向后爬伸,迎风面前缘部分结冰厚度基本相同,到后部急速降低。3) 当转速为600 r/min时,结冰已经无法生长到尾缘部分,尾缘部分不再发生结冰,非迎风面结冰延生变长,这与对称翼型结冰相同。4) 当转速为800 r/min时,叶片结冰主要集中在前缘部分,迎风面的结冰延伸变小,非迎风面的结冰延伸变大。综合对比可以发现,随着转速的增加,迎风面首先会被结冰完全覆盖,其后会出现前缘部分结冰和尾缘部分结冰,最后尾缘部分结冰消失,结冰全部出现在前缘部分,迎风面的结冰延伸距离要大于非迎风面。非对称翼型迎风面与非迎风面结冰均不平滑,由前缘向后先是平滑过渡,在结束部位急剧收缩。
当其他条件相同时,结冰时间不同,叶片表面仍满足上述结冰分布规律,所不同的是当叶片结冰时间由5 min增加10 min时,叶片表面的结冰量增大,厚度增加,结冰在叶片表面的爬伸距离不能看出明显变化。
2.2 结冰特征量分析为了定量的分析不同环境参数对叶片结冰的影响,根据叶片结冰评价方法,对叶片结冰的特征量进行分析。
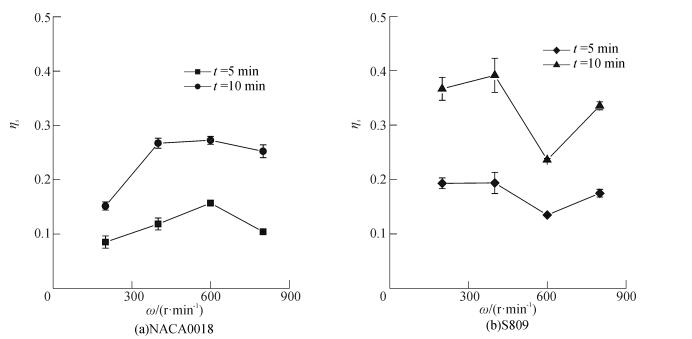
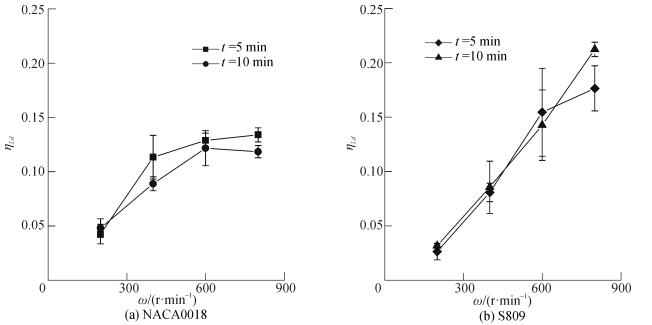
2.2.1 无因次结冰面积分析图 9给出了试验所用的两种叶片在不同工况下的无因次结冰面积ηs。总体来看,对于对称翼型的叶片结冰,其在低转速时结冰较少,随着转速增高,结冰呈现增长趋势,而在达到一定转速后又呈现降低趋势。而对于非对称翼型结冰,其在400 r/min时结冰要大于200 r/min,但是在600 r/min时急剧下降,在800 r/min时又出现了提升。这说明风机叶片的转速对结冰面结的影响很大,主要表现在低转速范围内,随着转速增大,叶片的相对速度攻角变小,虽然相对于来流来说叶片的迎风面始终没有发生变化,但是相对于叶片的相对速度而言,叶片的迎风面发生了变化,其水滴收集能力发生了变化,迎风面变化占主要因素;在高转速范围内,由于叶片运动相对速度攻角变化较小,迎风面的影响减弱,但是由于自身转速较高,其收集水滴增强,转速对结冰面积占主要因素。
|
| 图9 不同工况叶片无因次结冰面积 Figure 9 Dimensionless icing area of blade under different working conditions |
考虑时间对无因次叶片结冰面积影响可发现,对于任意工况下叶片在10 min的无因次结冰面积是5 min无因次结冰面积的两倍,可知在本文研究的结冰工况范围内,叶片无因此结冰面积与时间的关系可看作是线性关系。
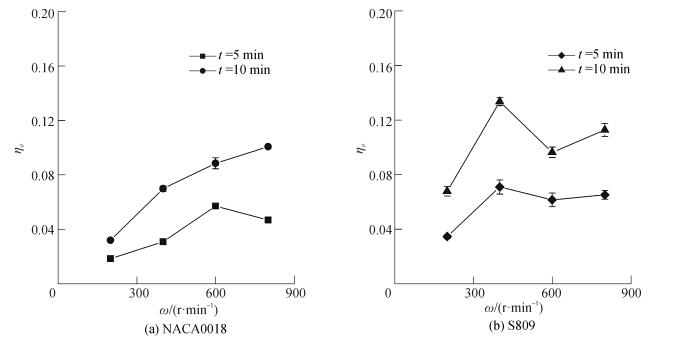
2.2.2 无因次驻点厚度分析图 10给出了试验所用的两个叶片在不同工况下的无因次结冰驻点厚度ησ。总体而言,对于对称翼型无因次结冰驻点厚度是随着转速呈现先增长后降低的趋势。这是由于随着旋转速度的增大,叶片结冰由流线型冰向角状型冰发展。对于非对称翼型,其无因次结冰驻点厚度在低转速时较小,随着转速增大,开始快速上升,但达到一定峰值时又开始降低,然后再继续增加。出现上述情况的主要原因还是在于在低转速范围内迎风面起主要作用,在高转速范围内转速起主要作用。
|
| 图10 不同工况叶片无因次结冰驻点厚度 Figure 10 Dimensionless icing stagnation thickness of blade under different working conditions |
考虑时间对无因次驻点厚度的影响可知,对于任意工况下叶片在10 min的无因次结冰驻点厚度是5 min无因次结冰驻点厚度的两倍,可知在本文研究的结冰工况范围内,叶片的无因次结冰驻点厚度与时间的关系可看作是线性关系。
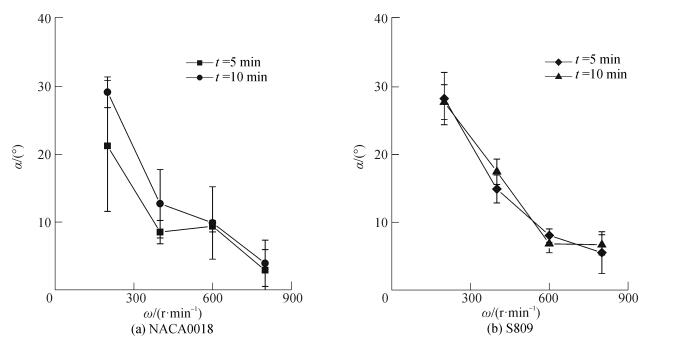
2.2.3 驻点偏转角分析图 11给出了试验所用的两个叶片在不同工况下的驻点偏转角α。总体而言,随着转速的增加,驻点偏转角呈现下降趋势,说明偏转角主要受到的是来流风速与自身转速的影响,主要为来流风速与叶片圆周速度的合速度方向。
|
| 图11 不同工况叶片结冰驻点偏转角 Figure 11 Blade icing stagnation angles under different working conditions |
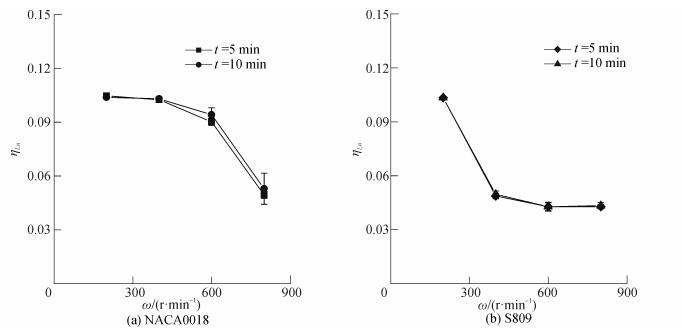
图 12给出了试验所用的两种叶片在不同工况下的无因次结冰上极限ηLu变化情况。可以发现对于对称翼型而言,当转速为200 r/min与400 r/min时,叶片的上极限覆盖了叶片的迎风面轮廓,当转速增加时,结冰上极限减小。对于非对称翼型,在200 r/min时叶片的上极限覆盖了叶片的迎风面轮廓,当转速增加时,结冰上极限逐渐减小,速度越大,其减小的趋势越低。
|
| 图12 不同工况叶片无因次结冰上极限 Figure 12 Dimensionless icing upper limit of blade under different working conditions |
图 13给出了试验所用的两种叶片在不同工况下的无因次结冰下极限ηLd。随着转速的增加,结冰下极限也在相应的增加。结冰下极限为旋转叶片的非迎风面,随着转速的增加其相对速度攻角减小,结冰下极限增加。
|
| 图13 不同工况叶片无因次结冰下极限 Figure 13 Dimensionless icing lower limit of blade icing under different working conditions |
综合比较叶片无因次结冰上极限和无因次结冰下极限可以发现,这两者不随时间变化而变化。
2.2.5 非对称翼型结冰评价上述分析了对称翼型和非对称翼型结冰的具有相同特性的结冰特征量,但是当转速为400 r/min时非对称翼型S809所结的不规则冰形将出现两个结冰区域,即前缘结冰和尾缘结冰,结合非对称翼型的不规则冰型评价方法,获得400 r/min时非对称翼型S809的结冰特征量如表 1所示。
| t/min | ηSf | ησf | α/(°) | ηLu | ηLd | ηSb | β/(°) | ησb | ηLb |
| 5 | 0.16 | 0.07 | 14.89 | 0.49 | 0.08 | 0.03 | 31.31 | 0.05 | 0.25 |
| 10 | 0.33 | 0.13 | 17.42 | 0.50 | 0.09 | 0.07 | 33.51 | 0.10 | 0.35 |
对于表 1中的数据,与对称翼型相同的不再进行分析,仅对有差别的结冰特征量进行分析。其中,后缘偏转角β随着结冰时间的增大有少量增加,同时无因次后缘结冰极限ηLd也有增加,其主要原因在于随着积冰的累积其结冰特征量发生变化,气动外形也发生变化,其值也相应的有所提升。同时无因次后缘结冰厚度ησb的增加也验证了上述观点。
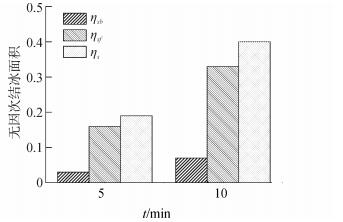
图 14给出了两次结冰时间下无因次前缘结冰面积ηSf、无因次后缘结冰面积ηSb及无因次总结冰面积ηs的关系图。可以发现无因次后缘结冰面积ηSf与无因次前缘结冰面积ηSb的比例变化较小,无因次前缘结冰面积ηSf要远大于无因次后缘结冰面积ηSb。
|
| 图14 前缘与后缘无因次结冰面积 Figure 14 Dimensionless icing area at the leading and trailing edge of blade |
通过对NACA0018翼型和S809翼型进行的绕轴旋转叶片结冰风洞试验获得的主要结论如下:
1) 本试验系统具有较高可重复性,可适用于对称翼型与非对称翼型的叶片结冰试验研究;
2) 旋转叶片翼型的转速不同,对结冰外形形式影响明显,低转速下叶片冰厚均匀,高转速下叶片前缘结冰增加,尾缘结冰减少;结冰时间对叶片结冰外形形式影响较小,但是随时间增加,叶片总量增加;对称翼型与非对称翼型间结冰存在较明显区别,非对称翼型结冰会出现前缘结冰和尾缘结冰同时存在的情况;
3) 对于各结冰特征量,无因次结冰面积、无因次驻点厚度会随着结冰时间的增加而呈线性增加,而其他结冰特征量随时间变化较小;转速不同对各结冰特征量有较明显的影响,在很大程度上决定了其发展趋势;对于非对称翼型在一定工况下会出现两个结冰区域,需要增加额外的特征量来分析结冰特征。
4) 旋转叶片的结冰风洞试验结果还无法完全反应实际的风力机叶片结冰情况,但实现缩小后的旋转叶片结冰风洞试验并建立起与其相对应的评价方法,就可以在之后的工作中通过选取合适的试验工况,利用相似准则的方法,对大型的风力机叶片结冰情况进行预测与分析,为大型风力机结冰研究提供试验基础。
| [1] |
胡燕平, 戴巨川, 刘德顺. 大型风力机叶片研究现状与发展趋势[J].
机械工程学报, 2013, 49(20): 140–151.
HU Yanping, DAI Juchuan, LIU Deshun. Research status and development trend on large scale wind turbine blades[J]. Journal of mechanical engineering, 2013, 49(20): 140–151. |
| [2] |
刘波, 贺志佳, 金昊. 风力发电现状与发展趋势[J].
东北电力大学学报, 2016, 36(2): 7–13.
LIU Bo, HE Zhijia, JIN Hao. Wind power status and de-velopment trend[J]. Journal of Northeast Dianli Uiniversity, 2016, 36(2): 7–13. |
| [3] |
程永卓. 浅谈中国风力机发电的现状与发展前景[J].
能源与节能, 2013(5): 19–20.
CHEN Yongzhuo. On the present situation and develop-ment propects of China's power generation[J]. Energy and energy conservation, 2013(5): 19–20. |
| [4] |
战培国. 国外寒冷地区风力机结冰问题研究[J].
航空科学技术, 2016, 27(2): 1–6.
ZHAN Peiguo. Review of the wind turbine icing in over-seas cold regions[J]. Aeronautical science & technology, 2016, 27(2): 1–6. |
| [5] |
任鹏飞, 徐宁, 宋娟娟, 等. 结冰对风力叶片影响数值的数值研究[J].
工程热物理学报, 2015, 36(2): 313–317.
REN Pengfei, XU Yu, SONG Juanjuan, et al. Numerical research on impact of icing on wind turbine blades[J]. Journal of engineering thermophysics, 2015, 36(2): 313–317. |
| [6] |
严晓雪, 朱春玲, 王正之. 风力机冰脱落轨迹仿真研究[J].
计算机仿真, 2015, 32(10): 123–127.
YAN Xiaoxue, ZHU Chunling, WANG Zhengzhi. Numerical simulation of ice shedding from turbine[J]. Computer simulation, 2015, 32(10): 123–127. DOI:10.3969/j.issn.1006-9348.2015.10.027 |
| [7] |
东乔天, 金哲岩, 杨志刚. 风力机结冰问题研究综述[J].
机械设计与制造, 2014(10): 269–272.
DONG Qiaotian, JIN Zheyan, YANG Zhigang. A review of icing effect on horizontal axis wind turbine[J]. Machinery design & manufacture, 2014(10): 269–272. DOI:10.3969/j.issn.1001-3997.2014.10.081 |
| [8] |
易贤, 王开春, 马洪林, 等. 大型风力机结冰过程水滴收集率三维计算[J].
空气动力学学报, 2013, 31(6): 745–751.
YI Xian, WANG Kaichun, MA Honglin, et al. 3-D numerical simulation of droplet collection efficiency in large-scale wind turbine icing[J]. Acta aerodynamica sinica, 2013, 31(6): 745–751. |
| [9] |
易贤, 王开春, 马洪林, 等. 水平轴风力机结冰及其影响计算分析[J].
太阳能学报, 2014, 35(6): 1052–1058.
YI Xian, WANG Kaichun, MA Honglin, et al. Computation of icing and its effect of horizontal axis wind turbine[J]. Acta energiae solaris sinica, 2014, 35(6): 1052–1058. |
| [10] |
易贤, 赵萍, 陈坤, 等. 水平轴风力机结冰探测器设计[J].
空气动力学学报, 2013, 31(2): 260–265.
YI Xian, ZHAO Ping, CHEN Kun, et al. Method of designing icing prober for an horizontal axis wind turbine[J]. Acta aerodynamica sinica, 2013, 31(2): 260–265. DOI:10.7638/kqdlxxb-2011.021 |
| [11] |
邓晓湖, 卢绪祥, 李录平, 等. 水平轴风力机叶片翼型结冰的数值模拟[J].
能源技术, 2010, 31(5): 266–271.
DENG Xiaohu, LU Xuxiang, LI Luping, et al. Numerical simulation of airfoil ice accretion process on horizontal-axis wind turbine blade[J]. Energy technology, 2010, 31(5): 266–271. |
| [12] |
蒋维, 李亚东, 李海波, 等. 水平轴风力机桨叶覆冰数值模拟[J].
太阳能学报, 2014, 35(1): 83–88.
JIANG Wei, LI Yadong, LI Haibo, et al. Simulation of icing on horozontal-axis wind turbine blade[J]. ACTA energiae solaris sinica, 2014, 35(1): 83–88. |
| [13] |
朱程香, 王珑, 孙志国, 等. 风力机叶片翼型的结冰数值模拟研究[J].
空气动力学学报, 2011, 29(4): 522–528.
ZHU Chengxiang, WANG Long, SUN Zhiguo, et al. Numerical study of wind turbine blade airfoil ice accre-tion[J]. Acta aerodynamica sinica, 2011, 29(4): 522–528. |
| [14] |
朱程香, 付斌, 孙志国, 等. 风力机防冰热载荷计算[J].
南京航空航天大学学报, 2011, 43(5): 701–706.
ZHU Chenxiang, FU Bin, SUN Zhiguo, et al. Calculation of wind turbine anti-icing heat load[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(5): 701–706. |
| [15] |
李岩, 迟媛, 冯放, 等. 垂直轴风力机叶片表面结冰的风洞试验[J].
工程热物理学报, 2012, 33(11): 1872–1875.
LI Yan, CHI Yuan, FENG Fang, et al. Wind tunnel test on icing on blade used for vertical axis wind turbine[J]. Journal of engineering thermophysics, 2012, 33(11): 1872–1875. |
| [16] |
刘钦东, 李岩, 王绍龙, 等. 攻角对NACA0018翼型明冰分布影响的风洞结冰试验研究[J].
中国科技论文, 2015, 10(23): 2716–2719.
LIU Qindong, LI Yan, WANG Shaolong, et al. A wind tunnel experimental study of glaze distribution effect on NACA0018 airfoil with the change of attack angles[J]. China science paper, 2015, 10(23): 2716–2719. DOI:10.3969/j.issn.2095-2783.2015.23.005 |
| [17] | NEIL B. Icing on a small horizontal axis wind turbine part1:glaze ice profiles[J]. Journal of wind engineering and industrial aerodynamics, 1992, 45(1): 75–85. DOI:10.1016/0167-6105(92)90006-V |
| [18] | GILLENWATER D, MASSON C, PERRON J. Wind turbine performance during icing events[J]. AIAA journal, 2008, 7(1): 1344. |
| [19] | KRAJ A G, BIBEAU E L. Phases of icing on wind turbine blades characterized by ice accumulation[J]. Re-newable energy, 2010, 35(5): 966–972. DOI:10.1016/j.renene.2009.09.013 |
| [20] | HAN Yiqiang, PALACIOS J, SCHMITZ S. Scaled ice accretion experiments on a rotating wind turbine blade[J]. Journal of wind engineering and industrial aerodynamica, 2010, 109: 55–67. |
| [21] |
舒立春, 任晓凯, 胡琴, 等. 环境参数对小型风力发电机叶片覆冰特性及输出功率的影响[J].
中国电机工程学报, 2016, 36(21): 5873–5878.
SHU Lichun, REN Xiaokai, HU qin, et al. Influences of environmental parameters on icing characteristics and output power of small wind turbine[J]. Proceedings of the CSEE, 2016, 36(21): 5873–5878. |
| [22] |
舒立春, 戚家浩, 胡琴, 等. 于洪杰. 风机叶片电加热防冰模型及分区防冰方法[J]. 中国电机工程学报, 2017, 37(5): 1448-1453.
SHU Lichun, Qi jiahao, HU qin, et al. Influences of envi-ronmental parameters on icing characteristics and output power of small wind turbine[J]. Proceedings of the CSEE, 2017, 37(5):1448-1453. |
| [23] |
李岩, 刘钦东, 王绍龙, 等. 小型垂直轴风力机叶片结冰风洞试验与数值计算[J].
空气动力学学报, 2016, 34(5): 568–572.
LI Yan, LIU Qindong, WANG Shaolong, et al. Wind tunnel test and numerical simulation on blade icing og small-scaled vertical axis wind turbine[J]. [J] ACTA aerodynamica sinica, 2016, 34(5): 568–572. |
| [24] |
李岩, 王绍龙, 郑玉芳, 等. 利用自然低温的风力机结冰风洞实验系统设计[J].
实验流体力学, 2016, 30(2): 54–58.
LI Yan, WANG Shaolong, ZHENG Yufang, et al. Design of wind tunnel experiment system for wind turbine icing by using natural low temperature[J]. Journal of experiment in fluid mechanics, 2016, 30(2): 54–58. |



