2. 东北林业大学 理学院, 黑龙江 哈尔滨 150040;
3. 东北林业大学 林学院, 黑龙江 哈尔滨 150040;
4. 哈尔滨理工大学 艺术学院, 黑龙江 哈尔滨 150040
2. School of Science, Northeast Forestry University, Harbin 150040, China;
3. School of Forestry, Northeast Forestry University, Harbin 150040, China;
4. Academy of Art, Harbin University of Science and Technology, Harbin 150040, China
为了缓解城市中心区交通堵塞,将用户从小汽车出行模式吸引到公交模式,成为城市交通规划研究领域亟待解决的课题。停车换乘(park-and-ride,P&R)设施的使用是解决该问题的有效手段。因此,为提高公共交通利用率,P&R设施的选址研究是停车规划和枢纽设施设计的热点问题。
以出行广义费用作为出行选择的衡量标尺是当前研究的常用方法。根据换乘广义费用应小于自驾广义费用这一假设,Holguin-Veras建立估算换乘人数的模型并对美国纽约市CBD进行P&R选址分析[1]。但该模型没有充分考虑P&R设施间的竞争,而是分别估算单个设施的用户需求量。竞争的含义是用户在各个选址方案之间和选址方案与驾车模式之间进行权衡。Felipe Aros-Vera[2]提出将P&R设施视为交通枢纽,应用基于P-枢纽(p-Hub)公式的空间优化模型来估算换乘的出行人数。该模型基于OD出行量采用多项logit公式来决定用户使用各个设施的比率,由此产生不同出行模式之间的竞争。卢晓珊等[3]建立了一个客流量最大、成本最小的双目标规划模型,然后利用线性加权技术将该双目标模型转化为含参数的单目标问题求解,但该模型的假设条件是不考虑设施容量问题,选址结果存在不确定性。然而,以上模型依然不能完全解决P&R设施选址问题。P&R设施的建设受到土地利用、路网结构、土地价格以及规划目标等诸多因素的影响。
本文假设出行者是理性的,并且出行广义费用为出行方式的决策要素,换乘的必要条件是换乘的广义费用低于自驾广义费用。本文利用p-枢纽方法研究在限定P&R设施系统吸引率下限及单个P&R设施容量上限的条件下确定最优化选址决策方案集的方法。P&R设施系统吸引率为选择P&R设施的人数与驾车出行人数的比值。
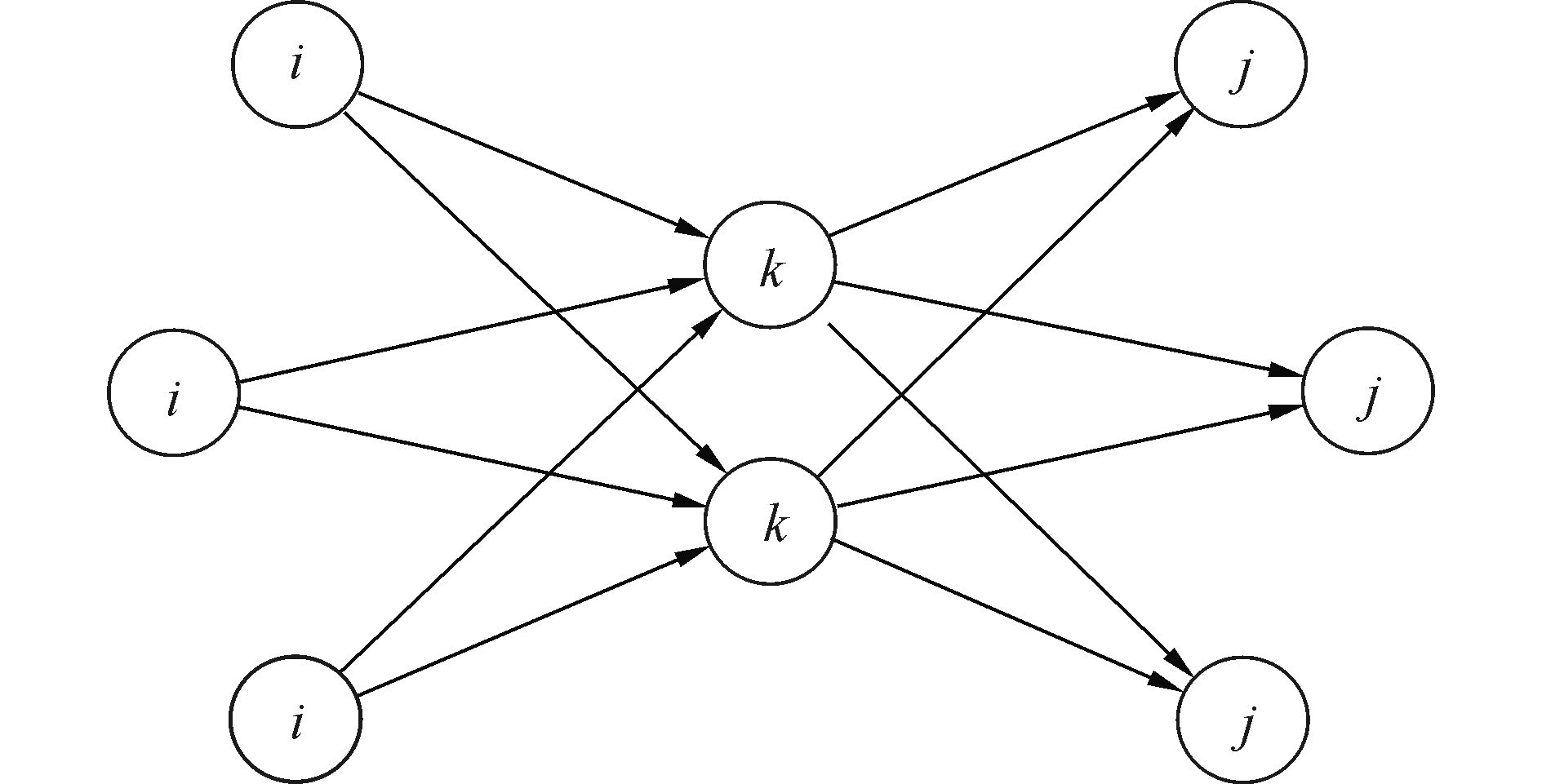
1 p-枢纽问题描述交通枢纽其运行过程是交通流从始点经由枢纽转运至终点。所谓p-枢纽问题是研究在交通网络当中设置p个枢纽来联接起止点,通过集散交通流来优化交通网络[4]。如图 1所示,i点表示出行始点,k点表示换乘设施,j点表示出行终点,箭头方向表示交通流的流动方向。k点作为交通枢纽,可以提供停车空间和换乘空间。
|
| 图1 p-枢纽网络图 Figure 1 Network of p-hub |
P&R系统的运作模式与p-枢纽问题一致,其用户需求是由在城市区域内从始点(居住地)到终点(办公地、购物地)的驾车出行者构成。因此,P&R设施作为中转站可以视为交通枢纽,出行者在此换乘更经济的出行模式继续后半段行程到达终点。值得注意的是,k点所提供的换乘空间尺度受到诸多因素的制约,因此换乘设施的容量应该被充分考虑。
确定停车换乘地址的备选集是优化选址的基础,在实践中至关重要。备选点的选择应该考虑以下四个方面:设施服务半径、交通系统便利性、社区整合、经济性[5]。
2 优化选址模型通常情况下,上角标是用来表示出行模式以及广义费用的类型,下角标是用来表示起始点、换乘点和终点。
2.1 假设条件在众多P&R系统方案下确定最优选址方案是非常复杂的问题。出于可行性,本文假设出行者为城市通勤者并且是理性的,并且出行广义费用为出行方式的决策要素。本文采用集计模型,将始点和终点以交通小区为单位进行选取。本文采用集计方法划分交通小区并认为OD相同的出行者选择模式(自驾或换乘)相同。否则,该问题过于复杂从而超出当前最优化理论的处理能力[2]。
由于换乘站备选点数量庞大,因此调研数据量巨大。而P&R设施投资相对较小,因此,利用大数据方法进行选址分析不可行[6]。本文考虑季节对出行选择的影响因素,引入步行舒适度的惩罚因子τ1。除此之外,本文考虑轨道交通工具内的舒适度与小汽车舒适度的差异,引入换乘公共交通乘车环境综合惩罚因子τ2,该惩罚因子综合反应载具环境包括拥挤度、隐私性、空气质量以及个人财产安全性等综合因素,该参数通过SP调查获得。
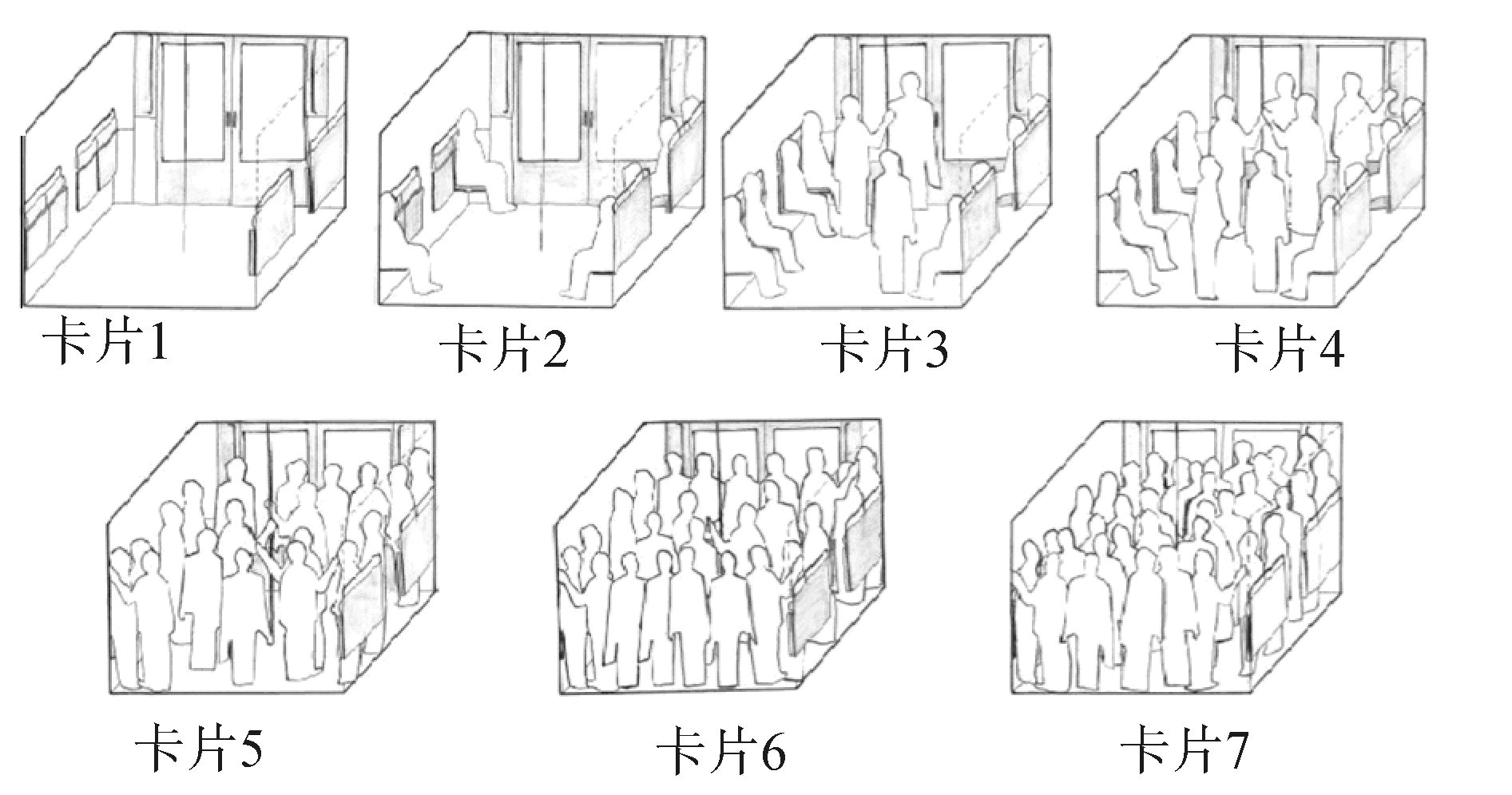
本文采用条件评估方法又称投标博弈法(contingent valuation method,CVM)[7]来估计换乘载客工具的拥挤成本,并研究不同舒适水平的等价变差。问卷方式是向受访者提出了一些假设场景,通过延长乘车时间来交换车厢内舒适度水平。所延长的时间记作WTTL(willingness to travel longer),在现场调查中使用了7张透视图(如图 2)来描述车厢内的早晚高峰的(7:30-10:00;17:00-19:30)场景。受访者根据自身经验选择一张透视图来预测下趟车的拥挤度,将它作为基准参考点,然后随机选择一张拥挤度小于它的透视图并进行二次投标来调查出行者对车厢舒适度相对于时间成本的偏好。调研者在延长时间为3、6、9、12、15、18共6档范围内随机投标,根据受访者第一轮的回答结果(同意或不同意)进行第二轮投标。例如:受访者在第一轮同意延长9 min,那么第二轮中随机增加延长时间(在12、15、18中随机选取);反之随机缩短延长时间(在3、6中随机选取)。本文以第二张透视图(拥挤度水平为1,1位乘客/m2)为基准,引入拥挤水平为j的时间乘子Tm(j)(即舒适度惩罚因子)。
|
| 图2 现场调查车厢拥堵水平透视图 Figure 2 Showcard used during the field survey |
做陈述性偏好的实证研究,在此分析下,车厢内拥挤度水平为j时的边际负效应可由βj*描述。两种拥挤度水平之间的替换边际率由βj*和β1*之比给出,恰为舒适度惩罚因子Tm(j) 。
针对于二次投标方法,采用双变量Probit模型来估计不同拥挤水平下换乘时间的边际负效应βj*。据此可计算出不同拥挤水平下的舒适度惩罚因子Tm(j)文献中给出了巴黎地铁中该值的取值范围1.05(拥挤度为2位乘客/m2的情况)~1.57(拥挤度为6位乘客/m2的情况).数据表明乘客对舒适度的偏好可表述为在最拥挤环境下(拥挤度为6位乘客/m2 )乘车1 min相当于在拥挤度水平为1(1位乘客/m2)的环境下乘车1.57 min。
根据随机效用模型的数据,可以得到拥挤成本和车厢密度之间的线性关系估计式。
据此,可以利用舒适度惩罚因子Tm(j)计算广义成本中的拥挤成本为:vTm(j)tkjT,IV。
其中,v表示时间成本。Tm(j)代表平均拥挤度为j时的舒适度惩罚因子即本文中的σ2。
2.2 出行选择分析在优化选址之前应该知道影响人们出行决策的基本原理,准确判断用户出行特征估算P&R设施用户需求量。在客户量需求模型中,判断出行者是否选择换乘模式是一个复杂的决策分析过程,相关考虑因素包括出行属性和特征及交通设施的竞争力[8]。出行模式的效能与相互竞争的交通设施所提供的服务水平密切相关。本文通过广义费用来刻画出行模式的效能。广义费用的构成表述如下:
自驾模式的广义费用:
| $g_{ij}^{A}=ut_{ij}^{A,IV}+f_{ij}^{A}+{{c}^{A}}d_{ij}^{A}+f_{j}^{1,p}$ | (1) |
式中:gijA为自驾模式从i点到j点的广义费用,元;v为时间价值,元/h;tijA,IV为自驾从i到j间行驶时间,h;fijA为自驾模式从i到j额外费用,元;cA为小汽车运行费用,元/km;dijA为自驾模式从i到j的出行距离,km;fjA,P为自驾模式在终点j的停车费,元。 换乘模式的广义费用:
| $\begin{align} & \ \ \ \ \ \ g_{ikj}^{PR}=v[t_{ik}^{A,IV}+{{\tau }_{1}}\cdot (t_{k}^{P,W}+t_{j}^{T,W})+ \\ & t_{kj}^{T,W}+t_{kj}^{T,S}+{{\tau }_{2}}t_{kj}^{A,IV}]+f_{ik}^{A}+f_{ik}^{T}+f_{k}^{A,P}+{{c}^{A}}d_{ij}^{A} \\ \end{align}$ | (2) |
式中:gikjPR为换乘模式从i点经k点到j点的广义费用,元;tikA,IV为自驾从i到k间行驶时间,h;τ1为季节对换乘过程中步行舒适度的惩罚因子;tkP,W为从停车场到换乘站的步行时间,h;tjT,W为从最近的车站到终点的步行时间,h;tkjT,W为换乘模式从k到j换乘等待时间,h;tkjT,S为换乘模式从k到j调度延误时间,h;τ2为换乘公共交通乘车环境综合惩罚因子;tkjT,IV为换乘模式从k到j间行驶时间,h;fikA为自驾模式从i到k的额外费用,元;fkjT为轨道交通从k到j的车票费用,元;fkA,P为自驾模式在换乘点停车费,元;cA为小汽车运行费用,元;dikA为自驾模式从i到k的出行距离,km。将广义费用代入Logit模型中来计算客户选择换乘设施的概率。
起止点为i,j的出行者在k点换乘的概率表达式为
| ${{p}_{ikj}}=\frac{{{x}_{k}}{{y}_{ikj}}{{\text{e}}^{-\theta g_{ikj}^{PR}}}}{{{\sum }_{\forall l\in K}}{{x}_{l}}{{y}_{ilj}}{{\text{e}}^{-\theta g_{ilj}^{PR}}}+{{\text{e}}^{-\theta g_{ij}^{A}}}}$ | (3) |
式中:xk为位置决策变量,yikj为成本决策变量,pikj为从i到j在k点换乘的出行选择概率,θ为出行者对出行费用的敏感度。
其中
在交通网络中对P&R设施进行优化选址,其目标是从换乘点备选集K中挑选出p个换乘点,使得换乘人数即需求总量达到最大化。数学建模为
| $\max z=\sum\limits_{k}{\sum\limits_{i,j}{{{h}_{ij}}{{p}_{ikj}}}}$ | (4) |
s.t.
| $g_{ij}^{A}=ut_{ij}^{A,IV}+f_{ij}^{A}+{{c}^{A}}d_{ij}^{A}+f_{j}^{1,p}$ | (5) |
| $\begin{align} & \ \ \ \ \ \ g_{ikj}^{PR}=v[t_{ik}^{A,IV}+{{\tau }_{1}}\cdot (t_{k}^{P,W}+t_{j}^{T,W})+ \\ & t_{kj}^{T,W}+t_{kj}^{T,S}+{{\tau }_{2}}t_{kj}^{A,IV}]+f_{ik}^{A}+f_{ik}^{T}+f_{k}^{A,P}+{{c}^{A}}d_{ij}^{A} \\ \end{align}$ | (6) |
| ${{x}_{k}}\in \{0,1\},\ \ \ \ \forall k\in K$ | (7) |
| $\sum\limits_{x}{{{x}_{k}}=p}$ | (8) |
| ${{y}_{ikj}}=\left\{ \begin{matrix} 1, & g_{ikj}^{PR}<g_{ij}^{A} \\ 0, & g_{ikj}^{PR}\ge g_{ij}^{A} \\ \end{matrix} \right.$ | (9) |
| ${{p}_{ikj}}=\frac{{{x}_{k}}{{y}_{ikj}}{{\text{e}}^{-\theta g_{ikj}^{PR}}}}{{{\sum }_{\forall l\in K}}{{x}_{l}}{{y}_{ilj}}{{\text{e}}^{-\theta g_{ilj}^{PR}}}+{{\text{e}}^{-\theta g_{ij}^{A}}}}$ | (10) |
| ${{D}_{k}}=\sum\limits_{ij}{{{h}_{ij}}}{{p}_{ikj}}\le {{c}_{k}}$ | (11) |
式中:hij为小汽车OD出行量,辆;pikj为从i到j在k点换乘的出行选择概率;Dk为选择换乘设施k的换乘车辆数;ck为P&R换乘设施k的容量上限。上述空间优化模型要求在满足若干约束条件(4)~(11)下,使P&R系统的用户需求总量即目标值z最大化。计算式(5)、(6)表示各种出行模式的广义费用。约束式(7)限定出行者只能换乘已选中的P&R设施。约束式(8)规定了P&R的设施总量。约束式(9)表示换乘的必要非充分条件是换乘的广义费用低于自驾的广义费用。而当自驾的广义费用高于或等于换乘的广义费用时,一部分出行者仍然会选择自驾,因为选择自驾的概率为
注意,概率pijk并不是决策变量。模型的决策变量分别是位置决策变量xk和成本决策变量yijk.
当决策变量取定后,其余的变量均可计算。式(4)~(11)建立了一个非线性整数规划模型。
本文考虑Logit模型的IIA特性,在下文的数值仿真中为尽量避免路径重合,引入换乘点之间的距离下限dmin,该模型针对所有间距大于dmin的换乘设施构成的系统进行选址优化,因此对于完善的轨道交通网络,多数情况下可采用MNL模型来估计出行模式选择概率。
4 求解算法由于p-hub问题已被证明是NP-hard问题[9],因此需采用启发式算法求解。启发式聚合集算法常用来解决优化选址中的p-hub问题[10-11]。本文采用三步式启发聚合集算法进行优化求解。
第一阶段:分别进行q次1-opt运算,即Teitz-Bart启发式算法。本文所用1-opt算法改编自文献[12]。每次都从一个随机的可行解即满足容量限定的P&R系统出发,经过1-opt运算得到改进解。改进解的特征是由一系列1-1优化替换所产生,并且不能再经过一次1-1替换得到更优的解。分别保存q次1-opt运算产生的结果,包括目标值和换乘站地址集,并将q个目标值从大到小排序,保存前r个目标值对应的结果(r≤q)。
在阶段一结束后构造启发式聚合集。
将上述r个改进解的换乘站地址集分别求并集与交集,构造聚合集CS与CS0。将所含地址个数分别记作v,u,即|CS|=v,|CS0|=u。
由于CS0必出现在最优解当中,故0≤u≤p≤v.再令聚合集CSf=CS-CS0。
第二阶段:分别进行s次2-opt运算。第一次运算是将阶段一中使目标值最大的换乘站地址集作为初始可行解,并将该地址集与CS0的差集记作R,称为2-opt运算中可变更地址集。而第二次至第s次的初始可行解是由CS0扩充得到,即从CSf中(随机)选出p-u个地址作为可变更地址集R,再将R与CS0的地址组合,如果满足容量限定则生成初始可行解。将阶段2的初始可行解进行2-opt算法优化得到改进解。改进解的特征是由一系列2-2优化替换所产生,并且不能再经过一次2-2替换得到更优的解。
第三阶段:将阶段二产生的s次运算结果,再分别进行一次1-opt运算,取当中目标值最大的改进解作为启发式算法的最优解。
1-opt算法:
1) 随机生成一个含p个地址的可行解,令S为对应的地址集,计算目标值z,令
2) 令
3) 令C=K/S,其中K是换乘点备选集,称C为1-opt运算中替换点备选集。
4) 若C=φ则到7),否则在C中随机挑一个P&R地址k再到5)。
5) 将C中地址k除去,并用k与S中的p个地址依次做替换,每一次替换后,新生成的P&R系统记作
判断1:如果该替换不满足容量限定,则进行下一次替换;如果满足容量限定则计算目标值并赋值给z*再作判断2。
判断2:如果z*>
判断3:如果第p次替换不满足容量限定或者仍有z*≤
6) 令z*=
7) 一次循环已经完成,如果
2-opt算法:
1) 对可行解计算目标值z,令
2) 令z0=
3) 令T=CSf/R 称T为2-opt运算的替换点备选集。因为|R|=p-u,|T|=v-p,所以在R与T中各挑出一对地址进行替换,共有
| $\begin{align} & t=[(p-u-1)+(p-u-2)+\cdots +1]\cdot \\ & \ \ \ \ [(v-p-1)+(v-p-2)+\cdots +1] \\ \end{align}$ |
种不同的替换方式。从第一次替换开始至t-1次替换结束对每次替换作下述判断:
判断1:判别当前替换是否满足容量限定。若不满足则跳到下一个替换。若满足则计算目标值并赋值给z*再作判断2。
判断2:若z*≤
对第t次替换作判断3。
判断3:如果满足容量限定且z*>
4) 一次循环已经完成。如果
1-opt运算中只要目标值被改进就将P&R地址集保存到S;2-opt运算是将t次替换中使目标值最大的可变更地址集保存到R。
5 实例分析本节针对二维路网的情形,做模拟仿真。所有的数值试验都是在工作站(Intel Core i7,3.4GHz)下进行,程序通过Visual Basic编写。
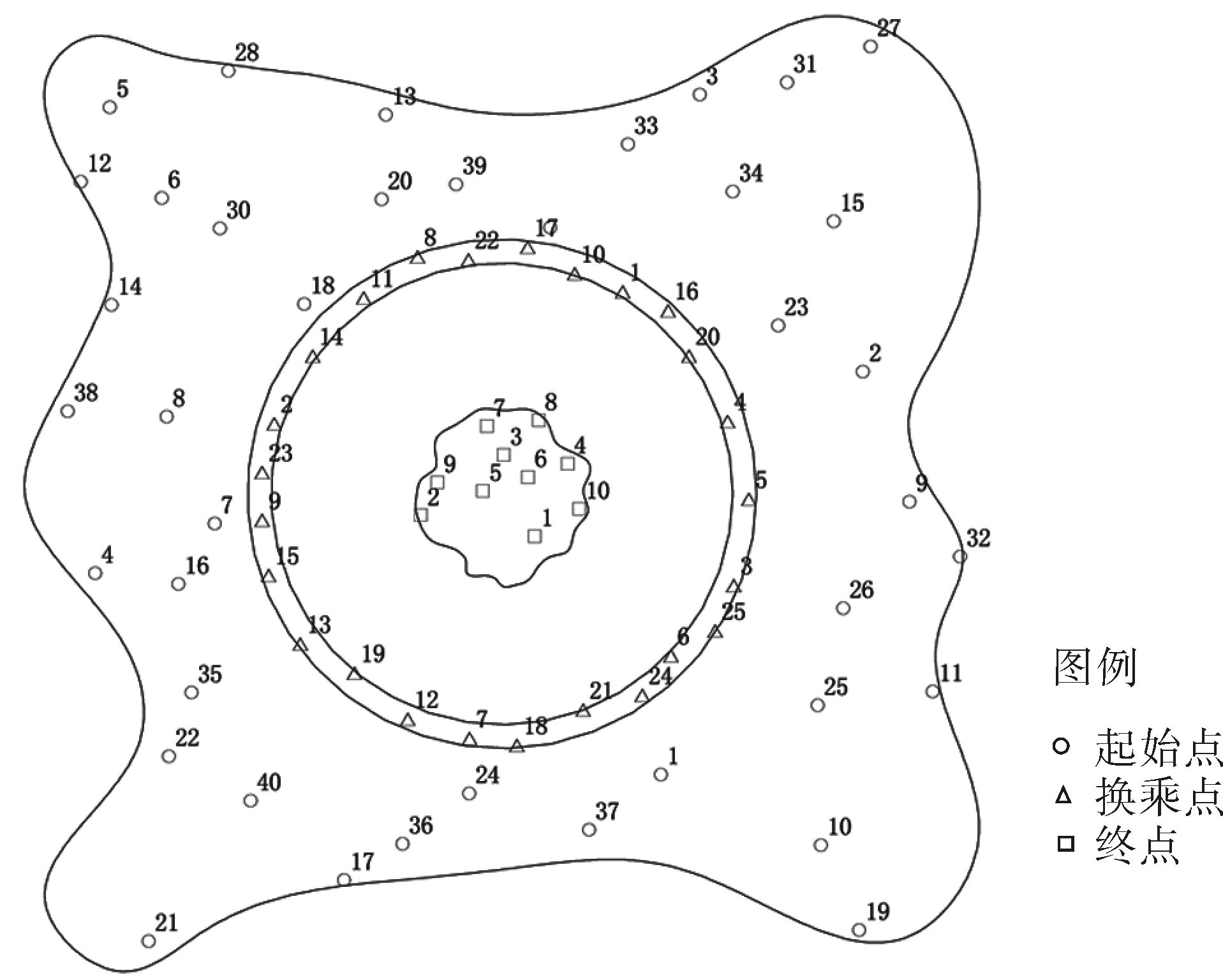
5.1 二维综合路网结构图 3描述了模拟假设的二维空间起止点与换乘点备选集的分布情况,核心区域为中央商务区包含出行终点直径约为3 km,内侧圆形区域表示交通堵塞区域,直径约为15 km,换乘点通常分布在堵塞区外围环形区域,距堵塞区1~1.5 km范围内[5, 13],环形区域的外围是居住区包含交通出行始点。该模拟结构图为单中心城市,城市尺度为纵横30 km,模拟假设为特大型城市。
|
| 图3 起止点与备选点分布图 Figure 3 Locations of OD and P&R candidates |
选用欧氏距离,燃油费与距离成正比。在处理实际问题时需要通过统计调查来标定出行者的价格敏感度参数θ,以便合理的制定取费标准来增加换乘设施的吸引率。现取价格敏感度θ=0.8,即出行者具有较高的价格敏感度,由于冬季对出行者带来不便,引入惩罚因子τ1来增加相应的时间成本[2, 14]。自驾模式的出行时间用tijA,IV表示,换乘模式的出行时间用tikA,IV+τ1·(tkP,W+tjT,W)+tkjT,W+tkjT,S+τ2tkjT,IV表示。在数值试验中时间用距离除以速度计算,在实际工程仿真中也可调用各路径的实时数据,如Google提供的交通实时数据。二维模型参数选取见表 1。表中,sijA,S为小汽车在非堵塞区的平均速度; sijA,C为小汽车在堵塞区的平均速度;skjT为轨道交通从k到j的平均速度。
| 出行参数 | 速度参数/km·h-1 | 时间参数/min | 价值参数/元 | 换乘票费/元 | 额外费用/元 | 其他参数 |
| K含25个换乘点 k分别取6,7,8 ck范围:750~1200 始点i共40个 终点j共10个 每对始终点出行量:25辆 总出行量10 000辆 dmin=4 km | sijA,S=60 sijA,C=15 skjT=25 | tijA,IV,tikA,IV,tkjT,IV 以上时间通过距离除 以相应的平均速度得出 tkP,W=11 tkjT,S=3 | v=26 cA=1 | 短途:2 中途:4 长途:6 | fijA=5 fikA=3 fkA,P=3 fjA,P=8 | τ1=1.7(冬季) τ2=1.2 θ=0.8 |
| 注:时间价值v按城市居民平均小时工资取值,惩罚因子τ1根据季节对步行速度的影响确定,τ2可通过问卷调研获得。 | ||||||
表 2中p为P&R设施数量,q为第一步启发式算法独立运行次数,r为第一步结束后选取最优解的个数,s为第二步和第三步启发式算法独立运行次数。
取参数p=7、q=10、r=4、s=5。p为P&R设施数量;q为第一步启发式算法独立运行次数;r为第一步结束后选取最优解的个数;s为第二步和第三步启发式算法独立运行次数;当容量限定为850时,优化算法在阶段三产生最优解。因此采用三步启发式算法是合理的,不能只进行1-opt或2-opt运算。
| 优化步骤 | 优化结果 |
| 阶段一排序后 的目标值以及 P&R地址集 | 8-10-15-20-2-24-7 (5 374); 6-8-20-5-15-7-2 (5 359); 10-4-15-8-21-12-2 (5 312); 7-8-10-20-9-13-24 (5 301) |
| CS | 8,10,15,20,2,24, 7,6,5,4,21,12,9,13 |
| CS0 | 8 |
| CSf | 10,15,20,2,24,7, 6,5,4,21,12,9,13 |
| 阶段二的目标值 以及P&R地址集 | 8-10-15-20-2-24-7 (5 374); 8-7-24-2-15-20-10 (5 374); 8-4-2-7-24-10-15 (5 363); 8-10-20-2-7-24-15 (5 374); 8-7-2-15-24-4-10 (5 363) |
| 阶段三的目标值 以及P&R地址集 | 8-10-15-20-2-24-7 (5 374); 8-7-24-2-15-20-10 (5 374); 8-20-2-7-24-10-15 (5 374); 8-10-20-2-7-24-15 (5 374); 8-7-2-15-25-4-10 (5 426) |
| 最优值/辆 | 5 426 |
| 排序后的最优地址集 | 10-15-25-2-7-8-4 |
| 注:表中括号内数字表示需求量最优值(辆)。 | |
P&R设施数量影响市政工程成本,因此,在满足需求的前提下,P&R设施数量不宜设置过低或过高。在模拟试验中,P&R设施数量分别取6、7、8,圆形堵塞区周长约45 km,现将设施间距离下限dmin取4 km,表 3~5显示了在不同容量限定下P&R系统选址方案。单个设施容量范围从750到1 200共分10级,每级间隔50个车位。括号外的数据代表优化选址后P&R设施的编号,括号内数据代表其吸引量。P&R设施编号的排列顺序根据其吸引量由大至小排列。最后两列分别代表在不同容量限定下,P&R系统的总吸引量和吸引率。根据表 3~5的结果显示P&R系统中单个P&R设施的吸引率与容量上限呈正相关。当容量上限在750~1 000范围内,优化选址结果扰动较大,但容量上限在1 050~1 200区段,优化结果趋于稳定即最优解中的半数以上选址点不随设施容量的增加而改变。如:选6个P&R设施,该区段共3个选址点一致,分别为11、19、3;选7个P&R设施,该区段共6个选址点一致,分别为14、19、1、3、22、21;选8个P&R设施,该区段共7个选址点一致,分别为14、19、1、3、22、21、4。表明系统中P&R设施数量的增加与选址稳定性成正相关。另外,在P&R设施数量不同的稳定的选址方案中比对一致的选址点(例如7个P&R设施与8个P&R设施稳定选址方案中的共同点:14、19、1、3、22、21),这些共同的稳定点应作为重要的选址对象。进一步分析可知存在个别选址点其吸引量随设施限定容量的增加而增多,如选址点14。该点值得决策者重点关注,并在周边交通承载力允许的条件下尽量扩大容量以满足未来发展需求。稳定性较好的优化选址方案其特征是P&R设施分布城市的多个方向,彼此相距一定的距离避免了设施间的竞争。并且吸引率较大的设施分布在始点密集区重心与CBD重心的连线附近。
| 容量上限/辆 | 6个停车换乘选址点 | 最优值/辆 | 吸引率/% | |||||
| 吸引率最多 | <————> | 吸引率最少 | ||||||
| 750 | 15(733) | 17(725) | 5(714) | 24(700) | 19(696) | 7(565) | 4 133 | 41.33 |
| 800 | 19(780) | 20(773) | 15(735) | 5(706) | 17(629) | 18(608) | 4 231 | 42.31 |
| 850 | 20(840) | 15(830) | 7(817) | 2(809) | 8(764) | 5(706) | 4 766 | 47.66 |
| 900 | 25(888) | 22(872) | 12(870) | 20(870) | 2(856) | 15(648) | 5 004 | 50.04 |
| 950 | 19(944) | 3(944) | 23(932) | 16(911) | 8(828) | 18(577) | 5 136 | 51.36 |
| 1 000 | 2(970) | 3(964) | 1(927) | 13(867) | 22(792) | 7(728) | 5 248 | 52.48 |
| 1 050 | 11(1 045) | 19(993) | 3(956) | 10(915) | 2(825) | 18(577) | 5 311 | 53.11 |
| 1 100 | 11(1 076) | 19(1 072) | 1(1 003) | 3(878) | 2(825) | 21(632) | 5 486 | 54.86 |
| 1 150 | 11(1 076) | 19(1 072) | 1(1 003) | 3(878) | 2(825) | 21(632) | 5 506 | 55.06 |
| 1 200 | 11(1 172) | 19(1 023) | 1(1 003) | 3(878) | 23(875) | 21(632) | 5 583 | 55.83 |
| 注:表中括号外数值表示P&R设施编号,括号外数值表示对应的吸引值。 | ||||||||
| 容量上限/辆 | 7个停车换乘选址点 | 最优值/辆 | 吸引率/% | ||||||
| 吸引率最多 | <————> | 吸引率最少 | |||||||
| 750 | 15(733) | 16(707) | 19(693) | 21(632) | 17(584) | 4(583) | 7(518) | 4 450 | 44.50 |
| 800 | 20(773) | 6(768) | 15(733) | 19(696) | 17(629) | 7(598) | 5(574) | 4 771 | 47.71 |
| 850 | 10(831) | 15(830) | 25(825) | 2(809) | 7(800) | 8(729) | 4(601) | 5 426 | 54.26 |
| 900 | 6(894) | 12(862) | 2(856) | 1(827) | 22(792) | 15(748) | 4(593) | 5 572 | 55.72 |
| 950 | 1(902) | 12(862) | 2(856) | 6(802) | 22(792) | 15(748) | 5(625) | 5 587 | 55.87 |
| 1 000 | 2(970) | 1(902) | 13(867) | 22(792) | 6(768) | 7(691) | 5(625) | 5 615 | 56.15 |
| 1 050 | 14(1 030) | 19(1 023) | 1(927) | 3(878) | 23(747) | 22(696) | 21(632) | 5 933 | 58.33 |
| 1 100 | 14(1 030) | 19(1 023) | 1(927) | 3(878) | 23(747) | 22(696) | 21(632) | 5 933 | 59.33 |
| 1 150 | 14(1 114) | 19(978) | 1(927) | 3(878) | 9(757) | 22(697) | 21(632) | 5 983 | 59.83 |
| 1200 | 14(1 114) | 19(978) | 1(927) | 3(878) | 9(757) | 22(697) | 21(632) | 5 983 | 59.83 |
| 注:表中括号外数值表示P&R设施编号,括号外数值表示对应的吸引值。 | |||||||||
| 容量上限/辆 | 8个停车换乘选址点 | 最优值/辆 | 吸引率/% | |||||||
| 吸引率最多 | <————> | 吸引率最少 | ||||||||
| 750 | 22(746) | 7(742) | 23(741) | 15(710) | 24(700) | 5(678) | 16(641) | 10(581) | 5 539 | 55.39 |
| 800 | 8(793) | 3(778) | 7(741) | 10(718) | 23(714) | 20(712) | 15(710) | 24(588) | 5 754 | 57.54 |
| 850 | 15(830) | 2(809) | 3(778) | 7(742) | 8(729) | 10(718) | 20(712) | 24(588) | 5 906 | 59.06 |
| 900 | 12(859) | 2(809) | 3(778) | 15(748) | 8(729) | 10(718) | 20(712 | 24(627) | 5 980 | 59.80 |
| 950 | 11(901) | 1(900) | 13(867) | 2(772) | 6(768) | 7(691) | 5(625) | 22(597) | 6121 | 61.21 |
| 1 000 | 14(988) | 19(944) | 3(928) | 23(746) | 10(716) | 20(712) | 8(583) | 18(577) | 6 194 | 61.94 |
| 1 050 | 14(1 030) | 19(1 023) | 1(827) | 3(797) | 23(747) | 22(696) | 21(632) | 4(503) | 6 255 | 62.55 |
| 1 100 | 14(1 030) | 19(1 023) | 1(827) | 3(797) | 23(747) | 22(696) | 21(632) | 4(503) | 6 255 | 62.55 |
| 1 150 | 14(1 114) | 19(978) | 1(827) | 3(797) | 9(757) | 22(697) | 21(632) | 4(503) | 6 305 | 63.05 |
| 1200 | 14(1 114) | 19(978) | 1(827) | 3(797) | 9(757) | 22(697) | 21(632) | 4(503) | 6 305 | 63.05 |
| 注:表中括号外数值表示P&R设施编号,括号外数值表示对应的吸引值。 | ||||||||||
城市规划决策者可以根据上述优化结果作选址决策分析,具体操作步骤如下:
1) 根据城市交通总体规划目标,确定预建P&R系统的吸引率下限,将低于吸引率下限的方案排除。
2) 对满足吸引率的P&R系统确定设施的最少数量(如表 4所示,假设规划目标中P&R系统吸引率下限为56%,则6个P&R设施无法满足要求,因此应增加设施数量。又如表 5所示,假设容量上限为900,P&R系统吸引率下限仍为56%则比较表 5和表 6可知,P&R设施数量至少为8个)。
3) 在剩余优化方案中,应充分考虑P&R设施周边实际交通路况,若周边道路交通不能承载预测数目的车辆,应将造成新的交通拥堵点的选址方案剔除,剩余方案构成决策方案集。
4) 实施的P&R设施的容量应介于模型估算的吸引量与限定容量上限之间。最终由规划专家综合考虑投资成本、吸引率以及城市用地现状、设施选址的稳定性等因素,在决策方案集中确定选址地点以及设施容量。
6 结论1) 在停车换乘选址分析中可以将换乘设施视为交通枢纽,以p-枢纽理论为基础构建二维城市综合路网的P&R系统优化选址模型。
2) 该问题可以采用启发式聚合集理论构造三步式搜索算法对模型进行求解。
3) 实际的案例中应考虑限定P&R设施停车容量上限,通过调整换乘站数量来优化P&R系统选址方案,以得到更符合实际的优化选址结果。
| [1] | HOLGUIN-VERAS J, REILLY J, AROS-VERA F, et al. Park-and-ride facilities in new york city economic analyses of alternative locations[C]//Transportation Research Record of the National Academies. Washington, 2012:123-130. |
| [2] | AROS-VERA F, MARIANOV V, MITCHELL J E. P-hub approach for the optimal park-and-ride facility location problem[J]. European journal of operational research, 2013, 226: 277–285. DOI:10.1016/j.ejor.2012.11.006 |
| [3] |
卢晓珊, 黄海军. 带有空间公平性约束的换乘停车场布局双目标规划模型[J].
系统工程理论与实践, 2014, 34(9): 2379–2385.
LU Xiaoshan, HUANG Haizhou. Bi-objective programming model for P&R facility location with spatial equity constraints[J]. Systems engineeringtheory & practice, 2014, 34(9): 2379–2385. |
| [4] | CAMPBELL J F, O'KELLY M E. Twenty-five years of hub location research[J]. Transportation science, 2012, 46(2): 153–169. DOI:10.1287/trsc.1120.0410 |
| [5] | AASHTO. Guide for park-and-ride facilities[S]. American:American Association of State Highway and Transportation Officials, 2004. |
| [6] | HOLGUIN-VERAS J, YUSHIMITO W F, AROS-VERA F, et al. User rationality and optimal park-and-ride location under potential demand maximization[J]. Transportation research part B, 2012, 46: 949–970. DOI:10.1016/j.trb.2012.02.011 |
| [7] | HAYWOOD L, KONING M. The distribution of crowding costs in public transport:new evidence from Paris[J]. Transportation research part A, 2015, 77: 182–201. DOI:10.1016/j.trb.2015.03.018 |
| [8] | ORTUZAR J D, WILLUMSEN L G. Modelling transport[M]. New York: John Wiley and Sons, 2001. |
| [9] | CAMPBELL J F, ERNST A T, DREZNER Z, et al. Facility location:applications and theory[M]. Berlin: Springer, 2002: 373-407. |
| [10] | ROSING K E, REVELLE C S. Heuristic concentration:two stage solution construction[J]. European journal of operational research, 1997, 97: 75–86. DOI:10.1016/S0377-2217(96)00100-2 |
| [11] | MARIANOV V, MIZUMORI M, REVELLE C. The heuristic concentration-integer and its application to a class of location problems[J]. Computers & operations research, 2008, 36: 1406–1422. |
| [12] | CHURCH R L, MURRAY A T. Business site selection, location analysis and GIS[M]. Hoboken: Wiley, 2008: 264. |
| [13] |
裴玉龙, 刘春晓. 停车换乘站位置选择及换乘需求预测[J].
长安大学学报, 2005, 25(1): 60–63.
PEI Yulong, LIU Chunxiao. Park and ride station location and its demand predicting[J]. Journal of Chang'an University, 2005, 25(1): 60–63. |
| [14] | RUDLOFF C, LEODOLTER M, BAUER D, et al. Influence of weather on transport demand case study from the Vienna, Austria, Region[J]. Transportation research record, 2015, 2582: 110–116. |



