船航行于海,受风、浪、流等外界强干扰作用产生六自由度运动,其中横摇尤为剧烈,不仅影响适航性及船载设备可靠性,而且大幅降低船体安全性与乘员舒适度。对于水面作战舰艇而言,直接影响武器精度,威胁战场生存能力[1-2]。因此,如何提高横摇稳定性成为船舶运动控制领域长期关注的研究热点。
减摇鳍作为迄今应用最为广泛的主动式减横摇特辅装置,其可靠性和有效性在多种船型上得以验证,但实际工程中减摇效果与理论预期相差较大[3]。究其原因,主要是由于减摇鳍是具有强干扰和模型不确定的非线性时变系统,导致控制误差较大。为此,学者提出一些控制策略[4-5],在一定程度上提高了减摇鳍系统性能,但忽视了系统反馈积累的较大误差,单纯依靠控制方法难以从根本上解决减摇鳍系统的控制问题,故需要改进反馈方式。针对反馈误差,最佳方案为运用直接检测的实际升力作为反馈,实时与船舶减摇所需的动态升力指令相比较,由误差信号驱鳍转动,直至达到期望的升力[6],减小升力实际值与理论值的误差。但在恶劣的海洋环境中很难实时检测升力,因此需要根据减摇鳍的具体结构特点设计专门的升力检测方法。
1 减摇鳍控制系统问题描述 1.1 横摇模型分析根据Conolly理论,装备一对减摇鳍的船体非线性横摇运动模型可表示为
| $ \begin{array}{*{20}{c}} {\left( {{I_x} + \Delta {I_x}} \right){{\rm{d}}^2}\theta /{\rm{d}}{t^2} + {N_1}{\rm{d}}\theta /{\rm{d}}t + {N_2}\left| {{\rm{d}}\theta /{\rm{d}}t} \right|{\rm{d}}\theta /{\rm{d}}t + }\\ {{G_1}\theta + {G_3}{\theta ^3} + {G_5}{\theta ^5} = - {K_\omega } - 2{L_\alpha }{l_\alpha }u} \end{array} $ | (1) |
式中:(Ix+ΔIx)d2θ/dt2为船体的惯性力矩,N1dθ/dt+N2|dθ/dt|dθ/dt为船体的阻尼力矩,G1θ+G3θ3+G5θ5为船体恢复力矩,Kω为扰动力矩,2Lαlαu为减摇鳍控制力矩,Lα为单鳍上升力,lα为鳍上水动力压力中心与鳍轴的距离,u为控制量。
理想状态下,如果减摇鳍的控制力矩完全抵消扰动力矩,则横摇运动停止,因此产生精准的控制力矩成为减横摇的关键。控制力矩需要根据扰动来确定,但海洋环境异常恶劣,如何准确有效地检测实际扰动力矩成为一个难题。
在鳍受到的动态水动力中,对船体起减摇作用的是升力。升力作用线垂直于水流相对速度和鳍的轴线。由于鳍的布置左右对称,当一舷的鳍产生的升力向上,则另一舷鳍产生的升力向下。因此,减摇鳍系统的控制问题很大程度上取决于如何精准检测和运用实际升力。
1.2 系统问题分析 1.2.1 系统反馈误差根据鳍在黏性流体中力系数计算理论[4],当鳍与水流成固定角度时,升力近似保持不变,如下
| $ {L_\alpha } = \frac{1}{2}{C_L}\left( \alpha \right)A\rho {V^2} $ | (2) |
式中:CL(α)为升力系数,ρ为流体密度,V为来流,A为鳍的投影面积。
由式(2)可知,升力系数与鳍角呈线性关系。在定常流情况下,在鳍失速前,鳍的静态水动力实验结果证实了这种关系。工程应用中,正是根据这种线性关系进行减摇鳍系统设计的,但鳍的真实水动力是复杂的动态特性。
针对鳍的水动力动态特性,船舶减摇与控制技术研究所进行了水池实验。限于篇幅,实验条件及结果见文献[4]。由实验结果可见,升力系数与鳍角的动态特性不是理想的线性关系,而是呈现一种闭合的扭曲梭形关系。因此,升力的理论估算值和实际检测值存在较大误差。
分析其影响因素,主要原因有以下几方面[3]:1)没有考虑前缘动壁效应;2)忽略实际条件,难以真正满足动力相似;3)多自由度耦合运动的干扰;4)斜流角简化为鳍转角。
因此,减摇鳍在实际海浪中的升力比水池实验结果更为复杂。理论静态升力与实际动态升力之间存在的较大误差,导致控制力矩的误差,难以准确抵抗海浪扰动力矩,必然降低减摇鳍的减摇效果。
1.2.2 控制策略误差在工程应用中,运用PID控制驱动减摇鳍抵抗海浪干扰,根据的是简化的船舶横摇线性模型。该模型作了如下假设:1)横摇运动是独立的,和船体的横荡运动、艏摇运动不存在耦合因素;2)船宽远小于波浪波长,正横浪时,波峰线平行于船舶中线面;3)波内压力场不因船体存在而受影响。
但实际上,在海浪中船的运动是一种复杂的六自由度综合运动,其中横摇、横荡和艏摇之间存在一定程度的影响;波内压力场也不是理想的,船体的存在必然会对波内压力场产生一定的影响。对于不同类型的船舶,因设计参数不同而使横摇周期Tφ和无因次阻尼系数nμ值不同。Tφ与船体横摇惯性矩和附加惯性矩有关。
由于船体外形复杂,以及船体与波浪之间的相互影响也十分复杂,故Ix与ΔIx的计算都是采用经验公式或实验来确定,因而是不确定的、可变的。nμ与横摇阻尼系数Nu有关,而船的横摇阻尼系数与船体形状、装载情况、横摇频率、横摇幅值、船体附近的流场、水粘性等多种因素有关,工程设计的PID控制忽略了上述影响。
因此,常规减摇鳍系统存在严重的非线性和不确定性问题。鳍角反馈误差和控制策略误差降低了减摇鳍的控制精度,造成限制减摇性能的瓶颈。
2 升力反馈设计为了实现减摇鳍的升力反馈控制,美国Sperry Marine公司[7]在中空的鳍轴内安装升力检测装置,但实际工程中在狭小的轴内安装与维修异常困难,因此没能实现推广应用。英国Rolls-Royce公司[8]在十字轴体内装传感器,但安装位置特殊易损坏,每次维修均需要船上坞,经济性差,且只适用于收放式减摇鳍,通用性不佳。日本三菱重工[9]在液压伺服系统中安装传感器,联合其他参数测量升力,改动虽小,但所需参数具有很强的非线性,与鳍型、角速度和船速等关联,还需进一步深入研究。船舶减摇与控制技术研究所[10-12]设计了鳍轴形变位移转化升力法,可实时检测升力,但存在轴承间隙死区问题。上述方法均较为繁琐,对原减摇鳍系统改动较大,不易工程实现。
近几十年来,常规减摇鳍广泛应用,优良性能得以证实。通过改进原鳍轴机构实现升力的检测,可继承其实用性和可靠性,弥补减摇鳍系统反馈不准确的缺陷。
2.1 鳍轴装置结构与常规减摇鳍相比,设计的新型鳍轴改进处是上支撑轴承处安装方形微动轴承座,轴承座内安装2个压力传感器,通过对鳍轴结构的受力分析,换算出鳍上所受的实际升力。改动小,不影响原设计的强度和密封要求,易于工程实现。
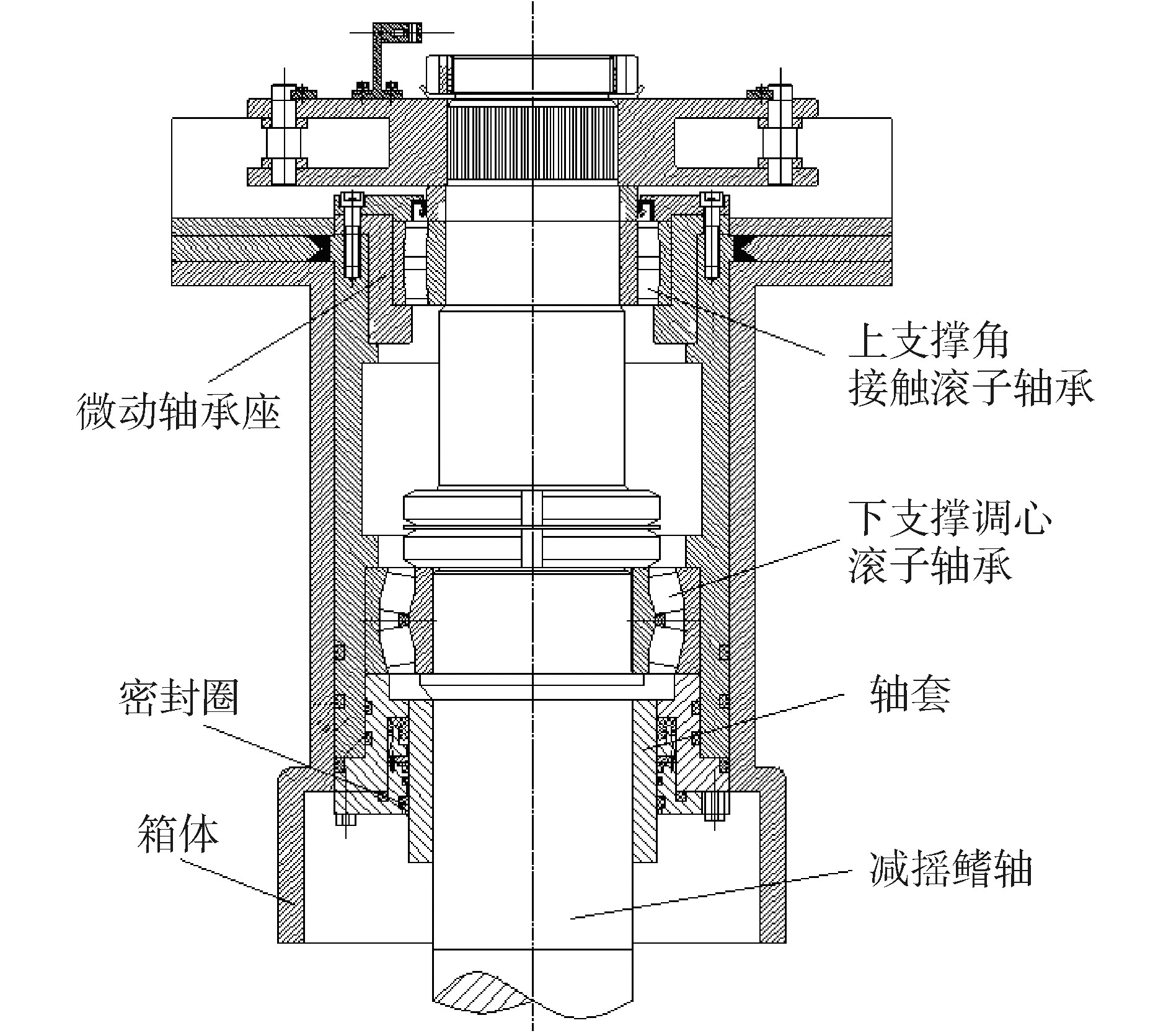
设计中,将上支撑轴承处设为受力测量点,有以下优点:1)位于船舱内,易于传感器的安装、检测和维修;2)根据力矩平衡原理,上支撑轴承的受力要比下支撑轴承受力小,对传感器的量程要求小。改进的新型减摇鳍轴结构如图 1所示。
|
图 1 新型鳍轴结构 Fig.1 New fin-axis structure |
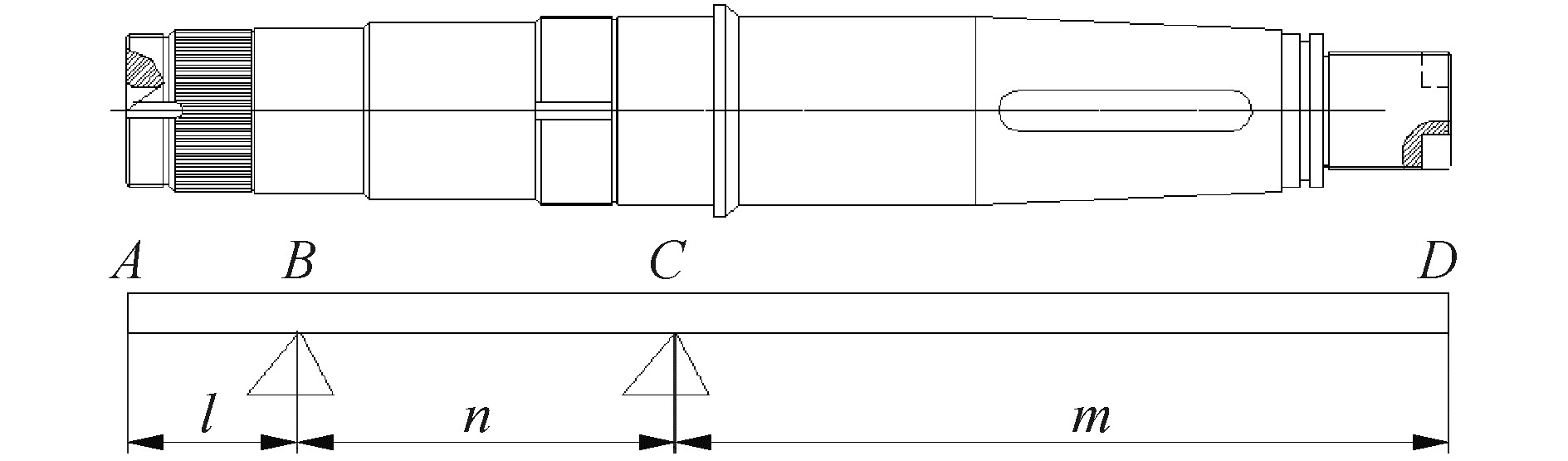
对鳍轴进行简化,轴体可近似成细长梁,上支撑的角接触滚子轴承和下支撑的调心滚子轴承形成2个简支点B和C。BC 段轴可近似等效为简支梁。在下支撑调心滚子轴承外侧部分悬空尺寸较长,CD段轴形成悬臂梁。鳍轴整体近似为简支梁和悬臂梁的复合梁结构,其简化形式如图 2所示。
|
图 2 鳍轴简化示意图 Fig.2 Schematic diagram of fin-axis |
鳍在海水中转动时,受到的水动力可近似看成作用于鳍压力中心D点的合力FD,支撑处B点和C点的支反力分别为FB和FC,驱鳍转动的液压缸在轴A点的不平衡力FA。
根据力矩平衡,可得
| $ {F_D}m - {F_A}\left( {l + n} \right) + {F_B}n = 0 $ | (3) |
则
| $ {F_D} = \frac{{{F_A}\left( {l + n} \right) - {F_B}n}}{m} $ | (4) |
因此,通过测量B点的支反力FB,配合FA即可得到鳍上的水动力,但如何方便有效地分解出其中的升力,就需要对传感器的安装方式进行专门设计。
2.3 传感器安装方式设计设计方形微动轴承座,当鳍受动态水动力作用时,鳍轴传动,设计的微动轴承座沿升力方向产生微动。相应的压力传感器测出上支撑点受到的升力。当鳍受到阻力作用时,由于它与升力方向垂直,微动轴承座将靠住箱体,且与压力传感器测力方向垂直,从而保证阻力分量不会影响到升力测量。
在箱体开孔安装一对压力传感器,为了保证测量的准确性,通过紧固器对传感器加一定的预应力,避免可能出现空隙带来死区问题,同时保证轴承座在平衡受力后结构稳定。
该方法有以下优点:1)通过机械结构,直接分解出鳍上升力;2)传感器的电路布局简单,安装维修方便;3)在轴承座的阻力侧安装压力传感器,可同时测量鳍上阻力,用途广泛。
通过改进鳍轴机构,实现升力的实时测量,不再依靠通过鳍角估算升力,设计系统的升力反馈,可降低系统的整体误差。
3 自适应模糊滑模控制器设计 3.1 系统描述由于减摇鳍受风浪流等强干扰,且运动模型的非线性和不确定性,因而很难用数学模型精准描述。滑模变结构控制作为一种强鲁棒性的控制策略,可用于解决此类非线性问题[12]。为此,利用自适应模糊化,可将滑模控制器中的切换项进行模糊逼近,使其连续化,解决系统输出抖振问题。
减摇鳍的非线性横摇运动系统可描述为
| $ \left\{ \begin{array}{l} {x^{\left( n \right)}} = f\left( {x,t} \right) + g\left( {x,t} \right)u\left( t \right) + d\left( t \right)\\ y = x \end{array} \right. $ | (5) |
式中: x∈R,u∈R,y∈R,
针对上述减摇鳍的非线性横摇运动系统,定义控制器的切换函数为
| $ s\left( {x,t} \right) = {k_1}e + {k_2}\dot e + \cdots {k_{n - 1}}{e^{\left( {n - 1} \right)}} + {e^{\left( {n - 1} \right)}} = \mathit{\boldsymbol{ke}} $ | (6) |
式中:
将滑模变结构控制律设计为
| $ u\left( t \right) = \frac{1}{{g\left( {x,t} \right)}}\left( { - f\left( {x,t} \right) - \sum\limits_{i = 1}^{n - 1} {{k_i}{e^{\left( i \right)}} + x_d^{\left( n \right)} - {u_{sw}}} } \right) $ | (7) |
其中usw=ηsgn(s),η>D, 则
| $ \begin{array}{*{20}{c}} {\dot s\left( {x,t} \right) = \sum\limits_{i = 1}^{n - 1} {{k_i}{e^{\left( i \right)}} + {e^{\left( n \right)}}} = \sum\limits_{i = 1}^{n - 1} {{k_i}{e^{\left( i \right)}} + f\left( {x,t} \right) + } }\\ {g\left( {x,t} \right)u\left( t \right) + d\left( t \right) - x_d^{\left( n \right)}} \end{array} $ | (8) |
将式(5)、(7)代入式(8),得
| $ s\left( {x,t} \right) \cdot \dot s\left( {x,t} \right) = ds - \eta \left| s \right| \le 0 $ | (9) |
当减摇鳍系统参数f、g和外界干扰d上界未知时,则控制律式(7)不适用。所以采用模糊系统
运用乘积推理机、单值模糊器和中心平均解模糊器设计相应的减摇鳍模糊控制系统,其输出分别为
| $ u\left( t \right) = \frac{1}{{\hat g\left( {x,t} \right)}}\left( { - \hat f\left( {x,t} \right) - \sum\limits_{i = 1}^{n - 1} {{k_i}{e^{\left( i \right)}} + x_d^{\left( n \right)} - \hat h\left( s \right)} } \right) $ | (10) |
| $ \left\{ \begin{array}{l} \hat f\left( {\mathit{\boldsymbol{x}}\left| {{\mathit{\boldsymbol{\theta }}_f}} \right.} \right) = \mathit{\boldsymbol{\theta }}_f^{\rm{T}}\xi \left( x \right)\\ \hat g\left( {\mathit{\boldsymbol{x}}\left| {{\mathit{\boldsymbol{\theta }}_g}} \right.} \right) = \mathit{\boldsymbol{\theta }}_g^{\rm{T}}\xi \left( \mathit{\boldsymbol{x}} \right)\\ \hat h\left( {s\left| {{\mathit{\boldsymbol{\theta }}_h}} \right.} \right) = \mathit{\boldsymbol{\theta }}_h^{\rm{T}}\phi \left( s \right) \end{array} \right. $ | (11) |
式中:
则θfT、θgT和θhT根据自适应律而变化。
| $ \left\{ \begin{array}{l} \hat h\left( {s\left| {\mathit{\boldsymbol{\theta }}_h^ * } \right.} \right) = {\eta _\Delta }{\mathop{\rm sgn}} \left( s \right)\\ {\eta _\Delta } = D + \eta ,\;\;\;\;\;\eta \ge 0\\ \left| {d\left( t \right)} \right| \le D \end{array} \right. $ | (12) |
设计自适应律为
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot \theta }}}_f} = {r_1}s\xi \left( x \right)\\ {{\mathit{\boldsymbol{\dot \theta }}}_g} = {r_2}s\xi \left( x \right)u\\ {{\mathit{\boldsymbol{\dot \theta }}}_h} = {r_3}s\phi \left( s \right) \end{array} \right. $ | (13) |
定义减摇鳍控制系统的最优参数为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\theta }}_f^ * = \arg \mathop {\min }\limits_{{\theta _f} \in {\mathit{\Omega }_f}} \left[ {\sup \left| {\hat f\left( {\mathit{\boldsymbol{x}}\left| {\mathop {{\mathit{\boldsymbol{\theta }}_f}}\limits_{x \in {{\bf{R}}^n}} } \right.} \right) - f\left( {x,t} \right)} \right|} \right]\\ \mathit{\boldsymbol{\theta }}_g^ * = \arg \mathop {\min }\limits_{{\theta _g} \in {\mathit{\Omega }_g}} \left[ {\sup \left| {\hat g\left( {\mathit{\boldsymbol{x}}\left| {\mathop {{\mathit{\boldsymbol{\theta }}_g}}\limits_{x \in {{\bf{R}}^n}} } \right.} \right) - g\left( {x,t} \right)} \right|} \right]\\ \mathit{\boldsymbol{\theta }}_h^ * = \arg \mathop {\min }\limits_{{\theta _h} \in {\mathit{\Omega }_h}} \left[ {\sup \left| {\hat h\left( {\mathit{\boldsymbol{s}}\left| {\mathop {{\mathit{\boldsymbol{\theta }}_h}}\limits_{x \in {{\bf{R}}^n}} } \right.} \right) - {u_{sw}}} \right|} \right] \end{array} \right. $ | (14) |
式中Ωf、Ωg和Ωh分别为θf、θg和θh的集合。
定义系统的最小逼近误差为
| $ \begin{array}{l} \omega = f\left( {x,t} \right) - \hat f\left( {\mathit{\boldsymbol{x}}\left| {\mathit{\boldsymbol{\theta }}_f^ * } \right.} \right) + \left( {g\left( {x,t} \right) - \hat g\left( {\mathit{\boldsymbol{x}}\left| {\mathit{\boldsymbol{\theta }}_g^ * } \right.} \right)} \right)u,\\ \;\left| \omega \right| \le {\omega _{\max }} \end{array} $ | (15) |
将控制律式(10)代入式(15),得
| $ \begin{array}{*{20}{c}} {\dot s = \sum\limits_{i = 1}^{n - 1} {{k_i}{e^{\left( i \right)}} + {x^{\left( n \right)}} - x_d^{\left( n \right)}} = \mathit{\boldsymbol{\varphi }}_f^{\rm{T}}\xi \left( x \right) + \mathit{\boldsymbol{\varphi }}_g^{\rm{T}}\xi \left( x \right)u\left( t \right) + }\\ {\mathit{\boldsymbol{\varphi }}_h^{\rm{T}}\varphi \left( s \right) + d\left( t \right) + \omega - \hat h\left( {s\left| {\theta _h^ * } \right.} \right)} \end{array} $ | (16) |
式中:φf=θf*-θf,φg=θg*-θg,φh=θh*-θh。
定义Lyapunov函数为
| $ V = \frac{1}{2}\left( {{s^2} + \frac{1}{{{r_1}}}\mathit{\boldsymbol{\varphi }}_f^{\rm{T}}{\mathit{\boldsymbol{\varphi }}_f} + \frac{1}{{{r_2}}}\mathit{\boldsymbol{\varphi }}_g^{\rm{T}}{\mathit{\boldsymbol{\varphi }}_g} + \frac{1}{{{r_3}}}\mathit{\boldsymbol{\varphi }}_h^{\rm{T}}{\mathit{\boldsymbol{\varphi }}_h}} \right) $ | (17) |
式中r1、r2和r3为正常数, 则
| $ \begin{array}{*{20}{c}} {\dot V = s\dot s + \frac{1}{{{r_1}}}\mathit{\boldsymbol{\varphi }}_f^{\rm{T}}{{\mathit{\boldsymbol{\dot \varphi }}}_f} + \frac{1}{{{r_2}}}\mathit{\boldsymbol{\varphi }}_g^{\rm{T}}{{\mathit{\boldsymbol{\dot \varphi }}}_g} + \frac{1}{{{r_3}}}\mathit{\boldsymbol{\varphi }}_h^{\rm{T}}{{\mathit{\boldsymbol{\dot \varphi }}}_h} = s\mathit{\boldsymbol{\varphi }}_f^{\rm{T}}\xi \left( x \right) + }\\ {\frac{1}{{{r_1}}}\mathit{\boldsymbol{\varphi }}_f^{\rm{T}}{{\mathit{\boldsymbol{\dot \varphi }}}_f} + s\mathit{\boldsymbol{\varphi }}_g^{\rm{T}}\xi \left( x \right)u\left( t \right) + \frac{1}{{{r_2}}}\mathit{\boldsymbol{\varphi }}_g^{\rm{T}}{{\mathit{\boldsymbol{\dot \varphi }}}_g} + s\mathit{\boldsymbol{\varphi }}_h^{\rm{T}}\mathit{\boldsymbol{\varphi }}\left( s \right) + }\\ {\frac{1}{{{r_3}}}\mathit{\boldsymbol{\varphi }}_h^{\rm{T}}{{\mathit{\boldsymbol{\dot \varphi }}}_h} + s\left( {d\left( t \right) - \hat h\left( {s\left| {\theta _h^ * } \right.} \right)} \right) + s\omega } \end{array} $ | (18) |
由于
| $ \hat h\left( {s\left| {\theta _h^ * } \right.} \right) = {\eta _\Delta }{\mathop{\rm sgn}} \left( s \right) $ | (19) |
则
| $ \dot V = sd\left( t \right) + s\omega - \left( {D + \eta } \right)\left| s \right| $ | (20) |
式中:
将自适应律式(15)代入式(20),得
| $ \dot V \le s\omega - \eta \left| s \right| $ | (21) |
根据模糊逼近理论,减摇鳍自适应模糊系统可实现使ω非常小,因此,通过取足够大的η可保证
根据改进常规鳍轴设计的升力反馈控制减摇鳍系统实验台如图 3所示。在液压伺服系统正向加载和反向加载时,测得传感器的电压值与升力之间的数据。采用最小二乘法,用线性比例特性来拟合升力测量曲线。对应的拟合函数为

|
图 3 减摇鳍实验台 Fig.3 Test bench of fin stabilizers |
| $ y = 1.5402x + 2.4559 $ |
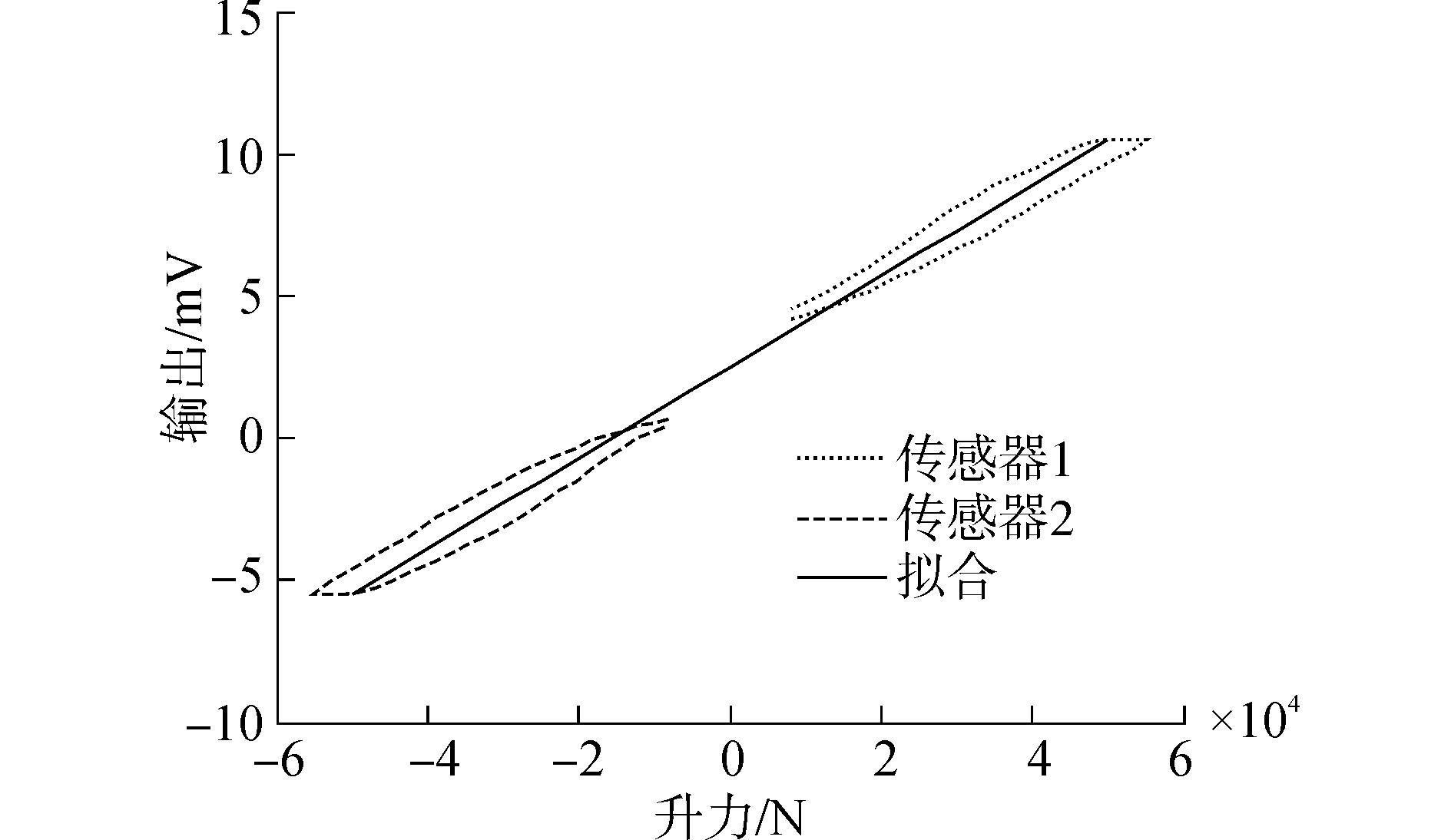
式中:2.455 9 mV为未加载时升力测量机构在升力传感器上反映出来的零位偏移电压。升力拟合结果如图 4所示。
|
图 4 升力测量值拟合曲线 Fig.4 lift curves obtained by fitting the data |
以装备某型减摇鳍系统的某船为例,进行仿真验证。横摇模型采用Conolly单自由度横摇运动模型,运用单参数谱模拟海浪随机运动。系统主要参数为:排水量D=1.5×106 kg,船长L=98.0 m,船宽B=10.2 m,吃水T=3.1 m,稳心高h=1.15 m,谐振周期Tφ=7.8 s,对应的升力反馈控制减摇鳍的船舶横摇非线性模型为
| $ \begin{array}{*{20}{c}} {{{\rm{d}}^2}\theta /{\rm{d}}{t^2} + 0.25174{\rm{d}}\theta /{\rm{d}}t + 0.7056\left| {{\rm{d}}\theta /{\rm{d}}t} \right|{\rm{d}}\theta /{\rm{d}}t + }\\ {0.64836\theta - 15.7696{\theta ^3} + 20.6562{\theta ^5} = }\\ { - 0.00973u - 0.39479e - 7{K_\omega }} \end{array} $ | (22) |
横摇角度指令θd(t)=0,切换函数为
| $ \left\{ \begin{array}{l} {\mu _{NM}}\left( {{x_i}} \right) = \exp \left[ { - {{\left( {\left( {{x_i} + 5{\rm{ \mathsf{ π} /3}}} \right)/\left( {5{\rm{ \mathsf{ π} /12}}} \right)} \right)}^2}} \right]\\ {\mu _{NS}}\left( {{x_i}} \right) = \exp \left[ { - {{\left( {\left( {{x_i} + 5{\rm{ \mathsf{ π} /6}}} \right)/\left( {5{\rm{ \mathsf{ π} /12}}} \right)} \right)}^2}} \right]\\ {\mu _Z}\left( {{x_i}} \right) = \exp \left[ { - {{\left( {{x_i}/\left( {5{\rm{ \mathsf{ π} /12}}} \right)} \right)}^2}} \right]\\ {\mu _{PS}}\left( {{x_i}} \right) = \exp \left[ { - {{\left( {\left( {{x_i} - 5{\rm{ \mathsf{ π} /6}}} \right)/\left( {5{\rm{ \mathsf{ π} /12}}} \right)} \right)}^2}} \right]\\ {\mu _{PM}}\left( {{x_i}} \right) = \exp \left[ { - {{\left( {\left( {{x_i} - 5{\rm{ \mathsf{ π} /3}}} \right)/\left( {5{\rm{ \mathsf{ π} /12}}} \right)} \right)}^2}} \right] \end{array} \right. $ | (23) |
根据排列组合,则用于逼近f(x, t)和g(x, t)的模糊规则共有25条。
定义切换函数s(t)的隶属函数为
| $ \left\{ \begin{array}{l} {\mu _N}\left( s \right) = 1/\left( {1 + \exp \left( {5s + 15} \right)} \right)\\ {\mu _Z}\left( s \right) = \exp \left( { - {s^2}} \right)\\ {\mu _P}\left( s \right) = 1/\left( {1 + \exp \left( {5s - 15} \right)} \right) \end{array} \right. $ | (24) |
自适应参数取r1=5,r2=1,r3=10。
考虑到实际应用,在仿真中采用减摇鳍实际工程改进型PID控制器作为参照:
| $ \begin{array}{*{20}{c}} {{u_{{\rm{PID}}}}\left( s \right) = }\\ {\left( {{k_1}\frac{1}{{{T_I}s + 1}} + {k_D}\frac{{{T_{D{\rm{1}}}}s}}{{\left( {{T_{D{\rm{1}}}}s + 1} \right)\left( {{T_{D{\rm{2}}}}s + 1} \right)}} + {k_p}} \right)\theta \left( s \right)} \end{array} $ | (25) |
式中:kp、kI、kD分别为控制器中比例、积分和微分环节的调节系数。为解决积分漂移,积分环节用惯性环节近似,TI为时间常数;为避免高频扰动,微分用间接微分环节代替,TD1、TD2对应的时间常数。θ为船舶横摇角。
其中,控制器参数为kp=6.90, kI=38.7, kD=2.06, TI=24.607, TD1=0.064, TD2=0.18。
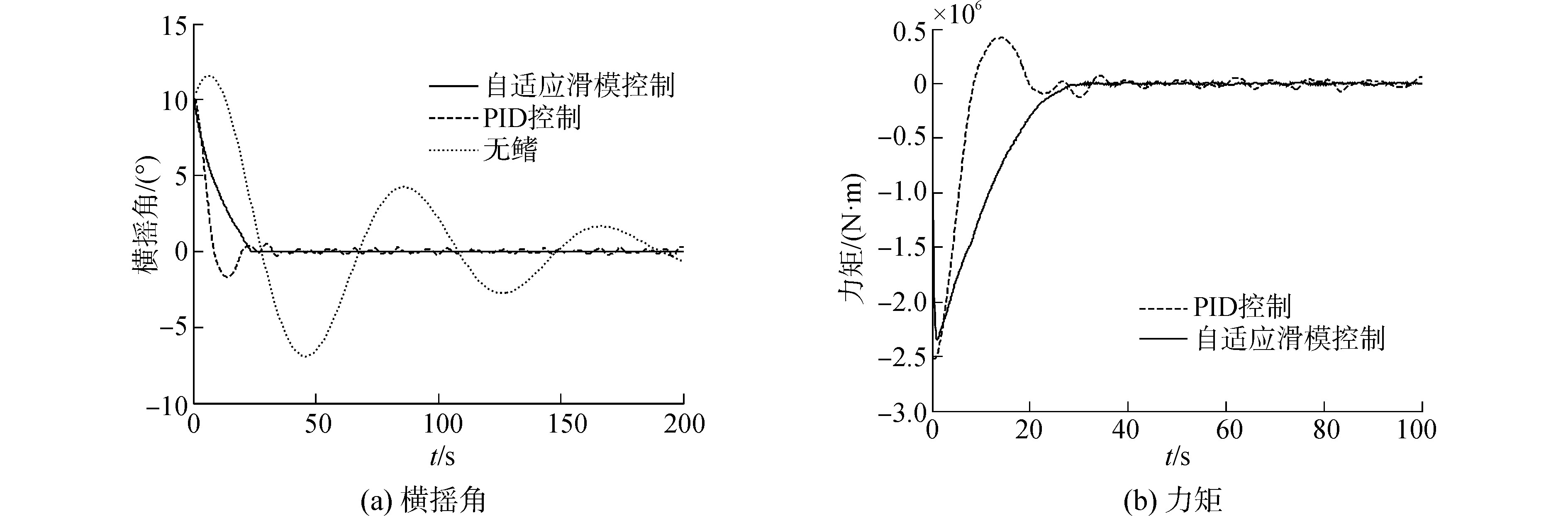
以横摇角10°时为例,在随机干扰作用下,分别运用PID控制和自适应滑模控制对横摇角和控制力矩进行动态仿真,对比结果如图 5所示。
|
图 5 动态响应仿真结果 Fig.5 Simulation results of dynamic response |
图 5选取100 s的横摇角和控制力矩的仿真结果,其中PID控制器在大约38 s时得到较为稳定的减摇效果,而设计的自适应滑模控制器在22 s左右时得到稳定状态,动态响应较快,且超调量整体较小,后者效果优于前者。PID控制器的控制力矩动态响应逊于自适应滑模控制器,且在一定范围内不断调整。
分别模拟船舶以10、20和30 kn速度航行,遭遇角分别为45°、90°和135°,在系统开环、常规PID控制系统和设计的自适应控制系统下的减摇性能。统计各种状态时的横摇角均值、方差和减摇效果百分比,如表 1所示。
| 表 1 减横摇统计表 Tab.1 Anti-rolling effect statistics |
综上可得,对于减摇效果,自适应控制为83.51%~96.03%,常规PID控制为80.51%~94.12%,前者优于后者。高航速时的要优于低航速时;斜浪状态差于正横浪状态。由于模型的摄动,PID控制的效果会受到影响。在低航速和斜浪时,系统非线性和不确定性较强,PID控制器的效果变差。本文设计的模糊化自适应滑模控制较常规PID控制具有更强的鲁棒性,能够较好地解决非线性和不确定性对系统的影响,提高减摇效果。
5 结论1) 改进鳍轴机构和传感器安装方式,直接从水动力中分解出升力并实现实时测量。
2) 设计切换模糊化的自适应滑模控制器,以提高不同海况下的减摇效果。
给出的升力检测方法需要机械改进,下一步研究配合电液伺服系统寻求更简单有效的方法以适用于旧型改造。
进一步研究在实际应用PID控制中加入自适应切换控制,扩大常规减摇鳍适用海况范围。
| [1] |
LIANG Lihua, SUN Mingxiao, ZhANG Songtao. Control system design of anti-rolling tank swing bench using BP neural network PID based on LabVIEW[J]. International journal of smart home, 2015, 69(6): 61-70. (  0) 0)
|
| [2] |
LIANG Lihua, SUN Mingxiao, ZHANG Songtao. A integrate control system design of WPC with active T-foil and transom stern flap for vertical motion improvement[J]. Journal of computational information systems, 2015, 11(9): 3217-3227. (  0) 0)
|
| [3] |
金鸿章, 王帆, 马玲. 零航速减摇鳍两步主从控制律设计[J]. 自动化学报, 2012(6): 1059-1064. JIN Hongzhang, WAN Fan, MA Ling. Design a two-step master-slave control law for zero-speed fin stabilizers[J]. Acta automatica sinica, 2012(6): 1059-1064. (  0) 0)
|
| [4] |
LIANG Lihua, SUN Mingxiao, LUAN Tiantian. Fuzzy input-based adaptive sliding mode control for vessel lift-feedback fin stabilizers with strong nonlinearity and uncertainty[J]. Shock and vibration, 2017(3): 1-13. (  0) 0)
|
| [5] |
LIANG Lihua, SUN Mingxiao, LUAN Tiantian. Design sliding mode control of fuzzy switching gain for lift-feedback fin stabilizers[C]//2016 IEEE International Conference on Mechatronics and Automation, 2016:1412-1417. http://ieeexplore.ieee.org/document/7558770/
(  0) 0)
|
| [6] |
梁利华, 孙明晓. 一种基于激光测距实时检测动态升力的鳍轴装置及方法[P]. 201710335524. X.
(  0) 0)
|
| [7] |
CHADWICK J, ETAL J. Roll stabilization system marine vessels[P]. US:2960959, 1960.
(  0) 0)
|
| [8] |
IVANF C, DEREK G, ROBEERT G. Lift measurement[P]. US:0196508, 2008.
(  0) 0)
|
| [9] |
SHUJI D, KASUHIDE M, TATSUNORI O. Fin stabilizer for vessel and control method and control program therefor[P]. US:263942, 2007.
(  0) 0)
|
| [10] |
梁利华, 孙明晓. 基于铁摩辛柯梁的减摇鳍空心轴机构设计与验证[C]//第35届中国控制会议论文集, 2016: 1-10. LIANG Lihua, SUN Mingxiao. Design and analysis of hollow fin-axis mechanism for fin stabilizers based on Timoshenko beam[C]//35th Chinese Control Conference. 2016:1-10 (  0) 0)
|
| [11] |
LIANG Lihua, SUN Mingxiao, SHI Hongyu, et al. Design and analyze a new measuring lift device for fin stabilizers using stiffness matrix of Euler-Bernoulli beam[J]. Plos one, 2017, 12(1): 1-13. (  0) 0)
|
| [12] |
LIU Jinkun. Sliding mode control design and Matlab simulation:the basic theory and design method[M]. Beijing: Publishing House of Tsinghua University, 2015: 313-322.
(  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


