无线异构网络在宏基站覆盖薄弱区域或热点地区部署例如中继、微微蜂窝站点、家庭基站等小型基站,通过缩短用户与基站间的距离使用户收到高质量信号,提高系统吞吐速率,近年来受到广泛的关注1。然而,蜂窝网络中部署小型基站不仅使网络拓扑结构变的非常复杂,同时频谱资源稀缺异构网络采用同频组网方式,小型基站的发射功率与宏基站发射功率相差甚远,使得微小区用户容易受到严重的跨层干扰,严重阻碍异构网络性能的提升,影响用户体验。
文献2针对中继站对相邻小区边缘用户产生的同频干扰,采用了一种基于随机化竞争(random competition,RC)的协作调度策略,通过在相邻小区边缘形成的中继协作区域内应用RC调度算法,减少同频干扰,提高小区边缘吞吐量。文献3提出了一种分层协作框架来实现资源块(resource block,RB)级别的协作传输来减少Macro和Pico基站间严重的跨层干扰。文献4介绍了一种增强小区间干扰协调(enhanced intercell interference coordination,eICIC,)技术消除跨层干扰,但此方法并不能彻底消除数据传输阶段的干扰。
此外,无线多输入多输出(multi-input multi-output,MIMO)传输系统采用空时处理技术进行信号处理,在多径环境下能极大提高频谱利用率,增加系统的数据传输速率5,是移动通信领域研究的主流技术之一。通过用户选择获取分集增益,是提升频谱效率、增强抵抗小区间干扰的能力以及提升用户与基站间的通信效率的又一有效方法6-7。文献8提出一种MIMO系统的用户选择算法。算法将被选用户总吞吐量作为选择标准,先确定信道容量最好的用户为选定用户;之后每选一个用户,都保证与已选定用户组成的用户组信道容量最大,虽使系统容量得到提升,但算法计算复杂度较大。
文献9提出了一种基于协作多点传输协调调度与波束形成(coordinated multiple point transmission coordinated scheduling and beamforming,CoMP-CSB)的用户选择干扰消除算法。此算法突破基站天线数对同时消除干扰用户数的限制,但当用户分布不均匀,基准用户与其他用户的干扰信号方向相差都很远,此时降低跨层干扰效果不佳。
为此,本文提出了一种新型的基于分组的用户选择算法,算法可以使用户任意分布情况下,突破发送天线数对去干扰用户数的限制,同时服务多个用户获取分集增益,有效提高系统性能。
1 无线异构网络系统模型考虑一个宏基站(macro)和微基站(pico)共存的无线异构下行传输系统,如图 1所示。系统由一个宏基站和L个微基站构成,宏基站覆盖的宏小区内有Km个服务用户;微小区内共有K个用户,从中选出Kp个服务用户,宏基站配置Nm根发送天线,微基站配置Np根发送天线,假设用户单天线接收。由于微基站的功率较小,当宏小区的用户远离微基站时,所受干扰较小10,故本文忽略微基站对宏小区用户的干扰。

|
| 图1 异构无线网络模型 Figure 1 Heterogeneous wireless network model |
假设信道衰落为独立块衰落(independent fading from block to block),信道向量全部服从瑞利分布。同时,假设基站能获得理想信道状态信息,用hilM表示宏基站与第l个微小区内用户i之间的信道向量,hjMM表示宏基站与宏小区内第j个用户之间的信道向量,hilP表示第l微小区内微基站与本小区内用户i之间的信道向量。微小区l内第i个用户的接收信号为
| ${\mathit{\boldsymbol{y}}_{il}} = \underbrace {{\mathit{\boldsymbol{h}}^P}_{il}{\mathit{\boldsymbol{v}}_{il}}{\mathit{\boldsymbol{x}}_{il}}}_{有用信号} + \underbrace {\sum\limits_{{K_p}} {{\mathit{\boldsymbol{h}}^P}_{il}{\mathit{\boldsymbol{v}}_{kl}}{\mathit{\boldsymbol{x}}_{kl}}} }_{微小区内多用户干扰} + {\rm{ }}\underbrace {\sum\limits_{k = 1}^{{K_m}} {{\mathit{\boldsymbol{h}}^\mathit{\boldsymbol{M}}}_{il}{\mathit{\boldsymbol{v}}_{kM}}{\mathit{\boldsymbol{x}}_{kM}}} }_{跨阶层小区间干扰} + \underbrace {{\mathit{\boldsymbol{z}}_{il}}}_{加性噪声}$ | (1) |
式中:xiM表示对用户uiM的U×1维的发送信号,
| $\begin{array}{l} {R_l} = {K_P} \times {\rm{E}}\{ {\rm{lb}}|{\mathit{\boldsymbol{I}}_U} + \mathit{\boldsymbol{v}}_{il}^{\rm{H}}{(\mathit{\boldsymbol{h}}_{il}^P)^H}\mathit{\boldsymbol{h}}_{il}^P{\mathit{\boldsymbol{v}}_{il}} \times \\ {${\mathit{\boldsymbol{I}}_U} + \sum\limits_{{K_p}} {\mathit{\boldsymbol{v}}_{kl}^H} {(\mathit{\boldsymbol{h}}_{il}^P)^H}\mathit{\boldsymbol{h}}_{il}^P{\mathit{\boldsymbol{v}}_{kl}} + \sum\limits_{k = 1}^{{K_m}} {\mathit{\boldsymbol{v}}_{kM}^H} {\rm{ }}{(\mathit{\boldsymbol{h}}_{il}^M)^H}\mathit{\boldsymbol{h}}_{il}^M{\mathit{\boldsymbol{v}}_{kM}}$^{ - 1}}|\} \end{array}$ | (2) |
由式(2) 可见,提高用户的信干噪比可以增强系统性能。因此,本文提出一种基于分组的用户选择算法,可在用户任意分布的情况下选出受到的跨层干扰影响最小、使系统容量最大的一组用户,提高系统性能。
2 用户选择算法为了减少用户接收到的干扰信号,本文采用迫零(zero forcing,ZF)线性预编码方案。基站运用ZF预编码消除干扰时能同时服务的最大用户数不大于基站发射天线数,当基站发射天线总数为N时,若基站为本小区(N-ξ)个用户提供服务,则该基站最多能消除邻小区内ξ个用户的跨层干扰,即基站自由度(degree of freedom,DOF)为ξ。若基站的服务用户数远远大于发射天线数,基站自由度ξ较小时,能被同时消除干扰的用户太少,系统性能提高不明显。而文献9提出一种基于CoMP-CSB的用户选择算法,本文称作已有算法(下同),巧妙地跨越了这一限制:当基站发射天线数为N时,若基站自由度ξ=1,则在邻小区中选信道状态最好的一个用户作为基准用户,本小区基站可以通过预编码消除对基准用户的跨层干扰。并且,此预编码矩阵可以降低邻小区内干扰信道与基准用户干扰信道方向相近的用户受到的跨层干扰,干扰信号方向越近,降低干扰效果越好。系统中被同时降低跨层干扰的用户数增加,系统性能显著提升。
然而,已有算法存在以下不足:异构网络中宏基站选定微小区内有用信号信道状态最好的用户作为基准用户,并消除其受到的跨层干扰;当微小区内用户分布不均匀时,基准用户的干扰信号很有可能与其他所有用户的干扰信号方向偏差都较大,那么即便采用文献9所提算法选出干扰方向最近的用户,它们的实际干扰方向仍存在较大差异,此时基准用户的预编码矩阵对最终服务用户干扰降低的效果不佳。针对已有算法的局限性,本文提出了异构网络中基于分组的用户选择算法。算法在宏基站选定基准用户之前,先通过一组分组向量,将受到来自宏基站干扰信道方向相近的用户分成一组,完成用户分组。再分别在每组中选出该组基准用户和与基准用户干扰信号方向最近的若干用户,最终选出使系统容量最大的一组用户作为最后服务用户。相比已有算法,本文算法先分组,再在各组中分别进行用户选择确定最终服务用户,即便用户分布不均匀也可以保证最终被选用户是使系统容量最大的一组用户,突破已有算法的局限性,提高系统性能。微小区内仍采用ZF预编码消除用户间干扰。
引入一个分组向量组C={w1,w2,…,wq},wf(f=1,2,…,q)是Nm×1维的向量,‖wf‖=1。本文研究的重点不是分组向量的选择对系统性能的影响,因此为了方便,本文采用随机向量。假设基站已知理想信道状态信息,令hilM(i=1,2, …,K)表示宏基站到微小区l内第i个用户的干扰信道向量。基站进行用户分组时,通过用户收到的干扰信号向量与分组向量间的内积或夹角来选择与其方向最接近的分组向量并得出相应分组向量的索引号f,将对应索引号相同的用户分成一组,得到分组Wf,(f=1,2,…,q)。分组完成后,分别在每个分组中选出该组的基准用户uWf1以及与其干扰信号方向最近的(KP-1) 个用户组成分组Vf,(f=1,2,…,q),用ZF预编码消除用户间干扰。比较各组选出用户的信道容量,将信道容量最大的用户作为最终被选用户。
综上所述,异构网络中基于分组的用户选择算法的具体步骤如下:
1) 初始化:微小区l内待选用户集:Ul={ul1,ul2, …,ulK},C={w1,w2, …,wq},Wf=φ,Vf=φ。
2) 用户分组:分别计算宏基站对微小区l内第i个用户uli的干扰信道向量
| $\begin{array}{l} {\mathit{\boldsymbol{f}}_{{u_{li}}}} = {\rm{arg}}\quad \mathop {{\rm{max}}}\limits_{\mathit{f} = 1,2,{\rm{ }} \ldots ,q} \left| {\mathit{\boldsymbol{\tilde h}}_{{\mathit{u}_{\mathit{li}}}\mathit{l}}^\mathit{M}\prime {\mathit{\boldsymbol{w}}_\mathit{f}}} \right| = \\ {\rm{arg}}\quad \mathop {{\rm{max}}}\limits_{\mathit{f} = 1,2,{\rm{ }} \ldots ,q} {\rm{sin}}(\angle (\mathit{\boldsymbol{\tilde h}}_{{\mathit{u}_{\mathit{li}}}\mathit{l}}^\mathit{M}\prime {\mathit{\boldsymbol{w}}_\mathit{f}})) \end{array}$ | (3) |
并将索引号相同的用户分为一组,此时
| $\left\{ \begin{array}{l} f = {f_{{u_{li}}}}\\ {W_f} = {W_f} + \{ {u_{li}}\} \end{array} \right.$ | (4) |
式中:
3) 用户选择:
① 各组中选出该组基准用户πf(Wf,1):
| ${{\pi }_{f}}({{W}_{f}},1)=\rm{arg}\,\rm{ma}{{\rm{x}}_{{{\mathit{u}}_{\mathit{li}}}}}{{_{\in }}_{{{\mathit{W}}_{\mathit{f}}}}}\|\mathit{\boldsymbol{h}}_{{{\mathit{u}}_{\mathit{li}}}\mathit{l}}^{\mathit{P}}\|_{\mathit{F}}^{2}$ | (5) |
② 分别计算宏基站对该组其他用户干扰信道
| $\mathit{\boldsymbol{\delta }}_{{\mathit{u}_{\mathit{li}}}}^\mathit{f} = \frac{{\left| {{{\mathit{\boldsymbol{\tilde h}}}^\mathit{M}}_{{\mathit{u}_{\mathit{li}}}\mathit{l}}\left( {{{\mathit{\boldsymbol{\tilde h}}}^\mathit{M}}_{{\mathit{\pi }_\mathit{f}}\mathit{l}}} \right)\prime } \right|}}{{\left\| {{{\mathit{\boldsymbol{\tilde h}}}^\mathit{M}}_{{\mathit{u}_{\mathit{li}}}\mathit{l}}} \right\|\left\| {{{\mathit{\boldsymbol{\tilde h}}}^\mathit{M}}_{{\mathit{\pi }_\mathit{f}}\mathit{l}}} \right\|}}$ | (6) |
式中:
③ 分别从如下子集中选出各组的第j个用户2≤j≤(KP-1):
| ${\mathit{\Psi }_\mathit{f}} = \{ {\mathit{j}_\mathit{f}} \in {\mathit{W}_\mathit{f}} - \{ {\mathit{\pi }_{\rm{f}}}({\mathit{W}_{\rm{f}}},1)\} \} $ | (7) |
用户j选择结果为
| $u_{lj}^{f}=\rm{arg}\ \rm{ma}{{\rm{x}}_{{{\mathit{u}}_{\mathit{lj}}}\in }}_{{{\Psi }_{\mathit{f}}}}{{\mathit{\delta }}^{\mathit{f}}}_{{{\mathit{u}}_{\mathit{lj}}}}$ | (8) |
| ${{\mathit{\Psi }}_{\mathit{f}}}={{\mathit{\Psi }}_{\mathit{f}}}-\{\mathit{u}_{\mathit{lj}}^{\mathit{f}}\}$ | (9) |
若Wf(f=1,2,…,q)中用户数小于Kp,则从其他分组中选择与该组πf(Wf,1) 干扰信道方向最近的用户组成Kp个用户。
④ 各组选出基准用户以及与其干扰信号方向接近的用户组成Vf(f=1,2, …,q):
| ${V_f} = {V_f} + \{ \mathit{u}_{\mathit{lj}}^\mathit{f}\} $ | (10) |
再从中选出最终服务用户组VF:
| $\begin{array}{l} {\mathit{\boldsymbol{R}}_{{\mathit{V}_\mathit{f}}}} = \sum\limits_{{u^f} = 1, \cdots ,{K_P}} {\mathit{\boldsymbol{E}}\{ {\rm{lb}}|{I_U} + \mathit{\boldsymbol{v}}_{ufl}^H{{(\mathit{\boldsymbol{h}}_{ufl}^P)}^H}\mathit{\boldsymbol{h}}_{ufl}^P{\mathit{\boldsymbol{v}}_{ufl}} \times } \\ [{\mathit{\boldsymbol{I}}_U} + \sum\limits_{{K_p}} {\mathit{\boldsymbol{v}}_{kl}^H} {(\mathit{\boldsymbol{h}}_{ufl}^P)^H}\mathit{\boldsymbol{h}}_{ufl}^P{\mathit{\boldsymbol{v}}_{kl}} + {\rm{ }}\sum\limits_{k = 1}^{{K_m}} {\mathit{v}_{kM}^H{{(\mathit{\boldsymbol{h}}_{ufl}^M)}^H}\mathit{\boldsymbol{h}}_{ufl}^M{\mathit{\boldsymbol{v}}_{kM}}{]^{ - 1}}|\} } \end{array}$ | (11) |
| ${V_F} = {\rm{arg}}\;\mathop {{\rm{max}}}\limits_{f = 1,2,{\rm{ }} \cdots ,q} {\mathit{\boldsymbol{R}}_{{V_f}}}$ | (12) |
本文算法利用用户受到干扰信号的方向信息,先将用户分组再进行用户选择,避免用户分布情况的不同对系统容量的影响。使用户在任意分布场景下,选出信道状态最好、使系统容量最大的一组用户作为服务用户,有效提升系统性能。
3 分组方案复杂度分析本节对文中所提用户选择算法进行了复杂度分析。为了方便计算,本文用flop来计量复杂度:1个flop定义一个实浮点数操作。由于信道矩阵为复数模型,对其乘法、除法运算均以复数考虑,每次复数加和乘分别为2个flop和6个flop11。对于维度为n的两个向量内积计算复杂度为6n flop,对于m×n的复值矩阵H,其Frobenius范数‖H‖F2运行2mn次实数加和2mn的实数乘,共4mn个flop。分组向量wq是Nm维向量,则计算一个分组向量需要的flop数为6Nm,若分组向量有q个,则总的flop数为(6Nm×q); 计算一个激活用户来自宏基站的干扰信道向量与分组向量的方向偏差需要的flop数为6Nm,分组向量的个数为q,则总的flop数为(6Nm×q×Kp),故完成用户分组需要的复杂度为
| ${C_g} = 6{N_m} \times q \times ({K_p} + 1)$ | (13) |
分组完成后计算用户到微基站信道范数需要的flop数为(4Np×Kp);每组中确定信道范数最大的用户作为第一被选用户uA,计算宏基站到各组任一激活用户的信道向量与到该组uA的信道向量的方向偏差需要的flop数为6Nm,共(Kp-q)次,需要的flop数为6Nm×(Kp-q),故完成用户选择需要的复杂度为
| ${C_c} = 4{N_p} \times {K_p} + 6{N_m} \times \left( {{K_p} - q} \right)$ | (14) |
本文采用ZF线性预编码方案消除干扰。ZF算法只涉及伪逆计算,对于m×n维复矩阵A,其伪逆运算需要的flop数为12mn2-5mn-n2。故用ZF算法消除各组用户间干扰需要的flop数为(12K×N2-5×K×Np-Np2),消除跨阶层干扰需要的flop数为(12×(Km+ξ)×Nm2-5×(Km+ξ)×Nm-Nm2),故ZF预编码共需要的flop数为
| $\begin{array}{l} {C_{ZF}} = q \times (12K \times {N^2}_p - 5 \times K \times {N_p} - \\ \quad \quad {N^2}_p + 12 \times ({K_m} + \xi ) \times {N^2}_m - \\ \quad \quad 5 \times ({K_m} + \xi ) \times {N_m} - {N^2}_m) \end{array}$ | (15) |
综上可知,本文用户选择算法复杂度为
| $C = {C_g} + {C_c} + {C_{ZF}}$ | (16) |
已有算法复杂度为
| $\begin{array}{l} C = {K_p} \times \left( {6{N_m} + 4{N_p}} \right) + \\ \quad \quad 12({K_m} + \xi ) \times {N^2}_m - 5({K_m} + \xi ) \times {N_m} - \\ \quad \quad {N^2}_m + 12K \times {N^2}_p - 5K \times {N_p} - {N^2}_m \end{array}$ | (17) |
本文算法较已有算法增加了一步用户分组,故复杂度有所提高。分组数q=1表示没有进行用户分组,即为已有算法。故本文算法与已有算法复杂度对比如表 1所示。
| q | K=2 | K=4 | K=6 |
| 1 | 64 Kp+992+728 Km | 64 Kp+1 336+728 Km | 64 Kp+1 680+728 Km |
| 3 | 208 Kp+2 976+2 184 Km | 208 Kp+4 008+2 184 Km | 208 Kp+5 040+2 184 Km |
| 4 | 256 Kp+3 968+2 912 Km | 256 Kp+5 344+2 912 Km | 256 Kp+6 720+2 912 Km |
| 5 | 304 Kp+4 960+3 640 Km | 304 Kp+6 680+3 640 Km | 304 Kp+8 400+3 640 Km |
表 1比较了在分组数不同、被选用户数不同情况下的算法复杂度。其中,假设宏基站的发射天线数Nm=8,微基站发射天线Np=4,并且假设宏基站天线自由度ξ=1。由表 1可知,分组数确定时,被选用户数越大,算法所需flop数越大,并且增量与基站覆盖范围内的总用户数无关。当被选用户数确定时,算法所需flop数随分组数的增大而增大,且增量和宏小区与微小区服务用户数有关。本文算法较对比算法增加了一步用户分组,故复杂度略高。
4 仿真结果与分析网络拓扑结构由一个宏基站,两个微基站组成。宏基站发射功率46 dB·m,覆盖范围半径250 m,家庭基站位置固定(在宏基站覆盖范围),发射功率30 dB·m,覆盖范围50 m,4个用户随机分布在家庭基站覆盖范围内,微基站随机分布在距宏基站DBS的圆周上,但微基站间彼此隔离。具体仿真参数如表 2所示。
| 参数名称 | 参数值 |
| 宏基站发射功率 | 46 dB·m |
| 微基站发射功率 | 30 dB·m |
| 宏基站覆盖半径 | 250 m |
| 微基站覆盖半径 | 50 m |
| 宏基站天线数 | 8 |
| 微基站天线数 | 4 |
| 每个用户配置天线数 | 1 |
| 宏基站到用户的路径 损耗GM,N | 128.1+37.6lgdM(dB12 |
| 微基站到用户的路径 损耗GF,N | 140.7+36.7lgdP(dB)12 |
| 微基站与距宏基站距离DBS | 100 m |
图 2与图 3分别给出了在用户分布不同的情况下本文算法与对比算法比较结果。系统假设宏基站空间自由度为1,用户分组数为4,系统选择的最终服务用户数也为4。两图都给出了不同天线配置下两种算法的对比。当宏基站发射天线数固定时,微基站发射天线越多,系统容量越大;当微基站发射天线数固定时,宏基站发射天线数越少,系统容量越大。如图 3所示,信噪比为20 dB,配置为Nm=16,Np=8时的系统容量比Nm=8,Np=4的系统容量大0.89 bit/s/Hz,比Nm=16,Np=4的系统容量大1.608 bit/s/Hz。发射天线数越多,则相应的发射总功率越大,因而用户受到的跨层干扰与宏基站的发射天线数成正比,系统容量和宏基站与微基站天线数的差值有关。

|
| 图2 用户均匀分布时本文算法与对比算法 Figure 2 Comparison between this algorithm and the comparing algorithm with user uniform distribution |

|
| 图3 用户不均匀分布时本文算法与对比算法 Figure 3 Comparison between this algorithm and the comparing algorithm with user non uniform distribution |
如图 2所示,用户均匀分布时相同天线配置下的两种算法微小区系统平均容量几乎一致。用户均匀分布时几乎很少出现服务用户与基准用户干扰信号方向相差很远的情况,故两种用户选择算法的差距不大。相应地,如图 3所示:随着信噪比的增加,本文算法较对比算法系统容量提升明显,性能更加优越。如当信噪比为20 dB,Nm=8,Np=4时,系统容量有近1.061 bit/s/Hz的增益。综上所述,本文算法较对比算法性能提升明显,在继承对比算法优势的基础上,完善算法应用场景,使得无论用户呈何种分布都可以通过用户选择提高系统性能。
图 4是不同的被选用户数对系统容量影响的对比图。图 4表明选择服务的用户数越小,系统的平均容量越大;而服务的用户越多,系统平均容量越小。这是因为仿真假设宏基站的自由度为1,宏基站只能消除1个选定用户的跨层干扰,其他用户根据与选定用户的方向偏差选择,最后选出的用户越多则与选定用户的方向偏差就越大,所以系统平均容量会随之减小;选择的用户数愈多,系统的总容量也越大,如图 5所示。

|
| 图4 被选用户数对系统平均容量的影响 Figure 4 Influence of the number of selected on the average capacity of the system |
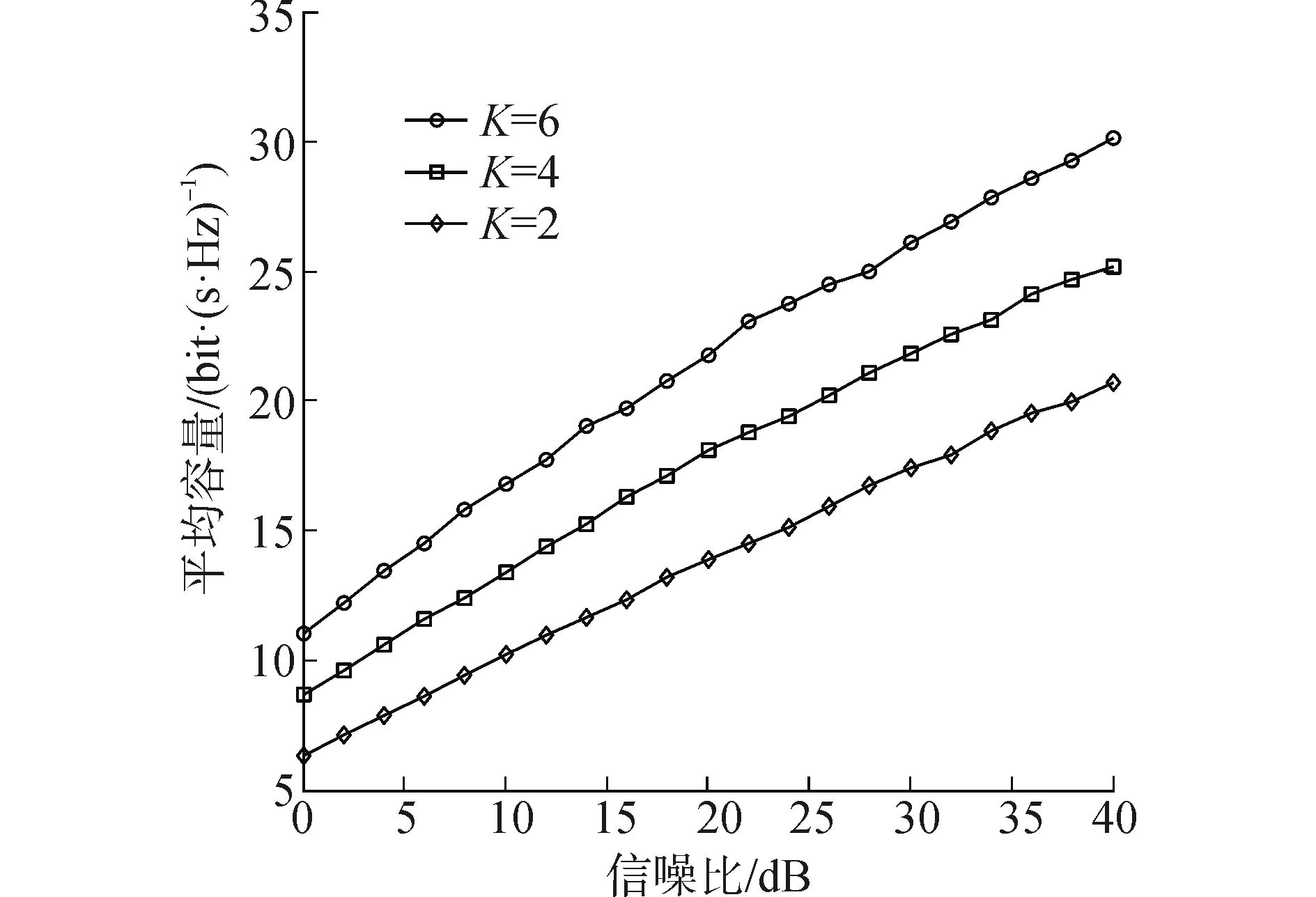
|
| 图5 被选用户数对系统总容量的影响 Figure 5 Influence of the number of selected on the total capacity of the system |
图 6给出了宏基站自由度不同对系统容量影响的对比图。仿真结果显示,当宏基站微基站天线配置确定时,自由度为2的系统容量较大,当信噪比为20 dB,Nm=8,Np=4时,自由度为2时的系统容量较自由度为1时的大2.633 bit/s/Hz。自由度越大代表宏基站能同时消除跨层干扰的微小区用户数就越大,系统容量相应也越大。

|
| 图6 宏基站自由度对系统容量的影响 Figure 6 Influence of the DOF of macro station on the capacity of the system |
1) 本文利用用户受到干扰信息方向的相近性,将用户分组;再进行用户选择,避免了当微小区内用户分布不均匀时,用户选择消除跨层干扰不理想的情况。
2) 当用户均匀分布时几乎很少出现服务用户与基准用户干扰信号方向相差很远的情况,故本文用户算法与现用户选择算法的性能优势不明显。
3) 在用户分布不均匀情况下,本文算法较对比算法性能提升明显,且随着信噪比的增加,本文算法性能更加优越。
4) 本文算法复杂度较现有算法有所增加,是在复杂度与系统性能间的折中方案。
| [1] |
谢龙. LTE-Advanced异构网络干扰协调技术研究[D]. 北京: 北京邮电大学, 2013.
XIE Long.Research on interference coordination technology of heterogeneous networks in LTE-advanced[D].Beijing: Beijing University of Posts and Telecommunications, 2013. |
| [2] |
曲桦, 徐西光, 赵季红, 等. 随机化竞争的LTE-A中继蜂窝小区边缘协作调度策略[J].
北京邮电大学学报, 2014, 03(3): 73–77.
QU Hua, XU Xiguang, ZHAO Jihong, et al. Collaborative scheduling scheme based on random competition for the edge of LTE-A relay-enhanced cell[J]. Journal of Beijing University of Posts and Telecommunications, 2014, 03(3): 73–77. |
| [3] |
张琛, 粟欣, 王文清, 等. 异构网络跨层协作传输技术研究[J].
通信学报, 2014, 35(8): 198–205.
ZHANG Chen, SU Xin, WANG Wenqing, et al. Research of cross-tier cooperative transmission technology in heterogeneous network[J]. Journal on communications, 2014, 35(8): 198–205. |
| [4] | BEATRIZ S, HUA W, KLAUS I P, et al. Multicell cooperative for LTE-advanced heterogeneous network scenarios[J]. IEEE wireless communications, 2013, 20(1): 27–34. DOI:10.1109/MWC.2013.6472196 |
| [5] | ERIK G. L, OVE E, FREDRIK T, et al. Massive MIMO for next generation wireless systems[J]. IEEE communications magazine, 2014, 52(2): 186–195. DOI:10.1109/MCOM.2014.6736761 |
| [6] |
韩东升, 杨维. 多基站协作系统中有限反馈性能分析[J].
北京邮电大学学报, 2013, 36(2): 79–83.
HAN Dongsheng, YANG Wei. Performance analysis of limited feedback in wulti-base-station coordination systems[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(2): 79–83. |
| [7] |
尤力, 高西奇. 大规模MIMO无线通信关键技术[J].
中兴通讯技术, 2014, 20(2): 26–28.
YOU Li, GAO Xiqi. Key technologies in massive MIMO wireless communication[J]. ZTE technology journal, 2014, 20(2): 26–28. |
| [8] | ZUKANG Shen, RUNHUA Chen, JEFFREY G A, et al. Low complexity user selection algorithms for multiuser MIMO systems with block diagonalization[C]//Conference Record of the Thirty-Ninth Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA: IEEE, 2005: 628-632. |
| [9] | UK J, HYUKMIN S, JONGROK P, et al. CoMP-CSB for ICI nulling with user selection[J]. IEEE transactions on wireless communications, 2011, 10(9): 2982–2993. DOI:10.1109/TWC.2011.072511.101661 |
| [10] | ZHIKUN Xu, CHEN Yangyang, GEOFFREY Y L, et al. Energy-efficient CoMP precoding in heterogeneous networks[J]. IEEE transactions on signal processing, 2014, 62(4): 1005–1017. DOI:10.1109/TSP.2013.2296279 |
| [11] | GOLUB G H, VAN L C F. Matrix computations[M]. Batlimore, Maryland, USA: The John Hopkisns University Press, 1996: 48-87. |
| [12] | 3GPP, CoordinatedMulti-Point Operation for LTE Physical Layer Aspects (Release 11), Feb. 2011[Online]. Available: ftp.3gpp.org, TR36.819 v0.0.1. |



