2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China;
3. Science and Technology on Underwater Acoustic Antagonizing Laboratory, Beijing 100036, China
水声信道的时变与频率选择性阻碍了大多数智能与高比特速率通信系统的实现,水声信道具有较长的时延扩展和显著的多普勒效应,对有效通信造成巨大挑战[1]。认知无线电[2-3](cognitive radio,CR)可以感知周围环境、提高频谱使用率,变换域通信系统(transform domain communication system,TDCS)以作为CR技术的候选方案[4]。TDCS是一种具有低截获率、抗干扰能力强的可靠性无线通信方式,能够自适应的改变发射信号的频谱,主动规避干扰,TDCS的优良特性为陆地战术无线通信与频谱利用率等问题提供了理论基础。1988年,German提出了该思想[5];1991年,Andren申请了一种低截获率通信系统的专利,但该专利并没有提供理论实现技术[6]。TDCS的概念最早是由美国军方提出并研究的。国内对TDCS的研究相对较晚,现已逐渐成为研究的热点[7-12]。
Donoho等于2004年提出了压缩感知(compressive sensing,CS)理论,打破了奈奎斯特采样定理采样频率限制,信号在变换域是稀疏的,与当前域相比可以用更少的采样点数、高概率精确的还原信号[13-14]。部分典型的水声信道具有明显的稀疏特性,即水声信道的大部分能量都集中在少数的延迟或多普勒值处。传统的最小二乘估计(least squares,LS)算法受高斯白噪声和子载波间干扰(inter carrier interference,ICI)的影响很大,在稀疏信道条件下存在噪声加强问题,因此LS算法不适合于稀疏信道估计[15-16]。由于基于压缩感知技术的稀疏信道估计的优势,因此在水声稀疏信道估计技术领域应用广泛,匹配追踪(matching pursuit,MP)信道估计具有低复杂度、计算效率高,但其估计性能差。正交匹配追踪(orthogonal matching pursuit,OMP)信道估计性能较LS好,但需要求解大量的LS问题,计算复杂度高[17-20]。
本文针对水声信道部分频带存在严重干扰问题,将变换域通信系统应用于水声通信,针对稀疏信道条件下的LS信道估计存在噪声加强问题,提出基于MMP-DCD稀疏水声信道估计算法,充分利用水声信道的稀疏特性。
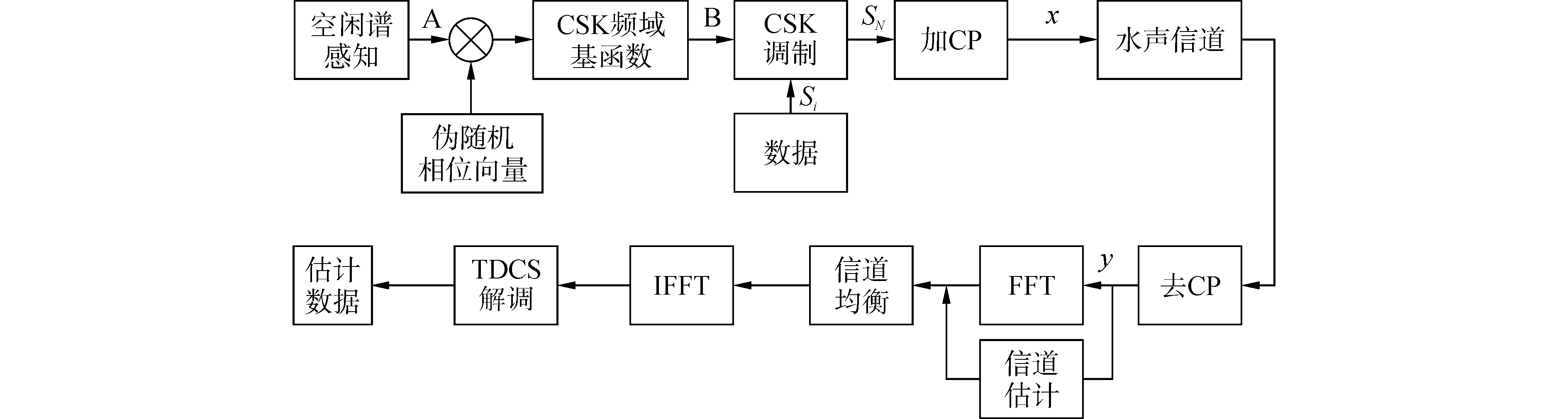
1 TDCS系统模型TDCS系统模型如图 1所示。空闲谱感知向量为 A=[A0 A1 …AN-1], 可用相应的认知无线电中的频谱感知技术用于感知通信频带范围内的未被占用的空闲频段(可对应于频域的子载波), N 表示子载波个数,对应位置被设定为0(表示该载波处的频谱空闲可用)或1(表示该载波处的频点已被占用)。利用 m序列产生伪随机相位向量,移位寄存器的级数为8。伪随机相位向量与A 相乘产生码移键控(code shift keying,CSK)时域基函数,再经过逆快速傅里叶变换(inverse fast fourier transform,IFFT)为频域基函数 B, 将其存储用于对数据进行CSK调制。
|
| 图1 TDCS系统模型 Figure 1 System model of TDCS |
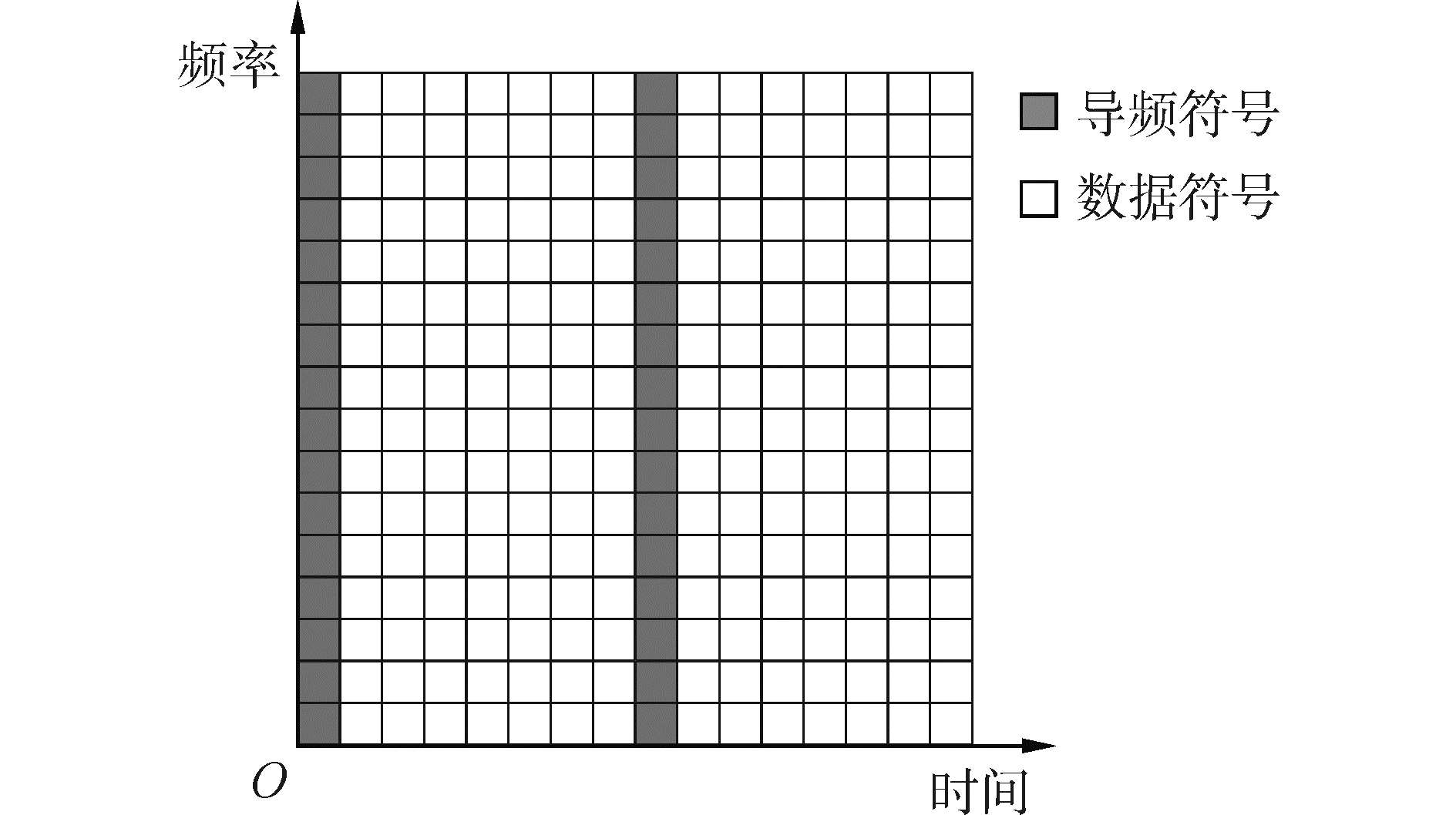
二元CSK属于直接序列(direct sequence,DS)扩频,在发射端产生64位伪随机码序列去调制待发送的数据序列,并在在接收端进行相关解调。为进行信道估计,在特定的子载波上插入导频,本文采用的是块状导频,如图 2所示。
|
| 图2 TDCS导频结构 Figure 2 Pilot structure of TDCS |
将要发射的数据插入导频符号形成新的数据,即数据 Si, 利用TDCS产生的基函数对数据 Si进行调制,SN 添加循环前缀(cyclic prefix,CP)后即为发射信号 xn。xn 通过TDCS信道并去掉循环前缀得到接收信号,即
| $ \mathit{\boldsymbol{y = Hx}} + \mathit{\boldsymbol{n}} $ | (1) |
式中:y=[y0 y1 … yN-1]T为接收到的信号,x=[x0 x1 … xN-1]T为发射信号,n=[n0 n1 … nN-1]T为高斯白噪声,H为信道卷积矩阵[23],表示为
| $ \mathit{\boldsymbol{H = }}\left[ {\begin{array}{*{20}{c}} {{h_0}}&0& \cdots &0&0& \cdots &{{h_2}}&{{h_1}}\\ {{h_{1}}}&{{h_0}}&{}& \vdots &0&{}& \vdots &{{h_2}}\\ \vdots &{{h_1}}&{}&0& \vdots &{}&{{h_{L - 1}}}& \vdots \\ {{h_{L - 1}}}& \vdots &{}&{{h_0}}&0&{}&0&{{h_{L - 1}}}\\ 0&{{h_{L - 1}}}&{}&{{h_1}}&{{h_0}}&{}&0&0\\ 0&0&{}& \vdots &{{h_1}}&{}& \vdots & \vdots \\ \vdots & \vdots &{}&{{h_{L - 1}}}& \vdots &{}&{{h_0}}&0\\ 0&0& \cdots &0&{{h_{L - 1}}}& \cdots &{{h_1}}&{{h_0}} \end{array}} \right] $ |
式中: L表示信道最大多途数,hk表示信道第k 条路径上的增益。
在TDCS的接收端,接收到的信号中导频向量为 yp,利用yp 可以估计信道,导频向量表达式为
| $ {\mathit{\boldsymbol{y}}_p} = \mathit{\boldsymbol{p}} * \mathit{\boldsymbol{h + n}} $ | (2) |
式中: p是导频符号,p=[p0 p1 … pN-1]T;n为噪声向量。 因为发射信号中添加了循环前缀,因此可以通过循环卷积来计算接收到的导频信号[21],即
| $ {\mathit{\boldsymbol{y}}_p} = \mathit{\boldsymbol{p}} \otimes \mathit{\boldsymbol{h + n}} $ | (3) |
式(3) 可以转化为
| $ {\mathit{\boldsymbol{y}}_p} = \mathit{\boldsymbol{Ch + n}} $ | (4) |
其中: C 表示导频矩阵:
| $ \mathit{\boldsymbol{C = }}\left[ {\begin{array}{*{20}{c}} {{p_0}}&{{p_{N - 1}}}& \cdots &{{p_{N - L}}}& \cdots &{{P_2}}&{{P_1}}\\ {{p_1}}&{{p_0}}&{}& \vdots &{}&{{p_3}}&{{p_2}}\\ \vdots &{{p_1}}& \cdots &{{p_{N - 1}}}&{}& \vdots & \vdots \\ {{p_{L - 1}}}& \vdots &{}&{{p_0}}& \cdots &{{p_{L - 1}}}&{{p_L}}\\ \vdots &{{p_{L - 1}}}& \cdots &{{p_1}}&{}& \vdots & \vdots \\ {{p_{N - 2}}}& \vdots &{}& \vdots &{}&{{p_0}}&{{p_{N - 1}}}\\ {{p_{N - 1}}}&{{p_{N - 2}}}& \cdots &{{p_{L - 1}}}& \cdots &{{p_1}}&{{p_0}} \end{array}} \right] $ |
发射信号 x 可以表示为[19]
| $ \mathit{\boldsymbol{x = }}\sum\limits_{i = 1}^N {{\alpha _i}{\mathit{\boldsymbol{\varphi }}_i} = \mathit{\boldsymbol{\psi }}} \mathit{\boldsymbol{\alpha }} $ | (5) |
式中:{φi}i=1N是一组正交基,Ψ=[φ1 φ2 … φN]为N×N维基矩阵,α=[α1 α2 … αN]T为N×1维列向量,且αi=〈X,φi〉=φkTx,如果系数α只有K个是非零的,K
若 x是K稀疏信号,则通过接收向量y的M个值,M
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} x = \boldsymbol{\varPhi} \psi \alpha }} $ | (6) |
式中: Φ为N×M测量矩阵,Φ 必须满足受限等距特性准则(restricted isometry property,RIP)[9]。
1.2 MMP-DCD稀疏信道估计算法Suhyuk Kwon提出了一种被称为多路径匹配追踪的算法(multipath matching pursuit,MMP)[17],在贪婪策略条件下执行树搜索,该算法能够同时搜索多个可能正确的候选支撑集,进而从观测向量中重构出稀疏信号。该算法所依托的两个基础有:1) 将寻找支撑集的过程看作是一个树形搜索的问题;2) 贪婪算法能够很好地解决此类问题。流程如下:输入:观测向量y,测量矩阵Φ,稀疏度K,路径数Qk=0,r0=y,S0={φ}
while k < K do
k=k+1,u=0,Sk=φ
for i=1 to |Sk-1| do
for j=1 to Q do
stemp=sik-1∪{
if stemp∉Sk
u=u+1
suk=stemp
Sk=Sk∪{suk}
用DCD算法求解
end if
end for
end for
end while
u*=argmin‖ruK‖22
s*=su*K
输出:
MMP算法保留若干组候选支撑集,而非像OMP那样只保留唯一的一组。在每次迭代更新支撑集时,对每组支撑集首先用相关的方法搜索出 Q 个与残差向量相关程度最大的原子,再分别对这些原子做检验,如果原子不再原有支撑集中,则将该原子纳入现有支撑集,否则忽略。且如果更新后的支撑集和之前的各个支撑集路径均不同,则更新成功。这样便形成了一个多分枝的树形结构。随着迭代次数的增加,支撑集树中的节点数目随之增加,这样可以同时将多组候选支撑集同时考虑,最终根据残差范数最小的原则在这些候选中选出最优者,作为整个问题的解。
在MMP算法中,需反复求解迭代过程中各个阶段的最小二乘问题,这使得该算法相对于常规的OMP算法来说运算量大为增加。Yuriy V. Zakharov等提出了一种不需要乘法和除法求解LS问题的DCD(dichotomous coordinate descent,DCD)算法,大大降低了求解LS问题的运算量,且该算法特别适合在FPGA等定点硬件平台上运行[11]。为解MMP运算量大的问题,本文提出用DCD算法取代原有的常规最小二乘求解方法,进而有效降低MMP算法运算量,DCD算法流程如下:
输入:测量矩阵 Φ,观测向量y,模值上限H,长度N
c=ΦHy,R=ΦHΦ, x=0,δ=H
for m=1 to Mb do
δ=δ/2,α=[δ,-δ,jδ,-jδ]
*
flag=0
for q=1 to N do
for t=1 to 4 do
if real {αtcp*}>Rp,pδ2/2 do
xp=xp+αt,
c=c-αtR(p), flag=1
end if
end for
end for
if flag=1
go to *
end if
end for
输出: x
2 仿真实验分析为了对本文提出的水声TDCS稀疏信道估计算法的有效性进行仿真,仿真中的声速剖面采用2015年11月的松花湖实测数据绘制,利用Bellhop获取水声信道冲击响应,湖底为细沙(密度为1.268 g/cm3,衰减系数为0.018 75 dB/波长)。仿真条件为:码片率4 k,采样率48 kHz,载频12 kHz,采用2阶CSK调制,Monte Carlo仿真次数10 000次,通信频带为8~16 kHz。编码方式采用码率为1/2的卷积码编码,硬判决Viterbi译码,生成矩阵为 g=[5,7]8, 下标8表示用8进制数表示。
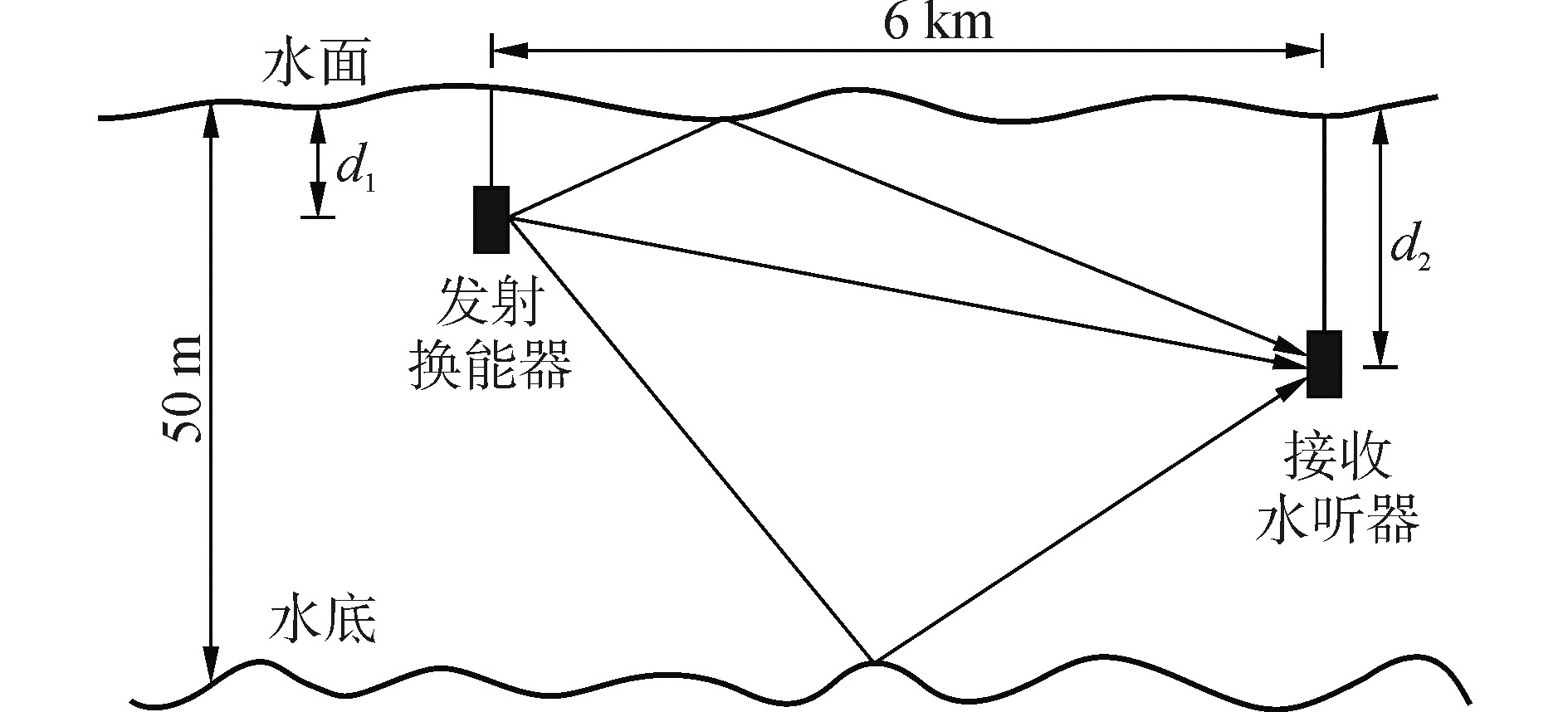
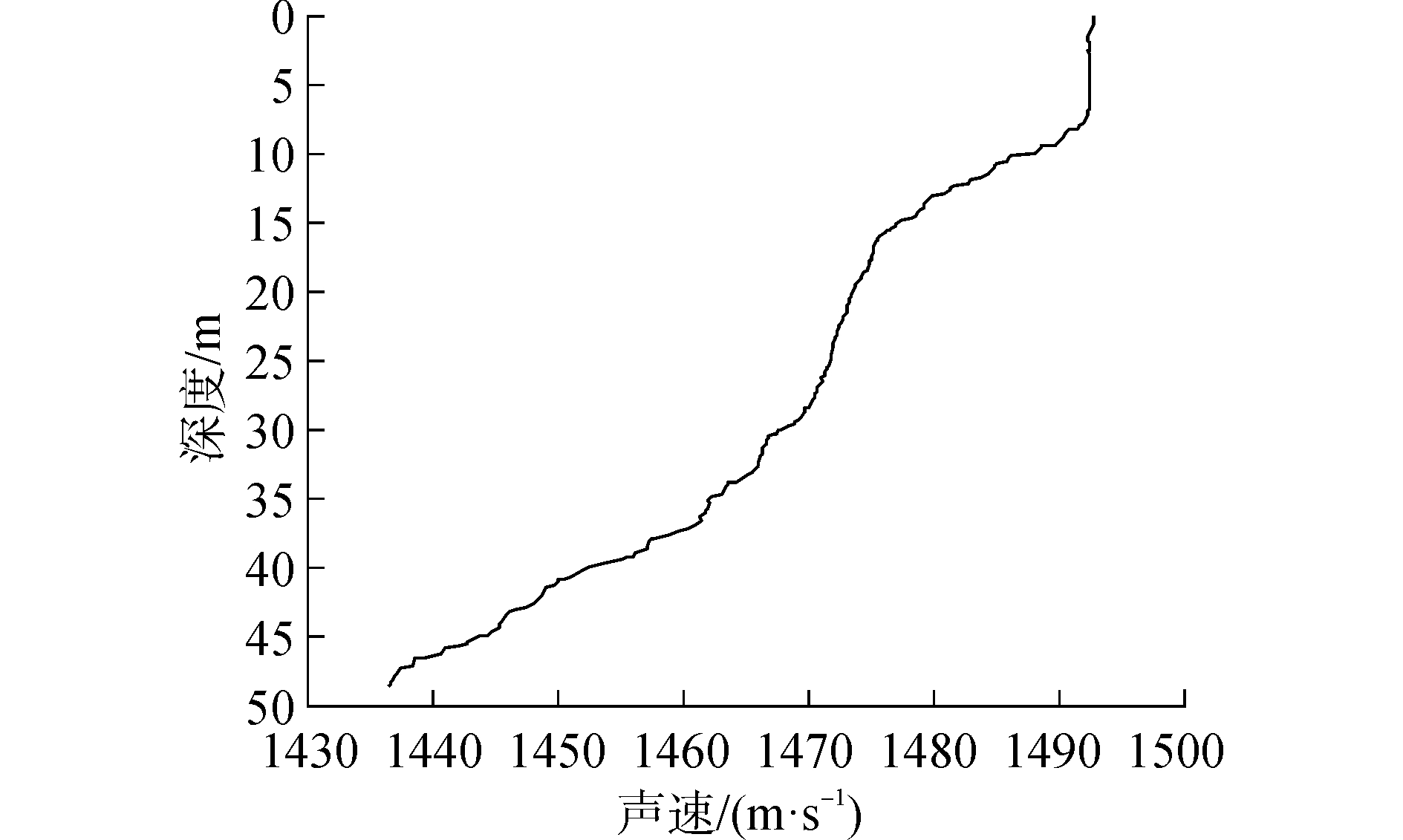
2.1 仿真实验配置图 3所示是仿真实验配置示意图。图中 d1表示发射换能器离水面的深度,d2 表示接收水听器离水面的深度,换能器与水听器之间的水平距离为6 km,换能器开角为30°,仿真中的发射换能器和接收水听器采用以下三种布放方式:1) 配置A:d1=10 m,d2=10 m;2) 配置B:d1=10 m,d2=40 m;3) 配置C:d1=40 m,d2=40 m。图 4是根据松花湖2015年11月湖试测得的声速剖面。
|
| 图3 仿真配置示意图 Figure 3 Diagram of equipment configuration |
|
| 图4 声速剖面 Figure 4 Sound speed profile |
图 5给出了利用Bellhop仿真得到的信道冲激响应,即三种配置下的幅度归一化信道冲击响应。从图 5可以看出,三种配置下水声信道均是稀疏的,即大部分的能量只集中在少数抽头上。三种配置下的信道多途扩展点数分别为152、114、88。
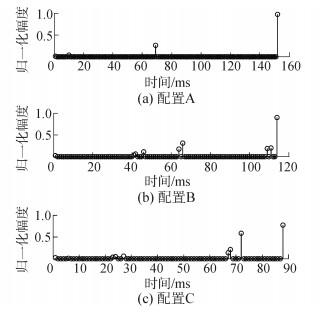
|
| 图5 三种配置信道冲激响应 Figure 5 Channel impulse response of three configurations |
图 6是通信频带为8~16 kHz时仿真信道的幅频特性,分别为三种配置信道幅频特性。图 6(a)中,虽然信道通过信道衰减最大约为4 dB,但是在频段上频率零点较多,在频率零点的位置,信号通过信道后能量损失严重。图 6(b)中频率零点个数较图 6(a)相对较少,在这些频率零点处,虽然信号通过信道衰减相对严重,最大达到5 dB,但在大部分频率点衰减的更平稳、衰减幅度更小。图 6(c)中,信号通过频率零点衰减特别严重,最大达到约35 dB。
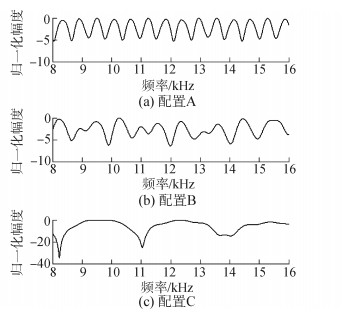
|
| 图6 三种配置信道幅频特性 Figure 6 Channel amplitude-frequency characteristics of three configurations |
图 7是通信频带为8~16 kHz时三种仿真信道的相频特性。图 7(a)~(c)分别为配置A信道相频特性、配置B信道相频特性、配置C信道相频特性。
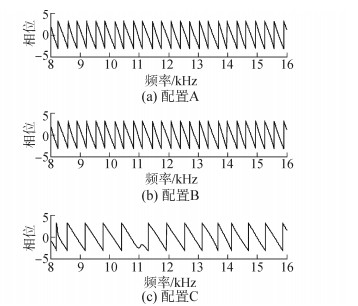
|
| 图7 三种配置信道相频特性 Figure 7 Channel phase-frequency characteristics of thress configurations |
图 8给出了三种配置条件下的基于LS和MMP-DCD算法的水声信道估计的均方误差曲线,其中CCSK基函数的长度为64。三种配置下LS算法估计的信道MSE基本一致,两种算法估计的信道MSE均随信噪比的增大而下降。配置A时,在低信噪比的环境下,本文提出的MMP-DCD算法的信道估计MSE明显优于LS算法,当SNR=-5 dB时,MMP-DCD信道估计MSE较LS算法有28 dB增益。这是因为LS算法没有考虑水声信道的稀疏特性,信道估计噪声加强,信道估计MSE较大。配置B时,MSE基本与配置A一致,当SNR=-5 dB时,MMP-DCD信道估计MSE比LS算法有28.7 dB增益。配置C时,信道估计MSE较配置A、配置B时增益增大。
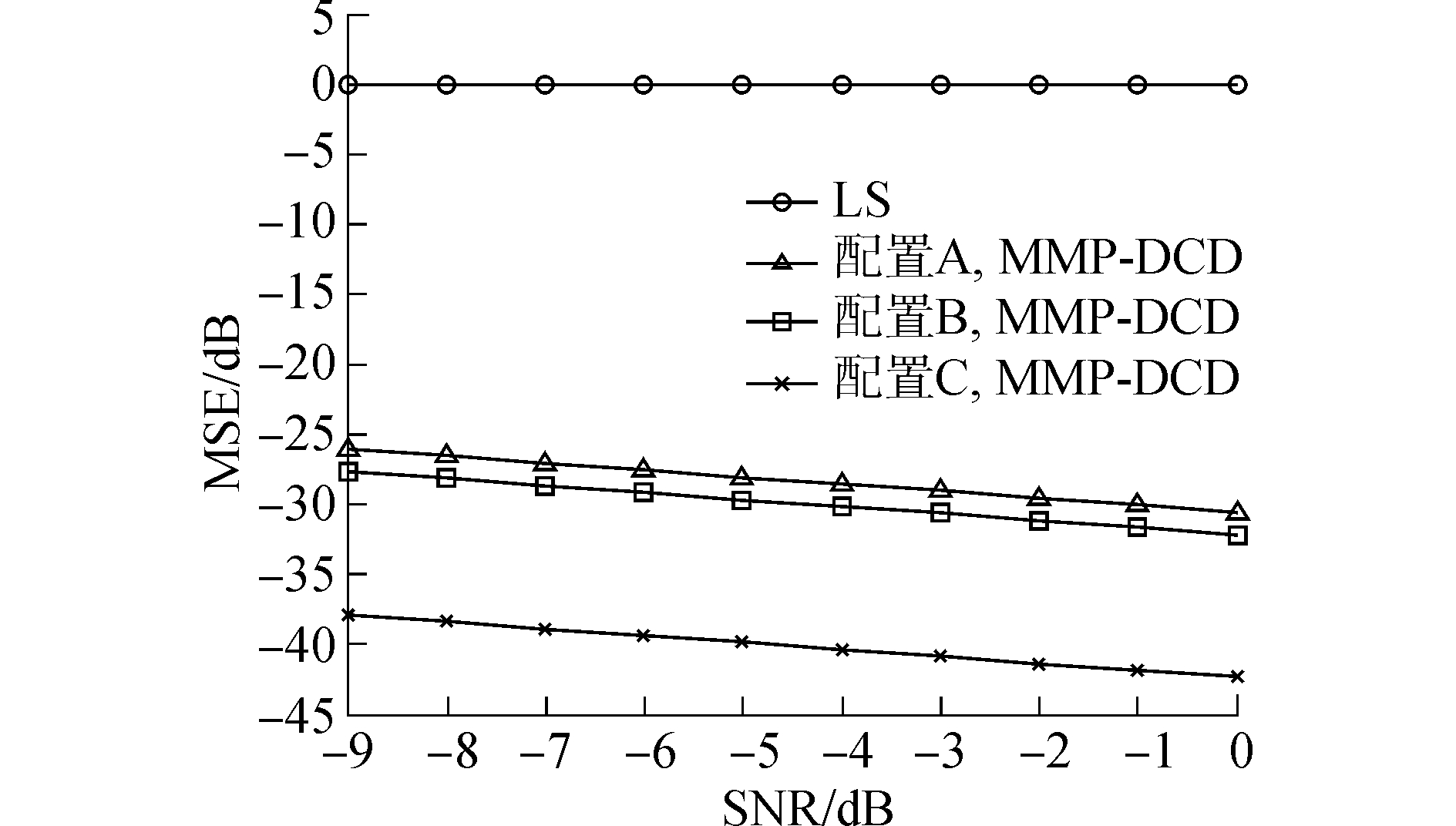
|
| 图8 基于不同信道估计算法的MSE曲线 Figure 8 MSE of different channel estimation algorithms of three configurations |
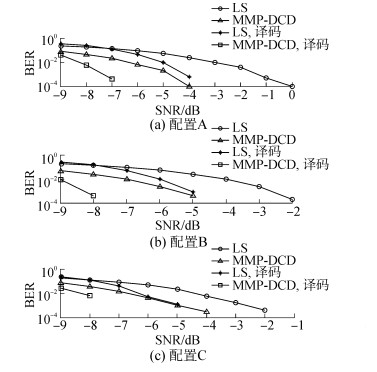
图 9给出了三种配置LS,MMP-DCD算法水声信道估计的误码率性能曲线。
|
| 图9 三种配置基于不同信道估计算法的BER曲线 Figure 9 BER of different channel estimation algorithms of three configuration |
图 9(a)为配置A信道估计BER随信噪比的变化曲线,由图可知LS、MMP-DCD、经过Viterbi译码的MMP-DCD算法估计的信道BER均随信噪比的增大而下降,但经过Viterbi译码的MMP-DCD、LS算法估计的信道BER比未经过译码时下降的更快。在误码率为0.001时,与LS算法相比,MMP-DCD算法约有3.4 dB增益,经过译码的MMP-DCD算法较经过译码的LS算法信道估计BER约有2.4 dB增益。在低信噪比下,未经过译码的MMP-DCD信道估计BER比传统经过译码的LS性能也要好。从图中可以看出,经过Viterbi译码的MMP-DCD算法信道估计BER最低,当SNR在-6 dB时为0,性能更好,增益明显。图 9(b)给出了配置B信道估计BER曲线,从图 9(b)可以看到,信道估计BER较图 9(a)有所改善,在SNR为-8~0 dB时,经译码的MMP-DCD信道估计BER为0。当误码率为0.001时,与LS算法相比,MMP-DCD算法约有2.8 dB增益,经过译码的MMP-DCD算法较经过译码的LS算法信道估计BER约有3.2 dB增益。与图 9(a)相比,图 9(b)中四种算法的信道估计BER都降低了,且4种算法信道估计BER趋近于0只需要更小信噪比,有1 dB增益。图 9(c)可以看出,当误码率为0.001时,与LS算法相比,MMP-DCD算法约有2.3 dB增益;误码率为0.01时,经过译码MMP-DCD算法较经过译码的LS算法信道估计BER约有2 dB增益。
3 结论1) 本文提出的MMP-DCD算法充分考虑了水声信道的稀疏特性,在低信噪比时,信道估计MSE、BER较传统LS算法有了明显改善,更适合用于稀疏水声信道估计。
2) 三中仿真实验配置条件信道估计结果表明,SNR=-5 dB时,MMP-DCD信道估计MSE比传统LS约有28 dB增益;BER为0.001时,MMP-DCD信道估计相比于LS算法约有2~3 dB增益。
| [1] | BERGER R, ZHOU Shengli, PREISIG C, et al. Sparse channel estimation for multicarrier underwater acoustic communication: from subquence methods to compressed sensing[J]. IEEE trans. signal process, 2010, 58(3): 1708–1721. DOI:10.1109/TSP.2009.2038424 |
| [2] | MITOLA J, MAGUIRE G Q, MAGUIRE J. Cognitive radio: making software radios more personal[J]. IEEE personal communications, 1999(6): 13–18. |
| [3] | MITOLA J. Cognitive radio: an integrated agent architecture for software defined radio[D]. Stockholm:Royal Institute of Technology, 2000. |
| [4] | CHAKREVARTHY V D, SHAW A K, TEMPLE M A, et al. Cognitive radio an adaptive waveform with spectral sharing capability[J]. IEEE WCNC, 2005(2): 724–729. |
| [5] | GERMAN, EDGAR H. Transfom domain signal processing study final report. Technical Report, Reistertown MD. Contract: Air Force F30602-86-C-0133[R]. August 1988. |
| [6] | ANDREN, CARL F, et al. Low probability-of-intercept communication system, Harris Corporation, US. Patent 5029184[p]. 1991. |
| [7] | HAN Chuan, WANG Jun, GONG Shuping, et al. Detection and performance of the OFDM-based transform domain communication system[C]//Circuits and system proceedings, 2006 International conference, Beijing, 2006: 1332-1336. |
| [8] | WANG Chuandan, ZHANG Zhongpei, LI Shaoqian. Interference avoidance using fractional fourier transform in transform domain communication system. Advanced Communication Technology[J]. The 9th International Conference. Beijing, 2007: 1756–1764. |
| [9] | CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE trans. info. theory, 2006, 52(2): 489–509. DOI:10.1109/TIT.2005.862083 |
| [10] | DONOHO D. Compressed sensing[J]. IEEE trans. theory, 2006, 52(4): 1289–1306. DOI:10.1109/TIT.2006.871582 |
| [11] | ZAKHAROV Y V, TOZER T C. Multiplication-free iterative algorithmfor LS problem[J]. Electron. lett., 2004, 40(9): 567–569. DOI:10.1049/el:20040353 |
| [12] | SAYED A H, KAILATH T. Recursive least-squares adaptive filters in'The digital signal processing handbook'[M]. (CRC Press, IEEE Press, USA, 1998), pp. 21.1-21.37. |
| [13] | TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE trans. inf. theory, 23007, 53(12): 4655-4666. |
| [14] | DAVENPORT M, WAKIN M B. Analysis of orthogonal matching pursuit using the restricted isometry property[J]. IEEE trans. inf. theory, 2010, 56(9): 4395–4401. DOI:10.1109/TIT.2010.2054653 |
| [15] | CAI T T, WANG L. Orthogonal matching pursuit for sparse signal recovery with noise[J]. IEEE trans. inf. theory, 2011, 57(7): 4680–4688. DOI:10.1109/TIT.2011.2146090 |
| [16] | ZHANG T. Sparse recovery with orthogonal matching pursuit under rip[J]. IEEE trans. inf. theory, 2011, 57(9): 6215–6221. DOI:10.1109/TIT.2011.2162263 |
| [17] | KWON S, WANG Jian, SHIM B. Multipath matching pursuit[J]. IEEE transactions on information theory, 2014, 60: 2986–3001. DOI:10.1109/TIT.2014.2310482 |
| [18] | COTTER S F, RAO B D. Sparse channel estimation via matching pursuit with application to equalization[J]. IEEE trans. commun., 2002, 50(3): 374–377. DOI:10.1109/26.990897 |
| [19] | WANG Biao, CHEN Yan. Sparse underwater acoustic channe estimation based on compressive sensing[J]. Information technology journal, 2013, 12: 1040–1044. DOI:10.3923/itj.2013.1040.1044 |
| [20] | ZAKHAROV Y V, NASCIMENTO V. Orthogonal matching pur-suit with DCD iterations[J]. Electrictionics letters, 2013, 49(4): . |



