燃气轮机作为一种先进的动力设备,在舰船、输气、发电等领域有着广泛的应用。对于航母舰载机和长时间在海洋环境中工作的船用燃气轮机来说,海洋大气中的盐雾气溶胶、尘埃颗粒等使燃气轮机通流部件承受着腐蚀、积垢及磨损等风险[1-6]。腐蚀、积垢及磨损等是造成燃气轮机叶片偏离设计工况甚至失效的常见形式,而叶片表面粗糙度增大则是最直接的表现形式,并且随着运行时间其表面粗糙度也相应增加。David Linden[7]对服役37个月的压气机进口导叶进行观察,由于点蚀等造成孔径甚至达到3.2 mm,深度为0.8 mm。在国内,霍武军等[8]对海军航空兵所用发动机压气机叶片的观察测量也表明海洋环境下叶片表面的点蚀蚀孔孔径可达20~30 μm,由于蚀孔内聚集H+、Cl-、SO42-等,有的蚀坑深度可达0.1~0.2 mm。卢明亮[9]在实验室条件下对不锈钢基材进行盐雾试验,在经过7、14和21 d后分别测量表面粗糙度发现由原来的2 μm分别增加到6.3、31.7和86.7 μm。由此可见,进行叶片表面粗糙度对压气机性能影响的相关研究具有非常重要的意义。
在近几十年中,国内外的一些学者开展了很多针对压气机叶片表面粗糙度的相关研究。在国外,Syverud等基于对GE J85-13的实验,得到叶片表面粗糙度对轴流压气机性能衰退的影响[10]。Back和Song等通过压气机平面叶栅粗糙度实验,考察不同粗糙度大小和分布位置对叶栅压力损失系数和效率损失系数的影响[11-12]。Mirko Morini等以NASA Stage37为对象,分别考察了均匀粗糙度和非均匀粗糙度对压气机总体性能衰退和内部流动特征的影响[13-14]。在国内,王松涛以NASA Stage35为计算模型分别计算了积垢和非均匀叶片粗糙度下压气机性能衰退规律和内部流场特征的变化规律[15-16]。李冬使用数值计算方法研究了某型压气机叶片光洁和粗糙下的性能对比[17]。卢明亮使用改变叶型尺寸的方法研究了叶片腐蚀后粗糙度对压气机性能变化的影响,结果表明叶片腐蚀后的压气机性能出现了一定程度的衰退[9]。这些研究少有采用等效沙粒模型方法来研究叶片表面粗糙度对压气机性能的影响。本文采用数值模拟的方法,以T3系列平板转捩实验为基础,验证了等效沙粒粗糙度计算方法的可行性,再以等效沙粒粗糙度模型为基础,以NASA Stage35型压气机为对象,研究了叶片表面粗糙度变化对压气机性能的影响。
1 等效沙粒模型数值方法本文采用商业软件CFX对研究对象进行全三维数值求解。CFX使用的壁面函数方法是Launder和Spalding所提方法的扩展。在对数规律的区域,流体近壁切向速度与壁面切应力呈对数的关系,并且使用经验公式连接平均流动的近壁边界条件和湍流输运方程[18]。近壁速度的对数关系为
| $ {u^ + } = \frac{{{U_t}}}{{{u_\tau }}} = \frac{1}{\kappa }\ln \left( {{y^ + }} \right) + C $ | (1) |
其中
| $ {y^ + } = \frac{{\rho \Delta y{u_\tau }}}{\mu } $ | (2) |
| $ {u_\tau } = \sqrt {\frac{{{\tau _w}}}{\rho }} $ | (3) |
式中:u+为近壁速度,uτ为摩擦速度,Ut为已知的距离壁面Δy距离处的切向速度,y+为距离壁面的无量纲距离,τw为壁面剪切应力,κ为Von Karman常数,C为与壁面粗糙度相关的常数。
壁面表面粗糙度能够明显增加近壁湍流产生项,这又反过来导致壁面切应力和传热系数的增加。为了使表面粗糙度的影响与实验数据更好的吻合,CFX使用如下关系式考虑粗糙度的影响。
| $ {u^ + } = \frac{1}{\kappa }\ln \left( {{y^ + }} \right) + B-\Delta B $ | (4) |
式中:B取5.2,偏移量ΔB是无量纲粗糙度h+(h+=huτ/υ) 的函数。
对于砂粒粗糙度,偏移量ΔB可以表达成如下形式:
| $ \Delta B = \frac{1}{\kappa }\ln \left( {1 + 0.3h_s^ + } \right) $ | (5) |
通常实际粗糙度是具有峰谷和不同形状和大小,通常以等效砂粒粗糙度ks描述,即具有相同的平均粗糙高度hs。根据无量纲砂粒粗糙度hs+将粗糙流动分为3种粗糙区域,分别为:1) 水利光滑区,0≤hs+≤5;2) 过渡粗糙区,5≤hs+≤70;3) 完全粗糙区,hs+≥70。对于水利光滑区具有完整的粘性底层,在过渡区粗糙单元开始破坏粘性底层,而在完全粗糙区粘性底层消失黏性影响可以忽略。
2 数值方法验证 2.1 T3系列平板转捩实验T3系列平板试验是90年代ERCOFTAC (European Research Community on Flow,Turbulence and Combustion) 在罗-罗公司所做的实验[19],是评价和验证各种转捩模型的经典模型。T3系列平板分为零压力梯度的T3A、T3B实验和带有压力梯度的T3C2、T3C3、T3C4、T3C5等,实验平板相同,前缘有圆角0.75 mm,长度为1.5 m。选取零压力梯度的T3A和T3B进行数值模拟来研究粗糙度对转捩的影响,具体的边界条件如表 1所示。
| 实验平板 | 进口速度/(m·s-1) | 进口湍流强度/% | 粘性比 | 压力梯度 |
| T3A | 5.4 | 3.0 | 13.0 | 无 |
| T3B | 9.4 | 6.0 | 100.0 | 无 |
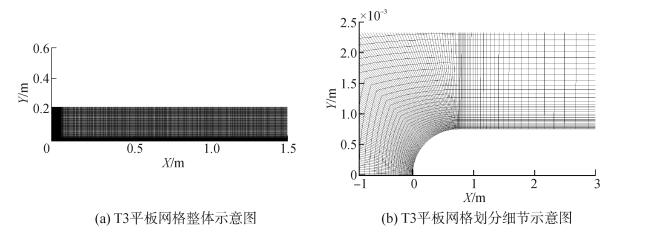
依据照实验中的几何尺寸建立了数值模拟所需的几何模型并进行了网格划分。根据经验值,边界层厚度约为2~3 mm,网格划分保证至少40个节点,平板壁面第一层网格点的y+ < 1,流向网格节点数为610,高度方向网格点数为140,展向取15个网格点,网格总数约为138万,如图 1所示。
|
| 图1 T3平板计算域网格划分示意图 Figure 1 The tablet domain mesh of T3 plate |
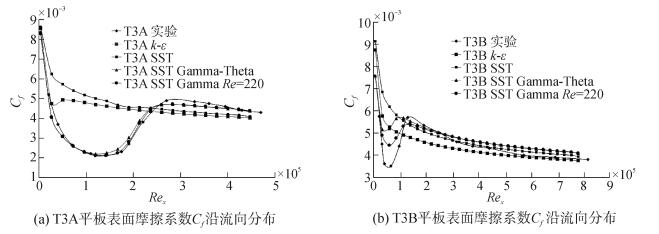
本文分别使用不同的湍流模型和和两种转捩模型模拟平板边界层转捩流动过程,图 2是T3A和T3B对应光滑条件下的不同模型的模拟结果以及与实验值的对比。
|
| 图2 T3A和T3B平板表面摩擦系数Cf沿流向分布 Figure 2 Surface friction coefficient Cf along flow direction of T3A and T3B plate |
图中的参数Re为使用SST模型的Gamma转捩模型时必须给定的转捩开始动量厚度雷诺数,横坐标Rex为基于边界层外主流速度和距平板前缘距离的雷诺数,Rex及表面摩擦系数Cf的义分别如下
| $ {{\mathop{\rm \mathit{Re}}\nolimits} _x} = \frac{{{U_e}x}}{v} $ | (6) |
| $ {C_f} = \frac{\tau }{{0.5\rho U_e^2}} $ | (7) |
式中:Ue为主流速度,ν为运动粘度系数,ρ为气体密度,τ为流向方向的壁面切应力。
从图 2(a)可以看出,SST模型的转捩模型Gamma Theta和Gamma的计算结果与实验值吻合较好,可以较准确地预测边界层转捩过程,而其他模型的计算结果与实验值差别很大,只是在湍流区域的计算值与实验值吻合较好。
2.3 粗糙度表面数值模拟方法验证为了考察粗糙度对边界层流动的影响,CFX软件对粗糙度的处理方法是在壁面函数的求解中加入粗糙度的敏感项 (等效砂粒粗糙度模型),本文通过使用CFX软件自带的等效砂粒粗糙度模型和构建Gauss型粗糙表面两种方法进行计算,考察粗糙度对边界层流动参数的影响以及两种方法计算结果的差别。基于上节的讨论,对边界层求解计算使用的湍流模型选用能够较准确预测转捩过程的SST Gamma模型。
为了能够观察到粗糙度特征对边界层流动影响的具体情况和特征,本节通过构造服从Gauss分布的粗糙平板进行数值模拟,进而研究粗糙表面上的流动情况。
在笛卡尔坐标系下,建立Gauss型粗糙表面模型时,x和y方向上的增量取Δx=40 μm、Δy=40 μm,基准面取Z=0,通过控制轮廓峰值高度R的取值,分别建立具有不同粗糙高度值的表面,这里取轮廓算术平均偏差Ra作为粗糙度的衡量参数,其定义如下
| $ {R_a} = \frac{1}{N}\sum\limits_{i = 1}^n {\left| {{Z_i}-Z} \right|} $ | (8) |
这里共建立了3个粗糙表面模型,在进行数值模拟时为了进行对比,另取光滑平板模型的情况,分别列入表 2,其中等效粗糙度ks与轮廓算数平均偏差Ra的经验关系式,取为ks=6.2Ra。
| 编号 | 峰值R/μm | 粗糙度Ra /μm | 等效值ks/μm |
| 光滑 | 0 | 0 | 0 |
| R1 | 10 | 2.75 | 17.05 |
| R2 | 20 | 5.50 | 34.10 |
| R3 | 30 | 8.25 | 51.15 |
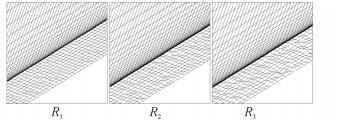
把T3平板实验的平板部分替换为构造的Gauss型粗糙表面,前缘部分圆弧仍采用光滑过渡,计算域其他边界不变,进行网格生成。平板宽度取0.4 mm,网格节点数为12,流向取12 000网格节点,并且在x为0.2~0.8 m加密处理,图 4为网格的局部展示。
|
| 图3 Gauss型粗糙度表面的网格划分示意图 Figure 3 Mesh of the Gauss rough surface |
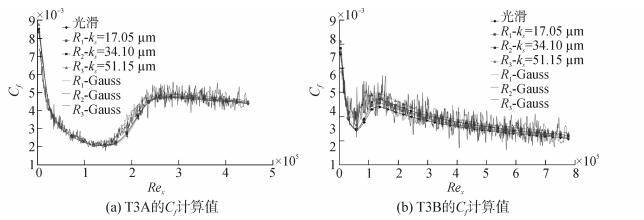
|
| 图4 两种方法对应的T3A和T3B的Cf计算值 Figure 4 Cf of T3A and T3B corresponding two methods |
以表 1中的边界条件对具有Gauss型粗糙表面的平板进行数值计算,同时按表 2在CFX软件中设置等效粗糙度进行计算,将计算结果表示在同一图中以便进行对比。图 4为两种方法计算得到的平板表面摩擦系数结果。从图中可以看出,对具有Gauss型粗糙度的T3平板的计算结果是波动的,这是因为表面摩擦系数的统计位置可能落在粗糙单元的峰顶或谷底,而两种不同位置的剪切应力存在着相对较大的差别,导至Cf值在某一小范围内跳动。同时可以看出Cf值的均值总体变化趋势和不同流动状态下粗糙度大小对其的影响与使用壁面函数法得到的计算结果都是一致的。
通过以上研究可知,采用壁面函数 (等效砂粒模型) 的研究方法虽然不能完全得到边界层内的流动特征,但是从整体来看,两种方法的计算结果是一致的。在工程问题中,一般只关注由粗糙度引起的宏观结果,而对附面层内的流动不作详细研究。因此,使用壁面函数的方法考察粗糙度的影响具有一定的工程应用价值,可以应用在研究粗糙叶片对压气机性能影响的研究中。
3 均匀表面粗糙度对压气机性能的影响 3.1 物理模型及网格划分为了研究表面粗糙度对压气机性能的影响,本文以NASA Stage35试验压气机为研究对象,该型压气机由一排转子与一排静子组成,其中转子叶片数目为36,静子叶片数目为46。设计转速为17 188.7 r/min,最大叶尖速度为454.456 m/s。整个计算域采用HOH型网格结构,并在叶片近壁区采用O型网格剖分,动叶叶尖间隙部分采用“蝶形网格”的结构进行划分。对叶片附近网格进行加密,设置第一层网格高度为10 μm。网格示意图如图 5所示。在网格划分完成后,叶片粗糙度按照CFX软件中对粗糙表面的壁面函数处理方法给定等效砂粒粗糙度ks,分别计算不同表面粗糙度对压气机气动特性的影响。其他边界条件设定如下:
|
| 图5 压气机计算域网格划分示意图 Figure 5 Mesh of the compressor domain |
进口:给定气流总压101 325 Pa,总温288.15 K;
出口:按径向平衡方程给定平均静压,调整压力值模拟压气机不同的工况点。
壁面:绝热,速度满足无滑移条件。
3.2 均匀粗糙度数值模拟结果本文采用等效砂粒粗糙度模型作为壁面函数的方法进行有关压气机表面粗糙度的数值模拟研究。表 3为在动叶叶片上附加的粗糙度,相对粗糙度ks/c是以叶顶弦长为参考值,取等效粗糙度与参考值之比作为无量纲化的粗糙度值。其中ks=1 μm时Rek < 90,可以认为是水力光滑,用以验证CFX软件中粗糙度模型的敏感性。
| 动叶编号 | ks/μm | Ra/μm | ks/c | Rek | 区域 |
| R1 | 1 | 0.16 | 1.79×10-5 | 25 | 光滑 |
| R2 | 5 | 0.81 | 8.93×10-5 | 124 | 粗糙 |
| R3 | 10 | 1.61 | 1.79×10-4 | 248 | 粗糙 |
| R4 | 25 | 4.03 | 4.46×10-4 | 621 | 粗糙 |
| R5 | 40 | 6.45 | 7.14×10-4 | 993 | 粗糙 |
| R6 | 55 | 8.87 | 9.82×10-4 | 1 365 | 粗糙 |
| R7 | 70 | 11.29 | 1.25×10-3 | 1 737 | 粗糙 |
| R8 | 85 | 13.71 | 1.52×10-3 | 2 110 | 粗糙 |
| R9 | 100 | 16.13 | 1.79×10-3 | 2 482 | 粗糙 |
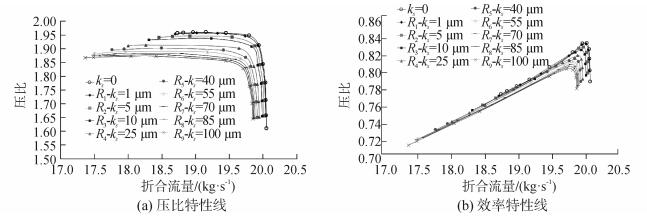
图 6为100%转速下对动叶附加不同粗糙度计算得到的压气机工作特性线。首先可以看出对于Stage35压气机,在其近堵塞工况下流量变化很小而在近失速工况下其压比几乎不变,粗糙度的增加并未改变压气机特性曲线的变化趋势和形态。对应ks=1 μm的压气机特性线与光滑情况几乎重合,可以认为流动处于水力光滑区。
|
| 图6 不同动叶表面粗糙度下的压气机级工作特性线 Figure 6 Characteristic line of the compressor with different roughness |
从图 6中可以看出,当动叶表面粗糙度ks由1 μm增大至100 μm时,压气机峰值效率减小3.5%,对应工况点的压比减小0.8%,总温比升高0.4%,同时粗糙度增加后的压气机最大压比与光滑情况下相比减小4.5%,这对于单级压气机来说是很大程度的衰退。
3.3 粗糙度对压气机损失的影响叶片粗糙度增大后,附面层内气体的摩擦损失以及吸力面分离区域扩大导致分离损失增大,因此压气机的效率、压比和流量等指标都相应下降。一般使用总损失系数
| $ \bar \omega = \frac{{{{\left( {{{P'}_{{\rm{ideal}}}}} \right)}_{{\rm{te}}}} - {{P'}_{{\rm{te}}}}}}{{{{P'}_{{\rm{le}}}} - {p_{{\rm{le}}}}}} \approx \frac{{{{P'}_{{\rm{le}}}} - {{P'}_{{\rm{te}}}}}}{{{{P'}_{{\rm{le}}}} - {p_{{\rm{le}}}}}} $ | (9) |
式中:上标“′”表示相对动叶叶片的参数,下标“le”和“te”分别表示前缘和尾缘,P和p则分别代表总压和静压。这里以前缘处的总压近似尾缘处理想过程的总压。
为了更好地描述叶片粗糙度对压气机总体性能的影响,使用效率损失系数ζ来衡量表面粗糙度对压气机效率参数影响的函数关系,效率损失系数的定义[20]为
| $ \zeta = 1-{\eta _{is}} $ | (10) |
取不同动叶粗糙度计算得到的峰值效率点作为参考工况,计算得到总损失系数
| 编号 | ks/μm | ks+ | ζ | 区域 | |
| R1 | 1 | 0.39 | 0.130 6 | 0.167 2 | 光滑 |
| R2 | 5 | 2.29 | 0.1332 | 0.170 7 | 粗糙 |
| R3 | 10 | 4.96 | 0.135 3 | 0.174 0 | 粗糙 |
| R4 | 25 | 13.91 | 0.139 9 | 0.180 1 | 粗糙 |
| R5 | 40 | 23.69 | 0.143 3 | 0.184 3 | 粗糙 |
| R6 | 55 | 34.06 | 0.146 7 | 0.187 7 | 粗糙 |
| R7 | 70 | 44.87 | 0.149 2 | 0.190 8 | 粗糙 |
| R8 | 85 | 56.07 | 0.152 2 | 0.193 4 | 粗糙 |
| R9 | 100 | 67.59 | 0.154 4 | 0.196 0 | 粗糙 |
从表5可以看出,随着表面粗糙度增加,动叶对应的总损失系数逐渐增加,压气机整级效率损失系数也逐渐增大。表面粗糙度对压气机损失参数的影响可以通过拟合得到一个确定的函数关系式,这里对无量纲粗糙度进行数学处理,取对数ln (ks++1) 为自变量,同时取压气机损失参数与光滑条件下的相对值为因变量拟合得到相应的关系。
以ks=1 μm水力光滑区域的计算结果为基准值,计算得到相应粗糙度条件下的总损失系数
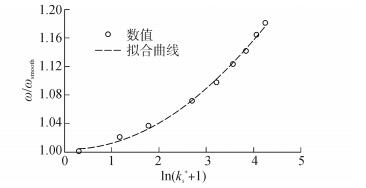
| $ \begin{array}{l} \frac{{\bar \omega }}{{{{\bar \omega }_{{\rm{smooth}}}}}} = 0.010\;3 \times {\left[{\ln \left( {k_s^ + + 1} \right)} \right]^2} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;0.002\;1\ln \left( {k_s^ + + 1} \right) + 1.003\;3\\ \frac{\zeta }{{{\zeta _{{\rm{smooth}}}}}} = 0.007\;3 \times {\left[{\ln \left( {k_s^ + + 1} \right)} \right]^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;0.010\;0\ln \left( {k_s^ + + 1} \right) + 0.997\;5 \end{array} $ |
|
|
图7
总损失系数相对值 |
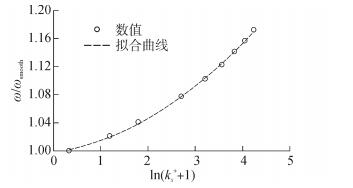
|
| 图8 效率损失系数相对值ζ/ζsmooth与ks+的关系 Figure 8 Relationship between ζ/ζsmooth and ks+ |
在一般工程问题中,在已知叶片平均粗糙度的情况下,根据上式可直接估算出压气机设计工况的总损失和效率损失。
4 结论1) 采用壁面函数 (等效砂粒模型) 的研究方法虽然不能完全得到边界层内的流动特征,但是该方法具有一定的工程价值,可以应用在研究粗糙叶片对压气机性能影响的研究中。
2) 动叶叶片表面粗糙度对压气机工作性能影响很大。当动叶表面粗糙度ks由1 μm增大至100 μm时,压气机峰值效率减小3.5%,对应工况点的压比减小0.8%,总温比升高0.4%,同时粗糙度增加后的压气机最大压比与光滑情况下相比减小4.5%,这对于单级压气机来说是很大程度的衰退。
3) 以不同动叶粗糙度计算得到的峰值效率点作为参考工况,计算得到总损失系数
| [1] |
孔祥鑫, 徐可君. 航空发动机叶片的腐蚀与防护[J].
航空科学技术, 1997(2): 24–26.
KONG Xiangxin, XU Kejun. Aeroengine blade corrosion and its control[J]. Aeronautical science and technology, 1997(2): 24–26. |
| [2] | KURZ R, BRUN K, WOLLIE M. Degradation effects on industrial gas turbines[J]. Journal of engineering for gas turbines and power, 2009(6): 62401–62407. |
| [3] | GRANOVSKIY A, MANAEV I, VASSILIEV V, et al. Effects of blade degradation on turbine performance[C]//ASME 2013 Turbine Blade Tip Symposium. American Society of Mechanical Engineers, 2013:V001T01A003. |
| [4] | CAGUIAT D E, ZIPKIN D M, PATTERSON J S. Compressor fouling testing on rolls royce/allison 501-K17 and general electric LM2500 gas turbine engines[C]//ASME Turbo Expo 2002:Power for Land, Sea, and Air. American Society of Mechanical Engineers, 2002:933-942. |
| [5] | HAMED A A, TABAKOFF W, RIVIR R B, et al. Turbine blade surface deterioration by erosion[J]. Journal of turbomachinery, 2005, 127(3): 445–452. DOI:10.1115/1.1860376 |
| [6] |
王松, 王国辉, 韩青, 等. 叶片积垢对压气机性能衰退的影响[J].
哈尔滨工程大学学报, 2014(12): 1524–1528.
WANG Song, WANG Guohui, HAN Qing, et al. Compressor performance deterioration caused by blade fouling[J]. Journal of Harbin Engineering University, 2014(12): 1524–1528. |
| [7] | LINDEN D H. Long term operating experience with corrosion control in industrial axial flow compressors[C]//Proceedings of the Fortieth Turbomachinery Symposium.[S.l.], 2011:93-106. |
| [8] |
霍武军, 孙护国. 海航发动机压气机叶片腐蚀与防护措施[J].
航空工程与维修, 2002(6): 39–41.
HUO Wujun, SUN Huguo. Corrosion and precaution for blades of aero-engine compressor in the navy air arm[J]. Journal of aviation maintenance and engineering, 2002(6): 39–41. |
| [9] |
卢明亮. 盐雾腐蚀对压气机性能影响的研究[D]. 哈尔滨工程大学, 2013.
LU Mingliang. Reaearch on the effects of salts spray corrosion on the compressor performance[D]. Harbin:Harbin Engineering University, 2013. |
| [10] | SYVERUD E, BAKKEN L E. The impact of surface roughness on axial compressor performance deterioration[C]//ASME Turbo Expo 2006:Power for Land, Sea, and Air. American Society of Mechanical Engineers, 2006:491-501. |
| [11] | BACK S C, HOBSON G V, SONG S J, et al. Effects of reynolds number and surface roughness magnitude and location on compressor cascade performance[J]. Journal of turbomachinery, 2012, 134(5): 051013. DOI:10.1115/1.4003821 |
| [12] | BACK S C, JEONG I C, SOHN J L, et al. Influence of surface roughness on the performance of a compressor blade in a linear cascade:experiment and modeling[C]//ASME Turbo Expo 2009:Power for Land, Sea, and Air. American Society of Mechanical Engineers, 2009:239-247. |
| [13] | MORINI M, PINELLI M, SPINA P R, et al. Computational fluid dynamics simulation of fouling on axial compressor stages[J]. Journal of engineering for gas turbines and power, 2010, 132(7): 072401. DOI:10.1115/1.4000128 |
| [14] | AIDI N, MORINI M, PINELLI M, et al. Performance evaluation of nonuniformly fouled axial compressor stages by means of computational fluid dynamics analyses[J]. Journal of turbomachinery, 2013, 136(2): . |
| [15] | CHEN S, SUN S, XU H, et al. Influence of local surface roughness of rotor blade on performance of an axial compressor stage[C]//ASME Turbo Expo 2013:Turbine Technical Conference and Exposition. American Society of Mechanical Engineers, 2013:V06AT35A015-V06AT35A015. |
| [16] | CHEN S, ZHANG C, SHI H, et al. Study on the impact of fouling on axial compressor stage[C]//ASME Turbo Expo 2012:Turbine Technical Conference and Exposition. American Society of Mechanical Engineers, 2012:1-8. |
| [17] |
李冬, 樊照远, 张娟, 等. 压气机叶片粗糙度对其性能衰退的影响研究[J].
航空发动机, 2009(5): 32–35.
LI Dong, FAN Zhaoyuan, ZHANG Juan, et al. Influence of blade roughness on compressor performance derterioration[J]. Aeroengine, 2009(5): 32–35. |
| [18] | CFX-Solver Theory Guide, ANSYS 13.0 Help[EB/OL]. 2010. http://www.doc88.com/p-908539666887.html. |
| [19] | SAVILL A M. A synthesis of T3 test case predictions[J]. Numerical simulation of unsteady flows and transition to turbulence, 1992: 404–442. |
| [20] | BOYLE R J, SENYITKO R G. Measurements and predictions of surface roughness effects on the turbine vane aerodynamics[C]//ASME Turbo Expo 2003, collocated with the 2003 International Joint Power Generation Conference. American Society of Mechanical Engineers, 2003:291-303. |



