高强度钢材目前已经被广泛使用在船舶与海洋结构物上,舰艇用钢强度更高。相对普通强度钢而言,高强钢的主要优点在于[1],使用可以大大减少钢材用量,减轻结构自重;减小焊缝尺寸,改善焊缝质量,提高疲劳寿命。缺点是低温韧性相对较差。电镜下对高强钢低温-60~-20℃冲击断裂试样断口图样的观察发现断口呈脆性断裂伴随较少量的延性断裂[2]。由于焊接工艺不过关、应力集中、材料自身缺陷以及疲劳等因素的客观存在,结构上会不可避免的产生裂纹。工作在低温环境下的含裂纹结构遭受外部砰击,撞击以及来自水中或空气中的爆炸冲击后,极易发生低应力开裂,裂纹将迅速扩展使结构在很短时间内断裂失效;而不是像无缺陷结构一样发生弹塑性变形以抵消外部冲击作用。解决动态断裂问题常用的数值方法有:1) 有限元的网格重构方法 (remeshingtechnique),裂纹必须和单元网格边界相一致,每扩展一次,需要重新划分网格。2) 单元间内聚力模型 (cohesive zone mode),在有限单元间插入带失效本构的接触单元 (cohesive element),预先设定扩展路径,利用接触单元的失效模拟动态裂纹扩展。3) 扩展有限单元法 (extended finite element method,XFEM),摆脱了传统有限单元法中裂纹对网格的依赖,不需网格重构和预设扩展路径即可实现裂纹的自动扩展。
已有的研究,大多基于以上三种数值方法并结合各自不同的断裂力学模型很好的解决了一些问题。A.R. Shahani等采用网格重构技术模拟了双悬臂梁试件的动态断裂过程[3]。Su Xiangting等在有限元的网格间嵌入接触单元,对混凝土试件的拉伸、扭转和三点弯曲冲击断裂试验的真实情况进行了模拟[4]。D. Grégoire等将扩展有限元和动态应力强度因子理论结合模拟PMMA试件的SHPB冲击断裂试验,二者吻合较好[5]。S Lee等采用XFEM模拟了海洋管道表面轴向半椭圆裂纹的低周疲劳扩展[6]。R Dimitri等使用XFEM研究了复合材料板的Ⅰ型和Ⅰ-Ⅱ复合型开裂,结果和理论解误差很小[7]。低温冲击断裂试验的实施较为困难,本文采用数值模拟方法研究。本文采用扩展有限元数值方法结合局部应力与损伤力学模型成功的预测了裂纹的扩展路径。同时分析了断裂能、初始裂纹长度和裂纹位置对扩展路径的影响。
1 XFEM数值理论扩展有限单元法于1999年由Belytschko等[8-9]提出,其基本原理是基于单位分解[10]的思想在常规有限单元法的位移模式中加进能反映裂纹面不连续和间断特性的扩充函数来加强常规有限元对位移场的近似。其位移逼近由连续和不连续两部分组成,连续位移采用标准有限单元法逼近,不连续位移根据所分析问题的不连续特性选取相应扩充函数来逼近。扩展有限单元法的提出引起了科学界的极大关注,得到了迅速发展和应用,主要用于解决夹杂界面、裂纹扩展和剪切带演化等不连续问题。
1.1 扩展有限元位移模式在常规有限元法中,单元形函数的集合就是一个单位分解,即
| $\sum\limits_{i = 1}^N {{N_i}\left( \mathit{\boldsymbol{x}} \right)} = 1$ | (1) |
基于单位分解的概念,位移场u(x) 可表示成控制域内的离散形式:
| $\mathit{\boldsymbol{u}}\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^N {{N_i}\left( \mathit{\boldsymbol{x}} \right)} {\mathit{\boldsymbol{u}}_i}$ | (2) |
扩展有限元为了反映裂纹附近区域的不连续性,在裂纹附近单元的位移场逼近函数中增添了基于单位分解法的扩充项[11],即
| $\mathit{\boldsymbol{u}}\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^N {{N_i}\left( \mathit{\boldsymbol{x}} \right)} {\mathit{\boldsymbol{u}}_i} + \sum\limits_{j = 1}^M {{N_j}\left( \mathit{\boldsymbol{x}} \right)} \psi \left( \mathit{\boldsymbol{x}} \right){\mathit{\boldsymbol{a}}_j}$ | (3) |
式中:Ni(x) 是节点标准有限元形函数,ψ(x) 是扩充函数,ui是标准节点自由度,aj为附加节点自由度。式 (3) 右端第一项是标准有限元近似,第二项是基于单位分解的扩充项近似。aj为新增加的节点自由度,它并无明确意义,是用于调整扩充函数ψ(x) 的幅值以对真实场达到最佳近似的待定系数。与传统有限元格式相比,最大区别在于单元节点处引入了多余自由度。在式 (3) 中,针对具体求解问题需要选用不同的扩充函数。构造扩充函数时,需要使其具有未知场u的真实解的某些特性以增加收敛速度,在实际使用中往往基于真实解的解空间来选取ψ(x)。
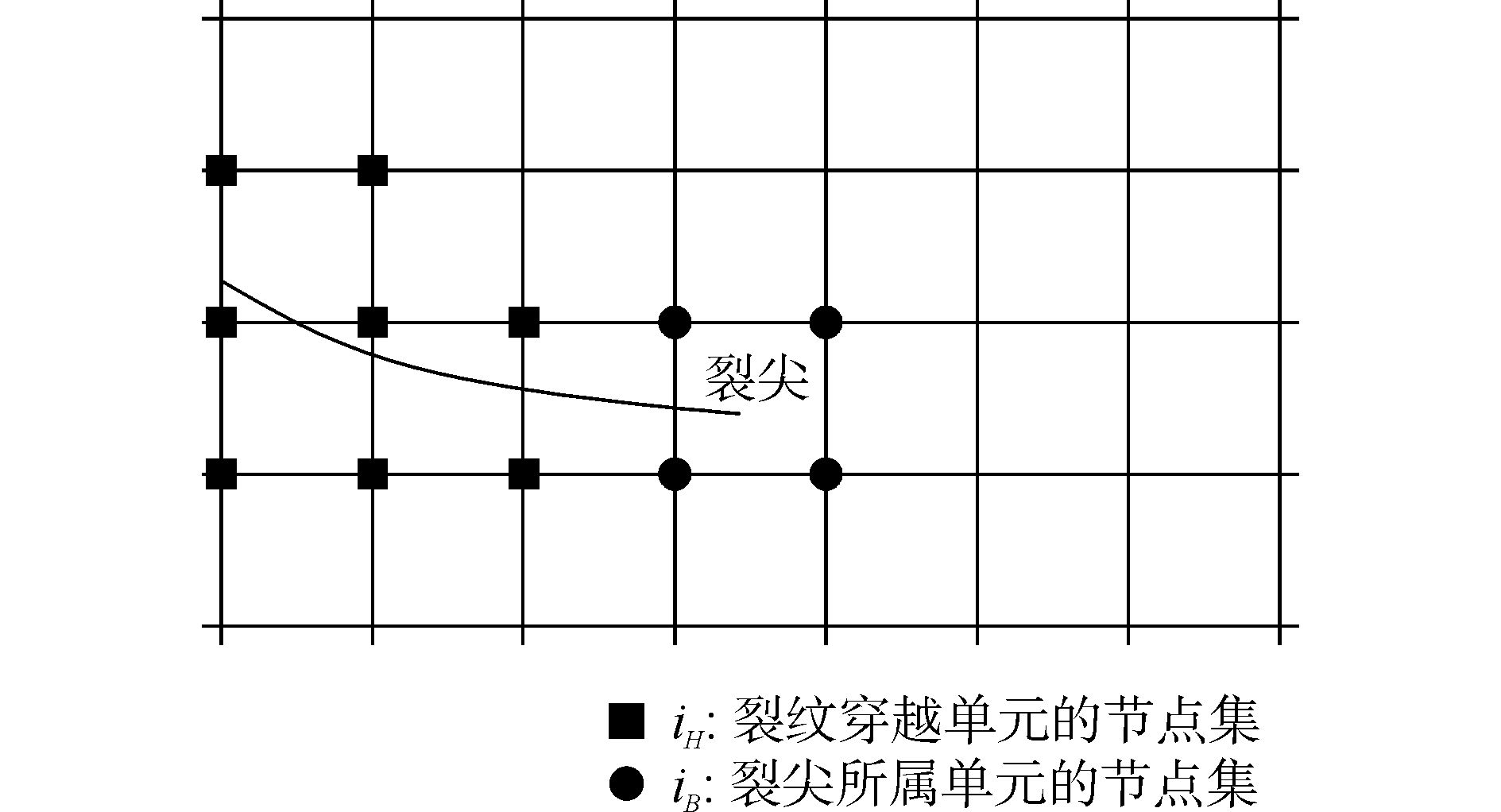
1.2 不同节点的扩充方式不同节点的扩充方式不一样,如图 1所示。
|
| 图1 裂纹区单元节点的扩充方式 Figure 1 Enrichment strategy of nodes in crack region |
图 1中iH和iB分别表示被裂纹完全穿过的单元的节点集合 (不包括iB) 和裂尖所处单元的节点集合。全部节点的集合用i0表示,则扩展有限元的位移逼近模式可表示为
| $\begin{array}{l} \mathit{\boldsymbol{u}}\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i \in {i_0}} {{N_i}\left( \mathit{\boldsymbol{x}} \right) \cdot } {\mathit{\boldsymbol{u}}_i} + \sum\limits_{i \in {i_H}} {{N_i}\left( \mathit{\boldsymbol{x}} \right) \cdot } H\left( \mathit{\boldsymbol{x}} \right) + \\ \quad \quad \quad \sum\limits_{i \in {i_B}} {{N_i}\left( \mathit{\boldsymbol{x}} \right) \cdot } \left( {\sum\limits_{k = 1, \ldots ,4} {{\psi _k}\left( x \right) \cdot {\mathit{\boldsymbol{b}}_{i,k}}} } \right) \end{array}$ | (4) |
对于被裂纹完全穿过的单元,裂纹面两侧的位移场发生跳跃,扩充函数为
| $\psi \left( \mathit{\boldsymbol{x}} \right) = H\left( \xi \right)$ | (5) |
式中:H(ξ) 为广义的Heaviside函数 (阶跃函数),在裂纹一侧等于1,另一侧等于-1,即
| $H\left( \xi \right) = \left\{ {\begin{array}{*{20}{l}} {1,} & {\xi \ge 0}\\ { - 1,} & {\xi <0} \end{array}} \right.$ | (6) |
对于裂尖单元,扩充函数的选取应能够反映裂尖的位移场特性,对于各向同弹性体,ψ(x) 可以是以下函数基的线性组合,即
| $\begin{array}{l} \quad \quad \quad \quad \quad \quad \quad {\psi _k}\left( {r,\theta } \right) = \\ \left\{ {\sqrt r {\rm{sin}}\frac{\theta }{2},\sqrt r {\rm{cos}}\frac{\theta }{2},\sqrt r {\rm{sin}}\frac{\theta }{2}{\rm{sin}}\theta ,\sqrt r {\rm{cos}}\frac{\theta }{2}{\rm{sin}}\theta } \right\} \end{array}$ | (7) |
式中:r和θ是在裂尖极坐标系中定义的位置参数。式 (5) 的扩充函数基正是线弹性断裂力学中平面复合型裂纹的裂尖位移场解析解的各项。用它们来构造裂尖形函数不仅可以表现裂纹面位移的不连续性质,同时可以精确捕捉裂尖位移场。这种类型的扩充函数称为裂尖扩充函数。由于裂尖扩充函数在计算程序中使用较为复杂,难以实现,本文的研究只采用阶跃函数扩充裂纹完全穿过的单元的节点,即裂纹扩展过程中将裂尖置于单元边界,将网格细化,可以计算得到较高精度的真实裂纹扩展情况。
1.3 裂纹追踪由于扩展有限单元法允许不连续面 (如裂纹等) 穿过单元,即网格独立于间断面,因此需要对不连续面进行几何描述,常用的方法是水平集方法 (level sets method)。另一方面,构造阶跃函数时候也需要借助水平集方法。
水平集方法是一种跟踪间断 (如裂纹、界面等) 运动的数值技术。其基本思想是将间断面γ看成高一维空间中某一函数φ(称为水平集函数) 的零水平集 (φ=0)。本文追踪裂纹使用的水平集函数是符号距离函数 (signed distance function),其表达式为
| $\xi \left( \mathit{\boldsymbol{x}} \right) = {\rm{min}}\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_r}} \right\|{\rm{sign}}({\mathit{\boldsymbol{n}}^ + }\cdot(\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_r}))$ | (8) |
式中:n+是间断处的单位法向量。对于不在间断处的任何点x,ξ(x) 是从点x到间断处γ的最短距离。并且对ξ(x) 以如下方式定义正负:如果点x所在的位置与n+指向一致,取正;如果点x在另一侧,取负。
2 局部应力与损伤力学模型局部应力与损伤模型关注断裂过程区的力学行为,由裂尖区的应力和损伤状态决定裂纹如何扩展,主要包括损伤起始和损伤演化,分别用于预测起裂和控制扩展,对脆性断裂和延性断裂都适用。
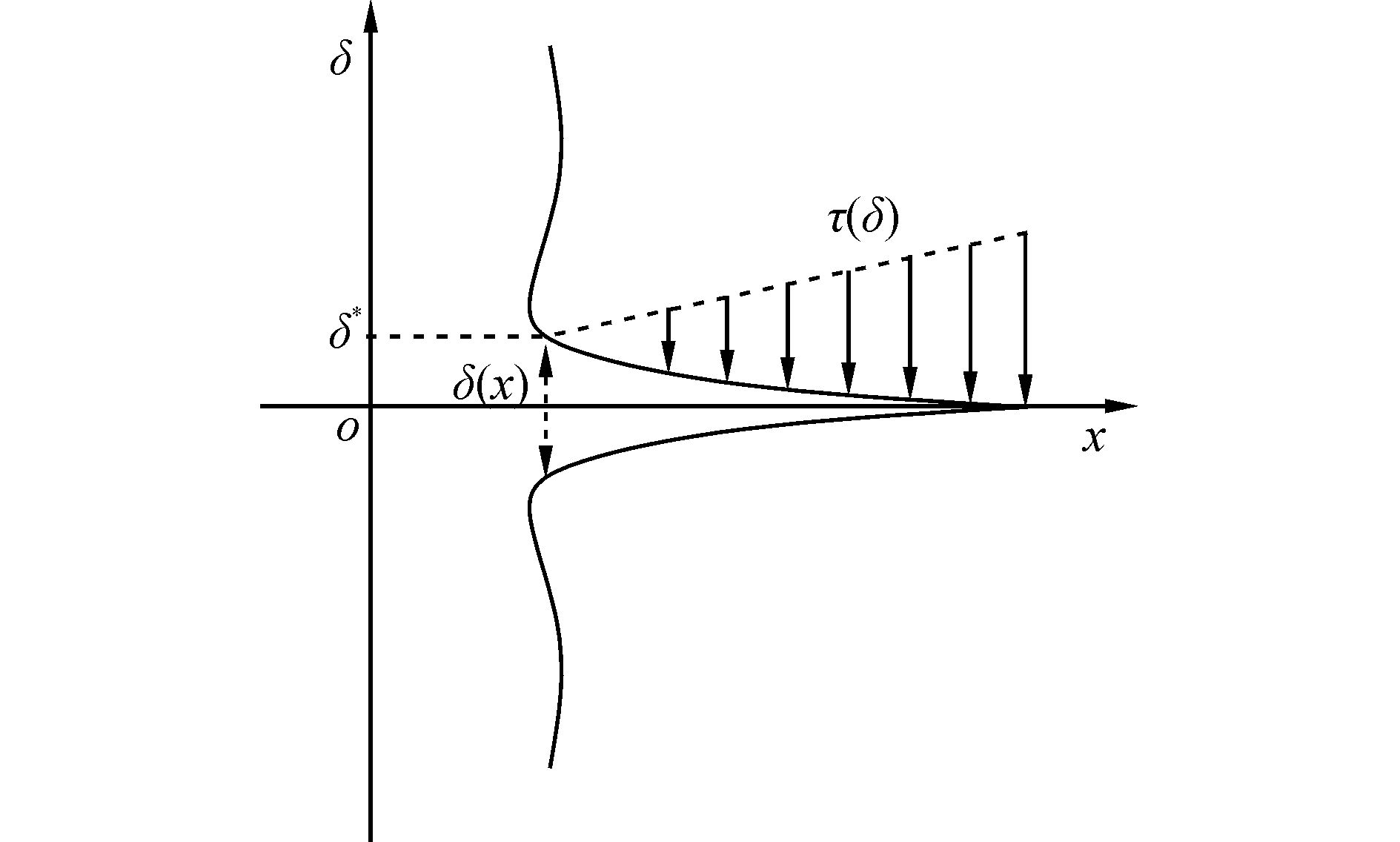
损伤起始即裂纹扩展方向垂直于裂尖点的最大主应力方向,最大主应力值达到损伤开始的临界值时裂纹开始扩展。关于损伤演化,在裂纹面间引入内聚力模型,该模型核心思想为裂纹的张开变形导致了内聚力τ(δ),它是张开位移δ(x) 的函数。内聚力随着裂纹张开位移的增大而减小,当裂纹张开位移增至δ*时,内聚力τ衰减为零,如图 2所示。
|
| 图2 内聚力裂纹模型 Figure 2 Cohesive crack model |
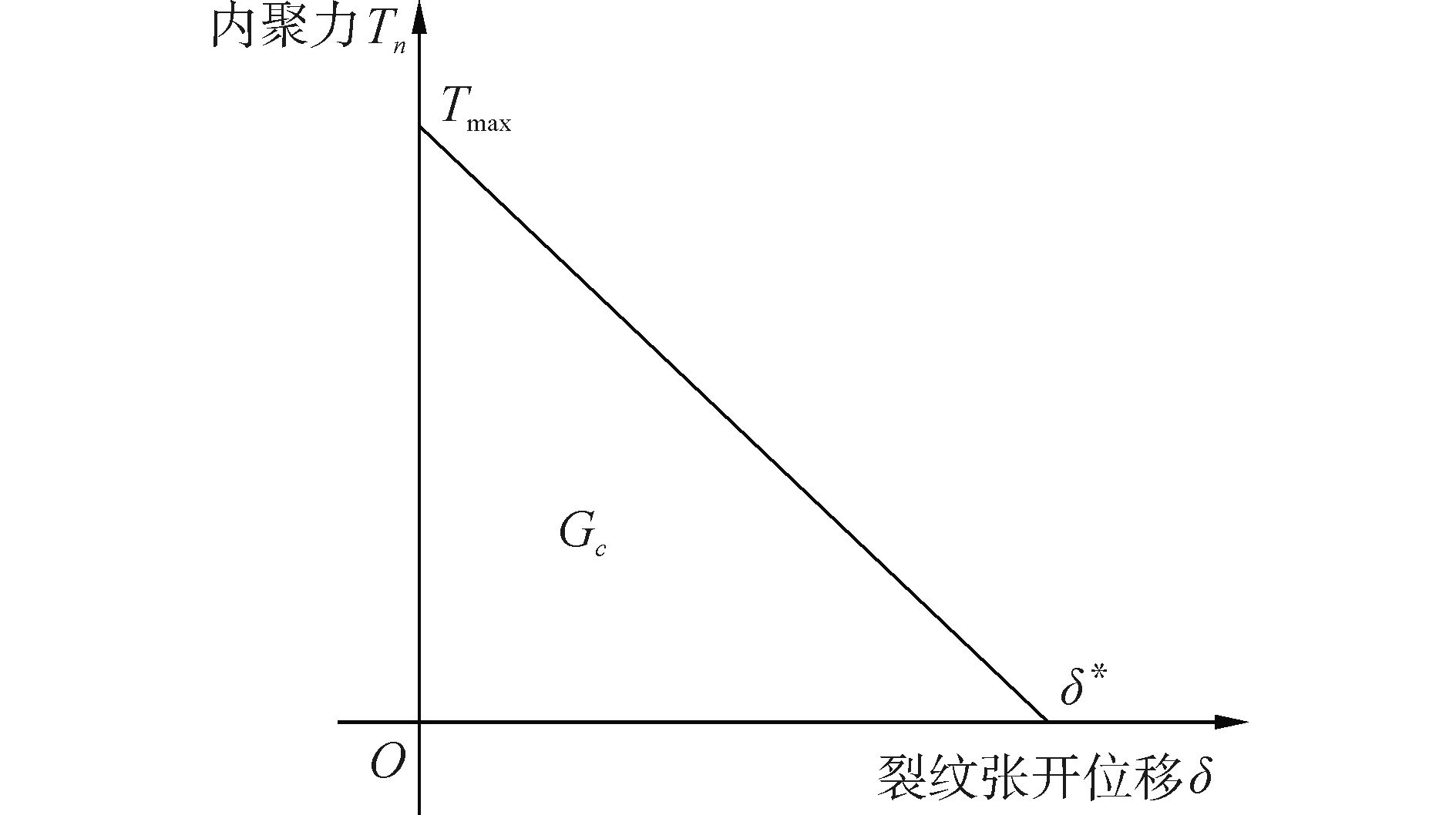
假定裂纹损伤起始前内聚力按线弹性关系发展至最大值Tmax,Tmax可由裂纹区域扩充单元的弹性材料属性计算得到;损伤起始后即裂尖张开后内聚力按图 3所示的线性关系退化。即
| ${\mathit{\boldsymbol{t}}_n} = \left( {1 - D} \right){\mathit{\boldsymbol{T}}_n}$ | (9) |
|
| 图3 内聚力-裂纹分离法则 Figure 3 Cohesive traction-separation law |
式中:Tn是矢量,包含一个法向和两个切向分量。Tn是损伤起始前计算出来的内聚力。损伤起始后的退化规律,也可以采用其他退化方式以更好的控制裂纹的真实扩展。Hillerborg等[12]将断裂能引入内聚力裂纹模型,损伤演化由损伤过程中耗散的能量Gc(断裂能) 来控制,其值等于图 3曲线下的面积。断裂能是材料本身的属性,可以通过实验测得。
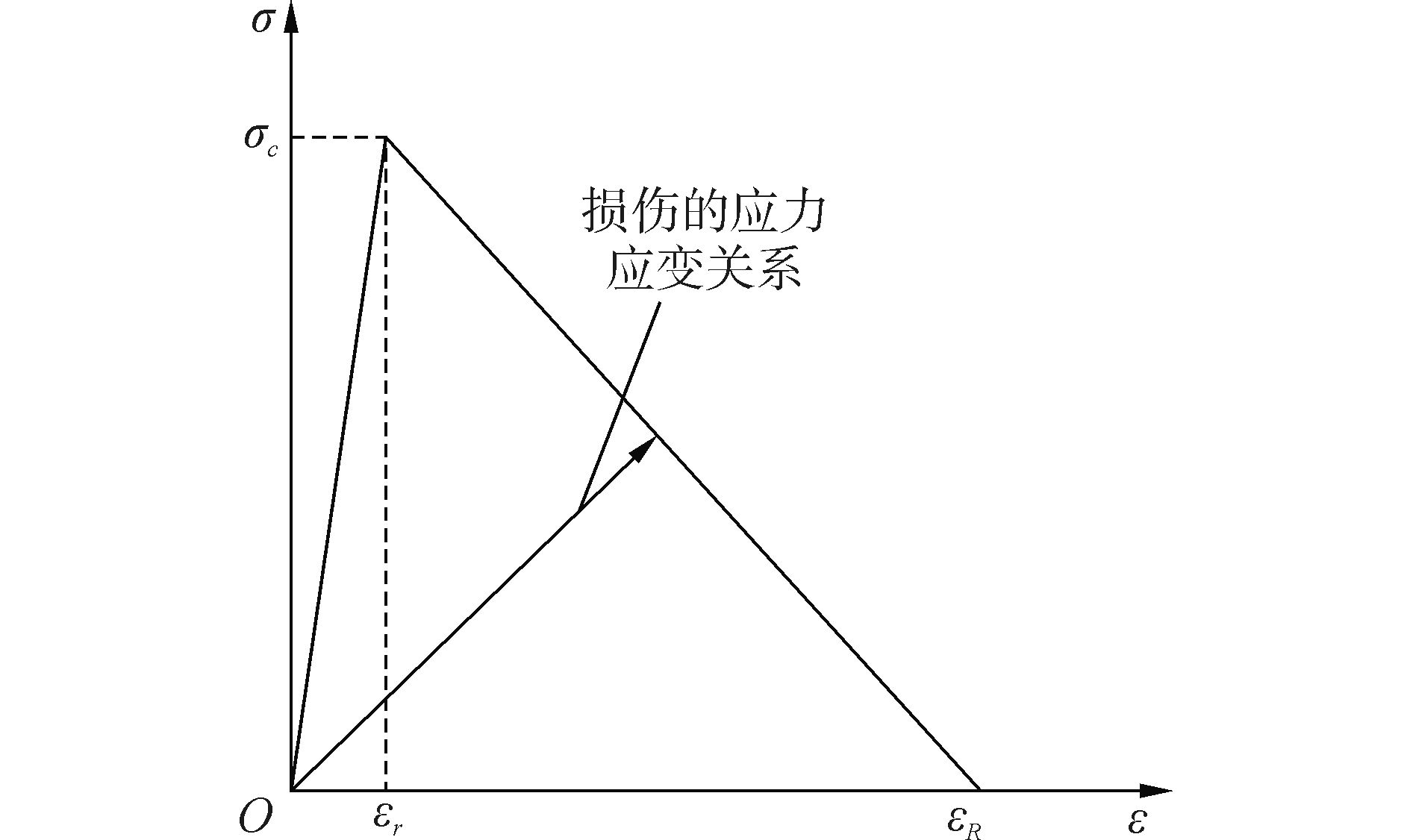
采用局部应力与损伤模型后,裂纹穿过区域的单元应力应变关系将按图 4中的曲线发展。εr点对应损伤起始时即裂尖开始张开时的应变,此时单元损伤指数D为0;εR点对应完全损伤即内聚力降为零时的应变,此时单元损伤指数D达到1。
|
| 图4 裂纹穿越单元的应力-应变关系 Figure 4 Stress-strain curve for element split by crack |
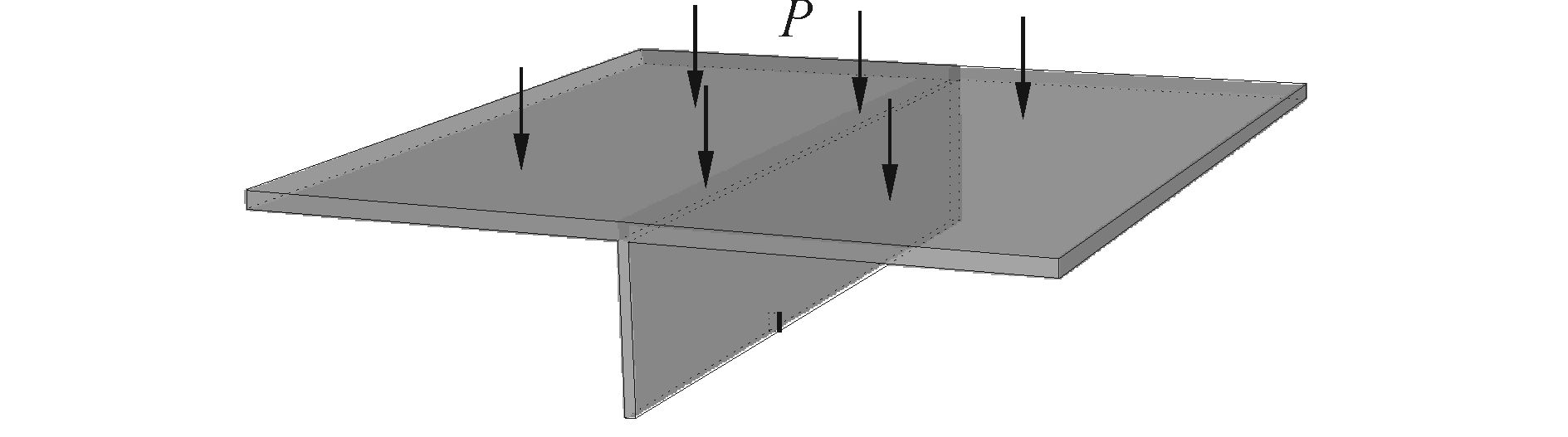
本文选取纵向加强结构的加筋板单元建立分析模型,如图 5所示。面板尺寸为0.6 m×0.6 m,厚度为12 mm,纵骨截面尺寸为120 mm×8 mm。面板和纵骨相交的两边采取简支约束,剩余两边自由。考虑实际结构中纵骨端部下端一般会有强框架支撑,在纵骨底部两端12 mm范围内约束其垂直面板方向的位移,整个面板均匀施加横向向内压力冲击载荷。
|
| 图5 分析模型 Figure 5 Analysis model |
所用材料为船用高强钢,屈服强度620 MPa,密度7 850 kg/m3,杨氏模量210 GPa,泊松比0.3。选取材料本构为Ramberg-Osgood模型,参数n为5,α为0.002。其应力应变关系为
| $E\varepsilon = \sigma + \alpha {(\frac{\sigma }{{{\sigma _0}}})^{n - 1}}\sigma $ | (10) |
式中:E是杨氏模量,船舶实际营运中最大名义弯曲应力范围为69~90 MN/m2 [2],大量断裂事故在正常营运中发生,即断裂应力值远低于材料屈服强度值。因此最大主应力定为80 MPa。低温动态断裂能Gc为
| ${G_c} = \frac{{K_{Id}^2}}{E}$ | (11) |
式中:KId是钢材在NDT (无塑性转变温度) 时的动态断裂韧度。欧文得出NDT温度下的KId[2]:
| ${K_{Id}} = C\sqrt m {\sigma _{yd}}$ | (12) |
式中:σyd为冲击动态屈服应力,一般高出屈服强度138 MPa左右[2],系数0.079 7≤C≤0.124 3。计算得到低温动态断裂能Gc约为40 kN/m。
|
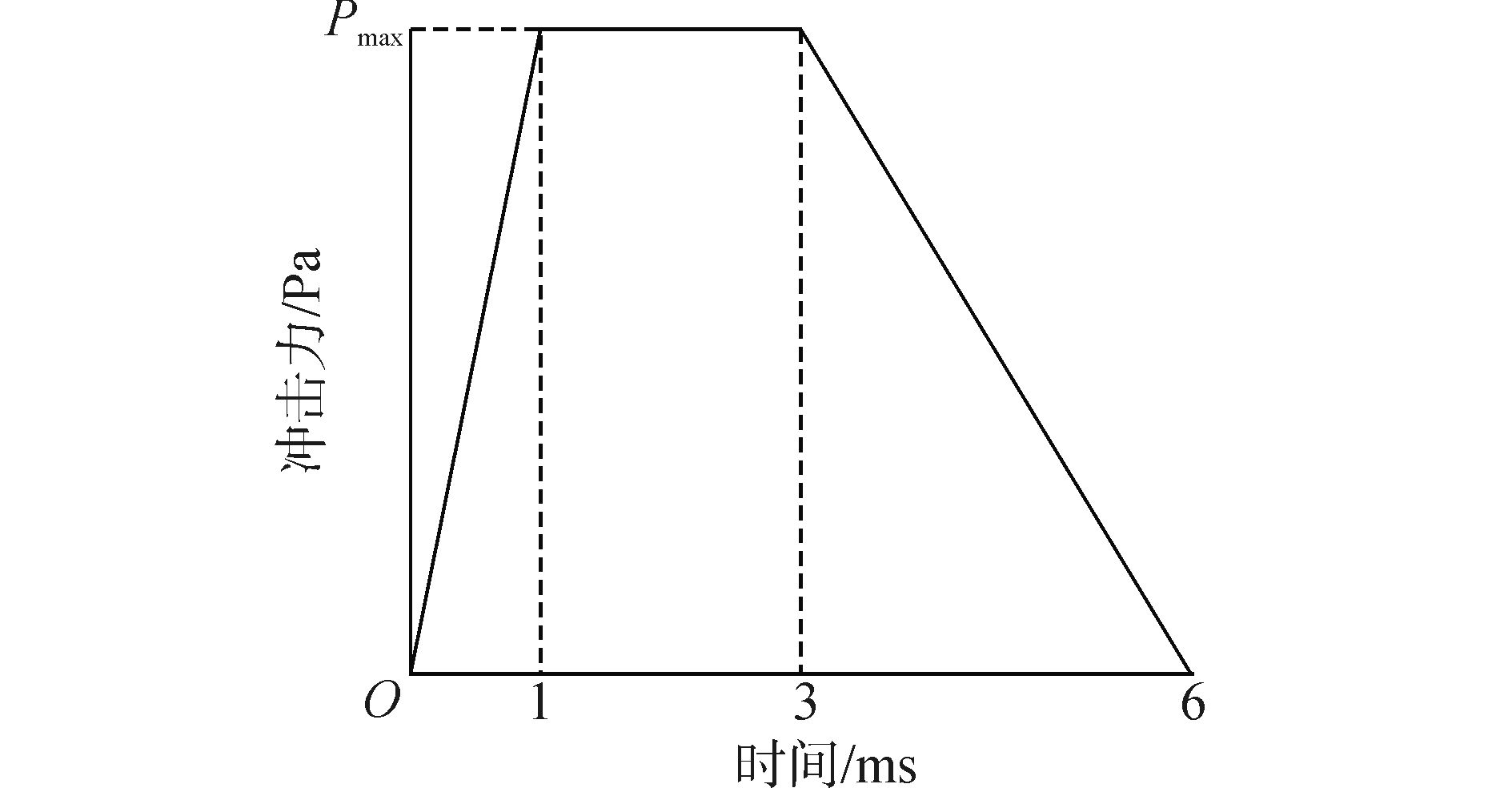
| 图6 冲击力时程曲线 Figure 6 The impact force-time history |
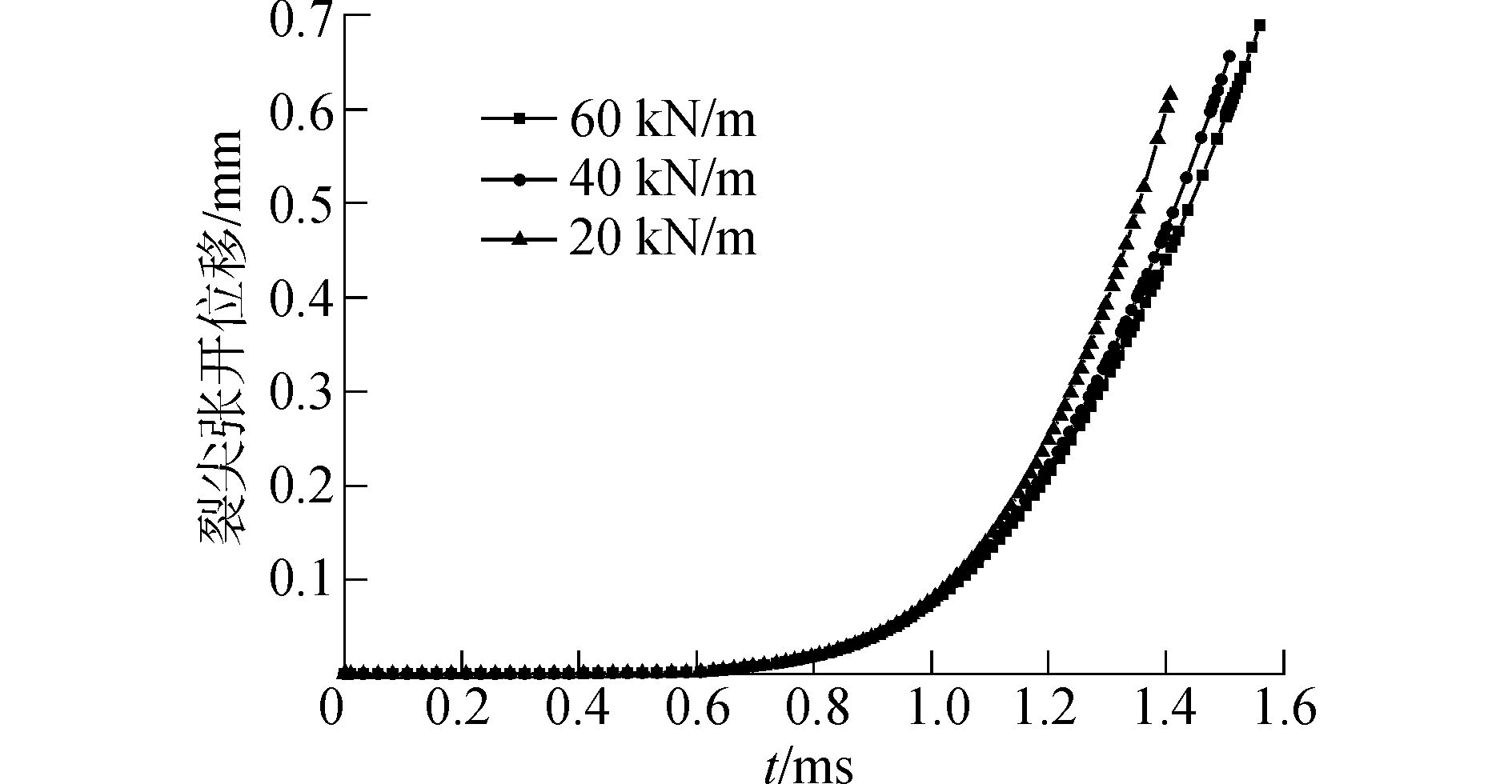
假定纵骨垂向中心线处下缘存在8 mm长初始裂纹,分析Pmax=0.5 MPa时的扩展情况。由于对称,裂纹呈Ⅰ型张开扩展,扩展路径为垂直于面板的直线,如图 7所示。温度降低,材料的断裂能也会减小[2]。改变低温范围内的断裂能,分别计算20、40和60 kN/m断裂能下的扩展发现不同断裂能下的裂纹扩展路径均为直线,均在t=0.590 ms时刻起裂,分别在1.407、1.508和1.560 ms时刻引起面板的开始断裂。此外,还得到不同断裂能下初始裂纹尖端的张开位移时程曲线,如图 8所示。

|
| 图7 Ⅰ型裂纹扩展 Figure 7 Crack propagation of mode I |
|
| 图8 裂纹尖端张开位移时程曲线 Figure 8 Crack tip open displacement-time history |
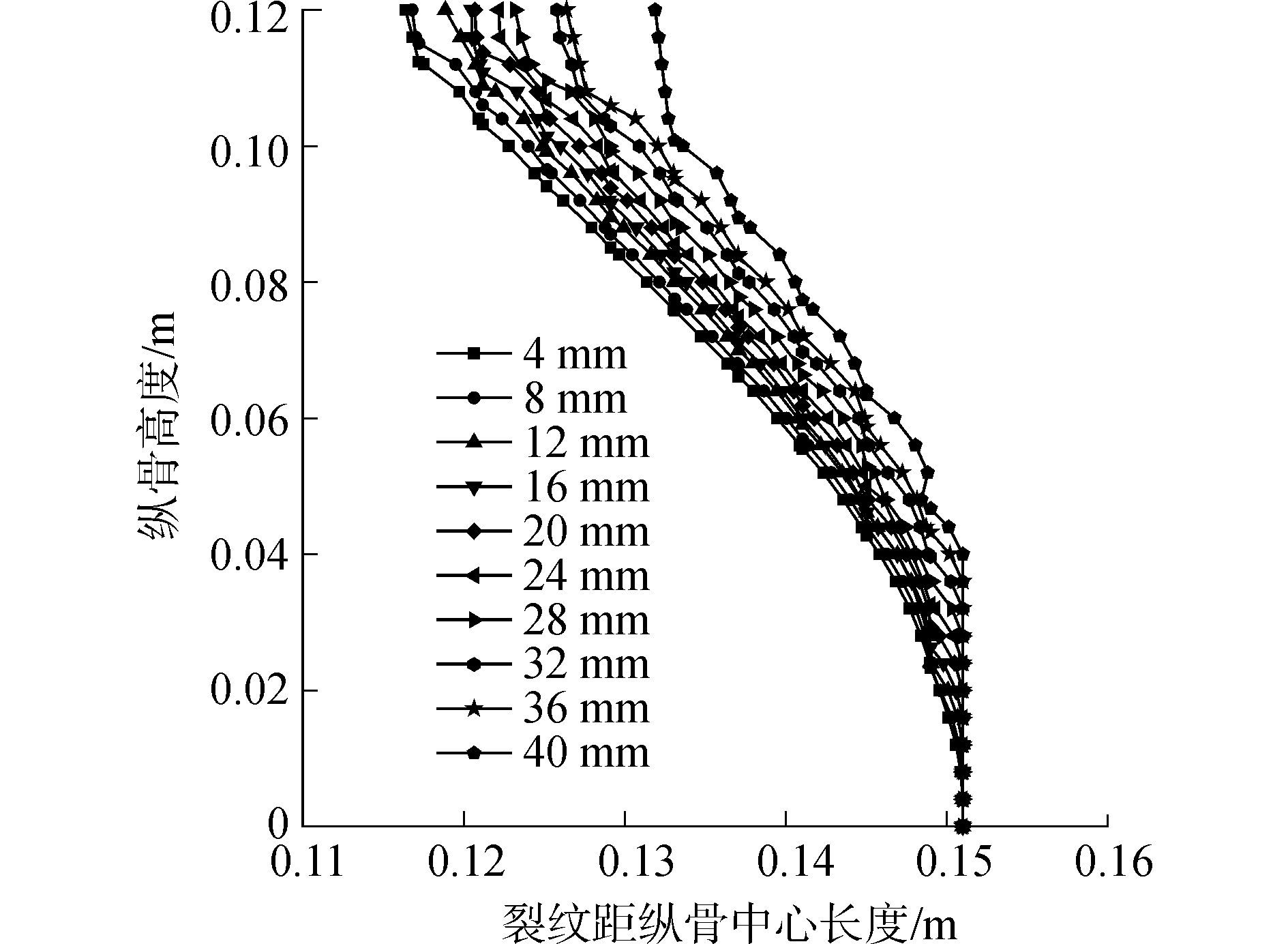
为了观察初始裂纹长度对裂纹扩展路径的影响,分析预测了Pmax=1.0 MPa时,距离纵骨中心0.151 m处,初始裂纹长度4~40 mm范围内的10道裂纹的扩展路径。图 9是纵骨上各裂纹路径的示意图,均呈Ⅰ-Ⅱ复合型扩展,自左向右依次代表 4~40 mm范围内按4 mm大小单调递增的各初始裂纹长度下的扩展路径,裂纹起裂时间见表 1。
|
| 图9 不同初始长度下的裂纹扩展路径 Figure 9 Crack propagation path for different initial crack lengths 注:图中坐标原点为纵骨垂向中心线和纵骨底边 (纵骨不与面板接触的一边) 的交点。 |
| 初始裂纹长度/mm | 起裂时间/ms |
| 4 | 0.540 |
| 8 | 0.515 |
| 12 | 0.498 |
| 16 | 0.470 |
| 20 | 0.448 |
| 24 | 0.436 |
| 28 | 0.430 |
| 32 | 0.418 |
| 36 | 0.412 |
| 40 | 0.398 |
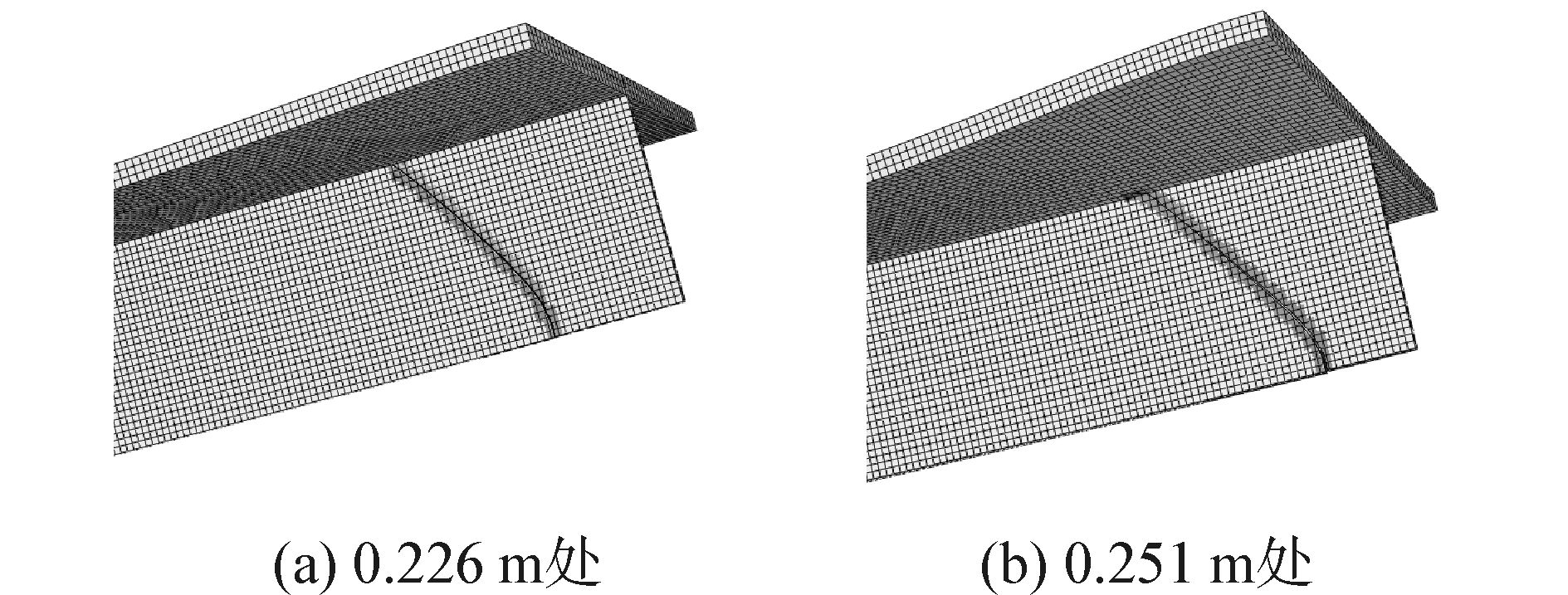
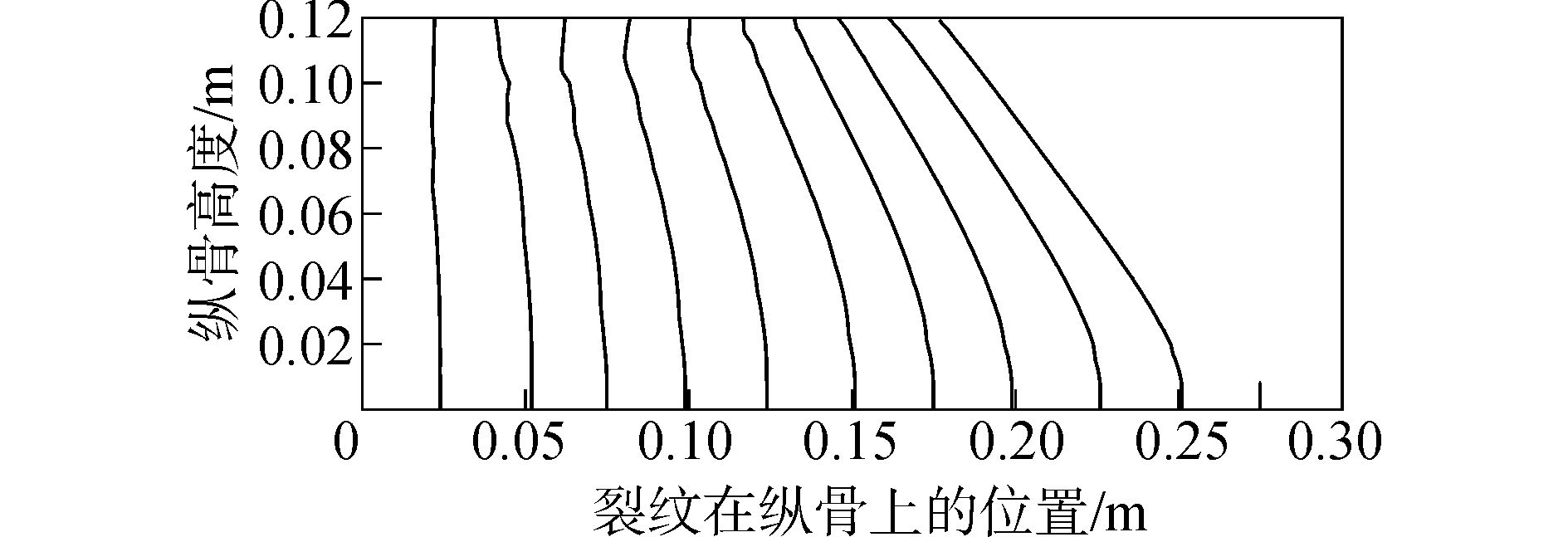
在纵骨垂向中心线外同一侧,约取25 mm间隔,分别计算Pmax=1.0 MPa时,11个不同位置处8 mm初始长度裂纹的扩展路径。图 10给出了距离纵骨垂向中心线0.226 m和0.251 m处的两道典型Ⅰ-Ⅱ复合型裂纹扩展路径的实体图。各个位置处的裂纹扩展路径示意图汇总为图 11(此图代表一半纵骨的投影图 (沿纵骨厚度方向投影),x、y轴分别表示纵骨的底边和垂向中心线,图的顶线代表纵骨和面板的交界线,右端边线为纵骨垂向边缘)。
|
| 图10 典型Ⅰ-Ⅱ复合型裂纹扩展 Figure 10 Typical mixed-mode Ⅰ-Ⅱ crack propagation |
|
| 图11 不同位置的裂纹扩展路径 Figure 11 Crack propagation path for multiple locations |
其中,距离纵骨垂向中心线较远的0.275 m处的裂纹,在整个载荷作用历程中,裂尖最大主应力未达到80 MPa,因此未发生起裂。各个位置裂纹的起裂时间见表 2。
| 裂纹位置/m | 起裂时间/ms |
| 0.024 | 0.457 |
| 0.052 | 0.465 |
| 0.075 | 0.472 |
| 0.099 | 0.478 |
| 0.124 | 0.492 |
| 0.151 | 0.515 |
| 0.175 | 0.545 |
| 0.199 | 0.592 |
| 0.226 | 0.695 |
| 0.251 | 0.894 |
| 0.275 | - |
综上所述,低温环境下位于加筋板骨材上的初始裂纹在外部横向冲击载荷作用下会迅速地扩展至面板,引起面板的断裂,在实际船舶与海洋结构物中表现为结构外板的断裂。这不仅会使结构承载力下降,还会造成外部海水涌入或者内部液体泄漏等灾难性事件。因此应经常检测外板内部的加强结构上是否存在裂纹 (尤其是低温服役环境下的军舰和破冰船),并在裂纹扩展路径或最终断裂位置上采取相应的措施修复和制止裂纹扩展,以确保构件的完整性和连续性。
4 结论本文方法适于解决低温冲击作用下加筋板骨材的动态裂纹扩展问题,可以有效的预测裂纹发展路径和最终引起面板断裂的位置,为实施裂纹修补和止裂提供指导。
1) 纵骨Ⅰ型裂纹扩展中,温度降低,材料断裂减小,裂尖张开位移速度加快,裂纹扩展速度加快,即结构抵抗裂纹扩展能力减弱。
2) 同一位置不同初始长度裂纹的Ⅰ-Ⅱ复合型扩展中,初始裂纹越长,裂纹起裂时间越早,裂纹路径的整体倾斜度 (裂纹扩展路径和裂尖初始方向的夹角) 越小,扩展到面板时的位置离纵骨中心越远。
3) 纵骨垂向中心线以外,不同位置同一初始长度裂纹的Ⅰ-Ⅱ复合型扩展中,裂纹离纵骨中心越远,扩展路径的整体倾斜度越大,起裂时间越晚,即越不容易起裂。
| [1] |
王元清, 林云, 张延年, 等. 高强度钢材Q460C低温力学性能试验[J].
沈阳建筑大学学报:自然科学版, 2011, 27(4): 646–652.
WANG Yuanqin, LIN Yun, ZHANG Yannian, et al. Experimental study on the mechanical properties of Q460C the high strength construction steel at low temperature[J]. Journal of Shenyang Jianzhu University:natural science, 2011, 27(4): 646–652. |
| [2] |
郑学祥.
船舶及海洋工程结构的断裂与疲劳分析[M]. 海洋出版社, 1988.
ZHENG Xuexiang. Fracture and fatigue analysis of s-hip and ocean engineering structures[M]. China oceanpress, 1988. |
| [3] | SHAHANI A R, FASAKHODI M R A. Finite element analysis of dynamic crack propagation using remeshing technique[J]. Materials & design, 2009, 30(4): 1032–1041. |
| [4] | SU X, YANG Z, LIU G. Finite element mod-elling of complex 3D static and dyna-mic crack propagation by embedding c-ohesive elements in abaqus[J]. Acta mechanica solida sinica, 2010, 23(3): 271–282. DOI:10.1016/S0894-9166(10)60030-4 |
| [5] | GRÉGOIRE D, MAIGRE H, RÉTHORÉ J, et al. Dynamic crack propagation under mixed-mode loading-comparison between experiments and XFEM simulati-ons[J]. International journal of solids & structures, 2007, 44(20): 6517–6534. |
| [6] | LEE S, MARTIN D. Application of XFEM to model stationary crack and crack propagation for pressure containing sub-seaequipment[C]//Proceedings of the ASME Pressure Vessels and Piping Conference, Vancouver, Canada, 2016, 63199. |
| [7] | DIMITRI R, FANTUZZI N, LI Y, et al. Numerical computation of the crack development and SIF in composite materials with XFEM and SFEM[J]. Composite structures, 2017, 160(3): 468–490. |
| [8] | MOЁS N, DOLBOW J, BELYTSCHKO T. A finite element method for crack growth without remeshing[J]. International journal for numerical methods in engineering, 1999, 46(1): 131–150. DOI:10.1002/(ISSN)1097-0207 |
| [9] | MOЁS N, BELYTSCHKO T. Extended finite element method for cohesive crack growth[J]. Engineering fracture mechanics, 2002, 69(7): 813–833. DOI:10.1016/S0013-7944(01)00128-X |
| [10] | MELENK J M, BABUŠKA I. The partition of unity finite element method:Basic theory and applications[J]. Computer methods in applied mechanics & engineering, 1996, 139(s 1-4): 289–314. |
| [11] | KHOEI A R. Extended finite element method:theory and applications[M].[S.l.]:John Wiley & Sons Inc, 2015. |
| [12] | HILLERBORG A, MODÉER M, PETERSSON P E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J]. Cement & concrete research, 1976, 6(6): 773–781. |



