2. 石家庄铁道大学 河北省大型结构健康诊断与控制重点实验室, 河北 石家庄 050043;
3. 河北省减隔震技术与装置工程技术研究中心, 河北 衡水 053000
2. Key Laboratory of Structural Health Monitoring and Control, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;
3. Hebei Engineering Technology Research Center of Seismic Isolation Technology and Equipment, Hengshui 053000, China
对于大型复杂结构、超出抗震设计规范规定的结构和使用新型材料的结构,需要通过结构试验才能准确把握其抗震性能。传统的结构抗震试验可以分为拟静力、拟动力和振动台试验。拟动力试验通过计算机数值模拟和物理加载试验的有效结合,可以慢速再现大比例模型(或足尺)结构在地震作用下的弹性-弹塑性-倒塌全过程反应,克服了拟静力和振动台试验方法的不足,具有良好发展前途和广泛应用前景[1]。由于结构控制技术的发展, 出现了与时间过程相关(如反馈控制的主动、半主动控制装置或TMD、TLD等)的控制装置,慢速的拟动力子结构实验测试无法反映这些时间相关的控制装置的性能或减振效果。基于这一难题,Nakashima等[2]于1992年在拟动力试验的基础上提出了实时子结构实验方法,该试验方法将结构分为数值子结构和试验子结构,将与速度、加速度相关且呈现复杂非线性的结构部分作为试验子结构,由真实试验模拟;结构其余部分作为数值子结构,由计算机模拟,通过作动器或振动台等加载装置的实时加载来使得两者在交接处变形协调、受力平衡。随着结构控制技术日益广泛地应用于工程实践,实时子结构实验吸引了越来越多学者的关注。
1 实时子结构试验方法的研究现状由于试件性能的速度相关性和试验加载的实时性,实时子结构试验在积分算法、加载控制方面比常规拟动力试验更复杂,同时也产生系统时滞等问题。
在常规拟动力或常规子结构试验中,显式积分方法只需下一时间步位移的显式表达;而实时子结构试验的显式积分方法还要求下一时间步速度的显式表达,因此导致常规拟动力试验中的显式算法在实时子结构试验方法中转变为隐式算法。2005年Wu等[3]基于常规拟动力试验的中心差分法,用位移的向前差分确定下一步速度,形成了实时子结构中心差分法,但这种方法比标准中心差分法的稳定性低,并且稳定性随试件阻尼的增加而降低。事实上,在将实时子结构试验的积分方法由隐式格式转化为显式格式方面,诸多学者进行了大量研究[4-9],但均存在一个问题:发展而来的实时子结构积分方法的稳定性较原方法低,且多为条件稳定,这难以满足自由度数目多、高阶自振频率高的大型复杂结构对于数值算法稳定性的要求。因此,寻求效率高、稳定性好的数值积分方法是目前实时子结构试验技术的研究方向之一。
时滞效应的补偿是实时子结构试验需要解决的另一个重要问题。时滞是指发送给液压伺服作动器信号和作动器到达指定位移之间的时间滞后。由于拟动力实验并不要求实时加载,时滞对实验的影响并不明显;但是实时子结构实验对加载的实时性要求很高,这使得时滞对实验结果的影响较大。Horiuchi等[10]认为时滞的影响可以看作结构的附加负阻尼,当负阻尼大于结构本身阻尼时,实验将失去稳定,即实验结果发散。Wallace等[11]确定了临界时滞的计算方法。Darby等[12]提出了一种能准确估计线性系统试件时滞的方法。吴斌等[13-14]分析了采用OS算法和中心差分法的时滞及立方外插补偿对实验稳定性的影响。实时子结构实验的时滞影响及其补偿方法仍有待进一步研究[15]。
可以看出,目前数值积分算法和加载系统的时滞问题是实时子结构试验技术所遇到的难题,直接针对这些难题研究其解决办法是其中的一条途径,也是目前大量学者正在进行的工作。但是发展实时子结构试验的另外途径,使其能够避开前述难题也是极其有意义的,本文拟在这方面进行一些探索。
2 全局迭代(global iteration)的实时子结构试验方法的原理为避开实时子结构试验理论方法和试验技术的瓶颈,本文提出全局迭代的实时子结构试验方法。不同于传统实时子结构试验中计算机数值计算部分在每一时间步均从子结构的伺服加载试验中获取反应,全局迭代实时子结构试验方法的数值计算和伺服加载系统分别在整个地震作用时间段内独立地进行计算或加载,它们之间传递整个地震作用时间内的子结构位移反应或恢复力时程,并以试验子结构的位移或力反应进行迭代收敛的判断。这种方法将实时子结构试验方法中的数值计算和伺服加载试验分为两个相对独立的部分,中间时间步不存在数据交互,避免了数值计算的稳定性和伺服加载时滞问题,其缺点是对子结构需进行多次伺服加载试验。
与传统实时子结构试验方法相同,全局迭代的实时子结构试验方法仍然选择地震作用下的薄弱部位、恢复力具有复杂非线性特征的部位或构件作为试验子结构,通过动力加载试验直接获取其恢复力;恢复力处于弹性或容易确定的构件作为计算子结构,通过数值计算进行模拟。
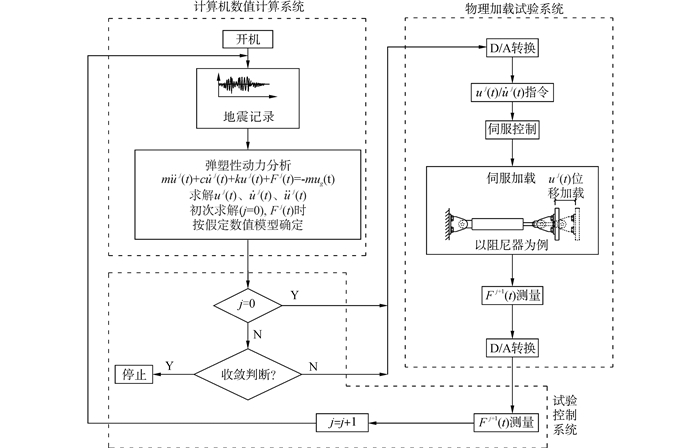
为使数值计算部分所采用的试验子结构的位移响应时程与其试验的恢复力相匹配,需进行迭代。以阻尼器为例,全局迭代的实时子结构试验方法的求解流程图如图 1。
图 1中,üg(t)是地震动时程,t∈[0, T],T是地震持续时间。uj(t)、
上述方法的迭代过程以整个地震持续时间为单位进行,这是“全局迭代”的由来。
图 1所示迭代过程通过比较两次迭代的位移时程uj(t)、uj+1(t)的差别。由于物理加载试验系统的位移控制和传感器的精度限制,在位移时程的较小值的区段,其相对误差较大,不能真实反映实际差别。因此采用各个时间点的相对误差作为收敛判断准则是不合适的。本文选择整个作用时间段[0, T]内的相对面积误差ε作为收敛判断准则:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\varepsilon = \\ \frac{{\int\limits_0^T {\left| {{u^{j + 1}}\left( t \right) - {u^j}\left( t \right)} \right|{\rm{d}}t} }}{{\int\limits_0^T {\left| {{u^j}\left( t \right){\rm{d}}t} \right|} }} \approx \frac{{\sum\limits_{t = \Delta t}^T {\left| {{u^{j + 1}}\left( t \right) - {u^j}\left( t \right)} \right|} }}{{\sum\limits_{t = \Delta t}^T {\left| {{u^j}\left( t \right)} \right|} }} \le {\varepsilon _0} \end{array} $ | (1) |
|
| 图1 全局迭代的实时子结构试验方法的求解流程图 Figure 1 Flow chart of global iteration real-time sub-structure test |
从下文的验证算例可以看出,收敛控制限值取2%时,位移时程可以判断为收敛,能够满足工程精度要求,因此本文取ε0=2%。
全局迭代的实时子结构试验的求解流程如下:
1) 计算机进行初始数值计算。
① 假定物理试验子结构的恢复力数值模型及参数;
② 根据假定的恢复力数值模型及参数,计算整个结构在地震作用时间内的反应,得到试验子结构的初始相对变形时程u0(t)和速度时程
2) 伺服加载系统进行第j次整个地震作用时间内的连续加载。
① 以计算机数值计算得到的试验子结构的相对变形uj-1(t)和相对速度
② 获取试验子结构的恢复力Fj(t)时程(t∈[0, T]),并将其传递给数值计算计算机。
3) 计算机数值计算部分进行第j+1次整个地震作用时间内的连续计算。
① 反应分析计算机根据物理加载试验得到的试验子结构的恢复力时程Fj(t)计算结构在整个地震作用时间内的反应。
② 提取试验子结构的相对变形时程uj+1(t)和速度时程
4) 全局迭代拟动力试验系统进行收敛性判断。
① 根据第j次和第j+1次数值计算得到的试验子结构的相对变形uj(t)和uj+1(t)判断收敛性,收敛性判断采用式(1)所示准则,若收敛,转至步骤5;若不收敛,转至下一步;
② 若j≥N, 迭代次数超过上限值N, 转至步骤6,否则转至下一步;
③ 用j+1代替j,进行下一次迭代求解,重复步骤2、3和4;
5) 全局迭代的实时子结构试验求解收敛,获取相应的结构反应,试验结束。
6) 求解不收敛,结束。
迭代次数超过上限值N,求解不收敛,结束。
从以上求解流程可以看出,本文提出的全局迭代的实时子结构试验方法中,除初始数值计算外,试验子结构的恢复力时程Fj(t)(t∈[0, T], j≥1)均采用物理试验的结果,仅是时间t的函数,与数值计算过程中的位移、速度等结果无直接关系。
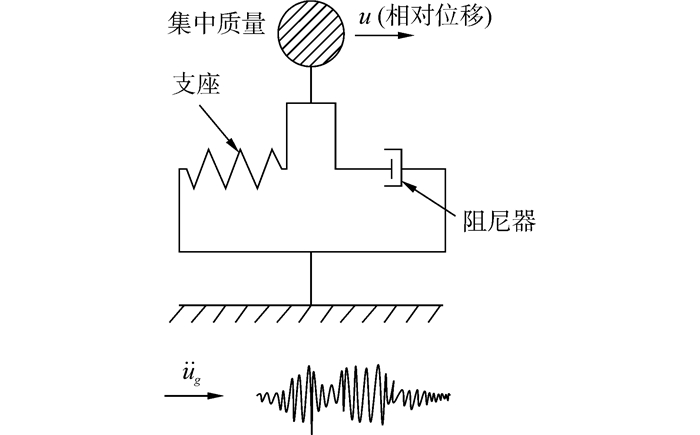
3 验证为验证上述试验方法,以高速铁路32 m常用跨径简支梁桥的简化模型为例进行计算,主梁采用双线整体无砟轨道箱梁,包括轨道结构和附属设施在内的上部结构总质量约为1 500 t,由四个支座支承,每个支座承担375 t。顺桥向采用盆式滑动支座与粘滞阻尼器组合的减隔震系统。
桥墩在顺桥向的刚度比支座的大很多,因此忽略桥墩的柔性。上述结构顺桥向地震反应计算模型可简化为图 2所示的单自由度体系,主梁简化为集中质量m=3.75×105 kg,相对于地面的位移记为u。支座采用理想弹塑性的非线性单元模拟,摩擦系数μ=0.01,屈服力Fy=36.77 kN,屈服位移Dy=0.003 m,初始刚度ke=1.226×104 kN/m,为避免数值计算的困难,屈服后刚度取为初始刚度的0.001倍;阻尼器速度指数α0=0.35,阻尼系数c0=35 kN·(s/m)α0。
|
| 图2 简化的单自由度模型 Figure 2 Simplified model of single degree of freedom |
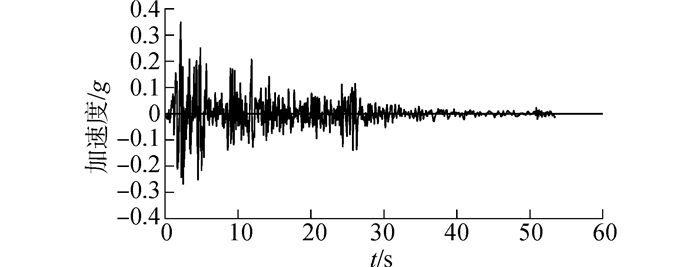
选择ElCentro波作为上述单自由度结构的水平地震动输入,如图 3所示。
|
| 图3 ElCentro地震波 Figure 3 ElCentro Ground motion record |
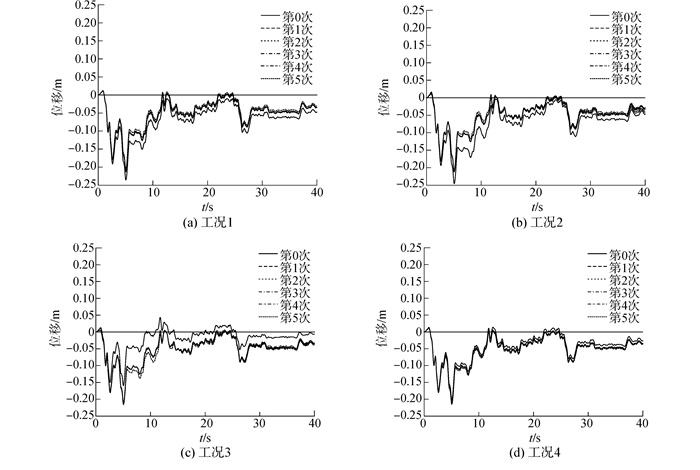
以粘滞阻尼器为试验子结构,其余部分进行数值计算模拟。假设初始数值计算时对阻尼器力学参数α和c的估计存在误差,误差大小为50%,存在四种可能的工况,如表 1所示。
| 工况 | 1 | 2 | 3 | 4 |
| 阻尼系数c | 0.5c0 | 0.5c0 | 1.5c0 | 1.5c0 |
| 阻尼器速度指数α | 0.5α0 | 1.5α0 | 0.5α0 | 1.5α0 |
每一工况,根据阻尼器恢复力数值模型,计算整个结构在地震作用时间内的初始反应,得到试验子结构的相对变形时程u0(t)和速度时程
|
| 图4 四种工况各次迭代的位移时程图 Figure 4 Displacement time history of each iteration of four cases |
用所示收敛判断准则计算四种工况各次迭代的收敛判断指标ε,如表 2所示。
| % | ||||
| 工况 | 1 | 2 | 3 | 4 |
| 第1次迭代 | 29.87 | 32.54 | 154.90 | 24.07 |
| 第2次迭代 | 12.27 | 13.03 | 12.03 | 6.53 |
| 第3次迭代 | 3.43 | 5.90 | 5.78 | 1.92 |
| 第4次迭代 | 1.14 | 2.60 | 2.83 | 0.63 |
| 第5次迭代 | 0.28 | 1.07 | 1.61 | 0.23 |
从表 2可以看出,对于四种工况,随着迭代的进行,试验子结构位移反应的相对面积误差ε的取值趋于减小,试验反应趋于收敛。不同工况的收敛速度不相同,但经过5次迭代之后,ε均小于2%,满足工程精度要求。
式(1)所列收敛准则比较了两次迭代的位移收敛情况。理论上,一般工程结构的位移趋于收敛时,结构其他反应指标(如速度、加速度等)也趋于收敛。以工况1为例,将其各次迭代的速度和加速度时程代入式(1)计算相应的相对面积误差,列于表 3。
| % | |||
| 反应指标 | 位移 | 速度 | 加速度 |
| 第1次迭代 | 29.87 | 5.38 | 2.03 |
| 第2次迭代 | 12.27 | 2.01 | 0.82 |
| 第3次迭代 | 3.43 | 0.85 | 0.42 |
| 第4次迭代 | 1.14 | 0.43 | 0.23 |
| 第5次迭代 | 0.28 | 0.20 | 0.12 |
从表 3中各反应的相对面积误差可以看出,各次迭代中位移、速度和加速度的收敛指标值具有相同的收敛趋势。这说明本文算例中,位移的收敛指标能够反映速度、加速度等反应的收敛情况。对于其他复杂结构,可进一步研究其他收敛指标(如平衡的或能量的收敛指标)的适用性。
以上算例表明,本文所提出的全局迭代的实时子结构试验方法是可行的,达到相对面积误差ε < 2%所需要的迭代次数不超过5次,可以接受。
4 迭代次数敏感性分析上文比较了数值模型参数初始估计的误差为50%的四种工况,为分析误差大小对收敛次数的影响,进一步计算两种工况:工况5和工况6,数值模型参数初始估计的误差分别为25%、75%。粘滞阻尼器速度指数α和阻尼系数c的误差变化关系与工况3对应,将这三种工况列于表 4。将上述三种工况各次迭代的收敛判断指标ε值列于表 5。
| % | |||
| 工况 | 5 | 3 | 6 |
| 阻尼系数c | 1.25c0 | 1.5c0 | 1.75c0 |
| 阻尼器速度指数α | 0.75α0 | 0.5α0 | 0.25α0 |
| % | |||
| 工况 | 5 | 3 | 6 |
| 第1次迭代 | 27.98 | 154.90 | 278.04 |
| 第2次迭代 | 7.89 | 12.03 | 24.25 |
| 第3次迭代 | 3.89 | 5.78 | 7.65 |
| 第4次迭代 | 1.32 | 2.83 | 3.08 |
| 第5次迭代 | 0.69 | 1.61 | 1.80 |
从表 5可以看出,初始参数的估计误差越小,迭代收敛的速度越快,收敛判断指标取值达到限值所需要的迭代次数越少。
5 方法适用性的讨论本文所提方法虽然能够避开传统实时子结构试验方法存在的数值积分稳定性和伺服加载时滞等难题,但是引入了一个迭代过程,需要对子结构进行多次伺服加载试验,因此本文方法的适用性是一个值得关注的问题。本文方法适用范围:
1) 特别适用于阻尼器作为试验子结构的情况。由于阻尼器可以重复利用,间隔一定时间后(需要等待粘滞液体温度下降),后续试验结果不受前次试验的影响,只需准备一个试验用阻尼器就能满足迭代需求,可以节约试验成本。
2) 适用于各个试验子结构的实物模型变异性较小的情况。对于对结构性能起控制作用的关键构件或复杂构件(如弹塑性支座、梁柱节点、墩柱塑性铰区域等),其在试验中将发生不可逆的弹塑性变形甚至破坏,因此需要制作多个变异性较小的模型,以满足迭代的需要。这就要求各试验模型的几何尺寸和材料特性等的差异较小。一般来说,只需对试件制作工艺稍加控制就能满足要求,如支座采用同批次生产加工、混凝土构件采用相同的工人师傅加工并进行同批次混凝土浇筑等。
按相同设计图纸和加工工艺生产的试验子结构的力学行为的可能存在变异,这种变异性对于本文方法迭代过程的稳定性、迭代次数和收敛控制指标可能存在影响,这一问题有待在进一步的工作中验证和研究。
6 结论传统实时子结构试验方法存在数值积分稳定性和伺服加载时滞等问题,为避开这些难题,本文探索了另一种实时子结构试验的途径,取得以下成果:
1) 提出全局迭代的实时子结构试验方法的概念和基本流程,并给出了收敛判断准则;
2) 通过算例对所提方法进行验证。结果表明,在数值模型参数初始估计的误差为50%的四种工况下,随着迭代进行,试验子结构位移反应的相对面积误差ε的取值趋于减小,试验反应趋于收敛。不同工况收敛速度不相同,但经过5次迭代后,ε均小于2%,满足工程精度要求,迭代次数可以接受。
3) 分析了数值模型参数初始估计误差对迭代次数的影响。比较了误差分别为25%、50%、75%三种工况时的迭代收敛情况,结果表明初始参数的估计误差越小,迭代收敛的速度越快,达到收敛限值所需要的迭代次数越少。
4) 对所提方法的适用性进行了初步讨论。
将本文方法应用于更多实际结构,对其做进一步理论及试验的验证和改进,是有待完成的工作。
| [1] |
倪志伟, 纪金豹, 杜阳阳. 拟动力试验方法的发展与展望[J].
灾害学, 2010, 25(S): 79–84.
NI Zhiwei, JI Jinbao, DU Yangyang. Development and prospect of pseudo-dynamic testing[J]. Journal of catastrophology, 2010, 25(S): 79–84. |
| [2] | NAKASHIMA M, KATO H, TAKAOKA E. Development of real-time pseudo dynamic testing[J]. Earthquake engineering & structural dynamics, 1992, 21(1): 79–92. |
| [3] | WU B, BAO H, OU J, et al. Stability and accuracy analysis of the central difference method for real-time substructure testing[J]. Earthquake engineering & structural dynamics, 2005, 34(7): 705–718. |
| [4] | CHANG S Y. Explicit pseudodynamic algorithm with unconditional stability[J]. Journal of engineering mechanics, 2002, 128(9): 935–947. DOI:10.1061/(ASCE)0733-9399(2002)128:9(935) |
| [5] |
吴斌, 保海娥. 实时子结构实验Chang算法的稳定性和精度[J].
地震工程与工程振动, 2006, 26(2): 41–48.
WU Bin, BAO Hai'e. Stability and accuracy of Chang algorithm for real-time substructure testing[J]. Earthquake engineering and engineering vibration, 2006, 26(2): 41–48. |
| [6] | ZHANG Yunfeng, SAUSE R, RICLES J M, et al. Modified predictor-corrector numerical scheme for real-time pseudo dynamic tests using state-space formulation[J]. Earthquake engineering & structural dynamics, 2005, 34(3): 271–288. |
| [7] | JUNG R Y, BENSON SHING P. Performance evaluation of a real-time pseudodynamic test system[J]. Earthquake engineering & structural dynamics, 2006, 35(7): 789–810. |
| [8] | BAYER V, DORKA U E, FVLLEKRUG U, et al. On real-time pseudo-dynamic sub-structure testing: algorithm, numerical and experimental results[J]. Aerospace science and technology, 2005, 9(3): 223–232. DOI:10.1016/j.ast.2005.01.009 |
| [9] | DARBY A P, BLAKEBOROUGH A, WILLIAMS M S. Improved control algorithm for real-time substructure testing[J]. Earthquake engineering & structural dynamics, 2001, 30(3): 431–448. |
| [10] | HORIUCHI T, INOUE M, KONNO T, et al. Real-time hybrid experimental system with actuator delay compensation and its application to a piping system with energy absorber[J]. Earthquake engineering & structural dynamics, 1999, 28(10): 1121–1141. |
| [11] | WALLACE M I, SIEBER J, NEILD S A, et al. Stability analysis of real-time dynamic substructuring using delay differential equation models[J]. Earthquake engineering & structural dynamics, 2005, 34(15): 1817–1832. |
| [12] | DARBY A P, WILLIAMS M S, BLAKEBOROUGH A. Stability and delay compensation for real-time substructure testing[J]. Journal of engineering mechanics, 2002, 128(12): 1276–1284. DOI:10.1061/(ASCE)0733-9399(2002)128:12(1276) |
| [13] | WU Bin, XU Guoshan, WANG Qianying, et al. Operator-splitting method for real-time substructure testing[J]. Earthquake engineering & structural dynamics, 2006, 35(3): 293–314. |
| [14] |
王倩颖, 吴斌, 欧进萍. 考虑作动器时滞及其补偿的实时子结构实验稳定性分析[J].
工程力学, 2007, 24(2): 9–14, 8.
WANG Qianying, WU Bin, OU Jinping. Stability analysis of real-time substructure testing considering actuator delay and compensation[J]. Engineering mechanics, 2007, 24(2): 9–14, 8. |
| [15] | WU Bin, WANG Qianying, BENSON S P, et al. Equivalent force control method for generalized real-time substructure testing with implicit integration[J]. Earthquake engineering & structural dynamics, 2007, 36(9): 1127–1149. |



