2. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001
2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
海洋环境噪声是海洋信道中的背景声场,任何声呐系统的设计和使用都要受到海洋环境噪声的影响。只有充分了解海洋环境噪声场的特性,才能合理设计与布放接收设备以及选择合适的信号处理方法,从而降低海洋环境噪声对水下设备的干扰,最大限度提高水下设备的性能[1]。此外,海洋噪声本身包含了水体、海面以及海底等环境特征信息,所以可以利用海洋环境噪声特性来反演海洋声学参数[2-5]。因此研究海洋环境噪声场的特性对水下探测以及海洋开发等活动都有着积极的意义。
海洋环境噪声模型是在噪声源研究基础上结合波导传播特性发展起来的,Cron最早于20世纪60年代开始了环境噪声模型的研究[6],该噪声模型采用的传播模型较为简单,没有考虑边界的影响,因此只适用于深海情形。各国学者后续对噪声预报模型进行了不断的改进[7-10],一方面,对噪声源的特性研究更加深入;另一方面,选取的声传播模型更加复杂,所以能处理的波导环境更加复杂。但是绝大部分噪声预报模型在处理噪声传播时都将海面当做绝对软边界处理,没有考虑海面粗糙度对噪声传播特性的影响。实际上,海面起伏会造成声波向各个方向散射,引起声波在传输过程中能量的衰减,尤其是对于正声速梯度波导,这种影响更加明显[11-15]。但尚未有文献对波浪起伏下噪声场空间进行研究。基于此,本文对这一问题展开研究。
一般认为风成噪声频段主要集中在500~30 000 Hz,实际上,在远离航道的浅海区域,海洋环境噪声在很宽的频带范围内(10~3 000 Hz)和风速都具有良好的相关性。Arasa等测量了不同海况下22~715 Hz频带范围的环境噪声,发现90 Hz以上噪声强度和风速相关性能够达到0.8以上[16]。Kewley[17]在南半球对30~800 Hz的噪声也进行了测量,当风速由5 m/s增加到20 m/s,100~800 Hz噪声强度普遍增加了约20 dB。这些研究都表明,低频噪声场也会显著受海面风速的影响。这里主要考虑海面起伏对低频噪声场空间特性的影响。首先,通过引进PM波浪谱模型[18]来描述海面粗糙度,基于小斜率近似方法[19]求解二维粗糙度谱下海面相干反射系数,并将海面反射损失引入到声传播模型中[20-21],求解出粗糙海面下声场本征值和本征函数;然后基于简正波理论给出了各向均匀与各向非均匀粗糙界面下噪声场空间特性预报模型;最后仿真分析了海面起伏对噪声场强度以及相关性的影响,并对结果进行了分析和总结。
1 波浪起伏海面下声传播模型声波入射到不平整界面上,除了向镜方向反射外,还会向其他方向上散射。当波浪起伏高度和声波波长比值较小时,能量主要都集中在镜反射方向,此时可以通过求解粗糙海面相干反射系数,并在声传播计算中予以考虑[12-15, 18-20],从而可以对粗糙界面下声场进行预报。所以求解粗糙界面下声传播问题的关键就在于求解粗糙海面的相干反射系数。
计算粗糙面声散射的方法有很多,如积分方法[22]、Kirchhoff近似[23]、微扰法[24]和小斜率近似方法等。其中积分方程方法给出了解析解,但是其计算量较大,一般作为其他近似方法准确性检验标准;Kirchhoff近似和微扰法是常用的研究方法,但是这两种方法有各自的适用范围,具有较大的局限性。而小斜率近似方法因为不用考虑粗糙面结构且求解精度较高,成为适用性较强的一种声散射预报模型。文献[19]对用小斜率近似来求解相干反射系数方法进行简单介绍。
考虑一维声散射,那么传递矩阵T可以写成
| $ \left\langle {\mathit{\boldsymbol{T}}\left\langle {{\mathit{\boldsymbol{k}}_{sx}},{\mathit{\boldsymbol{k}}_{ix}}} \right\rangle } \right\rangle = {\mathit{\boldsymbol{R}}_A}\left( {{\mathit{\boldsymbol{k}}_{ix}}} \right)\delta \left( {{\mathit{\boldsymbol{k}}_{ix}} - {\mathit{\boldsymbol{k}}_{sx}}} \right) $ | (1) |
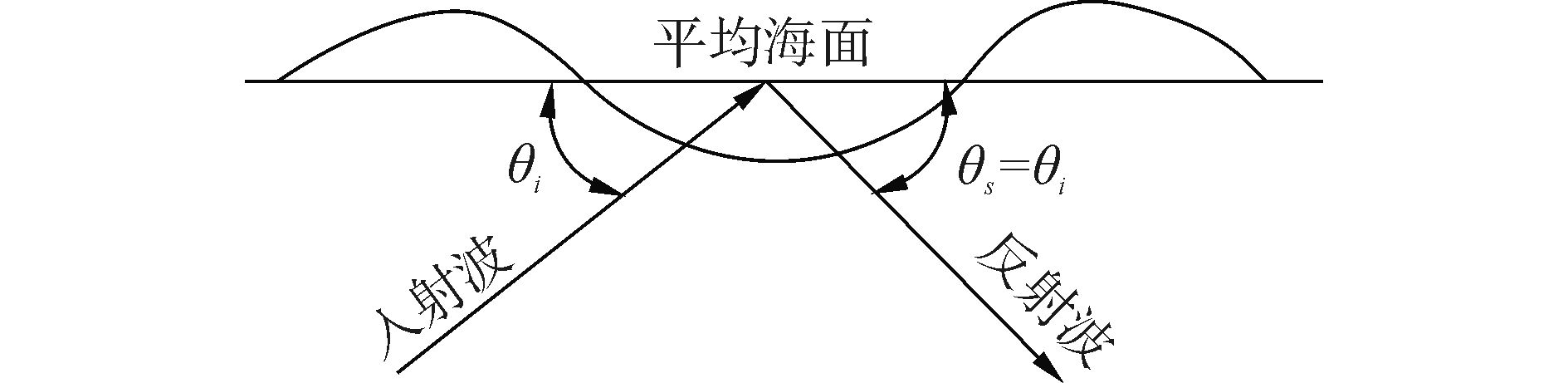
式中:RA为要求的相干反射系数,δ为单位脉冲函数,kix、ksx分别为入射波和散射波的水平波数,θi、θs分别为入射声波和镜向反射声波与平均海面之间的夹角(见图 1)。
|
图 1 一维随机粗糙表面散射几何模型 Fig.1 Scattering geometric model for one dimension random rough boundary |
用小斜率近似序列将传播矩阵展开并截取前两阶:
| $\left\langle \mathit{\boldsymbol{T}} \right\rangle = \left\langle {{\mathit{\boldsymbol{T}}_0}} \right\rangle + \left\langle {{\mathit{\boldsymbol{T}}_1}} \right\rangle $ | (2) |
其中:
| $\left\langle {{\mathit{\boldsymbol{T}}_0}} \right\rangle = - \exp \left[ { - \frac{{v_z^2{h^2}}}{2}} \right]\delta \left( {{k_{sx}} - {k_{ix}}} \right)$ | (3) |
| $\left\langle {{\mathit{\boldsymbol{T}}_1}} \right\rangle = {k_{iz}}\exp \left[ { - \frac{{v_z^2{h^2}}}{2}} \right]\delta \left( {{k_{sx}} - {k_{ix}}} \right)\int {{\rm{d}}KW\left( K \right)g\left( K \right)} $ | (4) |
其中:
| ${k_{iz}} = \sqrt {{k^2} - k_{ix}^2} ,{v_z} = {k_{iz}} + {k_{sz}}\\ g\left( K \right) = k{\beta _{i + 1}} + k{\beta _{s - 1}} - {v_z}\\ k{\beta _{i + 1}} = {\left[ {{k^2} - {{\left( {K + {k_{ix}}} \right)}^2}} \right]^{1/2}}{\mathop{\rm Im}\nolimits} \left( {{\beta _{i + 1}}} \right) > 0\\ k{\beta _{s - 1}} = {\left[ {{k^2} - {{\left( {{k_{sx}} - K} \right)}^2}} \right]^{1/2}}{\mathop{\rm Im}\nolimits} \left( {{\beta _{s - 1}}} \right) > 0$ |
式中:k为声波波数,W为一维海面粗糙度谱,h为海面波浪均方根波高。
将(3)、(4) 式代入到式(1),可以得到一维粗糙海面相干反射系数:
| ${R_A}\left( {{\theta _i}} \right) \approx \exp \left[ { - \frac{{v_z^2{h^2}}}{2}} \right]\left[ { - 1 + {k_{iz}}\int {{\rm{d}}KW\left( K \right)g\left( K \right)} } \right]$ | (5) |
式中:
由类似的过程可以得到二维粗糙界面下不同方位角
| $\begin{array}{l} {R_A}\left( {{\theta _i},{\varphi _i}} \right) \approx \exp \left[ { - 2k_{iz}^2{h^2}} \right]\left[ { - 1 - 2k_{iz}^2{h^2} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {2{k_{iz}}\int {W\left( \mathit{\boldsymbol{K}} \right)\sqrt {{k^2} - {{\left( {{\mathit{\boldsymbol{K}}_i} + \mathit{\boldsymbol{K}}} \right)}^2}} {\rm{d}}\mathit{\boldsymbol{K}}} } \right] \end{array}$ | (6) |
式中:θi、
| $\begin{gathered} {R_A}\left( {{\theta _i},{\varphi _i}} \right) \approx \exp \left( { - 2k_{iz}^2{h^2}} \right)\left[ { - 1 - 2k_{iz}^2{h^2} + } \right. \hfill \\ \;\;\;\;\;2k{k_{iz}}\iint {W\left( {K,\alpha } \right)\left[ {{{\sin }^2}{\theta _0} + 2\left( {K/h} \right) \times \cos {\theta _0} \times } \right.} \hfill \\ \;\;\;\;\;\;\left. {\left. {{{\left. {\cos \left( {\alpha - {\varphi _0}} \right) - {{\left( {K/k} \right)}^2}} \right]}^{1/2}}K{\text{d}}K{\text{d}}\alpha } \right]} \right] \hfill \\ \end{gathered} $ | (7) |
式中:RA
关于风浪谱的研究已经有很多,这里选择Pierson-Moskowitz风浪谱来描述海面粗糙度。P-M频谱S(ω)具有如下形式
| $S\left( \omega \right) = \frac{{{a_0}{g^2}}}{{{\omega ^5}}}\exp \left[ { - \beta {g^4}/{{\left( {\omega U} \right)}^4}} \right]$ | (8) |
式中:ω为表面重力波的频率;a0=8.1×10-3,b=0.74;g为重力加速度;U为海面上19.5 m高处的风速,m/s。深海重力波的频散关系具有如下形式
| ${\omega ^2} = gK$ | (9) |
风浪波数谱和频谱满足
| $\begin{array}{*{20}{c}} {W\left( K \right) = W\left( {K,\alpha } \right) = \sqrt {\frac{g}{{4{K^3}}}} S\left( {\sqrt {gK} } \right)\mathit{\Phi }\left( {K,\alpha } \right) = }\\ {\frac{{{a_0}}}{{2{K^4}}}\exp \left[ { - \beta {g^2}/\left( {{K^2}{U^4}} \right)} \right]\mathit{\Phi }\left( {K,\alpha } \right)} \end{array}$ | (10) |
式中:Φ(K, α)为方向分布函数,α为波数K对应的方向角,为了简化表达。一般定义逆风时α=0°,侧风时α=90°,主波浪方向为逆风方向。Φ(K, α)满足:
| $\int_{ - {\rm{\pi }}}^{\rm{\pi }} {\mathit{\Phi }\left( {K,\alpha } \right){\rm{d}}\alpha } = 1$ | (11) |
当Φ(K, α)为常数时,W(K)表示的是各向同性波数谱,也即各个方向海面粗糙度完全相同,其表达式为
| $W\left( K \right) = \frac{{{a_1}}}{{{K^4}}}\exp \left[ { - \beta {g^2}/\left( {{K^2}{U^4}} \right)} \right]$ | (12) |
式中:a1=0.637 4。当Φ(K, α)不为常数时,W(K)表示的是非各向均匀波数谱。这里选取方向分布函数Φ(K, α)=cos2α/π。最终得到非各向均匀二维波浪波数谱:
| $W\left( {K,\alpha } \right) = \frac{{{a_2}}}{{{K^4}}}\exp \left[ { - \beta {g^2}/\left( {{K^2}{U^4}} \right)} \right]{\cos ^2}\alpha $ | (13) |
式中:a2=1.29×10-3。无论对于各向均匀还是非各向均匀波浪谱W(K)都满足:
将式(12)、(13) 分别代入到式(7),可以分别得到各向均匀与非各向均匀粗糙界面下平均反射系数。各向均匀波浪谱下不同方向上海面相干反射系数都相同,而非各向均匀粗糙度谱下海面相干反射系数和方位角有关。将海面平均反射系数考虑到声传播模型KRAKENC[19]中,就能得到粗糙起伏界面下声场本征值和本征函数。由简正波模型理论可知,简谐点源的声场可以表示成一系列简正波的叠加:
| $p\left( {r,{z_s},z} \right) = \sqrt {\frac{{2{\rm{\pi }}}}{r}} \sum\limits_{m = 1}^M {{\phi _m}\left( {{z_s}} \right){\phi _m}\left( z \right)\exp \left( {{\rm{i}}{k_m}r} \right)} $ | (14) |
式中:zs、z分别为声源深度和接收深度,r为接收点距离声源的水平距离,km、
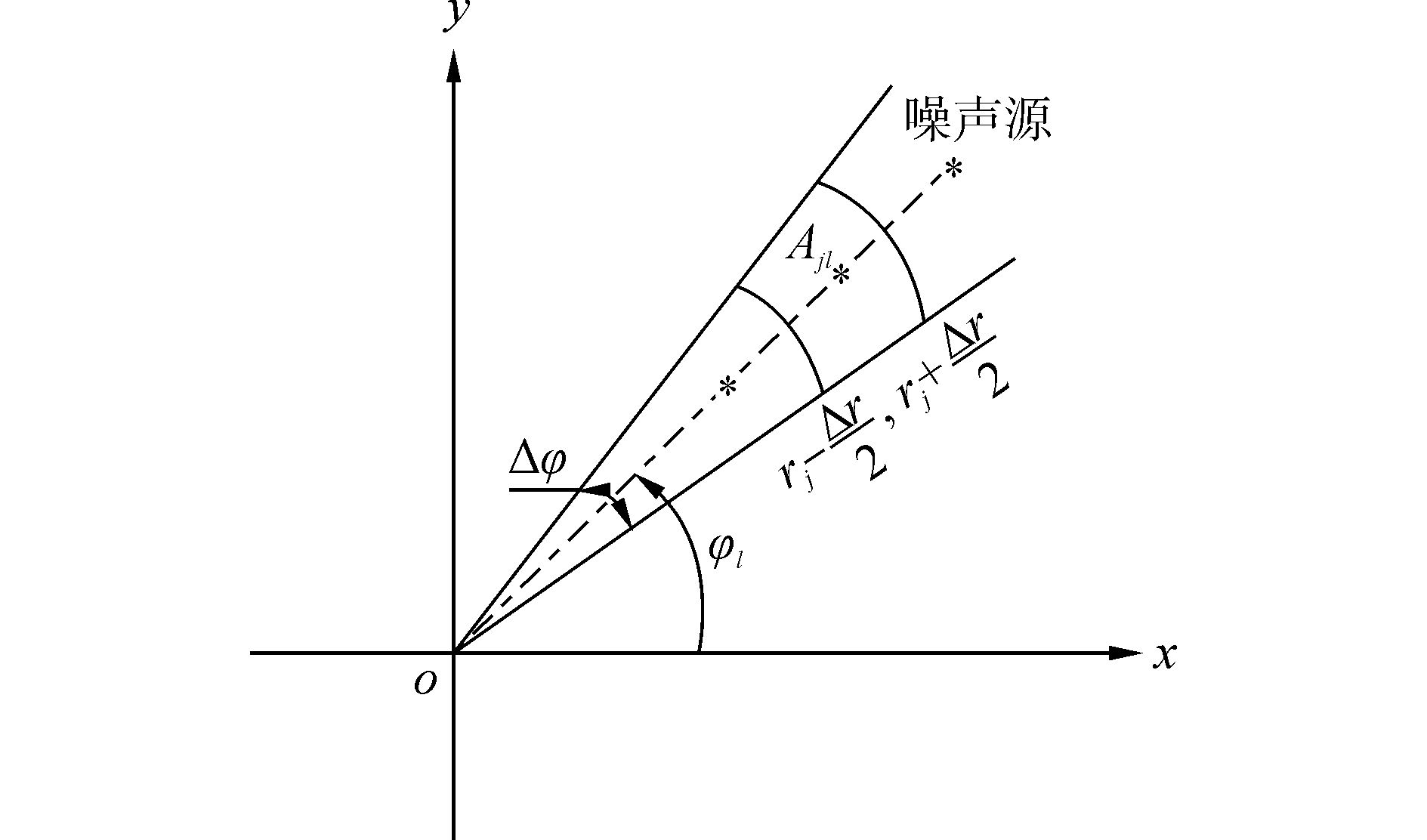
假设噪声源均匀分布在海面附近某一深度zs处,将噪声源平面按照图 2所示沿着半径方向和方位角方向进行均匀划分,第l个扇面与半径方向第j个区间段围成区域面积记为Ajl,由几何关系可知Ajl=rj
| $\begin{array}{*{20}{c}} {p\left( {{{\bar x}_n},{r_j},{z_s},{\varphi _l}} \right) = }\\ {\sqrt {2{\rm{\pi }}} \sum\limits_{m = 1}^M {{\varphi _{ml}}\left( {{z_s}} \right){\varphi _{ml}}\left( {{z_n}} \right)\frac{{\exp \left[ {{\rm{i}}{k_{ml}}\left( {{r_j} - {s_{nl}}} \right)} \right]}}{{\sqrt {{k_{ml}}\left( {{r_j} - {s_{nl}}} \right)} }}} } \end{array}$ | (15) |
|
图 2 噪声源平面划分示意图 Fig.2 Schematic diagram for dividing ambient noise source plane |
|
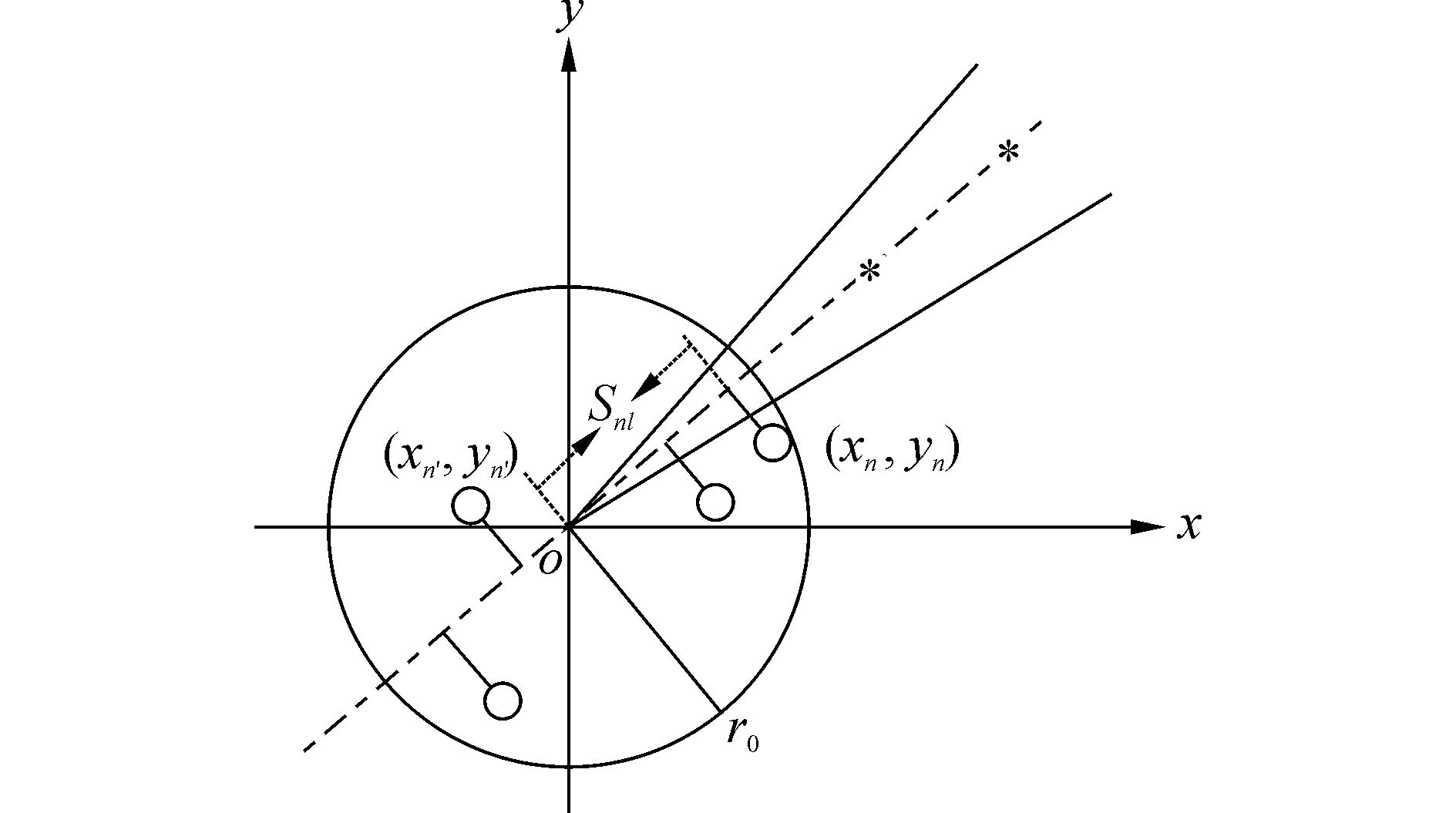
图 3 接收阵基元在xoy平面投影 Fig.3 The projection of receivers in the xoy plane |
式中:(rj-snl)表示Ajl区域内噪声源距离第n个接收基元的水平距离,kml、
所以整个界面所有噪声源在
| $\begin{array}{*{20}{c}} {{p_{{\rm{noise}}}}\left( {{{\bar x}_n}} \right) = }\\ {\sum\limits_{l = 1}^L {\exp \left( {{\rm{i}}{\psi _l}} \right)} \sum\limits_{j = 1}^J {\exp \left( {{\rm{i}}{\psi _j}} \right){I_{jl}}\sqrt {{A_{jl}}} p\left( {{{\bar x}_n},{r_j},{z_s},{\varphi _l}} \right)} } \end{array}$ | (16) |
式中:L和J分别为噪声源平面方位角和距离方向等分的份数。记空间
| $\begin{array}{l} {C_{nn'}} = \left\langle {{p_{{\rm{noise}}}}\left( {{{\bar x}_n}} \right)p_{{\rm{noise}}}^ * \left( {{{\bar x'}_n}} \right)} \right\rangle = \\ \sum\limits_{l = 1}^L {\sum\limits_{j = 1}^J {\sum\limits_{l' = 1}^L {\sum\limits_{j' = 1}^J {\exp \left[ {{\rm{i}}\left( {{\psi _l} - {\psi _{l'}}} \right)} \right]\exp \left[ {{\rm{i}}\left( {{\psi _j} - {\psi _j}} \right)} \right]} } } } \\ {I_{jl}}{I_{j'l'}}\sqrt {{A_{jl}}} \sqrt {{A_{j'l'}}} p\left( {{{\bar x}_n},{r_j},{z_s},{\varphi _l}} \right){p^ * }\left( {{{\bar x}_{n'}},{r_{j'}},{z_s},{\varphi _{l'}}} \right) \end{array}$ | (17) |
假设不同区域的噪声源不相关,则只有l=l′, j=j′这些项对应的项不为0,上式简化为
| $\begin{array}{l} {C_{nn'}} = \left\langle {{p_{{\rm{noise}}}}\left( {{{\bar x}_n}} \right)p_{{\rm{noise}}}^ * \left( {{{\bar x'}_n}} \right)} \right\rangle = \\ \sum\limits_{l = 1}^L {\sum\limits_{j = 1}^J {I_{jl}^2{A_{jl}}p\left( {{{\bar x}_n},{r_j},{z_s},{\varphi _l}} \right){p^ * }\left( {{{\bar x}_n},{r_j},{z_s},{\varphi _l}} \right)} } \end{array}$ | (18) |
将式(15) 代入到式(18),得到
| $\begin{array}{l} {C_{nn'}} = 2{\rm{\pi }}{I^2}\sum\limits_{l = 1}^L {\sum\limits_{j = 1}^J {\sum\limits_{m = 1}^M {\sum\limits_{m' = 1} {{r_j}\frac{{{\phi _{ml}}\left( {{z_s}} \right){\phi _{ml}}\left( {{z_n}} \right)}}{{\sqrt {{k_{ml}}\left( {{r_j} - {s_{nl}}} \right)} }} \times } } } } \\ \;\;\;\;\;\;\;\;\;\;\frac{{{\phi _{m'l}}\left( {{z_s}} \right){\phi _{m'l}}\left( {{{z'}_n}} \right)}}{{\sqrt {k_{m'l}^ * } \left( {{r_j} - {s_{n'l}}} \right)}}\left\{ {\Delta \phi \exp \left[ {{\rm{i}}\left( {k_{m'l}^ * {s_{n'l}} - } \right.} \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left. {\left. {{k_{ml}}{s_{nl}}} \right)} \right]} \right\} \times \left\{ {\Delta r\exp \left[ {{\rm{i}}\left( {{k_{ml}} - k_{m'l}^ * } \right){r_j}} \right]} \right\} \end{array}$ | (19) |
由于对于绝大部分噪声源都满足
| $\begin{array}{*{20}{c}} {{C_{nn'}} = 2{\rm{\pi }}{I^2}\sum\limits_{l = 1}^L {\sum\limits_{m = 1}^M {\frac{{\phi _{ml}^2\left( {{z_s}} \right){\phi _{ml}}\left( {{z_n}} \right){\phi _{ml}}\left( {{{z'}_n}} \right)}}{{\left| {{k_{ml}}} \right|}}} } \left\{ {\Delta r} \right.}\\ {\left. {\sum\limits_{j = 1}^J {\exp \left[ {{\rm{i}}\left( {{k_{ml}} - k_{m'l}^ * } \right){r_j}} \right]} } \right\}\left\{ {\Delta \varphi \exp \left[ {{\rm{i}}\left( {k_{ml}^ * {s_{n'l}} - {k_{ml}}{s_{nl}}} \right)} \right]} \right\}} \end{array}$ | (20) |
式中:第一个大括号中求和项可以用积分形式表示:
| $\begin{array}{*{20}{c}} {\int_{{r_0}}^{{r_J}} {\exp \left[ {{\rm{i}}\left( {{k_{ml}} - k_{m'l}^ * } \right)r} \right]{\rm{d}}r} = }\\ {\frac{{\exp \left[ {{\rm{i}}\left( {{k_{ml}} - k_{ml}^ * } \right){r_J}} \right] - \exp \left[ {{\rm{i}}\left( {{k_{ml}} - k_{ml}^ * } \right){r_0}} \right]}}{{{\rm{i}}\left( {{k_{ml}} - k_{ml}^ * } \right)}}} \end{array}$ | (21) |
式中:rJ为计算噪声源平面的最大距离。由于接收阵的水平尺寸相对于噪声源平面半径rJ非常小,当r0→0,rJ→∞时,上式简化为
| $\begin{array}{*{20}{c}} {{C_{nn'}} = \frac{{2{\rm{\pi }}{I^2}}}{2}\sum\limits_{l = 1}^L {\sum\limits_{m = 1}^M {\frac{{\varphi _{ml}^2\left( {{z_s}} \right){\varphi _{ml}}\left( {{z_n}} \right){\varphi _{ml}}\left( {{{z'}_n}} \right)}}{{\left| {{k_{ml}}} \right|{\mathop{\rm Im}\nolimits} \left( {{k_{ml}}} \right)}}} } \times }\\ {\left\{ {\Delta \varphi \exp \left[ {{\rm{i}}\left( {k_{ml}^ * {s_{n'l}} - {k_{ml}}{s_{nl}}} \right)} \right]} \right\}} \end{array}$ | (22) |
令
| $\left( {k_m^ * {s_{n'l}} - {k_m}{s_{nl}}} \right) = {\mathop{\rm Re}\nolimits} \left( {{k_{ml}}} \right){r_{nn'}}\cos \left( {{\beta _l} - {\gamma _{nn'}}} \right)$ | (23) |
当xn′=xn,yn′=yn
| $\Delta \varphi \exp \left[ {{\rm{i}}\left( {k_{ml}^ * {s_{n'l}} - {k_{ml}}{s_{nl}}} \right)} \right] = \Delta \varphi $ | (24) |
可以得到非各向均匀粗糙度谱下噪声场空间互谱密度函数表达式为
| $\begin{array}{l} {C_{nn'}} = \frac{{2{\rm{\pi }}{I^2}}}{2}\sum\limits_{l = 1}^L {\sum\limits_{m = 1}^M {\frac{{\varphi _{ml}^2\left( {{z_s}} \right){\varphi _{ml}}\left( {{z_n}} \right){\varphi _{ml}}\left( {{{z'}_n}} \right)}}{{\left| {{k_{ml}}} \right|{\mathop{\rm Im}\nolimits} \left( {{k_{ml}}} \right)}}} } \times \\ \;\;\;\;\;\;\;\;\;\left\{ {\Delta \varphi \exp \left[ {{\rm{i}}{\mathop{\rm Re}\nolimits} \left( {{k_{ml}}} \right){r_{nn'}}\cos \left( {{\beta _l} - {\gamma _{nn'}}} \right)} \right]} \right\} \end{array}$ | (25) |
对于各向均匀粗糙度谱,本征值和本征函数与方位角无关,式(25) 可以写成
| $\begin{array}{l} {C_{nn'}} = \frac{{2{\rm{\pi }}{I^2}}}{2}\sum\limits_{m = 1}^M {\frac{{\varphi _m^2\left( {{z_s}} \right){\varphi _m}\left( {{z_n}} \right){\varphi _m}\left( {{{z'}_n}} \right)}}{{\left| {{k_m}} \right|{\mathop{\rm Im}\nolimits} \left( {{k_m}} \right)}}} \\ \left\{ {\Delta \varphi \sum\limits_{l = 1}^L {\exp \left[ {{\rm{i}}{\mathop{\rm Re}\nolimits} \left( {{k_m}} \right){r_{nn'}}\cos \left( {{\beta _l} - {\gamma _{nn'}}} \right)} \right]} } \right\} \end{array}$ | (26) |
大括号项求和计算后等于2πJ0(Re(km)rnn′),则式(26) 最终简化成
| $\begin{array}{*{20}{c}} {{C_{nn'}} = }\\ {2{{\rm{\pi }}^2}{I^2}\sum\limits_{m = 1}^M {\frac{{\left| {{\phi _m}\left( {{z_s}} \right)} \right|_m^2\left( {{z_n}} \right){\phi _m}\left( {{{z'}_n}} \right)}}{{\left| {{k_m}} \right|{\mathop{\rm Im}\nolimits} \left( {{k_m}} \right)}}{J_0}\left( {{\mathop{\rm Re}\nolimits} \left( {{k_m}} \right){r_{nn'}}} \right)} } \end{array}$ | (27) |
式(27) 就是KI模型[8]表达式。
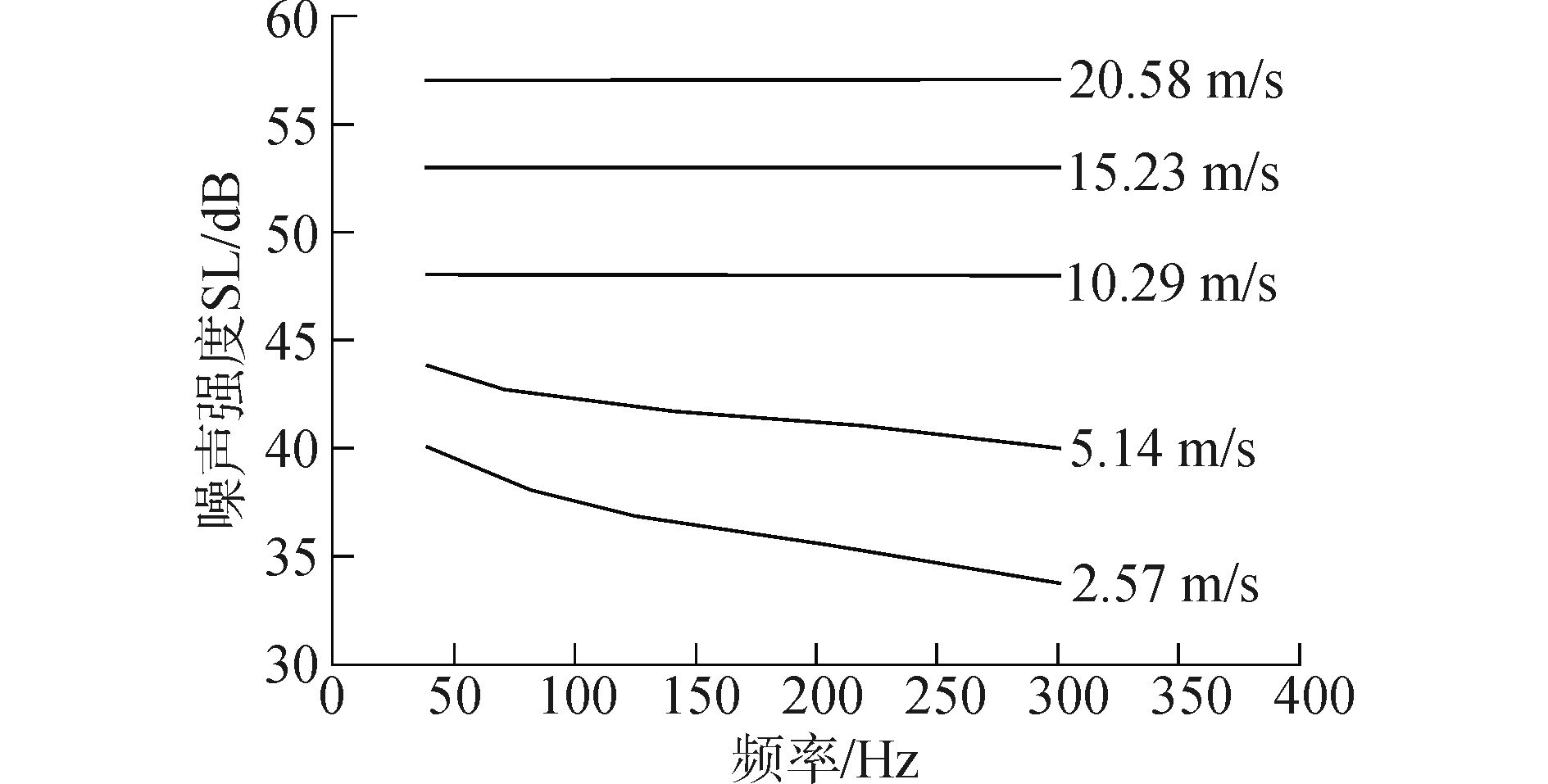
Kewley[24]通过大量的试验数据给出了低频噪声谱级SL与海面风速U和频率f间的关系(图 4),利用关系式I2=10SL(f, U)/10即可得到不同风速和频率下单位面积噪声源强度I2,图 4仅给出了5种风速下噪声谱级,其他风速下噪声谱级可以通过线性差值获得。
|
图 4 噪声谱级与频率和风速的关系 Fig.4 Ambient noise intensity versus fruquency and wind speed |
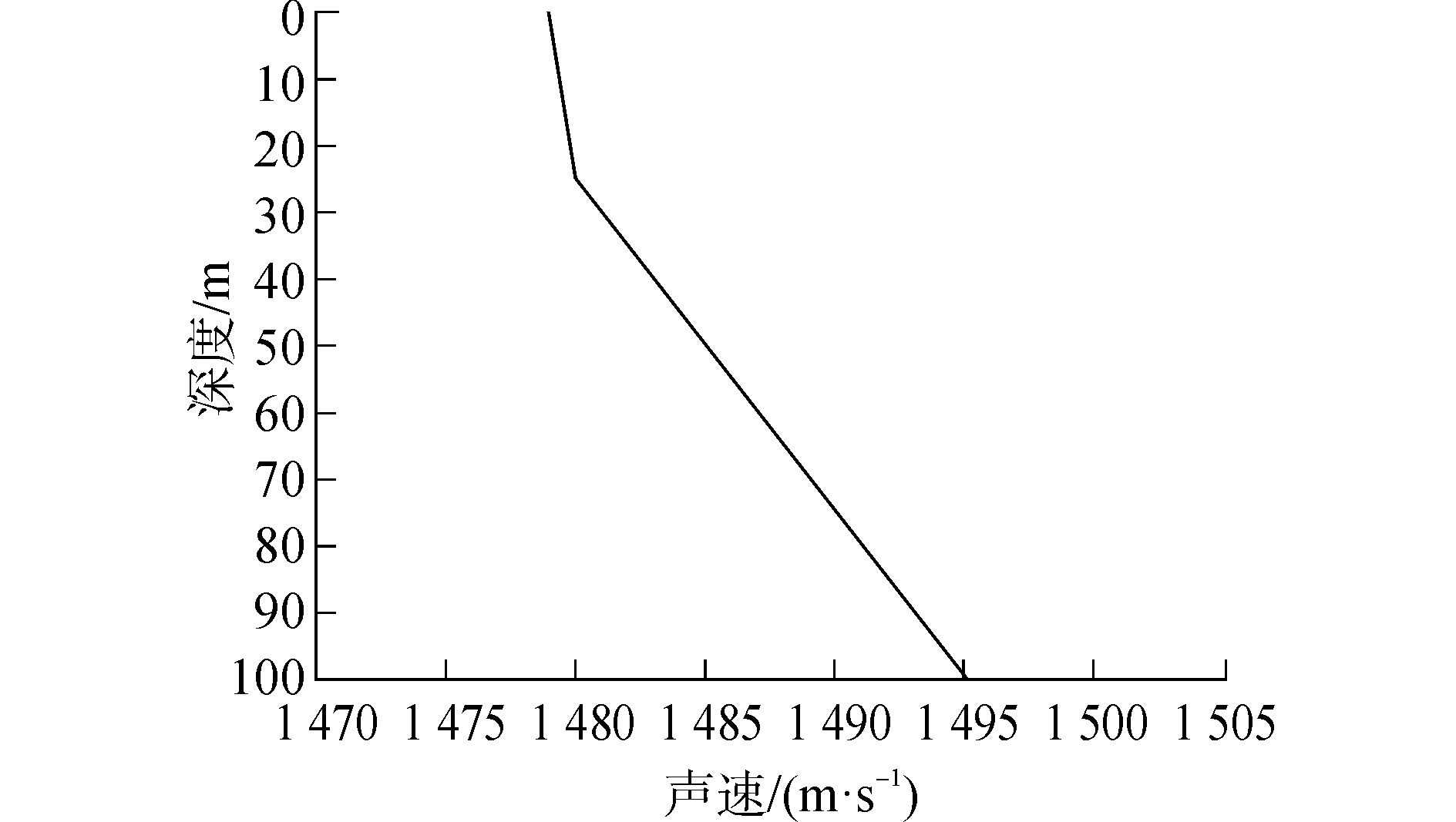
选取仿真环境如下:水深H1=100 m,水体密度ρ1=1.0 g/cm3,海底为弹性半无限空间。海底密度ρ2=1.8 g/cm3,海底纵波声速和横波声速分别为c1=1 800 m/s、c2=400 m/s,海底纵波和横波衰减分别为0.4 dB/λ、2.0 dB/λ。水体中声速剖面如图 5所示。
|
图 5 声速剖面 Fig.5 The sound speed profiles |
PM波浪谱是以风速作为输入量来描述海面粗糙度的,而气象站一般提供的是海况信息。表 1给出了不同海况对应的风速区间范围以及平均风速。为仿真简便,本文仿真中的不同海况下风速都是该海况下对应的平均风速。
| 表 1 海况和风速对应表 Tab.1 Wind speed as defined by sea state |
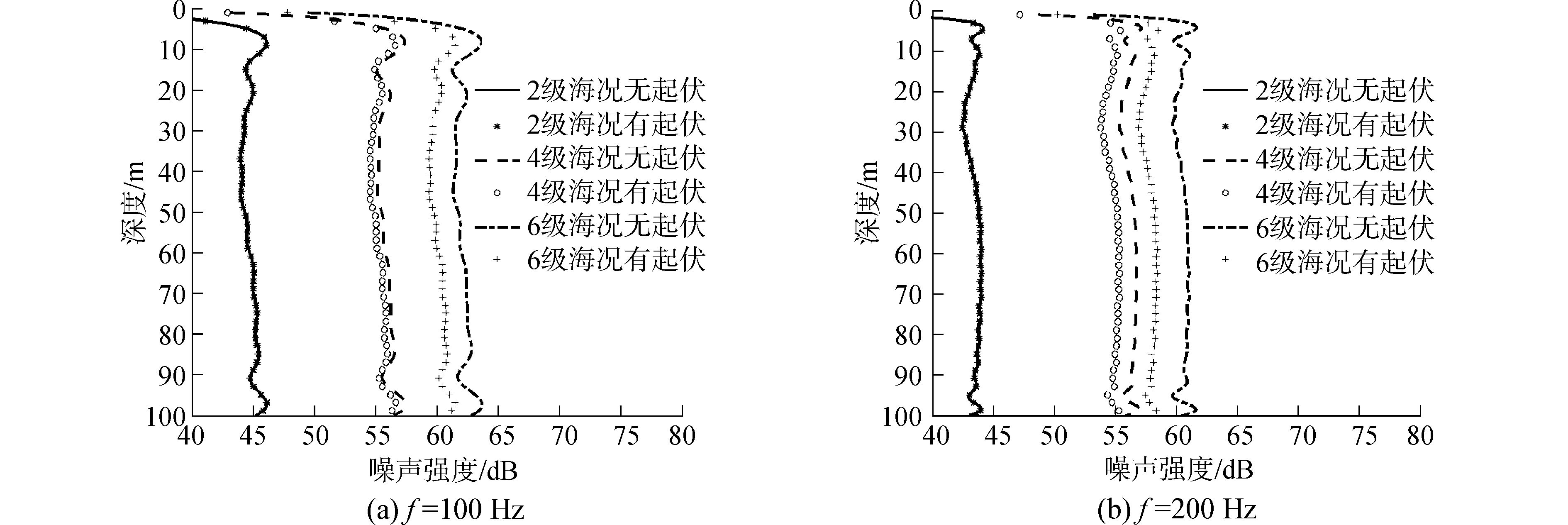
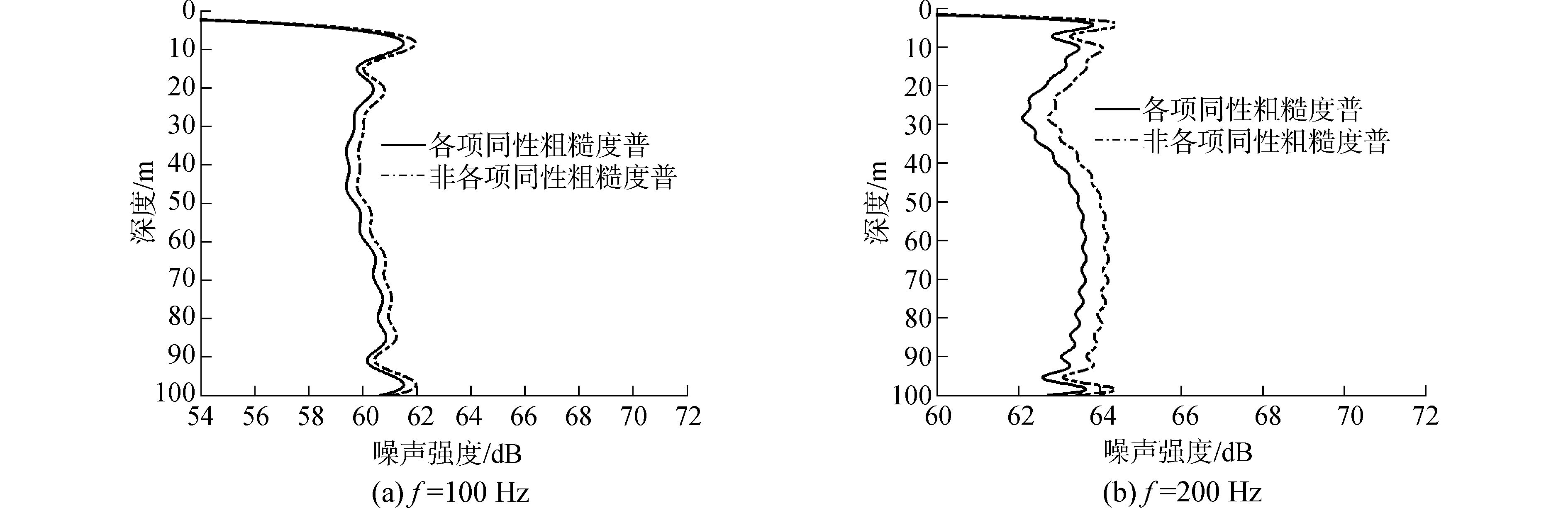
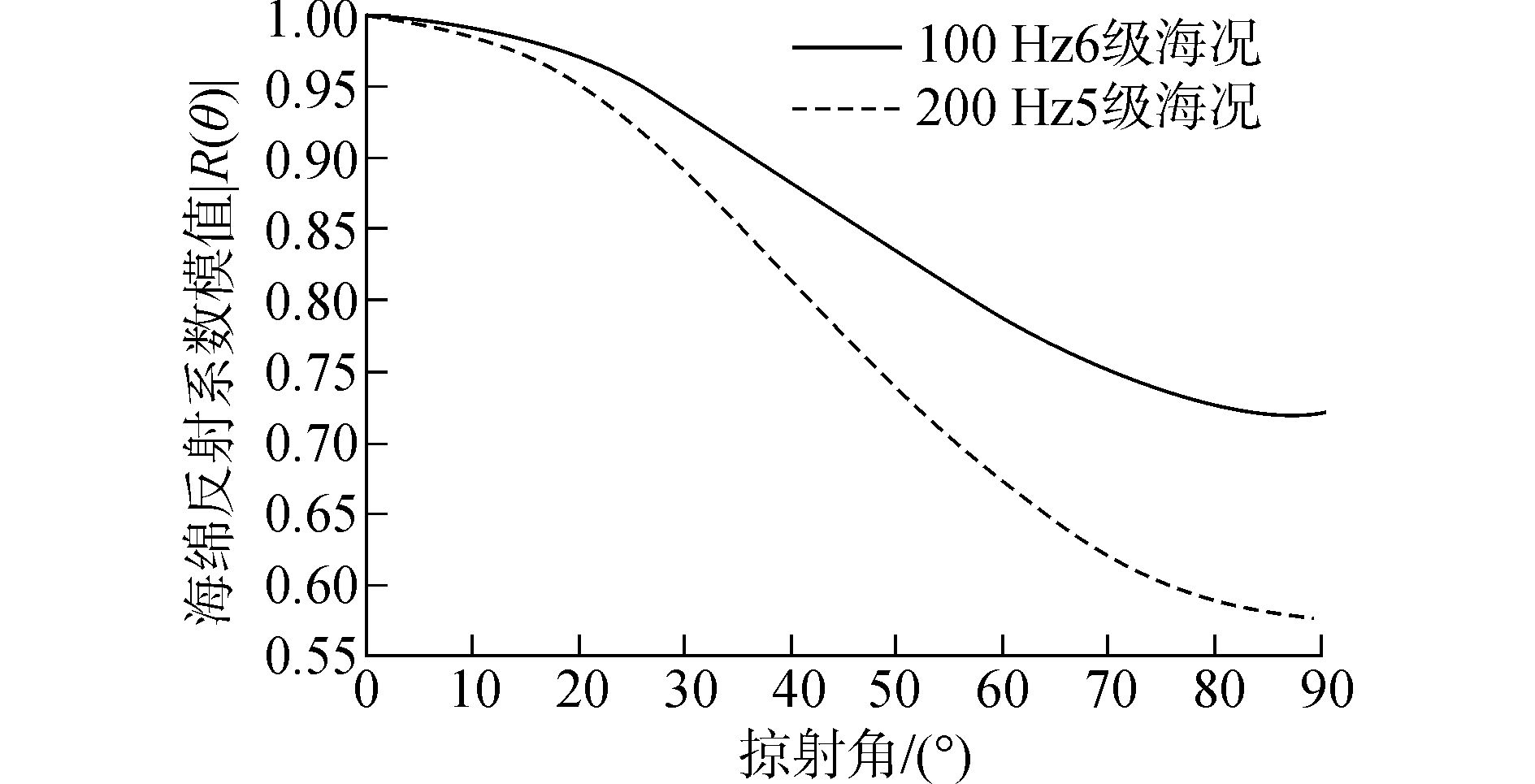
图 6(a)和(b)分别给出的是不同海况各向同性粗糙度谱下100 Hz和200 Hz的接收噪声强度。从图 6可以看到,随着风速增加,风生噪声强度增强,所以接收的噪声强度随着风速增加而逐渐增强,6级海况时噪声强度要显著高于2级和4级海况时的噪声强度。对比有无海面起伏时噪声强度可以看到,海面起伏会导致接收噪声强度减弱。这是因为部分能量被起伏海面散射到其他方向,海面相干反射系数模值小于1(见图 7),声波每次和海面作用后都有部分能量损耗,所以海面粗糙度越大,被海面损耗的能量越多,传播到接收点的能量变少,所以接收点噪声强度变弱。对于100 Hz声波,4级海况会使噪声强度减小0.4 dB,6级海况就能使噪声强度减小约2 dB。对于200 Hz声波,4级海况和5级海况会使噪声强度分别减小约1.7 dB和3.5 dB。同是4级海况,200 Hz噪声强度衰减要明显大于100 Hz噪声强度的衰减。这是因为200 Hz声波波长较小,更容易受粗糙海面影响,较多能量被散射到其他方向。图 8给出的是各向同性粗糙谱6级海况100 Hz声波和5级海况200 Hz声波的平均反射系数。可以看到后者反射损失明显大于前者,这也就解释了5级海况200 Hz噪声强度衰减大于6级海况100 Hz噪声强度的衰减。
|
图 6 100 Hz、200 Hz不同海况下噪声强度 Fig.6 Ambient noise intensity of 100 Hz and 200 Hz at different sea states |
|
图 7 各向均匀粗糙谱海面反射系数模值 Fig.7 Surface reflection under isotropic roughness spectrum |
|
图 8 100 Hz、200 Hz各向均匀与非各向均匀粗糙谱噪声强度 Fig.8 Ambient noise intensity of 100 Hz and 200 Hz under isotropic and anisotropic roughness spectrum |
图 8(a)和8(b)分别给出的是各向均匀与非各向均匀波浪谱作用下100 Hz和200 Hz噪声强度的对比,仿真所选择的海况分别为6级海况和5级海况。可以看到海面粗糙度的不均匀性对噪声强度的影响比较小,100 Hz二者引起的噪声强度差异约0.4 dB,200 Hz对应的噪声强度差异约0.6 dB。所以对于一般常见的海况。海面粗糙度的不均匀性对噪声强度的影响基本可以不予考虑。
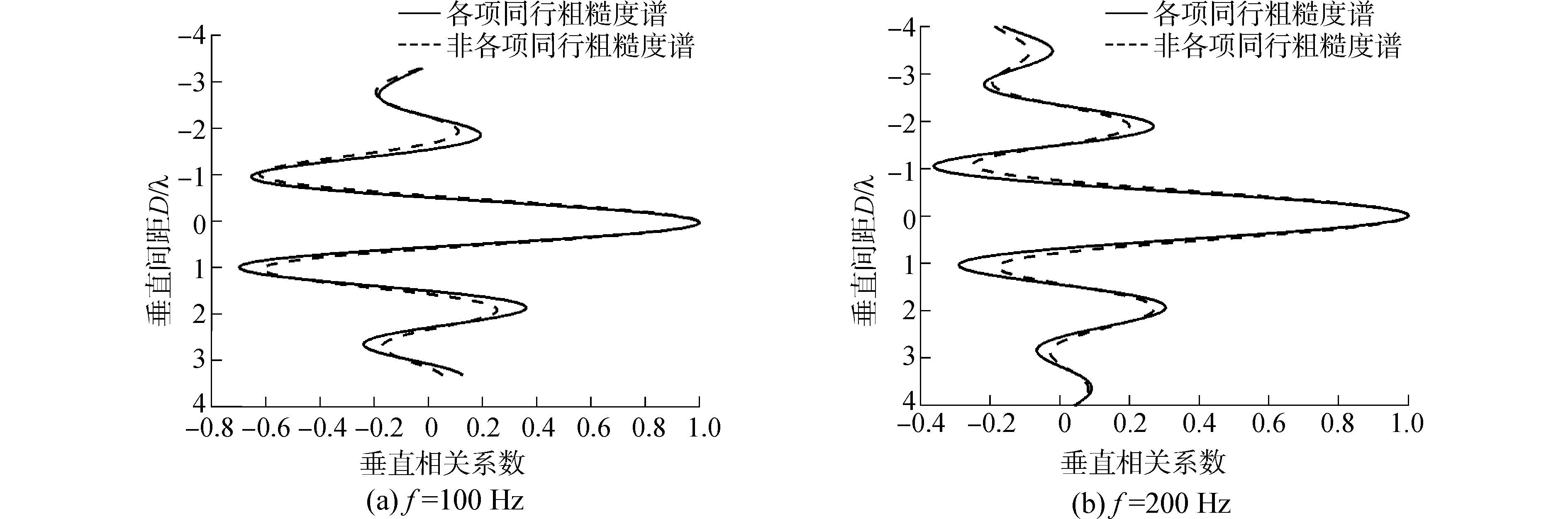
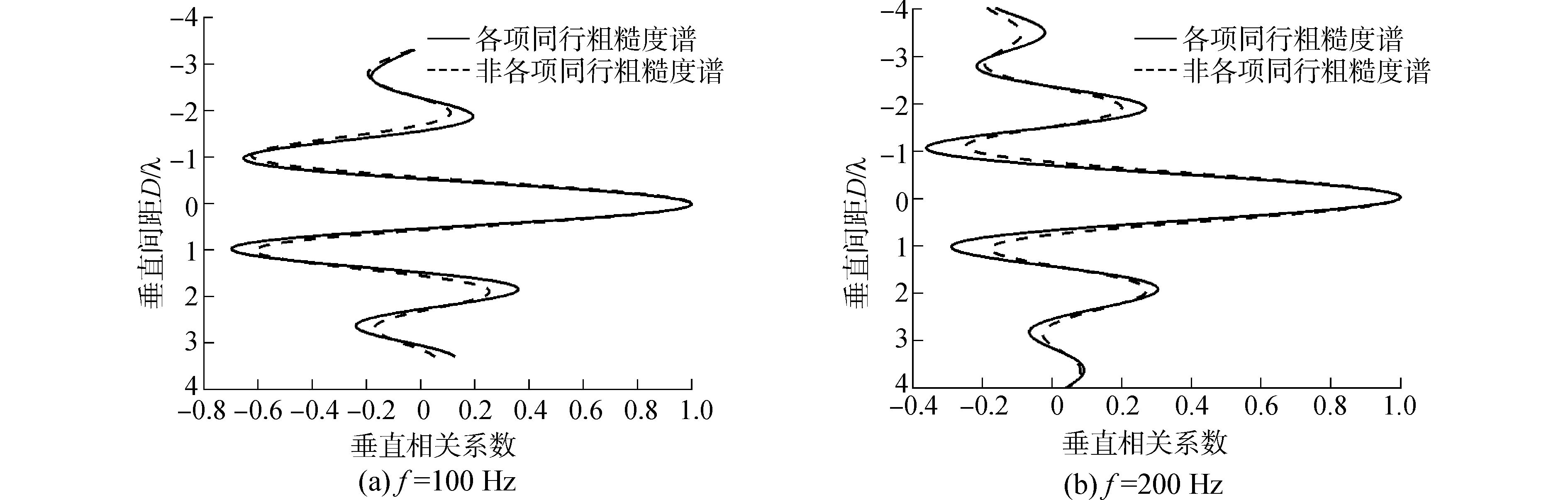
3.2 噪声垂直相关性图 9(a)和(b)分别给出的是不同海况各向同性粗糙度谱下100 Hz和200 Hz的噪声垂直相关系数。相对于理想海面,粗糙海面会使噪声场垂直相关系数幅度增大,而相关峰值和谷值对应的位置基本不发生变化。6级海况和5级海况使得100 Hz和200 Hz垂直相关第一个相关峰值分别增加了约0.18和0.1。图 10(a)和(b)给出了各向同性粗糙谱和非各向同性粗糙谱不同海况下100 Hz和200 Hz的噪声垂直相关性。由图可知,海面各个方向上粗糙度的不均匀性也只是改变噪声垂直相关系数的幅度,而对相关峰值和相关谷值对应的位置没有影响。
|
图 9 100 Hz、200 Hz不同海况下噪声垂直相关 Fig.9 Ambient noise vertical correlation of 100 Hz and 200 Hz at different sea states |
|
图 10 100 Hz、200 Hz各向均匀与非各向均匀粗糙谱噪声垂直相关性 Fig.10 Ambient noise vertical correlation of 100 Hz and 200 Hz under isotropic and anisotropic roughness spectrum |
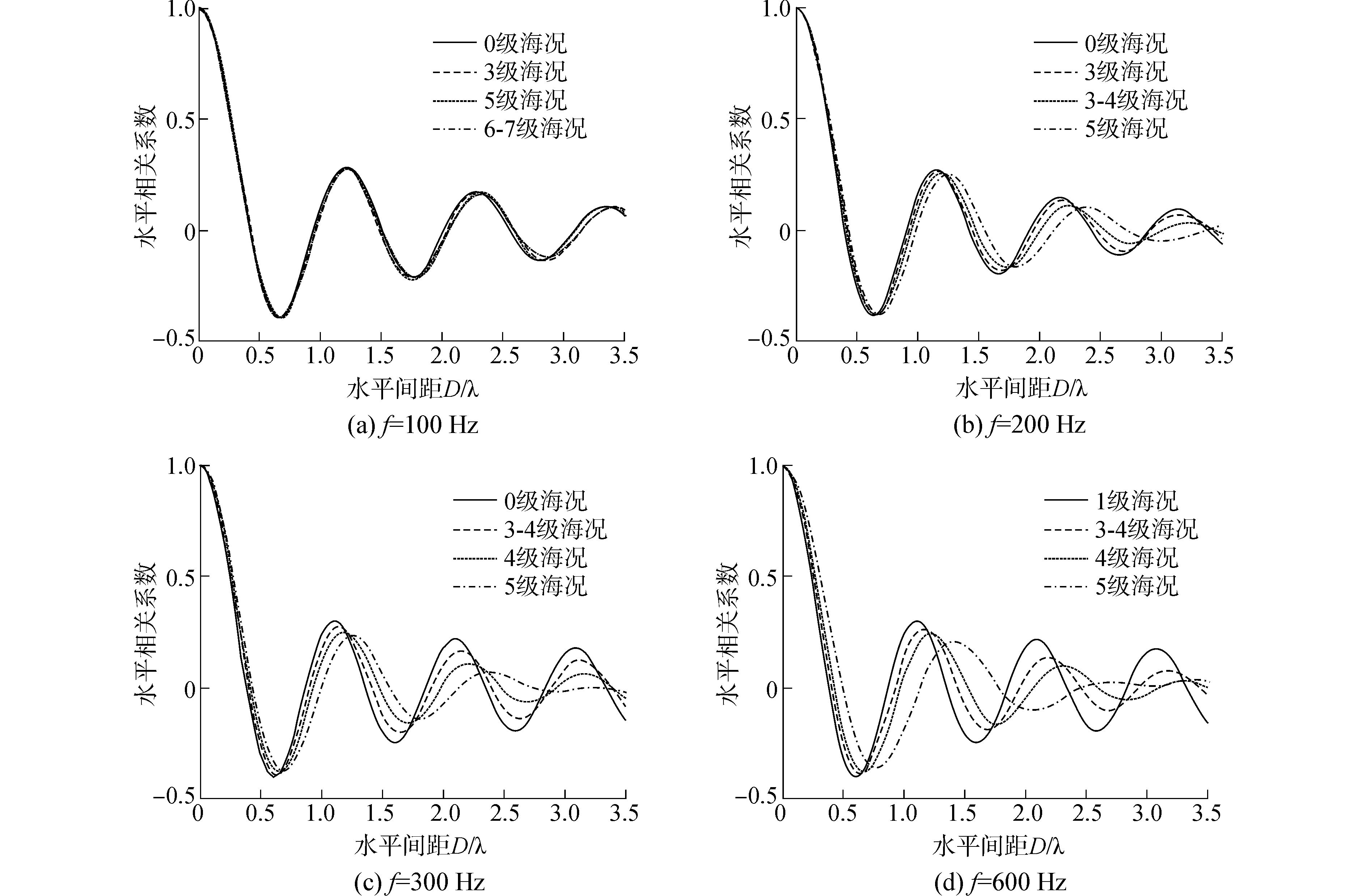
图 11(a)~(d)分别给出的是100、200、300、600 Hz各向均匀粗糙度谱下不同海况噪声场水平相关性。对于100 Hz,噪声场水平相关性基本不受海面粗糙度的影响,即使海面风速达到19 m/s,噪声场水平相关性也基本不发生改变。当声波频率增加到200 Hz,海况增加到5级,噪声场水平相关结构开始发生改变,随着海面粗糙度增加,噪声场水平相关半径逐渐增大,水平相关函数幅度变小,此外,相关峰和相关谷出现的位置也发生偏移。随着声波频率增高,这种变化越来越明显。当声波频率增加到600 Hz,噪声场水平相关性第一个相关峰的位置向右移动约0.3个波长。所以,当海面波浪起伏比较大时,在预报海洋环境噪声场水平相关特性就需要考虑海面粗糙度的影响。
|
图 11 不同频率下噪声场水平相关性 Fig.11 Ambient noise horizontal correlation at different frequency |
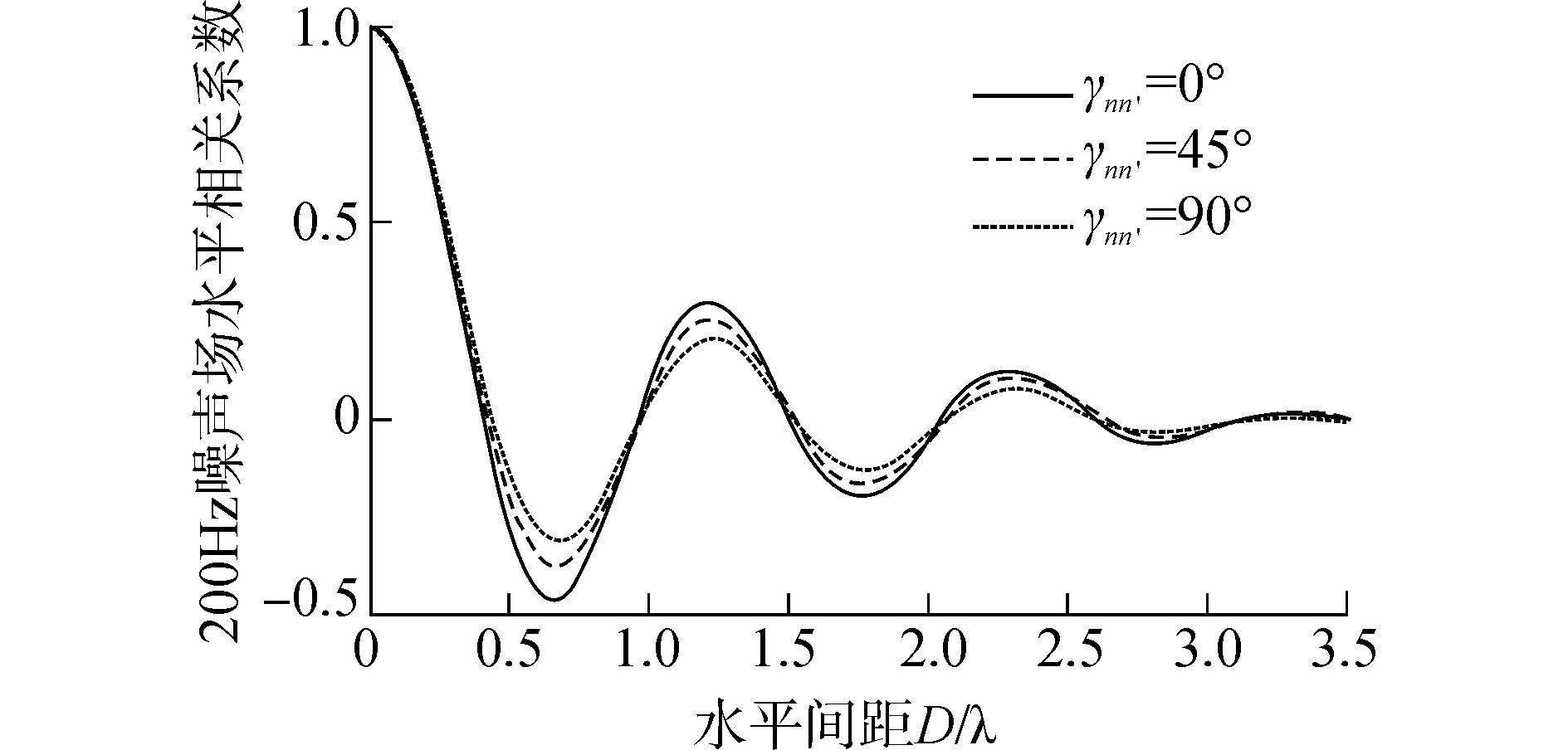
图 12给出的是非各向均匀波浪谱5级海况下不同方向上噪声水平相关性,声波频率为200 Hz。可以看到不同方向上噪声场水平相关性不完全相同,逆风(顺风)方向噪声场的水平相关半径要小于侧风方向噪声场的水平相关半径。2个正交方向上相关系数幅度差异约0.2。图 13给出的是频率为200 Hz的声波在5级海况逆风方向和侧风方向的海面相干反射系数。显然侧风方向的海面反射损失要小于逆风方向的海面反射损失,也即不同方向上声传播条件也不一致。这就造成了不同方向上噪声场水平相关性的差异。
|
图 12 5级海况不同方向上噪声场水平相关性 Fig.12 Ambient noise horizontal correlation of different direction at sea states 5 |

|
图 13 逆风方向和侧风方向海面反射系数 Fig.13 Surface reflection coefficient at headwind direction and sidewind direction |
1) 海面波浪起伏会使噪声强度减弱,其影响程度取决于声波频率以及海面粗糙度,但是基本不会影响噪声强度随深度变化的结构。海面粗糙度的不均匀性对噪声场强度影响非常弱,对于常见的海况,基本上可以不予考虑。
2) 海面波浪起伏只会影响噪声场垂直相关函数的幅度,不改变其相关峰与相关谷的位置。海面粗糙度的不均匀性对垂直相关性的影响亦是如此。
3) 随着风速增大,噪声场的水平相关半径也随之增大,相关函数的幅度衰减也随之变快,此外,相关峰的位置也会发生偏移。海面粗糙度和声波波长比值越大,这种效果越明显。由于不同方向上海面粗糙度不同,使得不同方向的声传播条件不同,所以不同方向上噪声场水平相关性也不相同,这是和KI模型最显著的差异。侧风方向的相关半径要大于逆风方向相关半径。
| [1] |
郭新毅, 李凡, 铁广朋, 等. 海洋环境噪声研究发展概述及应用前景[J]. 物理, 2014, 43(11): 723-731. GUO Xinyi, LI Fan, TIE Guangpeng, et al. Overview of ocean noise and application prospects[J]. Physics, 2014, 43(11): 723-731. DOI:10.7693/wl20141103 (  0) 0)
|
| [2] |
BUKINGHAM M J. Spatial coherence of wind-generated noise in a shallow ocean channel[J]. The journal of the acoustical society of America, 1981, 70(5): 1412-1420. DOI:10.1121/1.387096 ( 0) 0)
|
| [3] |
HARRISON C H, SIMONS D G. Geoacoustic inversion of ambient noise:A simple method[J]. The journal of the acoustical society of America, 2002, 112(4): 1377-1389. DOI:10.1121/1.1506365 ( 0) 0)
|
| [4] |
MARTIN S, CHRIS H H, MICHAEL B P. A passive fathometer technique for imaging seabed layering using ambient noise[J]. The journal of the acoustical society of America, 2006, 120(3): 1315-1323. DOI:10.1121/1.2227371 ( 0) 0)
|
| [5] |
HARRISON C H, BALDACCI A. Bottom reflection parameters deduced from ambient noise:simulation and experiment[C]//The Sixth International conference (ICTCA). Honclulu, USA, 2003.
( 0) 0)
|
| [6] |
CRON B F, SHERMAN C H. Spatial correlation functions for various noise models[J]. The journal of the acoustical society of America, 1962, 34(11): 1732-1736. DOI:10.1121/1.1909110 ( 0) 0)
|
| [7] |
PERKINS J S, KUPERMAN W A, INGENITOL F. Modeling ambient noise in three-dimensional ocean environments[J]. The journal of the acoustic society of America, 1993, 93(2): 739-752. DOI:10.1121/1.405437 ( 0) 0)
|
| [8] |
KUPERMAN W A, INGENITO F. Spatial correlation of surface generated noise in a stratified ocean[J]. The journal of the acoustical society of America, 1980, 67(6): 1988-1996. DOI:10.1121/1.384439 ( 0) 0)
|
| [9] |
HARRISION C H. Formulas for ambient noise level and coherence[J]. The journal of the acoustic Society of America, 1996, 99(4): 2055-2066. DOI:10.1121/1.415392 ( 0) 0)
|
| [10] |
林建恒, 高天赋. 简正波-射线混合风关海洋环境噪声模型[J]. 声学技术, 2003, 22(Z2): 119-121. LIN Jianheng, GAO Tianfu. A Hydride wind generated noise model of normal and ray[J]. Technical acoustic, 2003, 22(Z2): 119-121. DOI:10.3969/j.issn.1000-3630.2003.z2.037 (  0) 0)
|
| [11] |
GUY V NORTON, JORGE C. NOVARINI. The effect of sea surface roughness on shallow water waveguide propagation:A coherent approach[J]. The journal of the acoustic society of America, 1994, 99(4): 2013-2021. ( 0) 0)
|
| [12] |
KUPERMAN W A, INGENITO F. Attenuation of the coherent component of sound propagation in shallow water with rough boundaries[J]. The journal of the acoustic society of America, 1997, 61: 1178-1187. ( 0) 0)
|
| [13] |
USCINSKI B J. Sound propagation with a linear sound speed profile over a rough surface[J]. The journal of the acoustic society of America, 1993, 94: 491-498. DOI:10.1121/1.407061 ( 0) 0)
|
| [14] |
王先华, 彭朝晖, 李整林. 海面波浪起伏对声传播的影响[J]. 声学技术, 2007, 126(4): 551-556. WANG Xianhua, PENG Zhaohui, LI Zhenglin. Effects of wave fluctuation on sound propagation[J]. Technical acoustic, 2007, 126(4): 551-556. (  0) 0)
|
| [15] |
ERIC I T, FRANK S H, ELAM W T. Transport theory for shallow water propagation with rough boundaries[C]//Shallow Water Acoustic, Second International Shallow Water Acoustic Conference. American, 2010:99-105. http://meetings.aps.org/Meeting/MAR11/SessionIndex3/?VirtualSession=A
( 0) 0)
|
| [16] |
ARASE E M, ARASE T. Ambient sea noise in the deep and shallow ocean[J]. The journal of the acoustic society of America, 1967, 42: 73-77. DOI:10.1121/1.1910577 ( 0) 0)
|
| [17] |
KEWLEY D J, BROWNING D G, CAREY W M. Low frequency wind-generated ambient noise source levels[J]. The journal of the acoustic society of America, 1990, 88: 1894-1902. DOI:10.1121/1.400212 ( 0) 0)
|
| [18] |
THORSOS E I. Acoustic scattering from a Pierson Moskowitz sea surface[J]. The journal of the acoustic society of America, 1990, 88: 335-349. DOI:10.1121/1.399909 ( 0) 0)
|
| [19] |
KEVIN L. WILLIAMS, THORSOS. Examination of coherent surface reflection coefficient (CSRC) approximations in shallow water propagation[J]. The journal of the acoustic society of America, 2004, 116(4): 1975-1984. DOI:10.1121/1.1785617 ( 0) 0)
|
| [20] |
GÉRALDINE BOUCHAGE, MANELL E. ZAKHARIA. Assessment of the sea surface roughness effects on shallow water inversion of sea bottom properties[C]//Proceedings of 20th International Congress on Acoustics. Sydney, Australia, 2010:1-5.
( 0) 0)
|
| [21] |
WESTWOOD E K, TINDLE C T. A normal mode model for acoustic-elastic ocean environments[J]. The journal of the acoustic society of America, 1996, 100: 3631-3645. DOI:10.1121/1.417226 ( 0) 0)
|
| [22] |
ZHANG B, SN CHANDLER-WILDE. An integral equation method for rough surface scattering[J]. Joural of guidance control& dynamics, 2000, 23: 844-849. ( 0) 0)
|
| [23] |
THORSOS E I. The validity of the Kirchhoff approximation for rough surface scattering using a Gaussian roughness spectrum[J]. The journal of the acoustic society of America, 1988, 83: 78-92. DOI:10.1121/1.396188 ( 0) 0)
|
| [24] |
THORSOS E I, JACKSON D R. The validity of the perturbation approximation for rough surface scattering using a Gaussian roughness spectrum[J]. The journal of the acoustic society of America, 1989, 86: 261-277. DOI:10.1121/1.398342 ( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


