2. School of Management, Harbin Institute of Technology, Harbin 150001, China
住房过滤是住房市场中常见的一种现象,指的是随着时间推移为较高收入房客建造的住房发生老化、房屋价值降低,此类房客为了追求更好的住房而放弃现有住房,而较低收入房客会继续使用此类住房的过程。过滤理论研究居民与住房的动态变化,其中过滤产生的原因包括居民收入增加、新建住房进入住宅市场、以前的住房折旧、折旧住房价值降低等[1]。概括来讲,过滤是高收入居民向外迁居后由低收入居民占据其空置住房,形成的住房按社会等级向下过滤而居民向上过滤的持续动态过程[2]。从1975年开始,越来越多的专家开始将过滤理论引入到房屋的折旧问题研究中,住房功能不断降低,很可能越来越不能被当下社会所承认而部分退出住宅市场,这是早期过滤理论的基础。此后,陆续有一些学者开始尝试建立住房过滤模型,其中Sweeney的住宅过滤模型是最重要的模型之一[3]。由于住房市场的分层次结构和相互影响,住房过滤理论和梯度消费理论解释了住房市场存在的内部规律,是政府设计公共住房保障制度的重要理论基础[4]。过滤机制一直被认为是为低收入人群提供保障的重要机制,Rosenthal[6]依据过滤机制提出了“重复收入”的直接估算模型[5]。同时,过滤理论在住房市场和政策制定方面始终扮演重要角色,Dascher[7]从居住者选择居住地的角度扩展了Sweeney的经典过滤模型;赵佩佩[8]从住房过滤视角分析保障性住房的作用,并且提出了保障性住房规划的建设性意见;陈筱等[9]提出通过过滤模型来研究保障性住房的供给、质量监督、政策落实等;闫佳佳[10]借助过滤理论来研究保障性住房的信贷问题;Liu[11]建立了考虑住房过滤的住房市场模拟模型,并利用该模型从住房建设等级、属性预测和政策分析等方面对住房消费规律进行研究。
本文旨在运用住房过滤理论,结合我国保障性住房的现状,以出租型保障性住房为研究对象,设计保障性住房的租金模型。首先限定了保障对象,建立保障性住房过滤模型;其次以出租型保障性住房为研究对象,分别针对低收入者、中低收入者和夹心层设计了各自的过滤器模型,并对保障条件和租金进行限定;最后针对设计的定量租金模型进行简单的算例应用。
1 保障性住房过滤理论分析住房过滤反映了住房的生命周期各个阶段,是对住房经济行为的全面体现。房客的收入在住房过滤现象研究中具有重要地位,特别是从住房等级和收入等级两个相互联系的方面来研究住房供求结构,并对整个住房市场进行跟踪分析,具有重要的现实意义。
1.1 保障对象类别保障性住房主要是针对保障性人群建设的住房,一般是由政府负责建设,在特定时期也可由政府联合开发商建设,以低于市场的价格出售或出租给保障性人群,我国保障性住房形式主要有经济适用房、公共租赁房和廉租房三种。保障对象可根据收入水平、社会弱势群体、流动性等方面进行界定,本文按照收入水平对保障对象进行界定:1)低收入者:指城市无业、无劳动能力以及企业失业下岗人员,这类人员学历不高、劳动技能差、年龄偏大,在劳动力市场上为弱势群体,大多数此类人群的收入都低于城市最低保障线。2)中低收入者:这一部分人群的收入稍高于低收入者,但他们也很难在市区购买一套能够满足生活需要的住房,只能选择租住房子,且租住的房子大多比较老旧,采光、供暖、供水、供电等都很难满足理想的生活需要。3)夹心层:指既无法承受畸高的商品房价格又不具备申请经济适用房资格的人群,是住房保障政策无法惠及的城市居民。
1.2 保障性住房过滤机理住房过滤理论的基本原理是高收入阶层对于新房需求相当于间接补贴,进而满足不同收入阶层特别是低收入人群购房的需要。换句话说高收入人群对住房的新需求创造了消费者对新建住房质量的需求,假如把住房分为不同等级,那么开发商在同等价格条件下为了吸引更多的消费者购房会提高住房的质量;购房者搬到质量更好住房的同时留下旧住房,这些旧住房导致市场价格下降,也可让低收入家庭能够负担相应质量的住房,即价格的下降可以让低收入阶层负担质量相对较好的住房。住房过滤理论是基于一般均衡理论在长期过程中达到均衡的价格和数量,其核心是住房保障线的设定,可采用剩余收入法进行测算。
剩余收入法是一种测定住房支付能力的方法。假设家庭收入首先需要满足非住房的基本支出,如果剩余资金不足支付住房支出,则判定家庭存在住房能力问题,此时存在:
| $I - X < H$ | (1) |
式中:I表示收入,X表示非住房支出,H表示住房支出。这一测定方法反映了家庭住房支出、非住房支出和收入之间的平衡关系。通过这种方法得到的没有住房支付能力的人群并非全部无住房支付能力,因为可能是有些家庭消费过高导致的,因此必须设立一个“合理消费”。
假设在某一城市,存在着社会公认的住房支出的“合理消费”和非住房支出的“合理消费”:
| ${I^*} = {X^*} + {H^*}$ | (2) |
式中:H*表示住房支出的“合理消费”,X*表示非住房支出的“合理消费”,I*表示为达到最基本居住水平和最基本生活水平所需的可支配收入,即住房保障线。再构建:
| $G\left( y \right) = \int {_{y0}^y} g\left( y \right){\rm{d}}y$ | (3) |
式中:g(y)为保障人群收入的概率密度函数,y0表示受保障人群最低收入,y表示受保障人群收入,G(y)表示0时期收入低于y的居民数量。假设保障性住房的数量N刚好等于受保障人群的数量,将保障房的保障力度分为三个等级,从高到低分别为q1、q2、q3,对应的保障性住房供给量分别为x1、x2、x3,则有
| $G\left( y \right) = \int_{y0}^{{y_m}} {g\left( y \right){\rm{d}}y} = N$ | (4) |
| $N = {x_1} + {x_2} + {x_3}$ | (5) |
式中:ym表示受保障人群的最高收入,即保障线。保障性住房的最优解应该满足贫困等级与受保障等级相匹配的条件,即第i等级贫困的应该受到第i等级的保障福利。假设居民的收入函数为y(q),匹配条件可以写成:
| $G\left( {y\left( q \right)} \right) = L\left( q \right)$ | (6) |
式中:L(q)表示保障性住房的级别,可分别记为L(q1)、L(q2)、L(q3),且有:
当0≤G(y(q))≤x1时,G(y(q))=L(q1),表示收入为y(q)的居民保障性住房级别为L(q1);
当x1<G(y(q))≤x1+x2时,G(y(q))=L(q2)表示收入为y(q)的居民保障性住房级别为L(q2);
当x1+x2<G(y(q))≤x1+x2+x3时,G(y(q))=L(q3)表示收入为y(q)的居民保障性住房级别为L(q3)。
可以做如下假设:针对于同一类人群,把他们的受保障级别分为三类,包括A级家庭保障、B级家庭保障和C级家庭保障(A级需要最多的保障,B级较少,C级最少)。初始假设A、B、C家庭需要的保障服务分别为$A'B'C'$个单位(其中$A' > B' > C' > D' = 0$),一年后他们的收入水平提高,其中C家庭能够完全负担住房消费,他们就会搬离保障性住房;B家庭需要${C'}$个单位的保障服务,这样他们可能就会取代C家庭原来的位置;A家庭需要${B'}$个单位的保障服务,他们就会取代B家庭原来的位置,具体如图 1所示。
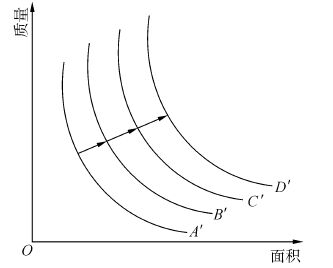
|
| 图1 保障性住房过滤模型 Figure 1 Affordable housing rents model |
本文选取的研究对象是出租型的保障性住房,因此对其租金研究具有重要作用。此处租金模型设计主要分为三部分:过滤器设计、保障条件限定以及租金限定,具体如图 2所示。
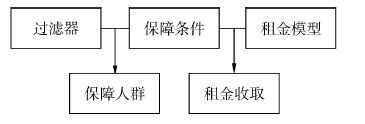
|
| 图2 租金模型构成 Figure 2 Rental model structure |
其中,过滤器用来筛选保障对象,保障条件针对过滤器的筛选进行限定,是过滤器筛选的标准;租金模型确定租金的收取模式,而保障条件可以辅助租金模型的设计,即租金模型的设计可借鉴保障条件的一些条件因素。
2.1 保障性住房的过滤器设计本文设计的过滤器如图 3所示。

|
| 图3 过滤器示意图 Figure 3 Schematic diagram of filtration |
政府通过过滤器来筛选保障人群,符合条件的保障对象进入保障房系统,不符合条件时退出保障房系统。此外不同受保障人群的过滤器是不同的,低收入者、中低收入者以及夹心层需要分别设计过滤器。
2.1.1 低收入者过滤器设计低收入者的收入水平没有最低限,那么仅需要过滤超过收入上限的人群即可。根据这一思想,低收入者的过滤器设计如图 4所示。
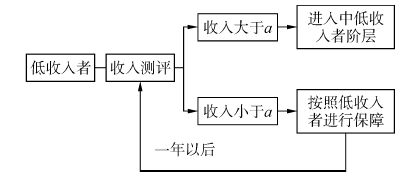
|
| 图4 低收入者过滤器 Figure 4 Low-income earners′ filtration |
具体过程是对申报的低收入者进行收入水平测评,当收入小于a时,则判定为低收入者家庭,获得低收入者保障性住房;否则进行中低收入者测评。同时,家庭收入是动态变化的,需要每隔一段时间重新测评。其中,低收入者过滤器中a的测定非常关键,代表满足家庭最基本生活需要的收入(不包含住房支出),后文研究将会具体求解。
2.1.2 中低收入者过滤器设计中低收入者的过滤可能朝两个方向发展,一方面是当中等收入者的收入低于某一水平线时,可能进入低收入者阶层,享受低收入者保障;否则可能就会退出保障性住房。有鉴于此,本文设计的中低收入者过滤器如图 5所示,具体的测评过程与低收入者相似,此处不再赘述。
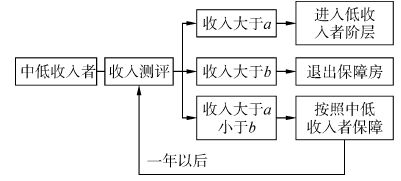
|
| 图5 中低收入者过滤器 Figure 5 Medium-and-low-income earners′ filtration |
夹心层人群的保障评价指标主要有三个方面:工资水平、学历以及工作年限,过滤器的设计也主要围绕这三个方面进行,具体如图 6所示。
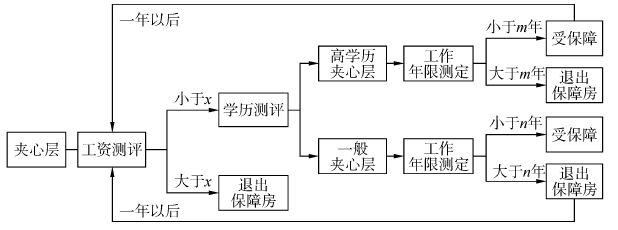
|
| 图6 夹心层人群过滤器 Figure 6 Sandwich layer population′ s filtration |
其中,夹心层人群除了收入测评之外,还需要进行学历和工作年限测评,具体方法是先分为高学历夹心层和普通夹心层,两者的保障力度有所区别,再测定工作年限:对于高学历夹心层,当其工作年限大于m a时,则退出保障性住房(这里的退出是指退出夹心层的保障房体系,有可能进入中低收入者和低收入者保障体系,下同。);对于普通夹心层,当其工作年限大于n a时,则退出保障性住房。
2.2 过滤器条件限定根据以上对低收入者、中低收入者以及夹心层的过滤器设计,需要对过滤器中的一些限定条件具体描述。
2.2.1 低收入者保障条件限定对于低收入者过滤器来说,主要是确定低收入者的最低收入线,以1.2节中研究的X*作为低收入者的准入线:X*表示非住房支出的合理消费,当家庭收入低于X*时,需要纳入低收入者群体。合理的非住房支出可以采用计量经济学中分析居民支出的ELES模型来确定。ELES模型表达式为
| $\begin{array}{l} {p_i}{q_i} = {p_i}{{\bar q}_i} + {\beta _i}\left( {I - \sum\limits_{j = 1}^n {{p_j}{{\bar q}_j}} } \right)\\ \left( {i,j = 1,2, \cdots ,n;\sum\limits_{i = 1}^n {{\beta _i} \le 1} } \right) \end{array}$ | (7) |
式中:pi为第i种商品的价格,qi为居民对于第i种商品的需求量,qi为居民对第i种产品的基本需求量,即最低消费需求量,βi为i种产品的边际消费倾向,I为家庭可支配收入。
在该模型中,piqi为居民对第i种产品的消费支出;piqi为居民对第i种商品的基本消费支出;${\beta _i}\left( {I - \sum\limits_{j = 1}^n {{p_j}{{\bar q}_j}} } \right)$为居民对第i种商品的超额消费支出。该模型表明,在一定收入水平价格之下,消费者首先满足基本消费需求piqi,在剩余的收入${I - \sum\limits_{j = 1}^n {{p_j}{{\bar q}_j}} }$中,按照βi的比例在消费第i种产品之间进行配比。
将式(7)变形为
| ${p_i}{q_i} = \left( {{p_i}{{\bar q}_i} - {\beta _i}\sum\limits_{j = 1}^n {{p_j}{{\bar q}_j}} } \right) + {\beta _i}I$ | (8) |
式中:piqi和${\sum\limits_{j = 1}^n {{p_i}{{\bar q}_j}} }$都是不变的常数,因此可以令
| ${\alpha _i} = {p_i}{{\bar q}_i} - {\beta _i}\sum\limits_{j = 1}^n {{p_j}{{\bar q}_j}} $ | (9) |
将式(9)代入式(8)得:
| ${p_i}{q_i} = {\alpha _i} + {\beta _i}I$ | (10) |
式(10)是一个简单的回归方程,可以根据调查的数据求出αi和βi的估计值${{\hat \alpha }_i}$和${{\hat \beta }_i}$,从而求得居民对于第i种商品的基本消费支出。再构建:
| ${p_i}{{\bar q}_i} = {{\hat \alpha }_i} + {{\hat \beta }_i}\sum\limits_{i = 1}^n {{{\hat \alpha }_i}/1} - \sum\limits_{i = 1}^n {{{\hat \beta }_i}} $ | (11) |
由式(11)可知存在${\sum\limits_{i = 1}^n {{p_i}{{\bar q}_i}} }$即为社会平均的居民满足基本生活需要的支出。则:
| ${X^*} = \sum\limits_{i = 1}^n {{p_i}{{\bar q}_i}} = \sum\limits_{i = 1}^n {{{\hat \alpha }_i}/} \left( {1 - \sum\limits_{i = 1}^n {{{\hat \beta }_i}} } \right)$ | (12) |
式中:X*即为非住房支出的合理消费,也就是图 4中的指标a。
此外,还可以参考当地的“低保线”作为低收入者的准入线:目前,国际上确定最低生活保障线的方法主要有生活需求法、国际贫困标准法、生活形态法、恩格尔系数法四种。
2.2.2 中低收入者保障条件限定根据图 5可知,中低收入者保障条件的限定主要是a和b的确定,在2.2.1 中已经给出了a的确定方法,此处主要研究b的求解办法。
在确定中低收入者保障线上限时,需要考虑到家庭生活基本开支,包括住房支出和非住房支出,故可结合1.2节进行保障准入线的研究,根据式(2)可得
| $I \ge {I^*} = {X^*} + {H^*}$ | (13) |
式中:I表示居民家庭收入。式(13)表明只有居民家庭的收入大于非住房支出和住房支出之和时,才能说明这个家庭具有住房支付能力,因此可将家庭收入I*作为保障性住房的准入线。那么I*=X*+H*就是图 5中的b,而X*是图 4中的a。
2.2.3 夹心层保障条件限定通过研究发现,工资收入和工作年限是限定夹心层的两个主要条件:
1 ) 工资限定条件的确定
假设夹心层的收入线I1,正常住房价格为Z1,政府设定夹心层毕业后Y年购买住房,X*是非住房支出合理消费,通货膨胀率为P,则有:
| $\begin{array}{l} {Z_1} = \left( {{I_1} - {X^*}} \right) + \frac{{\left( {{I_1} - {X^*}} \right)}}{{1 + P}} + \\ \frac{{\left( {{I_1} - {X^*}} \right)}}{{{{\left( {1 + P} \right)}^2}}} + \cdots + \frac{{\left( {{I_1} - {X^*}} \right)}}{{{{\left( {1 + P} \right)}^{Y - 1}}}} \end{array}$ | (14) |
化简得
| ${Z_1} = \frac{{{I_1} - {X^*}}}{P} \times \left[ {1 - \frac{1}{{{{\left( {1 + P} \right)}^Y}}}} \right]$ | (15) |
求得
| ${I_1} = \frac{{{Z_1}P}}{{\left[ {1 - \frac{1}{{{{\left( {1 + P} \right)}^Y}}}} \right]}} + {X^*}$ | (16) |
化简得
| ${I_1} = \frac{{{Z_1}P{{\left( {1 + P} \right)}^Y}}}{{{{\left( {1 + P} \right)}^Y} - 1}} + {X^*}$ | (17) |
式中:I1即为夹心层的收入线。
2 ) 保障年限的限定
对于夹心层的保障不可能是无限期的,一方面需要满足他们的住房需求,另一方面还需要激励他们早日买房,因此对于夹心层的保障需要设定年限。本文采取经验法来进行确定年限,具体操作方法就是根据当地的调查数据,统计之前Y年毕业的夹心层的平均购买住房的时间,通过这一时间来确定夹心层需要保障的年限。
2.3 保障对象租金限定保障性住房作为一种商品租给保障对象使用,需要收取一定的佣金,但是佣金额度需要适当把控。如果收取租金过多,保障性住房的“保障”意义就无法体现;如果收取租金额度太小,又会导致政府的财政压力过大,也会弱化建设方建设保障性住房的积极性。对低收入者、中低收入者和夹心层的租金收取需要分别进行研究。
2.3.1 低收入者租金收取从2.2.1节低收入者保障条件限定可知,低收入者的保障条件有两个:1)城市低保线;2)家庭的合理消费线。本文仅针对城市低保线分析,我国2015年重要城市低保线如表 1所示,其中低保线最高的上海是790元,比较低的南宁为250元。家庭收入低于这个水平线时基本生活需求无法满足,也就很难有额外的资金去支付保障性住房的租金。所以对于政府来说这一部分需要加大保障力度,可以免去租金。
| 地区 | 城市低保标准/元 | 调整日期 |
| 北京 | 710 | 2015年7月1日 |
| 上海 | 790 | 2015年4月1日 |
| 南京 | 700 | 2015年7月1日 |
| 重庆 | 365~385 | 2014年10月1日 |
| 天津 | 705 | 2015年4月1日 |
| 太原 | 453~505 | 2015年1月1日 |
| 杭州 | 660 | 2014年12月1日 |
| 石家庄 | 500 | 2013年12月 |
| 呼和浩特 | 515~565 | 2015年1月1日 |
| 武汉 | 580 | 2015年1月1日 |
| 长沙 | 450 | 2015年7月1日 |
| 广州 | 600 | 2014年1月1日 |
| 南宁 | 250 | 2014年1月1日 |
| 海口 | 450 | 2013年7月1日 |
| 成都 | 400~500 | 2014年11月1日 |
| 贵阳 | 425~530 | 2015年1月1日 |
| 昆明 | 475~530 | 2015年4月1日 |
| 拉萨 | 640 | 2015年 |
| 西安 | 480~510 | 2014年10月 |
| 兰州 | 387~515 | 2015年5月30日 |
| 西宁 | 373 | 2015年1月1日 |
| 银川 | 380 | 2015年 |
| 乌鲁木齐 | 380 | 2015年 |
| 沈阳 | 505~580 | 2015年7月1日 |
| 长春 | 350~435 | 2014年10月1日 |
| 哈尔滨 | 510 | 2014年10月1日 |
| 合肥 | 510 | 2015年1月1日 |
| 福州 | 最低工资标准36%~42% | |
| 南昌 | 450~480 | 2015年1月1日 |
| 济南 | 500~550 | 2015年4月1日 |
| 郑州 | 520 | 2015年7月1日 |
中低收入者的收入能够满足家庭的基本生活开支(除住房开支),但是又难以承受合适的住房租金压力,因此可用政府所需的住房建设成本来计算应该收取的租金,包括:前期费用、建筑安装工程费、基础设施费、公共配套费、开发间接费、财务费用、管理费用七项。假设上述七项成本之和为S,每年的管理费用为M,保障房每年的租金额为R,保障房的使用年限为T,报酬率为K,则有:
| $S = \left( {R - M} \right) + \frac{{\left( {R - M} \right)}}{{1 + K}} + \frac{{\left( {R - M} \right)}}{{{{\left( {1 + K} \right)}^2}}} + \cdots + \frac{{\left( {R - M} \right)}}{{{{\left( {1 + K} \right)}^{T - 1}}}}$ | (18) |
化简得
| $S = \frac{{R - M}}{K} \times \left[ {1 - \frac{1}{{{{\left( {1 + K} \right)}^T}}}} \right]$ | (19) |
求得
| $R = \frac{{SK}}{{\left[ {1 - \frac{1}{{{{\left( {1 + K} \right)}^T}}}} \right]}} + M$ | (20) |
化简得
| $R = \frac{{SK{{\left( {1 + K} \right)}^T}}}{{{{\left( {1 + K} \right)}^T} - 1}} + M$ | (21) |
式中R即为中低收入者家庭的租金。
2.3.3 夹心层租金收取普通夹心层和高学历夹心层的收入状况差异明显,因此需要分别收取租金。
1 ) 普通夹心层租金收取
夹心层的保障条件限定涉及工作年限以及收入水平,其中收入水平决定是否应该受到保障,而工作年限可以作为收取租金的参考因素:参加工作的年限越长,政府对其保障力度就应该越小,收取的租金越高。根据上述原理,本文设计的普通夹心层租金收取方法如表 2所示。表 2对工作年限、减免租金比例以及最大租住面积做出了限定。
| 参加工作 年限W/a | 减免租金 比例J/% | 最大租住 面积E/m2 |
| f~o | F | ${F'}$ |
| o+1~u | O | ${O'}$ |
| u+1~v | U | ${U'}$ |
| 注:f<o<u<v,F>O>U,$F' < O' < U'$ | ||
在表 2模式下,保障对象收取的租金为
| $R = eh\left( {1 - J} \right)$ | (22) |
式中:R表示租金,e表示实际租住面积,h表示市场平均租金单价。
假设某一城市的普通夹心层受保障额度如表 3所示。从表中可知:参加工作1~5 a可以减免租金40%,可租的最大面积为25 m2/人;6~10 a可减免租金20%,可租的最大面积为30 m2/人;11~15 a可减免租金10%,可租的最大面积为35 m2/人。如果一个参加工作3 a的人想居住面积为30 m2的房子,那么他可以在减免20%租金的情况下租住政府指定的30 m2住房;反之则不可。在实际操作中,如果政府财政状况较好,可以把减免的租金适当提高,最大的租住面积适当增加;反之则需要减少。
| 参加工作 年限W/a | 减免租金 比例J/% | 最大租住 面积E/m2 |
| 1~5 | 40 | 25 |
| 6~10 | 20 | 30 |
| 11~15 | 10 | 35 |
2 ) 高学历夹心层租金收取
高学历夹心层和普通夹心层的区别在于学历不同导致的平均收入不同,进而影响政府租金收取额度的差异化,但租金收取模式类似,具体租金收取方法如表 4所示。
| 参加工作 年限W/a | 减免租金 比例J/% | 最大租住 面积E/m2 |
| f1~o1 | F1 | ${F'}$1 |
| o1+1~u1 | O1 | ${{O'}_1}$ |
| u1+1~v1 | U1 | ${{U'}_1}$ |
| 注:f1<o1<u1<v1,F1>O1>U1,${{F'}_1} < {{O'}_1} < {{U'}_1}$ | ||
表 4模式下,收取租金额为
| ${R_1} = {e_1}{h_1}\left( {1 - {J_1}} \right)$ | (23) |
式中:R1表示租金,e1表示实际租住面积,h1表示市场平均租金单价。
在同一个城市,高学历夹心层的保障力度要小于普通夹心层,因此有
f1=f,o1<o,u1<u,v1<v;
F1<F,O1<O,U1<U;
${{F'}_1} > F',{{O'}_1} > O',{{U'}_1} > U'$。
取与表 3相同的城市,假设高学历夹心层的保障额度如表 5所示,从表中可知:参加工作1~3 a可减免租金30%,可租的最大面积为30 m2/人;参加工作4~6 a可减免租金15%,可租的最大面积为35 m2/人;参加工作7~10 a可减免租金8%,可租的最大面积为40 m2/人。
| 参加工作 年限W/a | 减免租金 比例J/% | 最大租住 面积E/m2 |
| 1~3 | 30 | 30 |
| 4~6 | 15 | 35 |
| 7~10 | 8 | 40 |
假设工作2 a的高学历夹心层租住一套28 m2的住房,市场租金单价为45 元/m2,由于保障福利,他所需支付租金为
| ${R_1} = 28 \times \left( {1 - 30\% } \right) \times 45 = 882元$。 |
居民住房是涉及到国家民生大计的问题,但是随着城市化的日益加快,我国城市住房的紧张状况逐步凸显,住房依然是困扰居民的一大问题。目前我国政府已经将完善住房保障制度纳入了政府职能,体现了保障性住房的现实重要性,同时保障性住房的理论研究已经取得长足发展,但是从过滤理论视角去研究保障性住房问题始终未能取得突破性进展。
本文从过滤理论出发,对出租形式的保障性住房租金进行研究,分别针对低收入者、中低收入者和夹心层三类受保障人群设计了保障性住房的租金模型。模型的设计包括过滤器、保障条件、租金限定三方面内容,主要得到以下结论:
1 ) 过滤器设计方面,不同保障对象的过滤器条件不同,低收入者根据社会合理消费来确定,中低收入者依据消费理论来计算,夹心层根据社会合理消费以及未来购房所需年份和住房价格来计算。
2 ) 保障条件方面,提出低收入者和中低收入者根据收入线限定,而夹心层根据收入线和工作年限限定。
3 ) 租金限定方面,保障性住房的租金收取应该主要针对中低收入者和夹心层,低收入者可免收租金,中低收入者根据成本收益法收取租金,夹心层根据学历和工作年限分层收取租金。总之,通过租金模型的设计,以期为我国保障性住房的政策制定提供重要参考。
| [1] |
刘望保, 闫小培, 曹小曙. 西方国家城市内部居住迁移研究综述[J].
地理科学, 2008, 28(1): 131–137.
LIU Wangbao, YAN Xiaopei, CAO Xiaoshu. Review on intra-urban residential mobility in the western country[J]. Scientia geographica sinica, 2008, 28(1): 131–137. |
| [2] |
塔娜, 柴彦威, 刘志林. 过滤理论的起源、概念及研究进展[J].
人文地理, 2011(1): 10–14.
TA Na, CHAI Yanwei, LIU Zhilin. The origin, concepts and research progress of filtering theory[J]. Human geography, 2011(1): 10–14. |
| [3] | SWEENEY J L. Quality, commodity hierarchies, and housing markets[J]. Econometrica: journal of the econometric society, 1974, 42(1): 147–167. DOI:10.2307/1913691 |
| [4] | GALSTER G. Comparing demand-side and supply-side housing policies: sub-market and spatial perspectives[J]. Housing studies, 1997, 12(4): 561–577. DOI:10.1080/02673039708720916 |
| [5] | ROSENTHAL S S. Are private markets and filtering a viable source of low-income housing? Estimates from a "Repeat Income" model[J]. American economic review, 2014, 104(2): 687–706. DOI:10.1257/aer.104.2.687 |
| [6] | HARRIS R. "Ragged urchins play on marquetry floors": the discourse of filtering is reconstructed, 1920s-1950s[J]. Housing policy debate, 2012, 22(3): 463–482. DOI:10.1080/10511482.2012.680481 |
| [7] | DASCHER K. Federal coordination of local housing demolition in the presence of filtering and migration[J]. International tax and public finance, 2012, 21(3): 375–396. |
| [8] |
赵佩佩. 我国大城市社会保障性住房供给效用的若干分析[J].
现代城市研究, 2007, 22(10): 63–69.
ZHAO Peipei. Some analysis on supply effects of social security houses in chinese large cities[J]. Modern urban research, 2007, 22(10): 63–69. |
| [9] |
陈筱, 汤玉刚. 住房过滤模型的发展与政策启示[J].
经济体制改革, 2009(5): 137–142.
CHEN Xiao, TANG Yugang. Development of housing filtering model and its policy implications[J]. Reform of economic system, 2009(5): 137–142. |
| [10] |
闫佳佳. 从住房过滤理论分析低收入群体的住房保障与信贷支持[J].
现代经济信息, 2011(12): 179.
YAN Jiajia. Analysis of housing security and credit support for low income groups from the housing filter theory[J]. Modern economic information, 2011(12): 179. |
| [11] | LIU Beibei. Housing needs of low-income floating population-in case of urban villages redevelopment projects in kunming, P.R. China[D]. Trondheim: Norwegian University of Science and Technology, 2011. |



