随着经济的发展,中国对能源的需求日益增大。在石油业迅猛发展的同时,海上溢油事故发生的几率也随之增大。石油的泄漏不仅会对海洋生态系统造成威胁,还会对渔业、海岸环境以及人类的可持续发展造成不可估量的严重后果[1]。因此,了解溢油在海面上的运动及变化规律,对于溢油事故发生时及时采取有效防治措施以降低溢油带来的危害具有极其重要的意义。位于山东半岛烟台港的栾家口港区南依陆地,北临渤海,东部岸线向东延伸,越过蓬莱市后进入黄海;西部岸线向西南延伸进入莱州湾。由于港口所在位置重要,一旦发生溢油事件将对该海域周边产业及海洋环境造成严重影响。
因此,以栾家口港区海域作为研究区域,建立溢油模型,并应用该模型对溢油事故展开数值试验,预测溢油漂移规律,本研究可为烟台港栾家口港区溢油事故采取迅速的应急措施提供有效的参考依据。
1 海上溢油模型及模型验证溢油进入水体后会发生一系列复杂的物理、化学变化,并最终消失在海洋环境中。其变化过程主要分为油膜的扩展、漂移以及风化过程。
油膜的扩展是指在惯性力、重力、粘性力以及表面张力的作用下,油膜各质点的相对运动。国内外众多学者对油膜扩展模型做了众多研究。早期,Blokker [2]以自由平面上的油作为研究对象,根据油膜的质量守恒,忽略表面张力以及粘性力,只考虑重力和溢油体积的影响,建立了油膜扩展公式。Fay将油膜的扩展分为惯性扩展阶段、粘性扩展阶段以及表面张力扩展阶段三个阶段,假定水面为平静,油膜在扩展过程中始终保持圆形,油膜在各个扩展阶段的特性用油膜直径D反映。Fay理论提出后,国内外众多学者对油膜的扩展进行了进一步的研究。赵文谦等[3]考虑了油膜的扩展和扩散作用,以及油膜边缘的消失过程,建立了油膜扩展范围公式。刘肖孔[4]在总结前人研究的基础上,将油膜扩展三阶段综合为一个公式进行表达。
油膜的漂移是指在在表面流以及风力因素的作用下,油膜的整体运动。国内外许多学者对油膜漂移过程进行了大量的研究。Nary模型[6]给出了考虑潮流、河流入流、风漂流以及地球自转科氏力的作用下的溢油漂移时间和位移计算公。SEADOCK模型将近海、外海的风速矢量通过权重系数协调,并与表面海流矢量叠加,以此来预测油膜在风、海流作用下的飘移涌动,得到油膜质心的位移。蒙特卡罗方法[7]将溢油看成大量的油粒子,通过运用溢油扩展预测程序显示溢油归宿轨迹。Delaware模型[8]考虑了地球旋转力以及波浪的影响,对潮流及风引起的油膜迁移建立位移公式。
溢油的风化过程主要包括溢油的蒸发、溶解、分散、乳化、吸附、沉降以及光氧化和生物降解[9]。
1.1 油膜的扩展本文采用Fay公式计算溢油的扩展根据油在水面的实际受力情况,考虑了油膜所受重力、表面张力、惯性力以及粘性力的作用,将油膜扩展的过程分为三个阶段,即重力-惯性力阶段、重力-粘性力阶段和表面张力-粘性力阶段[3]。
三个阶段的扩展半径:
重力扩展阶段:
| $ {{L}_{1}}={{K}_{1}}{{\left( gV\mathit {\Delta} \right)}^{1/4}}{{t}^{1/2}} $ | (1) |
粘性扩展阶段:
| $ {{L}_{2}}={{K}_{2}}{{\left[ g\left( 1-\mathit {\Delta} \right)\mathit {\Delta} \right]}^{1/6}}\upsilon _{w}^{-1/12}{{t}^{1/4}}{{V}^{1/4}} $ | (2) |
表面张力扩展:
| $ {{L}_{3}}={{K}_{3}}{{g}^{-1/4}}{{\delta }^{1/2}}\rho _{w}^{-3/4}{{t}^{3/4}} $ | (3) |
式中:Δ=1-ρ0/ρw,ρ0为油密度,ρw为水密度;L为油膜扩展直径,下标表示不同阶段;δ=δwa-δao-δow,δwa、δao、δow分别为水与空气间、油与空气间、油与水间的表面张力系数;υw为水的运动黏滞系数;K1=1.35、K2=1.60、K3=0.48为试验常数;t为时间,从溢油开始起算;V=
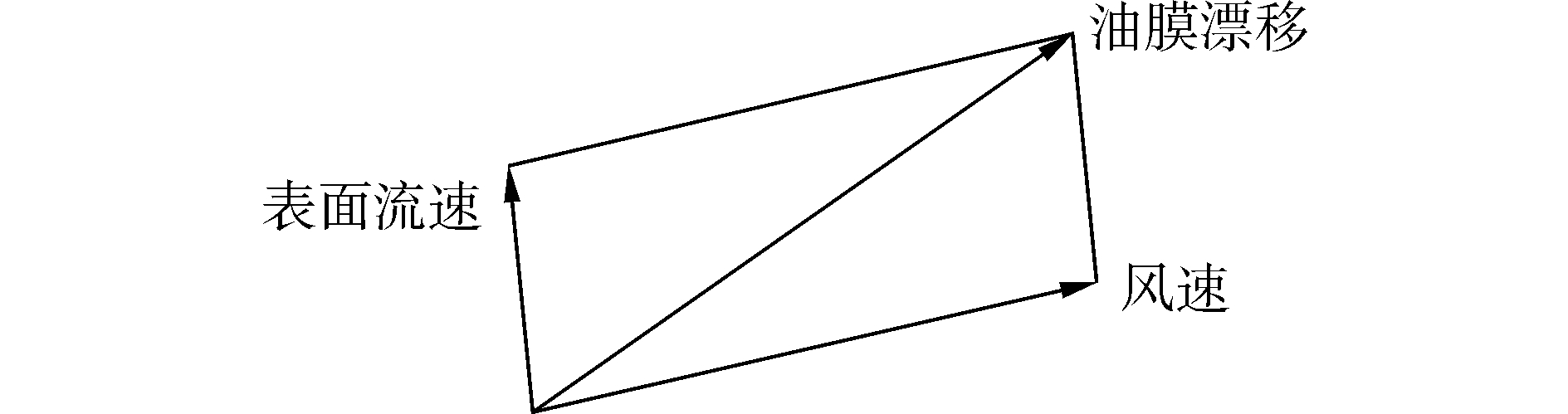
风场和表面流场是使油膜漂移的主要动力因素,如图 1所示[5]。
|
| 图1 迁移速度矢量合成示意图 Figure 1 Vector synthesis migration velocity |
| $ {{u}_{r}}\prime ={{u}_{c}}\prime +{{u}_{w}}\prime $ | (4) |
| $ {{u}_{c}}\prime ={{K}_{1}}{{u}_{c}} $ | (5) |
| $ {{u}_{w}}\prime ={{K}_{2}}{{u}_{f}} $ | (6) |
式中:ur′为油膜迁移速度;uc′为表面流速;uw′为风速;K1=1为潮流漂流系数;K2=0.035为(水面上10 m风速) 风漂流系数。
油膜厚度由质量守恒原理确定,公式为:
| $ \begin{align} & \frac{\partial \left( Ch \right)}{\partial t}+\frac{\partial \left( uCh \right)}{\partial x}+\frac{\partial \left( vCh \right)}{\partial y}= \\ & \ \ \ \ \ \ \ \ -({{\mathit \Phi }_{s}}+{{\mathit \Phi }_{b}}+R) \\ \end{align} $ | (7) |
式中:C为油膜浓度;h为油膜厚度;Φs为油膜上表面的油通量;Φb为油膜下表面的油通量;R为油膜物理、化学过程损失量。
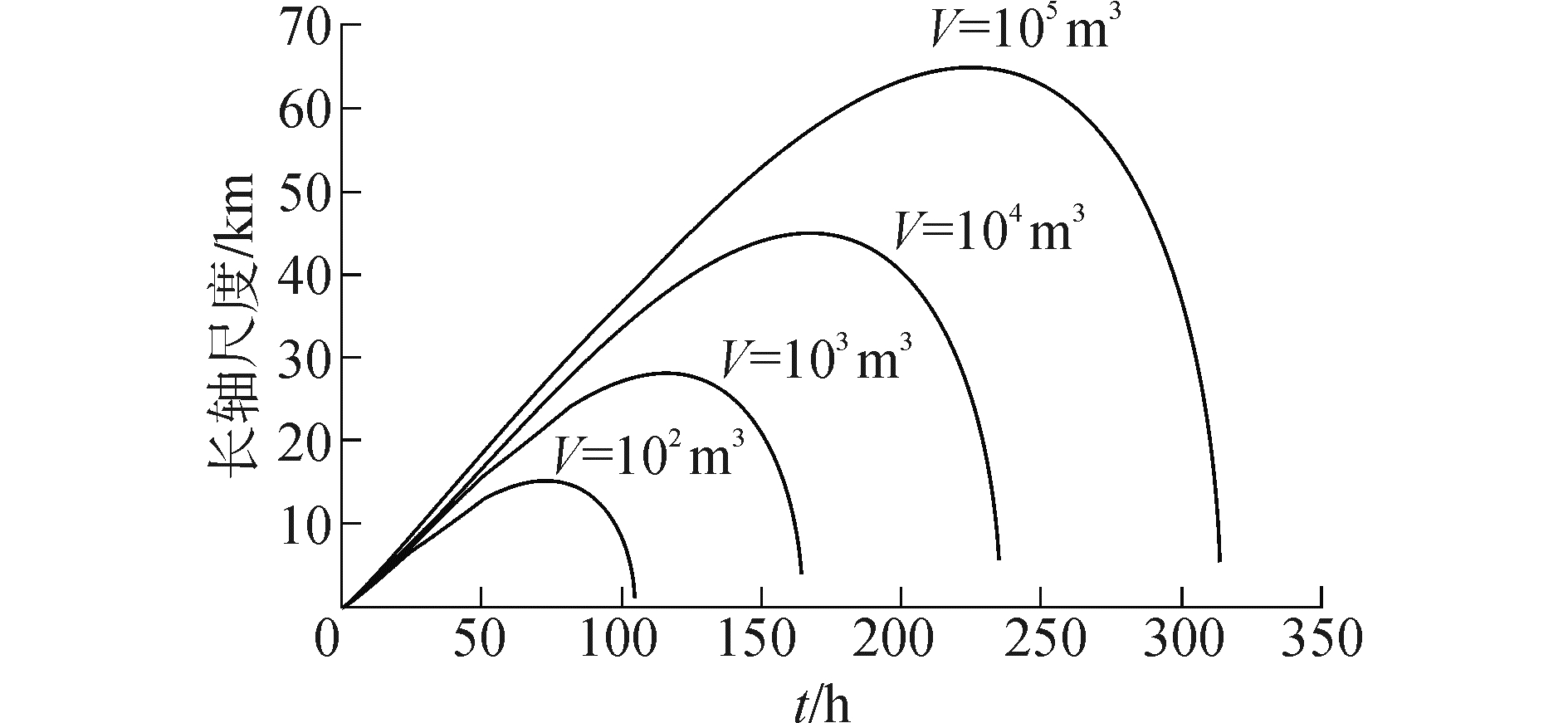
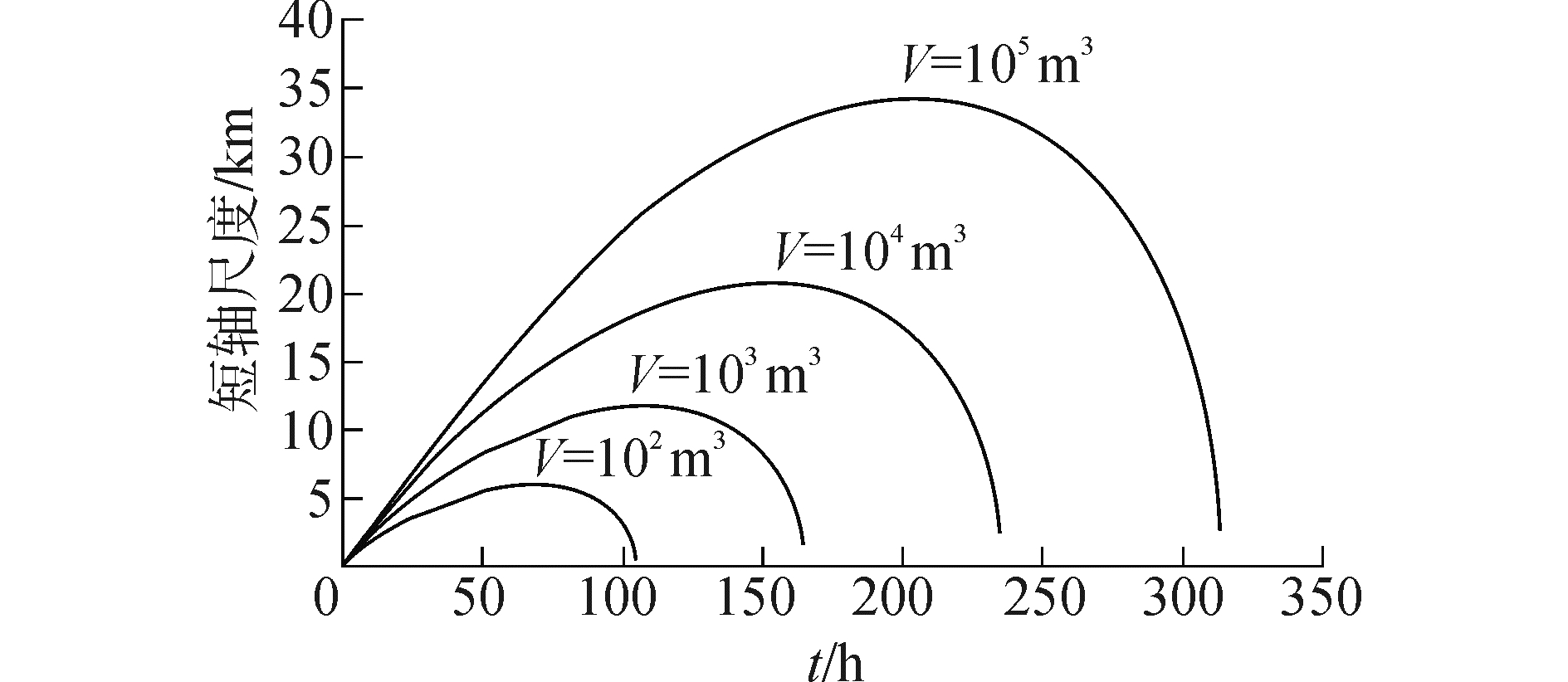
1.3 溢油模型的验证油膜自身的扩展和延展是溢油扩散与浓度扩散的主要区别之一。油膜扩延展体现于油膜长短轴尺度随时间的变化关系,本模型所采用公式给出的油膜长短轴尺度随时间的变化关系曲线见图 2和图 3,其中反映了油量对长短轴尺度的影响和油膜的最终消失时间,模拟结果与油膜分析研究基本一致。
|
| 图2 油膜长轴尺度随时间的变化曲线 Figure 2 Variation curve of oil slick long axis change in time |
|
| 图3 油膜短轴尺度随时间的变化曲线 Figure 3 Variation curve of oil slick short axis change in time |
油膜扩展公式通过水槽实验进行验证。模拟结果与实测结果对比如表 1所示,模拟计算结果和水槽试验过程见图 4、图 5,其中中间图为模拟结果,两侧为实验水槽中不同时刻的油膜扩展情况。
| 初始尺寸/cm | 结束尺寸/cm | 运动长度/m | 运动时间/s | |
| 计算值 | 15 | 21 | 1.17 | 30 |
| 实验值 | 15 | 22 | 1.20 | 30 |

|
| 图4 水槽实验时刻1油膜扩散漂移 Figure 4 Experiment of oil slick in flume in time-one |

|
| 图5 水槽实验时刻2油膜扩散漂移 Figure 5 Experiment of oil slick in flume in time-two |
考虑风应力作用的水动力模型的基本方程为浅水环流方程组[10],其中连续方程为
| $ \frac{\partial z}{\partial t}+\frac{\partial \left( uh \right)}{\partial x}+\frac{\partial \left( vh \right)}{\partial y}=0 $ | (8) |
运动方程为
| $ \begin{align} & \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+g\frac{\partial z}{\partial x}= \\ & -g\frac{\sqrt{{{u}^{2}}+{{v}^{2}}}}{{{c}^{2}}h}u+fv+\frac{{{\tau }_{xs}}}{\rho h}+{{M}_{x}} \\ \end{align} $ | (9) |
| $ \begin{align} & \frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+g\frac{\partial z}{\partial y}= \\ & -g\frac{\sqrt{{{u}^{2}}+{{v}^{2}}}}{{{c}^{2}}h}v-fu+\frac{{{\tau }_{ys}}}{\rho h}+{{M}_{y}} \\ \end{align} $ | (10) |
式中:
| $ \left\{ \begin{align} & {{M}_{x}}={{A}_{h}}(\frac{{{\partial }^{2}}u}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}u}{\partial {{y}^{2}}}) \\ & {{M}_{y}}={{A}_{h}}(\frac{{{\partial }^{2}}v}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}v}{\partial {{y}^{2}}}) \\ \end{align} \right. $ | (11) |
式中:u、v为在x、y方向的流速分量;z为水位;g为重力加速度;c为谢才阻力系数;h为水深;f为柯氏力系数;Ah为水平涡粘系数;ρ为水体密度;τxs、τys为在x、y方向的海面风应力分量。
确定风应力的经验公式为:
| $ \left\{ \begin{align} & {{\tau }_{xs}}=0.125{{C}_{D}}{{W}_{x}}\left| \boldsymbol{W} \right| \\ & {{\tau }_{ys}}=0.125{{C}_{D}}{{W}_{y}}\left| \boldsymbol{W} \right| \\ \end{align} \right. $ | (12) |
式中:CD为风拖曳力系数;Wx、Wy为在x、y方向的海面风速分量;W为风速矢量。CD按Heaps经验公式取值,经验公式为:
| $ {{C}_{D}}=\left\{ \begin{matrix} 0.564\times {{10}^{-3}},\ \ \ \ \ \left| \boldsymbol{W} \right|\le 4.917 \\ \begin{align} & \left( -0.12+0.13\left| \boldsymbol{W} \right| \right)\times {{10}^{-3}}, \\ & \ \ 4.917 < \left| \boldsymbol{W} \right| < 19.211 \\ \end{align} \\ 2.513\times {{10}^{-3}},\ \ \ \ \ \left| \boldsymbol{W} \right|\ge 19.221 \\ \end{matrix} \right. $ | (13) |
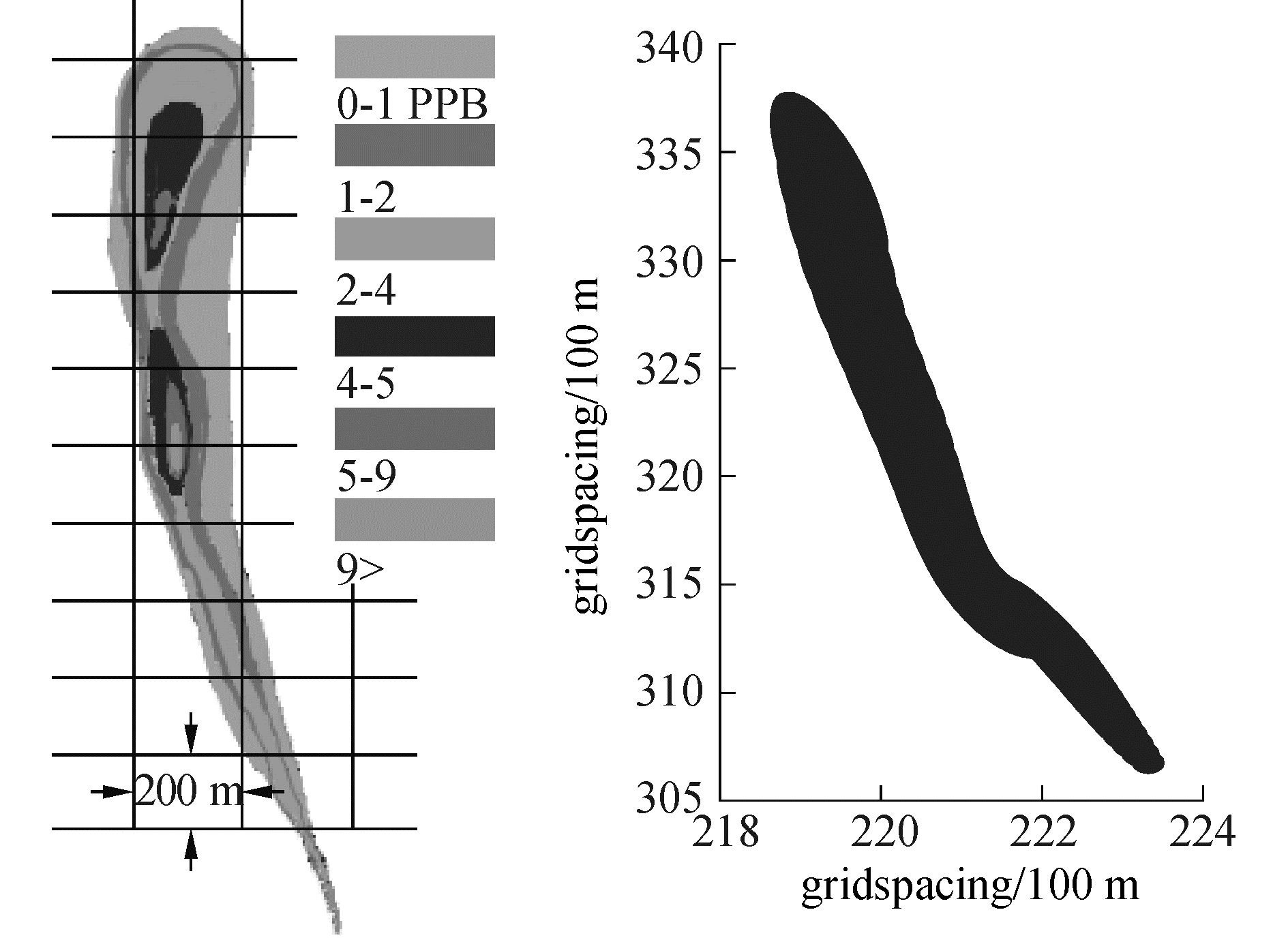
海区上现场示踪与模型计算结果的比较见图 6,可以看出扩散趋势和范围基本一致。其中染料示踪实验结果来源于中国科学院南海海洋研究所。
|
| 图6 染料示踪结果与溢油模型模拟结果比较 Figure 6 Comparison between simulation results and test results |
由于研究范围面积较大,同时要反映港口航道细部的地形地貌,采用有限元三角网格剖分模型,在港区、航道、人工岛附近将网格加密,形成单元个数为47 244,结点个数为24 350,模型网格最大空间步长约2 000 m,最小空间步长约25 m的网格,见图 7所示。

|
| 图7 网格剖分图 Figure 7 The model grids |
由于模型海区边界缺乏实测潮汐资料,需采用调和分析方法确定,天文潮可以用多个分潮的组合进行表示。将分潮组合的天文潮作为模型边界,通过调试和验证与模型内部的验证点比较达到一定精度。
3.2 模型边界条件模型海区边界缺乏实测潮汐资料,需采用调和分析方法确定[11],天文潮可以用多个分潮的组合表示为
| $ \zeta \left( t \right)=\sum\limits_{j=1}^{m}{{{f}_{j}}{{H}_{j}}}\text{cos}({{\sigma }_{j}}t+{{V}_{0j}}+{{u}_{j}}-{{K}_{j}}) $ | (14) |
式中:ζ(t) 为天文潮过程;f为平均振幅H的订正值,也称为分潮交点因子;H为平均振幅,是振幅调和常数;σ为分潮角频率,单位为1/平太阳时;t为时间;V0为分潮初相角;u为分潮初相角的订正系数;K为迟角,是幅角调和常数。模型潮位边界过程部分时间段见图 8~11。
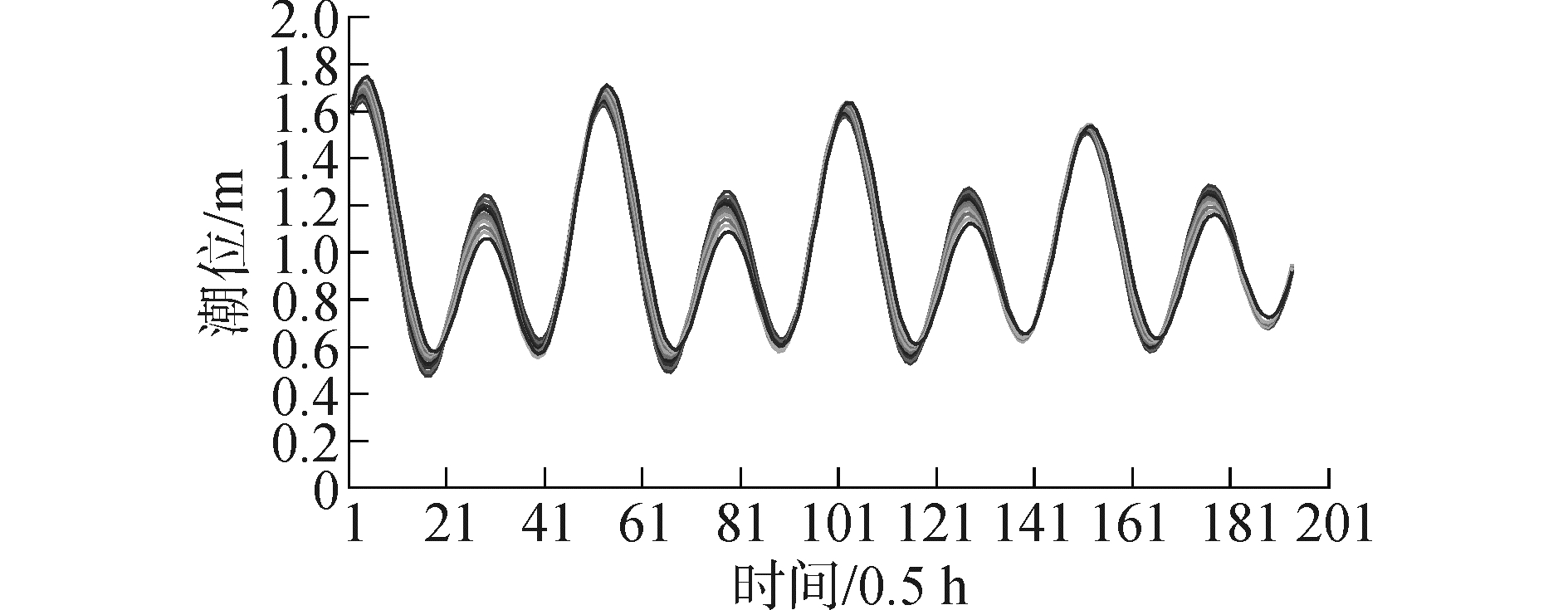
|
| 图8 模型东侧潮位边界过程 Figure 8 Tide level process of the east of model |
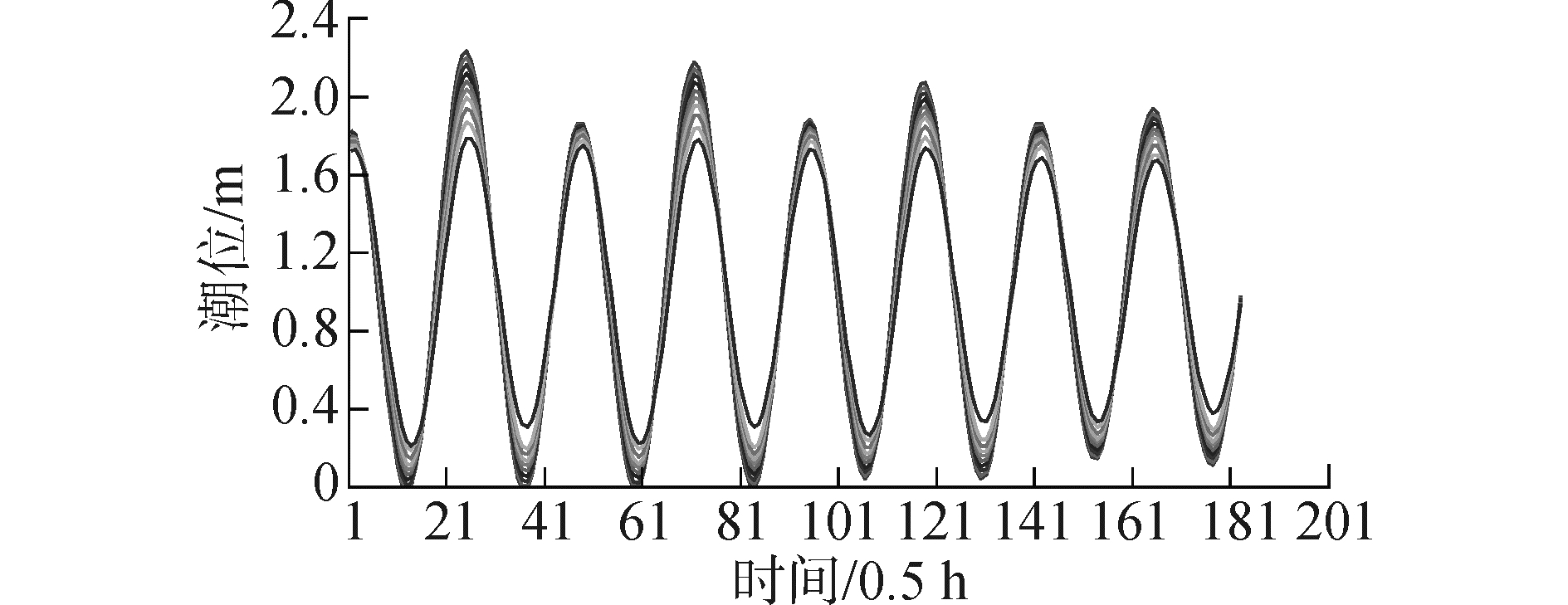
|
| 图9 模型东北侧潮位边界过程 Figure 9 Tide level process of the northeast of model |
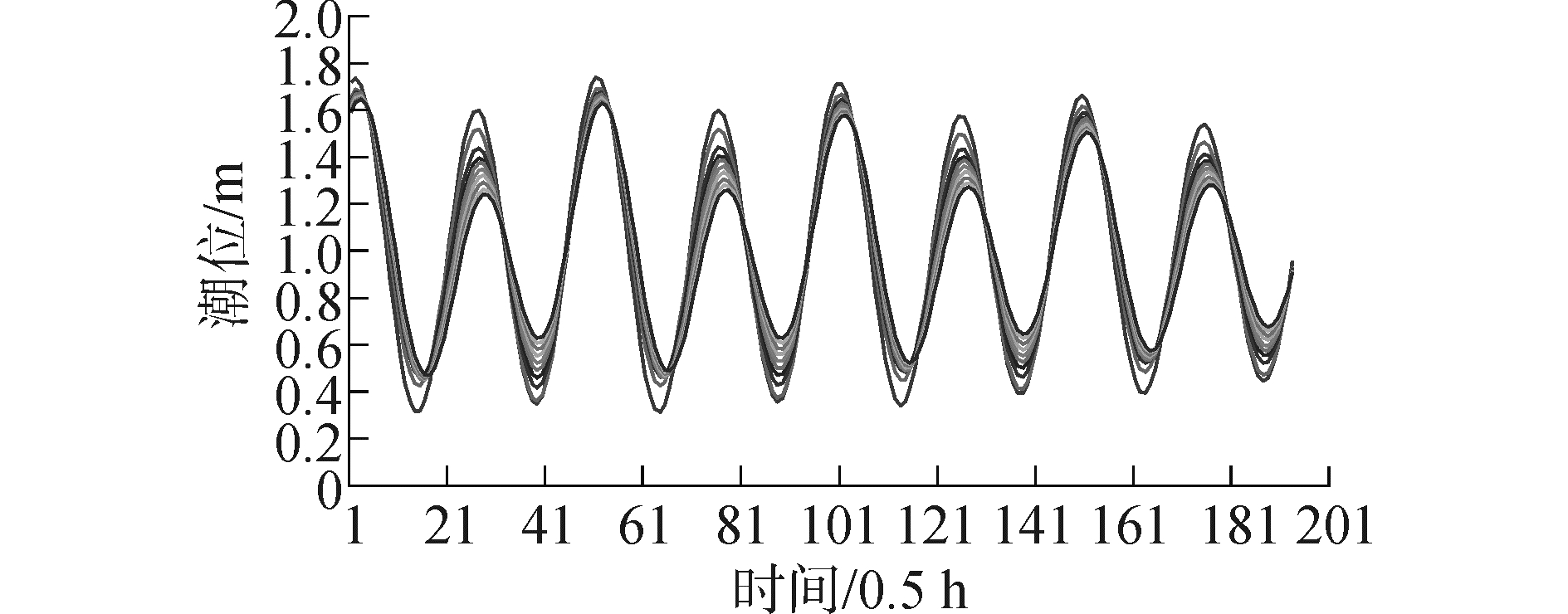
|
| 图10 模型西北侧潮位边界过程 Figure 10 Tide level process of the southwest of model |
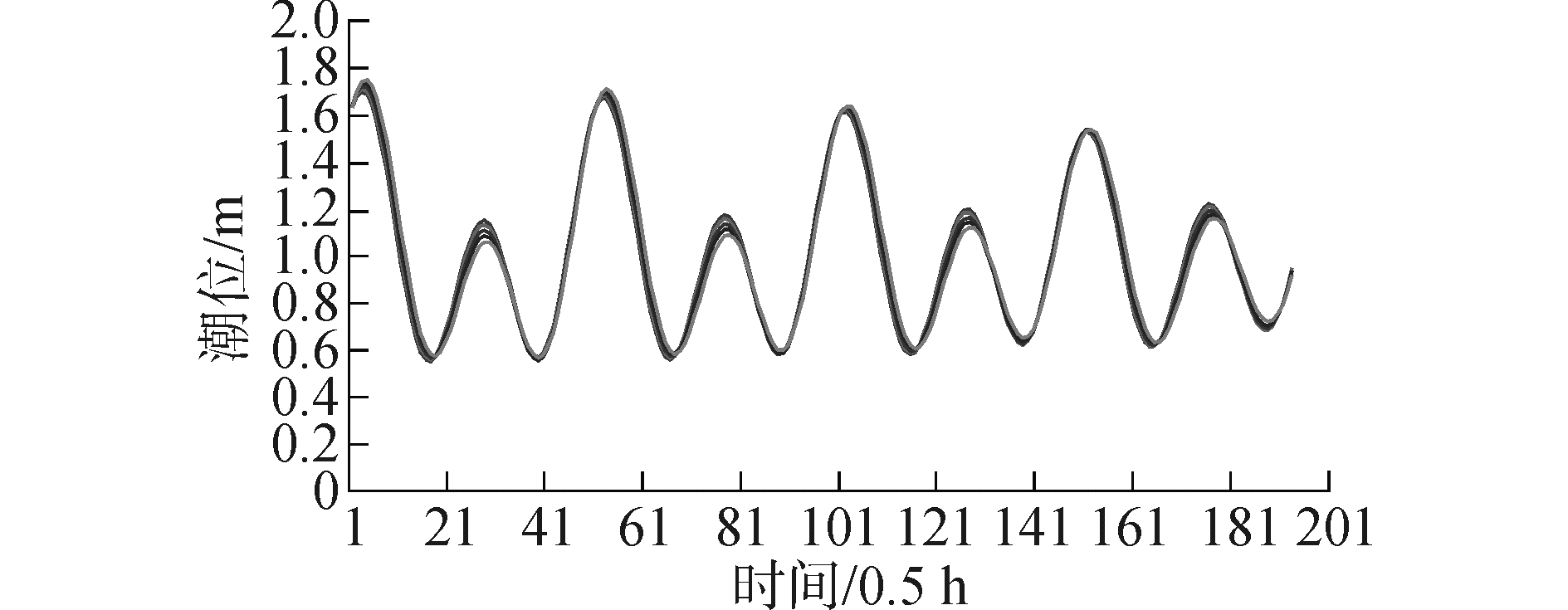
|
| 图11 模型西侧潮位边界过程 Figure 11 Tide level process of the west of model |
模型验证资料取自交通运输部天津水运工程科学研究所天津水运工程勘察设计院《蓬莱西海岸海洋文化旅游产业聚集区区域建设用海工程水文测验分析报告》,其中流速验证点为9个,潮位验证点为3个。验潮时间为2011年7月4日00:00~2011年7月14日14:30,历时10整天。其中包含了水文全潮测验大、小潮时间段。实际实测时间为:大潮:2011年7月5日10:00~2011年7月6日15:00(农历六月初五~六月初六),高潮~高潮。
小潮:2011年7月9日8:00-2011年7月10日13:00(农历六月初九~六月初十),低潮~低潮。大潮测验期间施测海域最大风速为5.2 m/s,风向为SSW,平均风速为2.4 m/s,风向以S~SW为主,测验期间施测海域海况良好,为1~2级,最大波高0.8 m (出现在U1测站)。小潮测验期间施测海域有雾,最大风速为7.6 m/s,风向为ENE,平均风速为3.8 m/s,风向以E~ENE为主,测验期间施测海域海况较好,为2~3级,最大波高1.2 m (出现在U1测站)。验证点如图 12所示,验证模型流速计算结果见图 13所示,验证模型流向计算结果见图 14所示(9点中任选2点)。验证点H1、H2、H3的潮位验证结果如图 15所示。
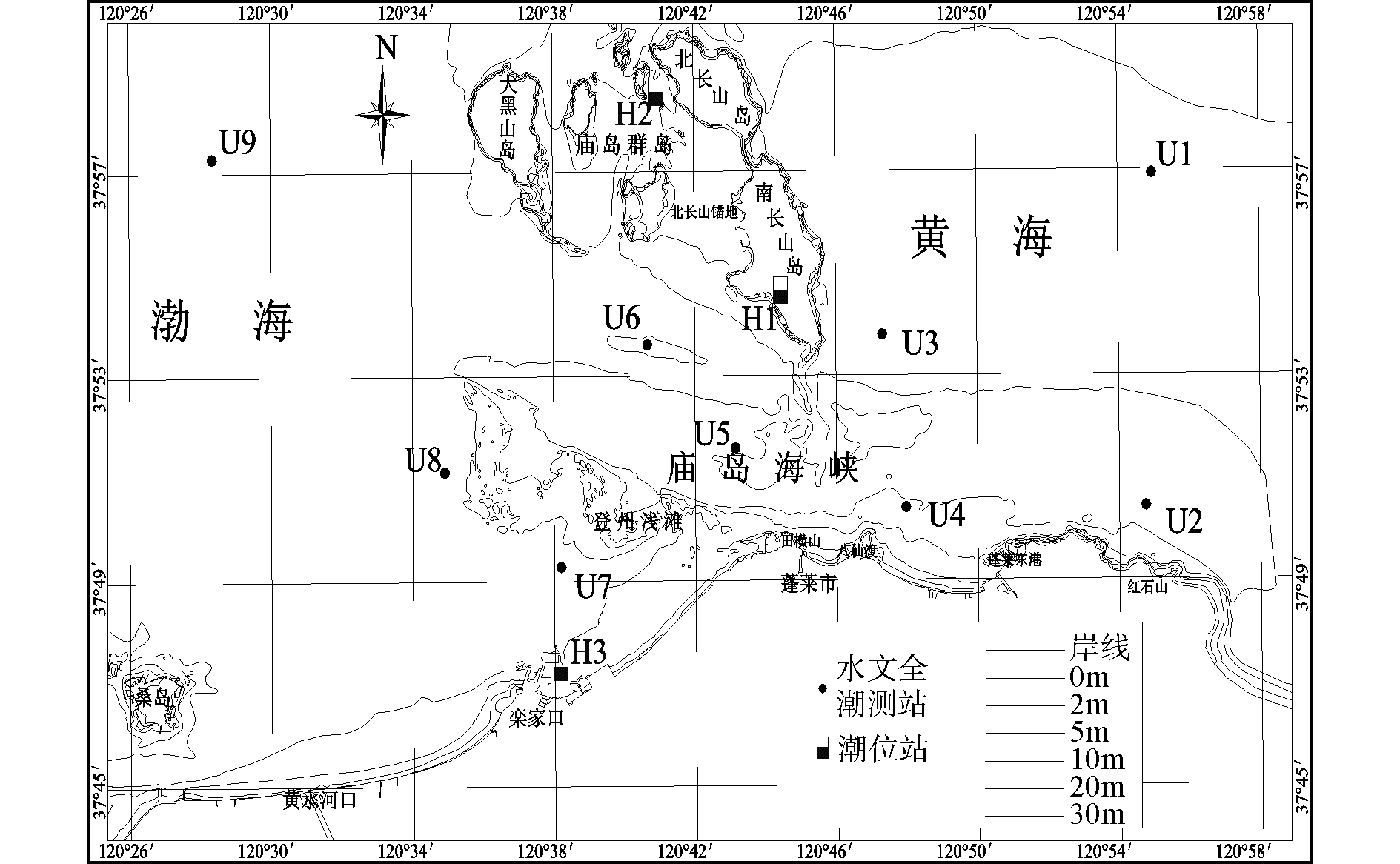
|
| 图12 验证点位置 Figure 12 Location of verification points |
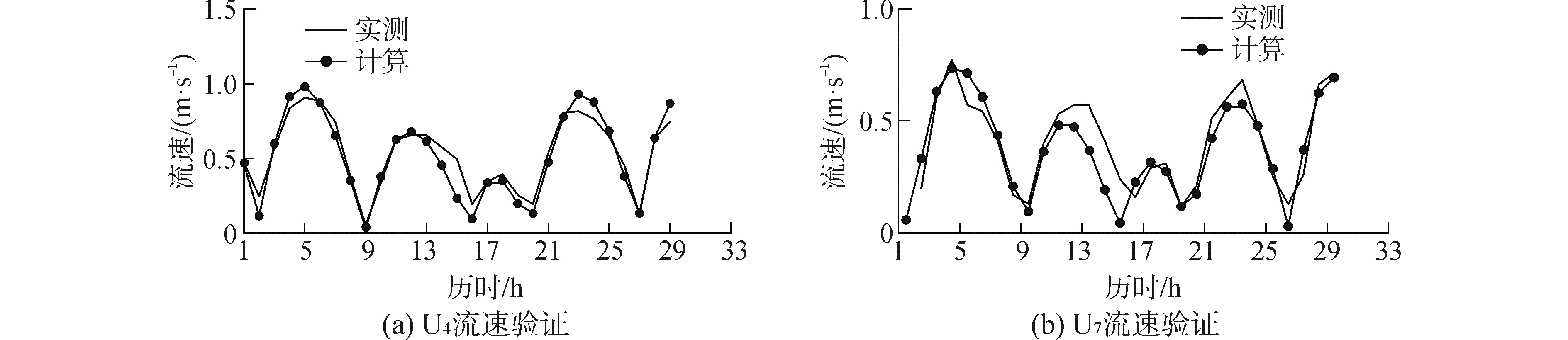
|
| 图13 U4和U7流速验证 Figure 13 Velocity verification of U4 and U7 |
从图可以看出,测点的潮位、流速以及流向与实测值基本一致,模拟结果较好的反映了海流特征,应用该模型进行溢油轨迹的预测具有较高的可靠度。
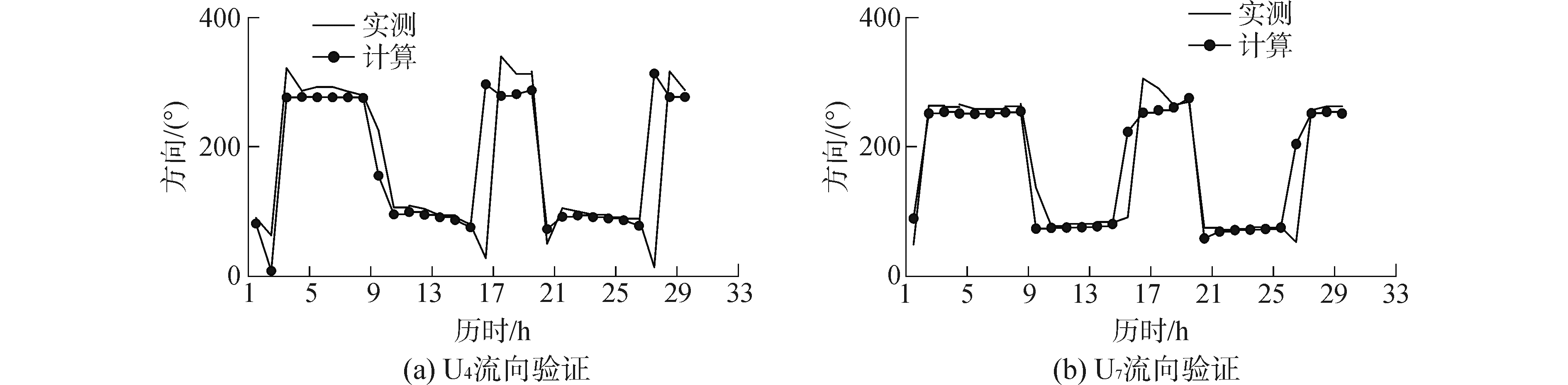
|
| 图14 U4和U7流向验证 Figure 14 Velocity direction verification of U4 and U7 |
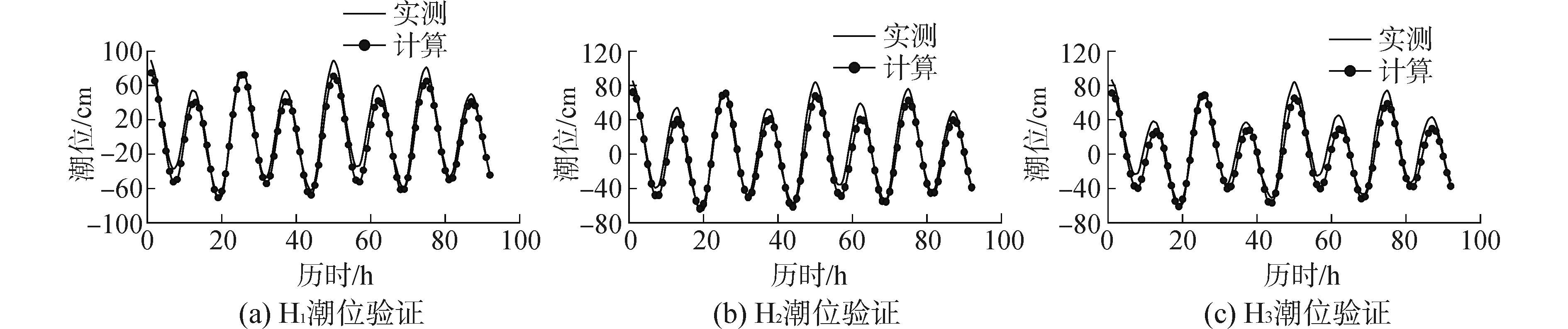
|
| 图15 H1、H2、H3潮位验证 Figure 15 Tide level verification of H1、H2、H3 |
海上溢油迁移的动力条件有潮流场、风场和油膜自身的延展构成。潮流场以潮流模型为基础考虑港口工程、航道北部防波堤和双鱼型人工岛海区溢油情况,以此流场为依据计算模拟48 h溢油扩散范围。风场应采用天津水运工程勘察设计院《蓬莱西海岸海洋文化旅游产业聚集区区域建设用海工程水文测验分析报告》中与潮流同期的水文全潮测验大潮风况波浪报表资料,同时参考烟台港的自然环境条件。由动力条件确定溢油环境考虑表 2列出的几种情况。
| 风况 | 无风 | SW | S | NW | NE |
| 风速/(m·s-1) | 0 | 4.9 | 2.0 | 3.4 | 2.7 |
| 潮流/h | 48 | 48 | 48 | 48 | 48 |
| 油膜 | 延展 | 延展 | 延展 | 延展 | 延展 |
| 说明 | 最大风向 | 不利风向1 | 不利风向2 | 不利风向3 |
表中最大风速、风向由实况资料确定,不利风向1为对庙岛海峡附近海域及岛屿的不利风向;不利风向2为对人工岛周边岸线的不利风向;不利风向3为对油品码头港池的不利风向。
3.5 结果与分析栾家口港区拥有万吨级油轮泊位,出港航道是油轮和船舶的必经之路,油品泄漏的突发事件有可能发生,本次模拟假定溢油点出现在出港航道的西端、中部和东端,临近港区、登州浅滩的实验区、人工岛和游船泊位,为高风险溢油区。溢油方式为瞬时溢油和连续溢油,瞬时溢油采用凝析油,溢油量为8 000 t,连续溢油采用低硫燃料油,溢油量为800 t/h,溢油时间为10 h。油品特征见表 3,其中API为美国协会采用的比重。海上溢油模型模拟时间步长为60 s;初始空间最小可分辨长度为15 m,为控制模拟时间,空间最大可分辨长度设计为100 m;模拟时间长度为48 h,采用随时间变化的潮位过程和潮流场分布,风况分别采用无风、SW、S、NW、NE5种风况。
| 油的名称 | 密度/(kg·m-3) | API比重 | 乳化含水量/% |
| 凝析油 | 830.5 | 38.80 | 74 |
| 低硫燃料油 | 972.0 | 14.08 | 80 |
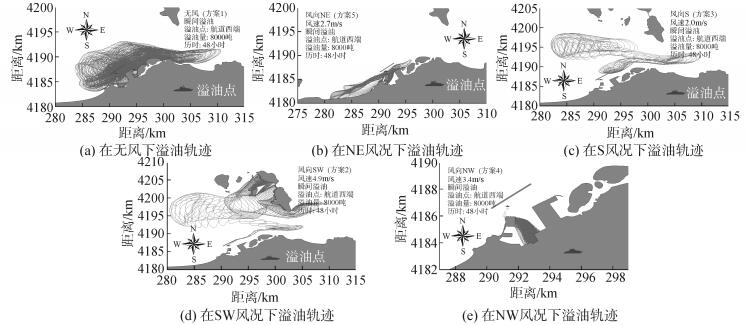
对于航道西部溢油点采用五种风况对其瞬时溢油进行模拟,得到溢油轨迹如图 16所示。
|
| 图16 输入和输出的自功率谱 Figure 16 Power spectrums of inputs and output |
由图 16可以看出,在航道西溢油点上瞬时溢油无风情况下,油膜随涨落潮流速迁移,由于航道附近涨落流速相当,油膜面积轨迹以溢油点为中心向周边辐射,当油膜伸展到庙岛海峡狭窄水道处时,落潮流速有所增加,出现向外海突出的油膜带。在东北风作用下,溢油后油膜随落潮流漂移一段距离后,在风速与涨潮流速联合作用,使油膜向西南方向运动,在途经客运泊位、港区时都有油膜侵入,部分油膜在48 h后漂移到港区西部的岸线处。在南风作用下,北防波堤对油膜沿风向移动具有阻挡作用,油膜贴近北防波堤后向落潮方向移动,移出北防波堤掩护区域后向庙岛群岛方向扩散,由于北防波堤的阻挡作用,使油膜脱离北防波堤后扩展不充分,油膜面积轨迹扫过的海区范围较小。在西南风作用下,北防波堤对油膜沿风向和涨落潮流向迁移没有阻挡作用,使溢油后油膜向落潮方向移动,移出北防波堤掩护区域后迅速向庙岛群岛方向扩散,油膜面积轨迹扫过的海区范围较大。在西北风作用下,溢油后油膜飘向港区附近,潮流速度较小,在西北风挤压下大部分油膜进入港区,油膜面积轨迹扫过大部分港区。溢油轨迹面积由大到小的风向依次为西南风、南风、无风、北风以及西北风。
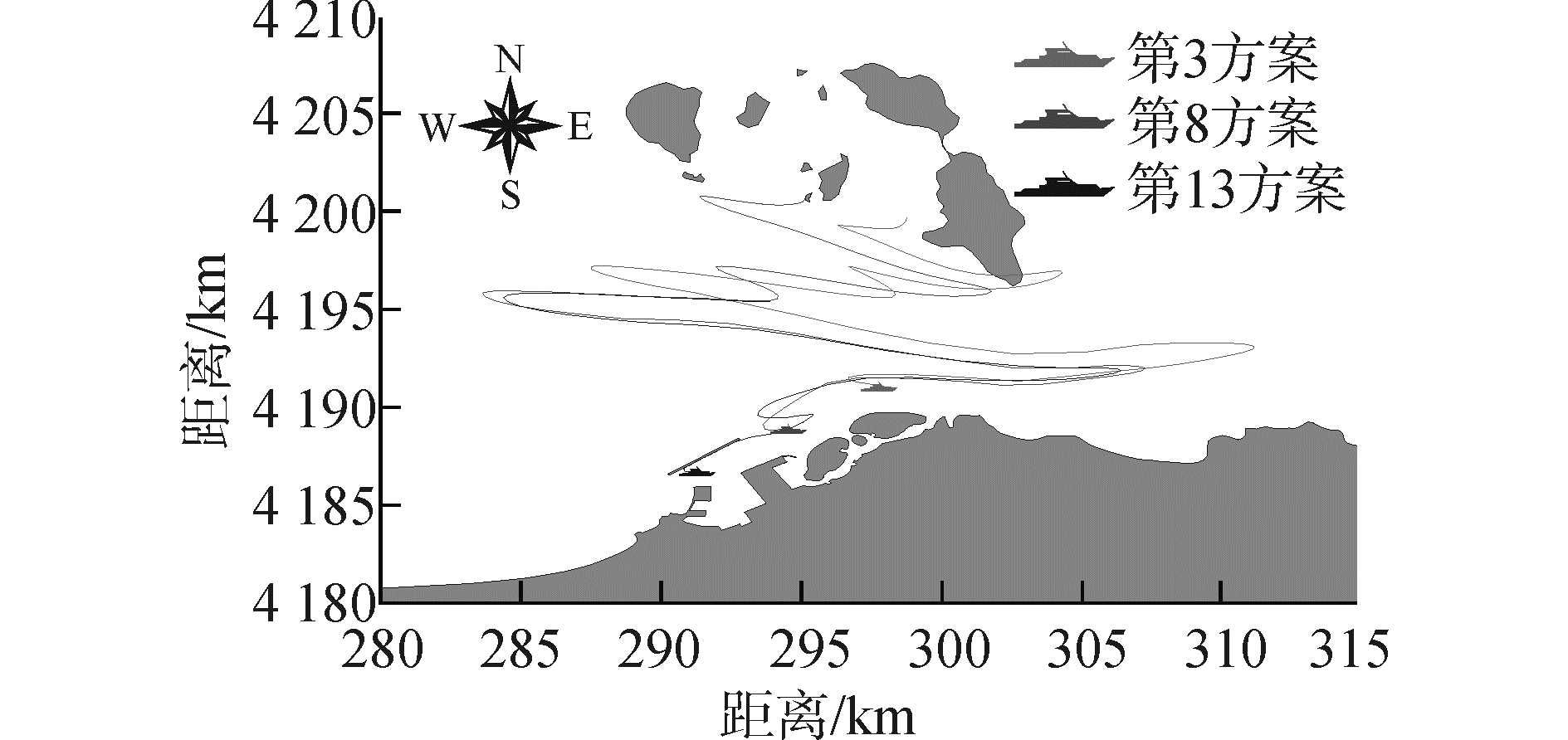
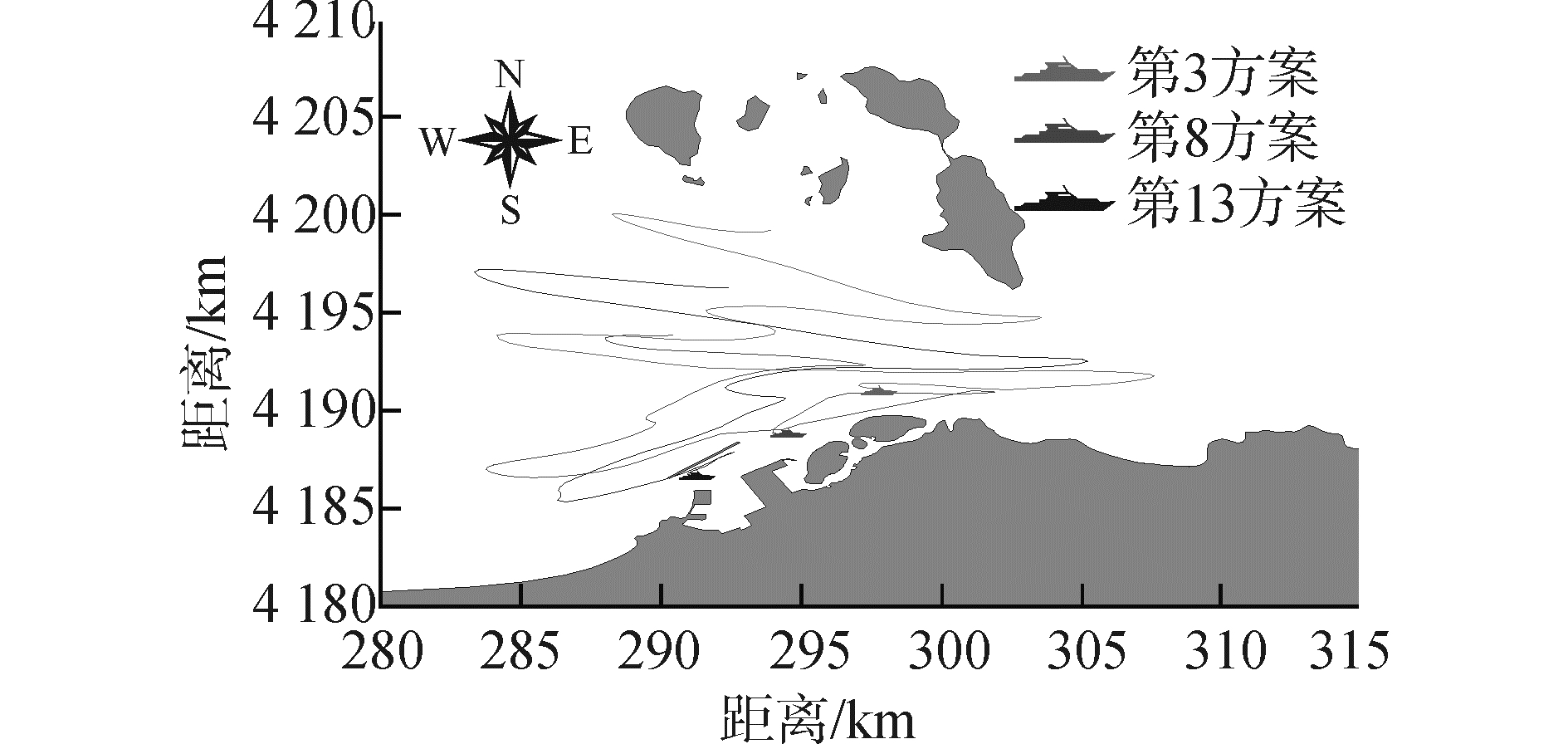
3.5.2 瞬时溢油与连续溢油的比较以油膜形心来表征油膜运动轨迹,如图 17、18所示,模拟了油膜在南风条件下不同溢油点瞬时溢油和连续溢油的运动轨迹。
|
| 图17 瞬时溢油油膜运动轨迹 Figure 17 Instant oil spill trajectory |
|
| 图18 连续溢油油膜运动轨迹 Figure 18 Continuous oil spill trajectory |
在南风作用瞬时溢油时,瞬时溢油量较大,当溢油点位于航道西部溢油后,油膜受南风作用很快与北防波堤相遇,潮流作用影响减小,南风使油膜贴近防波堤边壁,并使油膜沿边壁运动,直至油膜运动到北防波堤东端,脱离防波堤边壁,进入开阔海区。南风作用下连续溢油时,溢油量较小,溢油点位于航道西发生溢油后,油膜受南风作用虽向南偏移,但油膜面积较小,在没有接触到北防波堤之前,受涨潮流速影响油膜漂移出防波堤西端,随后在潮流和南风作用下,从北防波堤西侧进入开阔海区,之后呈“之”运动轨迹向庙岛群岛接近。从图中可以看出,瞬时溢油的运动轨迹向北延伸程度大于连续溢油向北延伸程度。
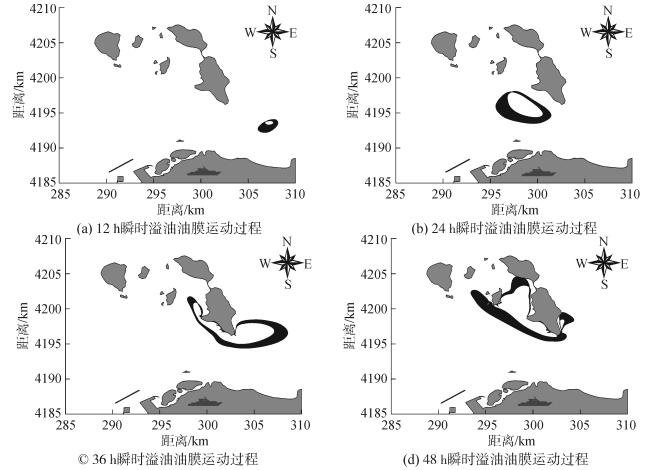
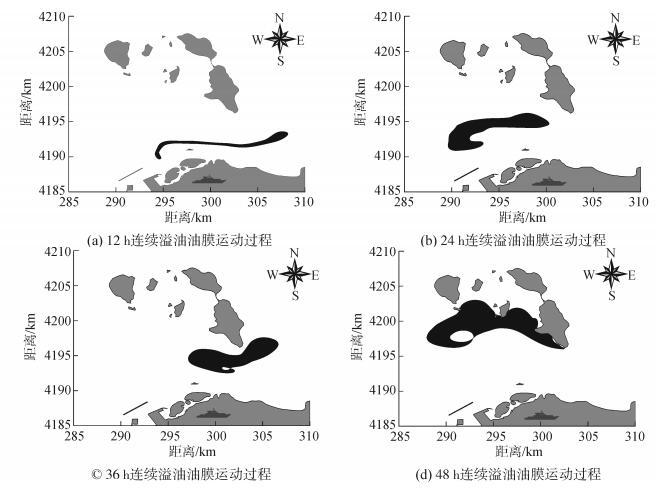
3.5.3 油膜运动过程分析对于瞬时溢油与连续溢油油膜的扩展面积进行比较。如图 19表示南风作用下溢油点位于航道东端瞬时溢油油膜运动过程。连续溢油的溢油总量与瞬时溢油量相同,但瞬时油量较小,油品的密度较大,溢油开始后溢油点新溢出的油膜与先前溢出的油膜混合,形成狭长的油带,油膜随潮流和风速进行迁移,同时油膜自身进行扩展。图 20表示南风作用下溢油点位于航道东端连续溢油油膜运动过程。
|
| 图19 瞬时溢油油膜运动过程 Figure 19 Instant oil spill motion process |
|
| 图20 连续溢油油膜运动过程 Figure 20 Continuous oil spill motion process |
油膜的迁移速度与油膜位置当地潮流速度和风速有关,油膜的扩展速度主要与溢油量成正比,与油品密度成反比,并受到周边地形的影响。瞬时溢油以近似椭圆形油膜形状漂移,破裂后一般形成不规则的多层圆环;连续溢油以狭长形油膜形状漂移,破裂后一般成形不规则的单层圆环。
不同风向及不同溢油方式下油膜扩散轨迹的模拟以及运动过程分析,对于溢油事故发生后能够及时有效的采取应急措施,减小污染扩散以及保护海洋生态环境具有重大意义。
4 结论在二维浅水环流方程组的基础上,综合考虑风、波浪等因素的影响建立了海上溢油数学模型,采用有限元方法进行离散。利用已建立的海上溢油数学模型对栾家口港区在不同动力条件、溢油点、溢油方式及油品种类分别进行模拟,得到油膜的扩散轨迹及运动过程,对海上溢油事故影响范围的预测以及有效应急措施的实施具有重要意义。
| [1] |
吴丹.渤海海洋溢油数学模型基本理论及应用研究[D].天津:天津大学, 2010:45-75.
WU Dan. Foundational theory and application research of mathematical modeling of oil spill on the sea in Bohai[D]. Tianjin:Tianjin University, 2010:45-75. |
| [2] | BLOKKER P C. Spreading and evaporation of petroleum products on water[C]//Proceedings of the 4th International Harbour Conference. Antwerp, the Netherlands, 1964:910-920. |
| [3] |
武周虎, 赵文谦. 海面溢油扩展、离散和迁移的组合模型[J].
海洋环境科学, 1992, 11(3): 33–40.
WU Zhouhu, ZHAO Wenqian. Oil spill expansion, dispersion and transportation jointed model on the sea[J]. Marine environmental science, 1992, 11(3): 33–40. |
| [4] | LIU S K, LEENDERTSE J J. A 3-D Oil spill model with and without ice cover[C]//Proceeding of Mechanics of Oil Slicks. Paris, France, 1981. |
| [5] |
张永良, 褚绍喜, 富国, 等. 溢油污染数学模型及其应用研究[J].
环境科学研究, 1991, 4(3): 7–17.
ZHANG Yongliang, CHU Shaoxi, FU Guo, et al. Study on the mathematical model of oil spill pollution and its application[J]. Research of environmental sciences, 1991, 4(3): 7–17. |
| [6] |
李冰绯.海上溢油的行为和归宿数学模型基本理论与建立方法的研究[D].天津:天津大学, 2004:21-70.
LI Bingfei. Study on the basic theory and establishing method of mathematical modeling of oil spill on the sea[D]. Tianjin:Tianjin University, 2004:21-70. |
| [7] |
娄安刚, 奚盘根, 黄祖珂, 等. 海面溢油轨迹的分析与预报[J].
青岛海洋大学学报, 1992, 24(4): 477–484.
LOU Angang, XI Pangen, HUANG Zuke, et al. Prediction of oil spill track and study on its dispersion over the sea[J]. Journal of ocean university of Qingdao, 1992, 24(4): 477–484. |
| [8] | WANG S, HWANG L S. A numerical model for simulation of oil spreading and transport and its application for predicting oil slick movement in bays[R]. NTIS Report AD0780424, 1974. |
| [9] | CHEN Haizhou, LI Daming, LI Xiao. Mathematical modeling of oil spill on the sea and application of the modeling in Daya Bay[J]. Journal of hydrodynamics, series B, 2007, 19(3): 282–291. DOI:10.1016/S1001-6058(07)60060-2 |
| [10] |
李大鸣, 刘川江, 吴丹, 等. 渤海海洋溢油的数学模型[J].
天津大学学报, 2012, 45(1): 50–57.
LI Daming, LIU Chuanjiang, WU Dan, et al. Mathematical model of marine oil spill in Bohai[J]. Journal of Tianjin university, 2012, 45(1): 50–57. |
| [11] |
宋志尧, 严以新, 茅丽华. 潮汐调和分析的一种算法[J].
海洋工程, 1997, 15(3): 40–45.
SONG Zhiyao, YAN Yixin, MAO Yihua. A tidal harmonious analysis method[J]. The ocean engineering, 1997, 15(3): 40–45. |
| [12] |
牟林, 邹和平, 武双全, 等. 海上溢油数值模型研究进展[J].
海洋通报, 2011, 30(4): 473–480.
MU Lin, ZOU Heping, WU Shuangquan, et al. Numerical model research on the ocean oil spill[J]. Marine science bulletin, 2011, 30(4): 473–480. |



