三体滑行艇是近年来所发展起来的一种新型的滑行艇艇型,相比于常规单体滑行艇,三体滑行艇在构型上的主要特征是起于船中的槽道分布于主艇体两侧。槽道在航行过程中不仅能够提供水动升力,当航速足够高时,槽道与艇体兴波脱离,还会提供气动升力来支持艇重,使得三体滑行艇具有远优于常规滑行艇的高速阻力性能。相关研究表明,三体滑行艇的槽道所产生的气动升力能够达到艇重的20%~30%[1];相比于具有单一槽道的双体滑行艇,虽然双体滑行艇在高速航行时所产生的气动升力可达到30~80%[2],但其槽道的气动压力中心通常位于重心之前,导致航行中的纵向稳定性变差;而三体滑行艇的气动压力中心则靠近艇尾,所产生的纵倾力矩能有效抑制海豚运动的发生,因而具有良好的高速运动稳定性。
目前,三体滑行艇已成为高性能类船舶的重要一支,有关其船体构型及水动力性能的研究也已成为滑行艇艇型研究中的热点问题。邹劲等[3]采用模型试验手段对三体滑行艇在静水和波浪中的水动力特性进行了系统的理论研究,对不同构型的模型在系列工况下的航行特性进行了分析[4],并尝试了在槽道内设置水翼、舭龙骨、喷气装置等设备来改善槽道的流动特性[5]。孙寒冰等[6]则采用数值手段对三体滑行艇主体部分所设置的引气槽结构进行了研究,讨论了不同拱度的引气槽对高速阻力性能的影响。Yousefi等[7]对现有的滑行艇水动力研究手段进行了总结,并采用基于FVM (finite volume method) 的Fluent软件对某单体滑行艇以及其加装槽道后的改进模型进行了对比研究。Morteza等[8]采用动网格方法结合船体六自由度运动方程实现了多槽道滑行艇两自由度静水拖航的模拟[9],Moghadam等[10]则采用相同的手段研究了槽道的截面形式对静水阻力性能的影响。
三体滑行艇槽道末段平直区域是槽道水气动力的主要作用区,对于全艇的阻力性能有着至关重要的影响。因此,本文采用CFX软件的FVM方法结合模型试验数据对该区域的高速流动特性进行了研究。
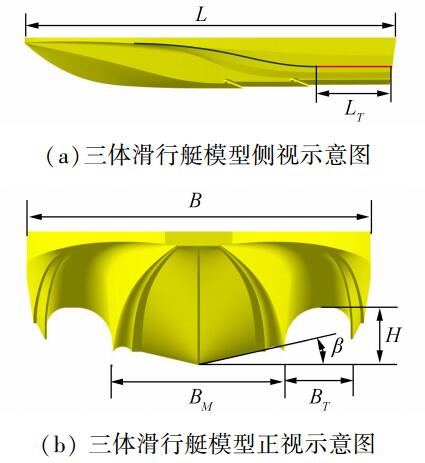
1 模型试验 1.1 模型简介本文研究的三体滑行艇模型侧视图如图 1(a)所示,槽道起始于船中之前,其前段呈反“S”型,后段则采用与基线平行的平直型,平直段LT的长度为0.2倍的船长L。从图 1(b)可以看出,主艇体占据了全艇绝大部分的排水体积;两侧的片体极为细长,其主要作用在于为槽道提供遮蔽并维持船体运动的平衡;槽道则由主体和片体所共同围成,为了与两侧壁面光滑过渡,在槽道顶的两端均采用了圆角处理。表 1中给出了以主艇体折角线宽BM进行无因次化后的主要尺度参数。
|
| 图1 三体滑行艇模型示意 Figure 1 Specification of planning trimaran model |
| 主要尺度 | 参数 |
| 总长L/BM | 5.5 |
| 总宽B/BM | 1.98 |
| 槽道宽BT/BM | 0.38 |
| 槽道高H/BM | 0.31 |
| 槽道平直段长度LS/BM | 1.1 |
| 主体斜升角β/(°) | 13 |
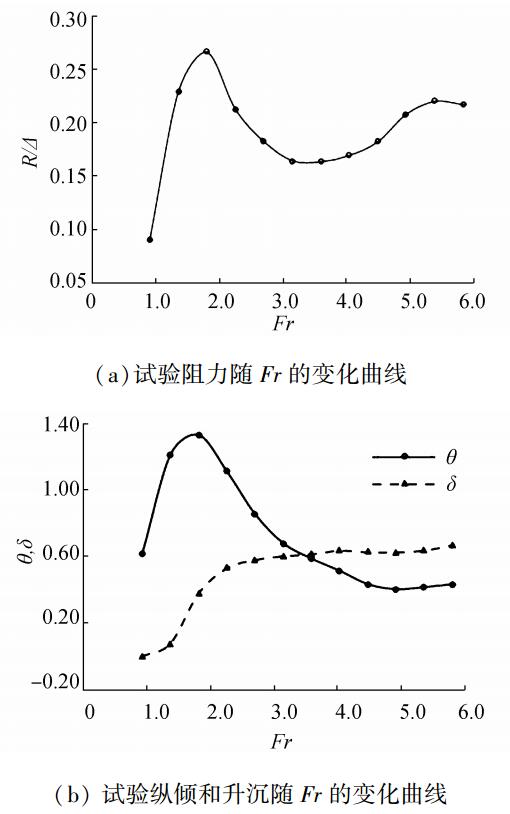
该三体滑行艇的模型试验于中航工业第605研究所高速水池完成,试验对容积弗劳德数Fr在3.14~5.83的工况进行了测试,图 2给出了试验中的阻力、纵倾及升沉随Fr的变化曲线,其中试验阻力由阻升比R/Δ表示,而无因次化升沉和纵倾表示为
|
| 图2 无因次化试验阻力、纵倾和升沉 Figure 2 Dimensionless resistance, trim angle and sinkage |
| $ \delta = \frac{{\delta '}}{{\bar T}} $ | (1) |
| $ \theta = \frac{{\sin \;\theta ' \cdot \bar T \times {{10}^2}}}{{{L_{WL}}}} $ | (2) |
式中:δ′和θ′分别为实际的升沉和纵倾值,T和LWL则表示模型静浮状态下的平均吃水与水线长。
图 3给了Fr=1.79, 2.24, 3.14和5.83时, 艇体首尾的兴波特性,结合试验数据及现象可以看出,在Fr为1.0~2.0,模型处于半滑行状态,逐渐增大的水动升力首先将艇艏部抬起,导致在此航速段出现明显的纵倾峰值并产生较大的兴波;加之艇体浸深较大,槽道几乎全部浸没于水中,其半封闭的几何特征在额外增加了全艇浸湿面积的同时产生了较大的形状阻力,因此在此航速段存在一个明显的低速峰值。

|
| 图3 不同航速下艇体首尾的兴波特性 Figure 3 Bow and stern wave characteristics at different speeds |
当Fr高于2.0后,随着航速的增加,艇体继续抬升,纵倾迅速减少,水动升力的进一步增大,艏部及艇体两侧兴波有了明显的削弱;艇艉的尾涡进一步向艇后延伸,使得尾封板完全暴露于空气之中;此时可认为模型已进入滑行状态,槽道前段壁面已开始与兴波波面脱离。
随着航速持续提升,艇体升沉的变化趋于缓和,而纵倾的仍有进一步减少的趋势,在Fr=3.14时,槽道前段已完全脱离水面,部分主体兴波被槽道吸收,并与槽道内的空气混合后在槽道尾端喷出,在艇尾形成明显的槽道尾流。当达到最高航速时(Fr=5.83),艇体两侧已几乎没有可见兴波,主艇体兴波基本上全部被槽道所吸收;而在尾封板处槽道顶部与槽道内的水气混合流脱离,使得槽道进入充分的通气状态;在此状态下,槽道的升力主要由其内部空气层的气动力所提供,槽道内浸湿面积大幅减少,从而降低了航行阻力,在阻力曲线则表现为高速段阻力随着航速的增加而减小,出现第二个阻力峰。
根据以上分析可以看出,三体滑行艇的阻力优势主要体现在阻力曲线相对平坦的高速段,其在低速段较大的阻力峰值会导致低速巡航时的功耗增大,故三体滑行艇正常工作航速应处于起滑之后的高航速下,相应地本文中数值研究也主要针对于此航速段的工况。
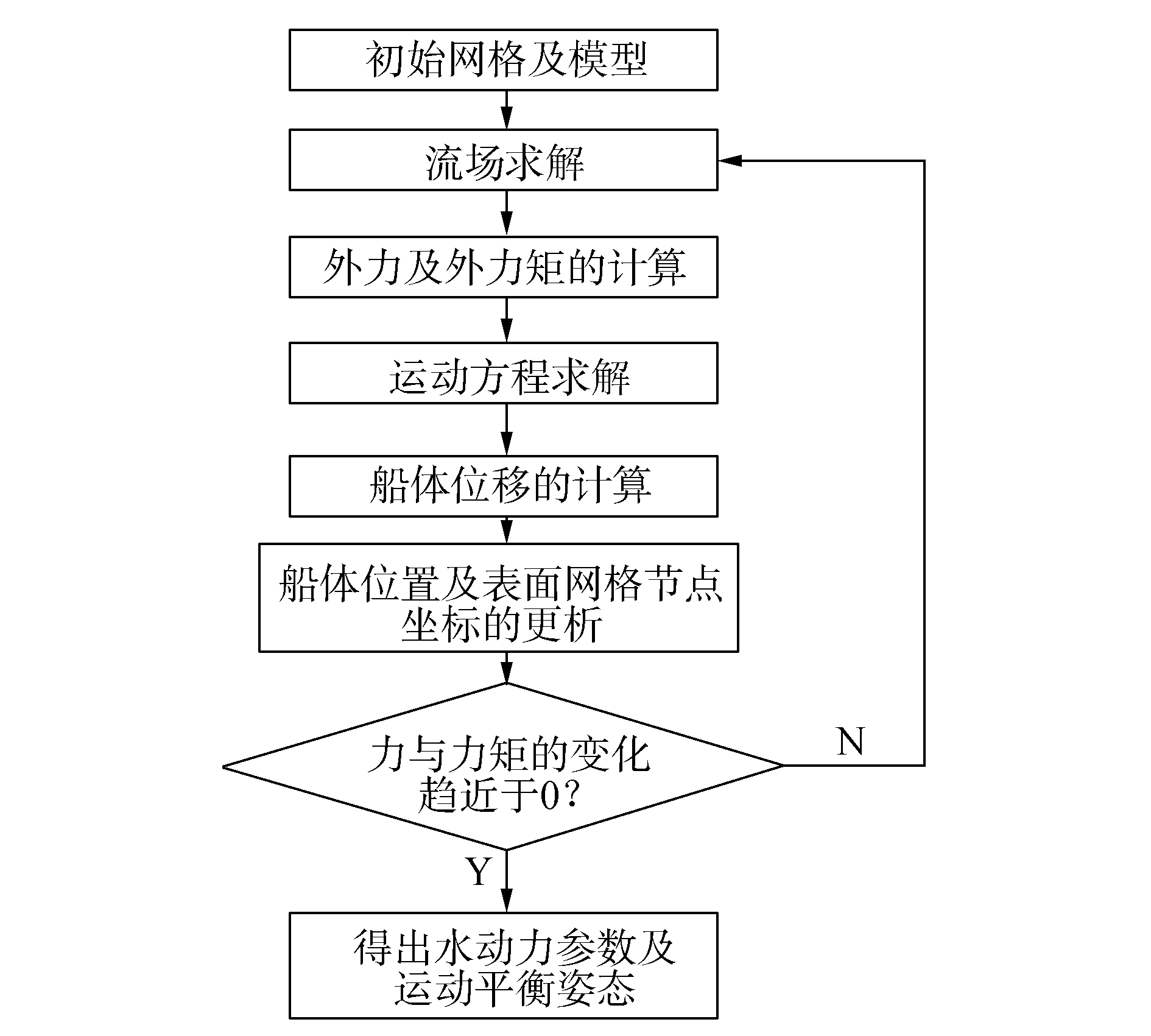
2 数值模型及有效性验证 2.1 数值计算方法简介在如上试验研究基础上,本文对3.14≤Fr≤5.83的工况进行了模拟,由于在高速航行时航行姿态的变化会对艇体的水动力特性产生较大的影响,在数值模拟的过程中计及了航行姿态的影响。图 4给出了具体的数值求解流程,本文采用RANS方程方法求解Navier-Stokes方程、结合SST (shear stress transportation) 湍流模型和VOF (volume of fraction) 方法完成了带自由液面粘性绕流场求解体系的建立,通过初始模型绕流的求解,即可得出作用于艇体表面的压力场和剪力场,艇体所受外力F和力矩M则由以下两式得出:
|
| 图4 数值求解流程图 Figure 4 Computational process |
| $ \mathit{\boldsymbol{F = }}\int_S {\left( {\mathit{\boldsymbol{\tau }}-p\mathit{\boldsymbol{I}}} \right)} \cdot \mathit{\boldsymbol{n}}{\rm{d}}S-\mathit{\boldsymbol{G}} $ | (3) |
| $ \mathit{\boldsymbol{M = }}\int_S {\left( {\mathit{\boldsymbol{r}}-{\mathit{\boldsymbol{r}}_G}} \right)} \left( {\mathit{\boldsymbol{\tau }}-p\mathit{\boldsymbol{I}}} \right) \cdot \mathit{\boldsymbol{n}}{\rm{d}}S $ | (4) |
式中:τ、I和G分别表示剪切力、压力和重力,n为船模表面的外法线向量,r和rG则分别为船壳表面任意一点以及重心处的位移矢量。而船体升沉X和和纵倾θ则由如下式所示的船体六自由度运动方程进行求解:
| $ \mathit{\boldsymbol{F = }}m\frac{{{{\rm{d}}^2}\mathit{\boldsymbol{X}}}}{{{\rm{d}}{t^2}}} $ | (5) |
| $ \mathit{\boldsymbol{M = }}\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\mathit{\boldsymbol{I}}\frac{{{\rm{d}}\mathit{\boldsymbol{\theta }}}}{{{\rm{d}}t}}} \right) $ | (6) |
进而可得出船体表面网格节点的位移,通过网格节点的移动即可实现船体运动的模拟。实际的求解过程可认为是流场求解与运动求解的耦合,当所受外力和力矩在一定的物理时间内的变化趋近于零时,可认为整个求解过程达到了收敛,此时所求得的船体姿态即为该工况下稳定航行时的平衡姿态。
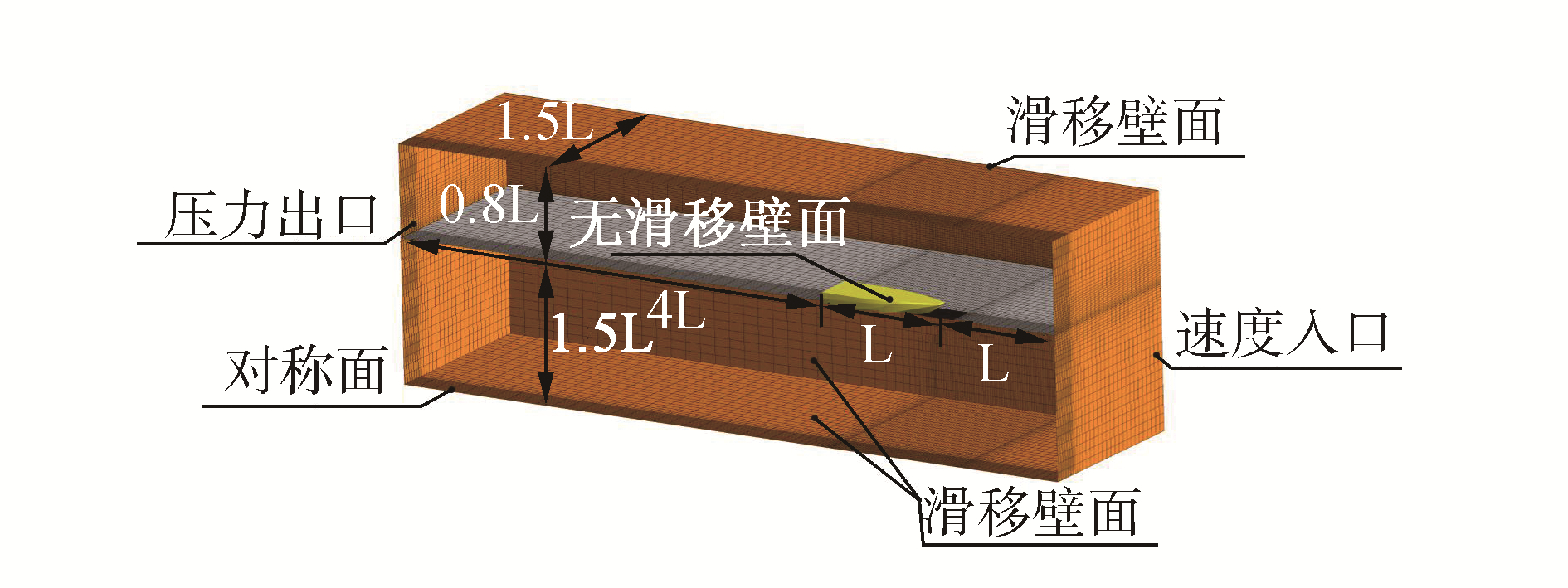
2.2 计算域的建立及网格划分如图 5所示,考虑到模型及流动的对称性,本文中计算域的建立只针对半侧船体进行,其在艇前、艇后、甲板以上、艇体以下、艇体左侧方向的尺度分别为1L、4L、0.8L、1.5L和1.5L。为了对三体滑行艇的复杂几何外形进行捕捉,本文中采用结构与非结构的混合网格进行整个计算域的离散。其中,在艇体表面采用三角形面网格进行划分,并由表面网格沿法线方向进行拉伸形成近场的边界层网格,在远场区域采用规则的结构化网格,在近远场的过渡区则采用非结构的四面体网格进行过渡,总网格数量约为8.4×105,艇体表面y+的范围为70~300。
|
| 图5 计算域及网格划分示意 Figure 5 Computational domain and mesh generation |
表 2中给出了计算值与试验值的对比,可以看出,在计算的速度范围内,计算姿态与试验值吻合度良好;而阻力计算值则在Fr>4.49的高航速下出现较大的误差,但整体趋势与试验值一致,并且对高航速下的阻力峰值点也有较为准确的捕捉。因此,本文中的计算方法能够较好的模拟出三体滑行艇在静水直航中的水动力特性,同时亦具有一定的计算精度,可用于本文中的计算与分析。
| Fr▽ | R/Δ | δ | θ | ||||||
| 计算值 | 试验值 | 误差/% | 计算值 | 试验值 | 计算值 | 试验值 | |||
| 3.14 | 0.172 | 0.165 | 4.13 | 0.592 | 0.605 | 0.655 | 0.679 | ||
| 3.59 | 0.171 | 0.164 | 4.56 | 0.611 | 0.616 | 0.554 | 0.587 | ||
| 4.04 | 0.178 | 0.170 | 4.75 | 0.633 | 0.638 | 0.490 | 0.513 | ||
| 4.49 | 0.185 | 0.183 | 1.23 | 0.655 | 0.628 | 0.457 | 0.432 | ||
| 4.93 | 0.193 | 0.209 | -7.67 | 0.677 | 0.627 | 0.432 | 0.402 | ||
| 5.38 | 0.196 | 0.221 | -11.42 | 0.730 | 0.638 | 0.431 | 0.414 | ||
| 5.83 | 0.190 | 0.218 | -13.13 | 0.706 | 0.672 | 0.429 | 0.432 | ||
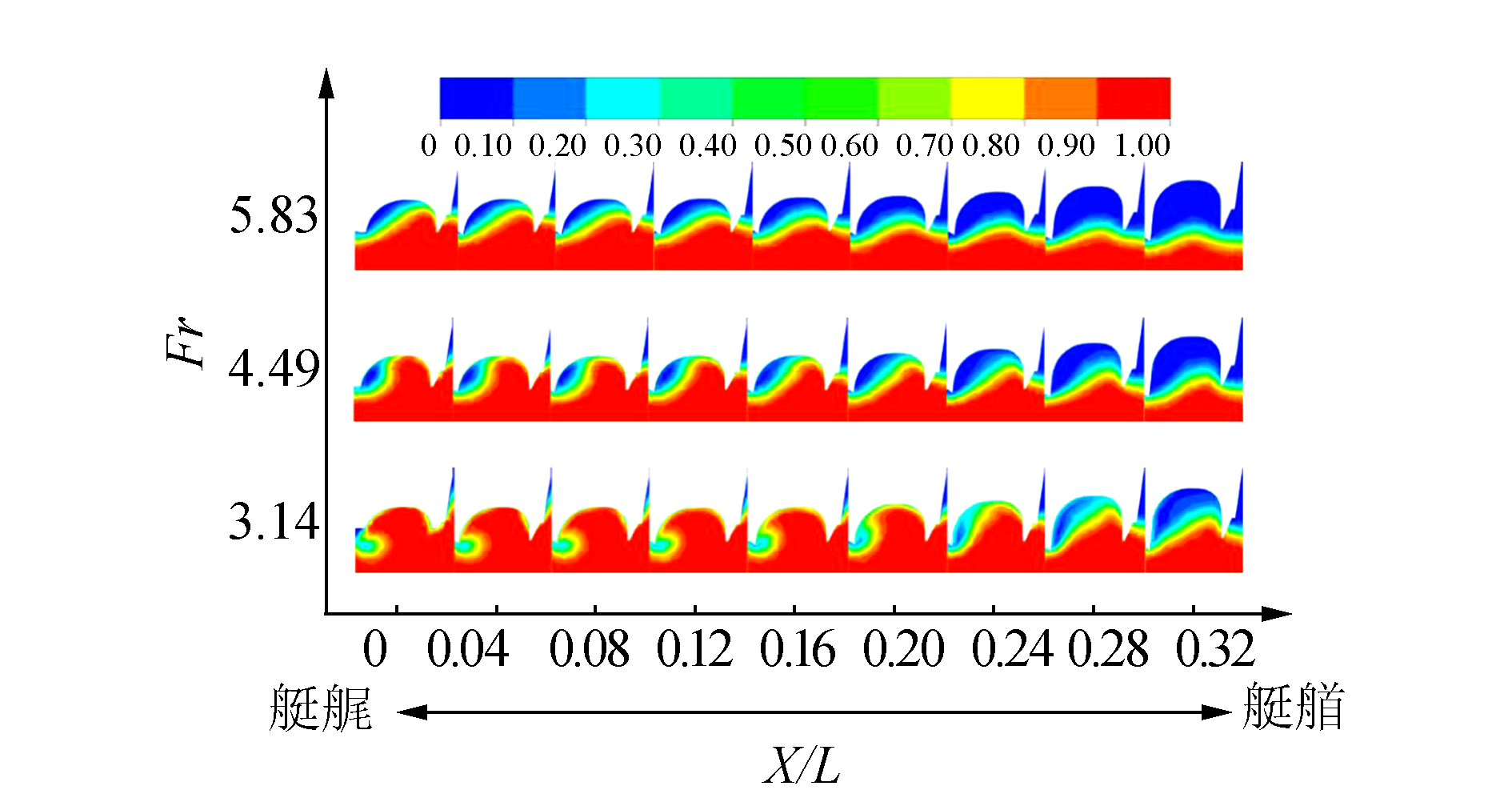
在试验过程中,由于模型的遮蔽,所观测到的现象主要为船体两侧兴波和尾流,为了能够直观的描述槽道内的流动特征,在计算结果的处理中利用0≤X/L≤0.32槽道各剖面处的水气分布云图表示了槽道内兴波和空气层的随航速的变化,如图 6所示,在Fr=3.14时,模型处于滑行状态的初始阶段,由于航行吃水较大,主片体兴波导致槽道的中后段浸没于水中,仅有极少量的空气分布于槽道两侧的壁面处;随着航速的提高,更多的艇体被抬离出水面,使得槽道内兴波被削弱,槽道壁面逐渐与兴波波面脱离,相应地通气量也逐渐增大;直至最高航速时,槽道与水面完全脱离,并形成完整的气层覆盖于兴波波面之上;此时槽道内的升力也由水动升力转化为气层的气动升力。
|
| 图6 不同航速下槽道系列剖面处的兴波波形 Figure 6 A series of transverse wave cuts in tunnel region at different speeds |
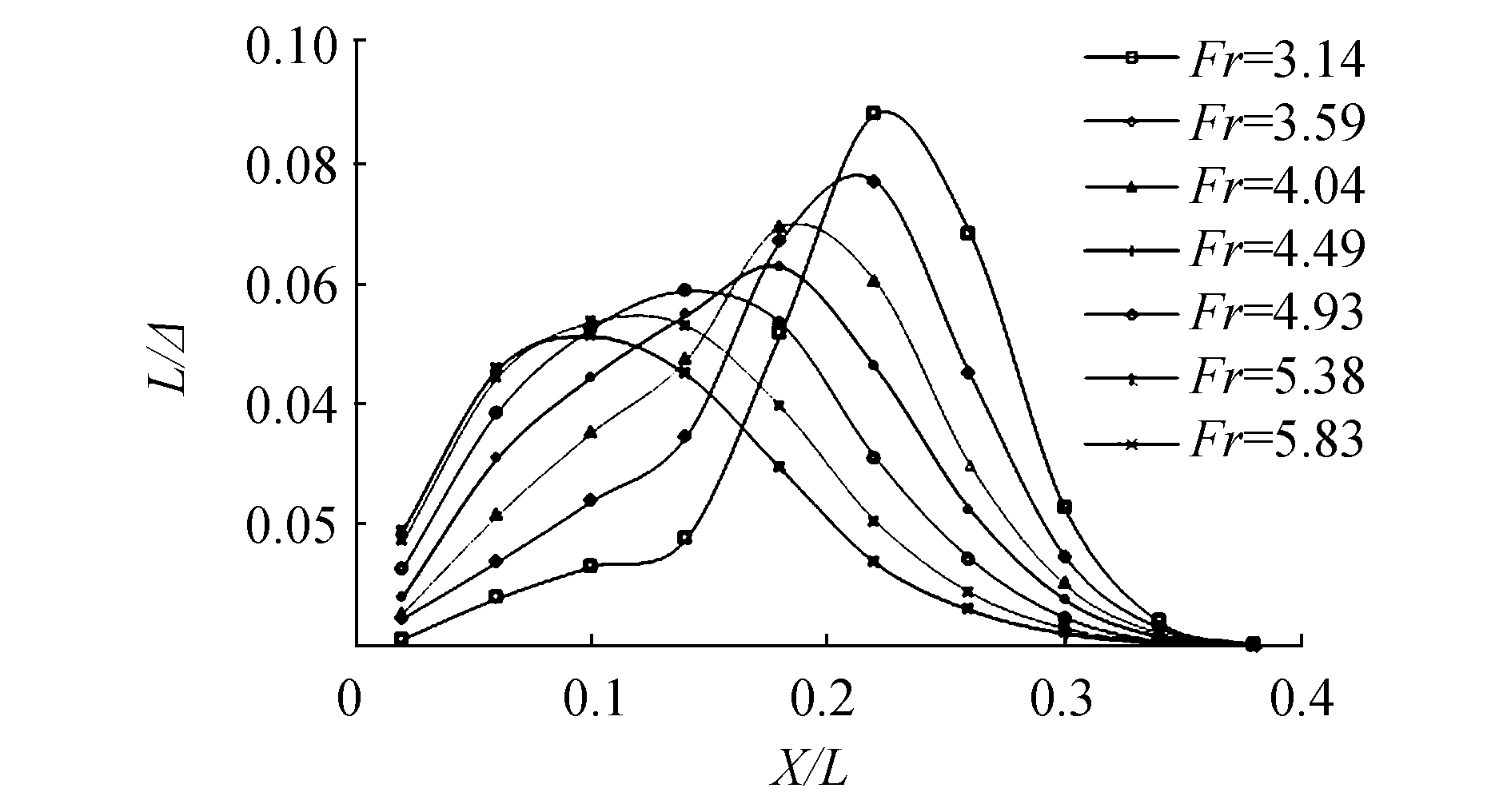
为了研究槽道内的升力在槽道内的分布情况,文中将0≤X/L≤0.4的槽道壁面沿纵向分为10段,并对每段壁面所提供的升力进行了监测,得出了槽道升力沿纵向的变化曲线,如图 7所示。结合槽道内的流动特性可以看出,主片体兴波对槽道升力有直接的影响,在Fr < 4.04时,随着兴波的减弱槽道升力的峰值也随之降低,并且随着槽道浸湿长度的减少,其峰值也向艇尾移动,这表示在此航速段水动升力仍是槽道升力的主要来源;当Fr>4.04时,虽然空气层的增长导致槽道浸湿面积的减少,但由于气动力逐渐增大并提供大多数的槽道升力,故槽道内升力分布的变化不再明显。
|
| 图7 槽道升力沿纵向的变化曲线 Figure 7 Tunnel lift varying along longitudinal directio |
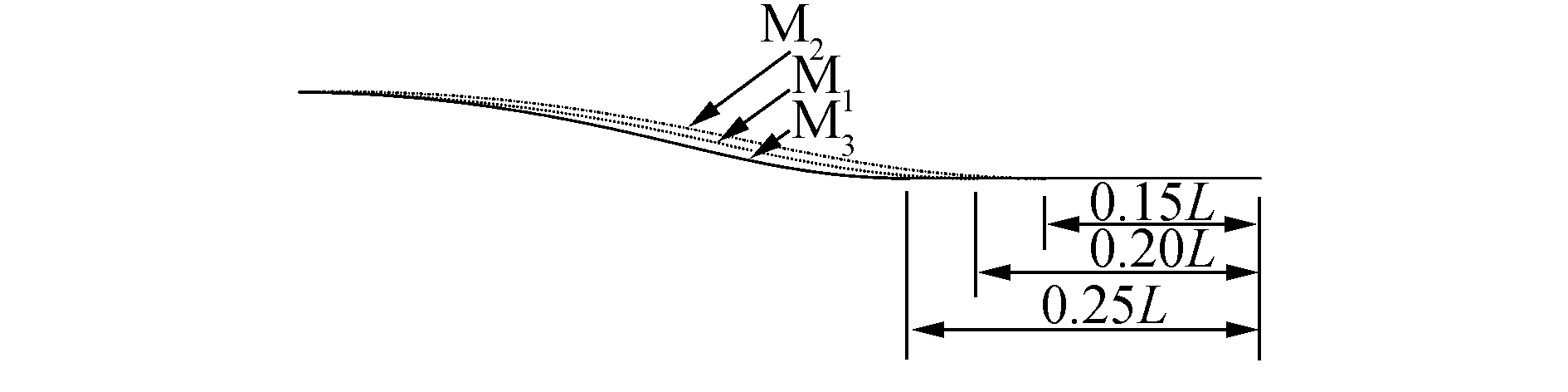
从图 7中槽道升力的作用区域来看,在高航速下的气动升力主要作用于0~0.2的槽道平直段,故在槽道构型的设计中,平直区域的确定对槽道的高速水气动力性能有着至关重要的影响。因此,本文在试验模型的基础上将槽道平直段长度分别调整为0.15L和0.25L,并利用上述数值手段对3种槽道进行了对比研究。图 8中给出了3种槽道中纵剖面形式的对比,为了便于文中的讨论,将试验模型命名为M1,槽道平直段缩短和增长后的模型则分别命名为M2和M3。
|
| 图8 不同槽道中纵剖面形式的对比 Figure 8 Comparison of longitudinal central section of different tunnels |
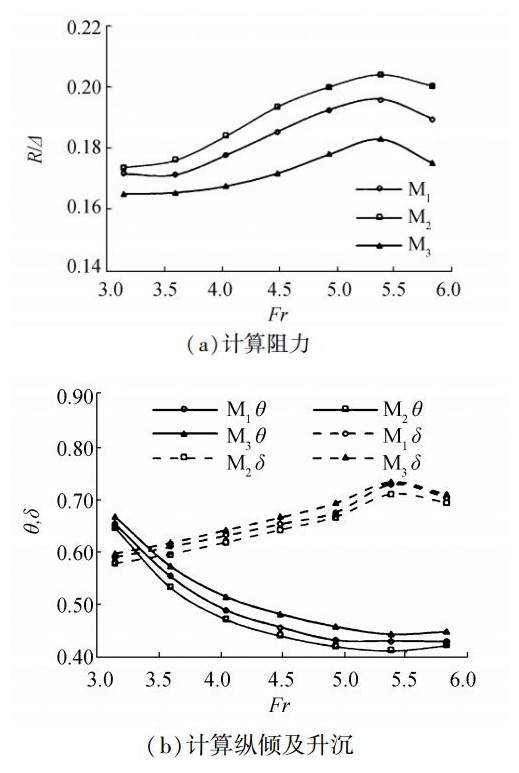
图 9中给出了三模型计算阻力和姿态的对比,可以看出,平直段的长度对模型阻力有着明显的影响,相比于原始模型M1,M2的阻力在计算的速度范围内有了不同程度的增大,其平均阻力增幅为3.7%。而M3的阻力则有所降低,并且随着航速的增大,阻力减额也愈发明显;在Fr=5.83时,其最大阻力收益为7.6%,各航速下的平均阻力收益则为6.0%。在航行姿态上,数值计算结果较好的体现出了不同模型之间的差异性,其中M2的航行纵倾和升沉较M1均有所降低,而M3则表现出相反的趋势。
|
| 图9 不同模型计算阻力及航行姿态的对比 Figure 9 Comparison of calculated resistance and hull behaviors |
由于槽道在航行过程中的主要作用是提供水气动升力,并维持船体的平衡,其所产生的动升力的大小是衡量槽道水气动力性能的重要指标。图 10中给出不同构型的槽道所产生的升力L的比较,可以看出,平直段长度的改变对槽道的水气动力性能产生了明显的影响,其中,M3的槽道升力要明显高于其余模型,较之M1,其槽道升力在各航速下的平均增幅为9.5%;而M2在不同航速下的槽道升力则较M1要小,其平均减额为7.4%。
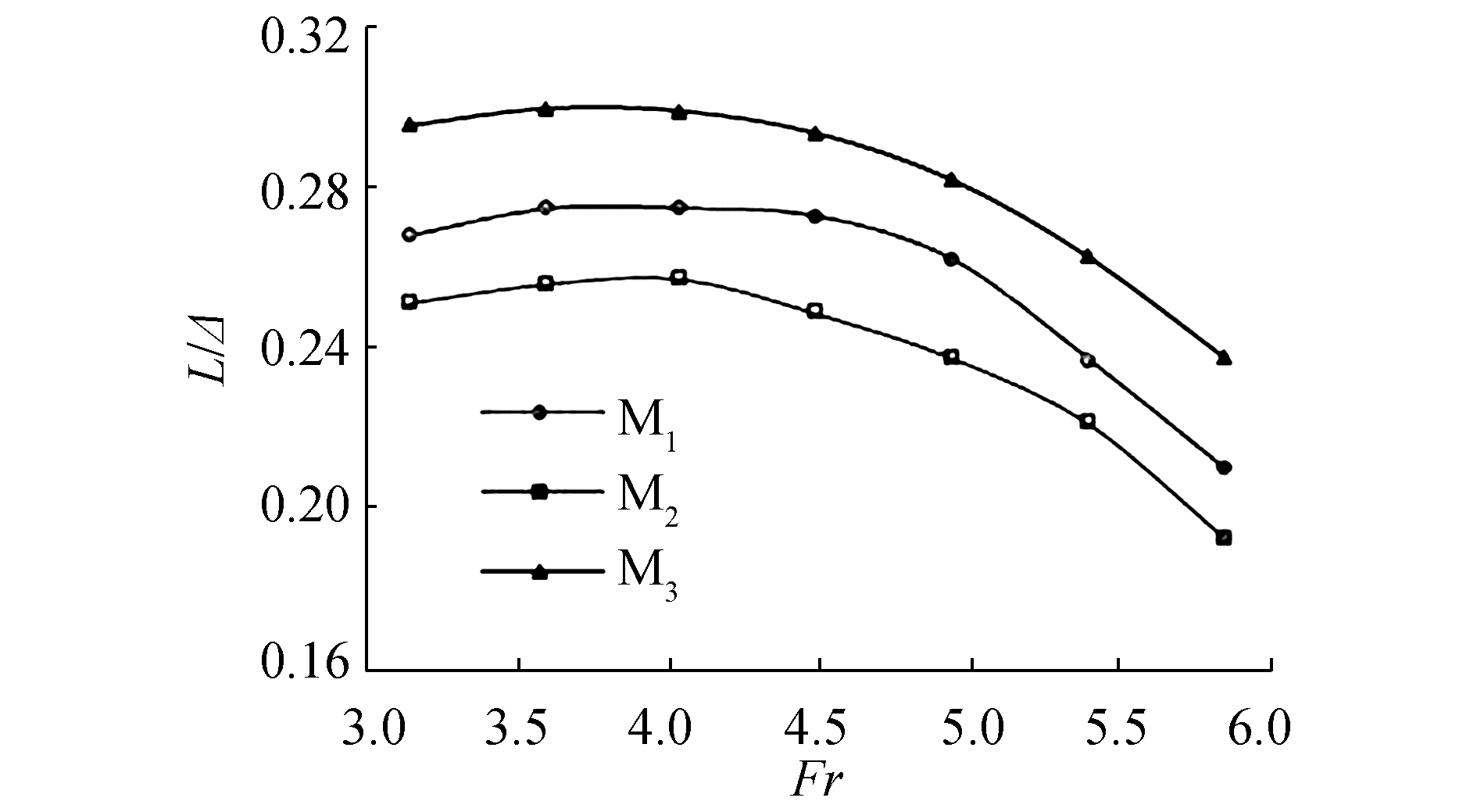
|
| 图10 不同构型槽道所产生的升力 Figure 10 Comparison of tunnel lift between different tunnel configurations |
此外,由于槽道位于艇体的中后部,在航行过程中槽道升力能够产生一个抑制航行倾角增大的纵倾力矩,其作用类似于尾压浪板[11],能够有效地减缓高航速下海豚运动的发生,提高艇体纵向运动的稳定性。图 11给出了不同构型的槽道所产生的纵倾力矩T的对比,可以看出,虽然M3的槽道提供了最多的升力,但其所产生的纵倾力矩较其余模型明显要小,这对高航速下的运动稳定性来说是不利的;与之相反的是,M2的槽道所产生的纵倾力矩则较原始模型略大。造成这种现象的原因是平直段长度的变化导致槽道压力中心的纵向位置(LCP) 发生改变,如图 12所示。M3槽道的压力中心相比与原始模型要明显前移,其在各航速下的平均移动距离为0.036L;而M2槽道的压力中心则向艇尾方向移动了0.017L的平均距离。两相比较,其结果是M3槽道的纵倾力臂减小,而M2槽道的纵倾力臂增大;对应地,槽道的纵倾力矩也表现出了相同的变化趋势。
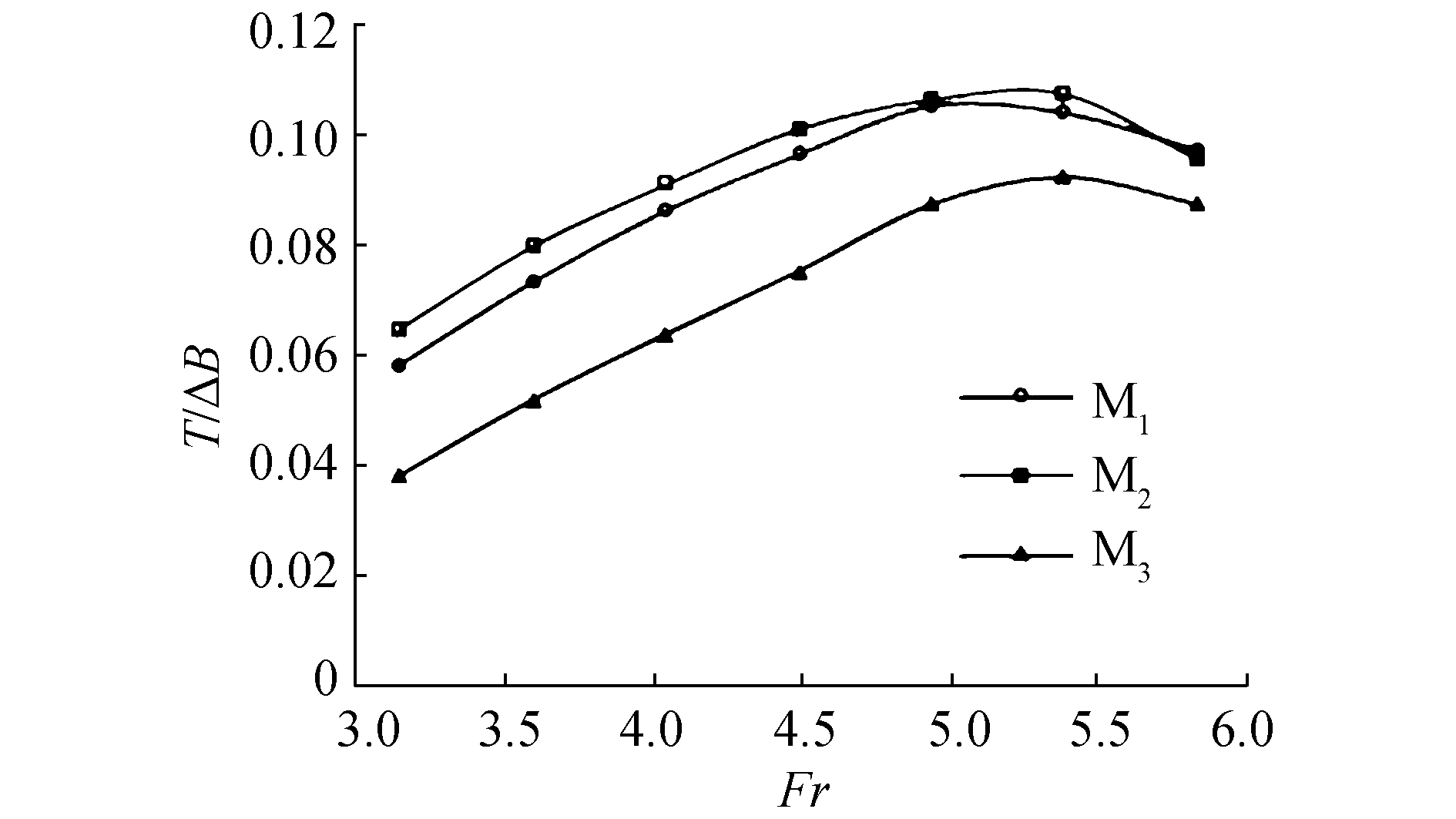
|
| 图11 不同构型槽道所提供的纵倾力矩 Figure 11 Comparison of tunnel trim moment between different tunnel configurations |
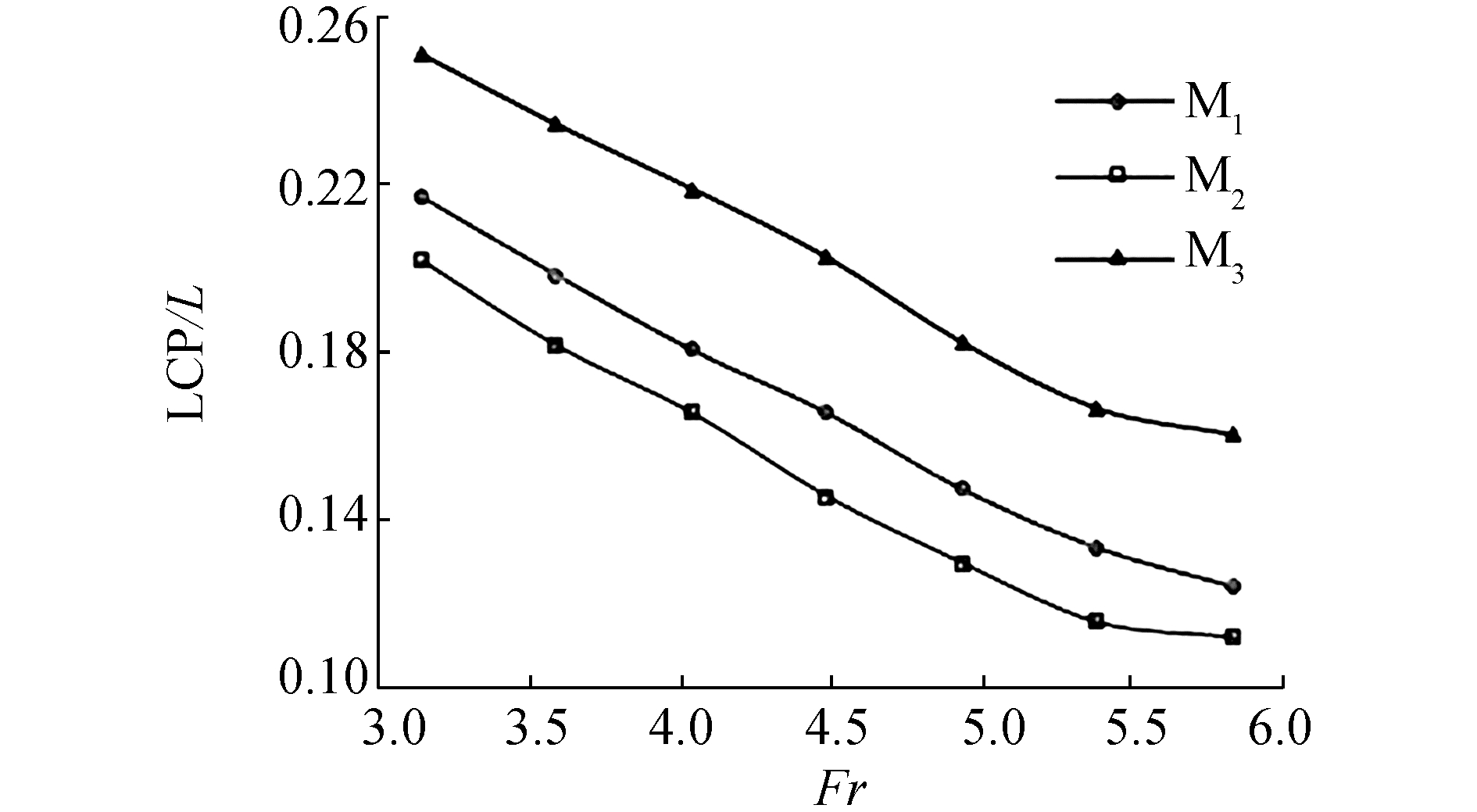
|
| 图12 不同构型的槽道压力中心的纵向位置 Figure 12 Comparison of LCP between different tunnel configurations |
本文结合试验现象和数值计算结果对槽道的水气动力作用机理进行了研究,讨论了槽道平直段长度对三体滑行艇阻力性能以及槽道水气动力特性的影响,计算结果具有较好的可信度,在三体滑行艇艇型设计中具有一定的参考价值。根据本文中的计算和分析,可得出以下结论:
1) 三体滑行艇的阻力优势主要体现在起滑之后的高速段,在此航速段,主艇体兴波逐渐被槽道所吸,槽道内通气量逐渐增大,并在Fr=5.83时与兴波波面脱离,进入全通气状态。
2) 槽道进入全通气状态后,其浸湿面积迅速减少,降低了此状态下的总阻力,使得高速段阻力曲线出现了明显的阻力峰。
3) 高航速下的气动升力主要作用于槽道的平直段。而将平直段长度增大,有利于提高槽道升力,并降低整体的航行阻力,但会导致槽道纵倾力矩的减小,不利于高航速下的运动稳定。而将平直段长度缩短则取得了相反的变化趋势。
4) 槽道升力的大小与三体滑行艇的阻力性能有着直接的相关性,在本文的计算模型中,槽道升力较大的模型,其阻力性能也更好。
| [1] | JIANG Yi, SUN Hanbing, ZOU Jin, et al. Analysis of tunnel hydrodynamic characteristics for planing trimaran by model tests and numerical simulations[J]. Ocean engineering, 2016, 113: 101–110. DOI:10.1016/j.oceaneng.2015.12.038 |
| [2] | COLLU M, WILLIAMS A W G, PATEL M H, et al. Aerodynamically alleviated marine vehicles (AAMV):development of a mathematical framework to design high speed marine vehicles with aerodynamic surfaces[C]//Proceedings of the 9th Internationnal Conference on High performance Marine Vessels. Shanghai, China, 2009. |
| [3] |
孙华伟, 邹劲, 黄德波, 等. 三体滑行艇阻力试验研究[J].
哈尔滨工程大学学报, 2011, 32(7): 858–861.
SUN Huawei, ZOU Jin, HUANG Debo, et al. Experimental study on a high-speed trimaran-planing boat[J]. Journal of Harbin engineering university, 2011, 32(7): 858–861. |
| [4] |
孙华伟, 黄德波, 邹劲, 等. 断阶3体滑行艇阻力试验研究[J].
华中科技大学学报:自然科学版, 2012, 40(1): 86–89.
SUN Huawei, HUANG Debo, ZOU Jin, et al. Experimental investigation on resistances from stepped trimaran-planing boats[J]. Journal of Huazhong university of science and technology:natural science edition, 2012, 40(1): 86–89. |
| [5] | MA Weijia, SUN Hanbing, ZOU Jin, et al. Test research on the resistance performance of high-speed trimaran planing hull[J]. Polish maritime research, 2013, 20(4): 45–51. |
| [6] |
蒋一, 孙寒冰, 邹劲, 等. 引气槽减阻特性的数值研究[J].
哈尔滨工程大学学报, 2016, 37(2): 151–156.
JIANG Yi, SUN Hanbing, ZOU Jin, et al. Numerical research on drag reduction characteristics of air ducts[J]. Journal of Harbin engineering university, 2016, 37(2): 151–156. |
| [7] | YOUSEFI R, SHAFAGHAT R, SHAKERI M. Hydrodynamic analysis techniques for high-speed planing hulls[J]. Applied ocean research, 2013, 42: 105–113. DOI:10.1016/j.apor.2013.05.004 |
| [8] | YOUSEFI R, SHAFAGHAT R, SHAKERI M. High-speed planing hull drag reduction using tunnels[J]. Ocean engineering, 2014, 84: 54–60. DOI:10.1016/j.oceaneng.2014.03.033 |
| [9] | GHASSABZADEH M, GHASSEMI H. Determining of the hydrodynamic forces on the multi-hull tunnel vessel in steady motion[J]. Journal of the Brazilian society of mechanical sciences and engineering, 2014, 36(4): 697–708. DOI:10.1007/s40430-013-0110-2 |
| [10] | MOGHADAM H K, SHAFAGHAT R, YOUSEFI R. Numerical investigation of the tunnel aperture on drag reduction in a high-speed tunneled planing hull[J]. Journal of the Brazilian society of mechanical sciences and engineering, 2015, 37(6): 1719–1730. DOI:10.1007/s40430-015-0431-4 |
| [11] | CELANO T. The prediction of porpoising inception for modern planing craft[J]. SNAME transactions, 1998, 106: 269–292. |



