2. College of Electrical Control Engineering, Heilongjiang University of Science and Technology, Harbin 150001, China
在排放法规日益严格和节能要求的双重压力下,将先进的电控燃油系统应用于柴油机已经迫在眉睫。电控双阀燃油喷射系统通过电控单体泵的溢流阀实现供油控制、通过电控喷油器的电磁阀实现喷油控制,能够实现快速的动态响应特性和柔性可调的喷油规律。尤其针对大功率柴油机要求,该燃油系统能够实现大循环喷油量、高喷油压力下每循环间燃油喷油特性的快速调节,并在低转速下产生高的喷射压力以及高喷射压力下的小循环喷油量的精确控制[1-2]。由于电控双阀燃油喷射系统集机械、液力、电磁于一体,循环喷油量由多物理场参数相互耦合作用下决定,所以该系统是一个多物理场参数相互耦合作用的非线性系统,尤其在双阀控制的燃油超高压瞬变流状态下,循环喷油量的稳定控制是双阀电控燃油系统的难题,而循环喷油量的稳定性是决定其成功匹配柴油机的前提和基础[3]。
文献[4]研究了全工况范围内电控双阀燃油喷射系统主喷油量随转速、脉宽的变化规律及特性参数变化所引起的主喷油量波动规律, 通过量化分析得出了各特性参数变化所引起的主喷油量波动百分比,为提高电控双阀燃油喷射系统工作的稳定性提供了理论基础。文献[5]通过对电控双阀燃油喷射系统进行线性分析得出:双阀系统中,不同控制模式下,相同时刻点的系统矩阵特征值分布变化较小,系统矩阵特征值分布只是随着喷射过程的推移,发生很大变化,整个系统是一个时变、非稳定的复杂系统。因此,本文通过对典型工况下喷油过程中系统的状态矩阵序列的秩与特征值分布进行分析,研究系统喷油过程的稳定性,从而为电控双阀燃油喷射系统喷油稳定性的控制提供理论依据。
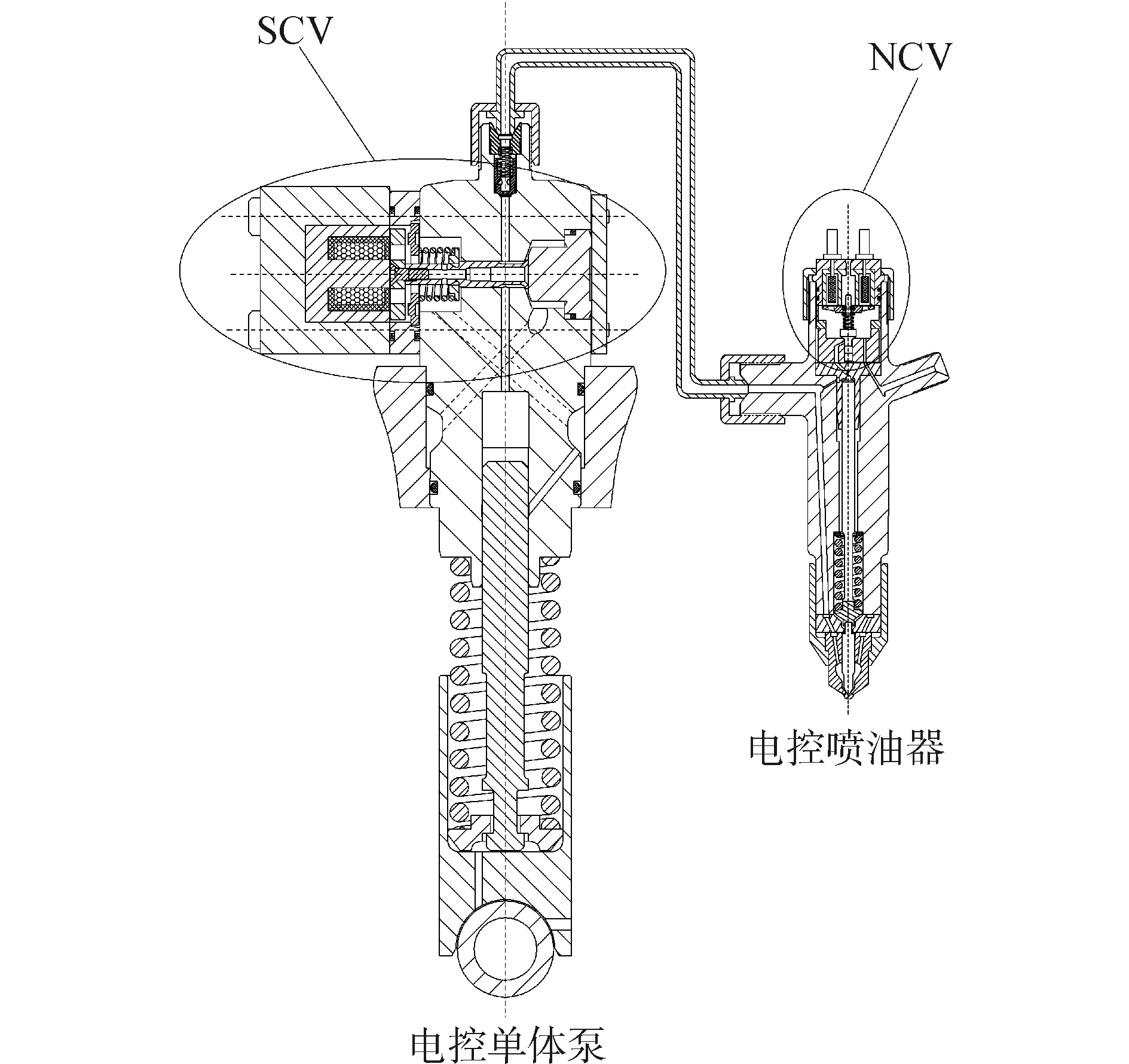
1 系统组成与工作原理电控双阀燃油喷射系统的组成及工作原理如图 1,其主要由电控单体泵和电控喷油器两部分组成。
|
| 图1 电控双阀燃油喷射系统结构原理图 Figure 1 Diagram of electronically controlled double-valve fuel injection system |
电控双阀燃油喷射系统通过电控喷油器替代传统电控单体泵系统中的机械式喷油器。喷油过程是通过电控单体泵端的溢流控制阀 (spill control valve,SCV) 和电控喷油器上的针阀控制阀 (needle control valve,NCV) 协同控制实现的。电控单体泵端的SCV主要实现供油控制。在SCV中的电磁铁不上电时,尽管单体泵的驱动凸轮顶起泵油柱塞,泵油柱塞腔中的燃油被压缩,但是由于SCV的开启,燃油经过SCV的泄油锥阀流回至低压油路,系统内不会建立起高压。当SCV的电磁铁上电时,泄油锥阀关闭泄油油路。泵油柱塞压缩柱塞腔中的燃油,高压油管内开始建立高压。电控喷油器上的NCV主要实现喷油控制。NCV在未上电时为关闭状态,针阀上端受到的液压力比下端高,针阀不能开启。当电磁阀上电时,NCV打开,针阀上端的高压燃油与低压油路连通,针阀抬起,燃油开始喷射[6-7]。
2 系统模型的建立与验证 2.1 模型建立电控双阀燃油喷射系统是集电、磁、机、液于一体的多物理场耦合系统,电场、磁场、机械运动和流场通过各自的控制方程及相互作用的变量耦合在一起。因此通过分析各个物理场之间的耦合关系,建立电磁场、机械运动、流场特性方程及高压油管内的压力波动方程如下。
1) 电磁场耦合方程:
| $ U = iR + \frac{{{\rm{d}}\lambda }}{{{\rm{d}}t}} $ | (1) |
| $ F = \frac{{{B^2}{A_l}}}{{2{\mu _0}}} = \frac{{{\mathit{\Phi }^2}}}{{2{\mu _0}{A_l}}} $ | (2) |
| $ \mathit{\Phi } = \frac{\lambda }{R} $ | (3) |
式中:U为线圈两端电压;i是电磁铁驱动电流,通过软件进行脉宽调制闭环控制;R为线圈电阻;r为线圈磁链值,等于线圈电感和电流的乘积;Φ为流经磁极面的磁通;Al为电磁铁的磁极面积;F为电磁铁产生的电磁力;B为磁感应强度;μ0为真空磁导率;R和λ与电磁铁的结构参数有关。
2) 柱塞腔运动方程:
| $ V\frac{{{\rm{d}}P}}{{{\rm{d}}t}} = {E_{\rm{v}}}A\frac{{{\rm{d}}L}}{{{\rm{d}}t}} $ | (4) |
| $ A = \frac{{\pi {d^2}}}{4} $ | (5) |
式中:V为柱塞腔容积,P为柱塞腔内燃油压力,Ev为燃油的可压缩性系数,A为柱塞顶面的横截面积,L为柱塞的运动位移,d为柱塞直径。
3) 阀杆机械运动方程:
| $ m\frac{{{{\rm{d}}^2}{x_1}}}{{{\rm{d}}{t^2}}} = {F_{{\rm{mag}}}} - {F_{\rm{f}}} - k\left( {{x_1} + {x_0}} \right) $ | (6) |
式中:m为运动件质量,包括阀杆、衔铁和弹簧等零件;x1为阀杆位移;Fmag为作用在衔铁上的电磁力;Ff为考虑到流场影响受到的力;k为弹簧刚度;x0为弹簧预变形量;t为时间。
4) 油管内的波动方程:
| $ \frac{{\partial u}}{{\partial x}} + \frac{1}{{{a^2}\rho }}\frac{{\partial p}}{{\partial t}} + \frac{u}{{{a^2}\rho }}\frac{{\partial p}}{{\partial x}} = 0 $ | (7) |
| $ \rho \left( {\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}}} \right) + \frac{{\partial p}}{{\partial x}} + 2k\rho u = 0 $ | (8) |
式中:ρ为燃油密度;p为压力;u为燃油速度;k为粘性阻力系数;a为油管压力波传播速度,简称声速。
式 (1)~(8) 为电控双阀燃油喷射系统的基本方程,再结合柱塞腔连续方程、初始条件和边界条件等,可以求解出电控双阀燃油系统喷射特性各种参数。基于上述方程,在AMESim仿真平台上建立了电控双阀燃油系统的数值仿真模型,如图 2所示。

|
| 图2 电控双阀燃油喷射系统仿真模型 Figure 2 Simulation model of electronically controlled double-valve fuel injection system |
为了验证模型的准确度,在试验台上对电控双阀燃油系统进行了试验,由于嘴端压力可以直接反映系统的喷射特性,试验中采用Kistler 4067高压传感器测量嘴端压力。图 3所示为在SCV控制模式下,循环喷油量为120 mm3的典型工况,凸轮转速分别为500、800和1 100 r/min时喷油器嘴端压力试验与仿真结果的对比图。由图 3可知,仿真值与实测值有很好的一致性,说明仿真模型能够准确预测电控双阀燃油喷射系统的喷油特性。

|
| 图3 典型工况下嘴端压力对比曲线 Figure 3 Comparison of measurement and simulation nozzle side pressure at different cam velocities |
为了分析系统稳定性,可以将系统在不同时刻点进行线性化,从而得到系统的状态矩阵A:
| $ \mathit{\boldsymbol{A = }}\frac{{\partial f\left( x \right)}}{{\partial x}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {f_1}}}{{\partial {x_1}}}} & {\frac{{\partial {f_1}}}{{\partial {x_2}}}} & \cdots & {\frac{{\partial {f_1}}}{{\partial {x_n}}}}\\ {\frac{{\partial {f_2}}}{{\partial {x_1}}}} & {\frac{{\partial {f_2}}}{{\partial {x_2}}}} & \cdots & {\frac{{\partial {f_2}}}{{\partial {x_n}}}}\\ \vdots & \vdots & \vdots & \vdots \\ {\frac{{\partial {f_n}}}{{\partial {x_1}}}} & {\frac{{\partial {f_n}}}{{\partial {x_2}}}} & \cdots & {\frac{{\partial {f_n}}}{{\partial {x_n}}}} \end{array}} \right] $ | (9) |
同理,可得到线性系统的控制矩阵B和输出矩阵C,则系统的状态空间表达式可表示为
| $ \begin{array}{l} \mathit{\boldsymbol{\dot X = AX + BU}}\\ \mathit{\boldsymbol{Y = CX}} \end{array} $ | (10) |
式中:X、Y、U分别为系统的状态变量、输出变量和控制变量[8]。
适当选取步长,获取喷油过程中各时刻点的系统状态矩阵表述,通过分析系统状态矩阵的秩与特征值分布来研究系统喷油过程的稳定性。由于电控双阀燃油喷射系统在喷油过程中,其各个组成部分的燃油压力、燃油流率及运动件的机械运动均为时间域内连续变化的状态量,结合电控双阀燃油喷射系统数值仿真模型,选取了凸轮转速、SCV驱动电流和NCV驱动电流为系统的控制变量,喷油压力、喷油率和喷油量为系统的输出变量。状态变量的选取如图 4所示,沿着燃油在系统内油路的流动过程,选取了燃油压力、流率、运动件速度和升程作为系统的状态变量。为提高计算准确性,考虑高压油管长度及管内沿程阻尼,将高压油管均分为6段,并将每段油管内的燃油压力及其两端流率作为状态变量,因此选取了3个控制变量、3个输出变量和37个状态变量。在AMESim平台对系统工作过程进行线性化处理,从而得到了电控双阀燃油喷射系统喷油过程中随时间变化的状态矩阵序列。

|
| 图4 电控双阀燃油喷射系统状态变量图 Figure 4 Selection of state variables in electronically controlled double-valve fuel injection system |
矩阵的秩是反映矩阵特性的重要参数,其值可用于确定线性系统的能控性和能观测性,对于不满足满秩条件的复杂控制系统,通过对状态矩阵进行秩分析,可以排除对系统状态无影响或影响很小的状态变量,实现对系统的降秩控制[9]。
图 5为NCV控制模式下,在凸轮转速800 r/min、喷油脉宽9.8℃aA的典型工况点,喷油过程中系统状态矩阵A的秩随时间的变化规律及其与系统控制电流、SCV升程、NCV升程、针阀升程和喷油速率的对应关系。图中的t1~t2对应SCV的关闭过程,t3~t4对应NCV的开启过程,t5~t6对应针阀的开启过程,t7~t10对应SCV的开启过程,t8~t9对应NCV的关闭过程,t9~t11对应针阀关闭的过程。

|
| 图5 系统状态矩阵的秩与关键参数的对应关系 Figure 5 Corresponding relation between the ranks of state matrices and key parameters |
如图 5所示,在SCV、NCV、针阀开始动作前与结束动作后,系统状态矩阵的秩都为31,说明电磁阀与针阀静止时,系统37个状态变量中只有31个相互独立,而当SCV阀杆、NCV阀杆或针阀阀杆开始动作时,它们的位移和速度会直接影响系统的状态,导致系统矩阵的秩瞬间变化。具体如下:
1)t1时刻之前,柱塞在凸轮驱动下开始压缩燃油,随着柱塞上行压油,柱塞腔内的燃油直接由密封锥面泄流至低压腔,电磁阀与针阀静止,系统状态矩阵的秩为31,说明此时系统37个状态变量中只有31个与系统有关。2)t1~t2时间段,SCV在电流作用下开始关闭,但未达到最大升程,由于SCV关闭过程中,阀杆的速度与位移瞬间发生了变化,系统矩阵的秩由31跳变至33。3)t2时刻,SCV关闭,泵油柱塞腔与低压油路的通道被切断,高压油管内开始建立高压。此时由于SCV的速度与位移不再变化,不再影响系统的状态,系统状态矩阵的秩由33降低到31。4)t3~t4时间段,NCV在电流控制下开始打开,但未达到最大升程,NCV阀杆的速度与位移与其他状态变量不再相关,系统矩阵的秩由31跳变为33。5)t4时刻,NCV达到最大升程,它的速度与位移不再变化,系统矩阵的秩由33降为31。6)t5~t6时间段,由于针阀的开启动作,针阀的速度与位移与其他状态变量由相关变为相互独立,使系统状态矩阵的秩由31上升到33。7)t6时刻,针阀达到最大升程,针阀的速度与位移不再变化,随着喷油进行,系统矩阵的秩从33降为31。8)t6~t7时间段,系统矩阵的秩维持在31,说明在该喷油过程中,系统矩阵中有31个相互独立的状态变量。9)t7~t8时间段,SCV打开过程中,泵油柱塞腔与低压油路通道被连通,NCV仍未关闭,系统矩阵从31变为33,对状态矩阵进行分析,得出此时状态矩阵中除NCV阀杆、针阀的速度与位移以外的33个状态变量线性无关。10)t8~t9时间段,NCV处于关闭过程,系统矩阵的秩从33升为35,此时只有针阀的速度与位移与其他状态变量相关。11)t9时刻,NCV关闭不再运动,而此时针阀开始关闭,分析得出此时系统仍有35个线性无关的状态变量,系统矩阵的秩保持在35不变。12)t10时刻,SCV完全打开并停止动作,系统状态矩阵的秩由35降至33,此时SCV阀杆的速度与位移与其他35个状态变量由独立变为相关。13)t10~t11时间段,系统仍在喷油,针阀处于关闭过程但未完全关闭,系统状态矩阵的秩为33。14)t11时刻,针阀彻底关闭,喷油结束,故系统矩阵的秩由33降低至31,对状态矩阵进行分析得出此时针阀的速度与位移与其他状态变量由独立变为相关,系统恢复至喷油之前的状态。
由以上分析可以看出,在喷油系统工作过程中,当SCV、NCV和针阀运动时,系统矩阵的秩增加,而在上述运动件都静止时,系统矩阵的秩为最小。因此可以通过对系统电磁阀驱动信号及SCV阀杆、NCV阀杆与针阀阀杆的运动特性进行分析,从而实现对系统状态矩阵序列的降秩处理,进而实现对喷油系统的降秩控制。
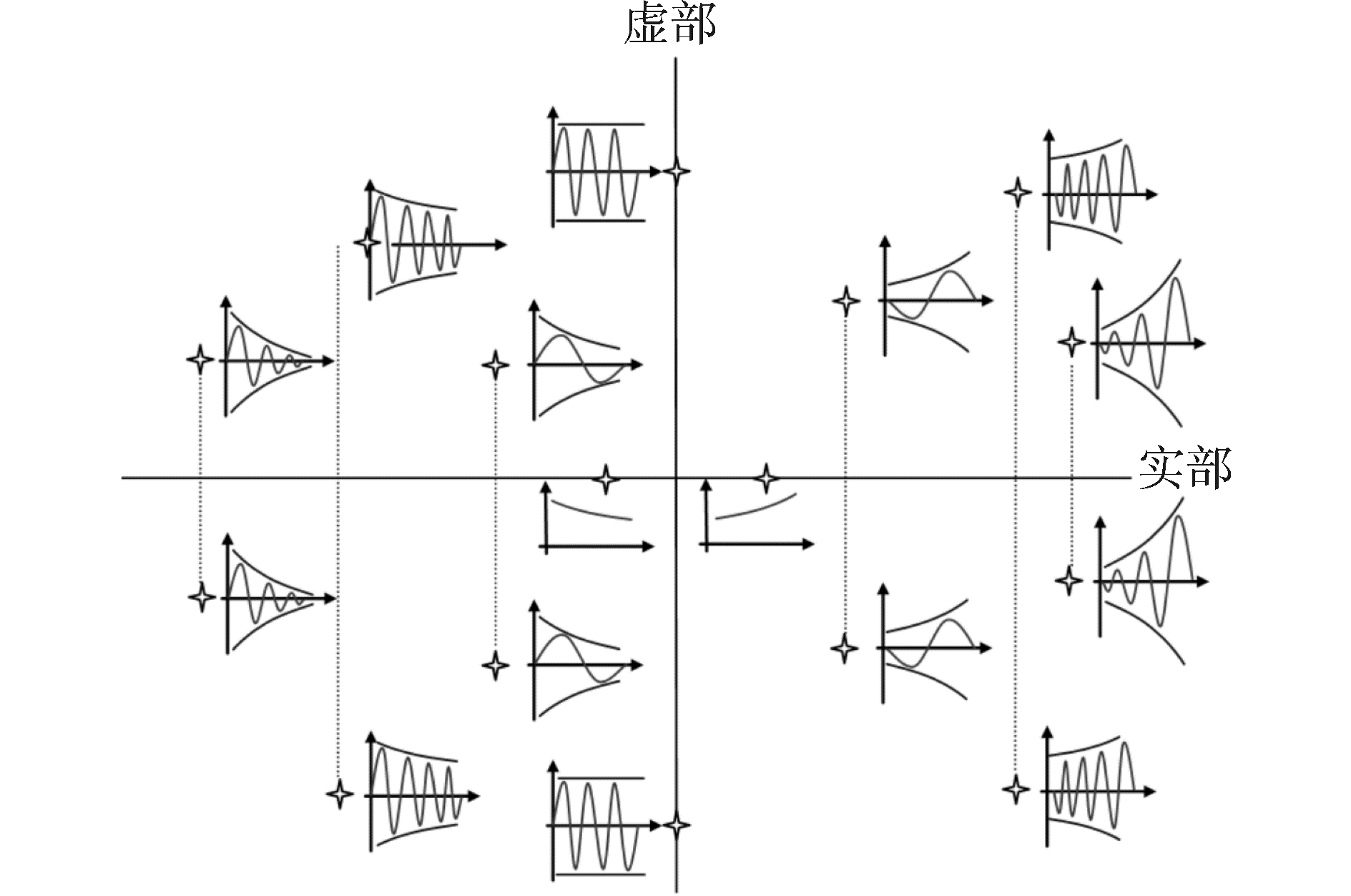
5 基于系统矩阵特征值分布的稳定性分析李雅普诺夫第一法的基本思路是通过系统状态方程的解来判别系统的稳定性。对于线性定常系统,只需解出特征方程的根即可作出稳定性判断。对于一般的非线性系统,则可通过线性化处理,近似得到线性化方程,然后再根据其特征根来判断系统的稳定性。因此,通过分析系统状态矩阵特征值在复平面域的分布情况即可判断系统的稳定性[10]。本文基于矩阵的秩的变化,将电控双阀燃油喷射系统喷油工作过程划分为12个时间段,在每个时间段中选取中间点作为典型时刻观察系统状态矩阵的特征值分布,以判断系统喷油工作过程中的稳定性变化。图 6为系统状态矩阵特征值在复平面域分布情况与系统稳定性的关系。特征值的实部决定系统的收敛与发散特性,即系统的稳定性。特征值位于正半平面实轴上则系统发散,不稳定;位于负半平面实轴上,系统收敛,稳定。特征值的虚部决定系统的振荡特性,特征值距离实轴越远,系统的震荡特性越强,且以实轴为对称轴的共轭特征值所反映的震荡特性相同。
|
| 图6 系统特征值分布与稳定性的关系 Figure 6 Relation between system stability and distribution of characteristic roots in the complex plane |
根据图 5系统矩阵秩的变化情况,将系统工作过程化分为0~t1,t1~t2,t2~t3,t3~t4,t4~t5,t5~t6,t6~t7,t7~t8,t8~t9,t9~t10,t10~t11,t11~0.012 s这12个阶段,在这12个阶段中选取每阶段中间时刻作为典型时刻点,分别求取了工作过程中典型时刻点对应的系统状态矩阵序列的特征值,并绘制了系统状态矩阵特征值在复平面的分布情况,如图 7所示。

|
| 图7 电控双阀燃油喷射系统工作过程典型时刻特征值分布 Figure 7 Eigenvalues distribution of state matrices on the complex plane at different time points |
如图 7(a)所示,在0~t1阶段,SCV未通电而阀杆开启,随着柱塞上行压油,柱塞腔内的燃油直接由密封锥面泄流至低压腔,此时系统内状态由低压供油系统决定。由于低压油泵持续脉动供油的固有特性,使低压油腔内的燃油压力存在周期性波动。因此系统状态矩阵序列的特征值主要集中在虚轴附近,表现出较强的弱阻尼振荡特性。
如图 7(b)所示,在t1~t2阶段,SCV阀杆开始动作,但未完全关闭。系统处于建压准备阶段,复平面的右侧系统状态矩阵序列的特征值逐渐增多,表明此时系统逐渐处于非稳定状态。这是由于在SCV阀杆关闭过程中,燃油的泄流通路被逐渐关闭,此时阀杆处的流动为三叉管流动状态,柱塞在供油凸轮驱动下上升,在柱塞压缩作用下,柱塞腔至喷油器嘴端油路内的燃油压力逐渐上升,流动为瞬变流,系统压力状态变化剧烈,系统的稳定性逐渐下降,小部分特征值由复平面左侧向右侧移动。
如图 7(c)所示,在t2~t3阶段,SCV完全关闭,系统处于建压阶段,系统状态矩阵序列的特征值大幅移向复平面的右侧,且主要集中在虚轴附近,表明此时系统处于非稳定状态,且存在明显震荡特性。这是由于在SCV完全关闭后,燃油的泄流通路被完全关闭,柱塞腔至喷油器嘴端油路内的燃油压力在柱塞压缩作用下迅速上升,系统压力状态变化剧烈,特征值大幅由复平面左侧向右侧移动。同时,由于此时NCV与针阀仍然处于关闭状态,柱塞腔至喷油器嘴端形成了两端闭口油路,燃油压力波在柱塞腔至喷油器嘴端之间往复传播、反射并不断叠加,使系统表现出显著的振荡特性,所以特征值集中分布在虚轴附近,且与实轴距离变大。
如图 7(d)、(e)所示,在t3~t4与t4~t5阶段,NCV开始打开至完全打开,针阀上端高压燃油与低压油路相连通,系统状态矩阵的特征值逐渐向左半平面移动,并逐渐向实轴靠拢,表明此时系统的阻尼增加,震荡减弱,稳定性增强。这是由于NCV打开,针阀上端压力降低,使得柱塞腔和喷嘴之间的压力波反射和叠加不断减弱,从而削弱了系统的震荡,使系统的稳定性有所提高。
如图 7(f)所示,在t5~t6阶段,针阀打开但未达到最大升程,系统开始喷油,此时系统在喷油孔处可能存在非稳定的瞬变流运动,可以看出右半平面系统状态矩阵的特征值有所增加,这是由于针阀打开瞬间,喷油器喷嘴处流动状态瞬间变化,系统的稳定性降低。
如图 7(g)所示,在t6~t7阶段,针阀达到最大升程,系统处于喷油阶段。与上一阶段相比,右半平面的系统矩阵特征值大幅降低,由于喷油过程中,SCV阀杆、NCV阀杆与针阀阀杆不再运动,对燃油流动的边界条件不再产生影响,整个系统的流动状态单一,提高了系统的稳定性,但仍保持了震荡特性。
如图 7(h)、(i)所示,在t7~t8与t8~t9阶段,SCV开始打开,系统开始泄流,NCV开始关闭,系统矩阵的特征值开始向复平面左侧移动且开始逐渐相实轴靠拢,系统的稳定性略微上升且震荡特性有所减弱。这是由于此时系统内的高压燃油经开启的密封锥面向低压腔泄流,燃油压力开始下降,相当于为系统引入了强阻尼作用,因此状态矩阵序列特征值沿阻尼增加的方向逐渐向实轴靠拢,系统表现出强阻尼特性。
如图 7(j)、(k)、(l)所示,在t9~t10、t10~t11与t11~0.012 s阶段,针阀在预紧力的作用下开始关闭至完全关闭,系统处于停止喷油准备阶段与喷油结束阶段。系统状态方程的特征值继续向复平面左侧移动并继续向实轴聚集,系统的稳定性上升的同时表现出强阻尼特性。这是由于喷油逐渐结束时,系统内的高压燃油经开启的密封锥面向低压腔泄流,燃油压力大幅下降,整个系统表现出对压力波的巨大衰减过程,所以系统状态方程的特征值延实轴展开,该阶段系统阻尼特性起主导作用。
6 结论1) 系统喷油过程中SCV、NCV和针阀的运动状态改变是系统状态矩阵秩发生变化的原因,当以上运动件由静止变为运动的瞬间,系统状态矩阵的秩增加,而在它们由运动变为静止时,系统状态矩阵的秩减小。
2) 低压供油系统的脉动供油与柱塞腔和喷油器嘴端之间的压力波反射、叠加是引起建压阶段系统振荡增强、稳定性下降的主要因素,针阀打开过程中喷油器喷嘴处流动状态的瞬间变化使喷油开始瞬间系统稳定性降低,针阀完全打开的喷油过程中由于系统流动特性单一,稳定性有所提高,系统喷油结束时燃油压力大幅下降形成的强阻尼作用使系统泄油阶段稳定性进一步增强。
3) 通过对系统状态矩阵序列特征值的分布及变化规律进行分析,揭示了双阀系统喷油过程中的稳定性变化规律及系统状态变化对稳定性的影响规律,为系统喷油稳定性的控制提供理论支撑。
| [1] | BEIDL C V, GILL D W, CARTELLIERI W, et al. The impact of emissions and fuel economy requirements on fuel injection system and noise of HD diesel engines:SAE tech-nical paper 980176[R]. 1998. |
| [2] | GREEVES G, TULLIS S, Barker B. Advanced two-actuator EUI and emission reduction for heavy-duty diesel engines:SAE technical paper 2003-01-0698[R]. 2003. |
| [3] | FAN Liyun, ZHU Yuanxian, MA Xiuzhen, et al. Quantitative analysis on cycle fuel injection quantity fluctuation of diesel engine electronic in-line pump system:SAE technical paper 2010-01-0875[R]. 2010. |
| [4] |
范立云, 文李明, 马修真, 等. 柴油机电控双阀燃油喷射系统喷油量影响因素研究[J].
内燃机工程, 2013, 34(2): 74–82.
FAN Liyun, WEN Liming, MA Xiuzhen, et al. Study of factors influencing delivery of electron-controlled double valve Injection system for diesel engine[J]. Chinese internal combustion engine engineering, 2013, 34(2): 74–82. |
| [5] |
文李明. 双阀电控单体泵燃油系统喷射特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
WEN Liming. Investigation on injection characteristics of double valves fuel system with electronically controlled[D]. Harbin:Harbin Engineering University, 2012. |
| [6] | CHAUFOUR P, MILLET G, HEDNA M, et al. Advanced modeling of a heavy-truck unit-injector system and its applications in the engine design process:SAE technical paper 2004-01-0020[R]. 2004. |
| [7] |
仇滔, 刘兴华, 刘福水, 等. 一种新型的双电磁阀燃油系统[J].
北京理工大学学报, 2008, 28(8): 674–677.
QIU Tao, LIU Xinghua, LIU Fushui, et al. Design for a new type fuel system[J]. Transactions of Beijing institute of technology, 2008, 28(8): 674–677. |
| [8] |
柏艳红, 陈聪, 孙志毅, 等. 基于AMESim的电液阀控缸系统线性化分析[J].
系统仿真学报, 2014, 26(7): 1430–1434.
BAI Yanhong, CHEN Cong, SUN Zhiyi, et al. Linear analysis of electro-hydraulic valve-controlled cylinder system based on AMESim[J]. Journal of system simulation, 2014, 26(7): 1430–1434. |
| [9] |
张科勋, 李进, 周明, 等. 柴油机空气系统降秩控制算法的应用范围[J].
机械工程学报, 2007, 43(12): 127–132.
ZHANG Kexun, LI Jin, ZHOU Ming, et al. Applicaton area of rank one control algorithm to diesel engine air system[J]. Chinese journal of mechanical engineering, 2007, 43(12): 127–132. DOI:10.3901/JME.2007.12.127 |
| [10] |
仝庆贻. 混杂系统稳定性及其在电力系统中的应用研究[D]. 杭州: 浙江大学, 2004.
TONG Qingyi. Research on stability of hybrid system and its applications in power systems[D]. Hangzhou:Zhejiang University, 2004. |



