海上起重设备在进行起重作业时,波浪会导致船舶产生复杂的运动,进而影响起重作业的安全。对海浪进行补偿和缓冲,以提高海上起重设备在高海况下作业的安全性和效率,是未来海上起重设备的发展方向。
目前,国内外已经发展出几种波浪补偿装置以及相应的控制模式。按能量的输入可分为主动补偿、被动补偿、主-被动补偿和半主动补偿[1]。主动补偿是采用检测并主动预测由船体引起的吊物升沉,控制执行机构主动补偿吊物的升沉,因还没有对应的能量回收方法,系统的能量损失大;被动补偿是采用运动隔离的方法,不对执行机构进行运动控制,不需进行能量的输入,有节能、简单可靠的特点,但补偿精度偏低;主-被动补偿是结合了主动补偿和被动补偿的特点,分时段进行主动和被动补偿,尽管其综合性能有所提升,但机构复杂、可靠性低,仍需消耗较大能量才能获得良好的补偿效果;半主动补偿则是通过控制被动补偿系统的阻尼和刚度实现补偿,补偿效果较被动补偿好,而且比主动补偿消耗能量少[2]。
半主动补偿一般采用阻尼刚度连续可调补偿的方式(多采用磁流变液技术),广泛应用于汽车悬挂、结构抗震及石油钻井中[3-5]。目前,这种补偿技术或者类似的调节技术已逐渐引入到了海上起重补偿领域,但还缺少统一、合理的补偿效果评价指标。
本文提出了一种借鉴半主动调节方式的基于阻尼阀的非连续可调补偿系统,建立其非线性动力学方程并线性化,分析这种可调被动变阻尼控制补偿方法在海上起重特有作业条件下的功能及其适用的范围,并探讨补偿器的综合评价指标,然后通过数值仿真分析系统线性、非线性刚度和线性、非线性阻尼对系统振幅的影响,最终提出了一种有较好补偿效果的基于阻尼调节的被动补偿方法。
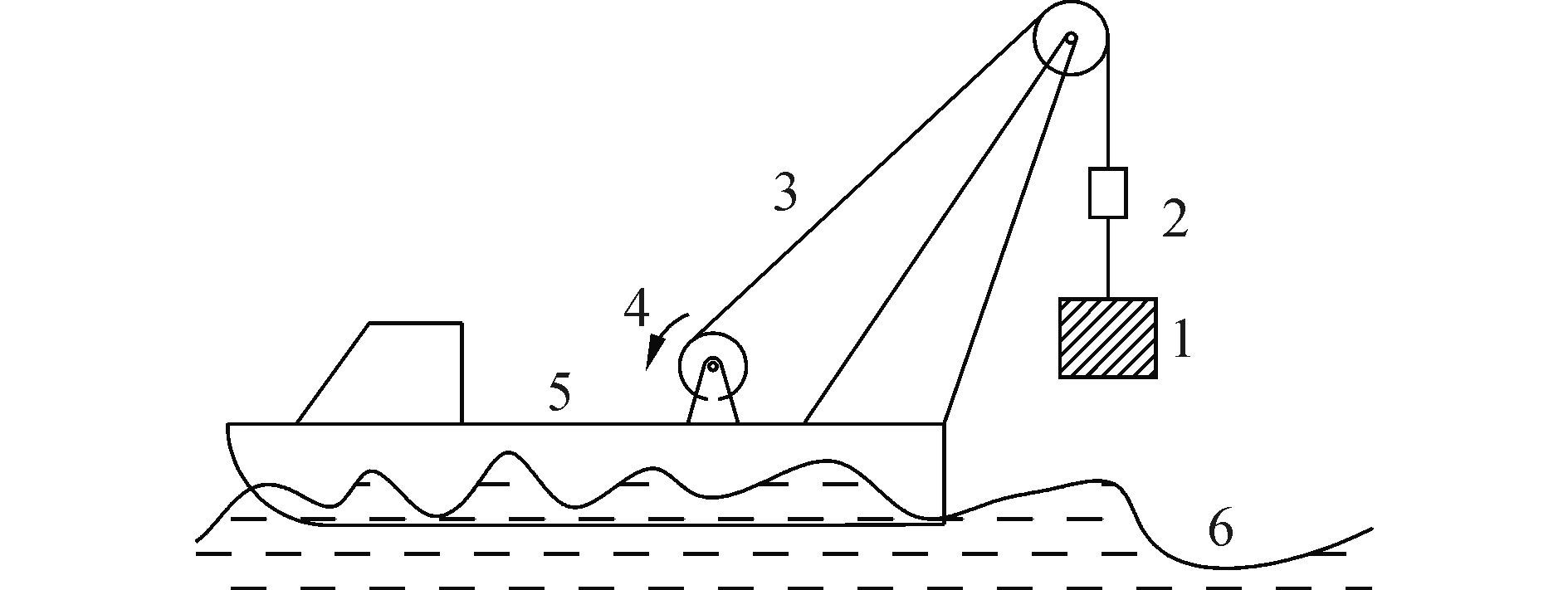
1 系统原理及分析 1.1 系统原理常用的液压缸起重补偿器主要形式分为压缩式和悬挂式,两者仅是结构形式不同,可以通过滑轮组进行互相转换,补偿特性类似。液压缸悬挂式起重补偿器原理如图 1所示。钢丝绳和吊重分别直接(或通过滑轮组)与补偿器的缸筒和活塞杆相连。活塞杆伸缩调节吊点的绝对位移,对系统的升沉进行补偿[1]。可调被动补偿是在被动补偿的基础上对阻尼和蓄能器充气压力进行调节,进而达到最优补偿效果。
|
注:1.吊重,2.补偿器,3.钢丝绳,4.卷扬机构,5.船体,6.海浪。 图 1 悬挂式补偿系统组成 Fig.1 Compensation system |
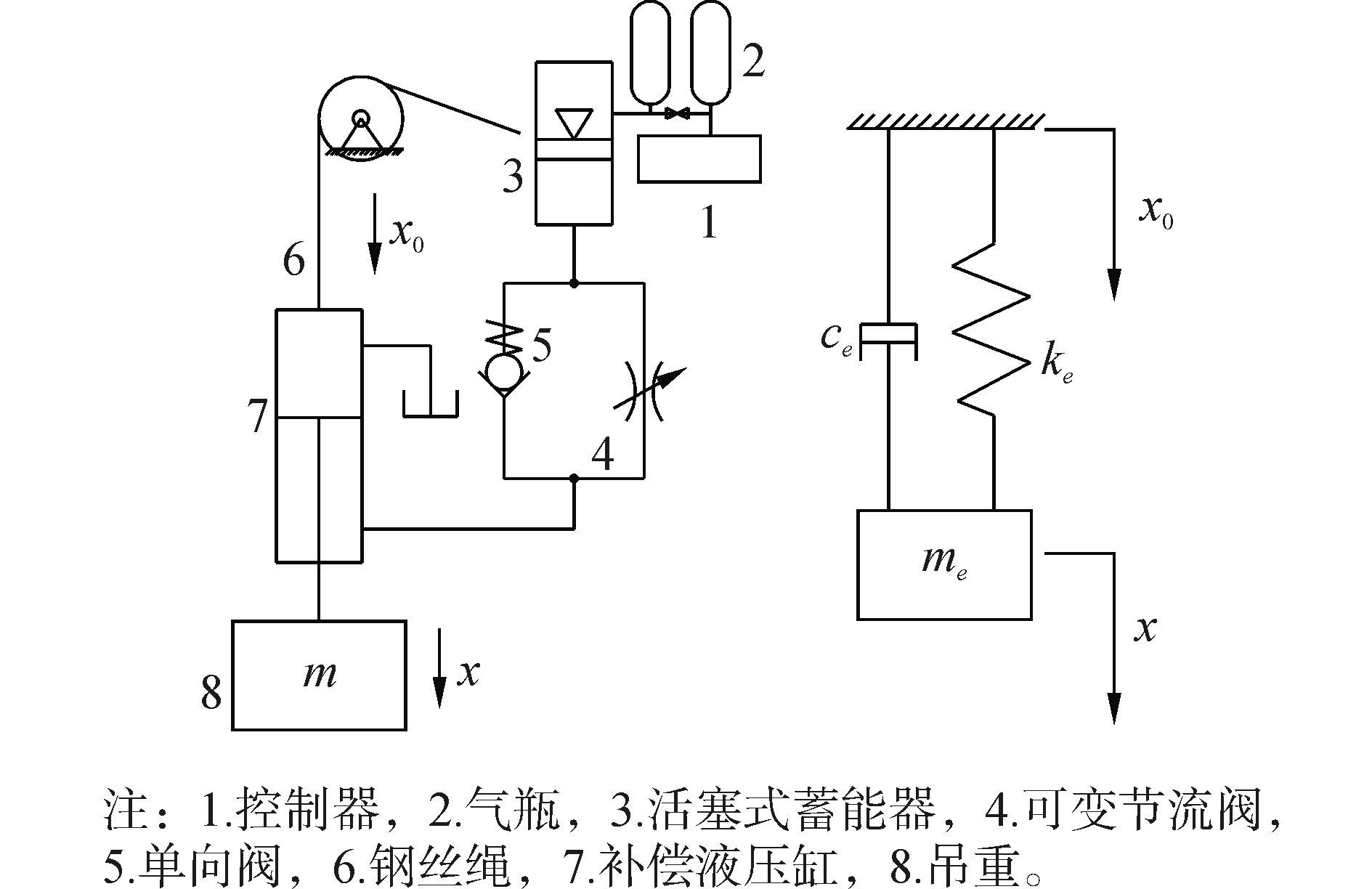
取起重机整体卷扬倍率比为1,可得起重补偿器系统简化模型如图 2所示。其中单向阀的作用是防止突然振动引起的压力冲击;节流阀的阻尼可调;补偿器的活塞式蓄能器和工作气瓶相连组成弹性元件。对于固定载荷或载荷变动范围不大的场合如深海采矿起重设备,水下机器人的收放等,不调节蓄能器的充气压力即可获得理想的补偿效果。本文所述系统采用备用气瓶储存高压气体以调节蓄能器充气压力,可以保持补偿液压缸的中位以适应不同载荷,备用气瓶的压力由空压机进行调节。
|
图 2 补偿器简化模型 Fig.2 Simplified compensator |
补偿系统的主要非线性原件有2个:1) 蓄能器,其等效刚度随气体压缩而增大;2) 系统的阻尼,主要为液压管路阻尼和节流阻尼。
本文的分析基于如下假定:1) 液压油不可压缩,不计液压油质量,不计系统泄漏;2) 不计液压缸的库伦摩擦和粘性摩擦,不计滑轮组的库伦摩擦和粘性摩擦。
将船体在波浪中的升沉运动简化为标准正弦函数,其频率和波浪圆频率相同,幅值与海浪的有义波高成正比:
| $ {x_0} = \alpha u = H\sin \left( {2{\rm{\pi }}\omega t} \right) $ | (1) |
式中:x0为起重船的升沉位移;u为海浪的波面函数;α为起重船升沉位移和有义波高的比例系数;H为船体升沉幅值;ω为波浪圆频率ω=1/T,T为波浪周期。
文献[6]已验证在其他条件相同情况下,采用标准正弦作为仿真输入比采用随机海浪作为输入,得到的位移补偿率低,而且单绳张力大。故本文采用标准正弦作为仿真输入是较实际随机波浪不利的工况,满足研究的要求。
吊重的绝对位移xabs和船体相对于吊重的位移x可以表示为
| $ \left\{ \begin{array}{l} {x_{{\rm{abs}}}} = {x_0} + {x_1} + {x_2}\\ x = {x_1} + {x_2} \end{array} \right. $ | (2) |
式中:x0为船体深沉位移,x1为活塞对于缸筒的相对位移,x2为钢丝绳伸长量。
由n0=1,p1=mg/A,得到蓄能器-液压缸的刚度[5]为
| $ \begin{array}{*{20}{c}} {{k_{{\rm{an}}}} = \frac{{{\rm{d}}{F_{{\rm{ac}}}}}}{{{\rm{d}}{x_1}}} = n{p_1}V_1^n{A^2}{{\left( {{V_1} - A{x_1}} \right)}^{ - \left( {n + 1} \right)}} = }\\ {nmgA{{\left( {\frac{{{p_0}{V_0}A}}{{mg}}} \right)}^n}{{\left( {\frac{{{p_0}{V_0}A}}{{mg}} - A{x_1}} \right)}^{ - \left( {n + 1} \right)}}} \end{array} $ | (3) |
式中:kan为非线性刚度,Fac为液压管路中的沿程压力损失在液压缸有效面积上产生的作用力,A为液压缸有效面积,p0为蓄能器充气压力,V0为蓄能器容积(由于蓄能器和气瓶看成一体,本文所述蓄能器容积及压力皆指蓄能器和气瓶的容积及压力),p1为静平衡时气体压强,V1为蓄能器平衡气体体积,n为补偿过程中气体状态指数,n0为初始气体状态指数,m为吊重质量。
补偿器的刚度为串联刚度kanx1=kropx2,故而船体相对于吊物的位移可以表示为
| $ x = {x_1} + {x_2} = {x_1}\left( {1 + \frac{{{k_{{\rm{an}}}}}}{{{k_{{\rm{rop}}}}}}} \right) $ | (4) |
式中:krop为钢丝绳的刚度系数,为常数。
由Poiseuille公式[6]:
| $ \Delta {p_{{\rm{pi}}}} = \frac{{128\mu {l_{{\rm{pi}}}}}}{{{\rm{\pi }}d_0^4}}\left( {A{{\dot x}_1}} \right) $ | (5) |
液压管路粘性阻尼为线性阻尼,其等效粘性阻尼系数为[7]。
| $ {c_{{\rm{pi}}}} = \frac{{{\rm{d}}\left( {{F_{{\rm{pi}}}}} \right)}}{{{\rm{d}}{{\dot x}_1}}} = \frac{{{\rm{d}}\left( {\Delta {p_{{\rm{pi}}}}} \right)}}{{{\rm{d}}{{\dot x}_1}}}A = \frac{{128\mu {l_{{\rm{pi}}}}}}{{{\rm{\pi }}d_0^4}}{A^2} $ | (6) |
式中:Fpi为液压管路沿程压力损失引起有效活塞面积上的作用力,Δppi为液压管路沿程压力损失,cpi为等效粘性阻尼系数,μ为油液的动力粘度,lpi为液压管路长度,d0为液压油管公称直径。
假定流经阻尼孔的流体运动为准恒定紊流,得节流阻尼系数[8]:
| $ {c_{\rm{O}}} = \frac{{{\rm{d}}\left( {{F_{{\rm{co}}}}} \right)}}{{{\rm{d}}\left( {{{\dot x}^2}} \right)}} = \frac{{d\left( {\Delta {p_{{\rm{co}}}}} \right)}}{{{\rm{d}}\left( {{{\dot x}^2}} \right)}}A = \frac{{\rho {A^3}}}{{2{{\left( {{c_{{\rm{Oq}}}}{A_{{\rm{ori}}}}} \right)}^2}}} $ | (7) |
式中:Fco为由孔口的压力损失在液压缸有效面积上产生的力,Δpco为孔口的压力损失在液压缸有效面积上引起的压力,ρ为油液的密度,cOq为节流孔流量系数,Aori为节流孔面积Aori=πdori2/4, dori为节流孔直径。
吊重在船体运动作用下发生强迫振动,系统的运动微分方程为[9]
| $ \begin{array}{*{20}{c}} {m\left[ {\left( {1 + \frac{{{k_{{\rm{an}}}}}}{{{k_{{\rm{rop}}}}}}} \right){{\ddot x}_1} + {{\ddot x}_0}} \right] + {c_{{\rm{pi}}}}{{\dot x}_1} + }\\ {{c_{\rm{O}}}{\rm{sign}}\left( {{{\dot x}_1}} \right)\dot x_1^2 + {k_{{\rm{an}}}}{x_1} = 0} \end{array} $ | (8) |
式(8) 中节流阻尼cO为非线性阻尼,所以基于阻尼调节的补偿器系统是典型的非线性非自治振动系统。尽管工程上可以采用数值方法进行求解,但并不能直观地体现各参数之间的关系[8],所以采用线性化的方法对其进行定性分析,以获得主要参数对系统性能的影响规律。
1.3 非自治系统线性化分析在实际系统中,由于krop≫kan,在线性分析时取x=x1,采用等效线性化方法[9],可假定等效的线性化方程如下
| $ m\left( {{{\ddot x}_0} + \ddot x} \right) + {k_{\rm{e}}}x + {c_{\rm{e}}}\dot x = 0 $ | (9) |
式中:ce为系统的等效阻尼,ke为系统等效刚度。
式(9) 可整理为
| $ \ddot x + 2\xi {\omega _{\rm{e}}}\dot x + \omega _{\rm{e}}^2x = H{\omega ^2}\sin \left( {\omega t} \right) $ | (10) |
式中:
将x=xabs-x0代入式(10),求出稳态解后可得吊物的绝对位移[9]为
| $ {x_{{\rm{abs}}}} = x + {x_0} = B\sin \left( {\omega t - \varphi } \right) $ | (11) |
其中:
| $ B = \frac{{H\sqrt {1 + {{\left( {2{\xi _{\rm{e}}}z} \right)}^2}} }}{{\sqrt {{{\left( {1 - {z^2}} \right)}^2} + {{\left( {2{\xi _{\rm{e}}}z} \right)}^2}} }} $ |
| $ \varphi = \arctan \left( {\frac{{2{\xi _{\rm{e}}}{z^3}}}{{1 - {z^2} + {{\left( {2{\xi _{\rm{e}}}z} \right)}^2}}}} \right) $ |
其中,
由式(6) 可得位移和加速度的放大系数βe大小相同,可以表示为
| $ {\beta _{\rm{e}}} = \frac{{B\omega _{\rm{e}}^2}}{{H\omega _{\rm{e}}^2}} = \frac{B}{H} = \frac{{\sqrt {1 + {{\left( {2{\xi _{\rm{e}}}z} \right)}^2}} }}{{\sqrt {{{\left( {1 - {z^2}} \right)}^2} + {{\left( {2{\xi _{\rm{e}}}z} \right)}^2}} }} $ | (12) |
对式(12) 求关于ξe的导数:
| $ \frac{{{\rm{d}}{\beta _{\rm{e}}}}}{{{\rm{d}}{\xi _{\rm{e}}}}} = \frac{{4\xi _{\rm{e}}^2\beta _{\rm{e}}^2{z^3}}}{{{{\left( {1 + {{\left( {2{\xi _{\rm{e}}}z} \right)}^2}} \right)}^2}}}\left( {{z^2} - 2} \right) $ | (13) |
当
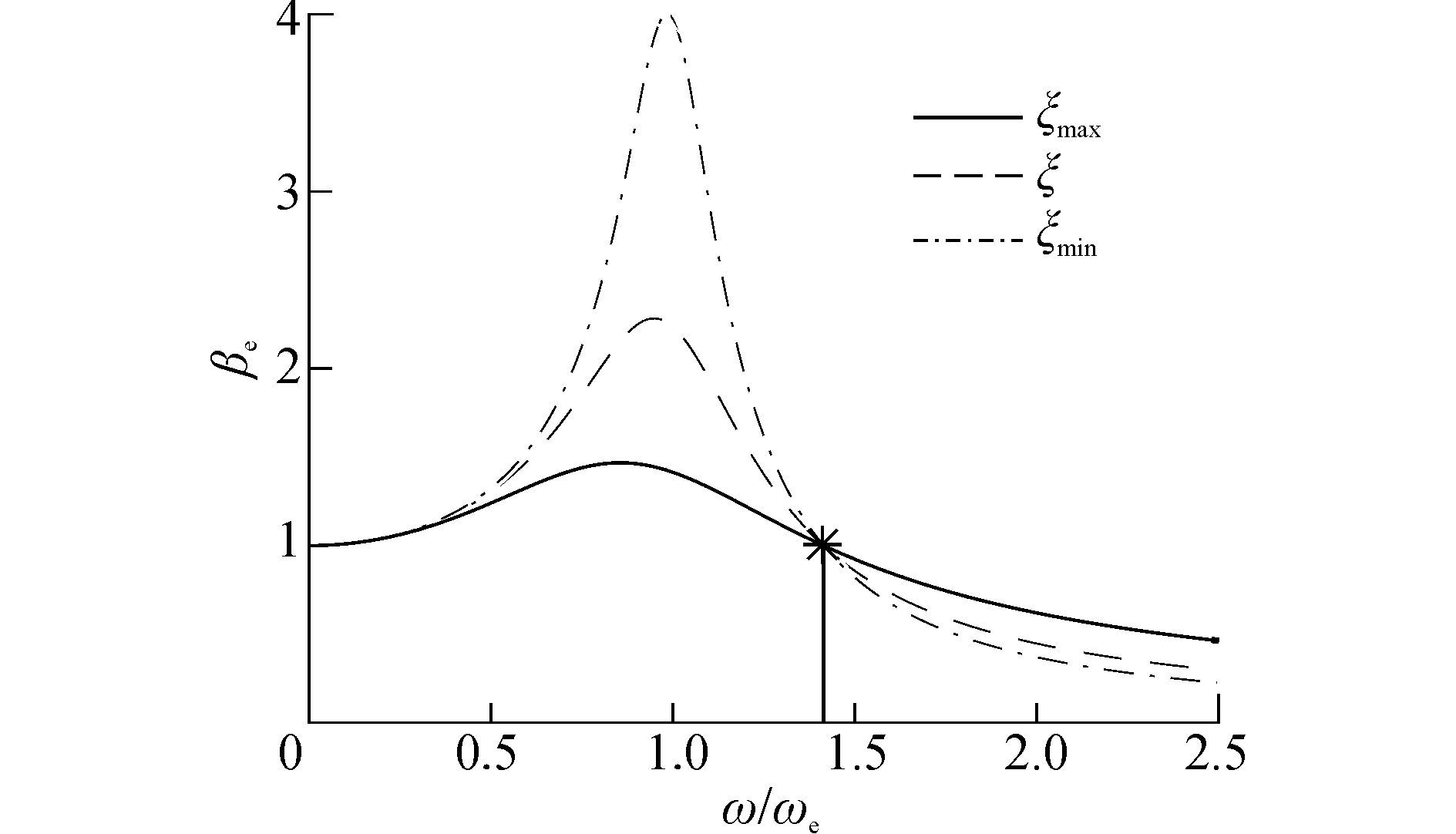
根据幅频特性可知,无论采取何种控制算法,基于阻尼调节的瞬时阻尼必然处在等效阻尼的上下限(ξmin和ξmax)之间,最终所取得的调节效果也必然介于二者之间,如图 3所示。而且只有z超过系统临界值时,减小ξe,才有可能同时减小位移峰值和加速度峰值。文献[6]已通过仿真验证了当V1过小时,xabs的峰值出现放大,根据式(14) 可知其原因是V1过小导致z小于系统临界值。
|
图 3 放大系数曲线 Fig.3 Curve of amplification coefficient |
假定蓄能器内的气体为理想绝热气体,可将其刚度线性化为[10]
| $ {k_{\rm{e}}} = \frac{{{p_1}n{A^2}}}{{{V_1}}} = \frac{{nmgA}}{{{V_1}}} = \frac{{{{\left( {mg} \right)}^2}n}}{{{p_0}{V_0}}} $ | (14) |
对式(7) 采用傅里叶级数展开的等效线性化方法[9],可得节流口的线性等效阻尼系数为
| $ \begin{array}{l} {c_{{\rm{Oe}}}} = \frac{4}{{{\rm{\pi }}B\omega }}\int_0^{\frac{{\rm{\pi }}}{{4t}}} {{c_{\rm{O}}}{{\left( {B\omega } \right)}^2}{{\cos }^3}\left( {\omega t} \right){\rm{d}}t} = \\ \;\;\;\;\;\;\;\;\frac{{4B\omega \rho {A^3}}}{{3{\rm{\pi }}{{\left( {{c_{{\rm{Oq}}}}{A_{{\rm{ori}}}}} \right)}^2}}} \end{array} $ | (15) |
总的线性等效阻尼系数为ce=cpi+cOe。
由式(14) 可得:
| $ {\omega _{\rm{e}}} = \sqrt {\frac{{ngA}}{{{V_1}}}} ,z = \sqrt {\frac{{{\omega ^2}{V_1}}}{{ngA}}} $ | (16) |
| $ {\xi _{\rm{e}}} = \left[ {\frac{{64\mu {L_{{\rm{pi}}}}{A^2}}}{{{\rm{\pi }}d_0^4}} + \frac{{2{B_{\rm{e}}}\omega \rho {A^3}}}{{3{\rm{\pi }}{{\left( {{c_{{\rm{Oq}}}}{A_{{\rm{ori}}}}} \right)}^2}}}} \right]\sqrt {\frac{{{V_1}}}{{nA{m^2}{g^2}}}} $ | (17) |
由式(14)~(17) 可知:1) 当m不同时,若系统能主动调节p0,则V1可保持不变;2)z仅和ω、V1、A有关,和m无关;3) 增大V0,获得较大V1,可以使得z增大,但也会使得ξe增大,所以增大V0并不总能有效减小βe;4) 减小A可有效减小ξe,增大z,故而利于减小系统βe;但A减小会导致系统压力过大,不利于系统的寿命和安全。由于海浪的激励可以视作一系列谐波的叠加,所以上述的分析结果可作为设计的参考。
2 评价指标现有的系统评价指标主要有两种:一种是采用单一变量,另一种是以加权参数为评价指标。第一种评价指标如Huster A.[11]定义了2个评价指标,位移补偿量率和张力补偿率为
| $ \left\{ {\begin{array}{*{20}{c}} {{\eta _{{\rm{position}}}} = 1 - {x_{{\rm{abs}}}}/{x_0}}\\ {{\eta _{{\rm{tension}}}} = 1 - {T_{{\rm{HC}}}}/{T_{{\rm{NHC}}}}} \end{array}} \right. $ | (18) |
式中:THC为采用补偿器的钢丝绳张力,TNHC为未采用补偿器的钢丝绳张力。
文中虽然对两个指标都做了评估,却采用张力补偿率达到70%作为设计的最终目的。这种方法的缺点是只考虑最终的补偿效果,而没有考虑瞬态振动对作业的影响。因为对于作业时间较短的起重过程,起吊初始阶段瞬态振幅会较长一段时间内影响起重作业,故而此时以最终的补偿率为评价指标并不合理。第二种评价指标如Driscoll等[12]认为不能取单一的变量作为评价指标,而定义了吊物位移和船体位移比值、钢丝绳张力和额定张力比值的均方根作为目标函数的基本变量,加权平均后构建目标函数并采用二次序列规划(SQP)寻取最优的刚度和阻尼值。这种方法的第一个缺点也是忽略了起吊时间的影响。第二个缺点是无需同时考虑位移补偿率和钢丝绳张力补偿率,因为根据上述的定性分析,位移放大系数和动力放大系数在整体上有同样的增减趋势,故而只需要考虑其一即可。
在保证安全的前提下,使系统达到最高的性能是补偿器设计要达到的指标,所以在保证钢丝绳张力在安全范围内的前提下,对位移进行最大限度的补偿。本文的研究只需考虑张力峰值是否超过限度,并专注于补偿器的位移补偿率。
微分方程的解为齐次通解和非齐次特解的叠加。通解为瞬态解,几个周期之后明显消减;非齐次特解为稳态解,持续作用。由于起重船单次作业的时间并不确定,所以并不能仅以较长时间之后残余的稳态解作为评价指标。本文按照海上起重动索要求,钢丝绳张力峰值满足安全系数不超过4,并以起吊后60~90 s(实际应用中可取不同时间段)时段吊物绝对位移量的峰值的算术平均值计算补偿率η,并以其作为系统的补偿效果的评价指标:
| $ \eta = \frac{1}{{{x_0}n}}\sum\limits_{i = 1}^n {\left( {{x_{{\rm{abs1}}}} + {x_{{\rm{abs2}}}} + \cdots + {x_{{\rm{abs}}n}}} \right)} $ | (19) |
式中:n为60~90 s中吊物绝对位移的峰值个数,xabs1,xabs2,…,xabsn为60~90 s中吊物绝对位移的峰值。
3 仿真分析 3.1 系统刚度采用变步长四阶-五阶Runge-Kutta法,仿真式(3) 的系统非线性刚度和式(14) 的系统线性等效刚度。分别取吊重质量m为12 t和6 t,其他参数如表 1所示。
| 表 1 系统刚度仿真参数 Tab.1 Variables of stiffness simulation |
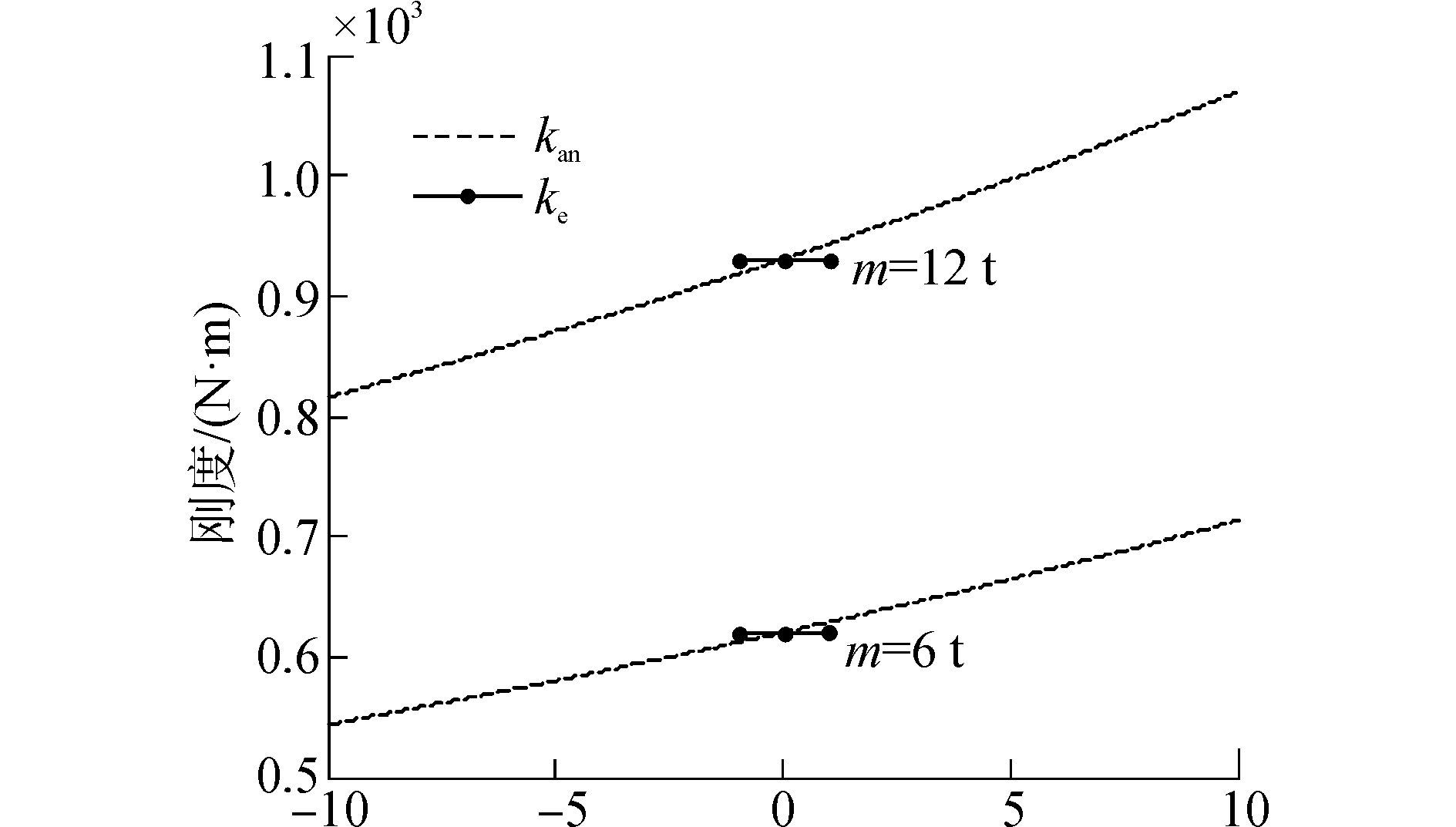
由式(14) 可知,等效刚度ke和m有关,m决定了刚度的初始水平,当m=12 t和m=6 t时的等效刚度如图 4所示。非线性刚度kan虽然整体上有较大的非线性,但在液压缸有限行程中基本呈线性且在ke的4.2%范围内变化。由文献[4]可知,海上起重补偿器的蓄能器容积V0往往较大,此时液压缸运动导致蓄能器的气体体积变化很小,从而决定了系统的刚度变化范围不会很大。仿真发现,采用线性等效刚度和采用非线性刚度仿真的结果基本相同。
|
图 4 非线性刚度和线性刚度对比 Fig.4 Comparison of nonlinear stiffness and linear stiffness |
为分析系统阻尼的特点,取仿真的浪级为四级浪,参考一般的半潜式钻井平台升沉位移与波高的模拟曲线确定起重船的深沉运动参数,见表 2[13],其他参数不变。假定补偿率为75%,绘制出一个周期内的阻尼的示功图,如图 5所示。
| 表 2 系统阻尼仿真参数 Tab.2 Variables of stiffness simulation |
|
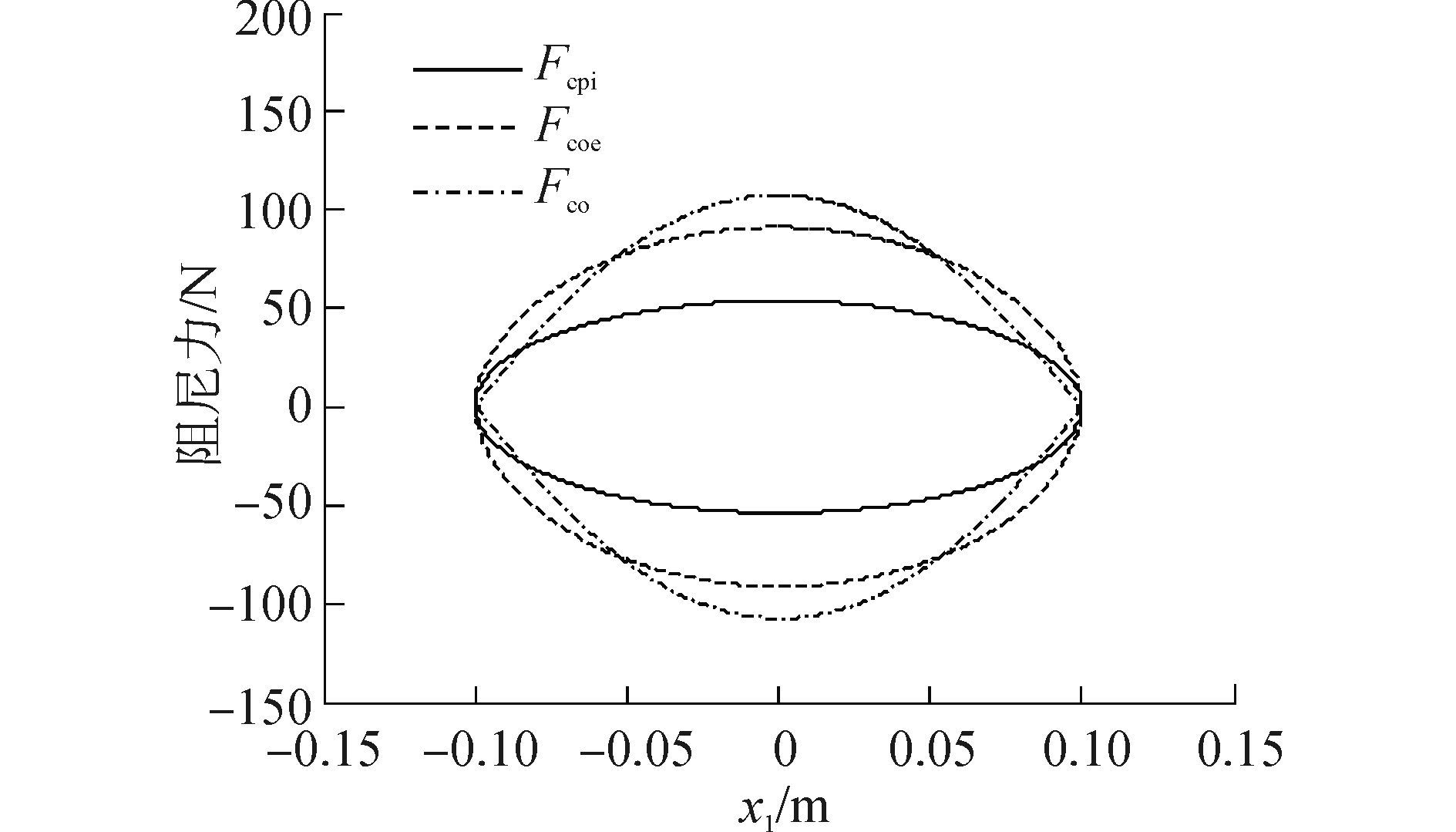
图 5 示功图 Fig.5 Ergogram |
图 5中的Fco是节流系数c0在液压缸上引起的阻尼力,Fcoe是线性等效阻尼系数coe在液压缸上引起的阻尼力,Fcpi是由液压管路的粘性阻尼引起的阻尼力。可见上述工况下,液压管路的粘性阻尼和节流孔的节流阻尼相比做功较少;非线性节流阻尼和线性化节流阻尼的做功相等,但做功趋势并不相同。
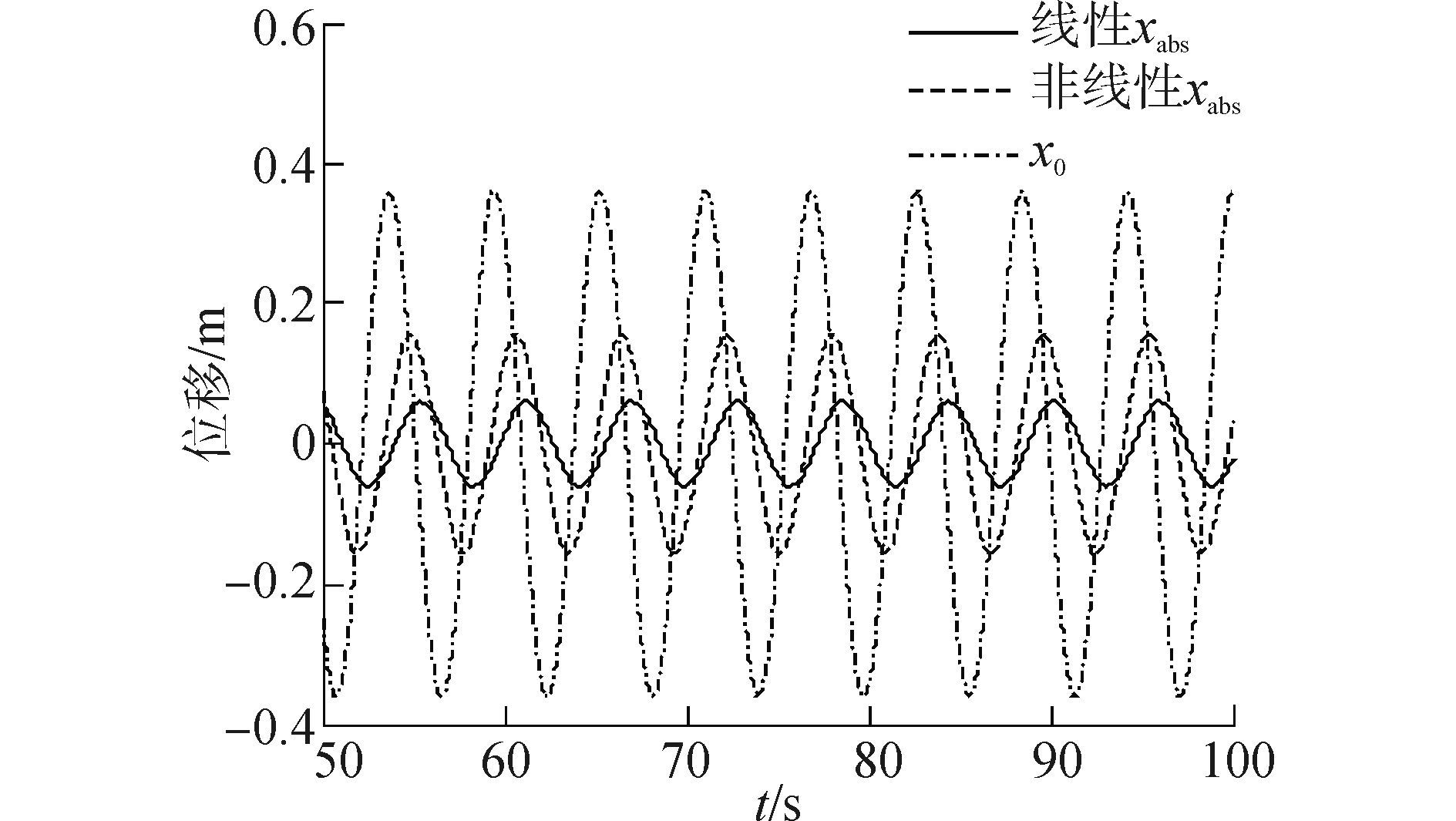
只取原模型即式(8) 和线性化之后的式(9) 求解其稳态分量,可得系统稳定后的吊物绝对位移曲线,如图 6所示。发现等效线性后的模型的补偿率为87.2%,而实际的非线性模型的补偿率只有67.8%,这主要是由于阻尼线性化导致的误差。
|
图 6 非线性化和线性化模型补偿效果 Fig.6 Compensation effect of nonlinear and linear model |
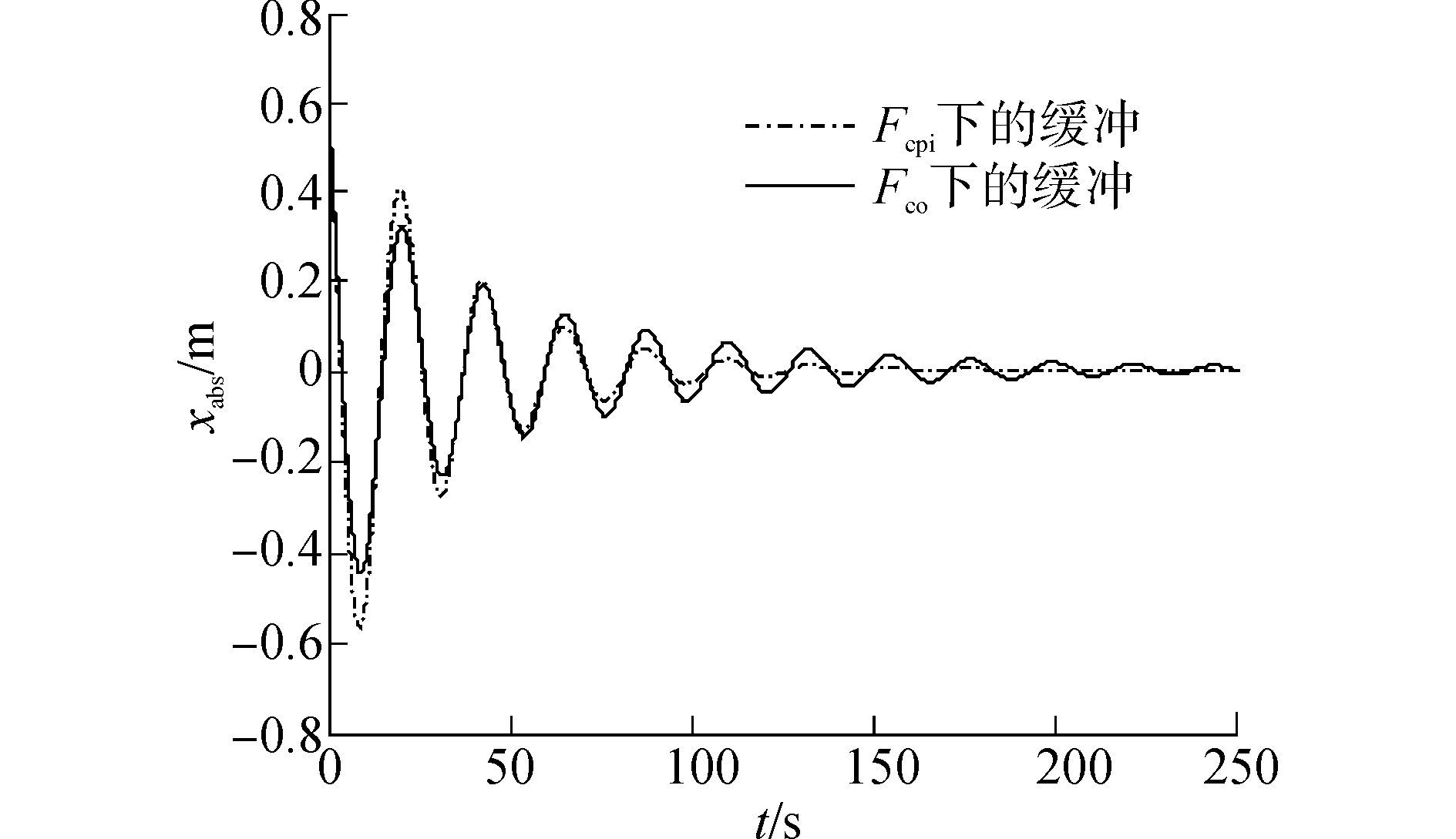
为分析系统阻尼对瞬态振动的作用,分别仿真只有非线性节流阻尼和油管的粘性阻尼的系统,起吊瞬间(假定质量突然加载)振动的瞬态分量如图 7所示。可见非线性阻尼力Fco对瞬态冲击引起的振动衰减效果明显,但幅值较低后不如粘性阻尼力Fcpi的效果。所以在起吊瞬间应加入节流阻尼以消减瞬态振动幅值。
|
图 7 非线性阻尼和线性阻尼对比 Fig.7 Comparison of nonlinear damping and linear damping |
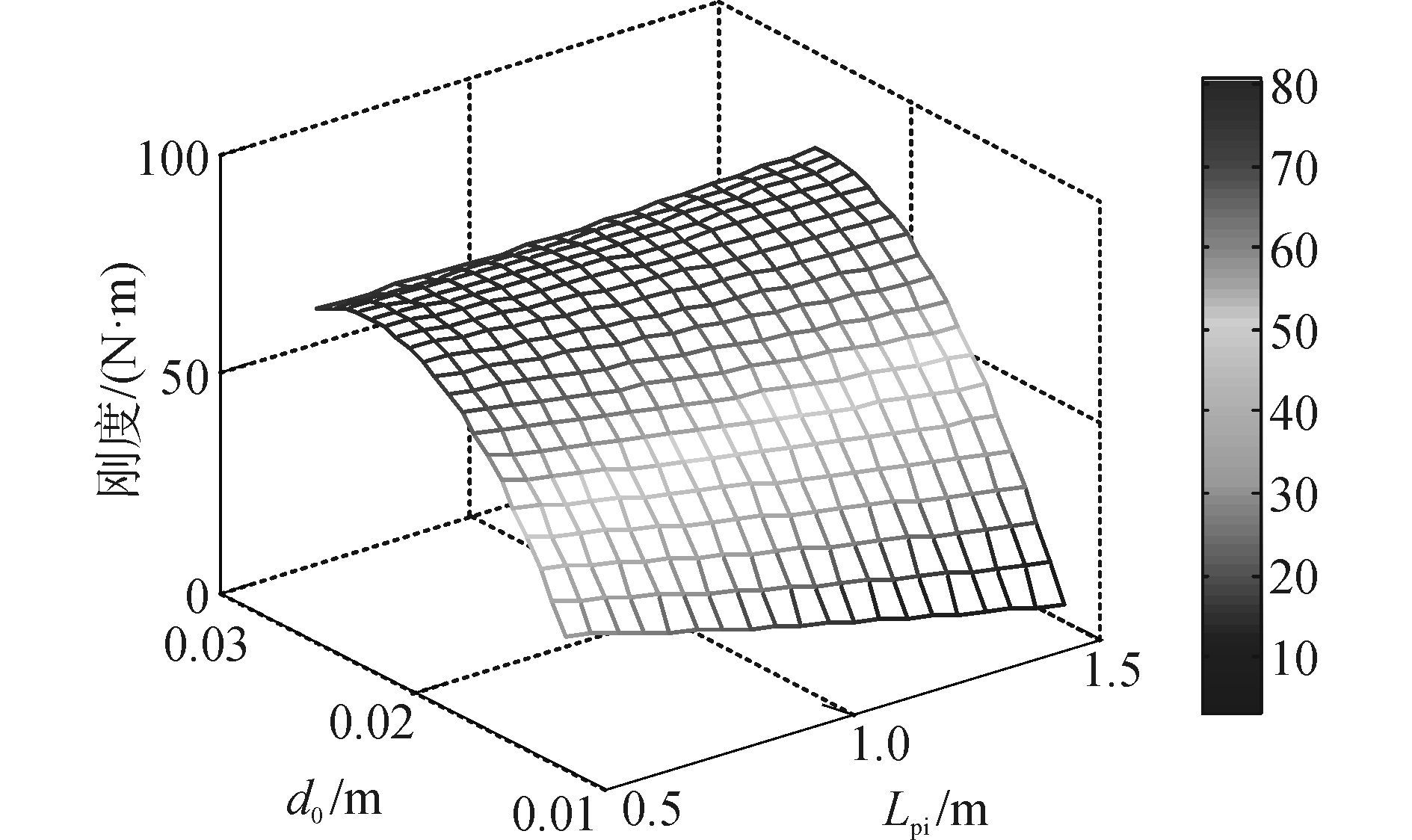
根据以上分析可知,如果频率比z超过特定值,减小阻尼比ξe可以减小放大系数,所以下文去除节流孔,只保留液压管作为阻尼元件并取液压管路直径d0增大和长度Lpi作为变参数进行仿真。
仿真得到补偿率η的响应面, 如图 8所示。可见d0增大和Lpi减小都会导致ξe减小,系统补偿率增加,但ξe过小则系统会趋于无阻尼强迫振动,瞬态振动幅值无法及时消减导致的系统持续振荡,所以在系统趋近Lpi=0.5 m,d0=0.03 m时,系统补偿率反而下降。
|
图 8 不同管长和直径下补偿率 Fig.8 Compensation rates with varied lengths and diameters |
由分析可知,等价阻尼比ξe和蓄能器平衡气体体积V1及活塞有效面积A有关。当无法增大V1时,若系统压力允许,减小A可以有效减小ξe,从而使得系统补偿率η提高。
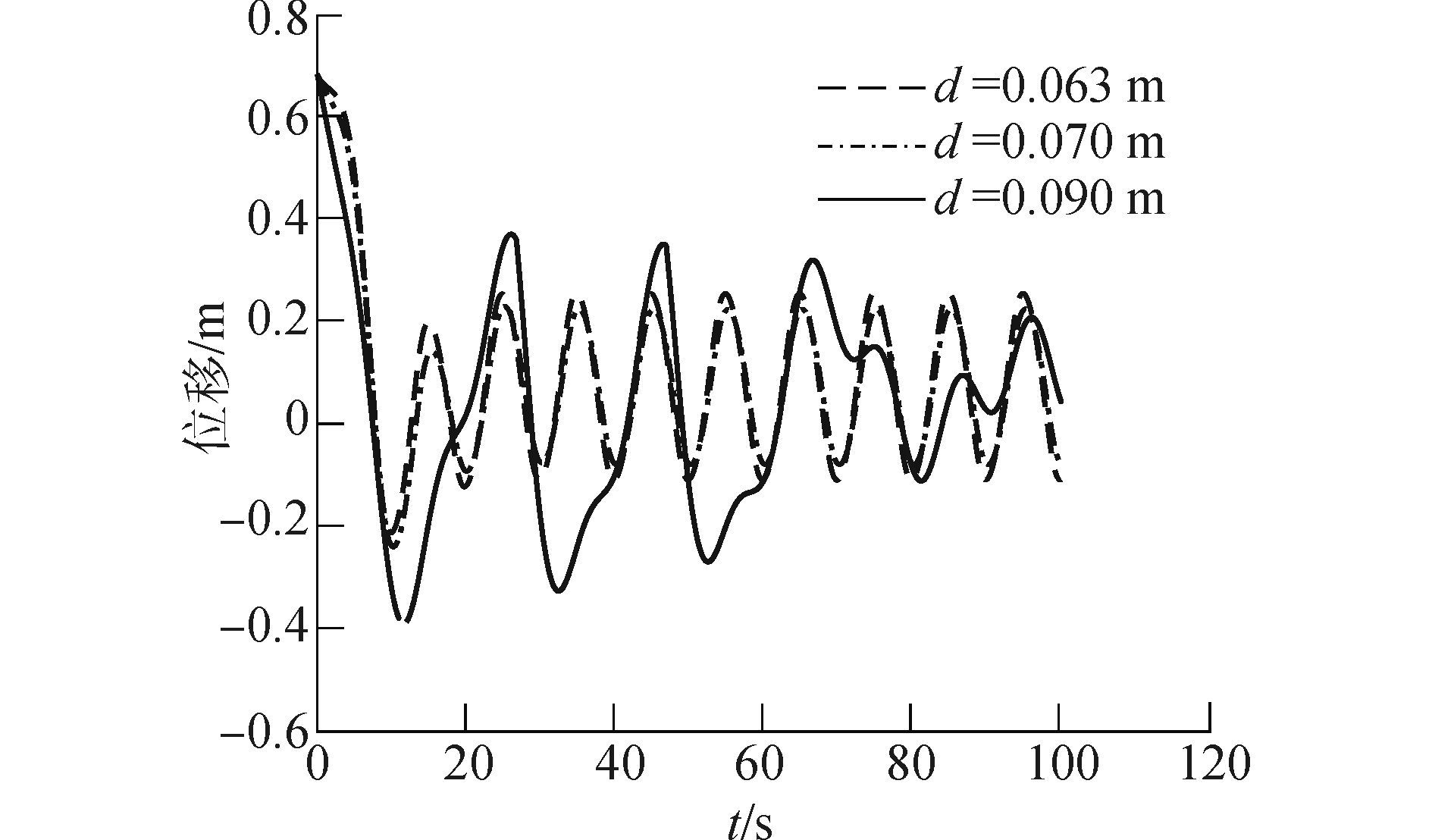
取同一系列补偿液压缸,其内径相同(0.125 m),杆径不同(0.09、0.07、0.063 m)的工况,假定吊物载荷瞬间施加在补偿系统上,进行仿真,结果如图 9所示。可见,在一定范围内减小A,能够提高η,但当A过小时系统由于z过小而产生振荡。
|
图 9 不同液压缸有效面积比较 Fig.9 Comparison of varied valid cylinder areas |
以上仿真结果和式(17) 中推导结果相符,即一定程度减小ξe(通过增大d0,减小lpi,减小A等)之后,吊物最终的稳态振动振幅会稳定在较小的值。但过小的ξe会导致吊物瞬态振动幅值衰减较慢,传统方法是增加系统阻尼提高ξe,这种方法虽然能够使得瞬态振动幅值在较短时间内衰减,但会使得最终的补偿率降低。
经过以上对非线性阻尼和粘性阻尼的效果分析可知,起吊时应加入节流阻尼对系统的瞬态响应进行消减,几个波浪周期之后再去除节流阻尼可得到较好的效果。
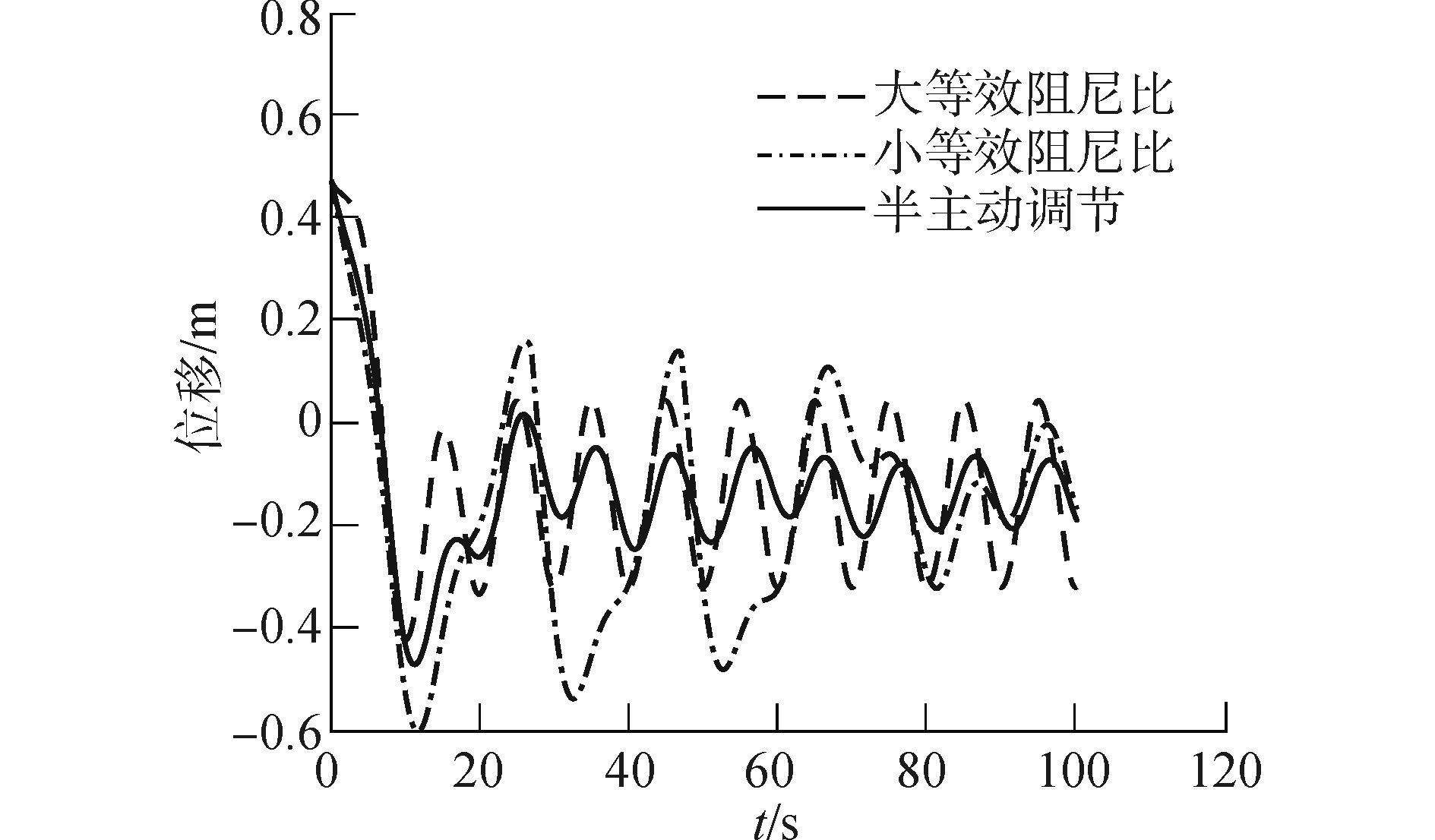
如图 10所示,若系统取较小的ξe(0.075,即杆径0.09 m时),会引起瞬态振动幅值无法消减;反之取较大的ξe(0.25,即杆径0.063 m时),会导致最终稳态振幅较大。所以可以采用较小的ξe,以得到较小的稳态振幅,并在开始起吊时加入节流阻尼,一定时间后(本文取50 s)后去除节流阻尼,可以迅速衰减瞬态振动。这种调节方式补偿率为77.7%,比取较大ξe时的补偿率47.2%和较小ξe时的补偿率64.8%都有较大提高。
|
图 10 阻尼调节效果 Fig.10 Effect of system with semi-active damping regulation |
然而一旦设计完成硬件条件不改变下,z便由船体的升沉频率决定,在越高海况下补偿效果越好,当海况较低的情况下补偿率反而下降;然而当海况较低时船体深沉的幅值也不大,所以吊重的幅值并不会随海况降低而增大。
4 结论1) 刚度线性化对系统的影响较小,而阻尼线性化之后会使得系统补偿量提高,即一定程度的误差,但其定性分析仍可作为设计参考;
2) 非线性阻尼力对瞬态冲击引起的振动衰减效果明显,但当瞬态振动振幅衰减后却不如线性阻尼力;
3) 在一定范围内减小系统的等效阻尼比能够提高系统的补偿率,但系统等效阻尼比过小导致瞬态衰减较慢,系统持续震荡;
4) 针对低阻尼比有利于提高补偿率,但系统易发生振荡的问题,提出了只在初始阶段加入节流阻尼的方法,获得了较好的效果。
| [1] |
ADAMSON J E. Efficient heave motion compensation for cable-suspended systems[EB/OL]. Houston:Ocean Works International, 2003. (2003-01)[2016-02-05].http://oceanworks.com/.
( 0) 0)
|
| [2] |
张彦廷, 黄鲁蒙, 孟德超, 等. 海洋钻机补偿绞车能耗计算与实验测试[J]. 石油学报, 2015, 36(5): 620-625. ZHANG Yanting, HUANG Lumeng, MENG Dechao, et al. Energy consumption calculation and experimental test for heave compensation drawworks of offshore rig[J]. Acta petrolei sinica, 2015, 36(5): 620-625. DOI:10.7623/syxb201505012 (  0) 0)
|
| [3] |
LIU Q, TANG Y, HUANG C, et al. Study on a mechanical semi-active heave compensation system of drill string for use on floating drilling platform[J]. Plos one, 2015, 10(7): e0133026. DOI:10.1371/journal.pone.0133026 ( 0) 0)
|
| [4] |
陈云微, 赵强. 车辆半主动座椅悬架滑模变结构控制[J]. 哈尔滨工程大学学报, 2012, 33(6): 775-781. CHEN Yunlue, ZHAO Qiang. Sliding mode variable structure control forsemi-active seat suspension in vehicles[J]. Journal of Harbin Engineering University, 2012, 33(6): 775-781. (  0) 0)
|
| [5] |
PISAL A Y, JANGID R S. Dynamic response of structure with semi-active tuned mass friction damper[J]. International journal of structural and civil engineering research, 2013, 2(1): 18-31. ( 0) 0)
|
| [6] |
NI J, LIU S J, LI X F. Modeling and simulation research on passive heave compensation system for deep sea mining[J]. Computer simulation, 2010, 27(5): 247-251. ( 0) 0)
|
| [7] |
杜艳霞. 阻尼可调油气悬架系统的非线性刚度特性分析[J]. 煤矿机械, 2012, 33(9): 126-128. DU Yanxia. Nonlinear stiffness characteristics analysis of damping adjustable hydro-pneumatic suspension system[J]. Coal mine machinery, 2012, 33(9): 126-128. (  0) 0)
|
| [8] |
蔡福海. 全地面起重机油气悬架系统仿真与优化[D]. 大连理工大学, 2006: 39-42. CAI Fuhai. Simulation and optimization of hydro-pneumatic suspension of all-terrain crane[D]. Dalian:Dalian University of Technology, 2006:39-42. http://cdmd.cnki.com.cn/Article/CDMD-10141-2007014481.htm (  0) 0)
|
| [9] |
闻邦椿. 机械振动理论及应用[M]. 北京: 高等教育出版社, 2009: 17-52.
( 0) 0)
|
| [10] |
WOODACRE J K, BAUER R J, IRANI R A. A review of vertical motion heave compensation systems[J]. Ocean engineering, 2015, 104: 140-154. DOI:10.1016/j.oceaneng.2015.05.004 ( 0) 0)
|
| [11] |
HAUSTER A, BERGSTROM H, GOSIOR J, et al. Design and operational performance of a standalone passive heave compensation system for a work class ROV[C]//OCEANS 2009, MTS/IEEE Biloxi-Marine Technology for Our Future:Global and Local Challenges. Biloxi, MS, USA, 2009:1-8.
( 0) 0)
|
| [12] |
DRISCOLL F R, BUCKHAM B, NAHON M. Numerical optimization of a cage-mounted passive heave compensation system[C]//OCEANS 2000 MTS/IEEE Conference and Exhibition. Nice, France, 2000:1121-1127
( 0) 0)
|
| [13] |
方华灿. 海洋石油钻采设备理论基础[M]. 北京: 北京工业出版社, 1984: 283-305.
( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


