2. School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China
刀盘作为全断面岩石掘进机 (tunnel boring machine,TBM) 的核心部件,工作在极其恶劣的复杂地质环境下,承受随机冲击载荷,最常见的工程问题是疲劳裂纹失效 [1-3]。对刀盘的裂纹扩展寿命进行合理评估,有利于保障施工安全及掘进效率发生疲劳,而寿命评估的前提是获得刀盘裂纹尖端的应力强度因子。为此,有必要研究复杂应力状态下刀盘裂纹应力强度因子的分布规律以及不同裂纹参数的影响。近年来,国内外学者在TBM刀盘系统结构设计方面,已开展了一定的研究工作,如科罗拉多矿业大学的Ozdemir等[4]、宾夕法尼亚州立大学的Rostami等[5]、新加坡南洋大学的龚秋明等[6]、中南大学的夏毅敏团队[7-8]、大连理工大学的孙伟、霍军周[9-12]等。而关于TBM刀盘裂纹应力强度因子的研究还很少涉及,也没有其参数影响的相关文献报导。应力强度因子是用来表征裂纹尖端应力场奇异性的强度,是驱动裂纹扩展的关键参数。对于刀盘这类复杂板式箱体类结构而言,传统的理论计算和试验方法很难求解其裂纹应力强度因子。因此,数值计算方法成为工程问题求解的有效途径[13]。Mitsuya等采用动态有限元方法计算管道在裂纹扩展过程中的动态应力强度因子[14]。X.B.Lin等采用数值仿真和试验等手段研究裂纹前沿应力强度因子的分布及变化规律[15-16]。本文以辽西北引水工程刀盘为研究对象,在刀盘面板的薄弱部位预制初始表面裂纹,用奇异单元对裂纹尖端区域进行精细网格处理。同时,在已有的刀盘等效疲劳载荷谱基础上,应用有限元法直接求解复杂应力下刀盘裂纹的应力强度因子。并分析裂纹位置角、形状比及相对深度比值等裂纹参数对应力强度因子分布规律的影响。
1 应力强度因子的数值解有限元法求解应力强度因子可分为直接法和间接法,直接法是利用裂纹尖端附近节点位移或应力值推算尖端的应力强度因子,如位移法和应力法;而间接法则是先求出能量释放率 (J积分),再根据其定义折算应力强度因子。根据单元类型的不同又可分为常规单元有限元法和特殊单元有限元法,如奇异单元法。以下简单介绍位移法的理论基础。
构件中任意的三维裂纹及尖端坐标系可抽象成如图 1所示。

|
| 图1 裂纹尖端局部坐标系 Figure 1 Local coordinate of near crack tip |
根据线弹性断裂力学的解析解,由任意外载作用所产生的裂纹尖端附近区域的位移场和应力强度因子的关系可表示为[15]
| $ \eqalign{ &\left[\matrix{ u \hfill \cr v \hfill \cr w \hfill \cr} \right] = {{{K_1}} \over {4G}}\sqrt {{r \over {2{\rm{\pi }}}}} \left[\matrix{ \left( {2k-1} \right)\cos {\theta \over 2}-\cos {{3\theta } \over 2} \hfill \cr \left( {2k+1} \right)\sin {\theta \over 2} - \sin {{3\theta } \over 2} \cr 0 \cr \hfill \cr} \right] + {{{K_{Ⅱ}}} \over {4G}}\sqrt {{r \over {2{\rm{\pi }}}}} \cdot \cr &\left[{\matrix{ {\left( {2k + 3} \right)\sin {\theta \over 2} + \sin {{3\theta } \over 2}} \cr {\left( {3-2k} \right)\cos {\theta \over 2}-\cos {{3\theta } \over 2}} \cr 0\cr } } \right] + {{{K_{Ⅲ}}} \over {4G}}\sqrt {{r \over {2{\rm{\pi }}}}} \left[{\matrix{ 0 \cr 0 \cr {8\sin {\theta \over 2}} \cr } } \right] \cr} $ | (1) |
式中:r、θ为局部柱坐标系中的两个坐标分量;u、v、w分别为裂纹尖端任一点的径向位移、法向位移和切向位移;KⅠ、KⅡ、KⅢ分别为Ⅰ型、Ⅱ型及Ⅲ型应力强度因子;G为剪切模量;k为与材料泊松比λ有关的常数,对于平面应变问题:k=3-4λ,而对于平面应力问题:k=(3-λ)/(1+λ)。
若上、下裂纹表面 (θ=±π) 的某一点位移已知,则根据式 (1) 可导出裂纹的应力强度因子计算公式:
| $ \left[\matrix{ {K_{Ⅰ}} \hfill \cr {K_{Ⅱ}} \hfill \cr {K_{Ⅲ}} \hfill \cr} \right] = \mathop {\lim }\limits_{r \to 0} {{2G} \over {k + 1}}\sqrt {{{2{\rm{\pi }}} \over r}} {\left[{\matrix{ v \cr u \cr {\left( {k + 1} \right)w/4} \cr } } \right]_{\theta = \pm {\rm{\pi }}}} $ | (2) |
式 (1)、(2) 的最大优点就是可利用常规有限元程序计算裂纹尖端的应力应变场,进而换算应力强度因子。在三维裂纹计算中,沿裂纹前缘绝大部分范围为平面应变状态。对于平面应变状态,Ⅰ型裂纹的应力强度因子KⅠ可用裂纹面的位移表示:
| $ {K_{Ⅰ}} = {{Ev} \over {4\left( {1 - {\lambda ^2}} \right)}}\sqrt {{{2{\rm{\pi }}} \over r}} $ | (3) |
通过有限元法求出裂纹尖端节点不同r值下的KⅠ值,采用最小二乘法经过线性回归绘制KⅠ的最佳直线,由外推法得到裂纹尖端处KⅠ值。KⅡ和KⅢ计算原理相似,只是代入不同方向的位移量而已。
式 (3) 是有限元法中的位移法求解应力强度因子的基本公式,采用的是常规单元划分网格,其位移模式不能反映裂纹尖端的奇异性,难以满足收敛性条件,即使采用很细的网格也不易获得足够精确的数值解。因此,国内外学者提出很多方法来解决这个难题,其中比较成熟的是奇异单元法。
奇异单元法是在裂纹尖端附近构造一种特殊单元,其余部位仍用常规单元进行网格划分。奇异单元中的位移插值函数包含所需要的奇异项,能够反映裂纹尖端网格的奇异性。该方法优点是裂纹尖端处的单元网格划分不必过细,也可获得较高精度的计算结果。有限元软件ANSYS中提供了一种求解三维裂纹问题的奇异单元,如图 2所示。裂纹尖端大部分区域处于平面应变状态,在求得应力应变解后,取裂纹尖端1/4节点的裂纹张开位移v(1/4)代替尖端位移,代入式 (3) 中即可求得应力强度因子:

|
| 图2 ANSYS提供的三维奇异单元 Figure 2 Three dimensional singular element in ANSYS |
| $ K = {{E{v_{\left( {1/4} \right)}}} \over {4\left( {1 - {\lambda ^2}} \right)}}\sqrt {{{2{\rm{\pi }}} \over {{r_{\left( {1/4} \right)}}}}} $ | (4) |
式中:r(1/4)为1/4节点到裂纹尖端的距离。
由于刀盘处于空间多点分布载荷的耦合作用下,裂纹部位呈现复杂的多向应力状态,本文采用同时考虑三种应力强度因子的复合型等效应力强度因子作为裂纹扩展的判据指标,其计算公式为[17]
| $ {{K}_{\text{ep}}}=\sqrt{{{\left( {{K}_{Ⅰ}}+{{K}_{Ⅱ}} \right)}^{2}}+K_{Ⅲ}^{2}/\left( 1-2\lambda \right)} $ | (5) |
子模型技术是分析模型中的部分区域,进而得到更精确结果的有限元技术,在很多工程案例中得到了应用。对于刀盘模型而言,要在整体模型上引入裂纹,其基体网格必须非常细密,导致计算量庞大,求解效率低下,且很难保证精度及收敛。因此,本文将子模型技术引入到求解复杂应力状态下刀盘裂纹的应力强度因子中,在分体薄弱部位预制初始裂纹,并切割出包含裂纹的子模型,进行精细网格划分。对于裂纹问题,子模型区域宽度B至少为裂纹长度的2.5~3倍[18],通过改变子模型区域大小,分析其对应力强度因子的影响,最终确定子模型区域宽度B为裂纹长度的5倍。
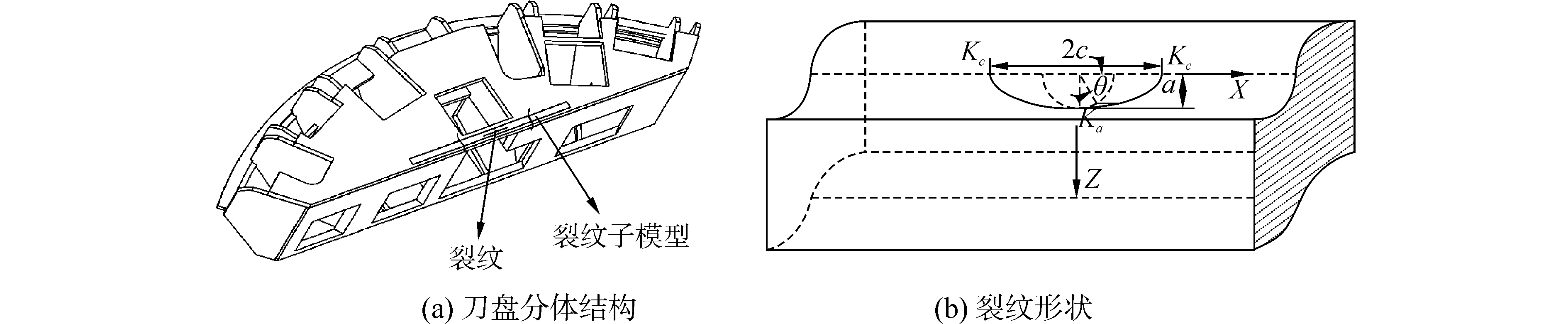
首先,建立不包含裂纹的刀盘分体模型,并用粗网格划分,通过静力分析判断出分体的薄弱部位,在此区域切割出包含裂纹体的子模型,并进行局部网格细化,如图 3所示。加载并求解整体模型,将得到的切割边界位移作为子模型的约束条件,进而计算裂纹尖端的应力强度因子。鉴于裂纹沿面板深度方向扩展所需能量最小,本文假定裂纹沿面板深度 (Z向) 和表面 (X向) 两个方向同时扩展,裂纹形貌呈现半椭圆形状,长半轴为c,短半轴为a,且长半轴方向与结合面法向垂直。裂纹尖端重点考虑裂纹最深处的应力强度因子Ka和裂纹表面自由端的应力强度因子Kc,二者共同驱动裂纹的扩展。
基于上述有限元子模型技术,合理等效刀盘分体结构,删除滚刀、焊缝等结构,分割出裂纹子模型。利用ANSYS软件对其进行网格划分,采用四面体单元划分裂纹子模型,奇异单元表征裂纹尖端的奇异性,其余结构采用六面体单元划分。同时经过严格控制整体网格大小和裂纹的网格参数,精细划分刀盘分体结构,提高求解效率和精度。建立含半椭圆型三维表面裂纹的刀盘分体有限元模型,如图 4所示。同时采用统计计数方法对滚刀及结合面载荷进行等效处理,将随机冲击载荷等效处理成8级恒幅载荷谱,其中结合面恒幅载荷如表 1所示[19]。

|
| 图4 含裂纹特征的刀盘分体有限元模型 Figure 4 The FEM model of cutter head piece with a surface crack |
| 幅值等级 | 切向载荷 | 法向载荷 | 轴向载荷 | ||||||||
| 幅值/kN | 累积循环次数 | 各级循环次数 | 幅值/kN | 累积循环次数 | 各级循环次数 | 幅值/kN | 累积循环次数 | 各级循环次数 | |||
| 1 | 509.89 | 1 | 1 | 540.67 | 1 | 1 | 3 980.97 | 1 | 1 | ||
| 2 | 491.24 | 4 | 3 | 518.97 | 5 | 4 | 3 852.48 | 13 | 12 | ||
| 3 | 453.94 | 74 | 70 | 475.56 | 141 | 136 | 3 595.50 | 695 | 682 | ||
| 4 | 407.31 | 2 100 | 2 026 | 421.43 | 3 789 | 3 648 | 3 274.28 | 21 973 | 21 278 | ||
| 5 | 351.36 | 34 700 | 32 600 | 356.19 | 64 948 | 61 159 | 2 888.81 | 185 052 | 163 079 | ||
| 6 | 295.41 | 220 700 | 186 000 | 291.08 | 359 252 | 294 304 | 2 503.34 | 325 192 | 140 140 | ||
| 7 | 239.46 | 609 679 | 388 976 | 225.91 | 786 302 | 427 050 | 2 117.87 | 379 972 | 54 780 | ||
| 8 | 183.51 | 907 555 | 297 876 | 160.86 | 974 286 | 187 984 | 1 732.40 | 898 017 | 518 045 | ||
加载第3级载荷幅值,求解刀盘分体有限元模型,提取等效应力分布结果如图 5所示。从应力分布云图中很明显可以看出,最大应力出现在裂纹尖端处,其应力场梯度变化很大,出现奇异性,且明显产生了一定范围的塑性区域。
3 复杂应力下刀盘裂纹应力强度因子参数影响分析刀盘的裂纹位置、形状及尺寸等是依据工程经验或统计方法设定。为进一步揭示刀盘的损伤机理,有必要分析这些与裂纹有关的参数对刀盘面板裂纹尖端应力强度因子的影响。以下主要分析裂纹位置角、形状比及相对深度这三个参数的影响。
3.1 裂纹位置角的影响图 4有限元模型中的初始裂纹位于刀盘分体的薄弱部位,是根据应力分布大小判定。初步判断其位于刀盘分体结合面和正滚刀刀座之间的面板上,且假定为半椭圆形表面裂纹。但裂纹放置的位置角还没有确定,文中规定裂纹位置角β表示裂纹尖端长半轴方向与子模型对称面的夹角,如图 6所示。

|
| 图6 裂纹位置角示意图 Figure 6 Schematic diagram of the crack position angle |
针对刀盘分体面板上裂纹位置角的不确定性,本节以含有相同裂纹尺寸的刀盘分体模型为研究对象 (a=10,c=20),在相同的疲劳载荷边界情况下,分析不同裂纹位置角下的裂纹尖端应力强度因子。这里给出β为0°、45°、60°、90°、120°及135°这几个角度的3种应力强度因子分布规律,如图 7所示。

|
| 图7 不同裂纹位置角的应力强度因子分布 Figure 7 Stress intensity factors distribution with different crack position angles |
由图 7可知:1) 总体而言,随着裂纹位置角β的增加,KⅠ绝对值呈现先增大后减小的趋势,KⅡ和KⅢ的绝对值基本关于β=90°对称的,且位置角不同时,裂纹尖端各点的扩展形式也不同。2) 当β=0°时,KⅠ最大,且均为正值,最大值出现在裂纹尖端最深处 (θ=90°),KⅡ和KⅢ值相对较小,裂纹主导的扩展形式为张开型。3) 当β>0°时,裂纹尖端的KⅠ值均小于0,说明裂纹面受压而不扩展,在β为0°~90°增大过程中,Ⅱ型和Ⅲ型应力强度因子呈现先增大后减小的趋势,而当β=45°时,KⅡ和KⅢ值均达到最大,此时裂纹尖端最深处以撕开型扩展形式为主,而尖端表面点处则以滑开型为主。4) 当β=90°时,KⅠ为负值,绝对值达到最大, KⅡ值接近0,起主导作用的扩展形式为撕开型;而当β>90°时,KⅠ值均小于0,随着位置角的继续增加,KⅡ和KⅢ值同上个阶段一样,先增大后减小,当β=135°二者达到最大,裂纹扩展形式与β=45°时一致。
由于裂纹扩展与裂纹尖端最深处和两个表面自由端处的应力强度因子关系最大,而在这两处的扩展形式为复合型,因此,按式 (5) 计算这两处的等效应力强度因子Keq,其中表面自由端两点取较大值,得到Keq随裂纹位置角的变化规律,如图 8所示。

|
| 图8 裂纹位置角对等效应力强度因子的影响 Figure 8 The influence of crack position angle to equivalent stress intensity factors |
由图 8可知,在相同载荷和裂纹尺寸的情况下,不同裂纹位置角下的裂纹尖端等效应力强度因子变化很大,基本是关于β=90°对称的,最深点处值略大于表面点处的值。当β为45°或135°时裂纹最深处和表面点的Keq均达到最大,说明此时裂纹扩展趋势最强,裂纹最容易扩展,对刀盘损伤影响最大。
3.2 裂纹形状比的影响裂纹形状比a/c是指半椭圆表面裂纹的短半轴和长半轴的比值,直接影响应力强度因子的大小和分布,该值在裂纹萌生时很难预测。因此以下分析不同裂纹形状比下的应力强度因子分布规律,这里分别取a/c为0.1、0.2、0.4、0.8和1五个数值。保持裂纹短半轴为10 mm及载荷边界条件不变,改变裂纹长半轴大小,计算得到不同形状比下的裂纹尖端应力强度因子KⅠ、KⅡ及KⅢ的分布如图 9所示。

|
| 图9 不同裂纹形状比的应力强度因子分布 Figure 9 Stress intensity factors distribution with different crack aspect ratios |
在相同的载荷约束及裂纹深度,不同的裂纹形状比情况下,对比分析以上结果可以发现:1) KⅠ值基本上是关于裂纹最深点 (θ=90°) 对称的,形状比越大,裂纹尖端大部分区域KⅠ值越小,且随着形状比的增加,裂纹尖端最深点处KⅠ值变小,表面点处的值变大;当a/c < 0.8时,KⅠ值呈现中间大两端小的趋势,而当a/c=1时,中间点的KⅠ值小于表面点的值,说明形状比越小,即越平直的裂纹,其尖端KⅠ值相差就越大,在深度方向扩展也越快,结构失效概率也会越高。2) KⅡ值的变化规律相对比较复杂,总体上小于KⅠ值,呈现中间小两端大的趋势,随着形状比的增加,中间点的KⅡ值总是接近0,说明裂纹形状基本不影响中心点的Ⅱ型应力强度因子,而左端 (θ < 90°)KⅡ值先减小,后增大,只是裂纹滑开方向发生了改变,右端值 (除表面点外) 总体上一直在增大。3) KⅢ值除表面点外同样小于KⅠ值,随着形状比的增加,中间区域几乎接近于0保持不变,两端逐渐减小,只是裂纹撕开方向相反;当a/c>0.8时,裂纹尖端 (除表面点外) 各点KⅢ值在一个很小的范围内变化,基本上保持不变,说明对于接近圆形的裂纹,裂纹形状对Ⅲ型应力强度因子基本没有影响,对平直裂纹两端值影响较大。
3.3 裂纹相对深度的影响裂纹相对深度a/t是指裂纹短半轴 (深度) 与刀盘面板厚度t的比值,该值大小同样对应力强度因子影响较大。这里分别取a/t为0.1、0.2、0.3、0.5和0.7这5个数值,保持裂纹形状比为0.2及载荷边界条件不变,计算得到不同相对深度下的裂纹尖端应力强度因子KⅠ、KⅡ及KⅢ如图 10所示。

|
| 图10 不同裂纹相对深度的应力强度因子分布 Figure 10 Stress intensity factors distribution with different crack depth ratios |
由图 10可知:1) 裂纹尖端的KⅠ、KⅡ及KⅢ值均随着裂纹深度的增加而增大,且每条曲线的变化规律有很大差异,相同深度下裂纹尖端最深处KⅠ占主导,表面点则是3种开裂形式都存在。2) KⅠ值呈现中间大两端小的趋势,且基本关于θ=90°对称的,说明裂纹尖端最深处以张开型扩展形式为主。3) KⅡ和KⅢ值则是中间小,两端大,其中裂纹中间点的KⅢ值基本为0保持不变,该处的KⅡ值则是随裂纹深度的增加缓慢增大;除a/t=0.7外,裂纹表面点的KⅢ值也是随深度的增加而缓慢增大,而此处的KⅡ值则快速增大。
4 结论1) 刀盘裂纹位置角β对3种应力强度因子的大小和方向均有很大影响, KⅠ绝对值随位置角呈现先增大后减小的趋势,KⅡ和KⅢ的绝对值基本关于β=90°对称,不同位置角下裂纹尖端的扩展形式也不同;当β为45°或135°时,裂纹最深处和表面点的等效应力强度因子均达到最大,对刀盘损伤影响也最严重,在工程中对这种带倾斜角度的裂纹要格外注意,防止因疲劳裂纹扩展导致结构的异常失效。
2) 裂纹形状比对KⅠ值影响最大,当形状比小于0.8时,KⅠ值呈现中间大两端小的趋势,形状比等于1时,中间点的KⅠ值小于表面点的,越平直的裂纹,两处的KⅠ值相差就越大,裂纹沿深度方向的扩展趋势也越强,结构也越容易失效,而形状比对裂纹尖端中间区域的KⅡ和KⅢ值则几乎没有影响。
3) KⅠ、KⅡ及KⅢ值均随着裂纹深度的增加而增大,相同深度下裂纹尖端最深处Ⅰ型应力强度因子占主导,以张开型扩展形式为主,表面点则是3种开裂形式都存在。
今后将开展刀盘的裂纹扩展寿命分析,并展开刀盘特征结构件的疲劳损伤试验,揭示TBM刀盘的损伤机理,间接验证分析结果的准确性。
| [1] |
陈树进, 刘志华, 齐鹏, 等. TBM刀盘整修技术[J].
建筑机械, 2012(6): 118–120.
CHEN Shujin, LIU Zhihua, QI Peng, et al. The rebuilding technology of TBM cutter head[J]. Construction machinery, 2012(6): 118–120. |
| [2] |
黄文鹏. 节理密集带地质硬岩TBM刀盘损坏形式及对策[J].
隧道建设, 2012, 32(4): 587–593.
HUANG Wenpeng. Study on damage of hard rock TBM induced by tunneling through joint-densely-developed hard rock section and countermeasures[J]. Tunnel construction, 2012, 32(4): 587–593. |
| [3] |
齐梦学, 李宏亮, 王雁军. 全断面硬岩掘进机全面整修技术研究与应用[J].
建设机械技术与管理, 2009(3): 97–102.
QI Mengxue, LI Hongliang, WANG Yanjun. Research and application of refit technology of all-section rock tunnel boring machine[J]. Construction machinery technology & management, 2009(3): 97–102. |
| [4] | ACAROGLU O, OZDEMIR L, ASBURY B. A fuzzy logic model to predict specific energy requirement for TBM performance prediction[J]. Tunnelling and underground space technology, 2008, 23: 600–608. DOI:10.1016/j.tust.2007.11.003 |
| [5] | HASSANPOUR J, ROSTAMI J, ZHAO J. A new hard rock TBM performance prediction model for project planning[J]. Tunnelling and underground space technology, 2011, 26: 595–603. DOI:10.1016/j.tust.2011.04.004 |
| [6] | GONG Q M, ZHAO J, HEFNY A M. Numerical simulation of rock fragmentatin process induced by two TBM cutters and cutter spacing optimization[J]. Tunnelling and underground space technology, 2006, 21: 263. DOI:10.1016/j.tust.2005.12.124 |
| [7] | XIA Yimin, OUYANG Tao, ZHANG Xinming, et al. Mechanical model of breaking rock and force characteristic of disc cutter[J]. Journal of central south university, 2012, 19: 1846–1852. DOI:10.1007/s11771-012-1218-8 |
| [8] |
夏毅敏, 陈卓, 林赉贶, 等. 某供水工程TBM刀盘破岩过程动静态响应特性[J].
哈尔滨工程大学学报, 2016, 37(5): 732–737.
XIA Yimin, CHEN Zhuo, LIN Laikuang, et al. Static and dynamic response characteristics of TBM cutterhead's rock-breaking process:case study of a diversion project[J]. Journal of Harbin Engineering University, 2016, 37(5): 732–737. |
| [9] | HUO Junzhou, SUN Wei, CHEN Jing, et al. Disc cutters plane layout design of the full-face rock tunnel boring machine (TBM) based on different layout patterns[J]. Computers & industrial engineering, 2011, 61: 1209–1225. |
| [10] | SUN Wei, LING Jing, HUO Junzhou, et al. Study of TBM cutterhead fatigue damage mechanisms based on a segmented comprehensive failure criterion[J]. Engineering failure analysis, 2015, 58: 64–82. DOI:10.1016/j.engfailanal.2015.08.041 |
| [11] | HUO Junzhou, WU Hanyang, YANG Jing, et al. Multi-directional coupling dynamic characteristics analysis of TBM cutterhead system based on tunnelling field test[J]. Journal of mechanical science and technology, 2015, 29(8): 3043–3058. DOI:10.1007/s12206-015-0701-1 |
| [12] | SUN Wei, LING Jingxiu, HUO Junzhou, et al. Dynamic characteristics study with multidegree-of-freedom coupling in TBM cutterhead system based on complex factors[J]. Mathematical problems in engineering, 2013, 2013(3): 657–675. |
| [13] |
张朋, 田佳林, 韩鲁佳. 基于非结构混合网格人椅系统外流场数值模拟[J].
应用科技, 2015, 42(5): 42–45.
ZHANG Peng, TIAN Jialin, HAN Lujia. Numerical simulation of the flow fields around the aircraft ejection seat system based on unstructured hybrid grids[J]. Applied science and technology, 2015, 42(5): 42–45. |
| [14] | MASAKI M, HIROYUKI M, NORITAKE O, et al. Calculation of dynamic stress intensity factors for pipes during crack propagation by dynamic finite element analysis[J]. Journal of pressure vessel technology, 2014, 136(1): 1–8. |
| [15] | LIN X B, SMITH R A. Finite element modeling of fatigue crack growth of surface cracked plates-Part Ⅰ:the numerical technique[J]. Engineering fracture mechanics, 1999, 63(5): 503–522. DOI:10.1016/S0013-7944(99)00040-5 |
| [16] | LIN X B, SMITH R A. Finite element modeling of fatigue crack growth of surface cracked plates-Part Ⅲ:Stress intensity factor and fatigue crack growth life[J]. Engineering fracture mechanics, 1999, 63(5): 541–556. DOI:10.1016/S0013-7944(99)00042-9 |
| [17] | CHRISTOPHER R S. Uncertainty quantification in crack growth modeling under multi-axial variable amplitude loading[D]. Nashville:Vanderbilt University, 2010:127-129. |
| [18] | DIAMANTAKOS I D, LABEAS G N, PANTELAKIS S G, et al. A model to assess the fatigue behavior of ageing aircraft fuselage[J]. Fatigue fract engng mater struct, 2001, 24(10): 677–686. DOI:10.1046/j.1460-2695.2001.00423.x |
| [19] | LING Jing, SUN Wei, HUO Junzhou, et al. Study of TBM cutterhead fatigue crack propagation life based on multi-degree of freedom coupling system dynamics[J]. Computers & industrial engineering, 2015, 83: 1–14. |