双目立体视觉是机器视觉的一种重要形式。双目立体视觉测量系统主要分为图像获取、摄像机标定、特征提取与匹配、三维重建。由于空间的三维景物被投影到二维图像时,视角问题、场景中的光照条件、景物几何形状和物理特性、噪声干扰和畸变、相机特性等都被综合到了图像的灰度值中,因此,要准确地对包含诸多不利因素的图像进行无歧义的特征提取与匹配是很困难的。特征提取是为了得到匹配赖以进行的图像匹配基元,发展至今,有Soble算子[2]、Canny算子[3],Moravec算子[4]、Harris角点检测[5]和尺度不变特征变换 (scale invariant feature transform,SIFT)[6]特征提取算法。特征匹配主要利用匹配基元间的相似属性建立相似测度函数,在约束条件下得到双目图像的匹配点对。约束条件主要集中在寻找搜索的范围和相似度的计算两个方面。Marr提出的唯一性约束、相容性约束、视差梯度约束、连续性约束[7]都围绕这两个方面。Marr提出的约束条件是最基本的,随着立体匹配的发展,视差范围约束、最大向量角准则[8]、极线约束[9-10]等也被发展与应用。
针对立体视觉算法中冗余特征点以及误匹配的问题,提出了尺度旋转不变角点的检测方法,解决冗余特征点多、计算量大的问题。本文将极线约束匹配算法、最大视差梯度算法以及最大向量角准则相结合,提高匹配正确率。利用实验室室内拍摄的盒子图像以及水池拍摄的水波纹图像对本文改进的算法进行验证。
1 特征点提取算法利用特征点代替图像中所有像素点能够减少计算量。依据算法应用的背景不同,特征点的分类也不同。本文选择角点作为感兴趣的特征点。针对Harris算法冗余角点过多的问题,引入尺度旋转不变角点,兼具尺度不变性和旋转不变性。尺度不变性角点,即为同时存在于多个尺度空间的角点。对尺度不变角点及其附近像素点计算方向描述子,选定幅值最大的方向为主方向,幅值不低于最大值80%的方向为辅方向。具有单一主辅方向的角点为尺度旋转不变角点。若存在多个辅方向,说明该点在任何一方向上的变化都很缓慢,属于空白部分,或者该点在任何一方向上变化都很快,属于噪声部分。提取尺度旋转不变角点的具体步骤如下:
1) 生成多尺度空间。假设一个图像I(x, y) 的尺度函数定义为L(x, y, σ),则可以通过该图像I(x, y) 与高斯函数G(x, y, σ) 卷积运算得到尺度函数L(x, y, σ):
| $ \begin{array}{l} \mathit{\boldsymbol{L}}\left( {x,y,\sigma } \right) = \mathit{\boldsymbol{G}}\left( {x,y,\sigma } \right) \otimes \mathit{\boldsymbol{I}}\left( {x,y} \right)\\ \mathit{\boldsymbol{G}}\left( {x,y,\sigma } \right) = \frac{1}{{2\pi {\sigma ^2}}}\exp \left( { - \frac{{{x^2} + {y^2}}}{{2{\sigma ^2}}}} \right) \end{array} $ |
式中:L(x, y, kσ) 表示第k层尺度空间函数,G(x, y, kσ) 表示为高斯卷积核函数,其高斯正态分布的标准偏差为kσ,k>1。
2) 对每一层尺度空间图像,分别计算其角点响应值R,并设定一个合适的阈值,对于小于阈值的角点响应值R,将其置零:
| $ \mathit{\boldsymbol{R}} = \left\{ {\mathit{\boldsymbol{R}}:det{\mathit{\boldsymbol{M}}_k} - \alpha {{\left( {{\rm{trace}}{\mathit{\boldsymbol{M}}_k}} \right)}^2}} \right\} < t $ |
3) 在5×5的窗口中进行局部非极大值抑制,取其中极大值点的位置点作为每一层尺度空间图像L(x, y, kσ) 中的角点。
4) 确定方向,图像中任意角点的幅值m(x, y) 和方向θ(x, y) 计算公式如下
| $ \begin{array}{*{20}{c}} {m\left( {x,y} \right) = \sqrt {{{\left( {L\left( {x + 1,y} \right) - L\left( {x - 1,y} \right)} \right)}^2} + {{\left( {L\left( {x,y + 1} \right) - L\left( {x,y - 1} \right)} \right)}^2}} }\\ {\theta \left( {x,y} \right) = \arctan \left[ {\frac{{L\left( {x,y + 1} \right) - L\left( {x,y - 1} \right)}}{{L\left( {x + 1,y} \right) - L\left( {x - 1,y} \right)}}} \right]} \end{array} $ |
式中:L是检测到的每一个角点各自所位于多尺度空间图像上的尺度。
2 立体匹配算法立体匹配算法将左右图中的特征点实现一对一匹配。立体匹配过程中,经常出现一对多误匹配现象。针对该问题,本文采用多约束条件匹配,提高匹配的精度。首先采用极线约束,计算左图特征点在右图上的极线,取极线上下20像素范围内的角点作为候选点,结合视差梯度与最大向量角约束,实现一对一精确匹配。具体计算步骤如下:
1) 对左图中的角点pl,计算其右图对应的极线约束方程:
| $ {l_{pr}} = \mathit{\boldsymbol{F}}{p_l} $ |
式中:F为相机的基础矩阵。利用极线条件约束后,能够减少一定数量的无匹配角点。
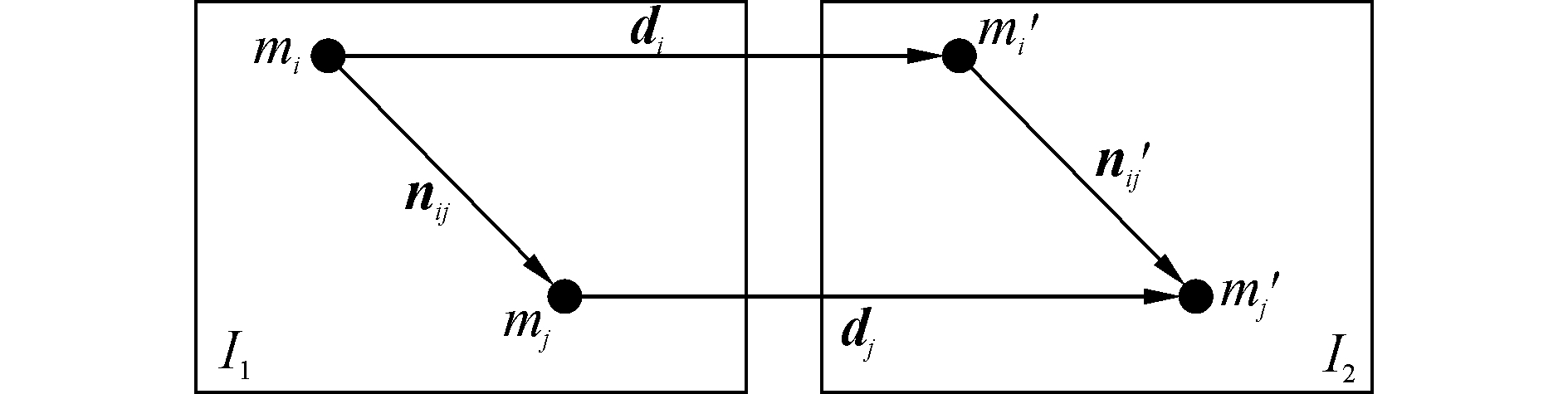
2) 计算视差梯度约束。如图 1所示,左图I1中有一角点mi,它的坐标为 (ui, vi),与其相匹配的角点m′i位于右图I2中,它的坐标为 (u′i, v′i),di表示m1到m′i的向量。左图I1中另一角点mj,它的坐标为 (uj, vj),与其相匹配的角点m′j位于右图I2中,它的坐标为 (u′j, v′j),dj表示mj到m′j的向量。计算左右两幅图中该点对与其他角点对之间的视差梯度Gd,根据视差梯度的定义可知,视差梯度约束的公式如下:
|
| 图1 视差梯度约束 Figure 1 Disparity gradient constraint |
| $ {G_d} = \frac{{\left\| {{\mathit{\boldsymbol{d}}_j} - {\mathit{\boldsymbol{d}}_i}} \right\|}}{{\left\| {\left[ {\left( {{m_j} - {m_i}} \right) + \left( {{{m'}_j} - {{m'}_i}} \right)} \right]/2} \right\|}} \le K $ |
式中:Gd为视差梯度, K为视差梯度约束的阈值,一般取值为2。如果视差梯度值大于设定的阈值K时,则认为该点对违反了视差梯度约束,统计其违反的次数。
3) 依次计算出其他的匹配点对的视差梯度以及其违反的次数,找出其中违反次数最多的一组,剔除该组匹配点对,更新角点对。
4) 重复2)、3),直到没有违反视差度约束条件为止。
5) 若违反次数最多不止一组,则根据最大向量角准则约束条件,剔除θsum最大的一组。图中nij表示mi指向mj的向量,n′ij表示m′i指向m′j的向量。θi_sum表示两组向量夹角之和,mi和m′i分别与左图中其他角点组成的向量夹角之和,其具体计算公式如下
| $ {\theta _{i\_{\rm{sum}}}} = \sum\limits_{j = 1,j \ne i}^N {\left| {{\rm{arcos}}\frac{{{\mathit{\boldsymbol{n}}_{ij}} \cdot {{\mathit{\boldsymbol{n'}}}_{ij}}}}{{\left\| {{\mathit{\boldsymbol{n}}_{ij}}} \right\| \cdot \left\| {{{\mathit{\boldsymbol{n'}}}_{ij}}} \right\|}}} \right|} $ |
式中:N为左图中其他候选角点对个数。最大向量角准则是找出θsum最大的点,这点即是错误的匹配点,将其删除,继续寻找剔除,直到最精确的那一点作为最后的匹配角点。
3 试验结果与分析双目摄像机固定在三脚架上,摄像的高度、摄像机的间距以及夹角均可调。双目摄像机通过网络交换机与主控电脑相连。主控电脑采用ThinkPad T440计算机。主控平台上运行双目测量测试开发平台软件,由Visual C++6.0语言编写,实现图像的采集,标定等功能。本系统所采集的图像均为480×640。
3.1 小盒试验通过双目视觉系统对盒子进行拍摄,将双目摄像机调到与盒子等高的位置,调整两摄像机之间的角度,使左右摄像机均能拍到盒子。得到的左右两幅原图如图 2所示。

|
| 图2 双目摄像机摄取的小盒左右原图片 Figure 2 Binocular camera capturing left and right original images |
从图 3~5可以看出,Harris算法检测出的角点非常密集,过多的角点里面包含冗余信息,增加匹配算法的计算量,也会增加误匹配率。SIFT算法剔除了冗余角点,但是能够提供给后续匹配处理的角点数据量相对较少,匹配点的数量较少,导致后续的三维测量的精度较低。本文改进的算法所保留的角点数量介于两者之间,有效去处了冗余角点,同时还能保证足够的角点数量,为后续的匹配处理提供最优的角点数据库。虽然降低SIFT算法的角点响应阈值,能够增加角点数量,但这相当于增加了角点检测算法的噪声,给后续的匹配算法增加了计算量和误匹配率。本文提出的尺度方向不变角点在保证每层角点提取总基数的基础上,利用方向算子抑制冗余角点,提高角点提取的质量。

|
| 图3 Harris角点检测算法检测到的角点图 Figure 3 Corners showed by Harris corner detection algorithm |

|
| 图4 SIFT算法检测到的角点图 Figure 4 Corner showed by SIFT detection algorithm |

|
| 图5 改进的角点检测算法检测到的角点图 Figure 5 Corners showed by improved corner detection algorithm |
左右图匹配计算中,本文提出了在极线约束算法基础上,结合最大视差梯度以及最大向量角算法提高左右图匹配的准确率和后期三维测量精度。由于篇幅所限,本文只选取了一个点作为描述举例。图 6(a)是左图的角点 (842, 758),利用极线约束算法,取上下20个像素范围,在图 6(b)所描述的右图中找到了67个符合极线约束的角点,从图 6中可以看出,由于极线是一条贯穿右图的直线,因此可以用图中视差梯度以及最大向量角准则进一步剔除误匹配点。

|
| 图6 极限约束一对多的情况 Figure 6 One to many example of pole line contraint |
将视差梯度约束阈值设为2,视差约束后,右图剩余64个点,剔除3个点,如图 7(a)所示,利用最大向量角约束后,剩余一个角点 (791, 783),如图 7(b)所示。

|
| 图7 视差梯度约束取2匹配结果 Figure 7 Matching results of gradient of disparity value being 2 |
视差梯度约束阈值为1时,视差梯度约束后,剩余59个点,剔除8个点,如图 8(a)所示。利用最大向量角准则后,实现了匹配一对一结果,匹配点 (791, 783),结果如图 8(b)所示。

|
| 图8 视差梯度约束取1匹配结果 Figure 8 Matching results of disparity gradient constraint value being 1 |
处理结果显示,一对多的“多”较集中在正确匹配点周围。当视差梯度约束的阈值取2时,剔除的误匹配点较少,最终还是最大向量角准则的作用,得到一对一匹配结果。当一对多的“多”不集中在正确匹配点周围时,视差梯度约束2能剔除离正确匹配点较远的点,保留集中在正确匹配点周围的点集,再采用最大向量角准则,得到一对一。从实验效果来看,当视差梯度约束阈值为1时,能更有效地剔除那些远离正确匹配点的点集,保留更集中于正确匹配点周围的点集。因此,视差梯度约束阈值选择1较好。
选择的定位角点为小盒的上表面的三个角点以及底部的三个角点,标号1~6。特征值比值约束为[0.2, 10],相关系数阈值取0.7。利用本文算法得到113对匹配点,错误匹配21对,如图 9所示。

|
| 图9 左右匹配效果图 Figure 9 Matching results of the improved algorithm |
采用SIFT算法时,distRatio采用建议的0.65,匹配结果为匹配了18对,错误匹配2对,正确匹配16对,如图 10所示。

|
| 图10 SIFT算法的匹配结果 Figure 10 Matching results of SIFT algorithm |
从实验结果可以看出,SIFT算法所提取的特征角点少,正确匹配率高。匹配点对太少,导致后期的三维测量是离散点少,进行拟合时误差较高。
3.2 水池试验本文采集的实验图片是在哈尔滨工程大学船模实验室水池中船模航行时船侧水波纹图像。船模长度1.2 m。试验中,在船艏,船舯,船艉处分别放置了三组双目摄像设备,同时拍摄船模以不同的速度航行时,船周围所泛起的波浪照片,用于绘制船侧的波浪等高线图。图 11表示航模速度为1.701 kn时船模后部位置产生的波浪经过预处理后的图片。由于水池实验环境有许多噪声干扰,如光照影响,相机自身干扰,波浪反光等,获得的图片噪声太多,不能直接应用处理。本文改进的特征点提取算法处理结果如图 12所示。

|
| 图11 预处理原始左右灰度图的结果 Figure 11 The left and right original grayscale images after de-noising |

|
| 图12 改进算法的左右两图角点检测 Figure 12 The corner detection results of the improved algorithm |
本文所提出算法的匹配结果如图 13所示。视差梯度约束阈值为1,极线约束上下20像素,区域对应查找,特征值比值范围[0.2, 10]。左右匹配两点之间的距离范围为[2 085, 2 170],匹配点之间相关系数的阈值选取为0.7。

|
| 图13 改进算法匹配结果 Figure 13 Matching results of the improved algorithm |
图 14为Harris检测结果,阈值取0.000 000 4。左图检测出角点2 349个,右图检测出角点1 882。

|
| 图14 Harris角点检测结果 Figure 14 The corner detection results of Harris |
SIFT算法检测出左图角点993个,右图角点750个, distRatio采用建议的0.65,匹配点3对,正确匹配2,错误匹配1。SIFT算法检测出的特征点如图 15所示,图 16给出了SIFT算法最终的匹配结果。

|
| 图15 SIFT算法检测的特征点 Figure 15 The corner detection results of SIFT algorithm |

|
| 图16 SIFT算法匹配结果 Figure 16 Matching results of SIFT algorithm |
将小盒以及水池照片所有参数的各种对比数据统计在表 1中。
| 检测的特征点数 | 匹配点对数 | 正确匹配率/% | 总的运行时间/s | |||
| 小盒图片 | Sift | 左 右 |
508 861 |
18 | 88.89 | 0.199 321 |
| 本文提出的算法 | 左 右 |
4 553 4 201 |
113 | 81.42 | 120.757 8 | |
| 水池船后图片 | Sift | 左 右 |
993 750 |
3 | 67 | 0.235 925 |
| 本文提出的算法 | 左 右 |
2 349 1 882 |
100 | 81 | 48.924 524 | |
从表 1的统计数据中可以看出,SIFT算法在小盒图片的匹配中运算时间以及正确匹配率高于本文的算法。但在水池船后图片处理中,本文提出的算法正确匹配率远远高于SIFT算法,运算时间虽然高于SIFT算法,但是在合理运算时间范围内。主要原因在于两次实验所选取的角点响应阈值不同,因此可以看出角点响应阈值参数是一个非常重要并且敏感的参数,未来研究中将阈值参数定义为一个自适应参数算法会更加稳健。本文所进行的研究工作是基于立体双目波浪等高线绘制算法中的基础部分,是后续所进行三维波浪等高线绘制的基础,所匹配的点对数目直接影响等高线拟合精度。从上述数据对比可以看出,本文所提出的算法在处理基于双目立体视觉的水面图片时,在匹配率参数性能上面要高于SIFT算法。
4 结论双目立体视觉算法主要分为两个步骤,特征点提取以及立体匹配。本文以船模航行时船侧的波浪等高线测量为应用背景,提出了一种有效的立体视觉测量方法,主要贡献有以下两点:
1) 引入尺度方向不变算子,将其作为待提取的特征点,提高了特征点提取的质量,降低了冗余特征点数量,减少了匹配算法部分的计算量;
2) 在立体匹配算法部分,将极线约束方法与视差梯度和最大向量角算法相结合,提高了匹配精度。实验结果显示本文提出的算法在检测水面图片中,正确匹配率达到了81%。
| [1] |
陈小天, 沈振康. 机器人视觉导航[J].
系统仿真学报, 2008, 20(10): 5501–5503.
CHEN Xiaotian, SHEN Zhenkang. Robot visual navigation[J]. Journal of system simulation, 2008, 20(10): 5501–5503. |
| [2] | GONZALEZ R C, WOODS R E. Digital image processing[M]. 3rd ed. India: Pearson Education, 2009. |
| [3] | CANNY J. A computational approach to edge detection[J]. IEEE transactions on pattern analysis and machine intelligence, 1986, PAMI-8(6): 679–698. DOI:10.1109/TPAMI.1986.4767851 |
| [4] | MORAVEC H P. Obstacle avoidance and navigation in the real world by a seeing robot rover[D]. Stanford:Stanford University, 1980. |
| [5] | HARRIS C, STEPHENS M. A combined corner and edge detector[C]//Proceedings of the 4th Alvey vision conference. Manchester, UK:AVC, 1988:147-150. |
| [6] | LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International journal of computer vision, 2004, 60(2): 91–110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [7] | MARR D, VISION A. A Computational Investigation into the Human Representation and Processing of Visual Information[M]. San Francisco: Freeman and Company, 1982. |
| [8] |
解则晓, 陆文娟. 基于图像相似几何特征的双目匹配算法[J].
中国激光, 2014, 41(5): 0508002.
XIE Zexiao, LU Wenjuan. Binocular matching algorithm based on similar geometric Features[J]. Chinese journal of lasers, 2014, 41(5): 0508002. DOI:10.3788/CJL |
| [9] | TAN Xiao, SUN Changming, SIRAULT X, et al. Feature matching in stereo images encouraging uniform spatial distribution[J]. Pattern recognition, 2015, 48(8): 2530–2542. DOI:10.1016/j.patcog.2015.02.026 |
| [10] | SONG Tao, TANG Baoping, ZHAO Minghang, et al. An accurate 3-D fire location method based on sub-pixel edge detection and non-parametric stereo matching[J]. Measurement, 2014, 50: 160–171. DOI:10.1016/j.measurement.2013.12.022 |



