2. Navy Military Representative Office in Harbin 703 Institute, Harbin 150001, China
压气机通常消耗涡轮有效膨胀功的1/2~2/3[1], 而压气机作为燃气轮机的一个重要组成部分, 对燃气轮机的性能具有重大的影响。湿压缩技术通过向压气机内喷入雾化水滴, 可有效降低压缩功, 提高燃气轮机的效率[2-3], 近年来得到了极大的关注。
湿压缩过程中水滴的存在会对压缩过程产生热力学、空气动力学与机械性能的影响[4], 对水滴在压气机内运动的研究对进一步理解湿压缩技术具有重要意义。水滴进入压气机后不可避免的会在气流和叶片作用下发生力破碎, Neupert等[5]采用光谱分析法对亚音速压气机内部水滴颗粒的运动进行了实验研究, 发现只有大水滴在较高的气动力负荷下才会发生破碎;水滴与气流间热与力的相互作用对压气机内流场影响较大, 由于水滴与气流速度不可能保持一致, 滑移速度的存在会增加水滴与气流的热量和质量传递, 从而强化蒸发效果[6];Yang Huaifeng等[7]通过研究发现流速相对较高的水滴可以通过拖拽作用加速低速区的气流, 并且当水滴撞击到叶片温度低于零度的区域时可能出现结冰现象, 不利于压气机性能的提高。
湿压缩技术自从被提出以来, 由于其在提高压气机和燃气轮机效率上的巨大潜力和工程价值而受到大量学者关注和研究, 但目前对水滴在压气机内的运动研究并不完善, 本文以NASA Stage 35单级轴流压气机为研究对象, 应用ANSYS CFX对湿压缩过程进行了数值模拟, 通过追踪水滴在压气机内的运动轨迹, 研究了水滴流经压气机过程中速度、温度及气动力作用强度的变化, 分析了水滴在压气机内不同位置运动的湍流强度以及破碎强度的大小, 分析了影响湿压缩效果的重要因素。
1 湿压缩水滴运动模型 1.1 水滴运动破碎湿压缩技术向压气机内喷入的液态水量一般小于相同进出口条件下干压缩流量的3%, 水滴颗粒在气流中的运动分布属于稀疏态, 水滴间的相互影响可以忽略, 对气流中的水滴可以进行单独分析。由于喷入的水滴与气流间必然存在速度差异, 在粘性的作用下, 水滴会受到气流拖拽力的作用。同时压气机的增压作用使得气流具有较大的压力变化, 水滴在气流中运动时还会受到压力梯度力的作用。考虑到水滴自身的重力, 水滴在压气机叶栅内运动的运动方程可以表示为
| ${m_p}d{\mathit{\boldsymbol{u}}_p}{\rm{d}}t = {\mathit{\boldsymbol{F}}_d} + {\mathit{\boldsymbol{F}}_p} + {\mathit{\boldsymbol{F}}_g}$ | (1) |
式中:mp为水滴颗粒质量, up为水滴速度, Fd为气流对水滴的拖拽力, Fp为水滴受到的压力梯度力, Fg为水滴自身重力。
根据文献[8], 水滴在压气机内运动受到的拖拽力可以利用拖拽系数表示为
| ${\mathit{\boldsymbol{F}}_d} = {1 \over 2}{C_d}\pi {{d_p^2} \over 4}\rho {\left( {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{u}}_p^{}} \right)^2} = {1 \over 2}{C_d}\pi {{d_p^2} \over 4}\rho \mathit{\boldsymbol{u}}_s^2$ | (2) |
式中:ρ和u分别为气流的密度和速度, dp为水滴颗粒直径, us为气流与水滴间的滑移速度, Cd为拖拽力系数。根据文献[9], 当水滴雷诺数小于2×105时, 水滴在压气机内运动的拖拽力系数为
| ${C_d} = 0.4 + {{24} \over {R{e_p}}} + {6 \over {1 + \sqrt {R{e_p}} }}$ | (3) |
式中:Rep为水滴雷诺数, 其计算式为
| $R{e_p} = {{\rho {d_p}\left| {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{u}}_p}} \right|} \over \mu }$ | (4) |
水滴受到的压力梯度力等于作用在水滴上的压力梯度与水滴颗粒体积的乘积, 可表示为
| ${\mathit{\boldsymbol{F}}_p} = {V_p}\nabla p = pd_p^36\nabla p$ | (5) |
式中:Vp为水滴颗粒的体积, ∇p为作用在水滴上的压力梯度。
水滴所受到的重力计算式为
| ${\mathit{\boldsymbol{F}}_g} = {m_p}g = {{\pi d_p^3{\rho _w}g} \over 6}$ | (6) |
式中ρw为水的密度。
水滴在气流中的受力与自身的表面张力相互作用, 当气流施加给水滴的作用力可以克服水滴表面张力的时候, 水滴将会发生破碎。水滴的气动韦伯数为
| $W{e_l} = {{\rho {\mathit{\boldsymbol{u}}_s}^2{d_p}} \over {{\sigma _p}}}$ | (7) |
式中σp为水滴的表面张力系数。
当韦伯数大于1时, 水滴将会发生变形, 当韦伯数超过临界值时, 将发生气动力破碎, 根据水滴韦伯数Wel的变化范围, 液滴破碎后的形态如表 1所示。
| 破碎形态 | Wel范围 |
| 振荡破碎 | Wel<12 |
| 袋状破碎 | 12<Wel<50 |
| 袋状-蕊状破碎 | 50<Wel<100 |
| 条带状破碎 | 100<Wel<350 |
| 崩溃状破碎 | 350<Wel |
湿压缩过程中不可避免的会有水滴与叶片发生撞击, 水滴的形态在撞击后会发生较大的变化, 根据文献[10]给出了水滴撞壁韦伯数的变化范围, 水滴撞击叶片后的形态表 2所示。
| 破碎形态 | Wew |
| 粘附 | Wew≤1 |
| 反弹 | 1<Wew≤5 |
| 铺展 | 5<Wew≤Wes |
| 喷溅 | Wes<Wew |
Wew为水滴撞壁韦伯数, 其表达式为
| $W{e_w} = {{{\rho _w}{\mathit{\boldsymbol{u}}_n}^2{d_p}} \over {{\sigma _p}}}$ | (8) |
式中un为水滴撞击壁面的法向速度。
Wes为水滴撞壁临界韦伯数, 其表达式为
| $W{e_s} = {A_w}L{a^{ - 0.15}}$ | (9) |
式中:Aw为和壁面粗糙度有关的表面系数, La为拉普拉斯数。
1.2 水滴传热传质水滴在压气机内部的运动伴随着传热传质, 与干压缩相比, 压气机内的温度、流量和效率会发生改变[11], 所以传热传质是研究水滴运动的重要内容。
水滴的蒸发速度可以通过水滴与气流间的传质系数计算:
| ${{{\rm{d}}{m_p}} \over {{\rm{d}}t}} = {k_m}\left( {{\rho _s} - {\rho _g}} \right)\pi d_p^2 = \pi {d_p}{D_c}Sh\left( {{\rho _s} - {\rho _g}} \right)$ | (10) |
式中:km为水滴与气流间的传质系数, Dc为分子扩散系数, ρs为水滴表面附近气体密度, ρg为周围气体密度, Sh为舍伍德数, 其表达式为
| $Sh = {{{k_m}{d_p}} \over {Sc}}$ | (11) |
式中Sc为施密特数。
水滴与气流间的传热主要为蒸发传热和对流传热, 所以水滴传热方程可以表示为
| ${m_p}{C_w}{{{\rm{d}}{T_p}} \over {{\rm{d}}t}} = h\pi {d_p}^2\left( {T - {T_p}} \right) + {{{\rm{d}}{m_p}} \over {{\rm{d}}t}}\gamma $ | (12) |
式中:Cw为液态水比热, γ为蒸发潜热, h为对流换热系数, 可以通过努塞尔特数计算:
| $h = {{\lambda Nu} \over {{d_p}}}$ | (13) |
式中Nu为努塞尔特数。
综上, 水滴的传热方程可以表示为
| ${m_p}{C_w}{{{\rm{d}}{T_p}} \over {{\rm{d}}t}} = \pi {d_p}\lambda Nu\left( {T - {T_p}} \right) + \pi {d_p}{D_c}Sh\left( {{\rho _s} - {\rho _g}} \right)\gamma $ | (14) |
本文以叶轮机械领域典型的NASA Stage35单级轴流压气机为研究对象, 选取工业流动和传热模拟中广泛采用的k-ε湍流模型, 在压气机设计工况下对稳态湿压缩过程中水滴的运动进行数值模拟。压气机进口喷水速度为50 m/s, 温度288.15 K, 水滴颗粒尺寸服从Rosin Rammler分布, 喷雾量为相同工况下干压缩空气质量流量的百分比。转速为17 188.7 r/m, 动叶数为36, 静叶数为46, 计算域通道网格采用多块结构化, 叶片周围选用O型网格, 生成后的网格单元总数为688 232, 其几何结构及网格模型如图 1所示。

|
| 图1 NASA Stage 35几何模型及叶片网格 Figure 1 Geometric model and blade grids for NASA Stage 35 |
湿压缩过程中, 水滴颗粒在压气机内运动时会呈现不同的运动形态, 并影响湿压缩过程。本文在水滴平均直径10 μm, 喷雾量1%的情况下追踪水滴在压气机内的分布情况, 为了清晰观察水滴颗粒, 以0.05 ms为时间间隔显示水滴在运动轨迹上的形态, 并以重力大小为颜色区分, 将水滴放大后的分布如图 2所示。

|
| 图2 水滴运动轨迹 Figure 2 Motion trajectories of water droplets |
水滴喷入压气机内未受叶片扰动之前, 相同时间间隔内, 小水滴运动的距离更远, 随气流的加速性更好, 小水滴规律性的分布在大水滴之前。观察水滴重力分布, 水滴破碎主要发生在转子叶片前缘附近, 水滴流经压气机转子叶片前缘后, 许多较大的水滴颗粒消失。在叶片区域, 水滴更多的偏向于叶片压力面一侧运动, 并在压力面尾缘处以密集的粒子流形式向下流动, 而吸力面一侧的水滴在惯性和气流作用下在尾缘处具有较大程度的分离, 并以静子叶片区域最为明显。水滴经过转子叶片时, 一部分水滴会流入叶顶间隙, 但水滴数量较少, 尺寸较小。在静子叶片区域, 水滴更多的偏离轮毂面运动, 贴近轮毂处的水滴数目极少。
为了研究水滴在压气机内的运动情况, 本文追踪了平均直径10 μm、喷雾量1%的情况下, 三个位置相近且具有代表性的水滴颗粒。图 3为三个水滴颗粒的运动轨迹。水滴1只在气流中流动, 未发生破碎和碰撞;水滴2与叶片发生碰撞, 碰撞之后破碎为尺寸较小的液滴;水滴3发生了气动力破碎。

|
| 图3 水滴重力分布图 Figure 3 Distribution of water droplets colored by gravity |
图 4为追踪的三颗水滴的直径沿压气机轴向的变化。水滴1的初始直径为7.61 μm, 水滴2的初始直径为15.02 μm, 水滴3的初始直径为20.14 μm。图中0.2~0.45的相对位置为转子叶片作用较强区域, 0.45~0.7为静子叶片作用较强区域。水滴2和水滴3由于发生了撞击破碎和气动力破碎, 直径发生突变。观察水滴1, 由于本文研究的压气机为单级轴流压气机, 轴向距离较短, 水滴的蒸发程度较低。

|
| 图4 压气机内水滴直径 Figure 4 Droplet diameter in compressor |
图 5为水滴和气体流速大小沿轴向的变化。根据压气机的工作原理, 空气被吸入压气机转子域内后流速会有所增加, 而在流经静子叶片时, 动能转变为压力能, 流速有所降低, 流速在转子与静子交接位置附近达到最大值。观察水滴流速的变化, 在气流拖拽作用下, 水滴流速会随着空气流速变化而变化, 并不断趋近于气体流速, 在压气机出口位置处, 不同尺寸水滴以及气体的流速相差很小。观察水滴颗粒2, 水滴撞击叶片后速度发生突然跃增, 但随后在气流拖拽作用下逐渐降低并趋于气流流速。水滴撞击叶片后速度发生较大程度改变, 所以水滴必然会对叶片产生一定程度的冲击力, 湿压缩过程中水滴频繁的撞击会造成叶片的额外负载, 对叶片寿命造成一定损害。

|
| 图5 压气机内水滴和气体流度 Figure 5 Velocity of water droplets and gas in compressor |
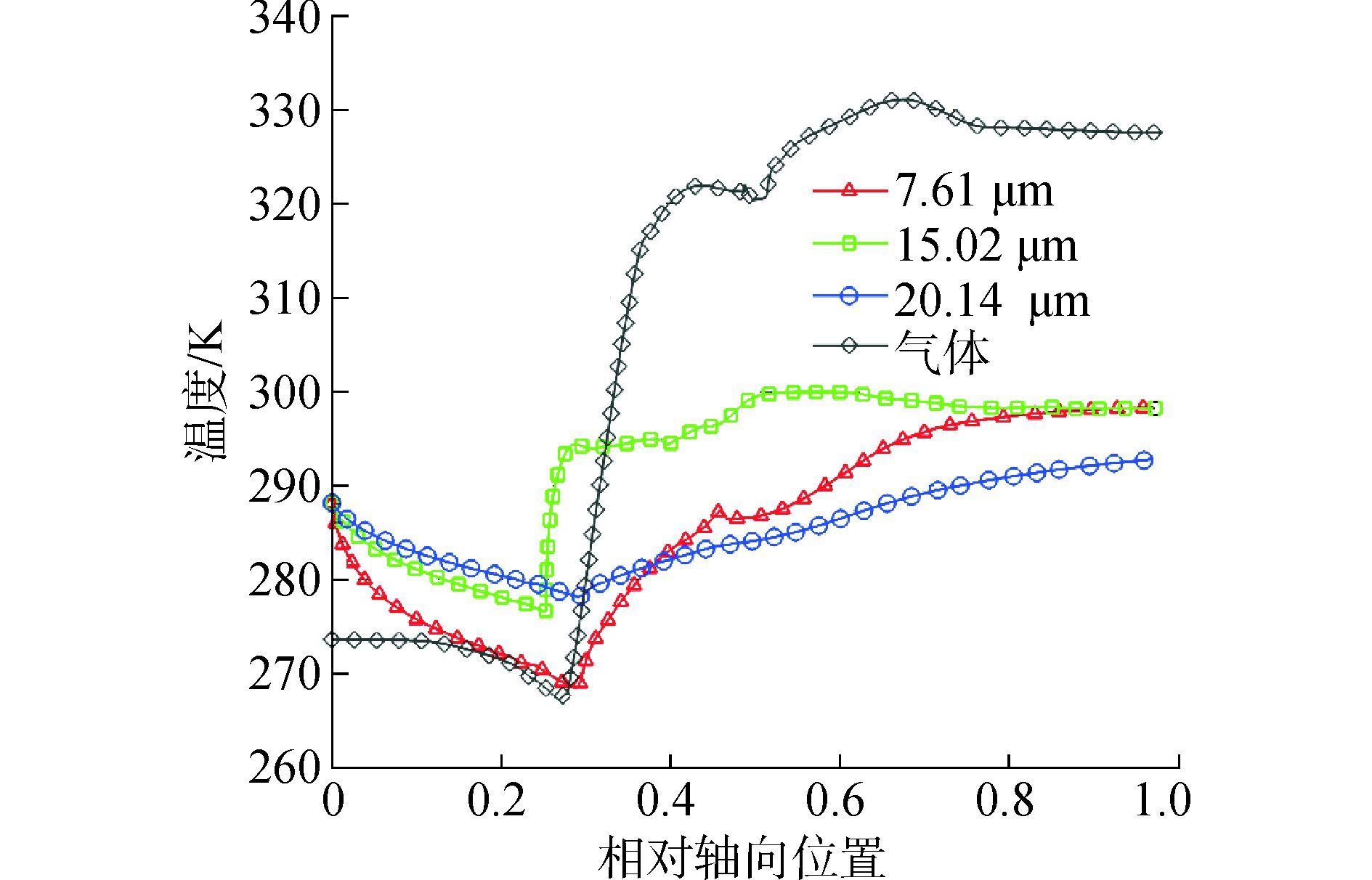
图 6为水滴和气体温度沿轴向的变化。
|
| 图6 压气机内水滴和气体温度 Figure 6 Temperature of water droplets and gas in compressor |
空气在被吸入压气机内而未流经转子叶片之前, 流速会有所增加, 温度会有所降低, 由于喷入的水滴温度要高于气流进口静温, 传热使得水滴温度也逐渐降低。气流流经转子叶片后, 压缩使得气体温度迅速升高, 在传热作用下, 水滴的温度也逐渐增加, 但水滴作为离散相, 从空气中吸热的速度较慢, 所以水滴温度的增加程度要远小于气体温度增加程度。观察不同尺寸水滴温度沿压气机轴向的变化, 较小的水滴颗粒其表面积与体积的比值较大, 水滴与气流间的传热强度较大, 温度降低和升高的速度均较快, 在压气机出口处的温度更高。初始直径为15.02 μm的水滴2在撞击叶片后破碎为较小的水滴, 所以其破碎后的温度升高较快。尽管初始直径为20.14 μm的水滴3也发生了气动力破碎, 但破碎程度较小, 水滴温度变化较慢。
图 7为气流和水滴间的滑移速度绝对值沿轴向的变化。由于喷入的水滴在压气机进口与气流存在一定的速度差异, 所以水滴的滑移速度相对较大, 随后在未流经叶片之前, 气流的拖拽作用使得水滴速度趋近于气体流速, 滑移速度有所减小, 但在转子叶片区域与静子叶片区域, 叶片的干扰使得气流和水滴的速度出现较大波动, 尤其以转子叶片区域最为强烈, 并在转子叶片前缘附近出现滑移速度峰值。由于水滴2撞击破碎后, 流速发生跃增, 所以撞击后水滴的滑移速度突然增大, 但破碎后的水滴颗粒较小, 随气流跟随性很好, 滑移速度很快降低。对比不同颗粒尺寸水滴的滑移速度, 水滴颗粒越大, 随气流的加速性越差, 与气流速度的差值越大, 在不同轴向位置所达到滑移速度较大值的情况越多。

|
| 图7 压气机内水滴和气体间的滑移速度 Figure 7 Slip velocity between water droplets and gas in compressor |
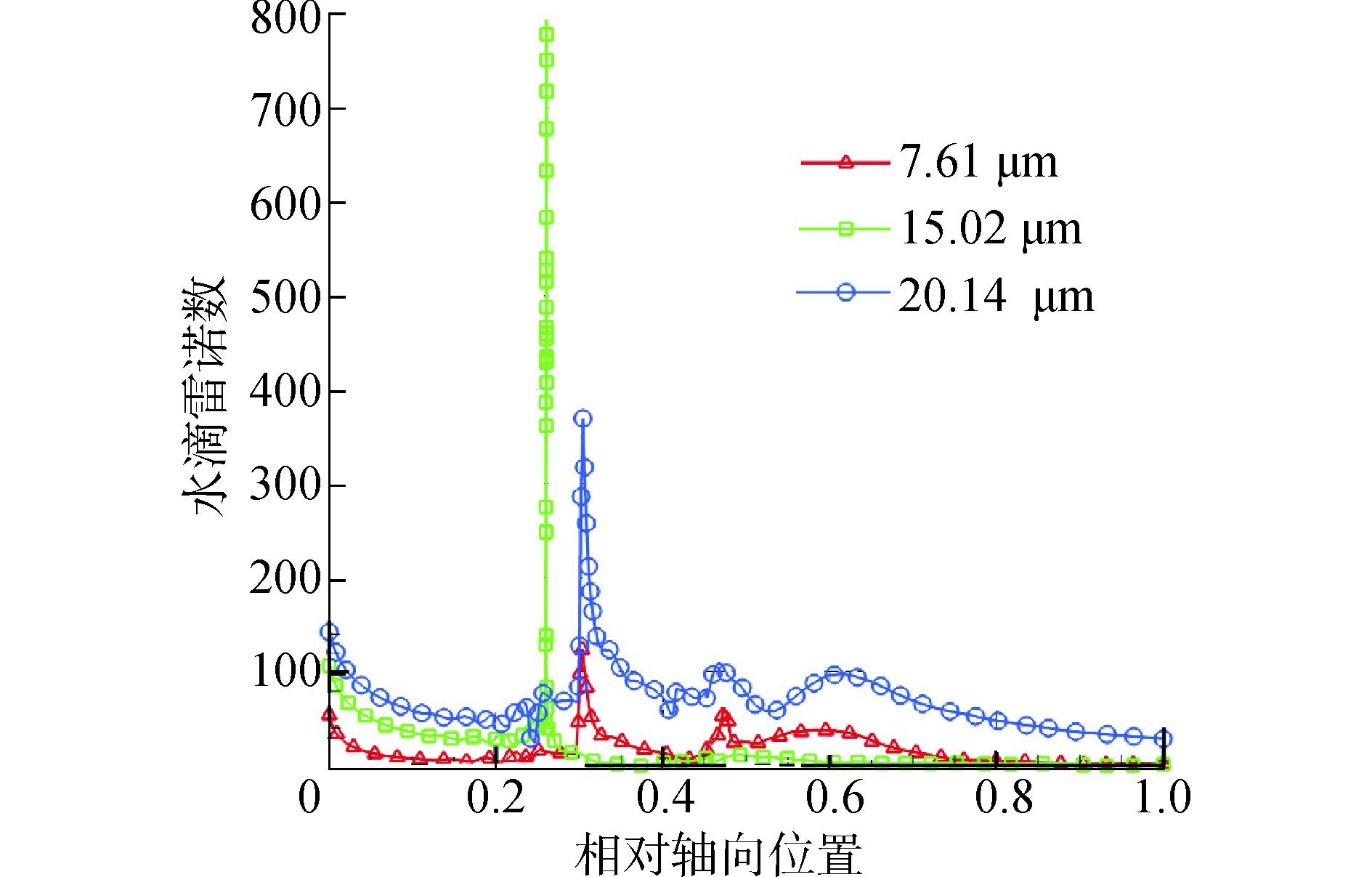
图 8为水滴雷诺数沿轴向的变化。水滴雷诺数沿压气机轴向位置的变化与滑移速度类似, 在转子叶片与静子叶片区域波动较大, 并在转子叶片前缘附近达到峰值, 尤其对于初始直径为15.02 μm的水滴2, 撞击后水滴流速的跃升使得水滴的雷诺数突然增加, 脉动强度突然增大。在叶片作用区域之外, 水滴的雷诺数会随着运动而逐渐减小, 脉动强度减弱。观察不同尺寸水滴雷诺数的数值可以发现, 水滴颗粒越大, 水滴的雷诺数在压气机内不同位置达到较大值的次数越多, 但湿压缩过程中水滴的雷诺数较小, 水滴的雷诺数在绝大多数位置均处于0.1~1 000的转捩区域内。
|
| 图8 压气机内水滴雷诺数 Figure 8 Reynolds number of water droplets in compressor |
水滴颗粒的韦伯数是判断水滴在气流中运动和破碎状态的重要参数, 图 9为追踪的三个水滴颗粒在压气机内不同相对位置的韦伯数。水滴在喷入压气机时存在初始破碎, 并且滑移速度较大, 所以水滴在压气机入口处的韦伯数较大。在转子和静子叶片区域, 由于叶片的扰动, 水滴的运动发生较大波动, 所以水滴的韦伯数出现较大波动, 并且转子域的波动幅度要远大于静子域, 尤其对于发生撞击破碎的水滴2, 速度的跃增使得水滴韦伯数急剧增加。但湿压缩过程中水滴的韦伯数整体较小, 水滴在压气机内绝大多数位置的韦伯数均处于0~5的范围内, 水滴发生振荡破碎的可能性较大。

|
| 图9 压气机内水滴韦伯数 Figure 9 Weber number of water droplets in compressor |
不同颗粒尺寸水滴达到临界破碎韦伯数所需要的滑移速度不同, 考虑到湿压缩过程中水蒸气的加入, 取本文研究过程中湿压缩气流平均的密度为1.3 kg/m3, 水滴表面张力系数0.072 N·m。
图 10为根据水滴气动力破碎临界韦伯数求得的水滴临界滑移速度。水滴颗粒越小, 达到相同临界韦伯数所需的滑移速度越大, 在颗粒尺寸为5 μm时, 临界韦伯数从1~350所对应的临界滑移速度分别达到105.25、364.59、744.21、1 052.47和1 968.99 m/s。图 7显示湿压缩研究过程中水滴的滑移速度一般较小, 大多数水滴均处于振荡破碎的范围内。

|
| 图10 水滴破碎临界滑移速度 Figure 10 Critical slip velocity for breakup of water droplets |
图 11为水滴在压气机内不同位置的气流拖拽力。由于水滴和气流间粘性作用的存在, 气流会对水滴产生拖拽力作用, 根据拖拽力的计算公式, 拖拽力受滑移速度影响较大, 所以水滴受到的拖拽力在转子及静子叶片区域出现较大波动, 并在转子叶片前缘附近出现峰值, 而在叶片作用较强的区域之外, 水滴流速在气流拖拽作用下不断趋近于气流, 滑移速度不断减小, 受到的拖拽力也逐渐减小。观察不同大小水滴的受力, 较大颗粒的水滴受到的气流拖拽力在压气机内绝大多数位置都要大于小颗粒水滴, 需要更大的拖拽作用而运动。由于拖拽力是在水滴和气流粘性存在的情况下产生的, 所以气流拖拽水滴运动的同时, 水滴也会对气流产生粘性阻力, 造成一定的损失。

|
| 图11 压气机内水滴拖拽力 Figure 11 Drag force of water droplets in compressor |
图 12为水滴颗粒在压气机内不同位置压力梯度力的变化。气流流经叶片区域时, 由于流动通道的缩小, 气体受到压缩, 逆向压力梯度增大, 所以水滴受到的压力梯度力在转子及静子叶片作用区域波动较大, 并在转子叶片前缘附近出现峰值。对于15.02 μm的水滴2, 水滴撞击转子叶片前缘破碎, 虽然颗粒尺寸减小, 但气流在流经叶片之间的通道时, 由于在叶片前缘处流动截面的突然减小而压缩, 产生较大的压力梯度, 所以水滴会受到较大的压力梯度力。观察不同大小水滴受到的压力梯度力, 较大的水滴颗粒由于体积较大, 受到的压力梯度力也较大。

|
| 图12 压气机内水滴压力梯度力 Figure 12 Pressure gradient force of water droplets in compressor |
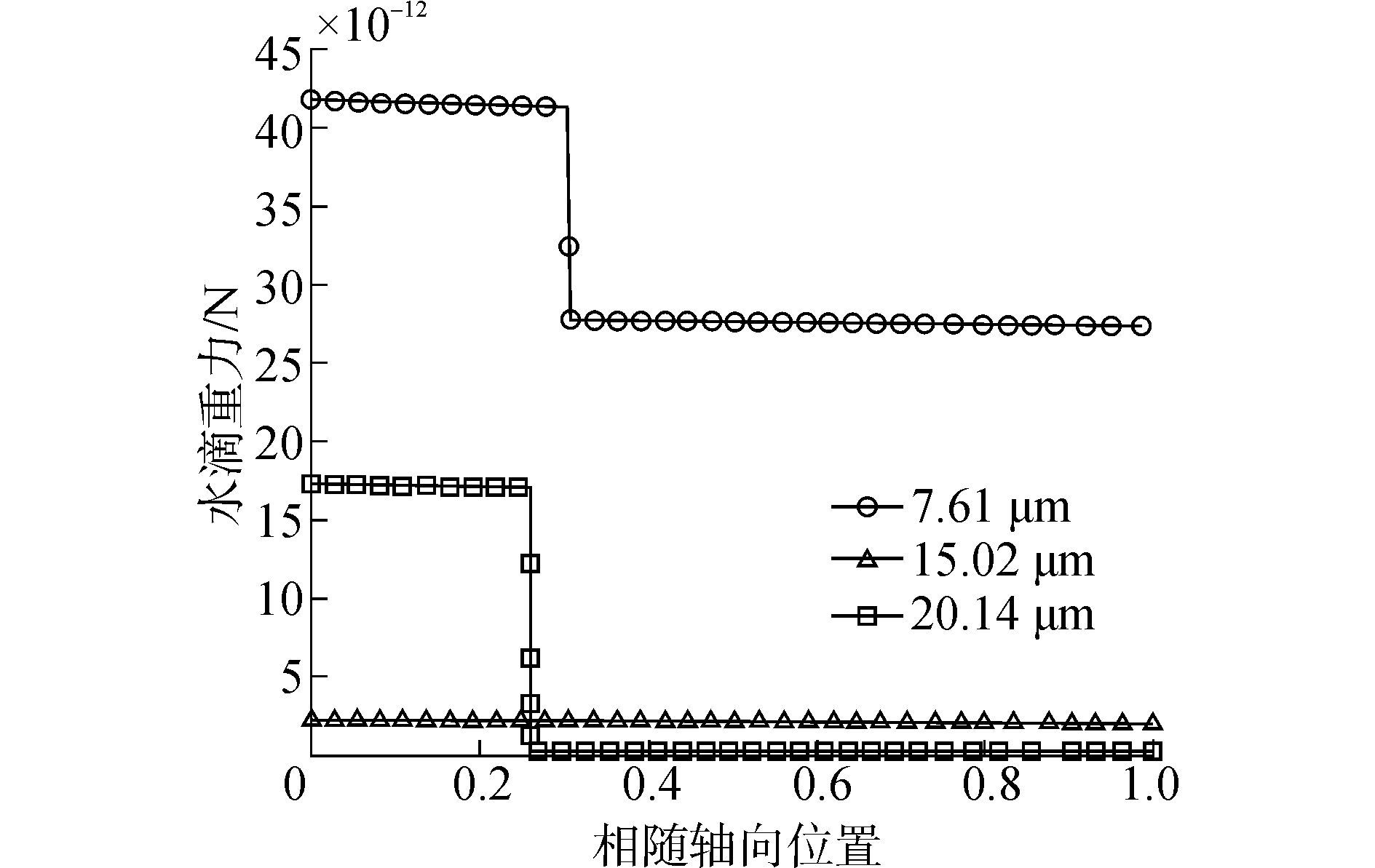
图 13为水滴颗粒在压气机内不同位置的重力变化。由于在蒸发及破碎作用下水滴的直径不断减小, 而液态水的密度在压气机内受温度及压力影响较小, 所以水滴的重力从进口到出口有所减小。
|
| 图13 压气机内水滴重力 Figure 13 Gravity of water droplets in compressor |
湿压缩过程中水滴所受到的作用力虽然较小, 但由于喷入的水滴处于微米级, 所以水滴会在微小作用力下运动。对比水滴受到的拖拽力、压力梯度力和重力大小可知, 压力梯度力及重力相比于拖拽力要小几个数量级, 可以忽略, 水滴在压气机内主要受到气流拖拽力的影响。
湿压缩过程中, 水滴颗粒的运动伴随着与气流之间质量和热量的传递, 而水滴在压气机内与气流的传热传质则是造成湿压缩与干压缩差别的重要因素[1]。图 14为压气机内的水蒸气质量。由图 6分析可知, 较小的水滴颗粒表面积与体积的比值较大, 水滴与气流的传热能力较强, 水滴的蒸发效果较好, 所以相同喷雾量情况下, 喷入较小的水滴颗粒在压气机内的蒸发量较大, 考虑到水滴破碎时分解为更小的水滴, 水滴的撞击破碎及气动力破碎有助于蒸发量的提高。在相同颗粒尺寸的情况下, 增加喷雾量使得压气机内液态水含量增加, 蒸发量也会增加, 但曲线的斜率随着喷雾量的增加有所降低, 增加喷雾量使得蒸发量增加的速率减弱, 这是因为增加喷雾量虽然使得压气机内整体的蒸发量增加, 但会使单个水滴的蒸发传热效果减弱, 蒸发速率和蒸发程度降低, 所以水滴整体蒸发量增加的速度降低。

|
| 图14 压气机内水蒸气质量 Figure 14 Mass of vapor in compressor |
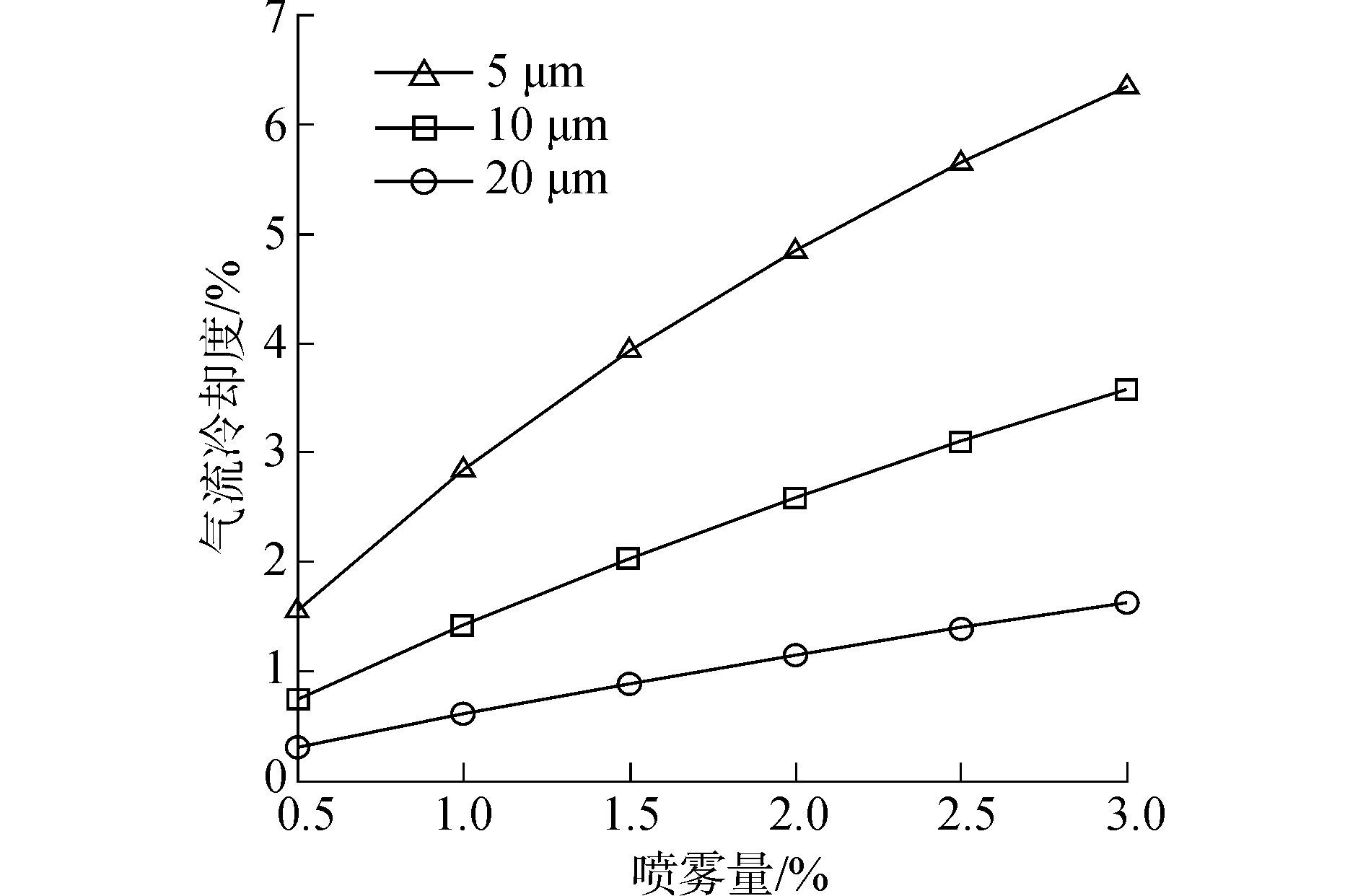
图 15为湿压缩相对于干压缩出口气流的冷却程度。
|
| 图15 气流冷却度 Figure 15 Cooling degree of gas |
图 14显示压气机内水蒸气质量会随着颗粒尺寸的减小和喷雾量的增大而增加, 而湿压缩过程中水滴的喷入对气流的冷却效果主要取决于液态水的蒸发冷却作用, 所以喷入的水滴颗粒越小, 喷雾量越大, 气流的冷却程度越高。在颗粒尺寸5 μm, 3%喷雾量情况下, 气流的冷却程度达到6.34%。
尽管水滴整体尺寸越小, 喷雾量越大, 压气机内水滴的蒸发量越多, 对气流的冷却程度越好, 但液态水蒸发量增加速率以及气流冷却程度的增加速率均会降低, 并且水滴与气流之间由于粘性而产生的拖拽作用会对气流造成一定的阻力损失, 水滴对叶片的撞击又会造成压气机的额外负载, 当喷雾量增加到一定程度时, 湿压缩过程中水滴蒸发带来的优化效果将弥补不了水滴喷入造成的损失, 压气机性能将会降低, 所以较小的水滴颗粒情况下选择适当大的喷雾量是应用湿压缩技术的一个关键因素。
3 结论1) 湿压缩过程中, 水滴在压气机内主要受气流拖拽力的作用, 运动雷诺数与韦伯数均较小, 发生振荡破碎的可能性较大, 并且主要发生在转子叶片前缘附近。
2) 较大的水滴颗粒传热传质能力较弱, 对气流造成的粘性拖拽损失较大, 发生破碎的可能性较高, 但大水滴破碎的同时降低了水滴的平局尺寸, 在一定程度上有利于促进水滴的传热传质。
3) 湿压缩过程中不可避免的会有水滴撞击到叶片表面, 不仅会对水滴的运动破碎产生影响, 同时会对叶片造成附加载荷, 对叶片的寿命造成损失。
4) 湿压缩过程需要综合考虑水滴产生的蒸发冷却效果、阻力损失与撞击作用的影响, 选取较小的水滴颗粒和适当的喷雾量来提高湿压缩效果。
| [1] | ZHENG Qun, SUN Yufeng, LI Shuying, et al. Thermodynamic analyses of wet compression process in the compressor of gas turbine[J]. Journal of turbomachinery, 2003, 125(3): 489–496. DOI:10.1115/1.1575254 |
| [2] | SUN Lanxin, ZHENG Qun, LI Yijin, et al. Understanding effects of wet compression on separated flow behavior in an axial compressor stage using CFD analysis[J]. Journal of turbomachinery, 2011, 133(3): 031026. DOI:10.1115/1.4003003 |
| [3] | SUN Lanxin, ZHENG Qun, LI Yijin, et al. Numerical simulation of a complete gas turbine engine with wet compression[J]. Journal of engineering for gas turbines and power, 2012, 135(1): 012002. DOI:10.1115/1.4007366 |
| [4] | ROUMELIOTIS I, ALEXIOU A, ARETAKIS N, et al. Development and integration of rain ingestion effects in engine performance simulations[J]. Journal of engineering for gas turbines and power, 2014, 137(4): 041202. DOI:10.1115/1.4028545 |
| [5] | NEUPERT N, OBER B, JOOS F. Experimental investigation on droplet behavior in a transonic compressor cascade[J]. Journal of turbomachinery, 2014, 137(3): 031009. DOI:10.1115/1.4028351 |
| [6] | WHITE A J, MEACOCK A J. Wet Compression analysis including velocity slip effects[C]//Proceedings of ASME Turbo Expo 2010:Power for Land, Sea, and Air. Glasgow, UK:ASME, 2010:953-963. |
| [7] | YANG Huaifeng, ZHENG Qun, LUO Mingcong, et al. Wet compression performance of a transonic compressor rotor at its near stall point[J]. Journal of marine science and application, 2011, 10(1): 49–62. DOI:10.1007/s11804-011-1041-x |
| [8] | NIKOLAIDIS T. Water ingestion effects on gas turbine engine performance[D]. Bedfordshire, England:Cranfield University, 2008:18-19. |
| [9] | WHITE F M. Viscous fluid flow[M]. 3rd ed. New York, NY: McGraw-Hill,, 2006. |
| [10] | BAI Chengxin, GOSMAN A D. Development of methodology for spray impingement simulation[R]. SAE Technical Paper 950283, 1995. |
| [11] | LUO Mingcong, ZHENG Qun, SUN Lanxin, et al. The effect of wet compression on a multistage subsonic compressor[J]. Journal of turbomachinery, 2013, 136(3): 031016. DOI:10.1115/1.4025570 |



