2. Zhejiang Provincial Key Laboratory of Part Rolling Technology, Ningbo 315211, China;
3. Central Research Institute of Building and Construction Co., Ltd, Beijing 100088, China
冷弯成形作为一种塑性成形的加工工艺,其所生产的产品与国民生活息息相关,随着冷弯型钢市场需求的逐年增长,对成形产品的质量也提出了更高的要求[1-3]。在冷弯成形的众多产品中,C型钢作为建筑施工的金属骨架、吊顶等广泛的应用于宾馆、候机楼、车站、游乐场、工厂、写字楼、顶棚等场所,其成形质量的好坏也影响着这些场所的使用。而冷弯产品的质量取决于合理的成形工艺参数[4-6],因此,探寻合理的成形工艺参数对提高冷弯成形产品的质量有着重要的工程应用意义。对冷弯成形工艺参数的研究发现当轧辊间距大于成形长度时,产生回弹,而轧辊间距过小时,板材弯曲褶皱;而间距的增大会减小板材边缘的异常塑性变形,而有限元仿真中进给速度施加在板材的前端或是板材与轧辊的接触面上,对成形产品纵向应变的大小并无明显的影响[7-9]。摩擦系数,板材的进给速度对板材的成形应变影响较小,而成型角增量的减小能有效降低成形应变并减小成形产品的弯曲缺陷[10-11]。仿真结果中的纵向应变可以通过有限元软件得到,然而实验中的板材应变的测量较难实现,通过对轧机轧辊的改造,使得应变测量仪可以通过上下轧辊的间隙而对板材成形的应变进行测量[12]。
本文以C型钢作为研究对象,以UC40冷弯机作为试验机,采用底线水平法而不是上、下山法布置轧辊[13-14],通过MSC.Marc对C型钢进行了成形过程的仿真,分析了板材不同层面及整体的应力、应变分布情况,此外,选取轧辊间距和板材进给速度两项工艺参数作为研究对象,以等效应力和等效应变作为成形质量的指标,摒弃了无法进行因素多水平试验的正交试验设计[15],而采用了均匀试验设计与有限元仿真相结合的方法,对C型钢成形的工艺参数进行了分析和优化。
1 C型钢成形的模型建立 1.1 模型的基本参数本文所使用的C型钢的基本尺寸及成形道次的辊花图如图 1(a)、(b)所示,加拿大的乔治·哈姆斯[16]以及日本的小奈弘[17]都提出过关于冷弯产品成形道次的计算公式,但由于冷弯产品的种类繁多,应用广泛,这些公式也并不具有普适性,不能给行业人员提供有效的理论参考;本文所采用的冷弯机共有十个道次,将其划分为四部分:第一部分为第一道次,作为咬入段,用于3 mm处的折弯,轧辊的咬入角为90°;第二部分为第二、三道次,用于5 mm处的折弯,轧辊成形角分别为 (60°、90°);第三部分为四到九道次,用于19 mm处的折弯,由于板材的塑性变形较大,故在此采取6个道次成形,轧辊成形角分别为 (19°、38°、57°、74°、85°、90°);第四部分为第十道次,作为过弯道次,成形角为95°,其目的是矫正回弹。另有两道次立辊L1和L2,分别位于第三、四道次间和第十道次后,同样为了矫正回弹。根据结构对称性,也为了减小计算量,提高求解效率,采取板材的一半进行建模,结构模型如图 2所示。
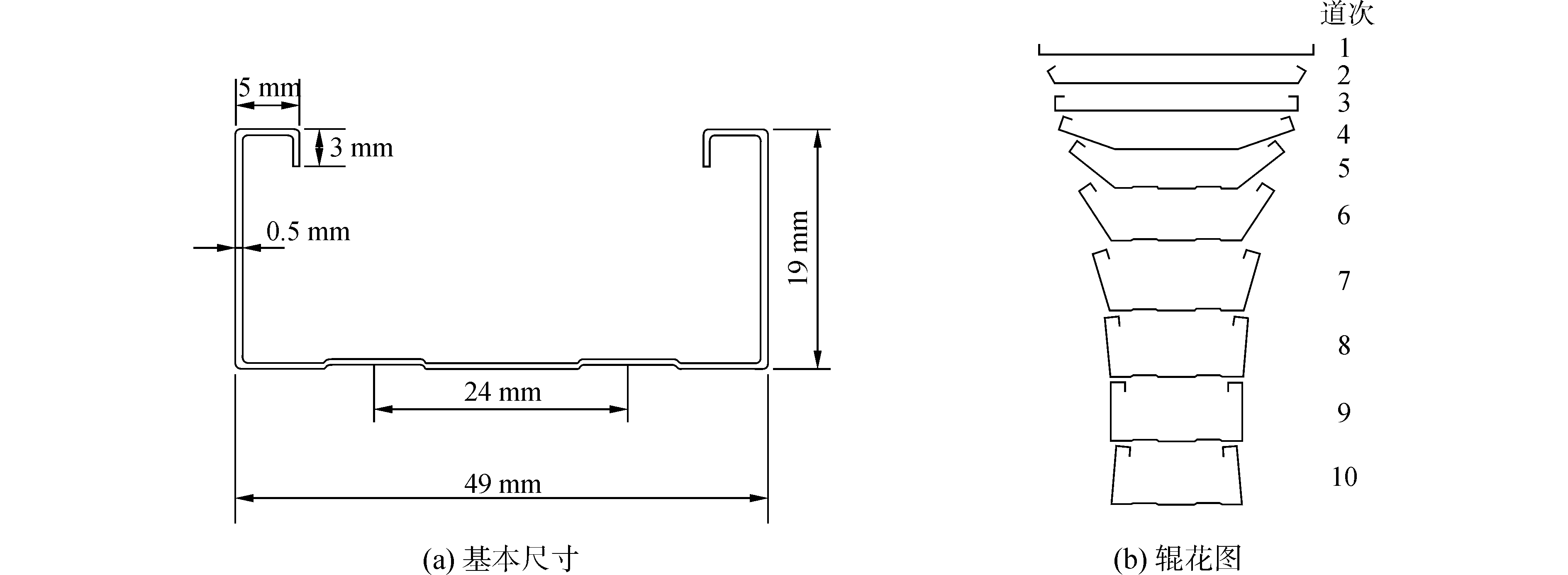
|
| 图1 C型钢的基本尺寸及成形过程 Figure 1 Basic dimensions and forming process of C-channel steel |

|
| 图2 冷弯成形的仿真模型 Figure 2 The simulation model of cold roll forming |
其中,模型的轧辊全部设置为刚体,板材采用双层八节点实体单元element7建模,建立的板材模型厚度为0.5 mm,宽度为47.5 mm,长度为47.5 mm,并对单元进行局部加密的网格划分,加密网格主要集中在成形第一、二部分道次的区域,即板材的边部。由于冷弯成形的特点为金属的塑性变形且具有回弹,故本文使用弹塑性有限元的方法,设置的板材弹性模量为210 GPa,泊松比为0.3,板材的进给速度为150 mm/s,轧辊间距为210 mm,板材与轧辊间的摩擦系数为0.2。
此外,板材的等效应力-等效应变关系[18]为
σ=617.2(0.001 292+ε)0.143
1.2 模型初始条件的设立实际的冷弯机下辊为驱动辊,上辊为从动辊,板材咬入冷弯机后,靠轧辊间转动的摩擦力带动板材进给,为了简化模型,便于计算,本文的模型将轧辊的上下两辊均设置为驱动辊,在板材的尾部设立推板,通过给推板一个不变的进给速度来带动板材的进给;为了保证进给过程中板材的理想进给,还需要对板材施加边界条件作为约束,施加的边界条件如图 3所示,在作为对称面的板材节点上固定了节点在Y、Z、Rx及Rz方向的自由度,避免板材在进给成形过程中出现滑移、褶皱等现象。

|
| 图3 板材的边界条件 Figure 3 Boundary conditions of the strip |
虽然本文所采用的板材为0.5 mm厚的带钢,但为了深入的研究和分析各层的应力及应变,并没有对薄壁实体采用壳单元或壳-体单元,而是采用了element7的体单元,虽然增大了计算量及计算时间,但体单元更真实的模拟了板材的实际成形状况,故在划分网格时将带钢在厚度上划分成双层厚度为0.25 mm的单元,并将板材定义为顶层、中间层、底层三层,如图 4所示,便于分层分析,并取位于板材中段的节点B1和节点B2作为分析对象;本文的等效应力为等效的冯·米塞斯应力 (以下简称等效应力),图 5(a)为板材中段的顶、中、底三层的等效应力分布,等效应力的几个峰值点分别位于C型钢成形的过弯段,三层的应力分布趋势相同,应力值相差较小,但板材的内层受力略大于中层和外层,图 5(b)中板材等效塑性应变 (以下简称等效应变) 的分布也证实了这点,等效应变的峰值点位置也与等效应力的大体相同。
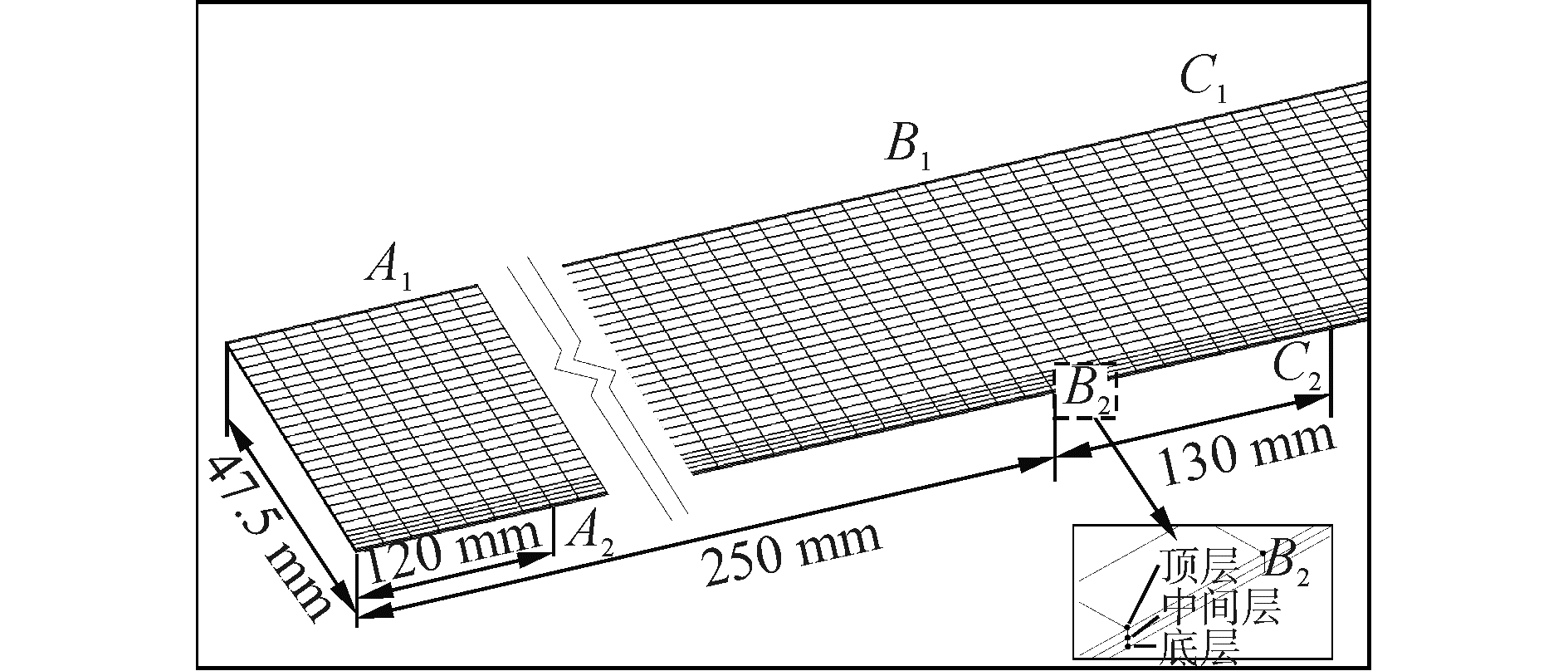
|
| 图4 测量节点分布 Figure 4 The distribution of measurement nodes |
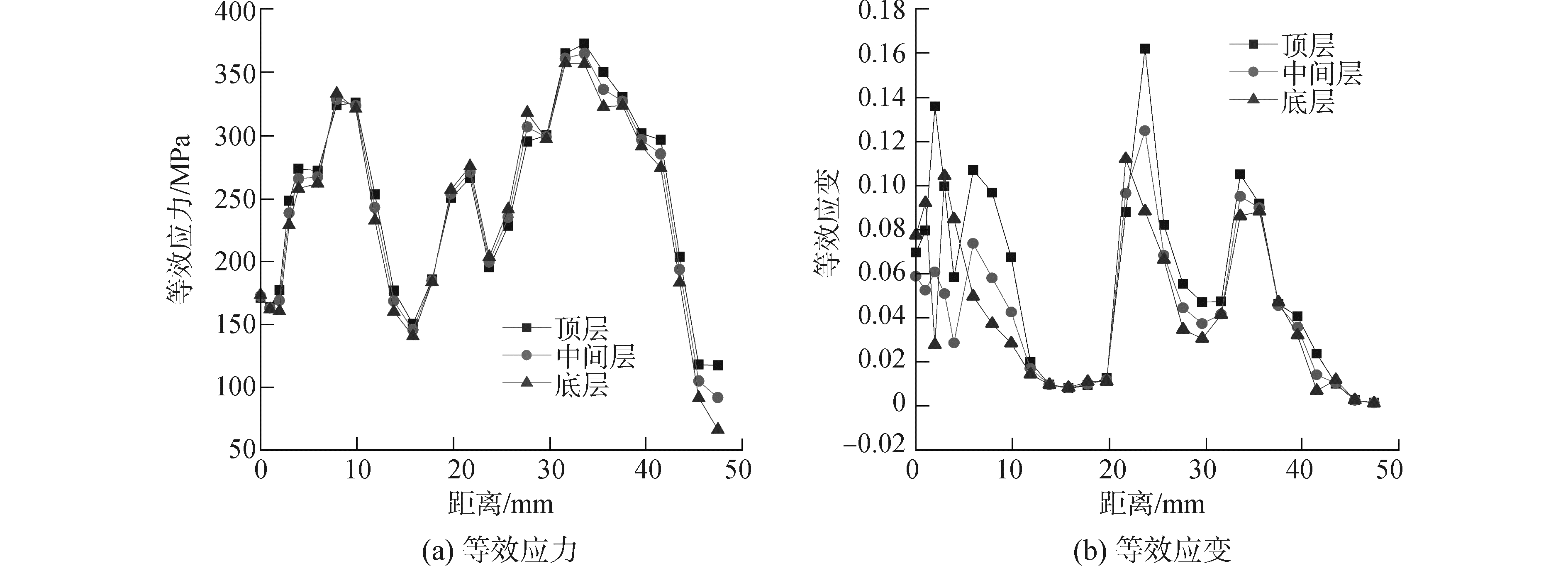
|
| 图5 节点B1至节点B2间三层应力和应变分布 Figure 5 The stress and strain distribution of three layers from node B1 to node B2 |
取图 4中板材前段节点A1、A2及板材后段节点C1、C2作为测量节点,对板材前段和后段对比分析。
图 6(a)中的板材等效应力云图显示了板材成形到第九道次后应力的整体分布,可见板材咬入段的成形质量较差,咬入段过后,成形质量有明显改善,由图 6(b)可知,在经过同一道次时,后段的等效应力大于前段,这主要与所设置的推板的推力有关,图中的C型钢成品为UC40冷弯机实验所得,由此可知仿真与实验的成形产品具有较好的一致性。由图 7(a)、(b)可以看出板材的大应变主要集中在咬入段和折弯处,且板材后段的等效应变也略大于前段。

|
| 图6 等效应力整体分布及前、后段应力对比 Figure 6 Equivalent stress distribution and stress comparison between front part to behind part of the strip |

|
| 图7 等效应变整体分布及前、后段应变对比 Figure 7 Equivalent strain distribution and strain comparison between front part to behind part of the strip |
均匀试验设计是采用均匀设计表安排试验,而用回归分析的方法进行数据分析的一种试验设计方法[19],相比于正交试验设计,均匀试验设计只考虑试验范围内试验点的均匀分散,不考虑试验点的整齐可比,但水平因素相对较多时,并不需要进行正交试验平方次的试验次数,从而使用较少的试验次数能够较多的因素水平数。本文以板材的进给速度和轧辊间距两项因素为研究对象,各取5个水平,如表 1。
| 因素 | 水平1 | 水平2 | 水平3 | 水平4 | 水平5 |
| 进给速度/(mm·s-1) | 50 | 100 | 150 | 200 | 250 |
| 轧辊间距/mm | 210 | 260 | 310 | 360 | 410 |
为了提高仿真试验结果的准确度,本文采取了比仿真试验次数增加一倍的均匀设计表U×10(10)10进行仿真试验设计,将均匀设计表理论上的10水平变为5水平的重复仿真试验,从而增加了仿真试验数据的准确度及可信度。本文采用的10组均匀试验方案如表 2所示。
| 试验号 | 进给速度/(mm·s-1) | 轧辊间距/mm | 最大等效应变 |
| 1 | (1)50 | (4)360 | 0.098 187 |
| 2 | (2)100 | (8)310 | 0.097 847 |
| 3 | (3)150 | (1)210 | 0.097 563 |
| 4 | (4)200 | (5)410 | 0.097 993 |
| 5 | (5)250 | (9)360 | 0.098 187 |
| 6 | (6) 50 | (2)260 | 0.098 168 |
| 7 | (7)100 | (6)210 | 0.098 238 |
| 8 | (8)150 | (10)410 | 0.098 192 |
| 9 | (9)200 | (3)310 | 0.098 45 |
| 10 | (10)250 | (7)260 | 0.098 168 |
| 优化 | 140 | 340 | 0.097 128 |
根据上述的试验方案进行仿真试验,测量结果为A1、A2间的节点在第三道次折弯处的最大等效应变,所得数据如表 2所示,均匀试验设计并不能按照正交试验设计一样进行方差分析,只能进行直观分析或是回归分析,直接观察可知:表 2中的试验方案3所测得的最大等效应变值最小,如果仅从这十组方案中选择工艺参数,方案3即为较优方案。由于均匀试验试验点分布的均匀性,经过大量实践证明,较优解与最优解的结果相差不大。
将表 2中的数据导入Matlab进行回归分析以求解最优方案,采用二次多项式的回归方式得到仿真试验数据的拟合方程为
y=0.097 014-3.746×10-6v+7.897×10-6d+1.317×10-8v2-1.1503×10-8d2
式中:y为最大等效应变,v为板材的进给速度,d为轧辊间距,两项工艺参数的影响指标见表 3,由逐步回归分析得到的标准化逐步回归系数的大小可以作为影响等效应变的参考指标,由表 3可知轧辊间距d对等效应变的影响大于板材的进给速度v;由线性回归分析得到的Fα为因素的临界水平值,以判定因素的影响是否显著,F为数据的实际水平值,通过F与Fα的比较发现,两工艺参数的影响均不显著,可见进给速度和轧辊间距两项工艺参数均不是影响产品质量的关键因素,但仍有一定的影响作用;对回归方程求解偏导,得到的最优条件为v=142.2 mm/s,d=343.3 mm,近似可得v=140 mm/s,d=340 mm,进行仿真验证,得到的数据如表 2中的优化所示,可见优化组的工艺参数相比前十组方案的等效应变均要小,由于两项工艺参数对板材成形的等效应变影响都很小,故优化后的应变值并没有明显的降低,但一定程度上减小了等效应变的峰值,可以作为工艺参数选用的参考,实际生产中,该两项参数的选取还要结合电机、场地大小等进一步考虑获得。
| 指标 | 进给速度v | 轧辊间距d |
| 标准化逐步回归系数 | 1.14 | 2.41 |
| F | 0.028 | 0.39 |
| Fα | 5.59 | 12.24 |
1) 板材采用体单元建模,虽然增加了计算时间,但更加真实地模拟了成形过程,分层分析发现总体上板材内层受到的应力相对于中层和外层较大,所产生的变形也较大,由于成形过程中板材折弯处的异常应变易使得附近区域产生异常应变,故在设计时更应着重考虑控制折弯处内层的应力应变。板材后段产生的等效应变也略大于板材的前段,由成形过程也易知板材在进给咬入段的成形质量较差,这主要是由于成形道次的第一部分咬入角太大且仅有一个道次,因此为了改善C型钢的成形质量,可以减小咬入角并增加咬入段的成形道次。
2) 相比于正交试验设计,利用均匀试验设计与有限元仿真模拟相结合的方法,能够对具有大量水平的因素进行组合试验且避免了庞大的试验次数,可以用于冷弯成形工艺参数的优化,在实际生产中,对工艺参数设计具有一定的参考价值。
3) 本文所采取的均匀试验设计因素采用5水平,且只将一个关键道次的等效应变作为指标,不管是因素、水平还是指标的数量都相对较少,进一步的研究可增加以上三者的试验基数;而针对于本优化方案的结果,可根据两因素对成形质量的影响程度在优化参数的数值附近进一步细化水平并进行试验,使得所得的结果更为精确;以上仿真试验的相关数据也需要实验的验证。
| [1] | DAVIS J M. Recent research advances in cold-formed steel structures[J]. Journal of constructional steel research, 2000, 55: 267–288. DOI:10.1016/S0143-974X(99)00089-9 |
| [2] | MACDONALD M, HEIYANTUDUWA M A, RHODES J. Recent developments in the design of cold-formed steel members and structures[J]. Thin-Walled Structures, 2008, 46: 1047–1053. DOI:10.1016/j.tws.2008.01.039 |
| [3] | SCHAFER B W. Review:The direct strength method of cold-formed steel member design[J]. Journal of constructional steel research, 2008, 64: 766–778. DOI:10.1016/j.jcsr.2008.01.022 |
| [4] |
曾国. 多道次辊弯成形冷弯型钢残余应力有限元仿真与实验研究[D]. 上海: 上海交通大学, 2009.
ZENG Guo. Simulation and experimental study on residual stresses for multi-stand roll-formed sections[D]. Shanghai:Shanghai Jiao Tong University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10248-2010033187.htm |
| [5] | ZENG G, LI SH, YU ZQ, et al. Optimization design of roll profiles for cold roll forming based on response surface method[J]. Materials and Design, 2009, 30: 1930–1938. DOI:10.1016/j.matdes.2008.09.018 |
| [6] |
付志强. 异型管连续辊弯成型工艺及计算机辅助设计系统研究[D]. 秦皇岛: 燕山大学, 2014.
FU Zhiqiang. Research on continuous roll forming process and the computer aided design system of shape tube[D]. Qinhuangdao:Yanshan University, 2014. |
| [7] | HONG S, LEE S, KIM N. A parametric study on forming length in roll forming[J]. Journal of materials processing technology, 2001, 113(1-3): 774–778. DOI:10.1016/S0924-0136(01)00711-7 |
| [8] | BUI Q V, PONTHOT J P. Numerical simulation of cold roll-forming processes[J]. Journal of materials processing technology, 2008, 202(1-3): 275–282. DOI:10.1016/j.jmatprotec.2007.08.073 |
| [9] | HEISLITZ F, LIVATYALI H, AHMETOGLU M A, et al. Simulation of roll forming process with the 3-D FEM code PAM-STAMP[J]. Journal of materials processing technology, 1996, 59(1/2): 59–67. |
| [10] | SAFDARIAN R, NAEINI H M. The effects of forming parameters on the cold roll forming of channel section[J]. Thin-walled structures, 2015, 92: 130–136. DOI:10.1016/j.tws.2015.03.002 |
| [11] | BIDABADI B S, NAEINI H M, TEHRANI M S, et al. Experimental and numerical study of bowing defects in cold roll-formed, U-channel sections[J]. Journal of constructional steel research, 2016, 118: 243–253. DOI:10.1016/j.jcsr.2015.11.007 |
| [12] | SENANAYAKE R S, COLE I M, THIRUVARUDCHELVAN S. The application of computational and experimental techniques to metal deformation in cold roll forming[J]. Journal of materials processing technology, 1994, 45(1-4): 155–160. DOI:10.1016/0924-0136(94)90334-4 |
| [13] | BIDABADI B S, NAEINI H M, TAFTI R A, et al. Experimental investigation of the ovality of holes on pre-notched channel products in the cold roll forming process[J]. Journal of materials processing technology, 2015, 225: 213–220. DOI:10.1016/j.jmatprotec.2015.06.008 |
| [14] | 李登超. 冷弯型钢及焊管生产技术[M]. 北京: 化学工业出版社, 2011: 20-21. |
| [15] |
胡盛德, 郭志旺, 肖颐, 等. 利用正交试验设计优化冷弯成形工艺参数[J].
轧钢, 2015, 32(3): 44–47.
HU Shengde, GUO Zhiwang, XIAO Yi, et al. Optimization of cold roll forming process parameters by orthogonal experimental design[J]. Steel rolling, 2015, 32(3): 44–47. |
| [16] |
乔治·哈姆斯. 冷弯成型技术手册[M]. 刘继英, 艾正青, 译. 北京: 化学工业出版社, 2009: 178-186.
HALMOS G T. Roll forming handbook[M]. LIU Jiying, AI Zhengqing, trans. Beijing:Chemical Industry Press, 2009:178-186. |
| [17] | 小奈弘, 刘继英. 冷弯成型技术[M]. 北京: 化学工业出版社, 2008: 9-13. |
| [18] |
李大永, 蒋劲茂, 彭颖红, 等. 辊弯成形过程仿真与参数优化[J].
系统仿真学报, 2007, 19(4): 893–896.
LI Dayong, JIANG Jinmao, PENG Yinghong, et al. Study on roll forming process simulation and roll diameters optimization[J]. Journal of system simulation, 2007, 19(4): 893–896. |
| [19] | 王岩, 随思涟. 试验设计与MATLAB数据分析[M]. 北京: 清华大学出版社, 2012: 208-232. |



