船舶在复杂的海况下运营,其结构常常会产生损伤,而这种潜在的损伤是造成船体结构整体失效的直接因素。船舶结构安全监测系统使用传感器对船体结构进行实时监测,检测并预报结构的早期损伤,从而引导相关人员采取措施,预防船体结构的破坏,这对于船舶安全航行具有很大的意义。为了能够真实地反映和预报船体结构,结构监测点位置以及传感器的布置形式的选取至关重要。结构监测点的布置是否合理直接影响到船舶结构安全监测系统对于船体结构监测的有效性。
为了能够更好地使用船体结构安全监测系统对船体结构进行监测,针对结构监测点布置这一问题,学者们进行了一系列的研究。Wang等[1]将光纤传感器应用于船体结构监测,根据船体的特点给出了传感器布置的位置。张岚[2]根据散货船结构的特点和典型损坏的形式对传感器的位置进行了系统地研究。金永兴等[3-4]则考虑了集装箱船结构疲劳事故发生的主要原因和结构特点,确定集装箱船结构监测点的位置。王为[5]将船体简化为Nishihara箱型梁结构,通过对结构进行有限元分析,对光纤光栅传感器的布置位置进行了优化。梁文彬[6]等则采用遗传算法对结构上监测点的分布进行了研究。申素梅[7]基于有限元静力计算,提出了自升式海洋平台桩腿桩靴结构监测方案。赵彦文[8]则考虑腐蚀对于结构的影响研究了传感器在油船结构中的布置。李志锋[9]通过有限元直接计算方法研究了海洋平台工作船和双体船中传感器的布置。贾连徽等[10]综合考虑海况信息下的结构应力响应,对结构监测点的位置进行了研究并给出相应的传感器布置方式。
然而以上研究成果大多只关注船体结构在环境载荷下的结构响应,缺乏对船体结构失效后船体总纵强度的损失、传感器损坏后导致的监测效率下降等因素的考虑。因此在前人研究的基础上,综合考虑船舶具体航行区域的海况、传感器失效以及结构失效对于总纵强度影响等因素,建立一套基于风险的结构监测点布置方法十分必要。同时, 说明相应传感器的布置形式,形成具有一定抗破损能力的船体结构监测体系。
1 船体结构监测点的布置方法 1.1 船体结构的短期失效概率根据波浪载荷理论,认为海浪在短时间内是均值为0的平稳正态随机过程。因此,线性的海浪波浪载荷所对应的随机过程亦将是均值为0的平稳正态的。由波浪载荷线性响应系统可知,波浪载荷的谱密度可以表达为
| $ {S_W}\left( {\omega, {H_{1/3}}, {T_z}} \right) = {H^2}\left( \omega \right){S_\zeta }\left( {\omega, {H_{1/3}}, {T_z}} \right) $ | (1) |
式中:Sζ(ω, H1/3, Tz) 为海浪谱密度函数,SW(ω, H1/3, Tz) 为波浪载荷的谱密度函数,ω为波浪圆频率,H1/3为有义波高,Tz为波浪的特征周期,H(ω) 应力响应的模。
根据船体结构图建立有限元模型来模拟实船结构。依据船舶装载手册和船舶实际的运营环境,通过海浪资料获得海浪谱密度函数,并对船体有限元模型施加外部载荷。使用有限元软件Nastran进行有限元分析,即可计算出各个工况下的船体结构任意部位的结构响应函数H(ω),根据式(1) 得到波浪载荷的谱密度函数SW(ω, H1/3, T2)。
假定船舶在波浪中航行的短期结构应力幅值服从瑞利分布[11],故结构应力幅值的概率密度函数和分布函数如下
| $ {g_d}\left( x \right) = \frac{{2x}}{{{k^2}}}\exp \left( {-\frac{{{x^2}}}{{{k^2}}}} \right) $ | (2) |
| $ {G_d}\left( x \right) = 1-\exp \left( {-\frac{{{x^2}}}{{{k^2}}}} \right) $ | (3) |
式中参数k可以根据波浪载荷的谱密度函数求得:
| $ {k^2} = 2\int\limits_0^\infty {{S_W}\left( {\omega, {H_{1/3}}, {T_z}} \right)} {\rm{d}}\omega $ | (4) |
根据序列统计原理,以瑞利为初始分布,可求得应力幅值的极值分布概率密度函数和分布函数为
| $ {f_d}\left( x \right) = n{\left[{1-\exp \left( {\frac{{{x^2}}}{k}} \right)} \right]^{n -1}}\frac{{2x}}{k}\exp \left( { -\frac{{{x^2}}}{k}} \right) $ | (5) |
| $ {F_d}\left( x \right) = {\left[{1-\exp \left( {-\frac{{{x^2}}}{k}} \right)} \right]^n} $ | (6) |
式中n为船舶的运营时期内遭遇应力峰值的个数。
在船体结构的承载能力上,本文主要考虑结构的屈服破坏,并假定钢材屈服极限服从正态分布,其概率密度函数表达式如下:
| $ {f_c}\left( x \right) = \frac{1}{{\sqrt {2{\rm{\pi }}} {\sigma _C}}}\exp \left[{-\frac{{{{\left( {x-{\mu _C}} \right)}^2}}}{{2\sigma _C^2}}} \right] $ | (7) |
式中:μC为均值,一般取钢材屈服极限;σC为相应的标准差。
引入结构可靠性理论,认为载荷对船体结构的作用为D,船体结构的承载能力为C,船体结构失效函数M=C-D,当C与D是独立的随机变量时,结构失效概率为
| $ {P_f} = P\left[{\left( {C-D} \right) < 0} \right] = \int_{ - \infty }^{ + \infty } {\left[{1-{F_d}\left( x \right)} \right]{f_c}\left( x \right){\rm{d}}x} $ | (8) |
联立式(6)~(8),即可求得船体结构在短期海况下的结构失效概率。
1.2 船体结构的加权失效概率船舶在长期航行时遭遇到不同浪向和频率的波浪,同时由于运营的需要,船体自身的装载状况也会改变,而这些船舶具体的运行环境因素也将在船体结构的失效中有所考虑。因此船体结构的加权失效概率由各短期失效概率再结合船舶营运中可能遭遇的各种海况的分布情况得到。通过分析船舶在具体航行环境下的浪向、波浪频率以及船舶装载工况出现的概率,对短期海况下的结构失效概率进行加权,从而获得船体结构加权失效概率:
| $ {{\bar P}_f} = \frac{1}{N}\sum\limits_i {\sum\limits_j {\sum\limits_k {{C_{{\alpha _i}}}} } } {C_{{T_j}}}{C_{{\beta _k}}}{P_f}\left( {{k_i}, {\omega _j}, {\beta _k}} \right) $ | (9) |
式中:
由于船体构件结构形式和位置的不同,导致了各个构件对于总纵船体强度的贡献各异。因此除考虑船体结构在波浪载荷作用下的失效概率以外,同时应该考虑结构失效对于船体总纵极限强度的影响[13]。通过有限元法,利用船体有限元模型计算结构完全失效后船体的剩余极限强度和完整船的极限强度,使用两者的比值作为衡量结构失效后对于船体总纵强度的影响,结构破损影响因子Cd的表达式为
| $ {C_d} = 1-\frac{{{M_d}}}{{{M_u}}} $ | (10) |
式中:Md为结构完全失效后船体的剩余极限强度,Mu为船体总纵极限强度。
1.4 传感器的布置在结构监测的实际操作中,通常将传感器焊接或使用高粘性胶将传感器粘连到被测结构构件上,而这导致了传感器的拆除和更换较为困难。同时考虑到船体航行周期时间长,在航运中不便进行维护和修理,为避免由于传感器失效导致的结构监测失效,通过冗余设计,两种具有一定抗损能力的传感器布置方式被给出[14-15],并对这两种布置方式所适用的结构构件以及传感器的自我检验进行了叙述,具体形式见图 1和图 2。

|
| 图1 双向传感器布置示意图 Figure 1 Layout of two-sensor |
|
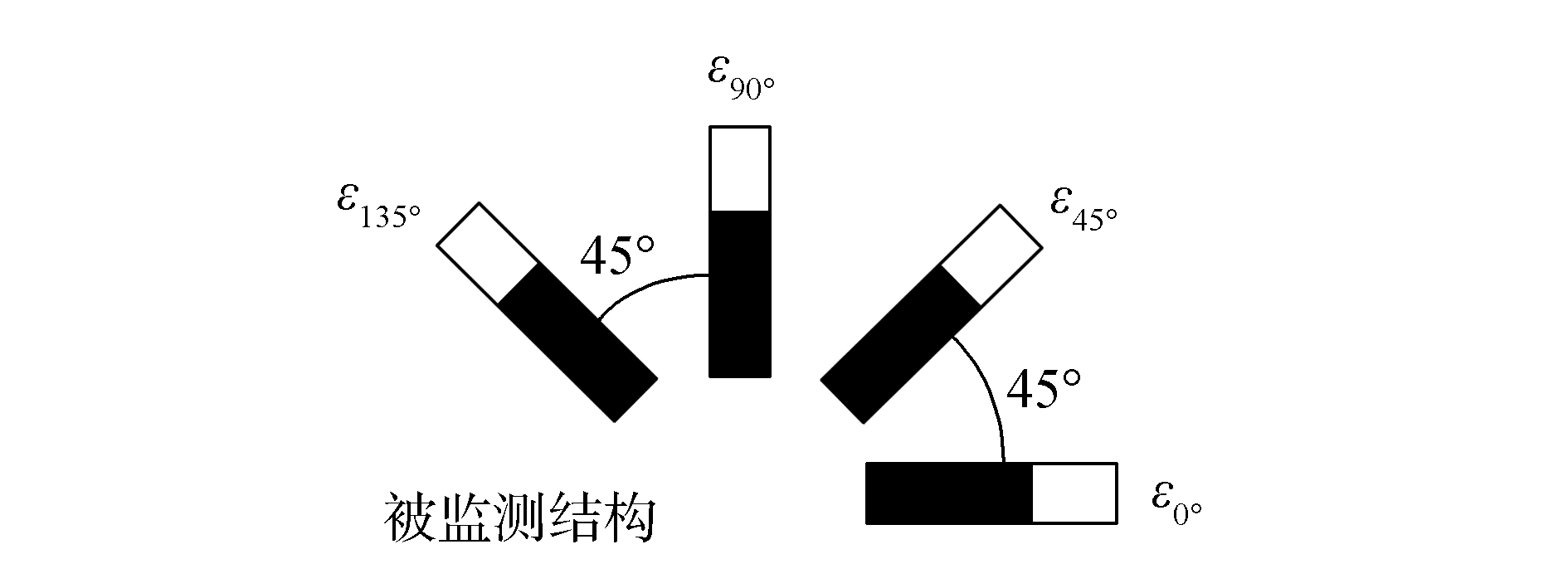
| 图2 四向传感器布置示意图 Figure 2 Layout of four-sensor |
对于纵骨、加强筋等骨材,其主要承受的应力为拉压应力。同时考虑到传感器能够布置的空间较小,故采用双向传感器监测构件上下表面的应变,由式(11) 虎克定律的应力与应变的关系,即可获得结构的应力状态。
| $ \sigma = E{\varepsilon _1} =-E{\varepsilon _2} $ | (11) |
式中:E为材料弹性模量, ε1为上表面应变, ε2为下表面应变。
而对于甲板、舱壁等板材,视其处于平面应力状态。监测点使用四向传感器布置,其主应力可以表示为
| $ \begin{array}{l} \sigma = \frac{E}{{\left( {1- {\mu ^2}} \right)}}\left[{\frac{{\left( {1 + \mu } \right)}}{2}\left( {{\varepsilon _{0^\circ }} + {\varepsilon _{90^\circ }}} \right)} \right. \pm \\ \frac{{\left( {1-\mu } \right)}}{2}\sqrt {{{\left( {{\varepsilon _{0^\circ }}-{\varepsilon _{90^\circ }}} \right)}^2} + {{\left( {{\varepsilon _{45^\circ }}-{\varepsilon _{135^\circ }}} \right)}^2}} \end{array} $ | (12) |
式中:μ为泊松比,ε0为与板材长边平行的传感器监测出的应变,ε45为与板材长边成45°角的传感器监测出的应变,ε90为与板材长边垂直的传感器监测出的应变,ε135为与板材长边成135°角的传感器监测出的应变。
对于处于平面应力状态的结构,采用第四强度理论,考察板材的Mises合应力值。根据计算出的主应力,可以计算出板材的Mises合应力值为
| $ {\sigma _{eq}} = \sqrt {\sigma _{\max }^2 + \sigma _{\min }^2-{\sigma _{\max }}{\sigma _{\min }}} $ | (13) |
| $ {\varepsilon _1} =-{\varepsilon _2} $ | (14) |
| $ {\varepsilon _{0^\circ }} + {\varepsilon _{90^\circ }} = {\varepsilon _{45^\circ }} + {\varepsilon _{135^\circ }} $ | (15) |
通过式(14) 和(15) 可知,在两种传感器的布置方式下都可以通过对比传感器监测的应变数据,实时检测传感器是否破损和松动,达到监测点处传感器自我检验的目的。
考虑到船体运营过程中一个传感器失效,由于采用了冗余设计,剩余的传感器仍然可以对结构进行有效监测。
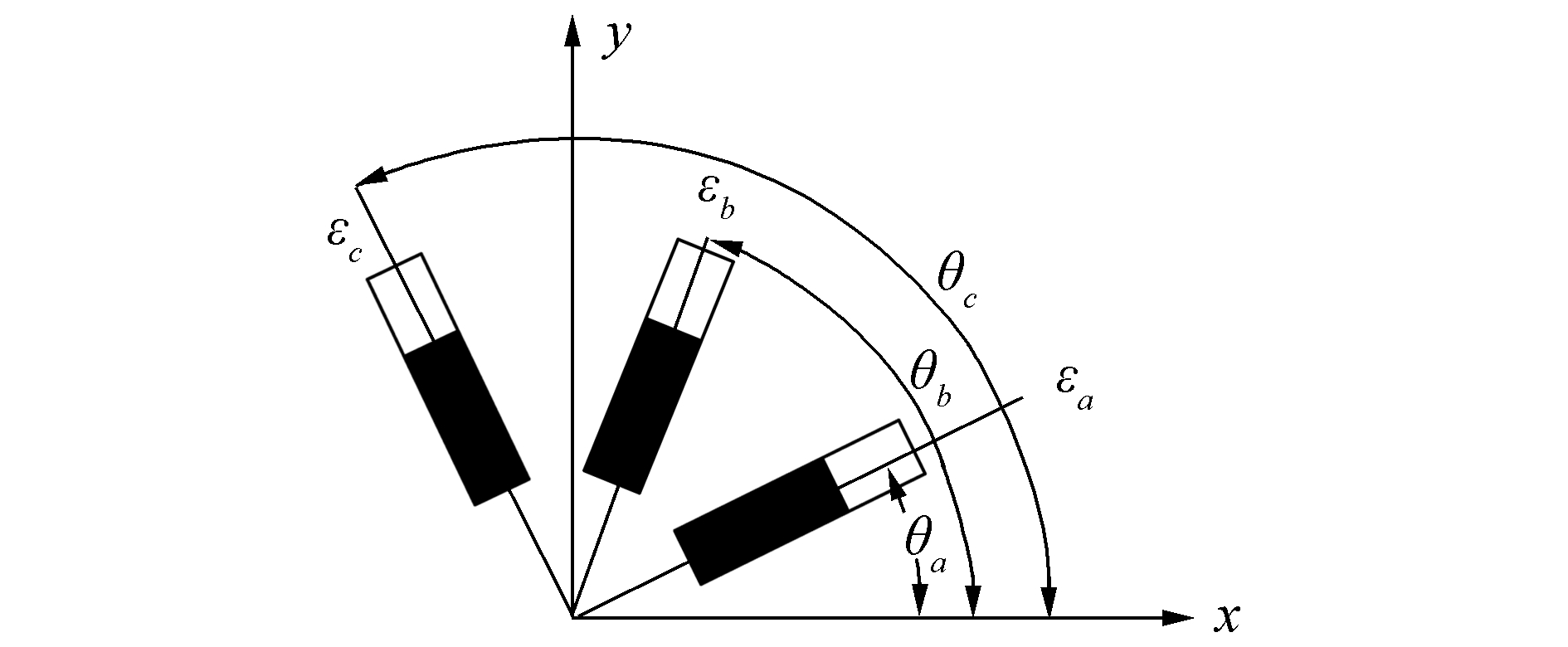
对于双向传感器布置来说,剩下的一个传感器仍可以继续对骨材的拉压应力进行监测。对于四向传感器布置来说,失去一个传感器后的任意3个传感器仍能组成三向传感器布置,具体如图 3。根据式(16) 中传感器监测出的应变和主轴(x轴和y轴) 应变的关系,利用高斯消去法求解方程组得到主轴应变,其中x轴与板材长边相平行,y轴与板材的短边相平行。
|
| 图3 三向传感器布置示意图 Figure 3 Layout of three-sensor |
| $ \left[{\begin{array}{*{20}{c}} {1 + \cos \;2{\theta _a}}&{1-\cos \;2{\theta _a}}&{-\sin \;2{\theta _a}}\\ {1 + \cos \;2{\theta _b}}&{1-\cos \;2{\theta _b}}&{ - \sin \;2{\theta _b}}\\ {1 + \cos \;2{\theta _c}}&{1 - \cos \;2{\theta _c}}&{ - \sin \;2{\theta _c}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{\varepsilon _x}}\\ {{\varepsilon _y}}\\ {{\gamma _{xy}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {2{\varepsilon _a}}\\ {2{\varepsilon _b}}\\ {2{\varepsilon _c}} \end{array}} \right] $ | (16) |
式中:θa为剩余传感器A与x轴的夹角,θb为剩余传感器B与x轴的夹角,θc为剩余传感器C与x轴的夹角,εa为剩余传感器A监测出的应变,εb为剩余传感器B监测出的应变,εc为剩余传感器C监测出的应变,εx为x轴方向上的应变,εy为y轴方向上的应变,γxy为剪应变。已知主轴应变,则板材的主应变为
| $ \varepsilon = \frac{{{\varepsilon _x} + {\varepsilon _y}}}{2} \pm \sqrt {{{\left( {\frac{{{\varepsilon _x}-{\varepsilon _y}}}{2}} \right)}^2} + {{\left( {\frac{{{\gamma _{xy}}}}{2}} \right)}^2}} $ | (17) |
板材的主应变与主应力的关系为
| $ \sigma _{\min }^{\max } = \frac{E}{{\left( {1-{\mu ^2}} \right)}}\left( {\varepsilon _{\min }^{\max } + \mu \varepsilon _{\min }^{\max }} \right) $ | (18) |
再根据式(17) 和(18) 中主应力和主轴应变的关系求得板的主应力,同样由式(13) 可以得到Mises应力,从而保证监测点能够继续有效监测。
如果全船使用同一类型的传感器进行监测,并假设单一传感器的失效概率为Pd,则对于双向传感器布置的监测点而言,其有效监测的概率为
| $ {P_s} = 1-P_d^2 $ | (19) |
对于四向传感器布置的监测点而言,其有效监测的概率为
| $ {P_s} = {\left( {1-{P_d}} \right)^4} + 4{P_d}{\left( {1-{P_d}} \right)^3} $ | (20) |
结构监测的风险分析主要考虑到结构的可靠性、传感器有效监测的可靠性以及结构失效后对于船体结构强度的影响[16]。根据结构风险评估理论,定义船体结构监测风险值为
| $ r = {{\bar P}_f}{P_s}{C_d} $ | (21) |
将船体结构离散成结构单元,定义结构单元ej为船体结构集合E的元素且为多元函数,函数与其结构的失效概率、船体结构强度的损失、结构的空间坐标以及风险值有关,其公式可以表示为
| $ {e_j} = \left[{{{\bar P}_{fi}}, {C_{{d_j}}}, {D_j}\left( {{x_j}, {y_j}, {z_j}} \right), {P_{{s_j}}}, {r_j}} \right], {e_j} \in E $ | (22) |
其中Dj(xj, yj, zj) 为结构单元中心点的空间坐标,且风险值有r1>r2>…rj(j=1, 2, …)。同法,定义结构监测单元si为结构监测点集合S的元素且为多元函数,函数的性质与结构单元一致,函数亦与其结构的失效概率、船体结构强度的损失、结构的空间坐标以及风险值有关,其公式可以表示为
| $ {s_i} = \left[{{{\bar P}_{fi}}, {C_{{d_i}}}, {D_i}\left( {{x_i}, {y_i}, {z_i}} \right), {P_{{s_i}}}, {r_i}} \right], {s_i} \in S $ | (23) |
本文选点方法分为初步筛选和二次筛选两步。对初步筛选监测点,主要考虑结构单元的失效概率和失效后所带来的船体总纵强度的损失,分别以结构的失效概率为纵坐标,以破损影响因子为横坐标,做出结构风险分布图,并对风险分布图进行分区归类。按照结构单元的失效概率将风险分布图分为3类,结构失效概率较高的为易损区,结构失效概率适中的为损伤区,结构失效概率较低为不易损区。同时,按照结构构件的破损影响因子也将风险分布图分为3类,破损影响因子较大为结构高损失区,破损影响因子适中的为结构中损失区,破损影响因子较低为结构低损失区。综合考虑失效概率和损失影响,最终结构风险分布图分为9区域,如Ⅰ-Ⅸ区。
在初步筛选中,要选取失效概率较高而破损影响不低的结构单元以及破损影响高的结构单元。因此对结构风险分布图划分优先级,并根据优先级由高至低将结构风险分布图划分将其中Ⅰ区为红色,Ⅱ区,Ⅳ区为橙色,Ⅲ区,Ⅴ区,Ⅶ区为黄色,Ⅵ区和Ⅶ区为绿色,Ⅸ区为蓝色。根据划分后的结构风险分布图,选取处于较高优先级的红色、橙色和黄色区域(即Ⅰ区、Ⅱ区、Ⅲ区、Ⅳ区、Ⅴ区、Ⅶ区) 的结构单元,这些结构单元所对应的中心点位置作为初选监测点的布置位置。
二次筛选是根据结构监测风险值的大小以及空间位置对初步筛选的监测点位置进行进一步筛选,引入搜索半径R来控制监测点的空间位置,使得监测点不会出现过于集中的现象,从而达到合理布置的目的。通过阶跃函数H构造结构监测单元si与结构单元ej的位置关系函数,位置关系函数为:
| $ {H_{ij}} = H\left( {\left| {{D_i}{D_j}} \right|-R} \right) = \left\{ \begin{array}{l} 1, \;\;\;\left| {{D_i}{D_j}} \right| \ge R\\ 0, \;\;\;\left| {{D_i}{D_j}} \right| < R \end{array} \right. $ | (24) |
式中:|DiDj|为监测单元si与结构单元ej各自中心点之间的距离, 当|DiDj|≥R时,结构单元ej与Hij的乘积仍为ej,即为保留结构单元ej。当时|DiDj|,结构单元ej与Hij的乘积为0,即剔除结构单元ej。由结构单元的定义可知,单元e1对应着结构风险值最大的结构单元,直接保留ej作为结构监测单元ej。然后通过结构监测单元si与结构单元ej的位置关系函数Hij进行判断,剔除以已选监测单元中心点位置为中心且半径为R的球域内的结构单元s1,在保留的结构单元中选取结构风险值最大的结构单元作为结构监测单元si,通过式(25) 逐步确定结构监测单元si,最终形成结构监测点集合S。
| $ \left\{ \begin{array}{l} {s_1} = {e_1}\\ {s_i} = \max {\left\{ {{e_2}\prod\limits_{n = 1}^{i-1} {{H_{n2}}}, {e_3}\prod\limits_{n = 1}^{i-1} {{H_{n3}}}, \cdots, {e_j}\prod\limits_{n = 1}^{i-1} {{H_{nj}}} } \right\}_{{r_j}}} \end{array} \right. $ | (25) |
通过筛选方法可知,结构监测单元si与结构单元ei具有同样的性质,在监测点集合S中的结构监测单元si对应的结构监测风险值仍满足r1>r2>…>ri。
2 船体结构监测点布置算例船舶在航行中往往船舯剖面所遭受的波浪载荷较大,而船舯剖面也是船体结构强度校核的重要位置。因此,应用上述方法对一条在中国沿海航行船舶的船舯剖面位置进行了结构监测点的布置,筛选步骤见流程图 5。该船总长241 m,型宽32 m,型深17.5 m,满载设计吃水10.8 m,具体有限元模型见图 4。
|
| 图5 船舯有限元模型示意图 Figure 5 Finite element model at the midship |

|
| 图4 布置方法流程图 Figure 4 Flow diagram of selection method |
根据船体结构构件的特点,将船舯剖面的结构离散成结构单元,并分为板材和骨材两类。其中板材为187个,骨材为152个,共计339个结构单元。通过船舶装载手册可知,船舶装载状态主要分为压载到港和满载出港两个装载状态。考虑到实船的航行海域为中国沿海海域,通过中国沿海海浪长期分布资料,可以获得在实际航行中船体可能遭遇的波高和波浪频率。由于船体左右舷对称,浪向范围以每30°递增从0°至180°,共取6个浪向;同时认为船在航行时,航速不变,正常运营航速为15 kn。利用有限元软件Patran/Natran进行有限元分析, 计算出各个工况下的结构响应函数H(ω)。海浪谱采用Pierson-Moskowitz单参数谱,计算船体结构的短期失效概率。
假定船舶航行10年的单一传感器破损失效的概率为0.5%,则监测点在双向和四向传感器布置下的有效监测概率分别为99.998%和99.985%。考虑船舶满载和压载装载状况,认为满载出港和压载到港在航行的时间均等,故装载分配系数Cα为0.5;同时假定浪向也符合均匀分布,故各个浪向的概率Cβ为1/6;而波浪的特征周期和有义波高的联合概率CT可以根据中国沿海海区波浪长期分布资料查表得到,根据式(9) 计算结构的加权失效概率。利用软件Abaqus进行非线性有限元分析,计算出完整船体的极限强度Mu和各个结构单元完全失效后船体的剩余极限强度Md,得到各个结构单元的结构破损影响因子Cd。根据结构单元的结构加权失效概率、结构破损影响因子和监测点有效监测率,计算结构单元的监测风险值。由于船舯结构单元较多,在此以主甲板的结构单元为例,说明结构监测点的布置过程,表 1和表 2分别列出了主甲板上板材和骨材前10个结构单元的信息。
| 序号 | 结构加权失效概率/% | 破损影响因子 | 风险值 | 位置 |
| e1 | 5.32 | 0.005 | 0.024 | 右舷距舯纵剖面3.8 m |
| e2 | 5.24 | 0.005 | 0.023 | 右舷距舯纵剖面3.4 m |
| e3 | 4.92 | 0.005 | 0.022 | 左舷距舯纵剖面3.4 m |
| e4 | 4.89 | 0.005 | 0.022 | 左舷距舯纵剖面3.8 m |
| e5 | 4.22 | 0.005 | 0.022 | 左舷距舯纵剖面2.6 m |
| e6 | 4.89 | 0.004 | 0.022 | 左舷距舯纵剖面5.8 m |
| e7 | 4.86 | 0.004 | 0.022 | 左舷距舯纵剖面6.2 m |
| e8 | 4.77 | 0.004 | 0.021 | 左舷距舯纵剖面5.4 m |
| e9 | 4.78 | 0.004 | 0.021 | 右舷距舯纵剖面6.2 m |
| e10 | 4.70 | 0.004 | 0.021 | 右舷距舯纵剖面5.0 m |
| 序号 | 结构加权失效概率/% | 破损影响因子 | 风险值 | 位置 |
| e37 | 5.21 | 0.002 | 0.011 | 左舷距舯纵剖面3.6 m |
| e38 | 4.85 | 0.002 | 0.010 | 舯纵剖面处 |
| e39 | 3.50 | 0.002 | 0.007 | 右舷距舯纵剖面3.6 m |
| e40 | 4.56 | 0.001 | 0.005 | 左舷距舯纵剖面6.0 m |
| e41 | 4.31 | 0.001 | 0.004 | 右舷距舯纵剖面5.2 m |
| e42 | 4.34 | 0.001 | 0.004 | 左舷距舯纵剖面6.3 m |
| e43 | 4.16 | 0.001 | 0.004 | 左舷距舯纵剖面6.7 m |
| e44 | 4.12 | 0.001 | 0.004 | 左舷距舯纵剖面6.0 m |
| e45 | 3.97 | 0.001 | 0.004 | 右舷距舯纵剖面6.4 m |
| e46 | 3.84 | 0.001 | 0.004 | 右舷距舯纵剖面4.8 m |
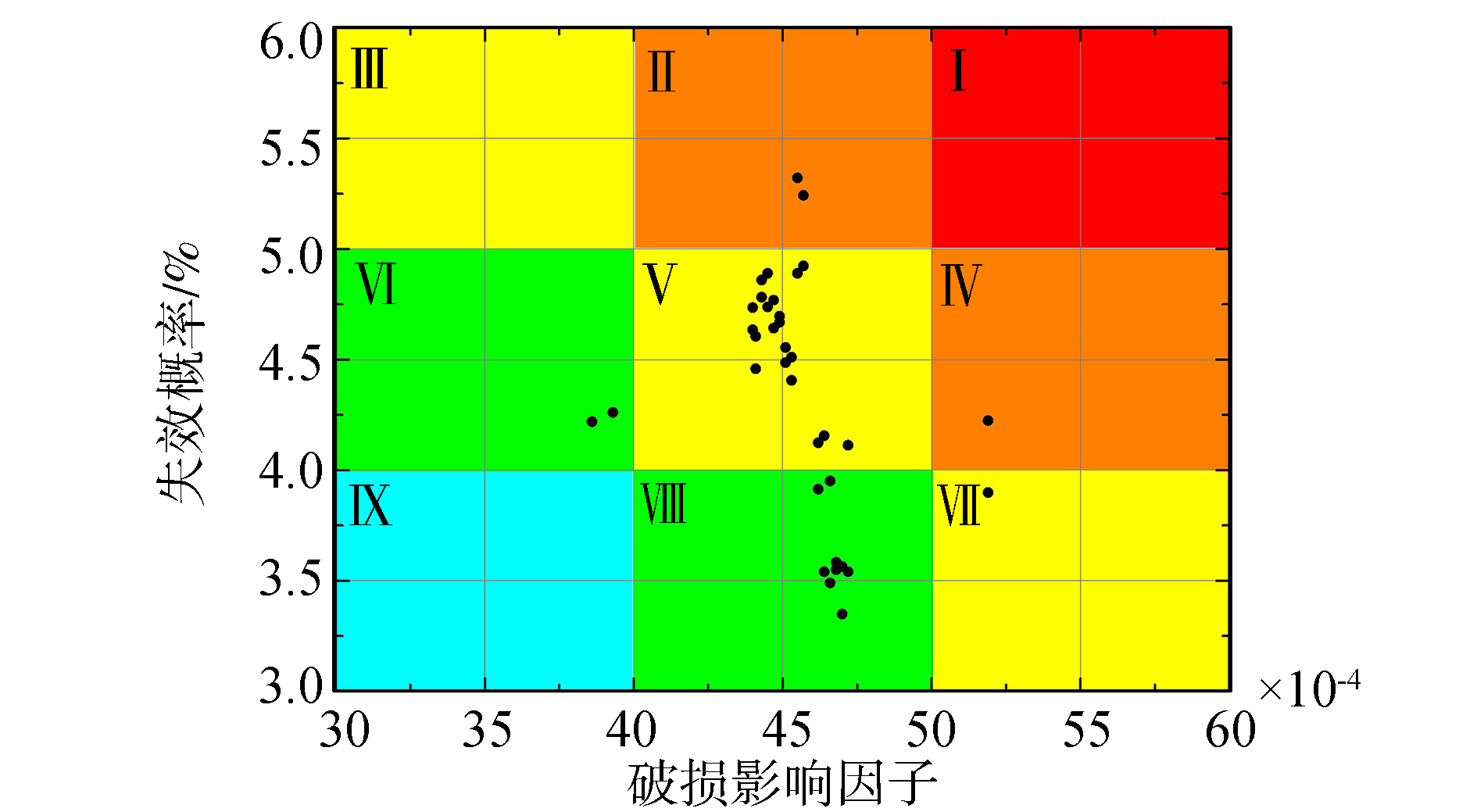
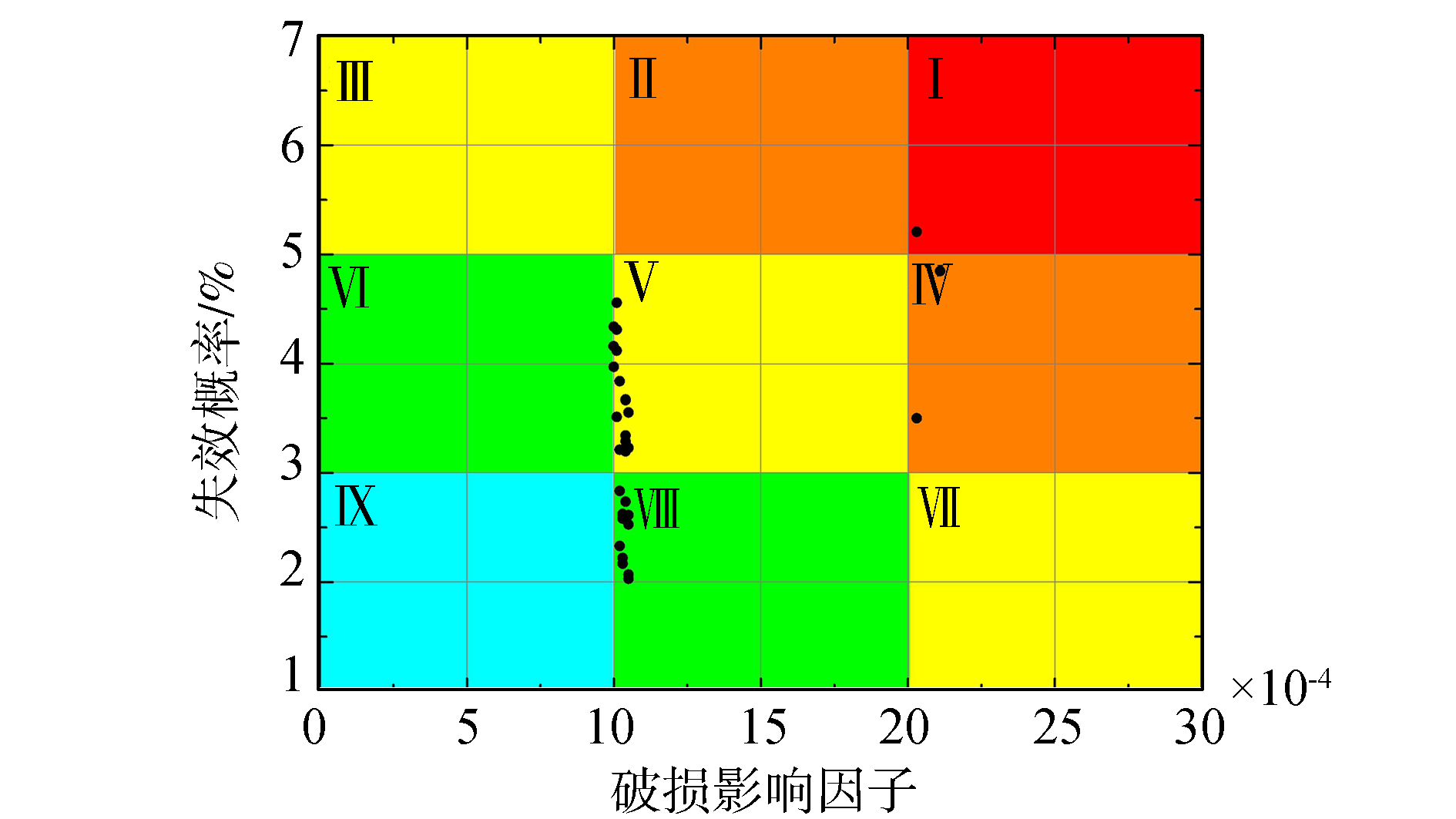
按照1.6节中所述方法,对结构监测的位置进行初步筛选。由于骨材和板材的传感器布置方式不同,故将两类构件分开进行初步筛选。对船舯主甲板的板材和骨材的初步筛选,具体见图 6~7。由风险分布图可知,主甲板的板材大多集中在Ⅴ区和Ⅷ区,失效概率主要分布于5%~3.5%之间,而破损影响因子主要位于[0.004, 0.005]区间内。而骨材也集中在Ⅴ区和Ⅷ区,由于甲板上骨材规格大多相同,使得骨材失效后对船体总纵强度的影响相差不多,破损影响因子保持在0.001左右;而失效概率主要分布于5.0%~2.0%。参照风险分布图,选取处于红色、橙色、黄色区域内的结构单元作为初步筛选后的单元,剔除绿色和蓝色区域里的结构单元。
|
| 图6 主甲板板材风险分布图 Figure 6 Risk distribution of structural plate element |
|
| 图7 主甲板骨材风险分布图 Figure 7 Risk distribution of longitudinal element |
取搜索半径R为1 m,对初步筛选后的结构单元进行进一步筛选。根据式(25),对初步筛选后的结构单元的位置进行比较,最终获得结构监测单元。主甲板上最终监测点的位置如表 3所示。
| 序号 | 风险值 | 传感器布置形式 | 位置 |
| s1 | 0.024 2 | 四向布置 | 右舷距舯纵剖面3.8 m |
| s2 | 0.022 5 | 四向布置 | 左舷距舯纵剖面3.4 m |
| s3 | 0.021 8 | 四向布置 | 左舷距舯纵剖面5.8 m |
| s4 | 0.021 2 | 四向布置 | 右舷距舯纵剖面6.2 m |
| s5 | 0.021 1 | 四向布置 | 右舷距舯纵剖面5.0 m |
| s6 | 0.020 8 | 四向布置 | 左舷距舯纵剖面7.0 m |
| s7 | 0.020 2 | 四向布置 | 左舷距舯纵剖面4.6 m |
| s8 | 0.019 4 | 四向布置 | 右舷距舯纵剖面0.2 m |
| s9 | 0.019 3 | 四向布置 | 右舷距舯纵剖面1.8 m |
| s10 | 0.019 0 | 四向布置 | 左舷距舯纵剖面2.2 m |
| s11 | 0.016 6 | 四向布置 | 左舷距舯纵剖面1.0 m |
| s12 | 0.003 3 | 双向布置 | 右舷距舯纵剖面2.8 m |
表 4列出了使用传统方法(文献[10]) 对甲板的监测点筛选结果。通过对比表 3和表 4可知,两种方法都选出12个监测位置,其中8个监测点位置相同,其余4个监测点位置相近。产生差异的原因在于传统方法在监测点的选择上以结构应力响应为依据,与风险评估方法在同一范围内筛选监测位置时,偏向选择结构应力响应较大的位置,而风险评估方法中加入了破损影响因子和传感器有效监测概率的影响,使监测点的位置偏向于结构监测风险值较高的位置。最终的监测点位置接近纵横舱壁与甲板、纵骨与甲板等结构交界处,而这些区域往往又是船舶建造规范和船体结构疲劳强度指南等相关船舶规范所指明的危险区域,这进一步验证了监测点选择的合理性。
| 序号 | 传感器布置形式 | 位置 |
| m1 | 三向布置 | 右舷距舯纵剖面3.8 m |
| m2 | 单向布置 | 左舷距舯纵剖面3.6 m |
| m3 | 三向布置 | 左舷距舯纵剖面5.8 m |
| m4 | 单向布置 | 舯纵剖面 |
| m5 | 三向布置 | 右舷距舯纵剖面6.2 m |
| m6 | 三向布置 | 左舷距舯纵剖面7.0 m |
| m7 | 三向布置 | 右舷距舯纵剖面5.0 m |
| m8 | 三向布置 | 左舷距舯纵剖面4.6 m |
| m9 | 三向布置 | 左舷距舯纵剖面2.6 m |
| m10 | 三向布置 | 右舷距舯纵剖面1.8 m |
| m11 | 单向布置 | 左舷距舯纵剖面1.6 m |
| m12 | 单向布置 | 右舷距舯纵剖面2.8 m |
风险评估方法使用了46个传感器,多于传统方法。虽然监测系统的成本有所升高,但与高昂的船体结构维修费用相比仍相对较少,因此从经济的角度仍然可行。而通过合理的增加传感器,新的监测方案使监测点位置处的传感器具有自我检验功能,能够实时有效地反馈结构监测点是否处于有效监测的状态,同时提高了监测位置的抗损能力。在保证所有监测点位置都能够有效监测的状态下,船体主甲板的整体有效监测率为99.84%,而使用传统方法进行结构监测点的布置,其整体有效监测率则为86.91%。由此可见,采用基于风险的监测点布置方法使得船体主甲板结构的有效监测概率提高了12.93%,极大地提高了船体结构监测的可靠性。
3 结论本文通过综合考虑船舶在航行环境下的结构失效、结构失效后对于总纵强度的影响以及监测有效性等多方面的因素,以结构监测风险值为衡准,建立了一套基于风险的船体结构监测点布置方法。
1) 通过算例可知,在保证监测点处传感器能够自我检验的同时,采用基于风险的结构监测点布置方法,使得监测位置更加合理。较之传统方法,基于风险的结构监测点布置方案有效地提高了船体结构整体的有效监测率,增强了船体监测的抗损能力,船体结构监测更加可靠。
2) 基于风险的结构监测点方法筛选出的位置分布均匀,有效地避免了由于结构应力集中现象所引起的监测点布置过于集中。
3) 通过在结构监测风险值中考虑结构有效监测的概率,将传感器的失效概率与结构监测点的布置联系起来,较之传统方法将监测点的选取和传感器的布置分开处理,更加符合实际,有利于建立完整的结构监测体系。
| [1] | WANG G, PRAN K, SAGVOLDEN G, et al. Ship hull structure monitoring using fibre optic sensors[J]. Smart materials and structures, 2001, 10(3): 472–478. DOI:10.1088/0964-1726/10/3/308 |
| [2] |
张岚.基于FBG技术的散货船结构监测传感器布置研究[D].湖北:武汉理工大学, 2008:28-48.
ZHANG Lan. Research on the arrangement of bulk carrier structure monitoring sensor based on FBG technology[D]. Wuhan:Wuhan University of Technology, 2008:28-48. http://cn.bing.com/academic/profile?id=72e17f14dad7dd6a623822f5d719ccb9&encoded=0&v=paper_preview&mkt=zh-cn |
| [3] |
金永兴, 胡雄, 施朝健. 集装箱船舶结构状态监测与评估系统[J].
上海海事大学学报, 2008, 29(3): 1–4.
JIN Yongxing, HU Xiong, SHI Chaojian. Supervision and evaluation system of container vessel hull structure[J]. Journal of Shanghai maritime university, 2008, 29(3): 1–4. |
| [4] |
胡雄, 孙德建, 金永兴, 等. 集装箱船舶结构状态的在线监测技术研究[J].
中国工程机械学报, 2009, 7(4): 459–462.
HU Xiong, SUN Dejian, JIN Yongxing, et al. Online monitoring technologies for container ship structures[J]. Chinese journal of construction machinery, 2009, 7(4): 459–462. |
| [5] |
王为.光纤光栅在船舶结构健康监测中的关键技术研究[D].天津:天津大学, 2010:32-52.
WANG Wei. Study of key technology on ship hull structural health monitoring with fiber Bragg grating[D]. Tianjin:Tianjin University, 2010:32-52. |
| [6] |
梁文彬.基于光纤光栅的船舶结构健康监测技术研究[D].天津:天津大学, 2011:37-46.
LIANG Wenbin. Study on ship hull structural health monitoring technology based on fiber Bragg grating[D]. Tianjin:Tianjin University, 2011:37-46. |
| [7] |
申素梅.自升式海洋平台桩腿桩靴结构监测方案研究[D].武汉:武汉理工大学, 2012:21-46.
SHEN Sumei. Study of jack-up offshore platform structure of the pile legs and boots monitoring program[D]. Wuhan:Wuhan University of Technology, 2012:21-46. |
| [8] |
赵彦文.基于光纤光栅传感器的油船结构状态监测研究[D].武汉:武汉理工大学, 2013:37-65.
ZHAO Yanwen. Research on oil carrier structure state monitoring base on fiber Bragg grating sensor[D]. Wuhan:Wuhan University of Technology, 2013:37-65. |
| [9] |
李志锋.基于FBG传感器的船舶强度状态监测[D].武汉:武汉理工大学, 2013:17-57.
Li Zhifeng. The ship strength monitoring based on FBG sensor technology[D]. Wuhan:Wuhan University of Technology, 2013:17-57. |
| [10] |
贾连徽, 任慧龙, 孙树政, 等. 船体结构应力监测点的选取方法研究[J].
船舶力学, 2013, 17(4): 389–397.
JIA Lianhui, REN Huilong, SUN Shuzheng, et al. Research on ship structural stress monitoring points selection method[J]. Journal of ship mechanics, 2013, 17(4): 389–397. |
| [11] | 杨代盛, 桑国光, 李维扬, 等. 船舶强度的概率方法[M]. 哈尔滨: 哈尔滨工程大学出版社, 2007. |
| [12] |
戴仰山, 沈进威, 宋竞正.
船舶波浪载荷[M]. 北京: 国防工业出版社, 2007.
DAI Yangshan, SHEN Jinwei, SONG Jingzheng. Ship wave leads[M]. Beijing: National Defense Industry Press, 2007. |
| [13] |
祁恩荣.完整和破损船体极限强度可靠性研究[D].无锡:中国船舶科学研究中心, 2003:70-77.
QI Enrong. Ultimate strength reliability analysis of intact and damaged ship hulls[D]. Wuxi:China Ship Scientific Research Center, 2003:70-77. |
| [14] | 欧贵宝, 朱加铭. 材料力学[M]. 哈尔滨: 哈尔滨工程大学出版社, 2002. |
| [15] | 潘信吉, 何蕴增. 材料力学实验原理及方法[M]. 哈尔滨: 哈尔滨工程大学出版社, 1995. |
| [16] |
唐文勇, 李典庆, 张圣坤. 基于风险的船体结构检测及维护研究综述[J].
船舶力学, 2005, 9(5): 143–154.
TANG Wenyong, LI Dianqing, ZHANG Shengqun. On the risk based inspection and maintenance planning for ship structures[J]. Journal of ship mechanics, 2005, 9(5): 143–154. |



