2. School of Computer Science and Engineering, Chongqing University of Technology, Chongqing 400054, China
湍流是一种气流运动,肉眼无法看见,而且经常不期而至。引发湍流的原因可能是气压变化、急流、冷锋、暖锋和雷暴,甚至在晴朗的天空中也可能出现湍流。湍流并非总能被预测出来,雷达也发现不了它。对气象雷达而言,湍流是指微粒速度偏差较大的气象目标,该定义与微粒的绝对速度无关,而与微粒速度的统计标准偏差有关。速度的偏差可理解为速度的范围或频谱,频谱越宽,湍流越大[1-3]。在湍流区域中,气流速度和方向的变化都相当急剧,因而不仅会使飞机颠簸,而且会使机体承受巨大的作用力,对飞行安全十分不利。所以,飞机总是十分小心地避免进入湍流区域。
Von-Karman和Dryden两种经典湍流模型一直受到人们的关注[4-6],但是这两种模型没有考虑非对称风场对湍流的影响。Kolmogorov等[7-10]认识到湍流的无特征尺度性,认为在Reynold数很大时,湍流是由相差很大的、各种不同尺度的涡旋组成。最大的涡旋直接由平均流畅的不稳定性及边界条件产生。大漩涡通过惯性又将能量输送或破裂成较小的漩涡。湍流研究的难点在于它含有大小不同尺度的湍流涡旋。
基于子波变换的尺度自相似性,Bezerra等[11-19]用子波变换的方法来研究湍流,其主要思路是首先运用傅里叶变换将空间域转换成域,寻找信号最强时的值,从而判断信号的主要成分或周期,同时借助小波变换观测信号在何种尺度上最强;此做法并没有发挥小波变换的优越性。
针对上述对湍流分析存在的问题,本文通过建立特定坐标系并提出湍流信号处理算法来分析湍流的危害程度。
1 曲线坐标系为了方便起见,将笛卡尔坐标系x-y-z写成y1, y2, y3,将圆柱坐标系r-φ-z,写成x1, x2, x3,这两个坐标系有如下的相互转换关系:
| $ \left\{ \begin{array}{l} {x^1} = \sqrt {{{\left( {{y^1}} \right)}^2} + {{\left( {{y^2}} \right)}^2}} = {x^1}\left( {{y^1},{y^2}} \right)\\ {x^2} = \arctan \frac{{{y^2}}}{{{y^1}}}{x^2}\left( {{y^1},{y^2}} \right)\\ {x^3} = {y^3} = {x^3}\left( {{y^3}} \right) \end{array} \right. $ | (1) |
| $ \left\{ \begin{array}{l} {y^1} = {x^1}\cos {x^2} = {y^1}\left( {{x^1},{x^2}} \right)\\ {y^2} = {x^1}\sin {x^2} = {y^2}\left( {{x^1},{x^2}} \right)\\ {y^3} = {x^3} = {y^3}\left( {{x^3}} \right) \end{array} \right. $ | (2) |
可以看出上面两组函数关系都是单值连续函数。任意曲线坐标系下的x1、x2、x3是笛卡尔坐标系y1、y2、y3的单值连续函数;除了原点 (0, 0, 0) 外,坐标转换的两个雅可比行列式J和J′均不为零,即在空间某一区域D内有
| $ J = \frac{{\partial \left( {{x^1},{x^2},{x^3}} \right)}}{{\partial \left( {{y^1},{y^2},{y^3}} \right)}} \ne 0,J' = \frac{{\partial \left( {{y^1},{y^2},{y^3}} \right)}}{{\partial \left( {{x^1},{x^2},{x^3}} \right)}} \ne 0 $ | (3) |
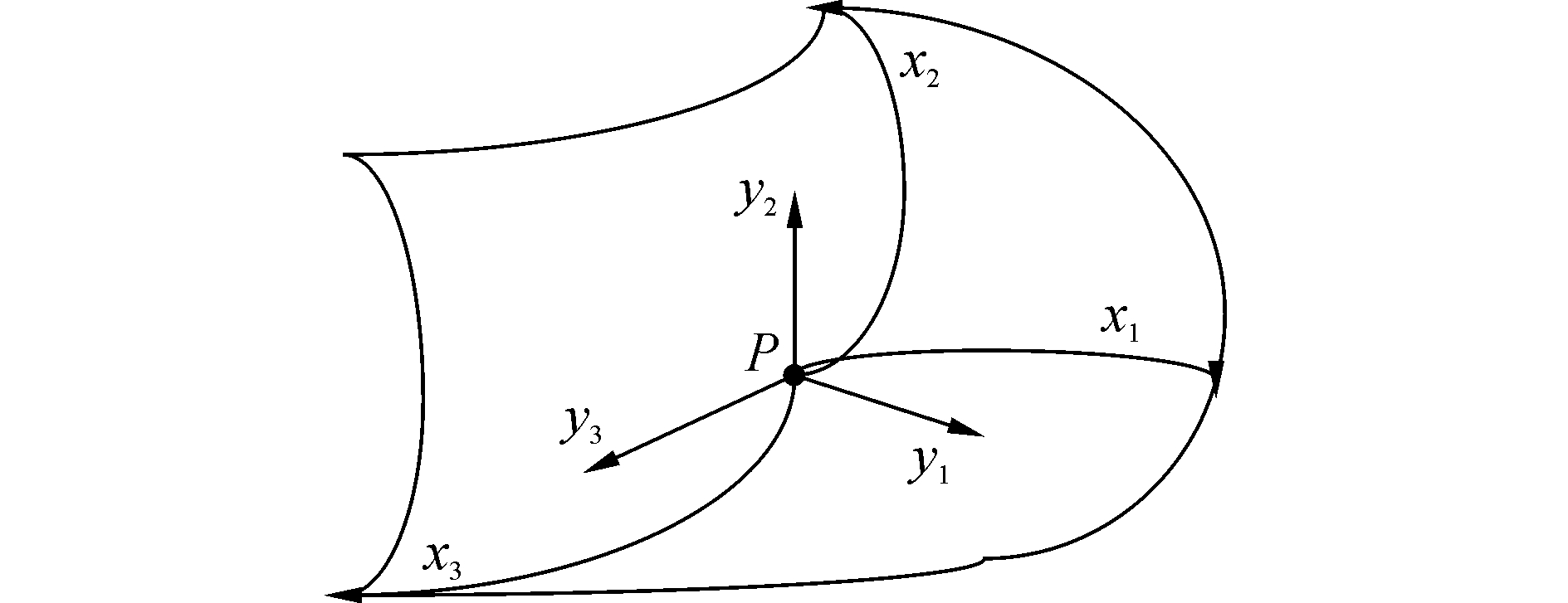
在此区域D中,点P和数组 (x1, x2, x3) 成为一一对应的,可以把x1、x2、x3当成P点的坐标 (如图 1)。这样x1、x2、x3就可构成曲线坐标系。
|
| 图1 区域D内的曲线坐标系 Figure 1 The curve coordinate system of area D |
现令ρ代表流体微团的平均密度,t为时间,V是绝对速度。由质量守恒定律和散度的定义可知,当速度场连续可微时有
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho \mathit{\boldsymbol{V}}} \right) = 0 $ | (4) |
流体微团运动方程的一般形式为
| $ \begin{array}{*{20}{c}} {\rho \frac{{{\rm{d}}\mathit{\boldsymbol{V}}}}{{{\rm{d}}t}} = \rho \mathit{\boldsymbol{F + }}\nabla \cdot \prod = }\\ {\rho \mathit{\boldsymbol{F}} - \nabla \rho + {\mathit{\boldsymbol{f}}_\tau }\left( {{\mathit{\boldsymbol{f}}_\tau } = \nabla \cdot \prod '} \right)} \end{array} $ | (5) |
| $ \prod = 2\mu \varepsilon - \left[ {p + \frac{2}{3}\mu \left( {\nabla \cdot \mathit{\boldsymbol{V}}} \right)} \right] \cdot \mathit{\boldsymbol{I}} $ | (6) |
| $ \prod ' = 2\mu \varepsilon - \frac{2}{3}\mu \left( {\nabla \cdot \mathit{\boldsymbol{V}}} \right) \cdot \mathit{\boldsymbol{I}} $ | (7) |
式中:F是单位质量流体所受的质量力与惯性力之和,Π是应力张量,fτ为粘性力,μ是一个与流体的粘性有关的比例常数,I是单位向量。
在曲线坐标系ξ、η、ζ下,根据流体力学结合拉梅系数可以推导出任一二维的曲线坐标系有
| $ \left\{ \begin{array}{l} \xi = \xi \left( {x,y} \right)\\ \eta = \eta \left( {x,y} \right) \end{array} \right. $ | (8) |
在满足式 (10)~(14) 及其他边界条件能够解出一组:
| $ \left\{ \begin{array}{l} x = x\left( {\xi ,\eta } \right)\\ y = y\left( {\xi ,\eta } \right) \end{array} \right. $ | (9) |
ξ、η=1, 2, 3, …求出所有网格点的坐标 (x,y),将这些网格点用光滑曲线连接起来,就是所需构筑的任意曲线坐标网格线。
3 湍流信号处理湍流是根据雨粒的速度偏差来定义的,且是随时间在不断变化的。湍流中雨粒的相对速度偏差越大,信号的多普勒宽度就越宽[18-20]。因此在机载多普勒气象雷达中,可以通过比较所接收到的信号的多普勒频谱的宽度来检测湍流目标。
分别对各个距离门湍流风场回波信号进行处理,提取回波风速、谱宽等参数。
湍流风场内,某一距离门的回波信号采样序列为A(n)=X(n)+jY(n),X(n)、Y(n) 分别为第n个脉冲采样信号的同向和正交分量,N为采样序列长度,Ts为回波信号采样时间间隔,可以得到回波信号的功率谱S(fi):
| $ S\left( {{f_i}} \right) = {\left| {\sum\limits_{n = 0}^{N - 1} {A\left( n \right)\exp \left( { - {\rm{j2}}\pi \frac{{ni}}{N}} \right)} } \right|^2} $ | (10) |
| $ {f_i} = \frac{i}{{N{T_s}}},i = 0,1 \cdots ,N - 1 $ | (11) |
平均频率是归一化功率谱的一阶矩,频谱宽度是归一化功率谱的二阶矩的平方根,湍流风场回波的平均多普勒速度和谱宽就由以下公式得到。
回波信号平均多普勒速度:
| $ \mathop f\limits^ \wedge = \frac{{\sum\limits_{i = 0}^{N - 1} {{f_i}S\left( {{f_i}} \right)} }}{{\sum\limits_{i = 0}^{N - 1} {S\left( {{f_i}} \right)} }} $ | (12) |
回波信号谱宽:
| $ \mathop {\sigma _f^2}\limits^ \wedge = \frac{{\sum\limits_{i = 0}^{N - 1} {{{\left( {{f_i} - \mathop f\limits^ \wedge } \right)}^2}S\left( {{f_i}} \right)} }}{{\sum\limits_{i = 0}^{N - 1} {S\left( {{f_i}} \right)} }} $ | (13) |
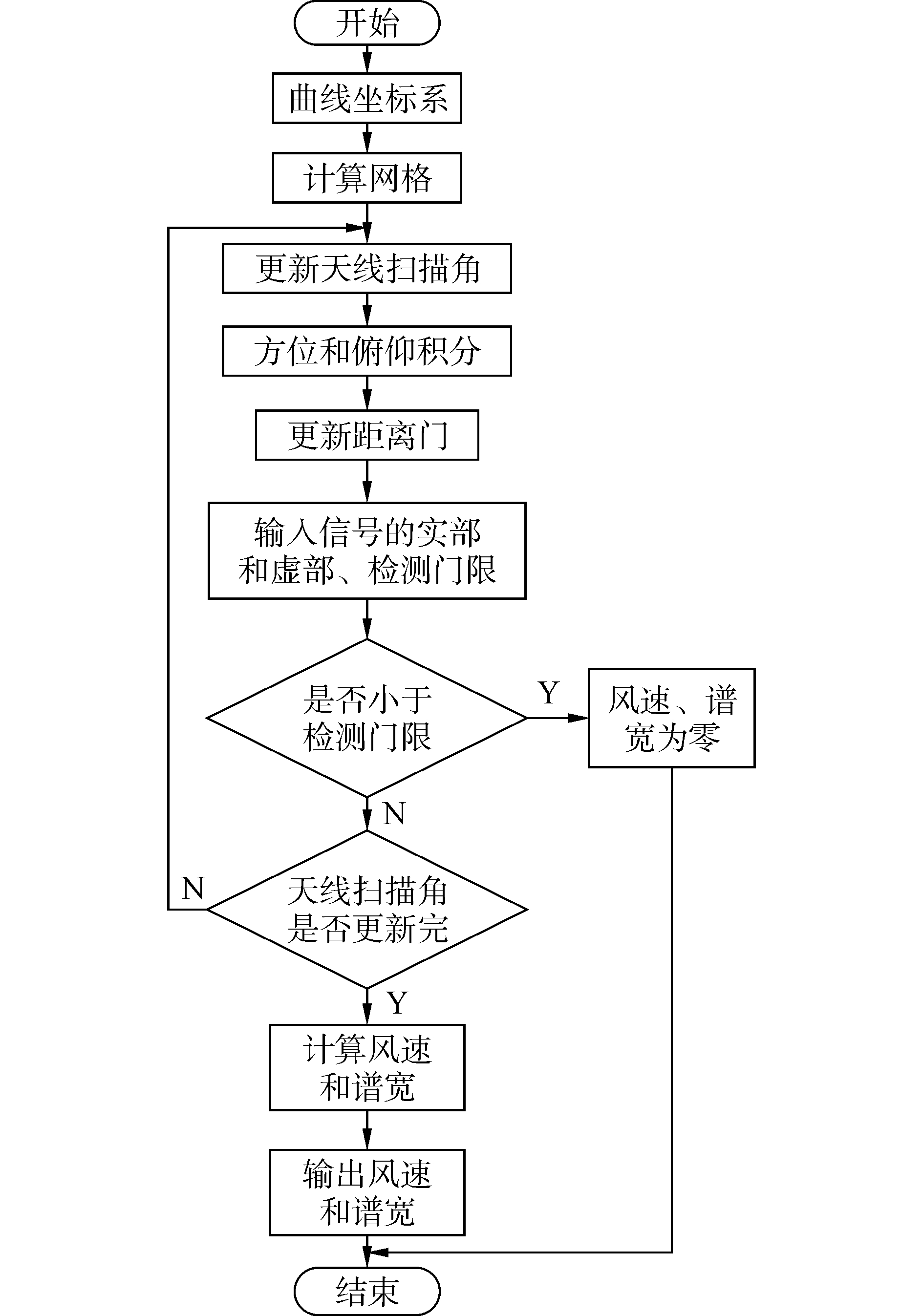
将式 (10) 分别代入式 (12)、(13),即可得到回波信号的平均多普勒速度与谱宽。其湍流回波信号处理流程图如图 2所示。
|
| 图2 回波信号处理流程图 Figure 2 The flow chart of echo signal processing |
为了定量分析湍流对飞行器等所造成的危害程度,这里引入危险因子概念。根据质量连续性定理,在给定高度上的垂直风速应当与水平质量散度成正比出危险因子F可定义为
| $ F \approx \frac{{{v_g}}}{g}\frac{{\partial {v_x}}}{{\partial x}} - kh\frac{{\frac{{\partial {v_x}}}{{\partial x}} + \frac{{{v_x}}}{R}}}{{{v_g}}} $ | (14) |
式中:vg为飞机地速,g=9.8 m/s2;Wx为水平风速;∂vx/∂x为水平风速分量变化率;h为飞机高度;k是比例系数;R为偏离微气流中心的距离。
4 仿真分析 4.1 仿真参数设置脉冲重复频率设置为3 500 Hz,脉冲宽度为1.5 μs,工作频率为9.0 GHz,最大不模糊风速为30.0 m/s,微暴中心距跑道接地点纵向距离为6 km,微暴中心距跑道接地点横向距离为171.2 m,微暴的范围为3 658 m×3 658 m×3 658 m。
对3 658 m×3 658 m×3 658 m的机场空间区域进行了120×120×50网格划分,每个网格大小为305 m×305 m×127 m。特征半径R为2 000 ft,取湍流的延伸直径1~3 km,水平风场高度为5 kft。x为垂直于飞机航向的,右为正;y为飞机航向为正,z为飞机跑道以上的地面高度,向上为正;风场的中心位置在 (x,y)=(1 829 m,1 829 m)。
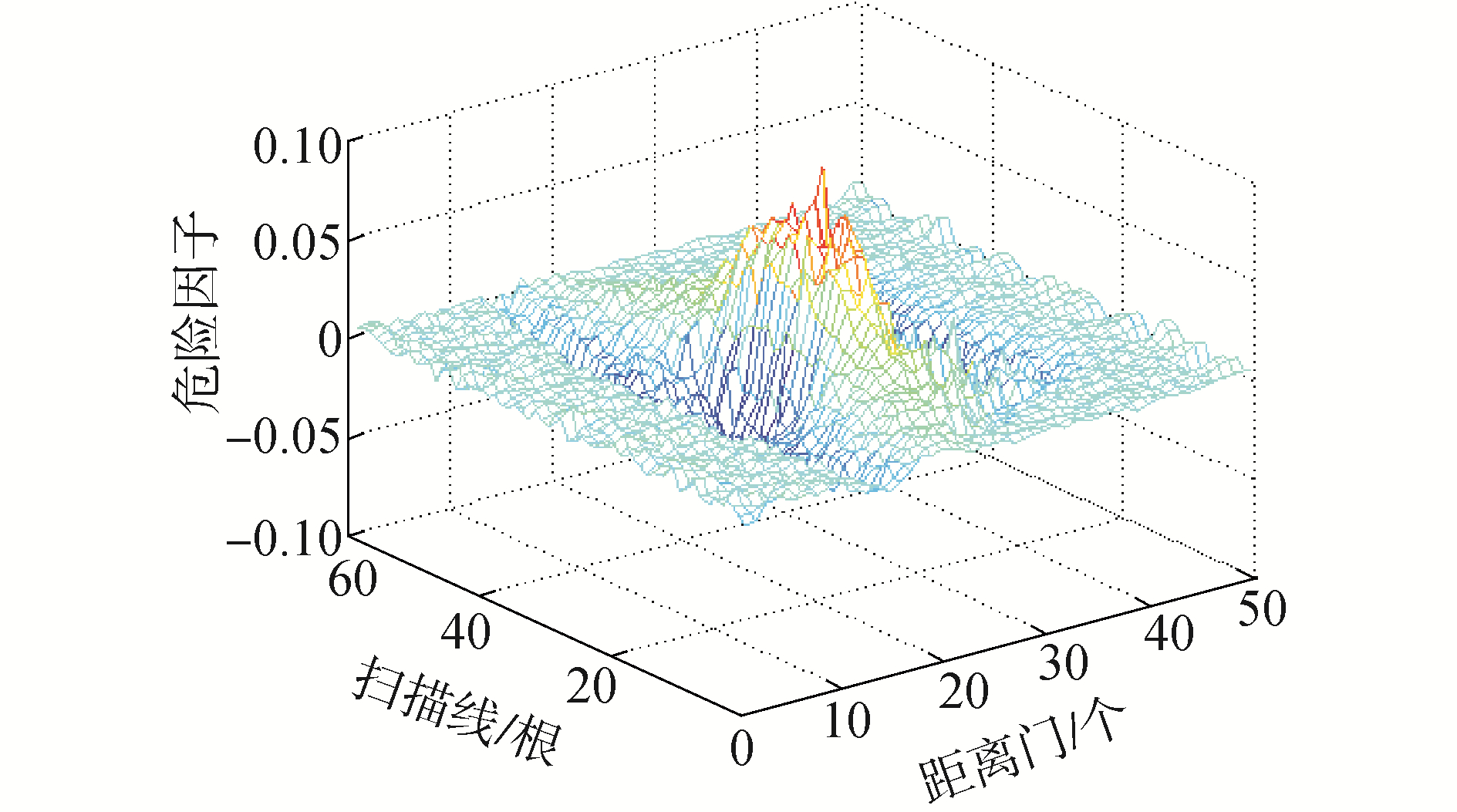
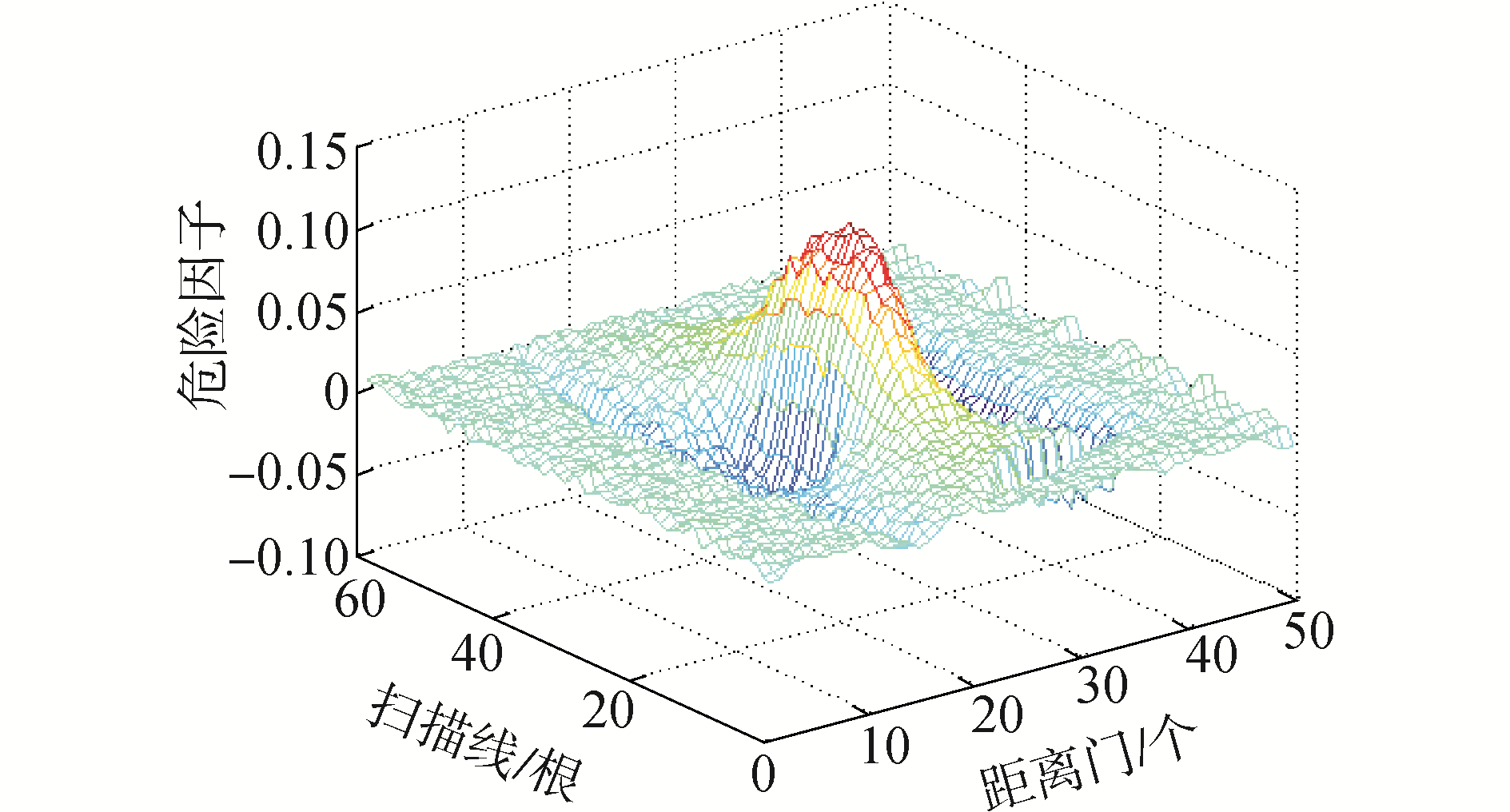
4.2 结果分析图 3是一个扫描面上,由湍流信号造成的回波信号的危险程度 (用危险因子衡量)。图 4是一个扫描面上的风速。通过比较图 3和图 4,可以看出,本文方法能较好地估计出湍流风场里的风速分布。
|
| 图3 设定回波信号的三维谱 (放大150倍) Figure 3 The three-dimensional spectrum of set echo signal |
|
| 图4 回波信号三维速度谱 (放大150倍) Figure 4 The three-dimensional spectrum of echo signal |
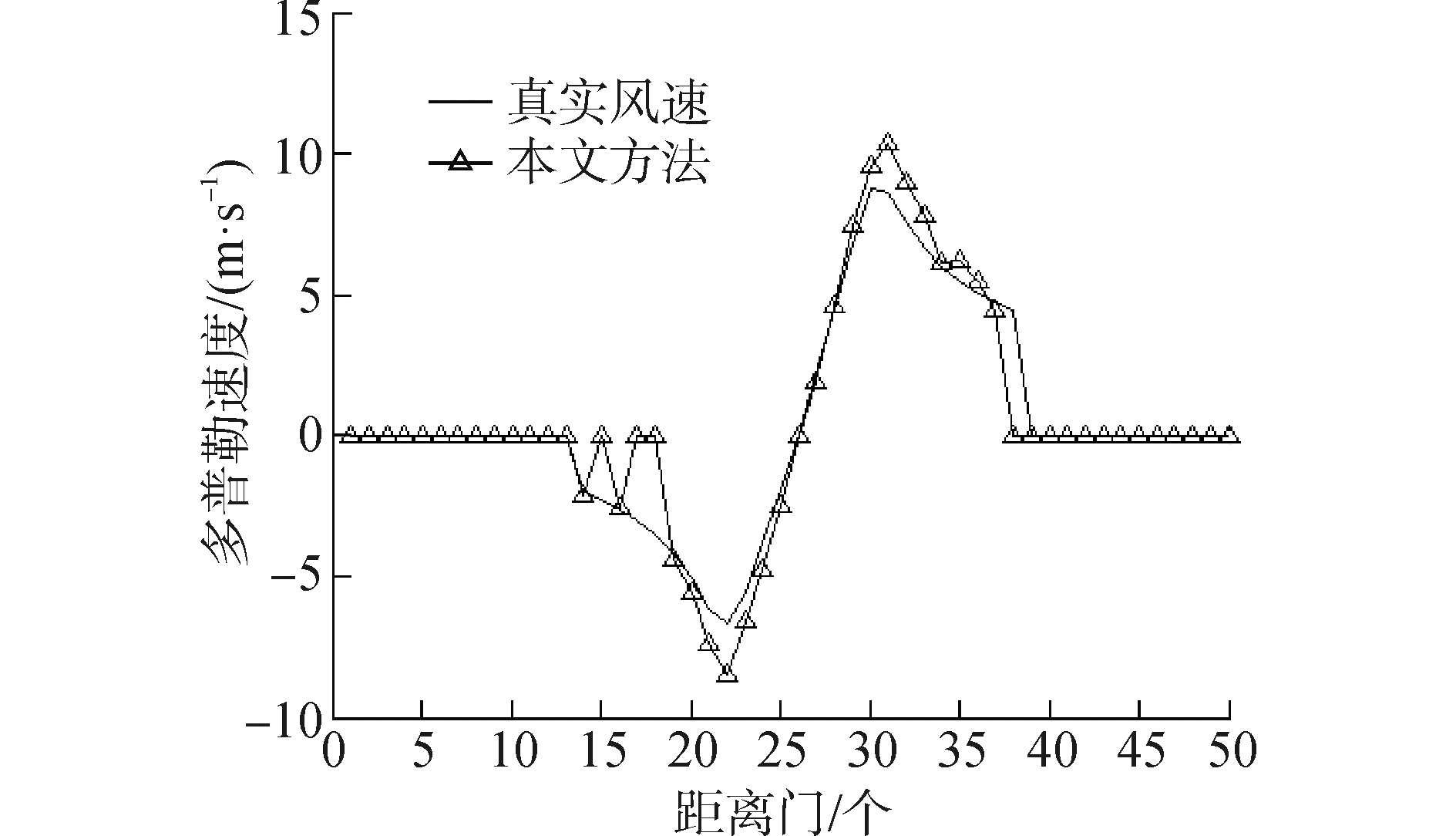
机载气象雷达在进行湍流信号处理时,对风场中各个距离门内的回波信号的谱宽进行估计,从而判断目标是否为湍流。图 5是第22根扫描线上,50个距离门上的估算风速和实际风速对比。通过图 5可以看出本文提出的湍流信号处理算法能够很好地对风速进行估计。
|
| 图5 50个距离门上的风速估值 (放大150倍) Figure 5 The estimate value of wind speed in 50 range bins |
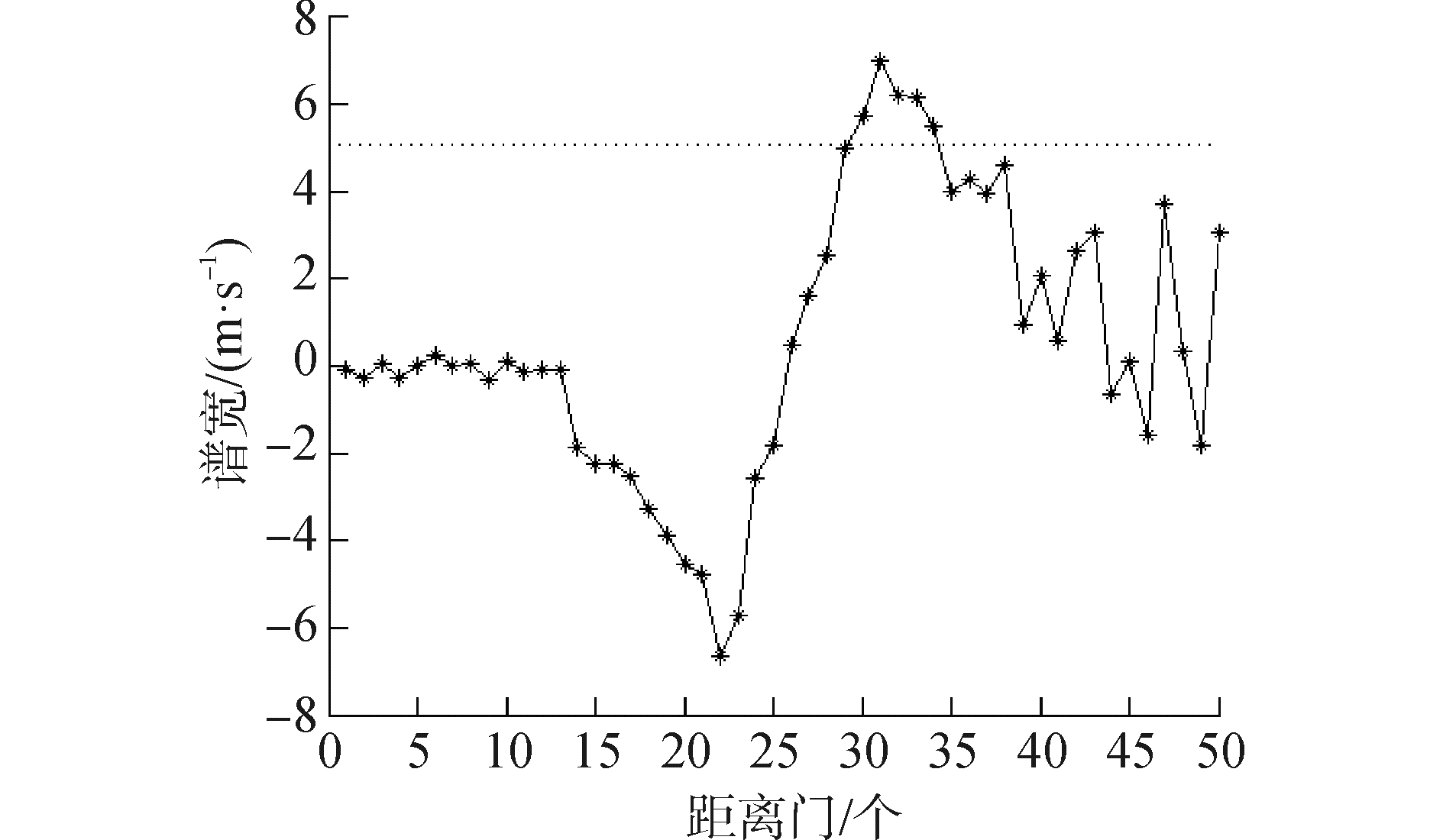
图 6是该扫描线上,50个距离门上的回波谱宽。为湍流检测的谱宽设置判决门限,图 6中设定了5 m/s为湍流判定门限,可以看出,在该扫描线上,第29、30、31、32、33等距离门单元上回波谱宽超出门限值,被断定为湍流目标。
|
| 图6 50个距离门上的回波信号谱宽估值 (放大150倍) Figure 6 The echo signal estimate value of spectrum width in 50 range bins |
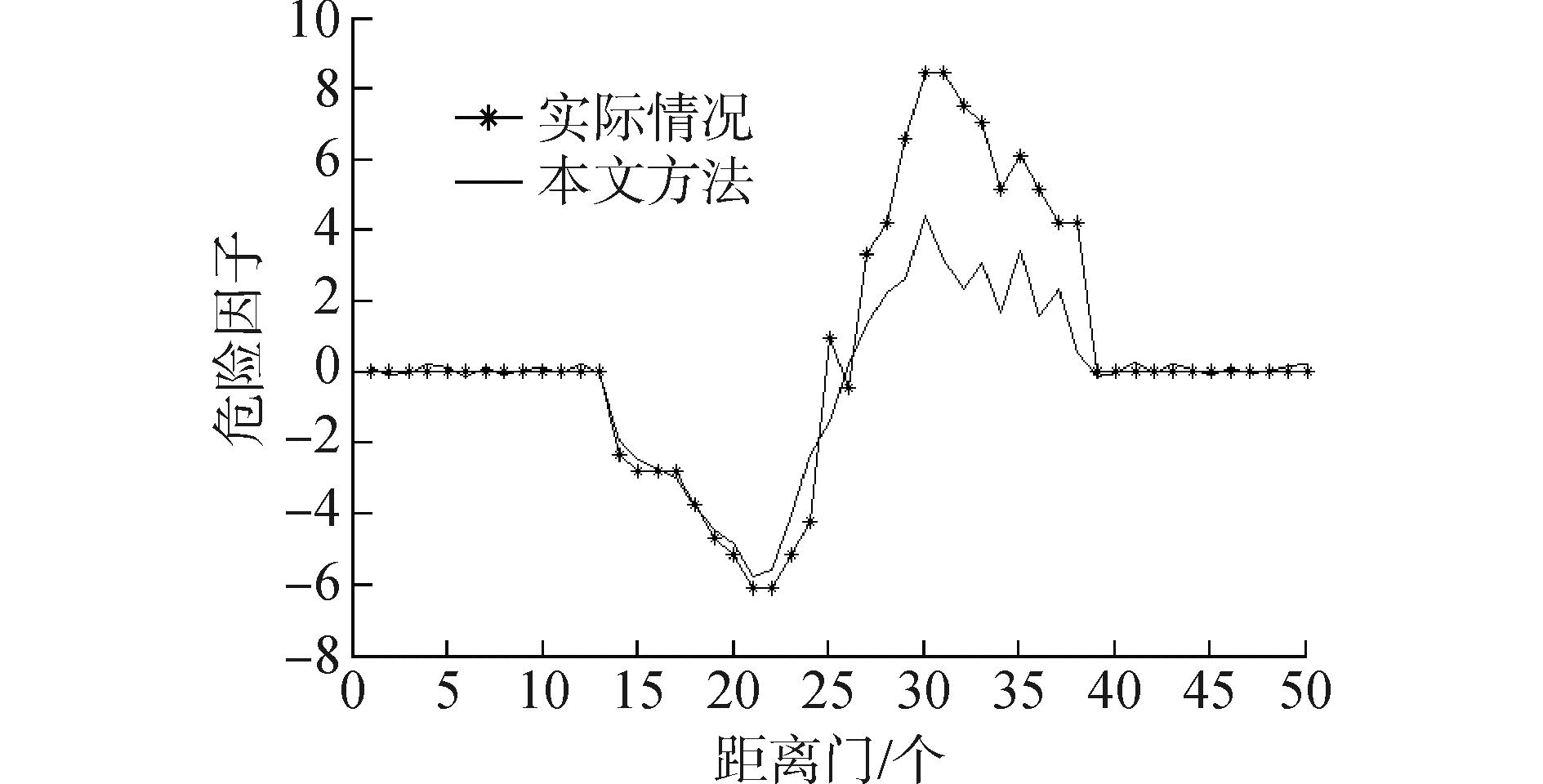
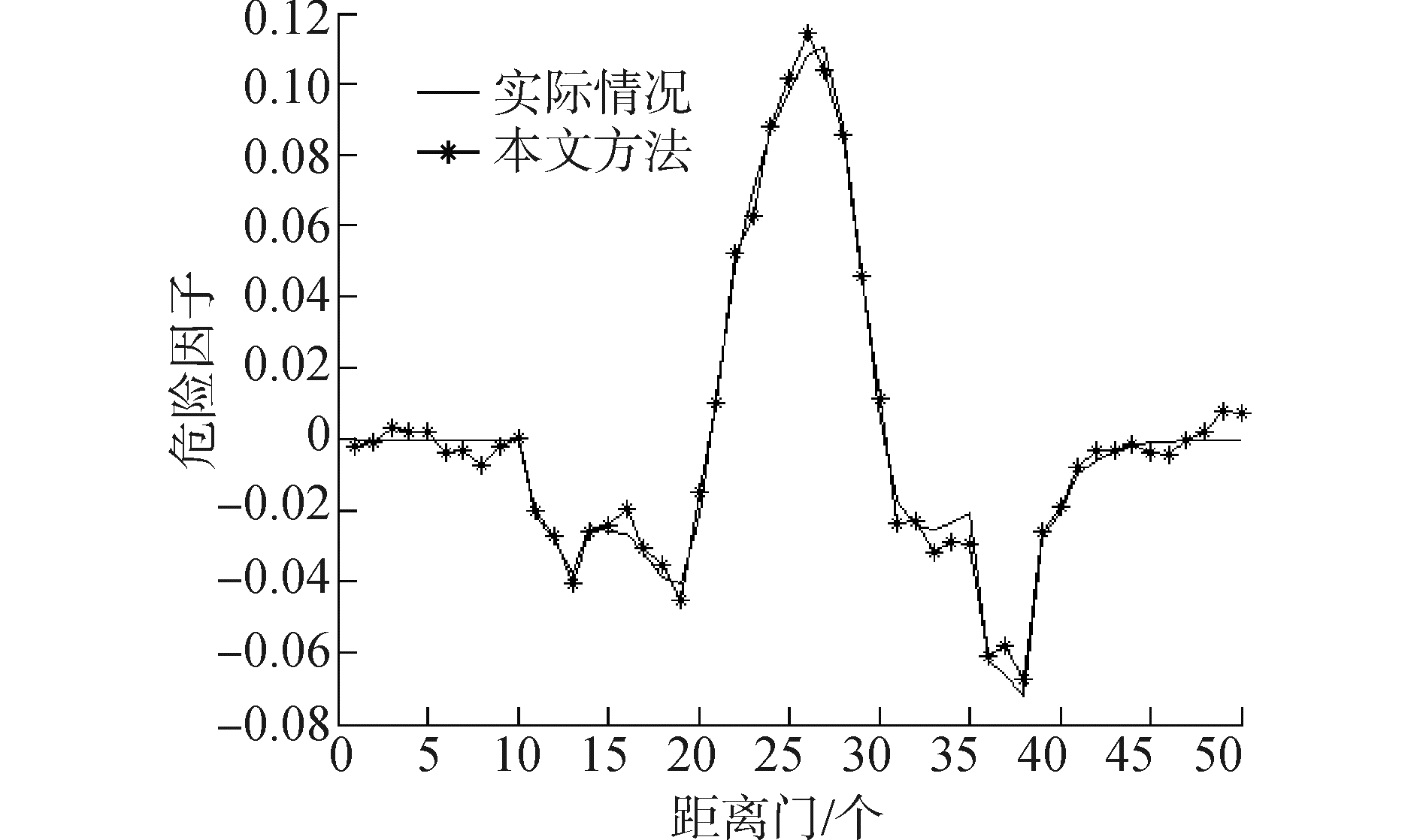
为了考虑地杂波的影响,本文分析了有、无地杂波两种情形下的危险因子变化曲线图。
通过图 7、8对比分析可以发现,无地杂波的情形要优于有杂波的情形。图 7中,在第25个距离门处,本文方法与实际情形下的危险因子差距较大;图 8中,在第25个距离门处,本文方法与实际情形下的危险因子的变化趋势很吻合。
|
| 图7 有地杂波情形下湍流危险因子分析 (放大150倍) Figure 7 The risk factor analysis with ground clutter |
|
| 图8 无地杂波情形下湍流危险因子分析 (放大150倍) Figure 8 The risk factor analysis with no ground clutter |
1) 建立了一种任意曲线坐标系,并结合湍流连续方程和运动方程建立了湍流计算网络数学模型,该网格计算模型能够很好的对湍流场进行剖分,以便于对湍流进行精确的仿真分析;
2) 建立了湍流危险程度的危险因子,结合多普勒效应并提出了一种湍流信号算法,该算法能够较好的反映湍流特性并能够对湍流进行检测和预测。
3) 提出的湍流信号处理模型和危险因子的数学模型可以作为微下击暴流风切变的参考模型;考虑到湍流的非线性,还可以进一步运用空时自适应处理和去卷积方法[21-25]来研究湍流的非线性等相关特性。
| [1] | GIL E, LAGUNA P, MARTÍNEZ J P, et al. Heart rate turbulence analysis based on photoplethysmography[J]. IEEE transactions on biomedical engineering, 2013, 60(11): 3149–3155. DOI:10.1109/TBME.2013.2270083 |
| [2] | GIBSON K B, NGUYEN T Q. An analysis and method for contrast enhancement turbulence mitigation[J]. IEEE transactions on image processing, 2014, 23(7): 3179–3190. DOI:10.1109/TIP.2014.2328180 |
| [3] | PURYEAR A L, SHAPIRO J H, PARENTI R R. Reciprocity-enhanced optical communication through atmospheric turbulence-Part Ⅱ:communication architectures and performance[J]. Journal of optical communications and networking, 2013, 5(8): 888–900. DOI:10.1364/JOCN.5.000888 |
| [4] | OREIFEJ O, LI Xin, SHAH M. Simultaneous video stabilization and moving object detection in turbulence[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(2): 450–462. DOI:10.1109/TPAMI.2012.97 |
| [5] |
刘式达, 付遵涛, 刘式适. 间歇湍流的分数阶动力学[J].
物理学报, 2014, 63(7): 074701.
LIU Shida, FU Zuntao, LIU Shishi. Fractional derivative dynamics of intermittent turbulence[J]. Acta physica sinica, 2014, 63(7): 074701. |
| [6] | TANG Xuan, WANG Zhaocheng, XU Zhengyuan, et al. Multihop free-space optical communications over turbulence channels with pointing errors using heterodyne detection[J]. Journal of lightwave technology, 2014, 32(15): 2597–2604. DOI:10.1109/JLT.2014.2330594 |
| [7] | BAKLAKOVA B A, BATRAKOVA A M, BOLOTINA V P, et al. Status of the free electron laser for the Siberian centre for photochemical research[J]. Nuclear instruments and methods in physics research section a:accelerators, spectrometers, detectors and associated equipment, 2001, 470(1/2): 60–65. |
| [8] | KOLMOGOROV V. Generalized roof duality and bisubmodular functions[J]. Discrete applied mathematics, 2012, 160(4/5): 416–426. |
| [9] | ZUO Yong, WU Jian, XIAO Houfei, et al. Non-line-of-sight ultraviolet communication performance in atmospheric turbulence[J]. China communications, 2013, 10(11): 52–57. DOI:10.1109/CC.2013.6674210 |
| [10] | WANG Ke, NIRMALATHAS A, LIM C, et al. Performance of high-speed reconfigurable free-space card-to-card optical interconnects under air turbulence[J]. Journal of lightwave technology, 2013, 31(11): 1687–1693. DOI:10.1109/JLT.2013.2256459 |
| [11] | COSTA F B. Fault-induced transient detection based on real-time analysis of the wavelet coefficient energy[J]. IEEE transactions on power delivery, 2014, 29(1): 140–153. DOI:10.1109/TPWRD.2013.2278272 |
| [12] | ASHRAFIAN A, VAHIDI B, MIRSALIM M. Time-time-transform application to fault diagnosis of power transformers[J]. IET generation, transmission & distribution, 2014, 8(6): 1156–1167. |
| [13] | SOGUERO-RUIZ C, LECHUGA-SUÁREZ L, MORA-JIMÉNEZ I, et al. Ontology for heart rate turbulence domain from the conceptual model of SNOMED-CT[J]. IEEE transactions on biomedical engineering, 2013, 60(7): 1825–1833. DOI:10.1109/TBME.2013.2243147 |
| [14] |
李成强, 张合勇, 王挺峰, 等. 高斯-谢尔模光束在大气湍流中传输的相干特性研究[J].
物理学报, 2013, 62(22): 224203.
LI Chengqiang, ZHANG Heyong, WANG Tingfeng, et al. Investigation on coherence characteristics of Gauss-Schell model beam propagating in atmospheric turbulence[J]. Acta physica sinica, 2013, 62(22): 224203. |
| [15] | TANG Xuan, XU Zhengyuan, GHASSEMLOOY Z. Coherent polarization modulated transmission through MIMO atmospheric optical turbulence channel[J]. Journal of lightwave technology, 2013, 31(20): 3221–3228. DOI:10.1109/JLT.2013.2281216 |
| [16] | VU B T, DANG N T, THANG T C, et al. Bit error rate analysis of rectangular QAM/FSO systems using an APD receiver over atmospheric turbulence channels[J]. Journal of optical communications and networking, 2013, 5(5): 437–446. DOI:10.1364/JOCN.5.000437 |
| [17] | KAUR P, JAIN V K, KAR S. Performance analysis of FSO array receivers in presence of atmospheric turbulence[J]. IEEE photonics technology letters, 2014, 26(12): 1165–1168. DOI:10.1109/LPT.2014.2316534 |
| [18] |
芮国胜, 张海波, 田文飚, 等. MMSE准则下近似最优MIMO分组并行检测算法[J].
电子学报, 2013, 41(10): 1881–1887.
RUI Guosheng, ZHANG Haibo, TIAN Wenbiao, et al. A near-optimal parallel detection algorithm based on channel partition and MMSE criterion[J]. Acta electronica sinica, 2013, 41(10): 1881–1887. |
| [19] | BENKHELIFA F, REZKI Z, ALOUINI M S. Low SNR capacity of FSO links over Gamma-Gamma atmospheric turbulence channels[J]. IEEE communications letters, 2013, 17(6): 1264–1267. DOI:10.1109/LCOMM.2013.043013.130119 |
| [20] | LIU Xiaopei, PANG WAIman, QIN Jing, et al. Turbulence simulation by adaptive multi-relaxation lattice boltzmann modeling[J]. IEEE transactions on visualization and computer graphics, 2014, 20(2): 289–302. DOI:10.1109/TVCG.2012.303 |
| [21] | ALADELOBA A O, WOOLFSON M S, PHILLIPS A J. WDM FSO network with turbulence-accentuated interchannel crosstalk[J]. Journal of optical communications and networking, 2013, 5(6): 641–651. DOI:10.1364/JOCN.5.000641 |
| [22] | ZHU Xiang, MILANFAR P. Removing atmospheric turbulence via space-invariant deconvolution[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(1): 157–170. DOI:10.1109/TPAMI.2012.82 |
| [23] | GREENE A D, HENDRICKS P J. Turbulent wake of a bridge pier in a tidal current[J]. IEEE journal of oceanic engineering, 2014, 39(2): 276–289. DOI:10.1109/JOE.2013.2249871 |
| [24] | VACHIRASRICIRIKUL S, NGAMROO I. Robust LFC in a smart grid with wind power penetration by coordinated V2G control and frequency controller[J]. IEEE transactions on smart grid, 2014, 5(1): 371–380. DOI:10.1109/TSG.2013.2264921 |
| [25] |
刘小洋, 李勇, 程宇峰. 机载脉冲多普勒雷达湍流信号的仿真分析[J].
系统工程与电子技术, 2012, 34(5): 920–924.
LIU Xiaoyang, LI Yong, CHENG Yufeng. Simulation and analysis of turbulence signals in airborne pulse Doppler radar[J]. Systems engineering and electronics, 2012, 34(5): 920–924. |



