复合式土压平衡盾构机作为掘进复合岩土地质的主要工具,对其掘进性能的研究具有重大意义,尤其在盾构刀盘方面的研究是决定盾构施工能否顺利进行的关键。在以软土为主的地层中,盾构机掘进时,由于很难监测刀盘面板上压力的变化趋势,主要通过监测压力舱隔板上的压力来反映刀盘面板上压力的变化趋势[1-2]。大多数学者都在探寻复合式盾构机刀盘开口与盾构系统压力传递的关系,采用数值模拟和试验台模拟相结合的方法。屈福政等[3-5]基于流体力学的方法对盾构刀盘进行仿真分析,建立了盾构密封舱动态平衡系统数学模型。胡国良等[6]基于盾构机模拟试验台,研究了同一埋深下同样地质条件下密封舱土压力随时间变化的规律。徐前卫等[7]运用相似理论和模型试验的原理研究了土压平衡盾构机在不同地层下的适应性。但由于试验条件有限,不可能多次更改刀盘开口方式,并不能完全做到各类开口方式的全面研究。本文正是基于此考虑,建立多种不同开口模式的刀盘,运用计算流体力学的方法研究刀盘系统压力与刀盘开口模式的关系。
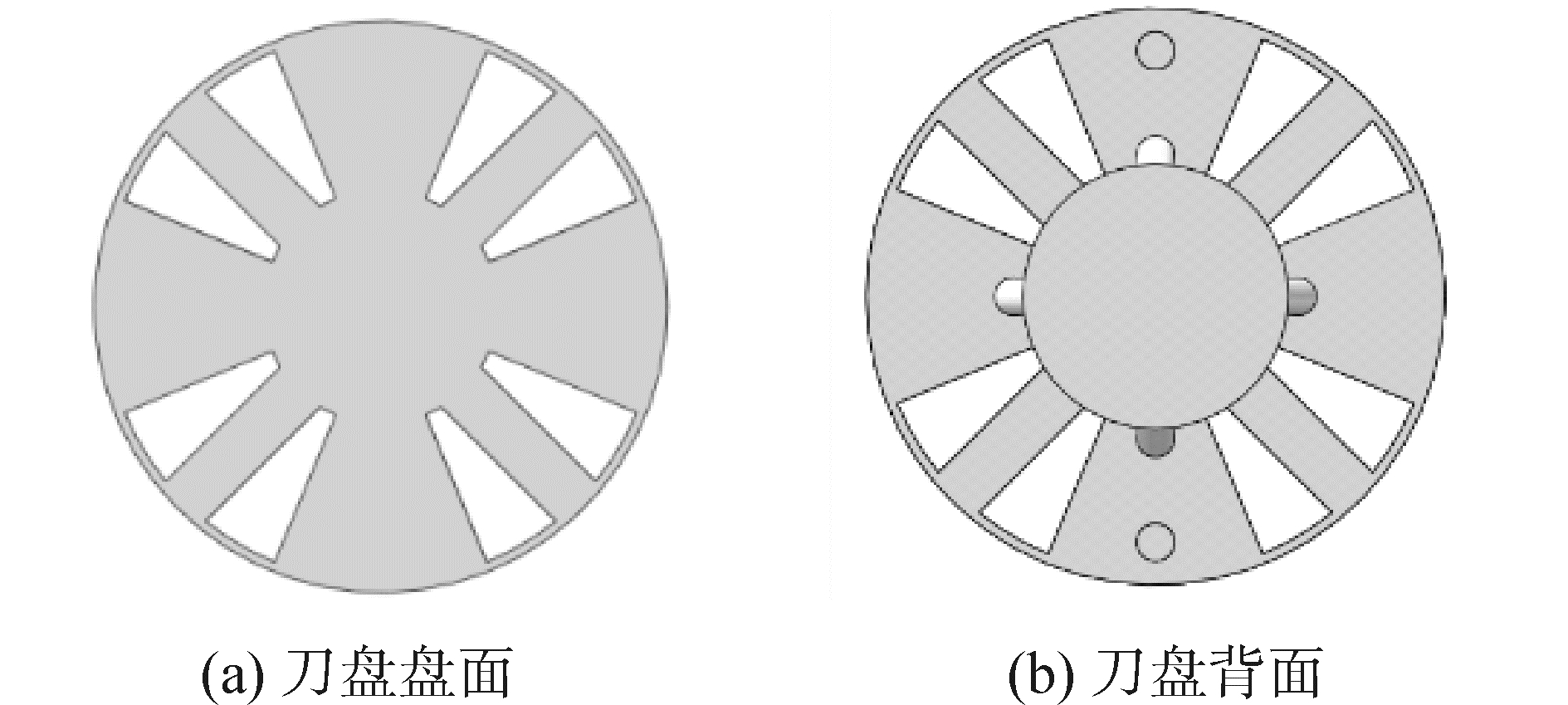
1 刀盘开口设计原理和过程 1.1 典型刀盘拓扑结构四辐条四辐板刀盘模型在国内应用比较广泛,本文将针对此类刀盘进行研究。依据拓扑学原理,把刀盘盘面上的滚刀、刮刀以及支撑板等零件去除,保留刀盘背面的搅拌棒和牛腿法兰,便得到了刀盘的拓扑结构,如图 1所示。后续将以此拓扑结构为基础,来对刀盘开口模式进行研究。
|
| 图1 典型刀盘拓扑结构 Figure 1 Topological structure of typical cutter head |
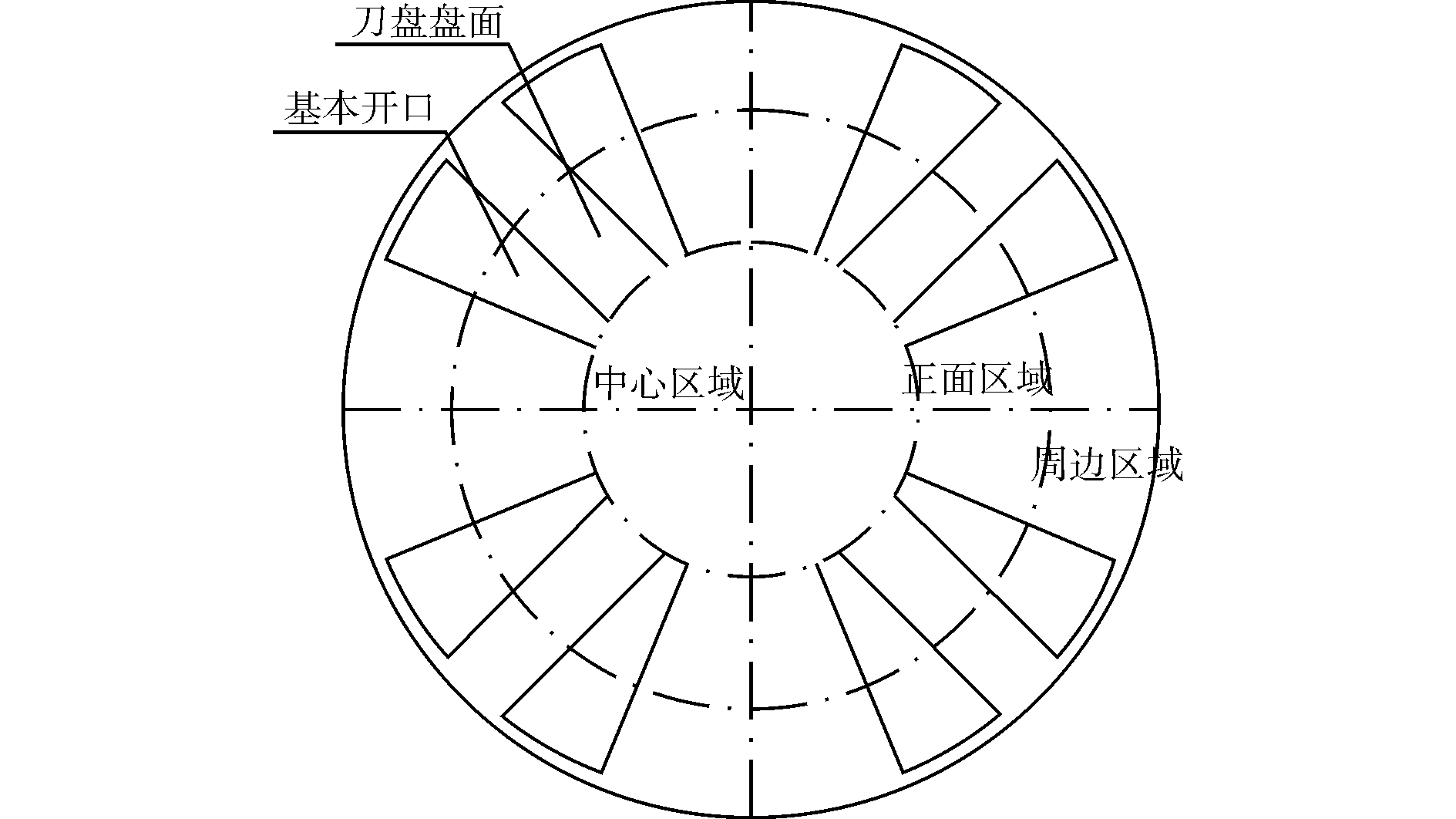
复合式盾构机刀盘上安装有三种刀具,分别是中心刀、正面刀具以及边滚刀,因此刀盘盘面也对应三大开口区域,分别是中心区域、正面区域和周边区域[8],如图 2所示。
|
| 图2 刀盘分区示意图 Figure 2 The partition of cutter head |
刀盘开口模式分析分为两种情况,分别是不同开口率分析和相同开口率分析[9-13]。不同开口率分析是指通过改变刀盘开口面积,来探索不同大小的开口率对刀盘系统压力传递的影响以便设计出最合适的刀盘开口率。相同开口率分析是指在刀盘开口面积相同的情况下,通过改变刀盘的开口位置,来探究其与刀盘系统压力的关系,以便设计出最合适的开口位置。对刀盘三大开口区域以及是否开口进行编号划分,把中心区域编号为1,正面区域编号为2,周边区域编号为3,不开口的情况编号为0,开口的情况编号为1。则中心区域不开口的情况表示为10,中心区域开口的情况表示为11,正面区域不开口的情况表示为20,正面区域开口的情况表示为21,周边区域不开口的情况表示为30,周边区域开口的情况表示为31。对上述所有情况进行统计归纳如表 1所示。
由典型刀盘结构可以衍生出八种不同开口模式刀盘,如图 3所示。这些开口模式是根据三个区域不开口 (有一种位置如图 3(a)),只开一个口 (有三种位置如图 3(b)、(c)、(d)),只开两个口 (有三种位置如图 3(e)、(f)、(g)),全部开口 (有一种位置图 3(h)) 四种情况生成的。这些开口模式是下文研究不定开口率和定开口率两种情况的基础。

|
| 图3 不同刀盘开口模式 Figure 3 Different opening modes of cutter head |
为便于对比,计算出上述所有刀盘的开口率,其中10-20-30开口率为24%,10-20-31、10-21-30、11-20-30开口率为33%,10-21-31、11-20-31、11-21-30开口率为40%,11-21-31开口率为49%。
针对不同开口率的情况,需要选择不同大小开口率的刀盘来进行研究。由上文可知有四种不同的开口率,因此每种开口率选择一种模式即可达到要求。这里选择开口率为24%的10-20-30, 开口率为33%的10-21-30,开口率为40%的11-21-30以及开口率为49%的11-21-31,这样开口率的变化区间就是24%~49%。
针对相同开口率的情况,需要选择开口率大小相同,但不同开口位置的刀盘来进行研究。此种情况下分别选择开口率为33%的三种开口模式 (10-20-31、10-21-30、11-20-30) 以及开口率为40%的三种开口模式 (10-21-31、11-20-31、11-21-30) 来进行研究。
2 流动性仿真分析Fluent适用于各种复杂外形的可压缩不可压缩流动计算,复合式土压平衡盾构机在掘进时需要对碴土进行改性处理,使碴土具备塑性流动状态,这种状态的碴土表现出一定程度的粘性,可以看做非牛顿流体[14]。非牛顿流体本身不可压缩,刀盘结构复杂,流体流过刀盘属于非定常流动[15-16],下面是在Fluent中进行流动性仿真分析。
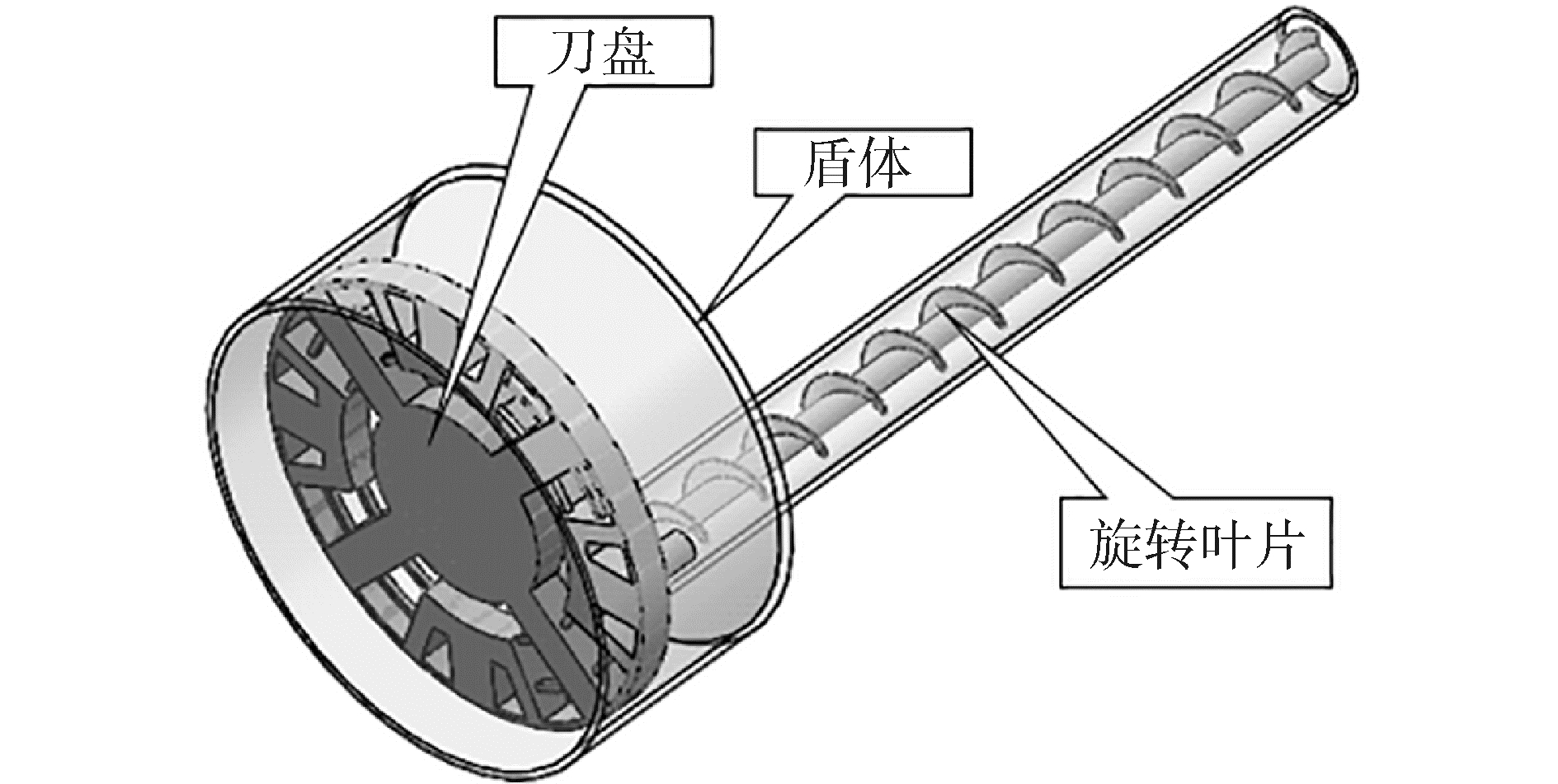
2.1 刀盘系统模型的建立刀盘系统模型包括静止部分和运动部分,其中静止部分主要是指盾构头部的盾体,螺旋输送机外围的套筒以及对刀盘起支撑作用的套筒,运动部分主要是指做旋转和移动运动的刀盘以及做旋转运动的螺旋叶片[17],除此以外,盾体内部充斥着大量的具有一定粘性的非牛顿流体。刀盘系统几何模型如图 4所示。
|
| 图4 刀盘系统几何模型 Figure 4 Geometric model of cutterhead system |
其中刀盘直径为6 100 mm,刀盘厚度为450 mm, 牛腿分布直径为3 000 mm,密封舱宽度为1 761 mm,螺旋套筒内径为1 100 mm,螺旋叶片长度为11 950 mm,螺旋叶片直径为800 mm,螺杆直径为175 mm,螺距为1 000 mm,叶片厚为70 mm。
2.2 流体参数设置在Fluent中非牛顿流体的模拟使用的是Bingham流体,流体模型采用Herschel-Bulkley模型[18],该模型模拟的“塑性流动状态”的流体性质与改良后的碴土最为相似。
查阅相关地质报告以及文献[19-20],得到满足Herschel-Bulkley本构模型的参数值,其中改性处理后的碴土密度为1 500 kg/m3,静剪切应力为15 000 Pa,屈服黏度为700 Pa·s,稠度指数为0.7,幂率指数为1.1,流体剪切速率范围为103~106 s-1。
2.3 边界条件设置边界条件设置主要是对盾构机实际工作过程中的相关掘进参数以及仿真计算过程中相关计算方法的设置,包括以下几个方面:
1) 刀盘的推进速度设为0.03 m/r,刀盘旋转速度设为2 r/min,螺旋输送机旋转速度设为9 r/min;
2) 入口边界条件采用速度入口,入口速度设为0.001 m/s,与刀盘推进速度相等,方向从流体入口指向出口,平行于刀盘系统轴线方向;
3) 采用压力出口边界条件,出口压力初始值设为0;
4) 流体流动形式为Transient (非定常流动),时间离散格式为一阶隐式,压力-速度耦合算法采用PISO;
5) 计算时间步长设为20,迭代时间步数设为50。
2.4 网格划分对刀盘系统进行网格划分,统计出各个部分的单元和节点如表 2所示。
| 刀盘系统 | 刀盘 | 盾体 | 螺旋叶片 | 流体 |
| Nodes | 99 583 | 215 963 | 61 600 | 522 734 |
| Elements | 483 540 | 914 363 | 49 629 | 2 759 252 |
在后续仿真研究中,对于不同开口模式的刀盘系统,刀盘网格划分会有所差异,其余部分完全相同,这样可以排除其他变量影响,有利于提高仿真结果的正确性。
3 数值计算结果及分析 3.1 变开口率下的流动性分析沿刀盘系统轴线方向依次选取泥浆入口,刀盘掘进界面、刀盘土舱隔板等五个表面作为后续分析的压力观测面。为了更直观地描述每个观测面的压力情况,定义等效压力值为
| $ {P_{{\rm{equ}}}} = \frac{1}{n}\sqrt {p_1^2 + p_2^2 + \cdots + p_n^2} $ |
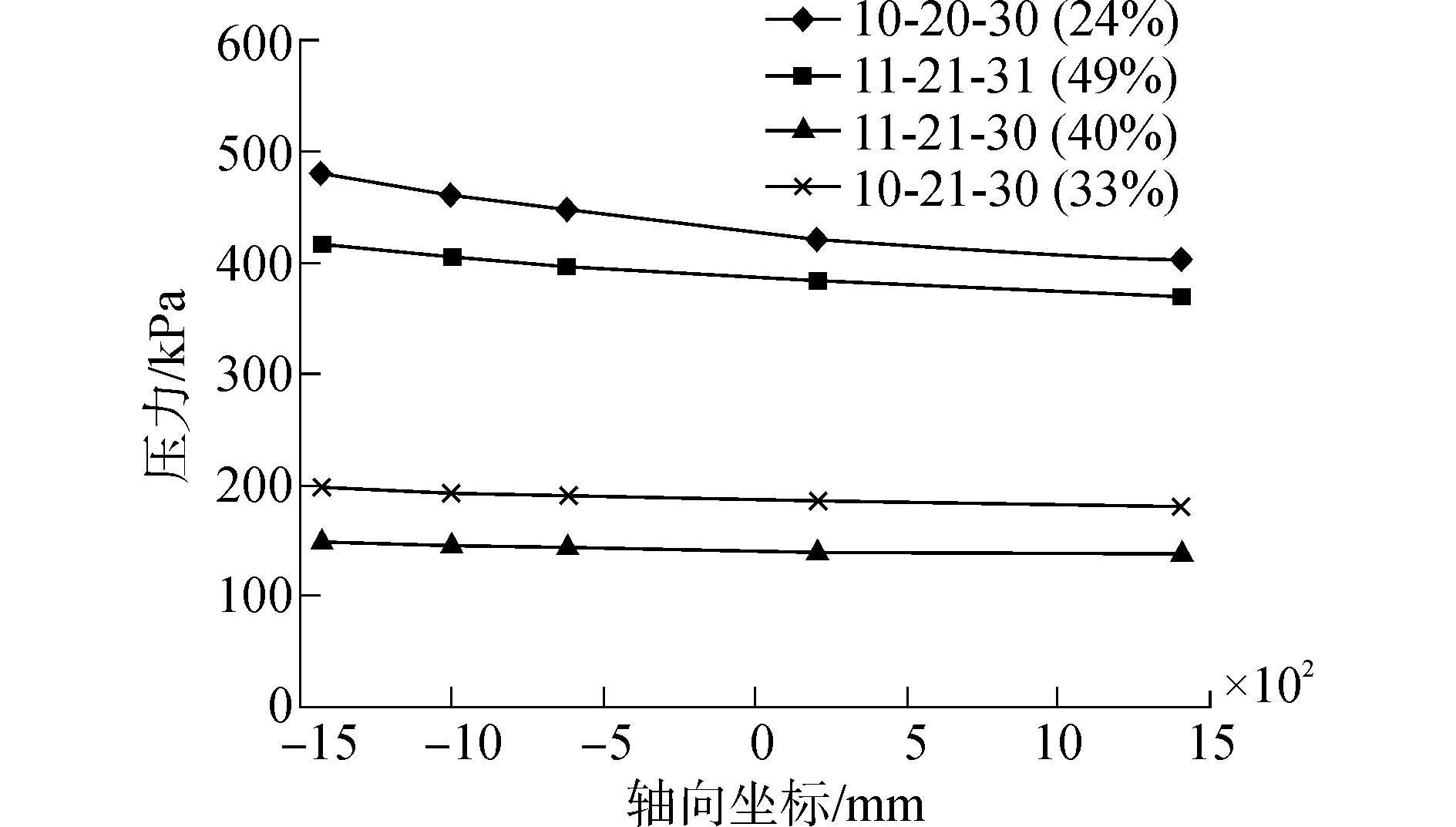
式中:Pequ表示观测面的等效压力值,Pn表示观测面上第n个节点的压力数值,n表示观测面内所有节点的个数。分别对四种不同刀盘开口模式的各个观测面进行等效压力值统计,得到四种开口模式下的刀盘系统轴向压力分布梯度如图 5所示。
|
| 图5 不同开口率的刀盘轴向压力传递曲线 Figure 5 The axial pressure gradient of different opening rate of the cutter head |
为了更好地描述刀盘系统轴向压力分布情况,引入压力传递系数α的概念,把刀盘土舱压力和开挖面入口压力的比值称作压力传递系数,它能够更加直观地反映刀盘系统压力传递情况。
对不同刀盘开口模式与压力传递系数之间的关系进行统计,并且对各个模式下的轴向压力传递曲线进行函数拟合,统计出相对应的拟合方程和相关系数,如表 3所示。
| 刀盘开口率k | α | R2 | 拟合方程 |
| 24% | 0.836 | 0.99 | P=427-0.027 6x+6.83×10-6x2 |
| 33% | 0.913 | 0.97 | P=186-0.005 9x+1.19×10-6x2 |
| 40% | 0.926 | 0.96 | P=140-0.003 7x+1.5×10-6x2 |
| 49% | 0.938 | 0.97 | P=385-0.016 7x+3.44×10-6x2 |
从图 5和表 3中可看出:随着开口率k的增大,压力传递系数α也逐渐提高,说明开口率越大的刀盘压力传递越流畅,刀盘对压力传递的阻碍越小,压力的轴向变化越小,从而碴土的流动性也越强。
刀盘轴向压力传递曲线都表现出明显的非线性关系,拟合出的曲线方程都是二次函数,并且二次函数每一项系数都是同一数量级,据此计算出的相关系数都是处于0.95~1,相关度非常高,说明不同刀盘开口模式下的压力传递规律是相似的,刀盘系统轴线方向的不同位置变化对压力数值的影响较大。
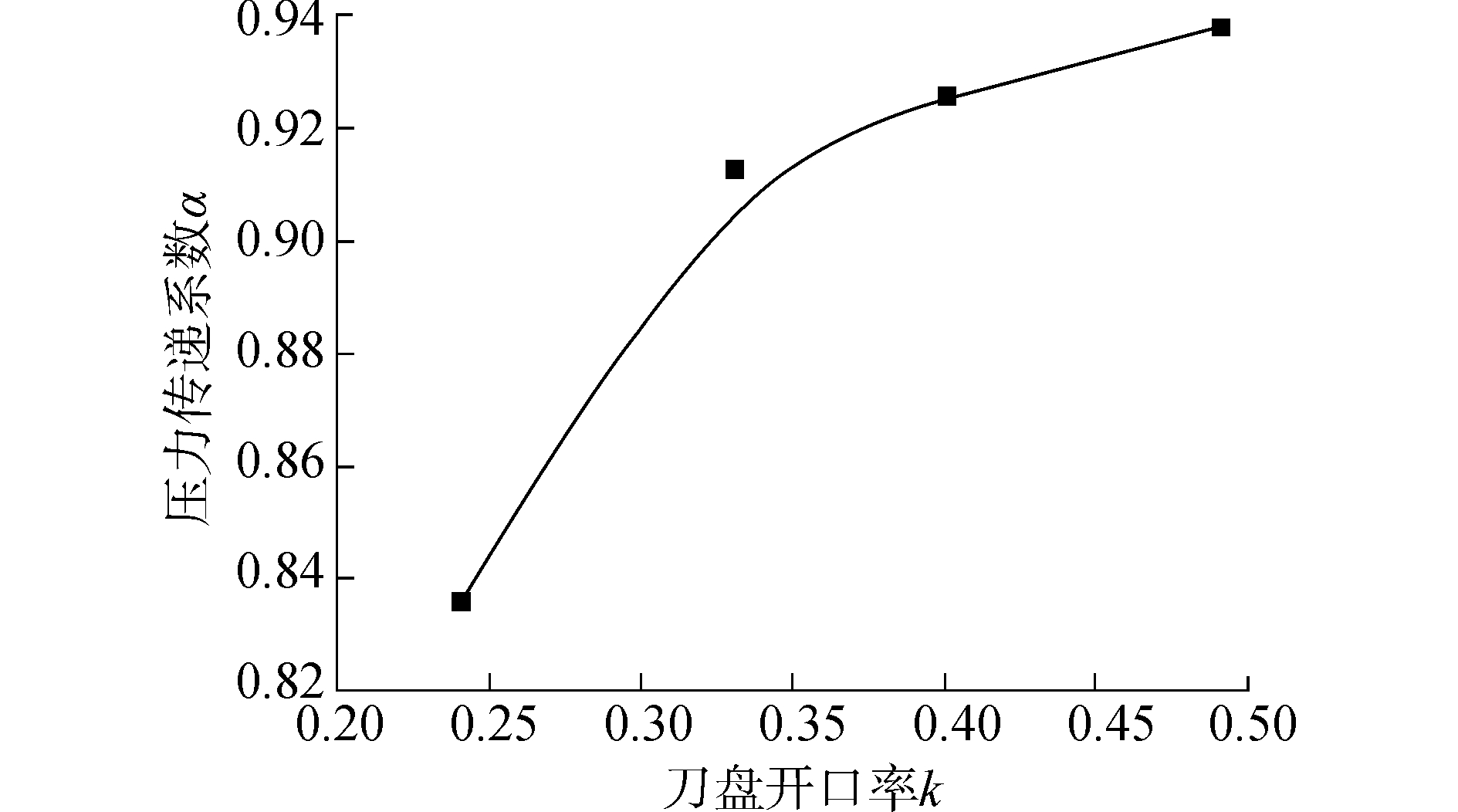
为了更加直观地比较刀盘开口率与压力传递系数的关系,将二者数值一一对应拟合出一条曲线,如图 6所示。
|
| 图6 刀盘开口率与压力传递系数的关系 Figure 6 The relationship between opening rate and pressure transfer coefficient |
对上述关系通过插值法进行函数拟合,得到三次函数关系如下
| $ \alpha = - 0.19 + 7.98k - 19.16{k^2} + 15.44{k^3} $ |
由上述刀盘开口率与压力传递系数拟合的三次函数可知,刀盘开口率与压力传递系数存在着确定的非线性关系。当压力传递系数无限接近于1时,理论上是可以得到一种最优的刀盘开口率。
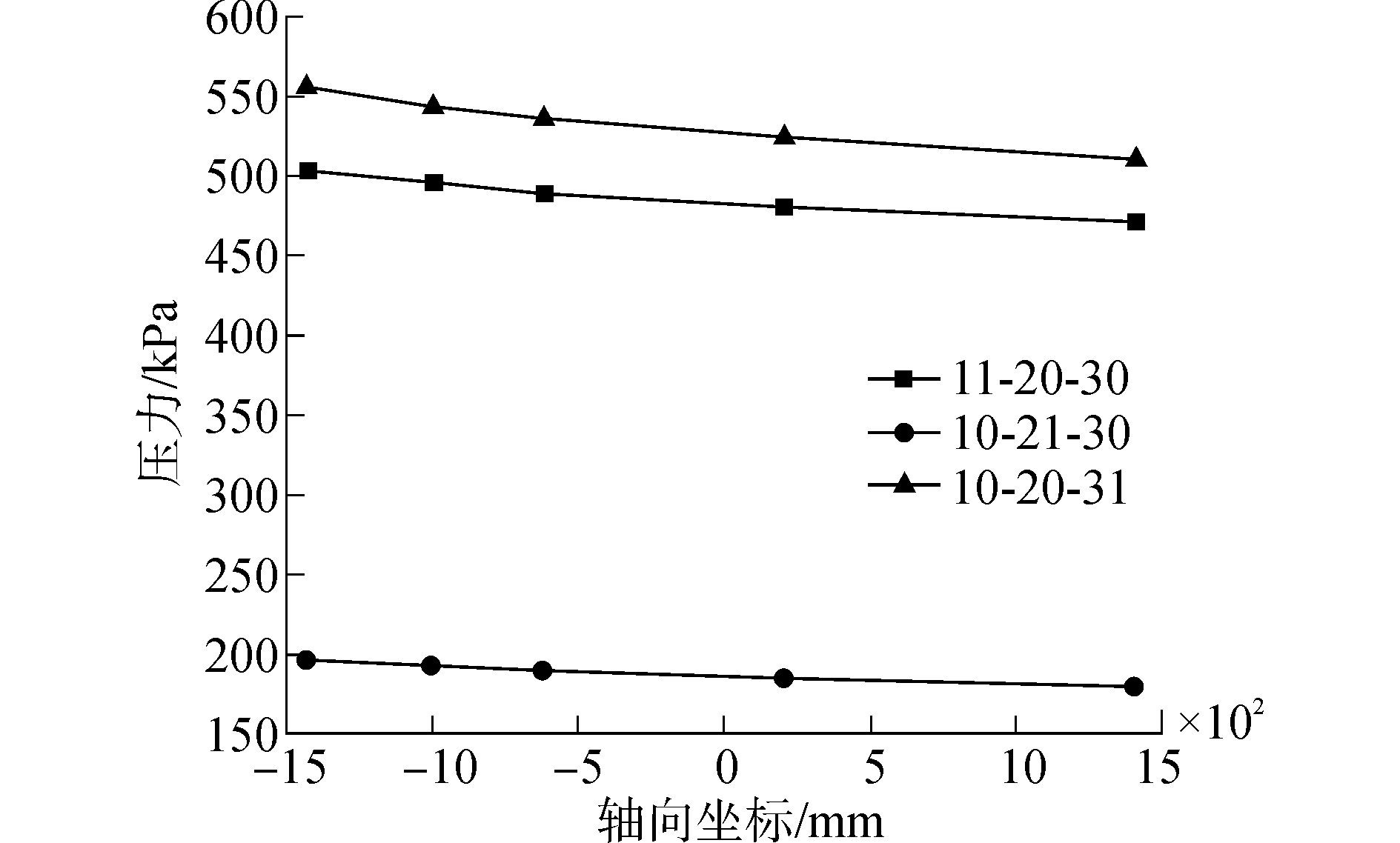
3.2 定开口率下的流动性分析开口率为33%的三种刀盘开口模式系统轴向压力传递曲线如图 7所示。
|
| 图7 盾构轴向压力传递曲线 (开口率33%) Figure 7 Shield axial pressure transmission curve (opening rate of 33%) |
从图 7中可以看出同一开口率不同开口位置模式下的系统压力值并不相同,其中周边区域开口的刀盘系统压力最大,中心区域开口的刀盘次之,正面区域开口的刀盘最小。分别计算出三种模式下的压力传递系数,并且对各个模式下的轴向压力传递曲线进行函数拟合,统计出相对应的拟合方程和相关系数,如表 4所示。
| 刀盘开口类型 | 压力传递系数 | 拟合方程 | 相关系数 |
| 10-20-31 | 0.917 | P=527-0.016x+3.33×10-6x2 | 0.99 |
| 11-20-30 | 0.877 | P=483-0.011 3x+2.51×10-6x2 | 0.97 |
| 10-21-30 | 0.913 | P=186-0.005 9x+1.19×10-6x2 | 0.97 |
根据表 4和图 7可以看出:在相同开口率的情况下,周边区域开口的刀盘压力传递系数最大,中心区域开口的刀盘压力传递系数最小,说明周边区域开口的刀盘对碴土流动性阻碍最小,中心区域开口的刀盘最不利于碴土的流动。三种刀盘开口模式中,压力传递曲线的拟合方程均呈现二次相关性,且相关系数都接近于1,它们都有着近似一致的压力变化规律。在开口率一定的情况下,要尽可能地增大周边区域开口面积,减小中心区域开口面积,这样有利于碴土比较顺利地流入土舱内部,减少碴土在刀盘前端堆积的数量,从而保持系统前后压力的平衡,实现刀盘掘进的有效进行。
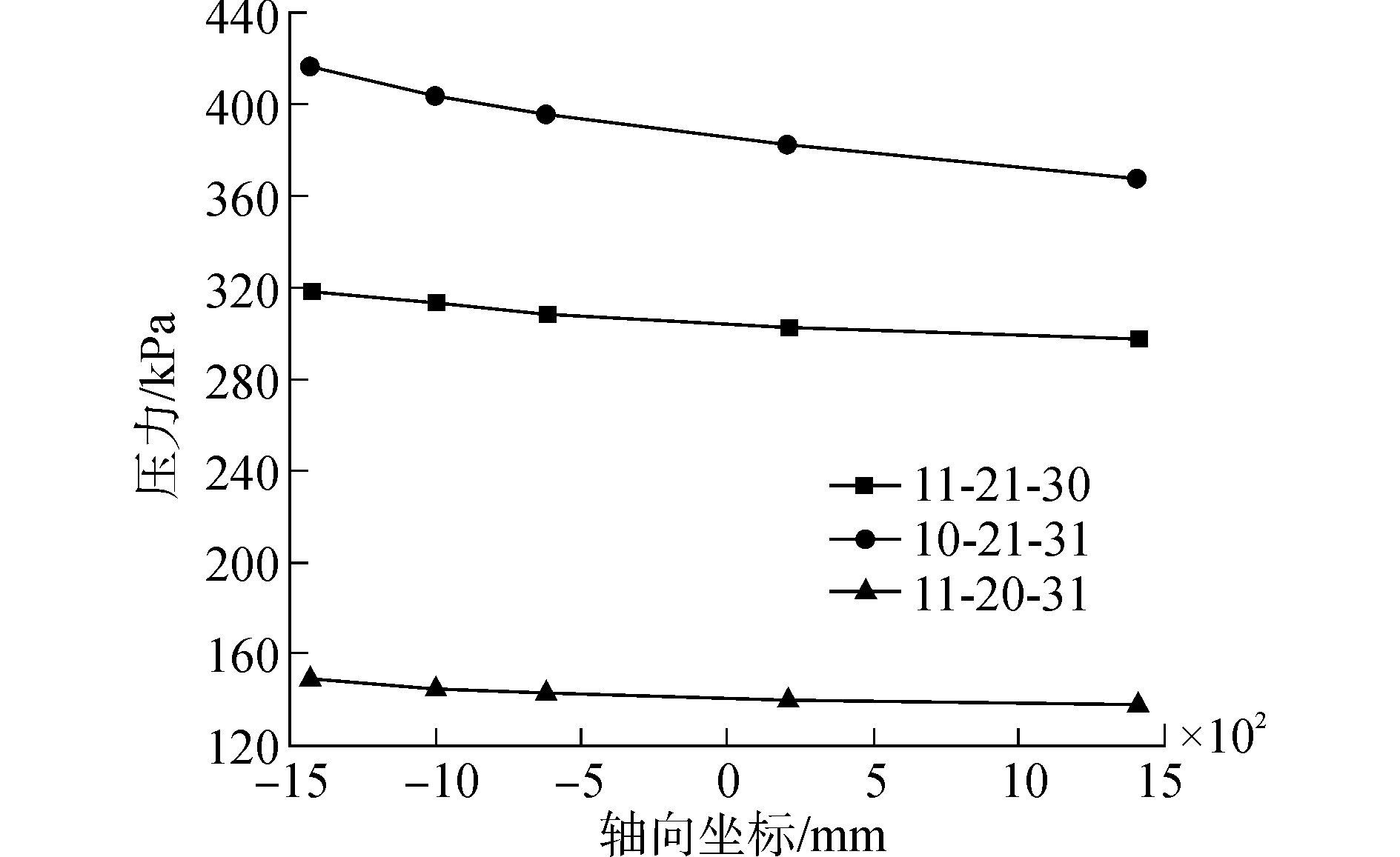
开口率为40%的三种刀盘开口模式系统轴向压力传递曲线如图 8所示。
|
| 图8 盾构轴向压力传递曲线 (开口率40%) Figure 8 Shield axial pressure transmission curve (opening rate of 40%) |
由压力传递曲线计算出压力传递系数,并对压力传递曲线进行函数拟合以及相关系数统计得到表 5。
| 刀盘开口类型 | 压力传递系数 | 相关系数 | 拟合方程 |
| 10-21-31 | 0.927 | 0.99 | P=385-0.016 7x+3.44×10-6x2 |
| 11-20-31 | 0.926 | 0.98 | P=140-0.003 7x+1.51×10-6x2 |
| 11-21-30 | 0.934 | 0.96 | P=304-0.007 3x+2.14×10-6x2 |
由图 8和表 5可知,其分布规律与开口率为33%的刀盘大致相同,但存在一些不同点:
由拟合的曲线函数以及对应的相关系数可以看出,刀盘系统压力值随位置的变化关系更加趋近于二次函数的变化趋势,其中10-21-31型刀盘的相关系数更是达到了0.99,已经可以认为压力和位置是完全相关的,说明当开口率较大时刀盘系统压力梯度呈现明显的二次非线性关系。
由三种开口模式的压力传递系数可以看出,三种压力传递系数都很大,而且数值极其接近,最大数值差只有0.008,说明开口率较大时碴土能够顺利地进入土舱内部,开口位置对碴土流动性的影响较小。
4 结论1) 刀盘开口模式与刀盘系统压力关系密切,总体来说,无论是在不定开口率还是定开口率下,盾构系统沿轴向压力呈现明显的递减趋势,但两种情况下的表现又各不相同。
2) 在不定开口率的情况下,开口率在24%~49%的刀盘,轴向压力梯度均呈现二次函数变化,刀盘开口率与压力传递系数呈现三次函数关系,据此可为变开口率刀盘结构设计提供理论依据。
3) 在定开口率的情况下,刀盘开口率为33%时,应尽量减小刀盘中心开口面积,能有效改善土体流动性;而刀盘开口率为40%时,开口位置对碴土流动性的影响降低,此时可增加正面和中心开口面积以降低该区域形成泥饼的可能。
本文研究了复合式盾构刀盘开口模式与压力传递的关系,下一步将针对特定开口模式搭建盾构系统试验台,进行实验研究,提取相关数据与仿真结果进行对比,使研究结果更具说服力。
| [1] |
中国土木工程学会. 2014中国隧道与地下工程大会 (CT-UC) 暨中国土木工程学会隧道及地下工程分会第十八届年会优秀论文汇编[C]. 杭州: 中国土木工程学会隧道及地下工程分会, 2014.
China Civil Engineering Society. 2014 Chinese tunnel and underground engineering conference (CTUC) and tunnel and underground engineering branch of China civil engineering society the 18-th annual conference proceedings good[C]. Hangzhou:China Civil Engineering Society of Tunnel and Underground Engineering Branch, 2014. |
| [2] |
李守巨.
盾构机土仓压力控制技术[M]. 大连: 大连理工大学出版社, 2011.
LI Shouju. Control of pressure in soil chamber in shield tunneling[M]. Dalian: Dalian University of Technology Press, 2011. |
| [3] |
刘畅, 孙铁兵, 孟庆琳, 等. 土压平衡盾构密封舱压力场模拟实验台设计[J].
中国机械工程, 2011, 22(1): 19–22, 27.
LIU Chang, SUN Tiebing, MENG Qinglin, et al. Design of experimental table for simulating pressure field of working chamber of earth pressure balanced shield[J]. China mechanical engineering, 2011, 22(1): 19–22, 27. |
| [4] | WU Li, QU Fuzheng. Discrete element simulation of mechanical characteristic of conditioned sands in earth pressure balance shield tunneling[J]. Journal of central south university of technology, 2009, 16(6): 1028–1033. DOI:10.1007/s11771-009-0170-8 |
| [5] | QU Fuzheng, WU Li, SUN Wei. Analysis of chamber pressure for earth pressure balance shield machine by discrete numerical model[C]//Proceedings Second International Conference on Intelligent Robotics and Applications. Berlin Heidelberg, 2009:402-411. http://link.springer.com/content/pdf/10.1007%2F978-3-642-10817-4_40.pdf |
| [6] |
胡国良, 龚国芳, 杨华勇, 等. 盾构掘进机模拟试验台液压系统集成及试验分析[J].
农业机械学报, 2005, 36(12): 102–105.
HU Guoliang, GONG Guofang, YANG Huayong, et al. Hydraulic system integration and experimental analysis of shield tunnelling machine for simulator test rig[J]. Transactions of the Chinese society for agricultural machinery, 2005, 36(12): 102–105. |
| [7] |
徐前卫, 朱合华, 廖少明, 等. 砂土地层盾构法施工的地层适应性模型试验研究[J].
岩石力学与土程学报, 2006, 25(S1): 2902–2909.
XU Qianwei, ZHU Hehua, LIAO Shaoming. Model experimental study on stratum adaptability of tunnel excavation with EPB shield machine in sandy stratum[J]. Chinese journal of rock mechanics and engineering, 2006, 25(S1): 2902–2909. |
| [8] |
林赉贶. 土压平衡盾构机刀盘开口特性及刀具布置方法研究[D]. 长沙: 中南大学, 2013.
LIN Laikuang. Research on opening characteristic and cutter's layout method of EPB shield cutterhead[D]. Changsha:Central South University, 2013. |
| [9] |
虞诗强, 霍军周, 吴承原, 等. EPB盾构机刀盘开口模式与刀盘盘体结构耦合设计[J].
机械设计与制造, 2013(10): 242–245.
YU Shiqiang, HUO Junzhou, WU Chengyuan, et al. Coupling design of EPB-TBM cutting wheel opening model and cutting wheel body structure[J]. Machinery design & manufacture, 2013(10): 242–245. |
| [10] |
刘书亮. 土压平衡盾构密封舱土体与旋转刀盘的流固耦合分析[D]. 天津: 天津大学, 2010.
LIU Shuliang. FSI analysis of the cutterhead and the soil in chamber for EPB shield machine[D]. Tianjin:Tianjin University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10056-1011266841.htm |
| [11] |
刘建琴, 郭伟, 黄丙庆, 等. 土压平衡盾构刀盘开口率与刀盘前后压差的关系[J].
天津大学学报, 2011, 44(8): 659–664.
LIU Jianqin, GUO Wei, HUANG Bingqing, et al. Relationship between aperture ratio and fore-and-back pressure of EPB shield cutter head[J]. Journal of Tianjin university, 2011, 44(8): 659–664. |
| [12] |
王洪新. 土压平衡盾构刀盘开口率选型及其对地层适应性研究[J].
土木工程学报, 2010, 43(3): 88–92.
WANG Hongxin. Type selection of the head aperture ratio of EPB shield cutterheads and adaptability to stratum characteristics[J]. China civil engineering journal, 2010, 43(3): 88–92. |
| [13] |
王洪新. 土压平衡盾构刀盘开口率对土舱压力的影响[J].
地下空间与工程学报, 2012, 8(1): 89–93, 104.
WANG Hongxin. Influence of aperture ratio of cutterhead of EPB shield on earth pressure in the chamber[J]. Chinese journal of underground space and engineering, 2012, 8(1): 89–93, 104. |
| [14] |
杨玄. 非牛顿流体在旋流器中流动特性的数值模拟[D]. 青岛: 中国石油大学, 2010.
YANG Xuan. Numerical simulation of flow characteristics of non-Newtonian fluid in a hydrocyclone[J]. Qingdao:China University of Petroleum, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10425-2010281146.htm |
| [15] |
郭伟, 胡竟, 王磊, 等. 基于CFD的土压平衡盾构刀盘开口分布特征研究[J].
机械工程学报, 2012, 48(17): 144–151.
GUO Wei, HU Jing, WANG Lei, et al. Study on the opening distribution characteristics of earth pressure balance shield cutter head based on CFD[J]. Journal of mechanical engineering, 2012, 48(17): 144–151. DOI:10.3901/JME.2012.12.144 |
| [16] |
胡竟. 基于CFD数值模拟的盾构刀盘设计分析[D]. 天津: 天津大学, 2012.
HU Jing. The numerical simulation of earth pressure balance shield cutter head design based on CFD[D]. Tianjin:Tianjin University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10056-1013039785.htm |
| [17] |
孟庆琳. 盾构螺旋输送机承压输送机理研究及控制中的应用[D]. 大连: 大连理工大学, 2012.
MENG Qinglin. Research and application in control of conveying mechanism of screw conveyor under pressure of EPB shield[D]. Dalian:Dalian University of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10141-1012393319.htm |
| [18] |
章敏, 王星华, 汪优. Herschel-Bulkley浆液在裂隙中的扩散规律研究[J].
岩土工程学报, 2011, 33(5): 815–820.
ZHANG Min, WANG Xinghua, WANG You. Diffusion of Herschel-Bulkley slurry in fractures[J]. Chinese journal of geotechnical engineering, 2011, 33(5): 815–820. |
| [19] |
杨洪杰, 傅德明, 葛修润. 盾构周围土压力的试验研究与数值模拟[J].
岩石力学与工程学报, 2006, 25(8): 1652–1657.
YANG Hongjie, FU Deming, GE Xiurun. Experimental study and numerical simulation of earth pressure around shield machine[J]. Chinese journal of rock mechanics and engineering, 2006, 25(8): 1652–1657. |
| [20] | ROSTAMI J. Study of pressure distribution within the crushed zone in the contact area between rock and disc cutters[J]. International journal of rock mechanics and mining sciences, 2013, 57: 172–186. DOI:10.1016/j.ijrmms.2012.07.031 |



