2. UAV System Engineering Research Institute, China Aerospace Electronic Technology Research Institute, Beijing 100094, China
多水下机器人系统(multiple autonomous underwater vehicles system,MAUVS),是指由多个水下机器人组成的系统,通过协作完成特定的任务,例如通讯中继、协同定位、区域搜索、地形扫描、环境数据采集[1-5]。
协同编队属于多水下机器人紧耦合任务,是多水下机器人系统进行多种作业的基础,也是演示验证多机器人协同体系结构的重要手段。人们针对此问题提出了多种多样的方法:JIANG Dapeng等基于机器人智能提出了基于行为的编队算法[6-7];HOU S P等通过构造分层的人工势场函数,考虑AUV的动力学特性,提出了自适应的多水下机器人编队控制算法[8-9];CUI Rongxin等采用领航-跟随法,通过测量领航者的位置构造虚拟跟随者,形成参考轨迹,采用反步法设计跟随者的控制器,使其收敛于虚拟跟随者[10]。综合来看,领航-跟随法和人工势场法在多水下机器人方面有着较为广泛的应用,各种方法都或多或少地借鉴了其中的思想。而基于行为法中,具体基本行为的构造也经常采用上述两种方法。
相位耦合振子模型(coupled phase oscillator),用于描述自然界和工程中具有周期特性的群体系统[11-12],例如心肌细胞的起搏、萤火虫的闪动。VICSEK Tamas等在离散时间下,针对单位速度进行平面运动的质点,提出了艏向一致的控制算法[13]。REZA Olfatisabe等将相位耦合振子模型扩展到多维球空间,并讨论了在此之上的一致性问题[14]。ANTONIS Papachristodoulou等设计Lyapunov函数,在具有时延和切换拓扑条件下保持了群体的一致性[15]。PALEY Derek A等通过控制振子群体质心的动量,提出了艏向一致、绕相同圆心转动的控制算法[16]。
传统的领航-跟随法拓扑结构固定,具有明确的领航者、跟随者,对于领航者的依赖性较强,一旦领航者丢失,则整个任务失败。相位耦合振子模型系统拓扑结构可变,利于适应复杂多变的外部环境。只要保证群体通讯拓扑联通,即可实现群体的协同运动。另外,水下机器人多采用螺旋桨、舵翼的控制形式,通过转艏实现水平面的机动,系统具有二阶非完整性。相位耦合振子模型通过控制振子艏向,完成群体运动,与之相符。
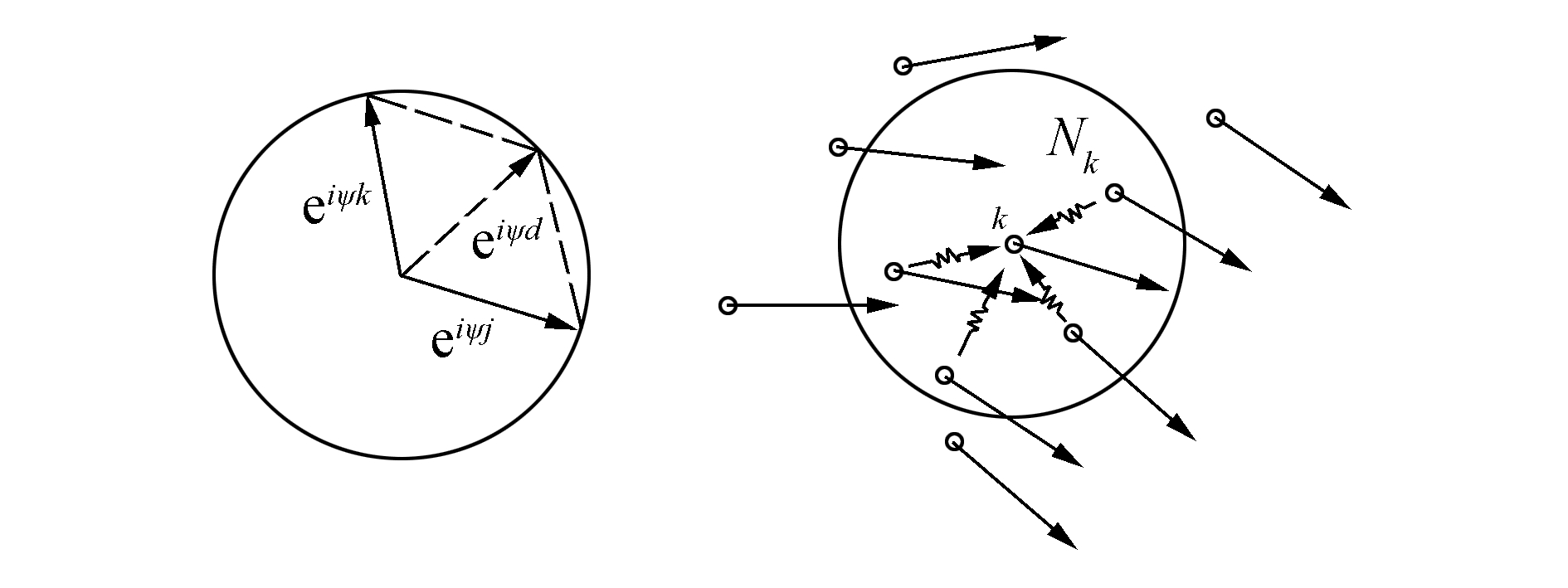
1 模型描述 1.1 相位耦合振子模型相位耦合振子模型采用复平面上的矢量eiψ表示振子的艏向角ψ。两者的区别在于:ψ处于线性空间,相加无法得到艏向均值(例如0°和270°的均值为135°,显然与需要的艏向不符);eiψ处于环形空间,具有周期性,矢量叠加可以求得艏向均值(如图 1(a))。这一特性给振子群体艏向一致的计算带来了很大便利。如图 1(b),直线箭头表示振子运动艏向,折线箭头表示信息传递,振子k可以感知到邻居振子j∈Nk的运动艏向,将艏向均值作为自己的期望艏向,从而与邻居振子保持一致。当所有振子都遵循这一原则调整自己的艏向,整个振子群体将达到艏向一致。
|
| 图1 相位耦合振子模型示意图 Figure 1 Diagram of coupled phase oscillator model |
在海洋探测的应用背景下,水下机器人的尺度远小于所运行环境的尺度。并且在弱机动条件下,水下机器人的纵向速度约等于合速度
| $ \left\{ \begin{array}{l} {{\dot \xi }_k}={{\rm{e}}^{{\rm{i}}\cdot{\psi _k}}}\\ {{\dot \psi }_k}={r_k} \end{array} \right. $ | (1) |
水下机器人的首摇响应动力学模型采用一阶野本模型,并考虑其非线性影响,加入建模模型误差的不确定项d(t),假设误差为慢变过程,即d(ṫ)≈0。可知多水下机器人的运动学和动力学模型为
| $ \left\{ \begin{array}{l} {{\dot \xi }_k}={{\rm{e}}^{{\rm{i}}\cdot{\psi _k}}}\\ {{\dot \psi }_k}={r_k}\\ {{\dot r}_k}=-\frac{{{r_k}}}{T}-\frac{{\alpha {r_k}^3}}{T}+\frac{{K{\delta _k}}}{T}+{d_k}\left(t \right) \end{array} \right. $ | (2) |
式中:K为回转性指数,表示单位舵角下的回转角速度;T为应舵指数,表示对操舵响应的快慢;α表示非线性项系数;δ表示舵角。
下文将设计合适的舵角控制律,使多水下机器人系统按照期望的队形运动:1) 艏向一致的协同编队航行;2) 采用LOS制导算法的,多水下机器人协同梳状搜索。
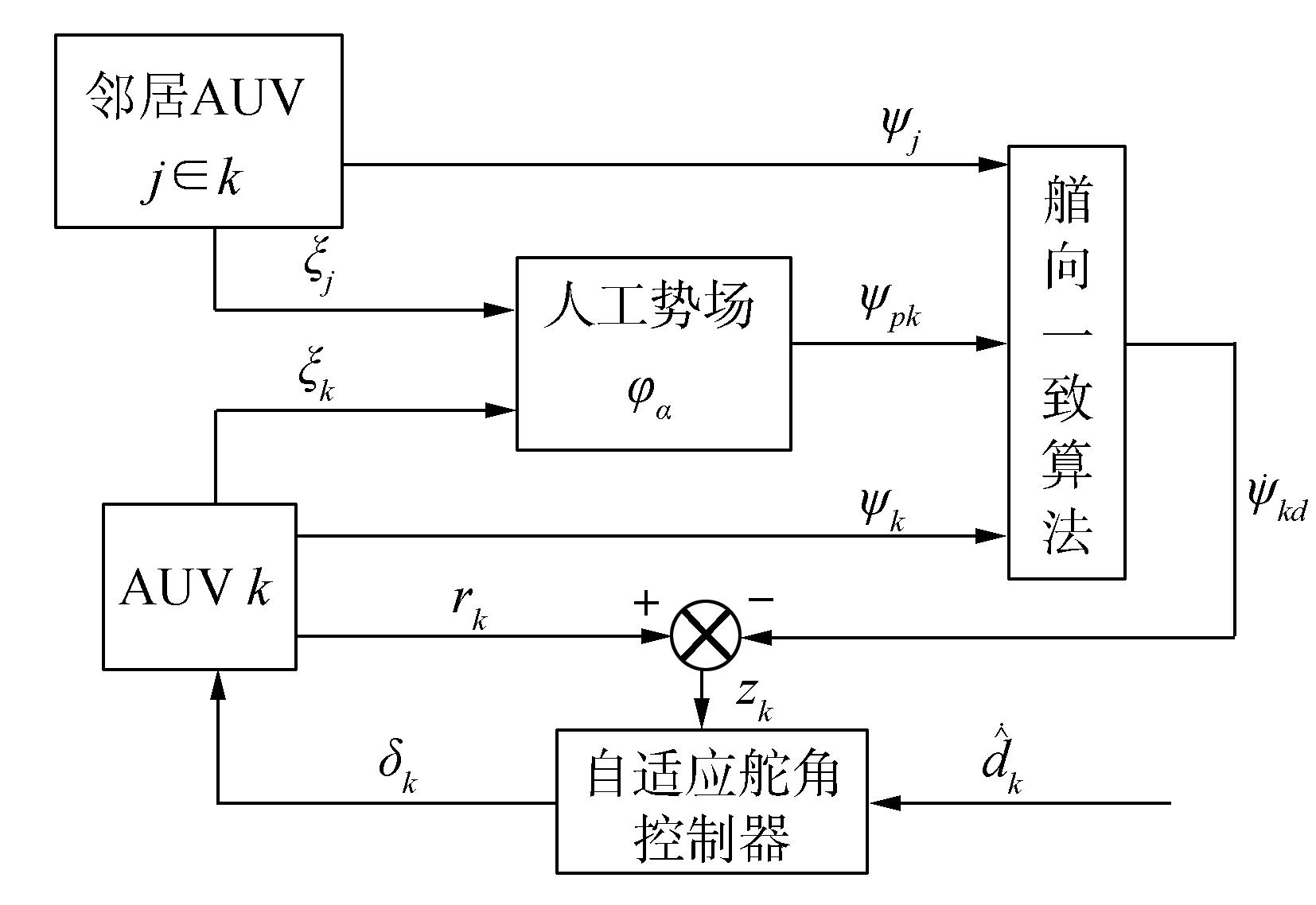
2 控制系统设计实现多水下机器人的编队控制,需要解决两个问题:个体之间具有一个合理的相互距离,群体具有相同的艏向。如图 2,第k个水下机器人通过通讯系统获知邻居水下机器人j∈Nk的位置,代入人工势场函数φα,计算所受到的势场力,将合力方向作为期望的运动方向ψpk。通过耦合振子的相位一致算法,获得期望的艏向变化率
|
| 图2 多水下机器人系统编队信息流框图 Figure 2 Information frame of MAUV formation |
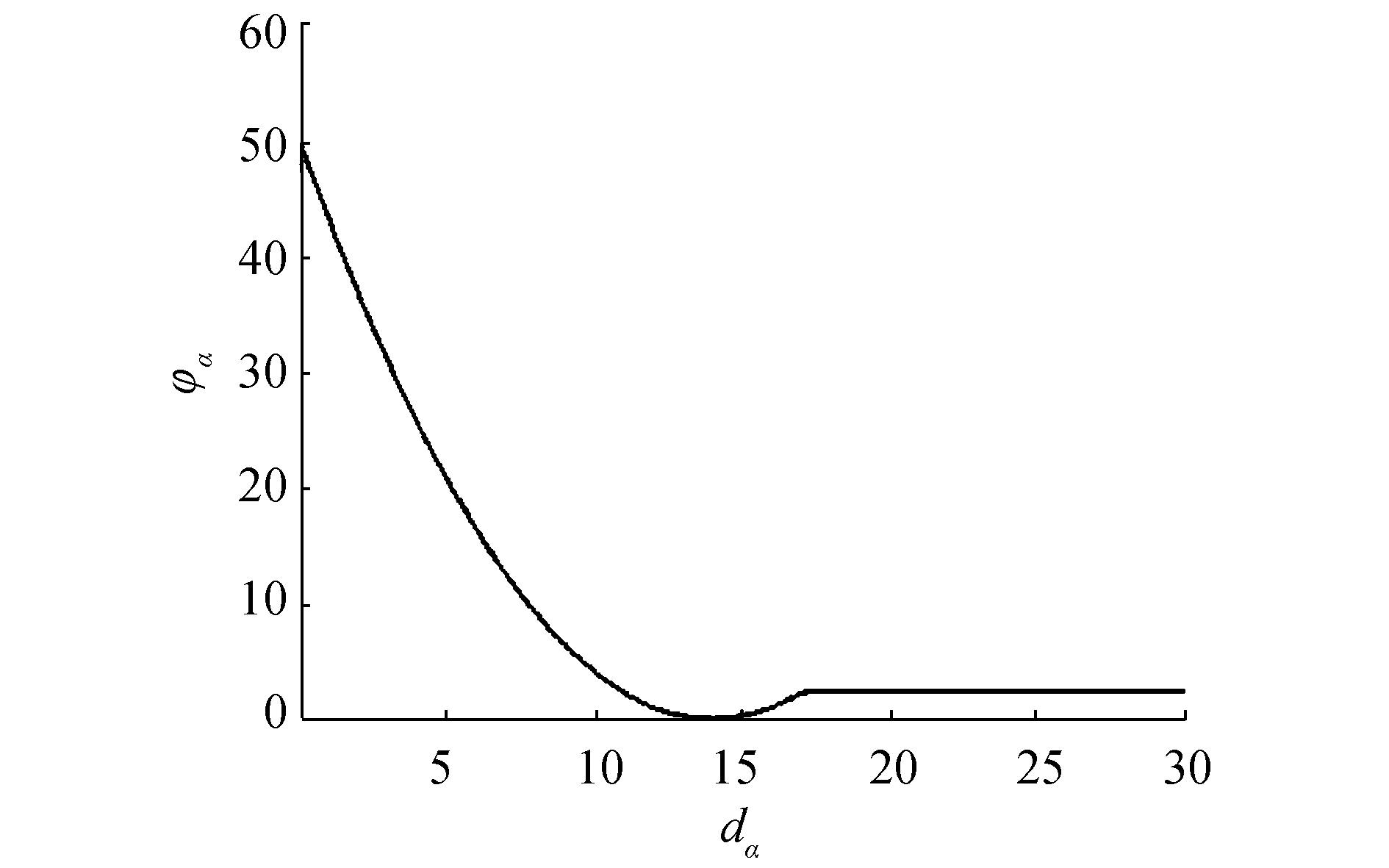
通过设计人工势场实现群体的聚合与避碰,当水下机器人之间的距离大于期望值时,产生相互的吸引力,小于期望值时,产生相互的排斥力。如果选取势函数
|
| 图3 人工势场函数 Figure 3 Artificial potential function |
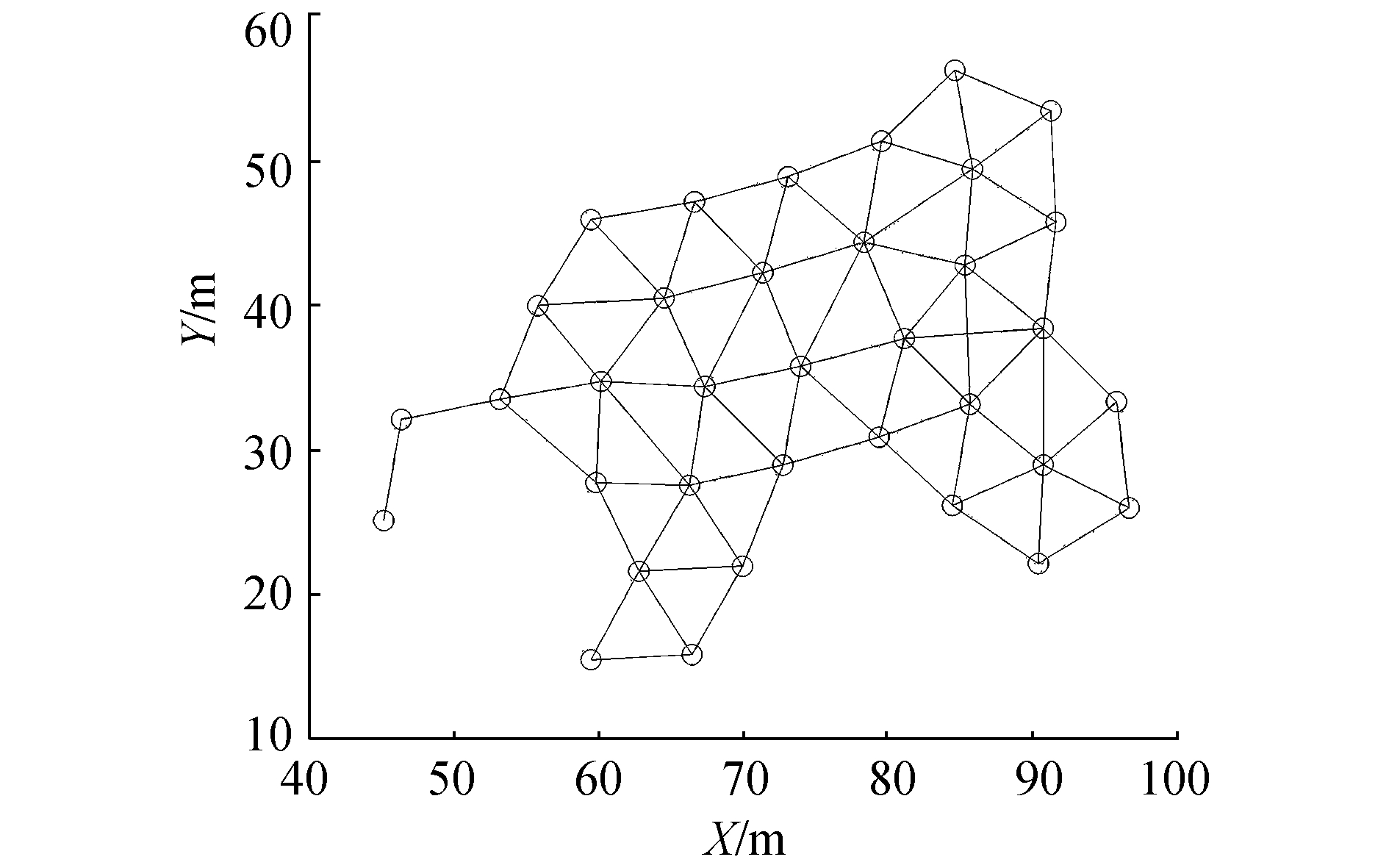
|
| 图4 多水下机器人形成的晶格状队形 Figure 4 Latticed formation of MAUV |
其中,dα表示期望的相互距离,此时为势能的最小值。也可以选用其他的势函数,或者多种势函数的组合,以形成更为复杂的队形。设人工势场势能和势场梯度分别为
| $ {V_1}({\mathit{\boldsymbol{\xi }}_k})=\sum\limits_{j \in {N_k}} {{\varphi _\alpha }} \left({\left\| {{\mathit{\boldsymbol{\xi }}_k}-{\mathit{\boldsymbol{\xi }}_j}} \right\|} \right) $ | (3) |
| $ \begin{array}{*{20}{c}} {\nabla {V_1}\left(\mathit{\boldsymbol{\xi }} \right){|_{\xi={\xi _k}}}=\sum\limits_{j \in {N_k}} {\nabla {\varphi _\alpha }} \left({\left\| {\mathit{\boldsymbol{\xi }}-{\mathit{\boldsymbol{\xi }}_j}} \right\|} \right){|_{\xi={\xi _k}}}=}\\ {\sum\limits_{j \in {N_k}} f({\mathit{\boldsymbol{\xi }}_k}, {\mathit{\boldsymbol{\xi }}_j})\cdot{\rm{ }}{\mathit{\boldsymbol{n}}_{j, k}}} \end{array} $ | (4) |
式中:nj,k=(ξk-ξj)/‖(ξk-ξj)‖表示由水下机器人j指向水下机器人k的单位向量,f(ξk, ξj) 表示力函数的幅值,其正负决定吸引、排斥。则有期望的水下机器人的艏向:
| $ {\psi _{{p_k}}}={\rm{arg}}(\sum\limits_{j \in {N_k}} f({\xi _k}, {\xi _j})\cdot{n_{j, k}})+{\rm{\pi }} $ | (5) |
选取Lyapunov函数为
| $ {V_2}=\frac{1}{{2N}}\left\langle {{{\rm{e}}^{{\rm{i}}\psi }}, \left({\boldsymbol{L}+\beta I} \right)\cdot {{\rm{e}}^{{\rm{i}}\psi }}-\beta {{\rm{e}}^{{\rm{i}}{\psi _p}}}} \right\rangle $ | (6) |
式中,eiψ=[eiψ1eiψ2 … eiψN]T;L为N阶通讯拓扑图的Laplacian矩阵,I为单位对角阵;β>0为队形保持系数;〈
| $ {{\dot V}_2}=\frac{1}{N}\sum\limits_{k=1}^N {\left\langle {i \cdot {{\rm{e}}^{{\rm{i}}\psi k}}, \left({\mathit{\boldsymbol{L}}{_k}+\beta {\mathit{\boldsymbol{I}}_k}} \right)\cdot {{\rm{e}}^{{\rm{i}}\psi }}-\beta {\mathit{\boldsymbol{I}}_k}\cdot{{\rm{e}}^{{\rm{i}}{\psi _p}}}} \right\rangle } \cdot {{\dot \psi }_k} $ | (7) |
期望的控制输入为
| $ \begin{array}{*{20}{c}} {{{\dot \psi }_{kd}}=-{K_1} \cdot \left\langle {{\rm{i}} \cdot {{\rm{e}}^{{\rm{i}}\psi k}}, \left({{\boldsymbol{L}_k}+\beta {\boldsymbol{I}_k}} \right)\cdot {{\rm{e}}^{{\rm{i}}\psi }}-\beta {\boldsymbol{I}_k}\cdot{{\rm{e}}^{{\rm{i}}{\psi _p}}}} \right\rangle, }\\ {{K_1} > 0} \end{array} $ | (8) |
对领航的水下机器人可在复数内积中加入制导项η Ik·eiψ-eiψg,其中eiψg为规划算法给出的制导角。
2.3 自适应舵角控制器定义误差变量zk=rk-
| $ {z_{\dot k}}={r_{\dot k}}{\rm{ }}-{{\ddot \psi }_{kd}}=-\frac{{{r_k}}}{T}-\frac{{\alpha {r_k}^3}}{T}+\frac{{K{\delta _k}}}{T}+{d_k}- {{\ddot \psi }_{kd}} $ |
选取Lyapunov函数为
| $ {V_3}={V_2}+\frac{1}{2}\sum\limits_{k=1}^N {{z_k}^2} $ | (9) |
对V3求导:
| $ \begin{array}{l} {{\dot V}_3}=\sum\limits_{k=1}^N {\left({\frac{1}{N} \cdot \left\langle {{\rm{i}} \cdot {{\rm{e}}^{{\rm{i}}\psi k}}, \left({{L_k}+\beta {I_k}} \right)\cdot } \right.} \right.} \\ \;\;\;\;\;\;\left.{\left.{{{\rm{e}}^{{\rm{i}} \cdot \psi }}-\beta \cdot{{\rm{e}}^{{\rm{i}}{\psi _p}}}} \right\rangle \cdot {{\dot \psi }_k}+{z_k} \cdot {{\dot z}_k}} \right) \end{array} $ | (10) |
选取滑模函数S=zk,则有舵角控制律为
| $ \begin{array}{l} {\delta _k}=\left({\frac{T}{K}\frac{{{r_k}}}{T}+\frac{{\alpha \cdot{r_k}^3}}{T}-D \cdot {\rm{sign}}({z_k})+{{\ddot \psi }_{kd}}-{K_2}\cdot{z_k}-} \right.\\ \;\;\left.{\frac{{\;1}}{N} \cdot{{\rm{e}}^{{\rm{i}}\cdot{\psi _k}}}, \left({{\boldsymbol{L}_k}+\beta {\boldsymbol{I}_k}} \right)\cdot{{\rm{e}}^{{\rm{i}}\cdot\psi }} - \beta \cdot{{\rm{e}}^{{\rm{i}}\cdot{\psi _p}}}} \right), {K_2} > 0 \end{array} $ | (11) |
由于系统建模误差上限D较难准确确定,取
| $ {V_4}={V_3}+\frac{1}{{2\gamma }}\sum\limits_{k=1}^N {{{\tilde d}_k}^2} $ | (12) |
对(12) 求导可得:
| $ \begin{align} & {{{\dot{V}}}_{4}}=\sum\limits_{k=1}^{N}{\left( -\frac{{{K}_{1}}}{N} \right.}\cdot {{\left\langle i\cdot {{\text{e}}^{\text{i}{{\psi }_{k}}}},\left( {{L}_{k}}+\beta {{I}_{k}} \right)\cdot {{\text{e}}^{\text{i}\psi }}-\beta \cdot {{\text{e}}^{\text{i}{{\psi }_{p}}}} \right\rangle }^{2}}- \\ & \ \ \ \ \ \ \left. {{K}_{2}}\cdot {{z}_{k}}^{2}+{{d}_{k}}\cdot {{z}_{k}}-{{{\hat{d}}}_{k}}\cdot \left| {{z}_{k}} \right|+\frac{1}{\gamma }{{{\tilde{d}}}_{k}}\cdot {{{\dot{\tilde{d}}}}_{k}} \right)= \\ & \ \ \ \ \ \ \sum\limits_{k=1}^{N}{\left( -\frac{{{K}_{1}}}{N} \right.}\cdot {{\left\langle i\cdot {{\text{e}}^{\text{i}{{\psi }_{k}}}},\left( {{L}_{k}}+\beta {{I}_{k}} \right)\cdot {{\text{e}}^{\text{i}\psi }}-\beta \cdot {{\text{e}}^{\text{i}{{\psi }_{p}}}} \right\rangle }^{2}}- \\ & \ \ \ \ \ \left. {{K}_{2}}\cdot {{z}_{k}}^{2}+{{{\hat{d}}}_{k}}\cdot {{z}_{k}}-{{{\hat{d}}}_{k}}\cdot \left| {{z}_{k}} \right|+{{{\tilde{d}}}_{k}}\cdot {{z}_{k}}-\frac{1}{\gamma }{{{\tilde{d}}}_{k}}\cdot {{{\dot{\tilde{d}}}}_{k}} \right) \\ \end{align} $ |
令
| $ \begin{matrix} {{\delta }_{k}}=\frac{T}{K}\left( \frac{{{r}_{k}}}{T}+\frac{\alpha \cdot {{r}_{k}}^{3}}{T}-{{{\hat{d}}}_{k}}\cdot \text{sign}({{z}_{k}})+{{{\ddot{\psi }}}_{kd}}- \right. \\ \ \ {{K}_{2}}\cdot {{z}_{k}}-\left. \frac{\ 1}{N}\cdot \langle i\cdot {{\text{e}}^{\text{i}{{\psi }_{k}}}},\left( {{K}_{k}}+\beta {{I}_{k}} \right)\cdot {{\text{e}}^{\text{i}\psi }}-\beta \cdot {{\text{e}}^{\text{i}{{\psi }_{p}}}}\rangle \right) \\ {{{\ddot{\psi }}}_{kd}}=-{{K}_{1}}\left[ \sum\limits_{j\in {{N}_{k}}}{\left\langle {{\text{e}}^{\text{i}{{\psi }_{k}}}},{{\text{e}}^{\text{i}{{\psi }_{j}}}} \right\rangle \left( {{{\dot{\psi }}}_{k}}\cdot {{{\dot{\psi }}}_{j}} \right)+} \right. \\ \left. \left\langle {{\text{e}}^{\text{i}{{\psi }_{k}}}},{{\text{e}}^{\text{i}{{\psi }_{{{p}_{k}}}}}} \right\rangle {{{\dot{\psi }}}_{k}} \right]{{{\dot{\hat{d}}}}_{k}}=\gamma \cdot {{z}_{k}} \\ \end{matrix} $ |
以REMUS模型[18]的水动力系数(见表 1) 进行仿真试验,艇体全长L=1.33 m,直径为0.191 m,质量m=30.51 kg,转动惯量Iz=3.45 kg·m2,单只舵翼的面积Sδ=6.65×10-3 m2,T=0.343 4,K=-0.643 0,K、T系数的计算参考文献[19]。选取非线性项系数α=5,控制参数K1=3,K2=3,γ=0.3。建模误差选取为实际模型的50%,即Tn=0.5T,Kn=1.5K,αn=1.5α,并加入白噪声作为外界干扰。仿真结果如图 5~8。
| Ṅr/(kg·m2) | Nv/(kg·m·s-1) | Ẏv/kg | Yv/(kg·s-1) | Nr/(kg·m2·s-1) | Nδ/(kg·m2·s-2) | Yr/(kg·m·s-1) | Yδ/(kg·m·s-2) |
| -4.88 | -30.7 | -35.5 | -66.6 | -6.87 | -6.15 | 9.67 | 9.64 |
|
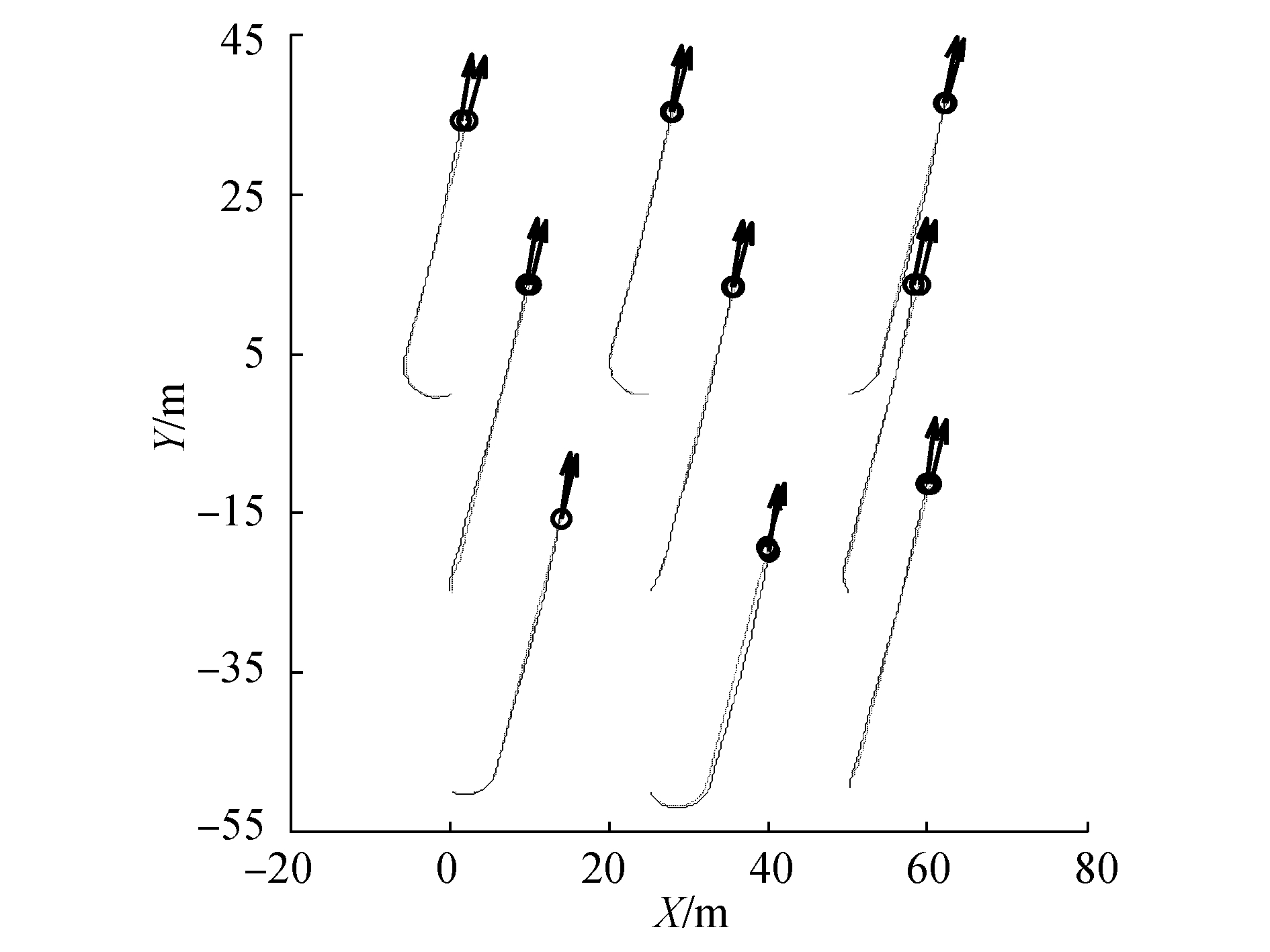
| 图5 多水下机器人运动轨迹 Figure 5 Trajectory of MAUV |
|
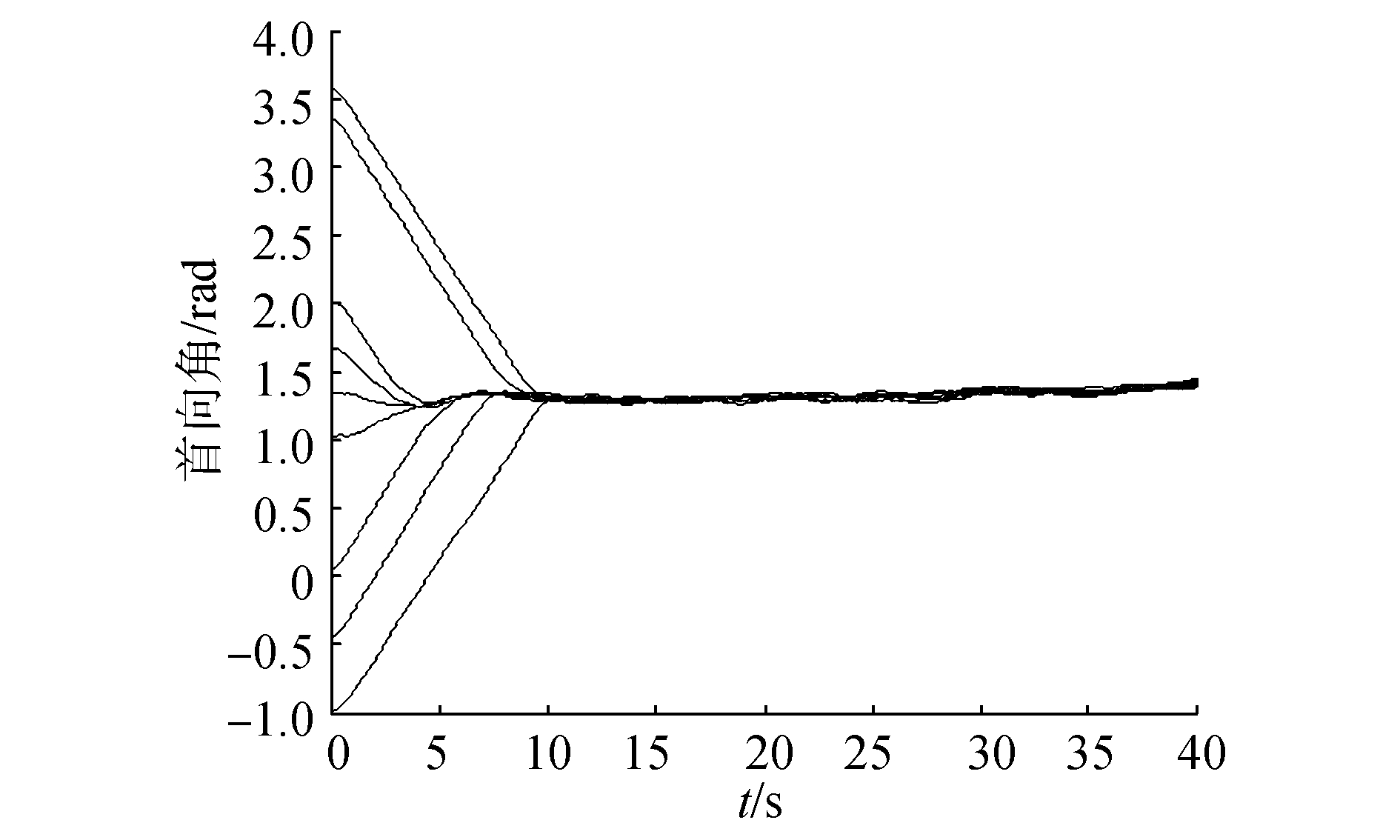
| 图6 多水下机器人艏向角 Figure 6 Heading of MAUV |
|
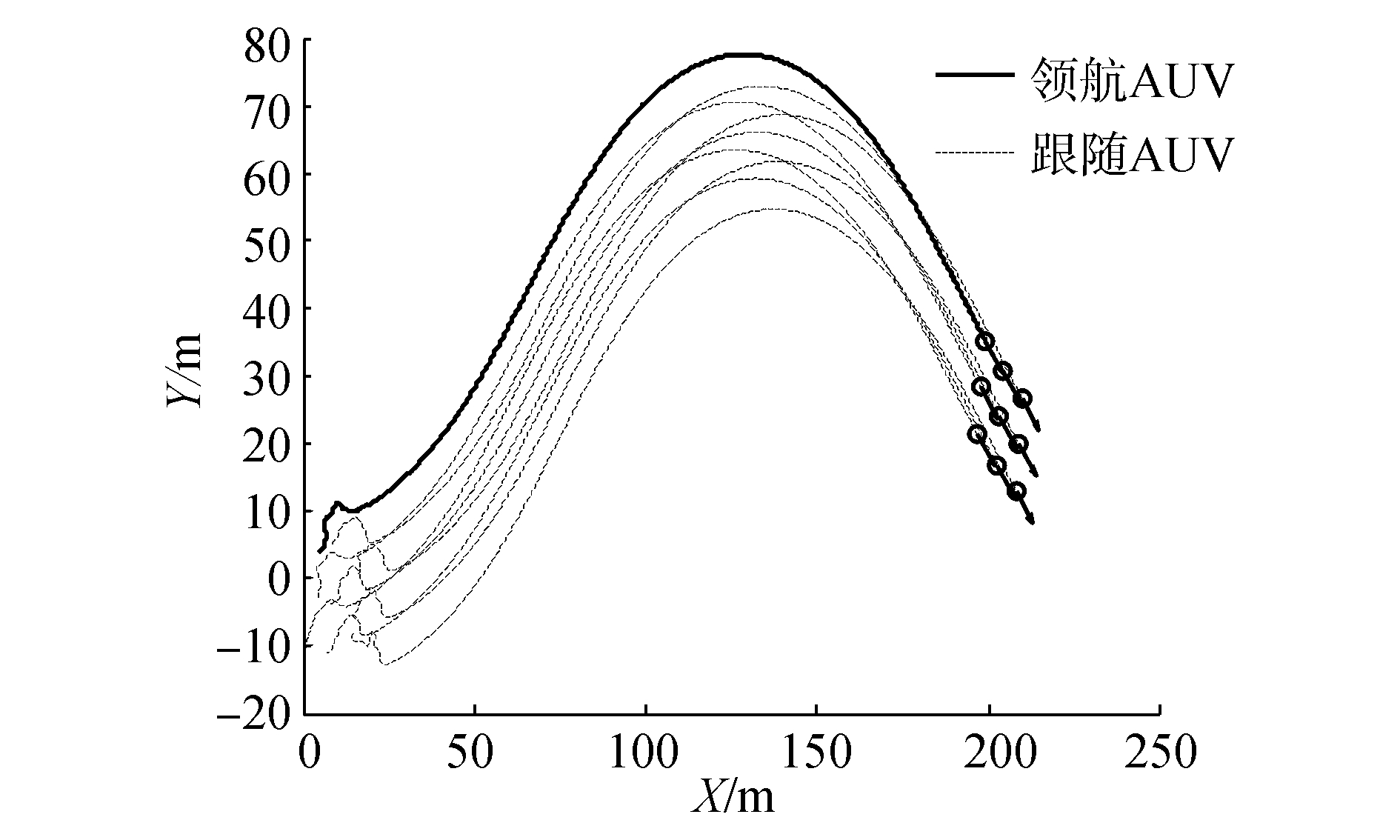
| 图7 具有领航者下多水下机器人曲线轨迹 Figure 7 Curve trajectory of MAUV with leader |
|
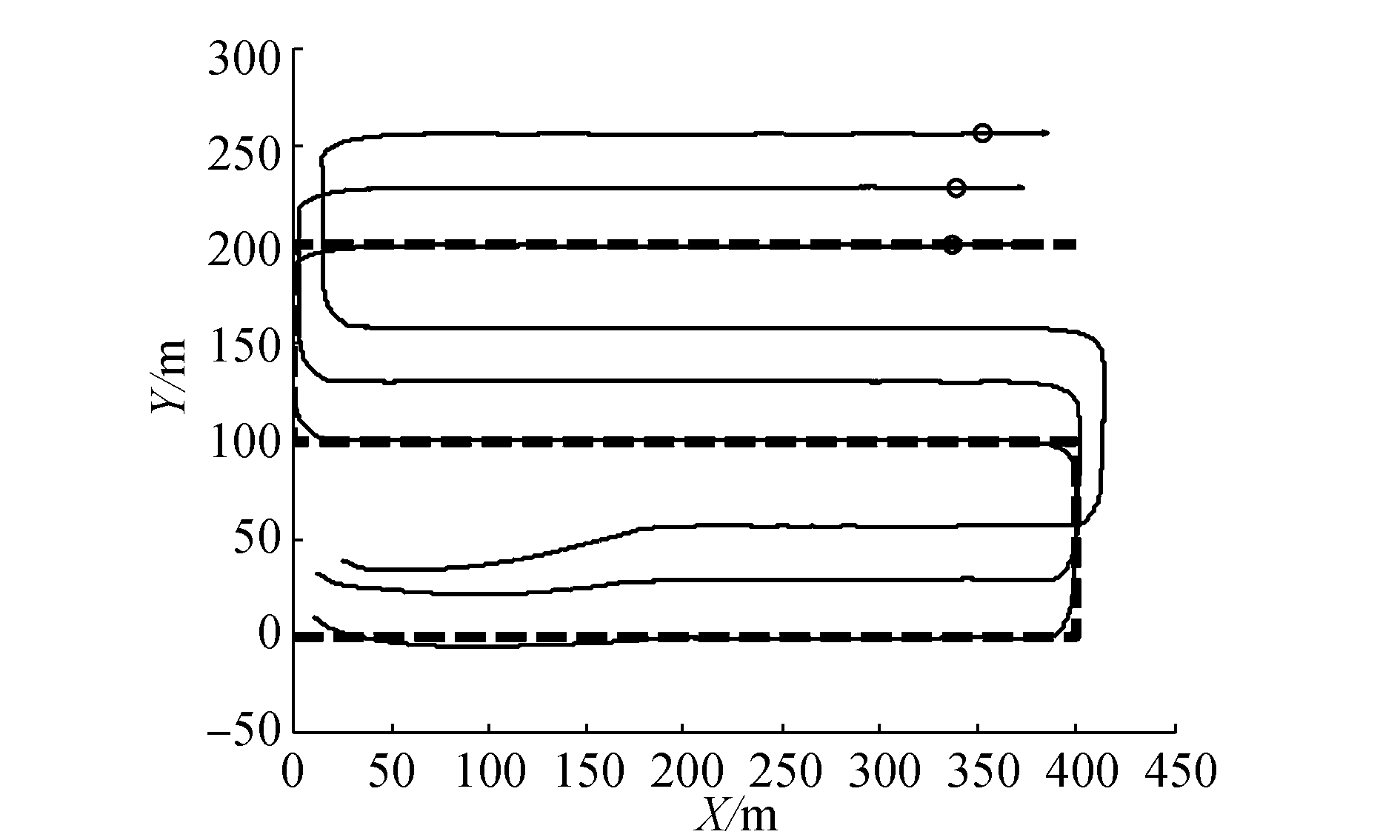
| 图8 LOS制导算法下多水下机器人梳状扫描 Figure 8 MAUV pectinate scanning using LOS guidance laws |
图 5为无领航者条件下9个水下机器人的运动轨迹,实线、虚线分别为有建模误差和环境干扰的条件下、理想条件下,多水下机器人的运动轨迹;圆圈代表当前水下机器人的位置;箭头代表水下机器人的艏向角,即速度的方向。图 6为9个水下机器人的艏向角随时间变化的曲线,初始时刻多水下机器人的艏向角在(-π, π]范围内的随机分布。由图可见,经过一定时间的调整,多水下机器人的艏向趋一致,收敛至一个艏向均值,在外界干扰的作用下,有小幅的波动,但仍表现出较好的稳定性。多水下机器人相互之间保持了较好的相对距离,逐渐形成类晶格状的队形。通过比较实际条件和理想条件下多水下机器人的运动轨迹可知,自适应舵角控制器,有效地抵制了建模误差和外界干扰的影响,使实际轨迹趋向于理想值。
图 7为在有领航者条件下9个水下机器人曲线运动轨迹。领航者的艏向以π/4为幅值,做正弦周期性变化,从而形成近似正弦曲线的运动轨迹。跟随者则随同领航者做相似的运动。在仿真初期,水下机器人群体经过一定时间的调整逐渐形成队形,并达到相同的艏向,并在行进过程中表现出良好的稳定性。仿真实验表明基于相位耦合振子模型的自适应编队控制算法,可有效适用于多水下机器人曲线运动和曲线路径跟踪的应用场景。
图 8为在有领航者条件下3个水下机器人梳状扫描的运动轨迹。水下机器人的初始位置在50 m×50 m的矩形区域内随机产生,设置相互间的期望距离为30 m。扫描的路径点为:(0, 0),(400, 0),(400, 100),(0, 100),(0, 200),(400, 200)。由图可见,领航者在LOS (line of sight) 制导算法下,由初始位置收敛至扫描路径。跟随者则随同领航者进行路径扫描,并产生了期望距离的偏移。3个水下机器人对扫描区域,进行了有效的覆盖,只进行单一条次的实验,就完成了对未知区域的有效探测。在扫描过程中,3个水下机器人保持了稳定的相互距离和艏向一致性,即使在通过直角转弯的过程中,也具有良好的队形。
4 结论本文基于相位耦合振子模型提出了一种多水下机器人协同编队的新方法。理论推导和仿真实验表明,所提出的算法可有效实现多水下机器人的编队形成和编队保持,保证艏向一致,在建模误差和外界干扰的影响下,具有良好的稳定性。同时,编队算法对路径形状并不敏感,可有效适用于直线路径跟踪和曲线路径跟踪。在领航者具有规划信息的条件下,整个编队可以跟随领航者跟踪期望的路径。相比于单个水下机器人,多水下机器人编队进行海洋区域扫描,可以增大扫描路径间隔,减小扫描作业时间和母船等待时间,极大地提高作业效率和经济性,表明所提出的算法在环境探测领域中具有实际的应用价值。
| [1] | ABREU P, BAYAT M, BOTELHO J, et al. Cooperative control and navigation in the scope of the EC CADDY project[C]//Proceedings of OCEANS 2015-Genova. Genova, Italy, 2015:1-5. |
| [2] | DE SOUSA J B, PEREIRA J, ALVES J, et al. Experiments in multi-vehicle operations:the rapid environmental picture atlantic exercise 2014[C]//Proceedings ofOCEANS 2015-Genova. Genova, Italy, 2015:1-7. |
| [3] | BAHR A, LEONARD J J, MARTINOLI A. Dynamic positioning of beacon vehicles for cooperative underwater navigation[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. Vilamoura, Algarve, Portugal, 2012:3760-3767. |
| [4] | BOLONI L, TURGUT D, BASAGNI S, et al. Scheduling data transmissions of underwater sensor nodes for maximizing value of information[C]//Proceedings of IEEE Global Telecommunications Conference. Atlanta, GA, United States, 2013:438-443. |
| [5] | RAMP S R, DAVIS R E, LEONARD N E, et al. Preparing to predict:the second autonomous ocean sampling network (AOSN-Ⅱ) experiment in the Monterey Bay[J]. Deep sea research part Ⅱ:topical studies in oceanography, 2009, 56(3/4/5): 68–86. |
| [6] | JIANG Dapeng, PANG Yongjie, QIN Zaibai. Coordinated control of multiple autonomous underwater vehicle system[C]//Proceedings of the 8th World Congress on Intelligent Control and Automation. Ji'nan, China, 2010:4901-4906. |
| [7] | DJAPIC V. Unifying behavior based control design and hybrid stability theory for AUV application[D]. Riverside:University of California, 2009:72-105. |
| [8] | HOU S P, CHEAH C C. Can a simple control scheme work for a formation control of multiple autonomous underwater vehicles[J]. IEEE transactions on control systems technology, 2011, 19(5): 1090–1101. DOI:10.1109/TCST.2010.2076388 |
| [9] |
黄海, 张强, 张树迪, 等. 欠驱动AUV自适应编队控制策略[J].
哈尔滨工程大学学报, 2015, 36(5): 633–637, 643.
HUANG Hai, ZHANG Qiang, ZHANG Shudi, et al. Adaptive formation control strategy for under-actuated AUVs[J]. Journal of Harbin engineering university, 2015, 36(5): 633–637, 643. |
| [10] | CUI Rongxin, GE S S, VOON Ee How B, et al. Leader-follower formation control of underactuated AUVs with leader position measurement[C]//Proceedings of IEEE International Conference on Robotics and Automation. Kobe, Japan, 2009:979-984. |
| [11] | WINFREE A T. Biological rhythms and the behavior of populations of coupled oscillators[J]. Journal of theoretical biology, 1967, 16(1): 15–42. DOI:10.1016/0022-5193(67)90051-3 |
| [12] | KURAMOTO Y. Self-entrainment of a population of coupled non-linear oscillators[M]//ARAKI H. International Symposium on Mathematical Problems in Theoretical Physics. Berlin Heidelberg:Springer, 1975, 1:420-422. |
| [13] | VICSEK T, CZIRóK A, BEN-JACOB E, et al. Novel type of phase transition in a system of self-driven particles[J]. Physical review letters, 1995, 75(6): 1226–1229. DOI:10.1103/PhysRevLett.75.1226 |
| [14] | OLFATI-SABER R. Swarms on sphere:a programmable swarm with synchronous behaviors like oscillator networks[C]//Proceedings of the 45th IEEE Conference on Decision and Control. San Diego, CA, USA, 2006:5060-5066. |
| [15] | PAPACHRISTODOULOU A, JADBABAIE A. Synchronization in oscillator networks:switching topologies and non-homogeneous delays[C]//Proceedings of the 44th IEEE Conference on Decision and Control, and the European Control Conference. Seville, Spain, 2005:5692-5697. |
| [16] | PALEY D A, LEONARD N E, SEPULCHRE R, et al. Oscillator models and collective motion[J]. IEEE control systems magazine, 2007, 27(4): 89–105. DOI:10.1109/MCS.2007.384123 |
| [17] | OLFATI-SABER R. Flocking for multi-agent dynamic systems:algorithms and theory[J]. IEEE transactions on automatic control, 2006, 51(3): 401–420. DOI:10.1109/TAC.2005.864190 |
| [18] | PRESTERO T. Verification of a six-degree of freedom simulation model for the REMUS autonomous underwater vehicle[D]. Massachusetts:Massachusetts Institute of Technology, 2001:102-112. |
| [19] | 施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995: 43. |



