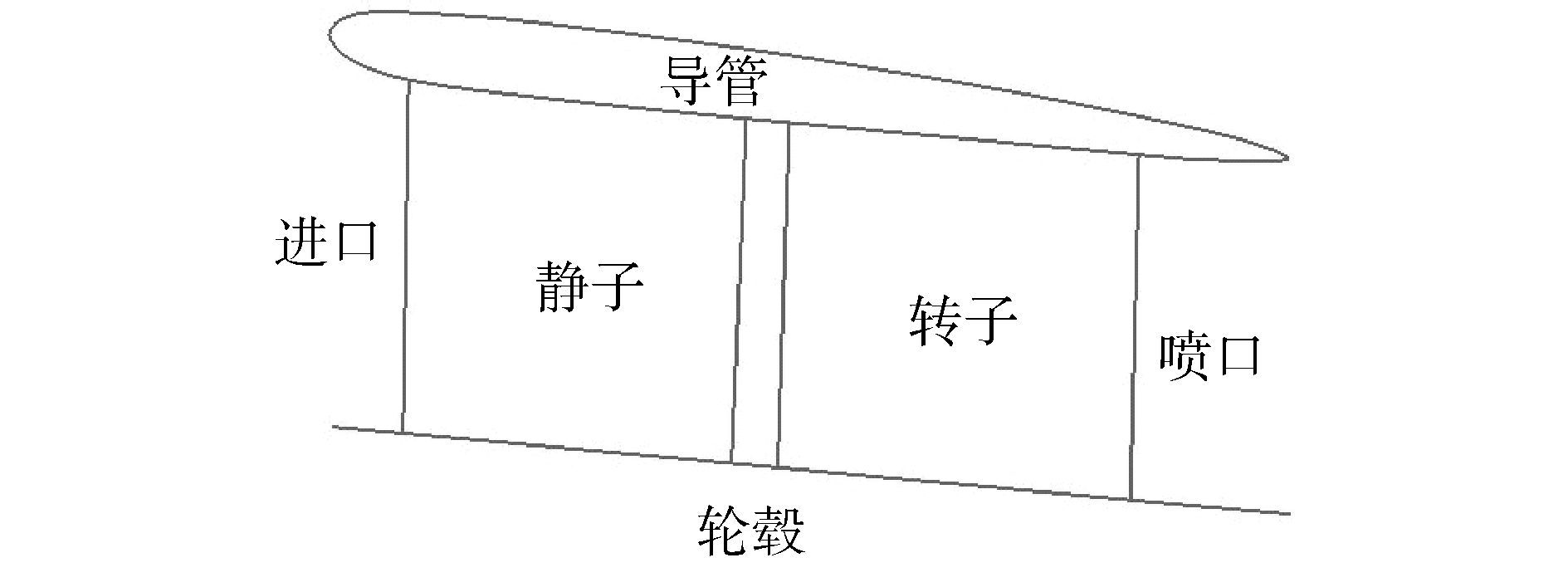
泵喷推进器主要由导管、转子和静子组成[1],分为两类:一类是静子布置在转子的前面,称为前漩式;另一类是静子布置在转子的后面,称为后漩式[2]。导管的存在能够保护转子叶片,减少转子叶梢滑流损失,防止水草缠绕、叶片碰损和落水者人身安全威胁,类似于导管桨。静子的存在虽然加大了过流面积而增大摩擦损失,却能够使转子来流产生预旋或吸收转子尾流的旋转能量,使得射流轴向分量高达99.4%以上,同时用于固定导管。上述优点使得泵喷的安全性、推进效率高于螺旋桨和导管桨。此外泵喷还具有水下辐射噪声低,临界航速高等优点[3]。近年来泵喷在潜艇(如美国seawolf、Virginia攻击核潜艇和英国Trafalgar、Astute攻击核潜艇),鱼雷(Mark50、Mark18等),摩托艇、两栖登陆战车等领域逐步得到发展。
反问题设计方法主要分为流场计算和叶片形状计算2个部分,叶片形状基于流场计算结果进行迭代改进并一次性确定出最优叶轮[4],摆脱依赖传统设计经验,重复模型校验和叶轮改进的繁琐过程。基于该方法,肖若富将某混流泵进一步优化,水力效率提高3.2%[5]。杨魏利用自编程序,将三维反问题设计方法应用到离心风机叶轮的设计计算中,并指出三维反问题设计方法可运用到各种叶轮机械[6]。靳栓宝基于三维反问题设计方法和CFD数值模拟研究了叶片重载位置对轴流泵抗空化特性和水力效率的影响[7],所设计混流泵在设计点效率达到90.5%[8]。常书平基于三元反问题设计方法,研究了转子叶片随边轮毂到轮缘环量(即负载)分布规律对混流泵的性能影响[9]。和螺旋桨相比,喷水推进轴流泵本身具有流量大、推进效率高、抗空泡能力强和噪声低的特点[10]。本研究结合三维反问题设计和CFD数值模拟手段,设计了一款前漩式泵喷推进器,旨在设计出一款推进性能优于某国外滑行艇原配螺旋桨的泵喷。
1 泵喷选型及三维反问题设计方法已知滑行艇阻力曲线f=R(Vs)、排水量mship、设计航速、所用主机功率PD、转速n和齿轮箱减速比。假定传动系统效率ηm为0.97,泵喷效率ηm一般为0.9左右,相对旋转效率ηr用于反映进流不均匀对泵喷效率的影响程度,其大小可近似取为0.99。待求参数有泵喷喷速比μ、出口直径Dj、流量Q、扬程H。设α为船体边数为ψ,喷口射流速度为Vj,则泵喷有效功率为
| $ {P_{PE}} = \frac{1}{2}\left( {1 + \psi } \right)\rho QV_j^2 - \frac{1}{2}\beta \rho QV_s^2 $ | (1) |
泵喷有效推力功率为
| $ {P_{TE}} = \rho Q{V_s}\left( {{V_j} - \alpha {V_s}} \right) $ | (2) |
在求取泵喷推进器主要设计参数时以喷射效率最佳为出发点,求出使得喷射效率最大时的喷速比:
| $ {\eta _j} = \frac{{{P_{TE}}}}{{{P_{PE}}}} = \frac{{2\left( {\mu - \alpha } \right)}}{{\left( {1 + \psi } \right){\mu ^2} - \beta }} $ | (3) |
式中:μ=Vj/Vs,两边求导可得到最佳喷速比为
| $ {\mu _{{\rm{opt}}}} = \alpha + \sqrt {{\alpha ^2} - \beta } $ | (4) |
μopt的确定用于后续泵喷喷口的尺寸、扬程等其他重要参数的选取。
考虑到船体推力减额的作用,船体运动动力学方程为
| $ \frac{{{P_{TE}}}}{{{V_S}}}\left( {1 - t} \right) - R = {m_{{\rm{ship}}}}a $ | (5) |
式中:t为推力减额,该值随航速不同而变化;R为裸船阻力;a为船体运动加速度。
当船体阻力与推力平衡时,船体航速稳定,加速度为零,可求得喷口喷射速度为
| $ {V_j} = \mu {V_S} $ | (6) |
泵的扬程:
| $ H = \frac{{\left( {{\mu ^2} - \beta } \right)V_S^2}}{{2g}} $ | (7) |
泵的流量:
| $ Q = \frac{{{p_{PE}}}}{{\rho gH}} $ | (8) |
进而确定喷口直径:
| $ {D_j} = \sqrt {\frac{{4Q}}{{{\rm{\pi }}Vj}}} $ | (9) |
泵喷比转速:
| $ {n_s} = \frac{{3.65n{Q^{1/2}}}}{{{H^{3/4}}}} $ | (10) |
式(1)~(10) 中多个模块的计算用到了船体边界层模块计算结果的反馈,船体计算模块中进流面直径为α,进流面上流量Q以及α和β值的确定更加复杂。
对于中小型船舶采用Prandtl公式求取边界层厚度δ更加合适[11],Prandtl公式为
| $ \delta = 0.37{L_x}{\left( {\mathit{Re}} \right)^{ - 1/5}} = 0.37{L_x}{\left( {\frac{{{V_s}{L_x}}}{v}} \right)^{ - 1/5}} $ | (11) |
式中:Lx为船艏至进流面的纵向距离,Re为船舶运动雷诺数,ν为水的运动粘度。边界层厚度内相应过流面内流量为
| $ {Q_\delta } = \int_A {{V_s}{{\left( {\frac{y}{\delta }} \right)}^{\frac{1}{n}}}{\rm{d}}A} $ | (12) |
式中n为边界层速度分布指数。
当泵喷进流面直径d<δ时,
| $ {Q_1} = \frac{1}{8}\int\limits_0^{2{\rm{\pi }}} {{d^2}{V_s}{{\left( {\frac{y}{\delta }} \right)}^{\frac{1}{n}}}{\rm{d}}\theta } $ | (13) |
当d≥δ时,
| $ {Q_2} = \frac{1}{8}\int\limits_{{\theta _1}}^{\pi - {\theta _1}} {{d^2}{V_s}{{\left( {\frac{y}{\delta }} \right)}^{\frac{1}{n}}}{\rm{d}}\theta } + \frac{1}{8}\int\limits_{\pi - {\theta _1}}^{2\pi + {\theta _1}} {{d^2}{V_s}{\rm{d}}\theta } $ | (14) |
首先根据航速求取进流面处边界层厚度进而求取边界层内进流面流量Qδ,在此基础上将计算所得的边界层流量与泵喷流两计算值Q进行比较,分Q<Qδ和Q≥Qδ两种情况分别对进流面直径d、进流动量影响系数α和进流动能系数β进行求解,将这些参数输出到泵喷选型求解模块中,统一借助Matlab/Simulink仿真平台,搭建泵喷推进器选型程序,可最终确定泵喷选型。
泵喷选型后可初步确定出轴面投影图,在此基础上采用三维反问题设计方法对转子和静子叶片进行叶型求解。三维反问题设计方法包括流场计算和叶片形状求解两部分,流场计算时假设求解流场为无黏不可压有势流。需定义的求解条件有泵流量、转速、转子叶片数、静子叶片数和叶片负载分布。求解叶片形状时以涡片代替叶片对流动的作用,即假设叶片无限薄,原理同圆弧法叶片设计基本一致,涡片强度由周向环量2πrVθ决定[12-13]。流场计算时将三维速度场分解为周向平均速度和周向周期速度进行正命题求解,在柱坐标系中:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{\bar V}} + \mathit{\boldsymbol{\tilde V}} $ | (15) |
假设来流均匀无旋,V连续,∇·V=0,又固体壁面上满足V·n=0,可求得:
叶片区平均流动流函数方程:
| $ \frac{{{\partial ^2}\mathit{\Psi }}}{{\partial {r^2}}} - \frac{1}{r}\frac{{\partial \mathit{\Psi }}}{{\partial r}} + \frac{{{\partial ^2}\mathit{\Psi }}}{{\partial {z^2}}} = - r\left[ {\frac{{\partial f}}{{\partial z}}\frac{{\partial r{{\bar V}_\theta }}}{{\partial r}} - \frac{{\partial f}}{{\partial r}}\frac{{\partial r{{\bar V}_\theta }}}{{\partial z}}} \right] $ | (16) |
非叶片区平均流动流函数方程:
| $ \frac{{{\partial ^2}\mathit{\Psi }}}{{\partial {r^2}}} - \frac{1}{r}\frac{{\partial \mathit{\Psi }}}{{\partial r}} + \frac{{{\partial ^2}\mathit{\Psi }}}{{\partial {z^2}}} = 0 $ | (17) |
式中:n为壁面矢量,Ψ为引入流函数,f为叶片包角,rVθ为周向平均速度矩。
叶片区周期流动流函数方程:
| $ {\nabla ^2}\mathit{\Phi }\left( {r,\theta ,z} \right) = T\left( S \right) \cdot {\nabla ^2}r{{\bar V}_\theta } + T'\left( S \right)\left( {\nabla r{{\bar V}_\theta } \cdot \nabla S} \right) $ | (18) |
非叶片区周期流动流函数方程:
| $ {\nabla ^2}\mathit{\Phi }\left( {r,\theta ,z} \right) = 0 $ | (19) |
| $ \begin{array}{l} T\left( S \right) = \sum\limits_{K = 1}^\infty {\frac{2}{{KB}}\cos \left( {KBf} \right)\sin \left( {KB\theta } \right)} - \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_{K = 1}^\infty {\frac{2}{{KB}}\sin \left( {KBf} \right)\cos \left( {KB\theta } \right)} \end{array} $ | (20) |
式中:Φ为势函数,S为叶面位置函数,B为叶片数。
根据速度在叶片表面满足无滑移条件进行三维叶片形状的反命题求解,在无厚度叶面上,相对流速与叶面相切与叶片法向矢量正交,可得叶片设计方程:
| $ \left( {{{\bar V}_Z} + {v_{zb1}}} \right)\frac{{\partial f}}{{\partial z}} + \left( {{{\bar V}_r} + {v_{rb1}}} \right)\frac{{\partial f}}{{\partial r}} = \frac{{r{{\bar V}_\theta }}}{{{r^2}}} + \frac{{{v_{\theta b1}}}}{r} - \omega $ | (21) |
式中:ω为叶轮转速,rVθ为速度矩,反映周向环量值,即叶片负载。正反命题的求解和迭代实现以选型结构为基础的叶片形状和流场的三维计算,并最终确定出最优叶轮或静子。叶片负载分布决定叶片形状,叶片正面与背面的相对速度(Wb+-Wb-)的方向既垂直于法向矢量又垂直于旋度方向,则叶片正面与背面的速度跳跃为
| $ W_b^ + - W_b^ - = \frac{{2{\rm{\pi }}}}{B}\frac{{\left( {\nabla r{{\bar V}_\theta } \times \nabla S} \right) \times \nabla S}}{{\nabla S \times \nabla S}} $ | (22) |
沿流线应用无粘流场伯努利方程简化为
| $ {P^ + } - {P^ - } = \frac{{2{\rm{\pi }}}}{B}\rho {W_{mbl}}\frac{{\partial r{{\bar V}_\theta }}}{{\partial m}} $ | (23) |
式中:Wmbl为轴面相对叶面速度,m为叶片流线轴面投影长度,rVθ的值等于∂rVθ/∂m沿流线轴面投影长度的积分,因此作为叶片载荷的控制参数,其分布规律对混流泵性能有重要影响,这种加载方式能够更有效地控制设计结果[14-15]。确定出叶型后,对叶片进行NACA厚度分布,最后利用软件CFX对所得泵喷进行三维粘性流场计算以获得精确的水力特性。
2 CFD数值模拟验证及滑行艇敞水桨水力特性计算基于软件CFX,采用剪切应力输运(SST)湍流模型联立不可压连续方程对RANS方程进行求解,SST湍流模型通过混合函数在自由流动区域和近壁面区域分别调用k-ε湍流模型和k-ω湍流模型,综合二者的优点跳过壁面函数而较好地模拟粘性底层流动[16]。
2.1 数值模拟方法验证为验证数值模拟手段的可信性,首先以E779A桨和KaMeWa71sⅡ型喷水推进泵为对象进行数值计算。E779A桨直径为0.227 m,螺距为0.25 m,桨叶数为4叶,盘面比为68.9%,计算域设置及桨叶结构化网格如图 1所示,其中D为桨直径。
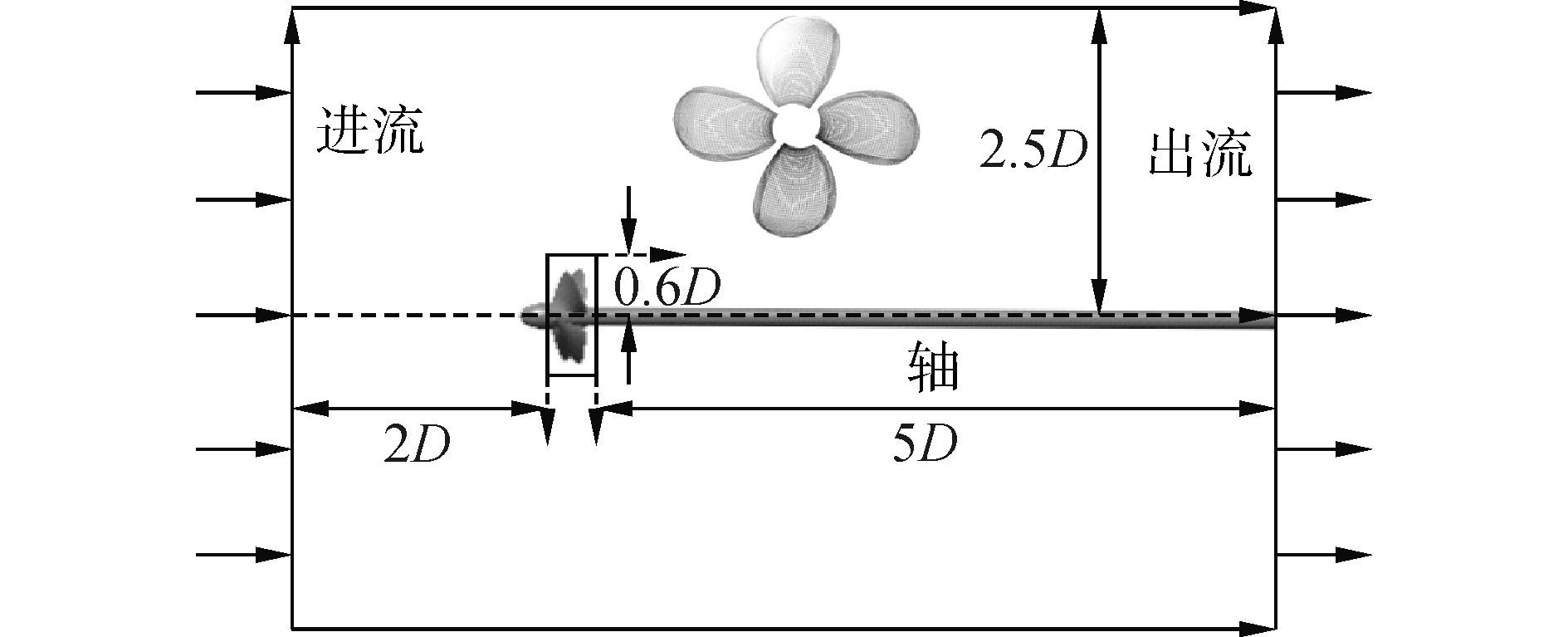
|
| 图1 敞水桨计算域与边界条件 Figure 1 Computational domain and boundary conditions |
参照文献[17]的试验条件,转速r=707.3 r/min,进速系数0.3≤J≤1.2,利用CFX软件求得不同进速系数下的推力系数Kt=T/(ρn2D4)、力矩系数Kq=Q/(ρn2D5)和推进效率η=JKt/(2πKq)的实际值。从图 2中可以看出,很大范围内推力系数和力矩系数与试验值吻合较好,最大误差为3.1%。
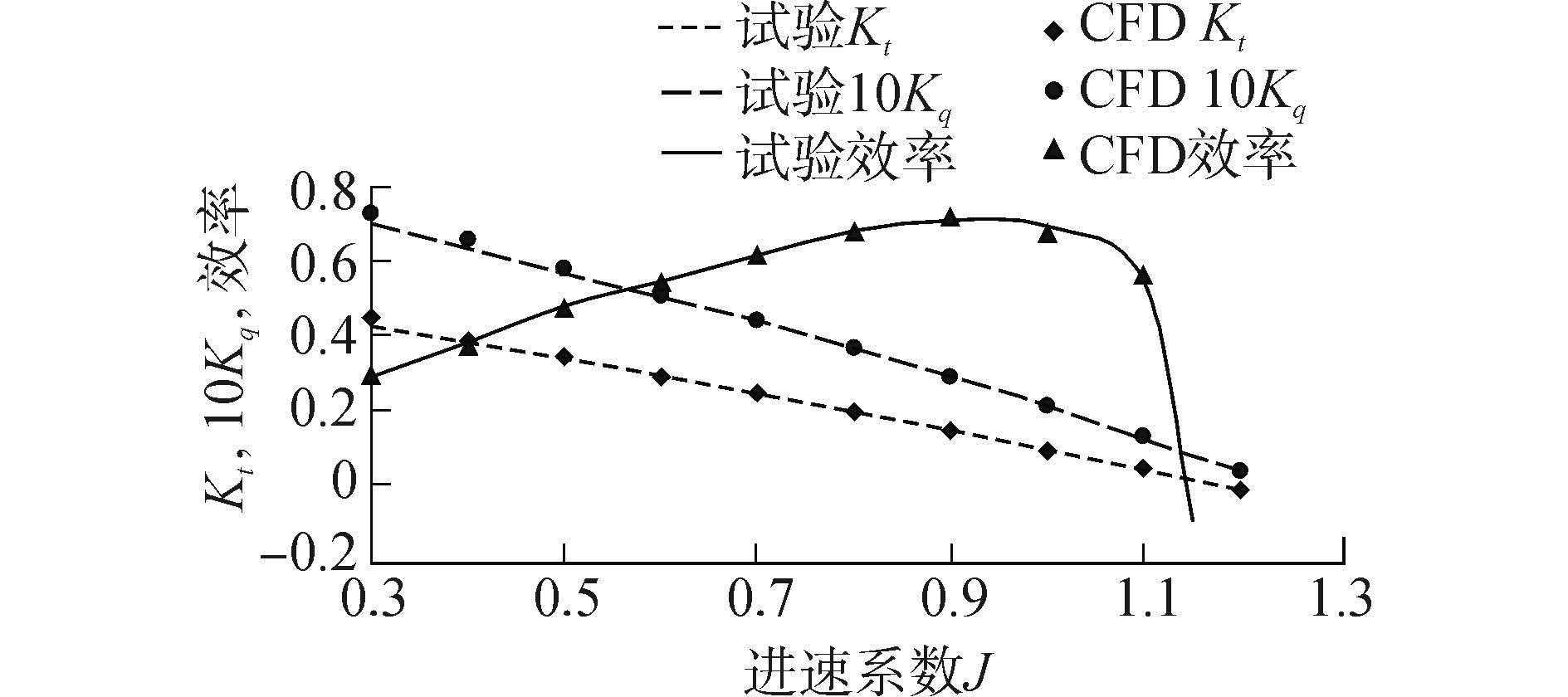
|
| 图2 数值模拟与实验值的对比 Figure 2 Results comparison with experimental data |
KaMeWa71sⅡ混流泵几何如图 3所示,叶轮进口直管处直径为710 mm,叶轮有6片,11片导叶,比转速ns=445,设计工况转速n0=880 r/min。
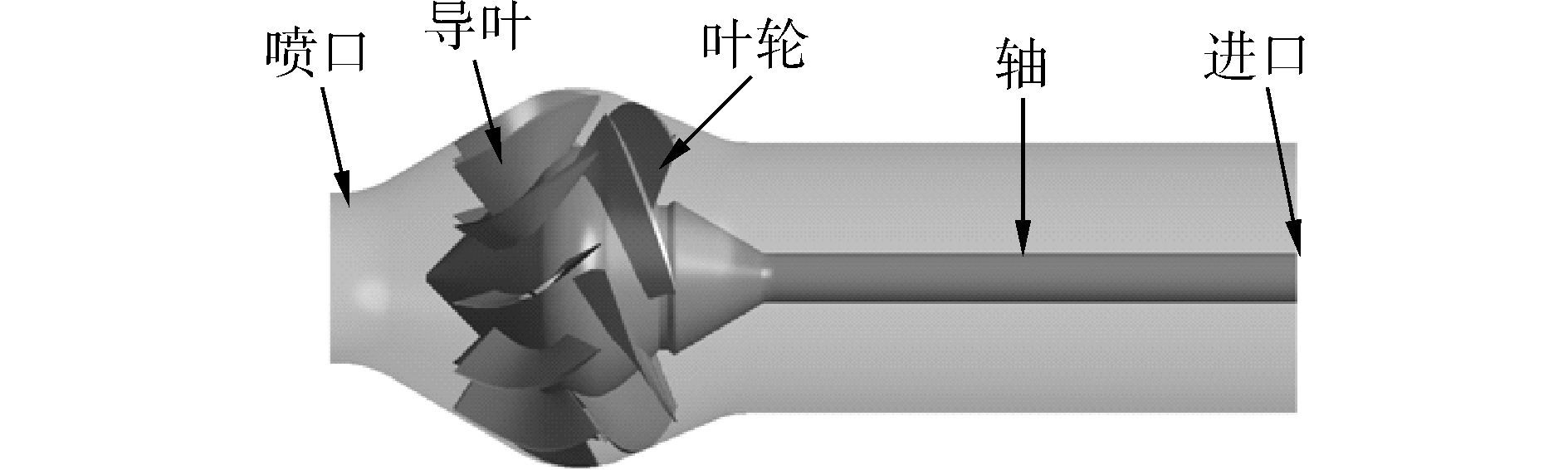
|
| 图3 KaMeWa71sⅡ混流泵几何 Figure 3 Geometry of KaMeWa71sⅡ mixed-flow pump |
对数值计算结果和厂商提供实验数据进行归一化处理,该混流泵功率对比情况见表 1,最大误差为1.9%,数值计算所得流线情况见图 4。
| 转速/(r·min-1) | 计算值/kW | 实验值/kW | 相对误差/% |
| 700 | 1.019 | 1 | 1.9 |
| 800 | 1.014 | 1 | 1.4 |
| 900 | 1.017 | 1 | 1.7 |
| 1 000 | 1.015 | 1 | 1.5 |
| 1 100 | 1.016 | 1 | 1.6 |
| 1 200 | 1.015 | 1 | 1.5 |

|
| 图4 喷泵流线图 Figure 4 Streamline of waterjet pump |
两个案例的验证表明,本文方法在螺旋桨和泵类旋转机械的数值计算上满足工程要求。
2.2 滑行艇原配螺旋桨水力特性计算国外滑行艇所用螺旋桨直径为0.347 m,艇满载最高航速可达38 km/h,桨叶为3叶,主机功率为42 kW,无减速齿轮箱,转速2 200 r/min。用同样方法对其进行进速系数0.3≤J≤1.2工况的敞水计算,求得相应工况下水力特性参数如表 2所示。
| J | 航速/(km·h-1) | Kt | 10Kq | 推力/N | 功率/kW | 效率/% |
| 0.2 | 9.16 | 0.407 | 0.662 | 7 935 | 103.0 | 19.6 |
| 0.3 | 13.74 | 0.366 | 0.603 | 7 131 | 94.0 | 29.0 |
| 0.4 | 18.32 | 0.325 | 0.546 | 6 336 | 85.1 | 37.9 |
| 0.5 | 22.9 | 0.283 | 0.488 | 5 507 | 76.0 | 46.1 |
| 0.6 | 27.48 | 0.240 | 0.428 | 4 668 | 66.7 | 53.4 |
| 0.7 | 32.06 | 0.197 | 0.369 | 3 831 | 57.4 | 59.4 |
| 0.8 | 36.64 | 0.156 | 0.312 | 3 034 | 48.7 | 63.5 |
| 0.9 | 41.22 | 0.116 | 0.255 | 2 251 | 39.7 | 64.9 |
| 1.0 | 45.8 | 0.074 | 0.192 | 1 440 | 29.9 | 61.3 |
| 1.05 | 48.09 | 0.053 | 0.157 | 1 017 | 24.5 | 55.8 |
| 1.1 | 50.38 | 0.029 | 0.121 | 574 | 18.8 | 42.8 |
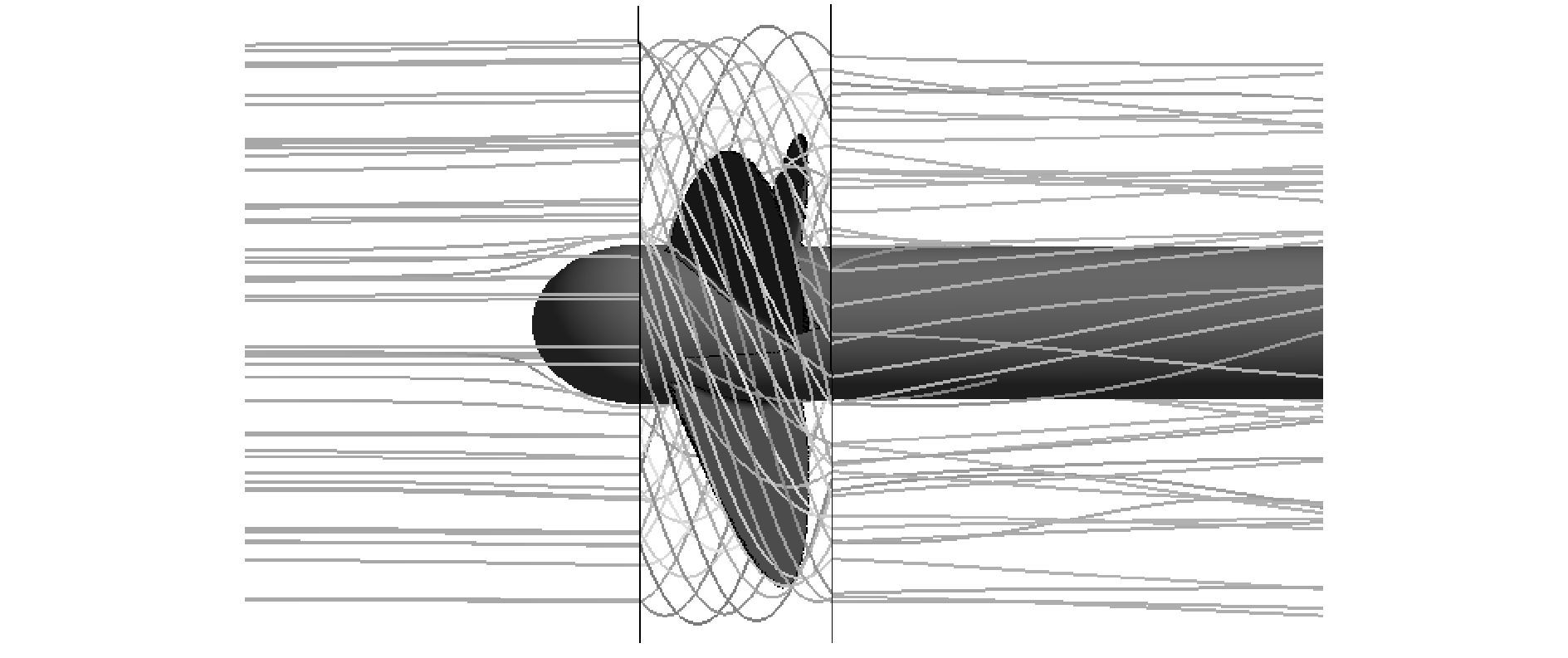
可知J=0.9为桨设计工况,且此时的航速和桨接收功率均与艇最高航速、主机功率接近,说明该国外螺旋桨是为匹配该艇特别制造,此时桨推进效率为64.9%,推力2 221 N,桨功率39.7 kW,取叶片表面相对压力云图如图 5所示,认为深色区域发生空化,可以看出在设计工况螺旋桨基本无空化。此时其流线情况如图 6所示。
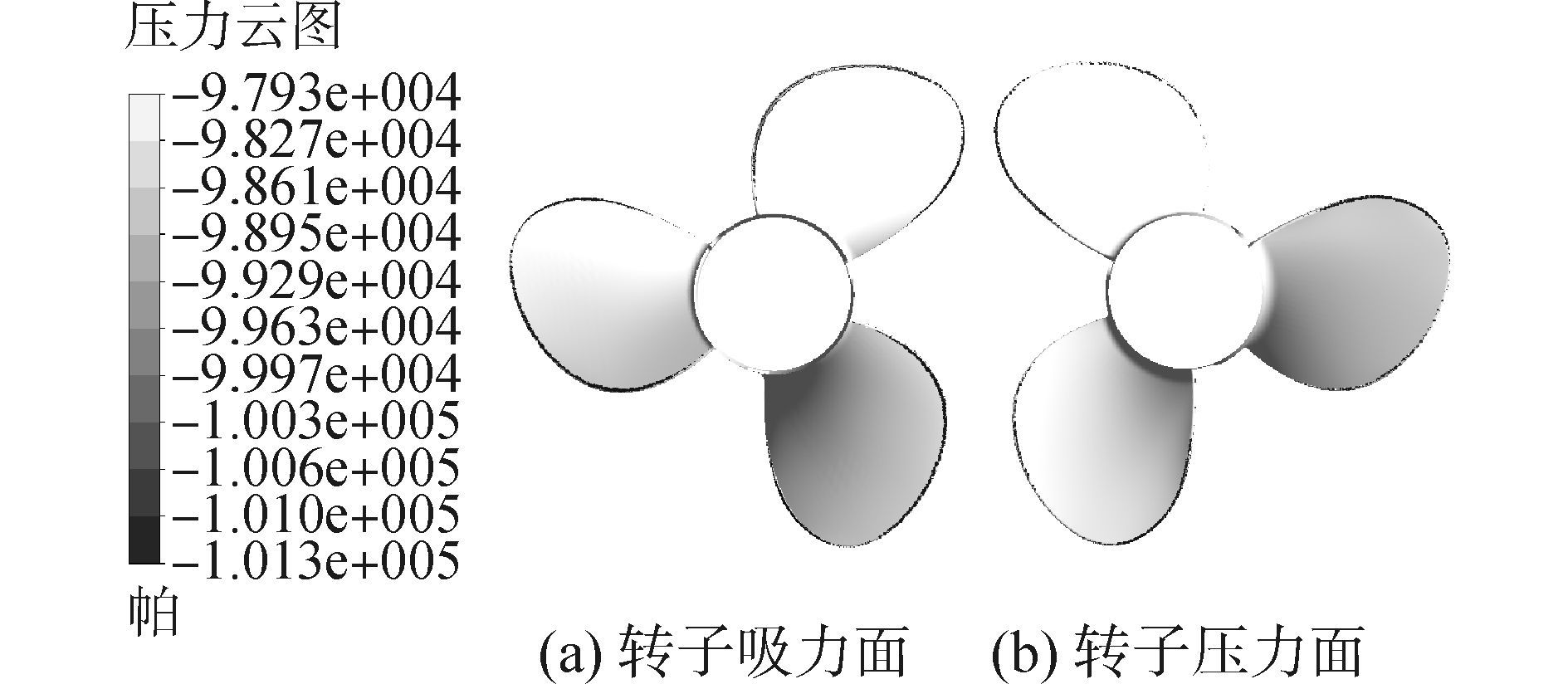
|
| 图5 桨叶空化情况 Figure 5 Pressure distribution in propeller blades |
|
| 图6 敞水桨流线图 Figure 6 Streamlines of open water propeller |
基于上述螺旋桨敞水特性,对泵喷设计提出要求为:转速为主机转速n=2 200 r/min,设计航速大于等于桨对应航速,本文定义为42 km/h,设计工况下泵喷功率小于41 kW,推力大于螺旋桨推力。滑行艇艇长Lx=5.6 m,满载(12人)排水量约为mship=1.7 t,泵喷设计需要厂家提供艇试航的阻力曲线,由于厂家未提供阻力曲线且滑行艇船型涉密,设计泵喷所用曲线是结合螺旋桨推力曲线和泵喷性能要求所定,泵喷选型结果为:流量Q=0.496 m3/s,H=7.4 m,喷口直径Dj=0.213 m,进口直径Ds=0.268 m,转子叶片数定义为4片,由以往设计经验可得,转子叶片叶顶间隙在0.1 mm内浮动对泵喷推力、功率、效率影响不大,结合现行的泵制造工艺,此处定义叶顶间隙为0.25 mm。静子导叶数定义为6片,轴面线如图 7。
|
| 图7 泵喷轴面投影图 Figure 7 Drawing of meridional cross-section of pumpjet |
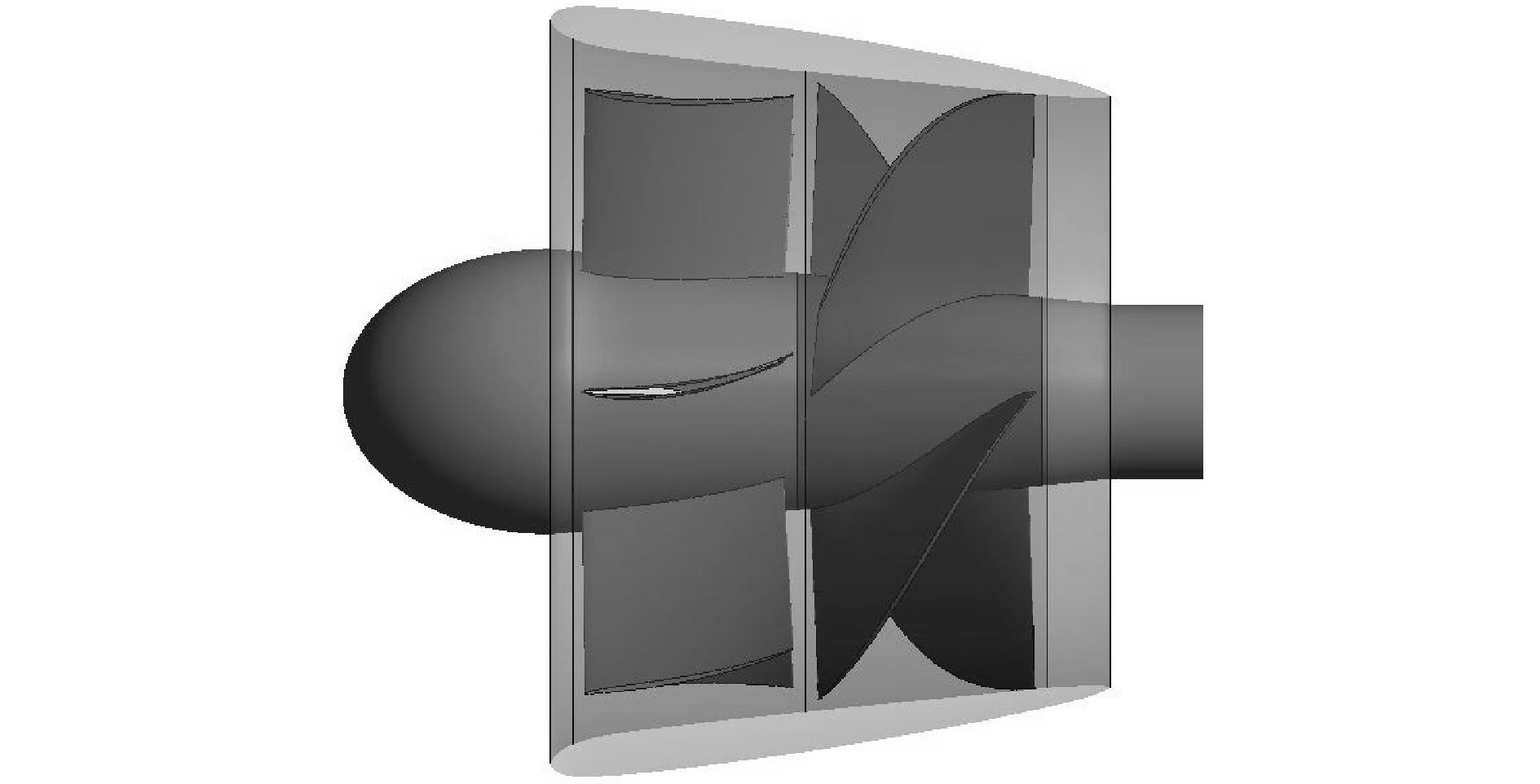
导管形状借鉴于19A导管改进而成,所有叶片均采用NACA翼型厚度分布规律进行加厚,最大厚度为5 mm,根据三维反问题方法求得转子和静子形状后匹配上导管并对叶片加厚,求得泵喷几何如图 8所示。
|
| 图8 泵喷三维形状 Figure 8 3-D shape for the pumpjet |
速度矩反映周向环量,即叶片负载,叶片负载决定叶片形状。设计过程假设进流无旋,故静子进口速度矩设置为0,假设转子能够完全回收导叶预旋,则转子出流无旋速度矩设置为0。静子出口和转子进口速度矩相等,结合转子进口轮毂半径和轮缘半径取参考半径
|
| 图9 转子叶片轮毂和轮缘处载荷分布 Figure 9 Rotor blade loading on hub and shroud |
|
| 图10 静子叶片轮毂和轮缘处载荷分布 Figure 10 Stator blade loading on hub and shroud |
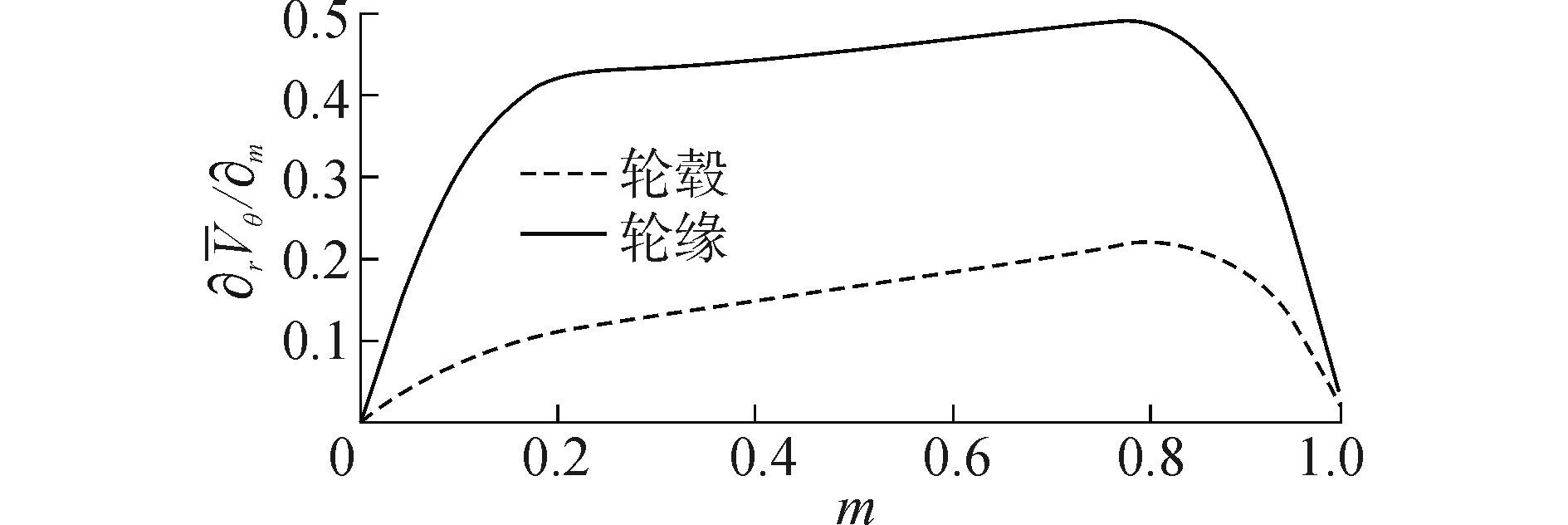
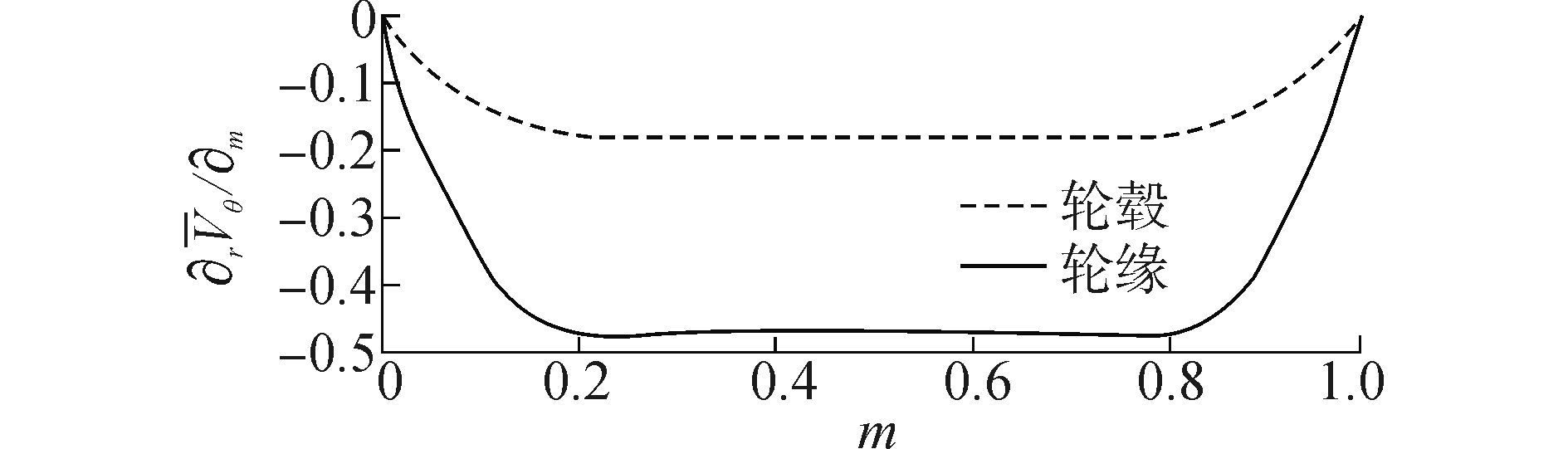
转子叶片轮缘、轮毂沿导边到随边的无量纲速度矩变化如图 11所示。可知,在每个完整叶片中,轮缘处速度矩无量纲值为0.36,轮毂处有0.13,其他位置由二者进行线性插值分布。
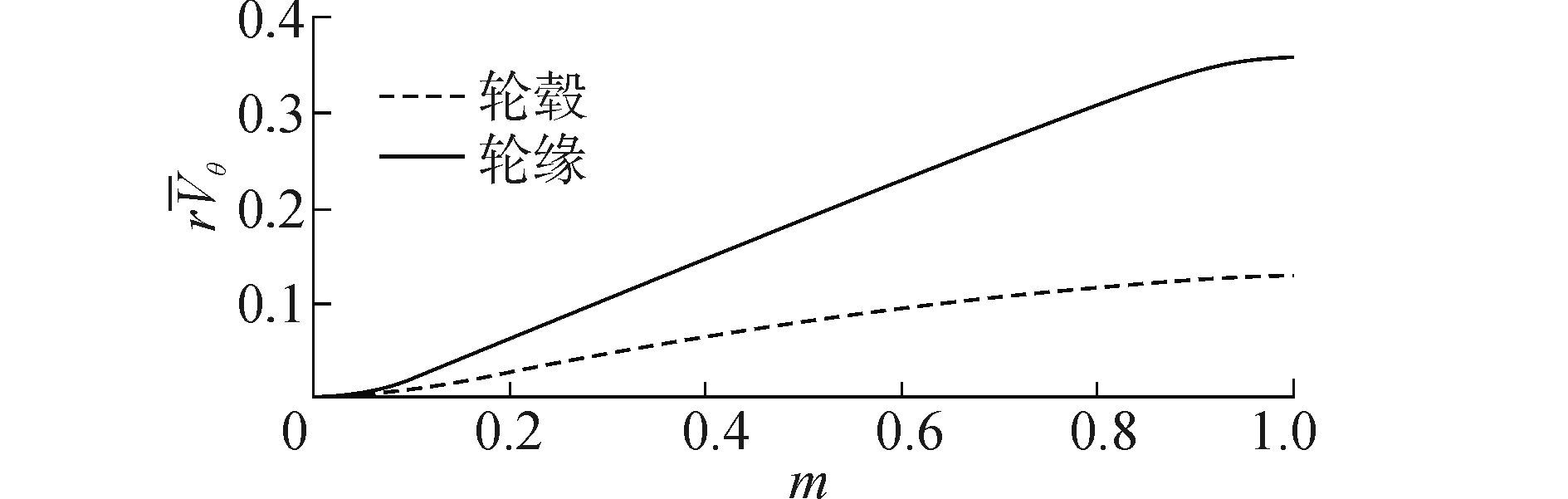
|
| 图11 速度矩沿轴面流线分布 Figure 11 Velocity moment distributions along meridional streamlines |
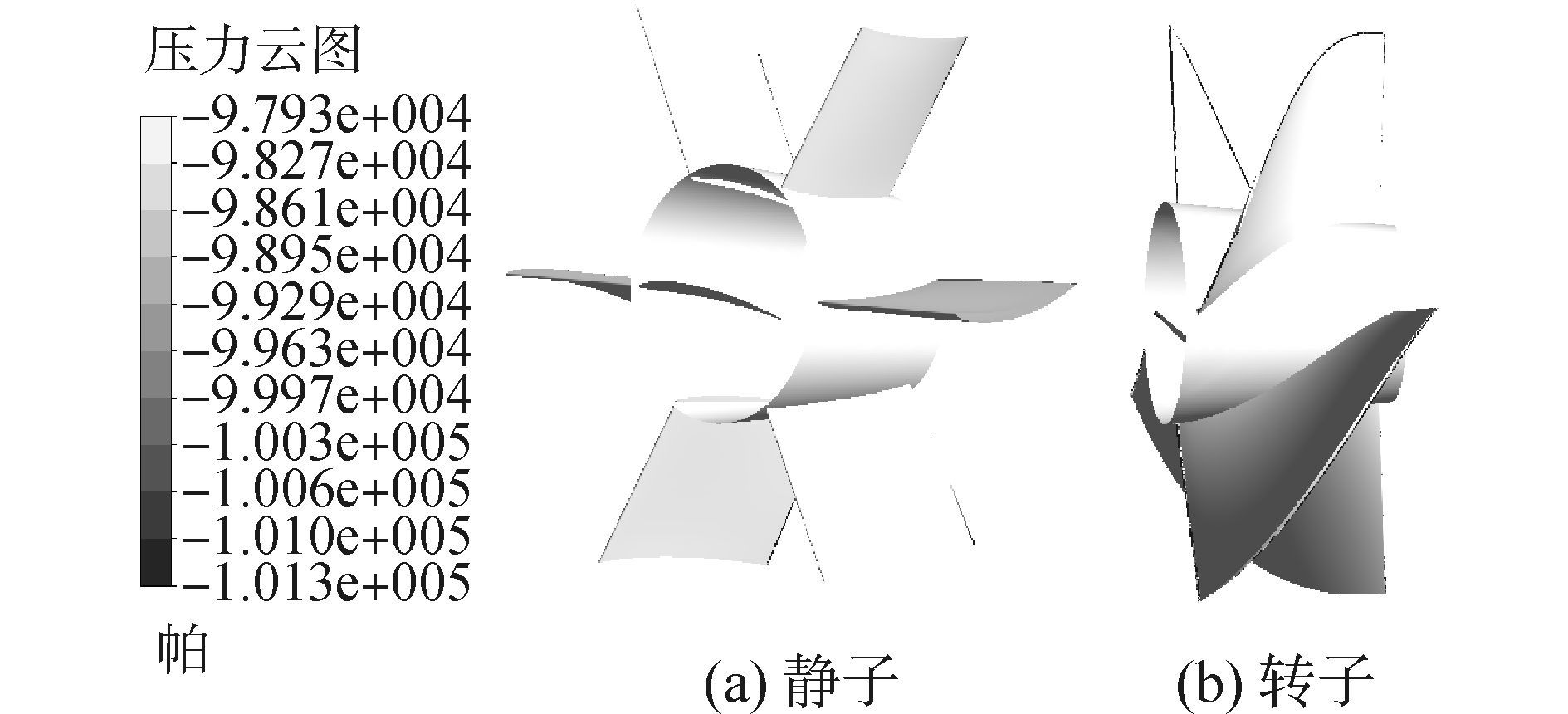
敞水泵喷计算采用全结构化网格如图 12所示,计算域设置同桨完全一致,转速同样为2 200 r/min,42 km/h下其流线和空化情况如图 13、14所示,同样,深色代表空化区,所设计泵喷没有产生空化。定义轴向分量概念为
|
| 图12 泵结构化网格 Figure 12 Structural mesh of pumpjet |
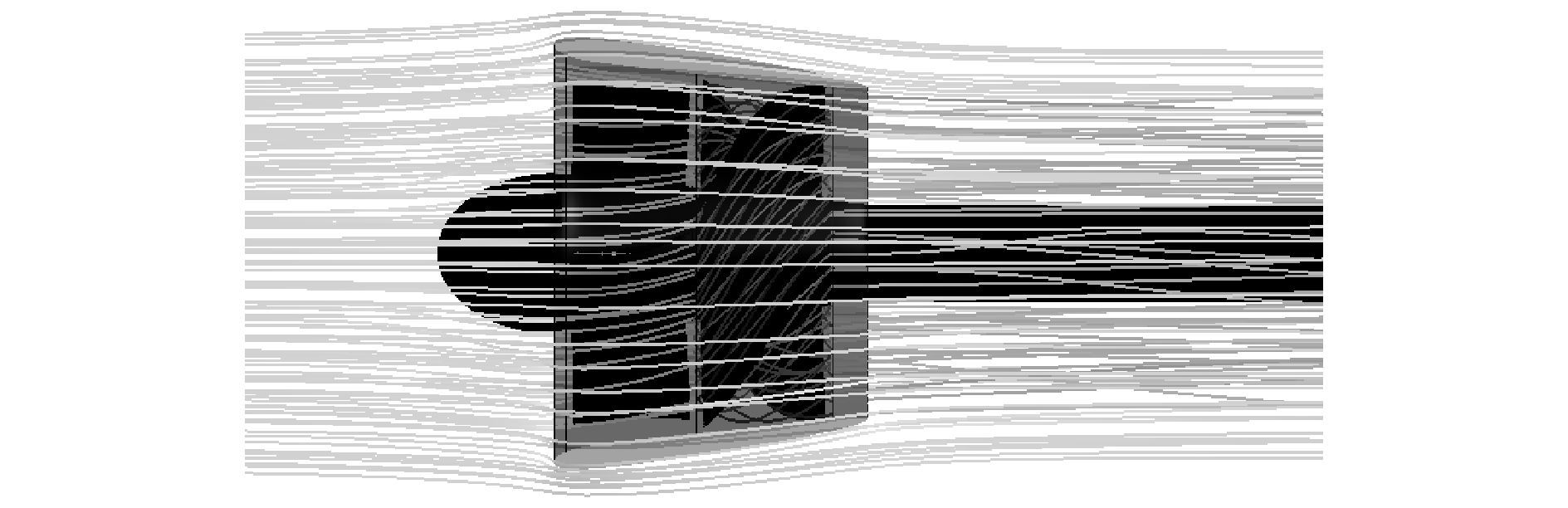
|
| 图13 泵喷敞水流线图 Figure 13 Streamlines of open water pumpjet |
|
| 图14 静子、转子表面压力分布 Figure 14 Pressure distribution in stator and rotor |
| $ \iint\limits_S {V_z^2/\left( {V_\theta ^2 + V_r^2 + V_z^2} \right)} $ | (24) |
式中:Vz、Vr、Vθ分别为泵喷出口的轴向、径向、周向速度,S为喷口面积,泵喷喷口轴向分量达到99.4%,用同样方法取得螺旋桨桨叶后等桨盘面出口处轴向分量为96.9%。
泵喷水力特性参数如表 3所示,在同一主机输出功率限制下,推进器接收功率约为39.7 kW。此时螺旋桨进流速度41.2 km/h,消耗功率39.7 kW,净推力2 251 N,推进效率64.9%,泵喷设计工况点对应进流速度为42 km/h,消耗功率39.7 kW,净推力2 320 N,推进效率68.2%。在消耗相同功率情况下,泵喷在对应更高航速下产生更大的推力,推进效率增加了3.3个百分点。
| 进流速度/(km·h-1) | 流量/(m3·s-1) | 推力/N | 功率/kW | 扬程/m | 推进效率/% |
| 38 | 0.481 | 2 591 | 41.2 | 7.70 | 66.9 |
| 42 | 0.493 | 2 320 | 39.7 | 7.22 | 68.2 |
| 44 | 0.499 | 2 184 | 39.0 | 6.97 | 68.4 |
| 46 | 0.506 | 2 047 | 38.3 | 6.71 | 68.3 |
| 48 | 0.513 | 1 909 | 37.8 | 6.43 | 67.3 |
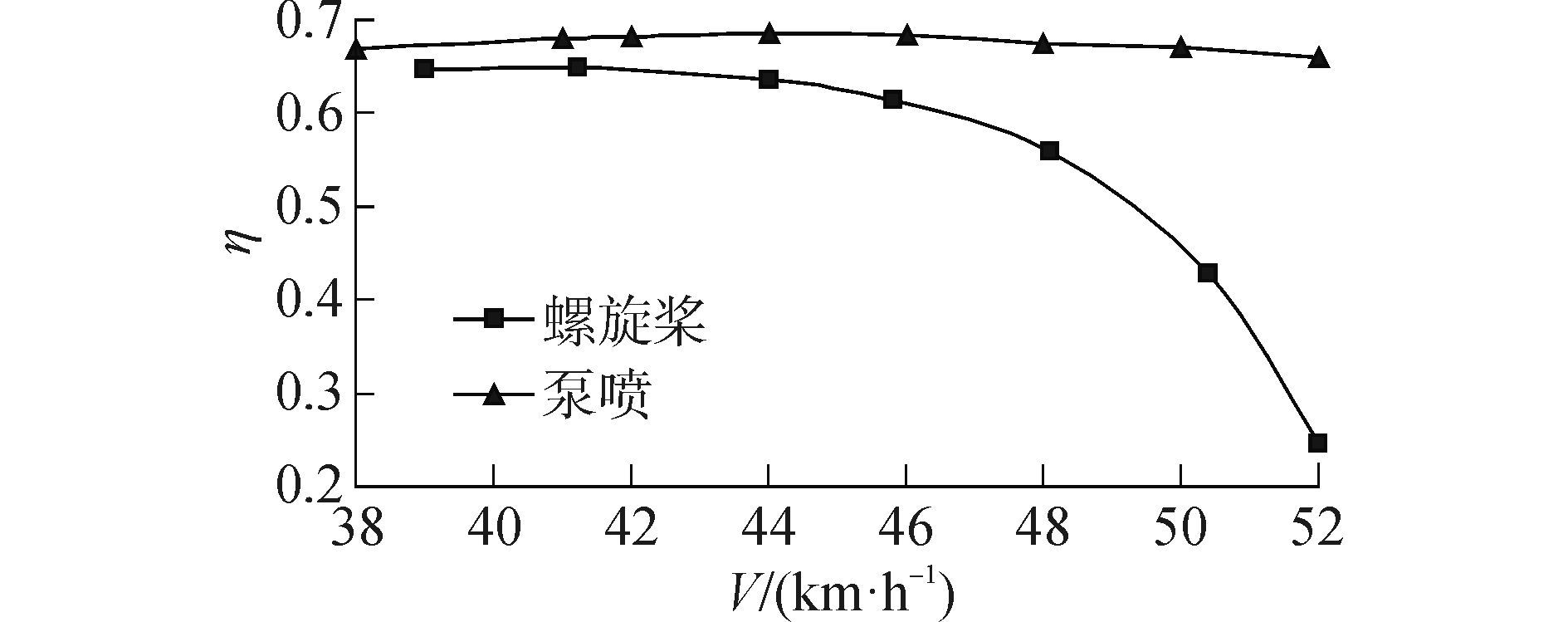
在主机输出功率范围内改变进流速度,泵喷推进器与螺旋桨的推进效率η对比曲线如图 15所示,可以看出在高速进流下,螺旋桨推进效率急剧下降,泵喷推进效率下降趋势缓和。因泵设计时是按满载(12人)工况设计,轻载情况下航速会有不同程度的提高,泵喷在较高航速下仍然具有较高的推进效率,具有更强的高速适应性。
|
| 图15 推进效率对比图 Figure 15 Results comparison of propulsion efficiency |
1) 基于三维反问题方法对泵喷推进器转子、静子进行设计,快捷高效。通过叶面速度矩实现叶片负载分布能够有效控制设计结果,改进的19A导管和叶片的NACA厚度分布解决了泵喷导管设计和叶片加厚问题。
2) 以E779a桨和71SII喷泵为对象验证了数值计算的可信性,在此基础上对所设计泵喷和对比桨进行了敞水水力特性计算。泵喷标称直径0.278 m,桨直径0.347 m,泵型紧凑。消耗相同的主机额定功率时,泵喷在对应更高的进流速度时仍产生更大的推力,推进效率增加了3.3个百分点。
3) 从敞水特性看,设计工况点以后随来流速度增加螺旋桨推进效率急剧下降,泵喷推进效率则较为缓和,泵喷具有更高的高速适应性,使得艇轻载高航速航行时仍具有较高效率。
另外,出于水草缠绕、叶片碰损及人身安全方面考虑,泵喷推进器相比螺旋桨具有很大优势。三维反问题方法泵喷设计在实际工程应用中具有较强的可行性。
| [1] |
潘光, 胡斌, 王鹏, 等. 泵喷推进器定常水动力性能数值模拟[J].
上海交通大学学报, 2013, 47(6): 992–937.
PAN Guang, HU Bin, WANG Peng, et al. Numerical simulation of steady hydrodynamic performance of a pumpjet propulsor[J]. Journal of Shanghai Jiao Tong University, 2013, 47(6): 992–937. |
| [2] |
刘文峰, 胡欲立. 新型水下集成电机推进装置的泵喷推进器结构原理及特点分析[J].
鱼雷技术, 2007, 15(6): 5–8.
LIU Wenfeng, HU Yuli. Analysis of construction principle and characteristics of pumpjet for underwater integrated motor propulsor[J]. Torpedo techinology, 2007, 15(6): 5–8. |
| [3] |
王天奎, 唐登海. 泵喷推进器-低噪声的核潜艇推进方式[J].
现代军事, 2006, 7(7): 52–54.
WANG Tiankui, TANG Denghai. Pumpjet propulsor-pow noise propulsor of nuclear submarine[J]. Conmilit, 2006, 7(7): 52–54. |
| [4] | BONAIUTI D, ZANGENEH M. On the coupling of inverse design and optimization techniques for the multiobjective, multipoint design of turbomachinery blades[J]. Journal of turbomachinery, 2009, 131: 021014. DOI:10.1115/1.2950065 |
| [5] |
肖若富, 陶然, 王维维, 等. 混流泵叶轮反问题设计与水力性能优化[J].
农业机械学报, 2014, 45(9): 84–88.
XIAO Ruofu, TAO Ran, WANG Weiwei, et al. 3-D inverse design and hydrodynamic performance optimization for a mixed-flow pump impeller[J]. Transactions of the Chinese society for agricultural machinery, 2014, 45(9): 84–88. DOI:10.6041/j.issn.1000-1298.2014.09.014 |
| [6] |
杨魏, 王福军, 王宏. 离心式叶轮三维反问题设计和数值计算[J].
排灌机械工程学报, 2012, 30(4): 632–635.
YANG Wei, WANG Fujun, WANG Hong. Three-dimensional inverse design and fluid flow numerical simulation for centrifugal impeller[J]. Journal of drainage and irrigation machinery engineering, 2012, 30(4): 632–635. |
| [7] |
靳栓宝, 王永生. 基于三元设计及数值试验轴流泵抗空化性能[J].
排灌机械工程学报, 2013, 31(9): 763–767.
JIN Shuanbao, WANG Yongsheng. 3-D design of axial-flow pump and numerical prediction of its cavitation performance[J]. Journal of drainage and irrigation machinery engineering, 2013, 31(9): 763–767. DOI:10.3969/j.issn.1674-8530.2013.09.006 |
| [8] |
靳栓宝, 王永生, 丁江明, 等. 混流式喷水推进泵三元设计及数值试验[J].
哈尔滨工程大学学报, 2012, 33(10): 1223–1227.
JIN Shuanbao, WANG Yongsheng, DING Jiangming, et al. Three-dimensional design and numerical experiment of mixed-flow waterjet with CFD[J]. Journal of Harbin Engineering University, 2012, 33(10): 1223–1227. |
| [9] |
常书平, 石岩峰, 周晨, 等. 出口环量分布对混流泵性能的影响[J].
农业机械学报, 2014, 45(1): 89–93.
CHANG Shuping, SHI Yanfeng, ZHOU Chen, et al. Effects of exit circulation distribution on performances of mixed-flow pump[J]. Transactions of the Chinese society for agricultural machinery, 2014, 45(1): 89–93. DOI:10.6041/j.issn.1000-1298.2014.01.015 |
| [10] |
常书平, 王永生, 靳栓宝. 轴流式喷水推进泵水力设计和性能检验[J].
哈尔滨工程大学学报, 2011, 32(10): 1278–1282.
CHANG Shuping, WANG Yongsheng, JIN Shuanbao. Hydraulic design and performance investigation of a waterjet axial flow pump[J]. Journal of Harbin Engineering University, 2011, 32(10): 1278–1282. DOI:10.3969/j.issn.1006-7043.2011.10.003 |
| [11] | SVENSSON R, GROSSI L.Trail results including wake measurements from the world's largest waterjet installation[C].International conference on waterjet propulsion latest developments. amsterdam:the royal institution of naval Architects(RINA), 1998. |
| [12] | 罗兴琦. 混流式水轮机转轮的全三维反问题计算与优化[D]. 北京: 清华大学, 1995. |
| [13] | 关醒凡. 现代泵技术手册[M]. 北京: 宇航出版社, 1995: 326-332. |
| [14] | GOTO A, NOHMi M, SAKURAI T, et al. Hydrodynamic design system for pumps based on 3-D CAD, CFD and inverse design method[J]. ASME journal of fluids engineering, 2002, 124(2): 329–335. DOI:10.1115/1.1471362 |
| [15] | BONAIUTI D, ZANGENEH M, AARTOJARVI R, et al. Parametric design of a waterjet pump by means of inverse design, CFD calculations and experimental analyses[J]. ASME Journal of fluids engineering, 2010, 132: 1–15. |
| [16] | LLOYD G, ESPANOLES A. Best practice guidelines for marine applications of computational fluid dynamics[R]. WS Atkins consultants and members of the NSC, marnet-cfd thernatic network, 2002. |
| [17] | Pumplinx demonstration on performance and cavitation of E779A Propeller. Geometry and experimental data courtesy of INSEAN, 2009, 09. http://www.insean.it. |



