2. 中国船舶及海洋工程设计研究院 上海市船舶工程重点实验室, 上海 200011;
3. 中国船舶工业集团公司 规划发展部, 北京 100048
2. Shanghai Key Laboratory of Ship Engineering, Marine Design & Research Institute of China, Shanghai 200011, China;
3. Development Dept., China State Shipbuilding Corporation, Beijing 100048, China
在船舶与海洋工程结构设计中,在满足强度要求前提下,减轻结构重量是提高结构设计水平的关键。其中,静强度设计方法已经基本成熟,其设计方法简单、可靠,计算分析与试验验证都相对容易。但是,船体结构经常会遇到瞬态载荷的作用,如船体受到的波浪砰击载荷,此时须对船体结构进行瞬态动力响应分析。对船体结构进行瞬态动力分析需要耗费大量的时间和精力,且计算结果受到较多参数的影响,计算过程不够稳定。因此,若能得到砰击载荷的等效静态载荷,将等效静态载荷作用于结构,分析得到与砰击瞬态载荷作用相同的回应结果,将大大提高计算效率。
人们对砰击载荷作用下结构的响应做了大量的研究,例如Jones等[1-5]预报了船体结构在砰击载荷作用下的结构破坏问题,并在这方面提出了一些有用的观点。Saitoh等[6]给出了钢板在脉冲载荷作用下永久变形的经验公式。Nurick等[7]对遭受脉冲载荷的方形薄板进行了试验研究。Cheong等[8]对在流固冲击载荷作用下矩形板的动力后屈曲特性进行了试验研究。Wang等[9]采用直接计算方法研究了FPSO艏部抗砰击设计。上述研究结果和方法为砰击载荷作用下船体结构设计提供了一定的试验和理论基础,但是对于砰击载荷作用下结构的等效静态载荷研究的文献较少。
实船及模型试验都已表明,砰击载荷具有局部性、瞬时性及压力峰值沿船体表面快速移动三个主要特征[10]。如果按砰击压力的峰值对肋骨强度做静力计算和设计的话,肋骨框架结构将会十分保守。文献[10]中引入砰击压力“折减系数”的概念,将动态砰击压力转化为与产生相同结构响应 (应力) 的等价均布静压力。“折减系数”量值反映了砰击压力的不均匀程度,可以看作主要是砰击载荷在空间分布上的“折减”。本文暂时不对砰击载荷在空间分布上的折减做研究。在对砰击载荷在空间上“折减”前,应对结构在砰击载荷作用下由于砰击载荷的瞬态性引起的动载荷系数进行研究,Sinha等[11]对此进行了相关的研究。
本文基于文献[12]的理论计算结果,对船体外板和舷侧板架施加砰击载荷,进行瞬态动力响应计算,分析结构在瞬态砰击载荷作用下的响应,并与结构在砰击载荷峰值作用下的静态分析进行对比,从而得到砰击载荷的等效静态载荷。
1 砰击载荷的计算合理地预报砰击载荷对船体结构设计和船舶航行安全至关重要。船底砰击载荷峰值较高,作用时间较短,可能引起局部构件的破坏,严重者造成船体破舱,带来不可估量的损失。与底部砰击相比,外飘砰击产生的水动力较小,作用面积较大,砰击过程持续时间要长得多[12]。目前对砰击载荷的预报一般有三种方法:1) 基于水动力数值分析;2) 基于试验测量;3) 基于经验公式,例如船级社规范。
砰击载荷可以用四个特征参数来表示:1) 起升时间直到砰击压力峰值;2) 压力峰值;3) 压力衰减形式;4) 压力作用时间,如图 1所示。

|
| 图1 典型砰击载荷压力时间历程曲线 Figure 1 Time history of typical slamming pressure |
等效静态载荷原理可表述为:线性静态分析中的结构等效静态载荷能够产生与对应时刻结构非线性动力学分析完全相同的系统响应场[13]。图 2给出了静态载荷的等效过程。由图可见,动力学分析中总的计算时间步为n+1步,在等效时,将每个计算时间步等效为静态分析的一个工况,并且要求由第si个等效静态载荷计算得到的系统响应等价于对应时间步的动态响应。因而,动力学分析中总的时间步数等于线性静态分析中总的工况数。同样,基于等效静态载荷计算的结构线性静态响应的包络线与非线性结构动态响应的包络线一致。根据这一原理可以求得对应于动力学分析每一时间步的每个静态工况的等效静态载荷feq0、feq1、feq2、…、feqn。

|
| 图2 静态载荷的等效过程 Figure 2 Equivalent process of static loads |
完全采用上述等效静态载荷原理对砰击载荷作用下船体结构强度进行评估,也将耗费大量的时间和精力,因此工程上广泛采用的做法是将动载荷简单处理为乘以动态载荷因子的静载荷,动态载荷因子由设计规范或工程师的经验决定。下面通过理论分析得到动态载荷因子。
在进行结构瞬态动力响应分析时,通过运用数值积分方法求解耦合方程。非线性动力学微分方程为
| $ \mathit{\boldsymbol{M\ddot u}}\left( t \right) + \mathit{\boldsymbol{B\dot u}}\left( t \right) + \mathit{\boldsymbol{Ku}}\left( t \right) = \mathit{\boldsymbol{P}}\left( t \right) $ | (1) |
式中:M、B、K分别为动态质量矩阵、动态阻尼矩阵和动态刚度矩阵,P(t) 表示t时刻外载荷列阵,u(t) 为位移向量。
用固定时间步长Δt,在离散时间点计算基本结构响应 (位移),利用中心差分法计算离散时刻的速度
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot u}}}_n} = \frac{1}{{2\Delta t}}\left\{ {{u_{n + 1}} - {u_{n - 1}}} \right\}}\\ {{{\mathit{\boldsymbol{\ddot u}}}_n} = \frac{1}{{2\Delta {t^2}}}\left\{ {{u_{n + 1}} - 2{u_n} + {u_{n - 1}}} \right\}} \end{array} $ |
外力取3个邻近时间点的平均值,得到运动方程:
| $ \begin{array}{l} \frac{\mathit{\boldsymbol{M}}}{{\Delta {t^2}}}\left( {{u_{n + 1}} - 2{u_n} + {u_{n - 1}}} \right) + \frac{\mathit{\boldsymbol{B}}}{{2\Delta t}}\left( {{u_{n + 1}} - {u_{n - 1}}} \right) + \\ \frac{\mathit{\boldsymbol{K}}}{3}\left( {{u_{n + 1}} - {u_n} + {u_{n - 1}}} \right) = \frac{1}{3}\left( {{P_{n + 1}} + {P_n} + {P_{n - 1}}} \right) \end{array} $ | (2) |
合并同类项,运动方程写为
| $ {\mathit{\boldsymbol{A}}_1}\left\{ {{u_{n + 1}}} \right\} = {\mathit{\boldsymbol{A}}_2} + {\mathit{\boldsymbol{A}}_3}\left\{ {{u_n}} \right\} + {\mathit{\boldsymbol{A}}_4}\left\{ {{u_{n - 1}}} \right\} $ | (3) |
式中:
本文材料采用理想弹塑性材料模型,材料参数如下:杨氏弹性模量E为2.06×1011 N/m2,泊松比γ为0.3,密度ρ为7 850 kg/m3,屈服极限σs为355 MPa。
3 动态载荷因子计算砰击载荷的等效静态载荷可以通过砰击载荷峰值乘以动态载荷因子 (CDLF) 得到。动态载荷因子与砰击载荷作用时间t1和结构固有周期T(一阶振动模态) 的比值有关。在相同的砰击载荷峰值Pm和不同t1/T比值作用下,本文通过一系列的非线性瞬态动力分析,得到结构的最大应力或变形。将瞬态得到的结构最大应力或变形与静态非线性分析值比较,得到动态载荷因子CDLF:
| $ {C_{{\rm{DLF}}}} = {\sigma _d}/{\sigma _s}\;或\;{C_{{\rm{DLF}}}} = {w_d}/{w_s} $ | (4) |
式中:σd和σs分别为动态载荷和静态载荷作用下结构的Von-mises应力,wd和ws分别为动态载荷和静态载荷作用下结构的变形。
3.1 船体板动态载荷因子计算及分析波浪砰击载荷通常作用在一个较大的局部范围内,因此可将砰击载荷视为均布载荷。此外,作为船舶板周界的支撑结构,如纵桁、纵骨、肋骨及肋板等,其刚度远大于船体板的刚度,因此可将船体板视为四边固支的矩形板[14]。
本文选取三种不同板的规格进行计算,见表 1。板按四周刚性固定,则板在空气中的固有频率f和固有周期T可按下式计算:
| 板 | 规格尺寸 /mm×mm×mm |
载荷峰值 Pm/kPa |
板固有周 期T/s |
作用时间 t1/T |
| Panel-1 | 1 800×600×12 | 0.2~0.9 | 0.005 21 | 0.05~2 |
| Panel-2 | 1 800×600×10 | 0.2~0.9 | 0.006 26 | 0.05~2 |
| Panel-3 | 1 800×600×14 | 0.2~0.9 | 0.004 47 | 0.05~2 |
| $ f = 5.537 \times {10^6}\frac{t}{{ab}}\sqrt {{{\left( {\frac{a}{b}} \right)}^2} + {{\left( {\frac{b}{a}} \right)}^2} + 0.6045{\rm{Hz}}} $ | (5) |
| $ T = \frac{1}{f}{\rm{s}} $ | (6) |
对于板Panel-1,对其加载静态载荷时,其回应如表 3所示。从表 2中可以看出,当静态载荷大于0.4 MPa时,板将进入塑性阶段。
| 载荷峰值Pm/MPa | 应力/MPa | 变形/mm | 应变 |
| 0.2 | 173.5 | 1.998 | 0.000 862 |
| 0.3 | 259.5 | 2.934 | 0.001 289 |
| 0.4 | 343.2 | 3.81 | 0.001 704 |
| 0.5 | 355 | 4.751 | 0.002 25 |
| 0.6 | 355 | 5.683 | 0.002 837 |
| 0.7 | 355 | 6.732 | 0.003 654 |
| 0.8 | 355 | 8.207 | 0.005 136 |
| 0.9 | 355 | 9.42 | 0.006 434 |
| t1/T | 应力/MPa | 变形/mm | 应变 | CDLF-stress | CDLF-deflection | CDLF-strain |
| 0.1 | 243.3 | 2.59 | 0.001 21 | 0.937 57 | 0.882 75 | 0.938 71 |
| 0.2 | 355 | 4.48 | 0.001 93 | 1.368 02 | 1.526 93 | 1.497 28 |
| 0.4 | 355 | 5.25 | 0.002 33 | 1.368 02 | 1.789 37 | 1.807 60 |
| 0.6 | 350.1 | 4.34 | 0.001 93 | 1.349 13 | 1.479 21 | 1.497 28 |
| 0.8 | 321.6 | 3.64 | 0.001 60 | 1.239 31 | 1.240 63 | 1.241 27 |
| 1.0 | 263.1 | 2.98 | 0.001 30 | 1.013 87 | 1.015 68 | 1.008 53 |
| 1.2 | 253.8 | 2.9 | 0.001 26 | 0.978 03 | 0.988 41 | 0.977 50 |
| 1.4 | 302.7 | 3.46 | 0.001 50 | 1.166 47 | 1.179 28 | 1.163 69 |
| 1.5 | 297.9 | 3.39 | 0.001 48 | 1.147 98 | 1.155 42 | 1.148 18 |
| 1.6 | 303.8 | 3.466 | 0.001 51 | 1.170 71 | 1.181 32 | 1.171 45 |
| 1.7 | 300.67 | 3.42 | 0.001 49 | 1.158 65 | 1.165 64 | 1.155 93 |
| 1.8 | 287.8 | 3.26 | 0.001 43 | 1.109 06 | 1.111 11 | 1.109 39 |
| 2.0 | 259.7 | 2.96 | 0.001 29 | 1.000 77 | 1.008 86 | 1.000 78 |
对板Panel-1施加如图 3所示的瞬态载荷,当峰值载荷不小于0.3 MPa时,t1/T=0.2,0.4时板进入塑性阶段,如表 3所示。表 3中给出了板遭受瞬态载荷时的应力、变形和应变值。图 4给出了板Panel-1在t1/T=0.8和Pm=0.3 MPa时其长边中点处Von-mises应力的时历变化曲线。

|
| 图3 理想化砰击载荷压力时间历程曲线 Figure 3 Idealized time curve of slamming pressure |

|
| 图4 Pm=0.3 MPa时Panel-1应力变化 Figure 4 Variation of von-mises stress of Panel-1 at Pm=0.3 MPa |
在各载荷峰值和t1/T工况下,动态载荷因子如图 5所示,图中CDLF-deflection和CDLF-strain分别为采用变形和应变作为计算参数时对应的动态载荷因子,NSR为英国劳氏军船规范[15]砰击载荷动态载荷因子。从这些图中可以看出,当板的应力大于屈服极限时,即板进入塑性阶段时,计算其动态载荷因子时应使用变形或应变作为计算参数;从计算结果来看,选取变形作为计算参数所得动态载荷因子与劳氏军船规范较接近,使用应变作为计算参数的结果偏于安全。

|
| 图5 不同砰击载荷作用下动态载荷因子 Figure 5 The DLF under different slamming loads |
按照式 (4) 计算动态载荷因子,得到Panel-1、Panel-2、Panel-3在不同峰值下的动态载荷因子,如图 6所示。

|
| 图6 砰击载荷作用下板动态载荷因子 Figure 6 The DLF of panel under slamming loads |
由上述计算结果可以看出,当0.25≤t1/T≤0.9和1.25≤t1/T≤1.75时,需要对结构进行瞬态动力响应分析,尤其是t1/T在0.25~0.9时,动态效应较明显。因此当0.25≤t1/T≤0.9和1.25≤t1/T≤1.75时,可以运用本文中的动态载荷因子对船体板进行静态响应分析。
3.2 船体骨材动态载荷因子计算及分析对于船体外板骨材,即舷侧纵骨或舷侧肋骨,可选取由骨材和外板组成的板架进行瞬态动力分析。其有限元模型如图 7所示,其骨材尺寸为HP240×12 mm,板厚为14 mm,强横梁尺寸为⊥12×600/16×200 mm。

|
| 图7 有限元模型 Figure 7 The finite element model |
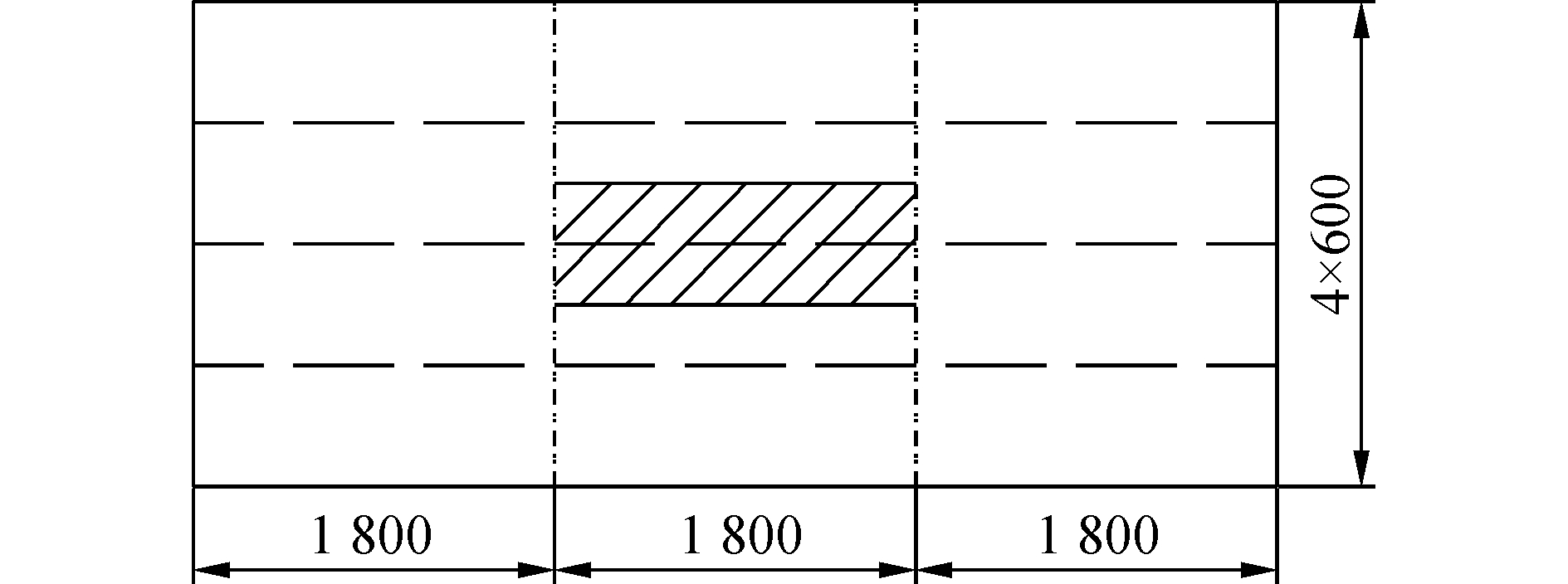
由于本文重点对骨材所受的动态载荷进行研究,因此施加的载荷范围如图 8中阴影线所示,边界条件为四周刚性固定。
|
| 图8 施加载荷范围 Figure 8 The region of loads |
通过对有限元模型进行模态分析,可得到纵骨及其带板的一阶垂向固有频率为280 Hz,如图 9所示。因此,舷侧纵骨一阶垂向固有周期T取为0.003 6 s。

|
| 图9 模态分析 Figure 9 The mode analysis |
对舷侧纵骨施加0.9 MPa的静态载荷,其静态分析结果为应力325.3 MPa,变形6.823 mm,应变0.001 32。动态响应分析结果见表 4,从表 4中可以看出,当0.5≤t1/T≤1.2时,骨材进入塑性阶段。
| t1/T | 应力/MPa | 变形/mm | 应变×10-3 | CDLF-stress | CDLF-deflection | CDLF-strain |
| 0.1 | 160.7 | 2.038 | 0.794 | 0.494 006 | 0.298 696 | 0.601 667 |
| 0.2 | 241 | 3.859 | 1.196 | 0.740 855 | 0.565 587 | 0.906 061 |
| 0.3 | 325.6 | 5.624 | 1.655 | 1.000 922 | 0.824 271 | 1.253 788 |
| 0.4 | 354.1 | 6.897 | 2.197 | 1.088 534 | 1.010 846 | 1.664 394 |
| 0.5 | 355 | 8.01 | 2.283 | — | 1.173 970 | 1.729 545 |
| 0.6 | 355 | 8.991 | 2.536 | — | 1.317 749 | 1.742 424 |
| 0.7 | 355 | 9.208 | 2.18 | — | 1.349 553 | 1.654 545 |
| 0.8 | 355 | 9.512 | 2.12 | — | 1.394 108 | 1.609 091 |
| 0.9 | 355 | 9.716 | 2.07 | — | 1.424 007 | 1.568 182 |
| 1.0 | 355 | 9.613 | 1.99 | — | 1.408 911 | 1.509 848 |
| 1.2 | 355 | 9.296 | 1.87 | — | 1.362 451 | 1.418 939 |
| 1.4 | 349.2 | 8.675 | 1.68 | 1.073 471 | 1.271 435 | 1.270 455 |
| 1.6 | 335.2 | 8.115 | 1.54 | 1.030 433 | 1.189 360 | 1.166 667 |
| 1.8 | 323.4 | 7.528 | 1.43 | 0.994 159 | 1.103 327 | 1.083 333 |
| 2.0 | 319.8 | 7.602 | 1.46 | 0.983 093 | 1.114 173 | 1.106 818 |
图 10给出了计算得到的船体骨材动态载荷因子,可以看出,船体骨材的动态载荷因子变化趋势与劳氏规范有差异,这是因为所建模型为板架,计算其骨材固有周期时与实际值存在一定误差,因此得到的动载荷存在一定误差,但CDLF-Strain和劳氏规范均在t1/T=0.5附近动载荷系数达到最大。

|
| 图10 船体骨材动态载荷因子 Figure 10 The DLF of stiffener |
本文应用非线性有限元方法,分别给出了船体外板和加筋板在砰击载荷作用下结构的瞬态动力响应和静态分析,得到了船体外板和骨材的动态载荷因子,并与劳氏规范[15]中动态载荷因子进行比较,验证了本文方法的正确性。计算结果表明,当0.25≤t1/T≤0.9和1.25≤t1/T≤1.75时,需要对结构进行瞬态动力响应分析,尤其是t1/T在0.25~0.9时,动态效应较明显。
一般而言,对于外飘砰击,由于砰击压力较小,砰击作用时间较长,因此其动态载荷系数较小,一般接近于1,实际计算时可以不考虑动态效应的影响。对于艏底砰击,由于砰击载荷较大,作用时间较短,且有附连水品质的影响,因此需要考虑动态效应的影响。
本文引入了动态载荷因子,给出了将瞬态载荷转化为静态载荷的方法和条件,可将复杂的瞬态动力分析转化为静态分析,为工程设计人员提供了一条可行且有效的技术途径。
| [1] | JONES N. A theoretical study of the dynamic plastic behavior of beams and plates under finite-deflections[J]. International journal of solids and structures, 1971(7): 1007–1029. |
| [2] | JONES N. Slamming damage[J]. Journal of ship research, 1973, 17(2): 80–86. |
| [3] | JONES N. Damage estimate for plating of ships and marine vehicles[C]. Proceedings of the International Symposium on Practical Design in Shipbuilding:PRADS'77, Tokyo, Japan, 1977, pp. 121-128. |
| [4] | JONES N. Structural impact[M]. Cambridge University Press, Cambridge, UK, 1997. |
| [5] | JONES N. Some recent developments in the dynamic inelastic behavior of structures[J]. Ships and offshore structures, 2006, 1(1): 37–42. DOI:10.1533/saos.2005.0007 |
| [6] | SAITOH T, YOSHIKAWA T, YAO H. Estimation of deflection of steel panel under impulsive loading[J]. The Japan society of mechanical engineers, 1995, 61: 2241–2246. |
| [7] | NURICK GN, SHAVE GC. The deformation and tearing of thin square plates subjected to impulsive loads-An experimental study[J]. International journal of impact engineering, 1996, 18(1): 99–116. DOI:10.1016/0734-743X(95)00018-2 |
| [8] | CHEONG HK, HAO H, CUI S. Experimental investigation of dynamic post-buckling characteristics of rectangular plates under fluid-solid slamming[J]. Engineering structures, 2000, 22(8): 947–960. DOI:10.1016/S0141-0296(99)00042-5 |
| [9] | WANG G, TANG S, SHIN Y. A direct calculation approach for designing a ship-shaped FPSO's bow against wave slamming load[C]. Proceedings of the 12th International Offshore and Polar Engineering Conference, Kitakyushu, Japan, 2002, Ⅳ:163-168. |
| [10] |
王辉. 船体结构局部强度设计中的砰击载荷确定方法[J].
中国造船, 2010, 51(2): 68–77.
WANG Hui. Slamming Load Determination in Local Structure Design of Ships[J]. Shipbuilding of China, 2010, 51(2): 68–77. |
| [11] | SINHA S, KAR S, SARANGDHAR D G. Development of simplified structural design formulation for slamming loads[C]. Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 2008. |
| [12] |
田喜民, 邹早建, 王福花. 大型船舶外飘砰击压力研究[J].
中国造船, 2014, 55(1): 1–10.
TIAN Ximin, ZOU Zaojian, WANG Fuhua. Numerical study on flare impact for large ships[J]. Shipbuilding of China, 2014, 55(1): 1–10. |
| [13] | KANG B S, SHYY Y K, HONG Q. Implementation of Equivalent Static Load Method in Flexible Multibody Dynamic Systems[C]. 7th World Congress of Structural and Multidisciplinary Optimization, Seoul, Korea, 2007:21-25. |
| [14] | 陈铁云, 王德禹, 黄震球. 船舶结构终极承载能力[M]. 上海: 上海交通大学出版社, 2005. |
| [15] | LLOYD's Register. Rules and Regulations for the Classi-fication of Naval Ships[S]. January 2011. |



