线性遗传编程算法 (linear genetic programming,LGP)[1]是遗传编程算法 (genetic programming,GP)[2]的变种算法之一,该算法继承了遗传编程算法的高度并行处理能力、强鲁棒性和全局搜索能力而被广泛地应用于诸多领域[3-5],并与其他智能优化算法[6]成为近期研究的热点。
早熟收敛与膨胀是线性遗传编程算法的两大问题。种群进化代数越多,膨胀程度越严重,计算适应度所需代价也越多。一般通过增加种群多样性减少早熟收敛的发生,但是算法需进化更多代才能收敛,加重种群的膨胀程度。因此,在增加种群多样性的过程中同时控制膨胀程度,对提高线性遗传编程算法的整体性能有着重要意义。
在增加种群多样性的研究问题上,主要有增加结构多样性和增加语义多样性两类方法。增加结构多样性是指增加种群在基因型方面的差异程度,此种方法首先定义结构距离度量个体间的差异程度,并在进化过程中增大个体间的结构距离,提高种群的多样性[7-9]。增加语义多样性是指增加种群在表现型方面的差异程度,并在进化过程中增大个体间的语义差异程度,以此提高种群的多样性[10-12]。
在控制种群膨胀程度的研究问题上,主要有限制个体的最大长度[2]、简约压力项[13-14]、双层锦标赛和比例锦标赛[15]等方法。这些方法主要通过限制个体的长度或使种群在搜索过程中偏向长度短的个体。
以上文献仅从增加种群多样性和控制种群膨胀的某一方面对线性遗传编程算法进行研究,但是增加种群的多样性会加重种群的膨胀程度,而控制种群的膨胀程度并不能保证保持种群的多样性。在线性遗传编程算法领域,鲜有文献对提高种群的多样性和控制膨胀结合起来综合研究。本文在优化种群年龄分层模型[16-17]的基础上,将该模型应用于线性遗传编程算法,用于减少算法早熟收敛的发生频率,同时控制种群的膨胀程度。
1 线性遗传编程算法及种群年龄分层模型 1.1 线性遗传编程算法线性遗传编程算法通过锦标赛选择适应度较大的个体参与复制、交叉和变异等遗传操作,以适应度为指引逐代搜索问题的最优解。线性遗传编程算法的个体采用程序指令序列的线性表示方式。设P(g)={X1,X2,…,XM}是规模为M的第g代种群,Xi=(xi1,xi2,…,xin) 为种群的第i个个体,长度为n,xij表示第i个体的第j行指令,线性遗传编程算法的个体表示如下:
void gp [double f[2])
{
r[4]=r[2]/r[0];
r[2]=f[0]-r[4];
//r[1]=r[0]/f[1];
r[4]=r[2]/7;
r[0]=r[0]+r[4];
}
根据对输出结果是否产生影响,指令分为有效指令和无效指令 (示例中选定r[0]作为个体的输出,第3行指令为无效指令)。有效指令中的运算符构成的序列称为有效运算符序列,表示为effOp (示例中,effOp= < /,-,/,+ >)。
1.2 种群年龄分层模型种群年龄分层模型由分层规则、L0层 (第0层) 新个体生成规则、个体年龄增长规则和个体升迁规则构成,分别定义如下:
分层规则:种群划分为L0~Lmax层,每层的子种群规模为M。每层的最大年龄限制AgeLimiti的计算为:
| $ \text{AgeLimi}{{\text{t}}_{i}}=\text{AGEGAP}\times \text{schem}{{\text{e}}_{i}} $ | (1) |
式中:AGEGAP用于控制各分层子种群的进化,第AGEGAP×(i-1) 代~第AGEGAP×i代 (i≥1),各分层的个体 (包括超龄个体) 在层内进化。schenmei表示元模式中第i层的值。Lmax层的个体没有最大年龄限制。元模式如表 1所示。例如,元模式采用多项式,AGEGAP=20,每层允许的最大年龄分别为20、40、80、180、…
| 元模式 | 每层允许的最大年龄 | ||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 线性 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 斐波那契 | 1 | 2 | 3 | 5 | 8 | 13 | 21 |
| 多项式n2 | 1 | 2 | 4 | 9 | 16 | 25 | 49 |
| 指数2n | 1 | 2 | 4 | 8 | 16 | 32 | 64 |
L0层新个体生成规则:在第AGEGAP×i代 (i≥0),在L0层随机生成新个体,用于填补原L0层中的个体升迁到L1层留下的空缺位置。
个体年龄增长规则:个体的年龄按照如下规则增长:1)L0层新生成的个体年龄为0;2) 变异算子产生的子代个体年龄为父代个体年龄加1;3) 交叉算子产生的子代个体年龄为父代个体年龄最大者的年龄加1;4) 复制算子选择的个体年龄加1。个体在同一代内发生多次复制、交叉和变异等遗传操作,年龄只增长一次。
个体升迁规则:第AGEGAP×i代 (i≥0),从Lmax-1~L0层,年龄超出本层允许最大年龄限制的个体将升迁到上一层,并替换上一层中适应度比该个体小的个体,如果该个体比上一层中所有个体适应度都小,则删除该个体。
种群年龄分层模型限制年龄相仿的个体在同一层竞争进化,因此该模型保护低年龄层的个体 (适应度通常较低) 以免受到高年龄层个体 (适应度通常较高) 的排挤,因此得以生存更长时间以搜索更广的区域;同时,该模型在L0层源源不断随机生成的新个体,随着年龄增长逐层升迁并替换高年龄层适应度低的个体。可见,在该模型中,种群不会由于出现超级个体而造成种群多样性丧失,甚至发生早熟收敛。因此,该模型是提高种群多样性的有效模型。
2 种群年龄分层模型在线性遗传编程算法的应用在种群年龄分层模型中,同批次生成的个体从L0层升迁到Lmax层过程中年龄一般相仿,因此这些个体有较大概率在整个升迁过程中保持在同一层,如果同批次生成的个体在低层出现了早熟收敛,有比较大的概率在整个升迁过程中都维持早熟收敛的状态,导致重复计算。为了提高各个分层子种群的多样性,本文首先定义个体间的有效运算符序列编辑距离,然后基于该编辑距离设计了双层锦标赛提高分层子种群的多样性。
2.1 基于双层锦标赛的分层子种群多样性策略 2.1.1 有效运算符序列编辑距离及计算算法定义1 有效运算符序列编辑距离:设effOpi、effOpj分别为个体Xi和个体Xj的有效运算符序列,将effOpi转换成effOpj所需的删除、插入和替换操作的集合称为effOpi到effOpj的编辑路径,而最短的编辑路径称为effOpi和effOpj的编辑距离。操作集合许可的编辑包括3种操作:将一个运算符替换成另一个运算符a→b,插入一个运算符Λ→b,删除一个运算符a→Λ(a,b表示为一个运算符,Λ表示空运算符)。
上述所提的3种操作中,每一个操作都有相应成本λ(·),分别以成本函数λ(a→Λ)、λ(Λ→b)、λ(a→b) 表示。假设将effOpi转换成effOpj,需要经过e1e2e3e4…en个操作,每个ei(i=1,2,…,n) 为一次操作。取E=e1e2e3e4…en为一连续的操作序列。因此,将effOpi经由操作集合E转换成effOpj总成本为λ(E):
| $ \lambda \left( E \right)=\sum\limits_{i=1}^{n}{\lambda \left( {{e}_{i}} \right)} $ | (2) |
则个体Xi和个体Xj的有效运算符编辑距离可以表示为
| $ \text{edit}\left( {{X}_{i}}, {{X}_{j}} \right)=\min \left\{ \lambda \left( E \right)\left| E \right.是其中的一条路径 \right\} $ | (3) |
假设成本函数λ(·)=1,求解有效运算符序列effOpi与effOpj的编辑距离的动态规划算法如算法1所示:
算法1:
输入:有效运算符序列effOpi及effOpj。
输出: edit (i,j),其中i=|effOpi|,j=|effOpj|。
1) if i=0 and j=0
2) return 0;
3) if i=0 and j!=0
4) return edit (i,j-1)+1;
5) if i!=0 and j=0
6) return edit (i-1,j)+1;
7) else
8) return
min{edit (i-1,j)+1,edit (i,j-1)+1,edit (i-1,j-1)+f(i,j)};
其中,当effOpi的第i个运算符不等于effOpj的第j个运算符时,f(i,j)=1;否则,f(i,j)=0。
2.1.2 双层锦标赛的分层子种群多样性策略种群年龄分层模型中各个分层子种群均采用标准的线性遗传编程算法。分层子种群通过锦标赛选择策略选择适应度高的父代个体参与复制、交叉和变异等遗传操作,从而产生子代个体。仅以适应度单一标准确定优胜个体容易导致种群在基因型上多样性的迅速减少,因此有必要以适应度和多样性两个标准确定优胜个体,以在不改变进化方向的前提下增加种群的多样性,从而减少早熟收敛的发生。
本文采用双层锦标赛选择策略融合适应度和多样性两个选择标准。在第1层中,每组锦标赛选择适应度较高的个体进入第2层;在第2层中,用算法1求出的有效运算符编辑距离衡量个体间的差异程度,选择有效运算符编辑距离最大的两个个体,作为最终的锦标赛选择结果。双层锦标赛选择策略如图 1所示。在第1层中,随机选择6个个体,分成3组分别进行锦标赛,每组锦标赛选择适应度较高的个体作为优胜个体,因此第1层锦标赛中共产生3个适应度相对较高的个体进入第2层锦标赛。在第2层中,选择有效运算符编辑距离最大的两个个体,作为整个锦标赛的选择结果。这样,双层锦标赛选择出在适应度高的前提下 (保证进化方向),差异程度尽量大 (提高多样性) 的两个个体。
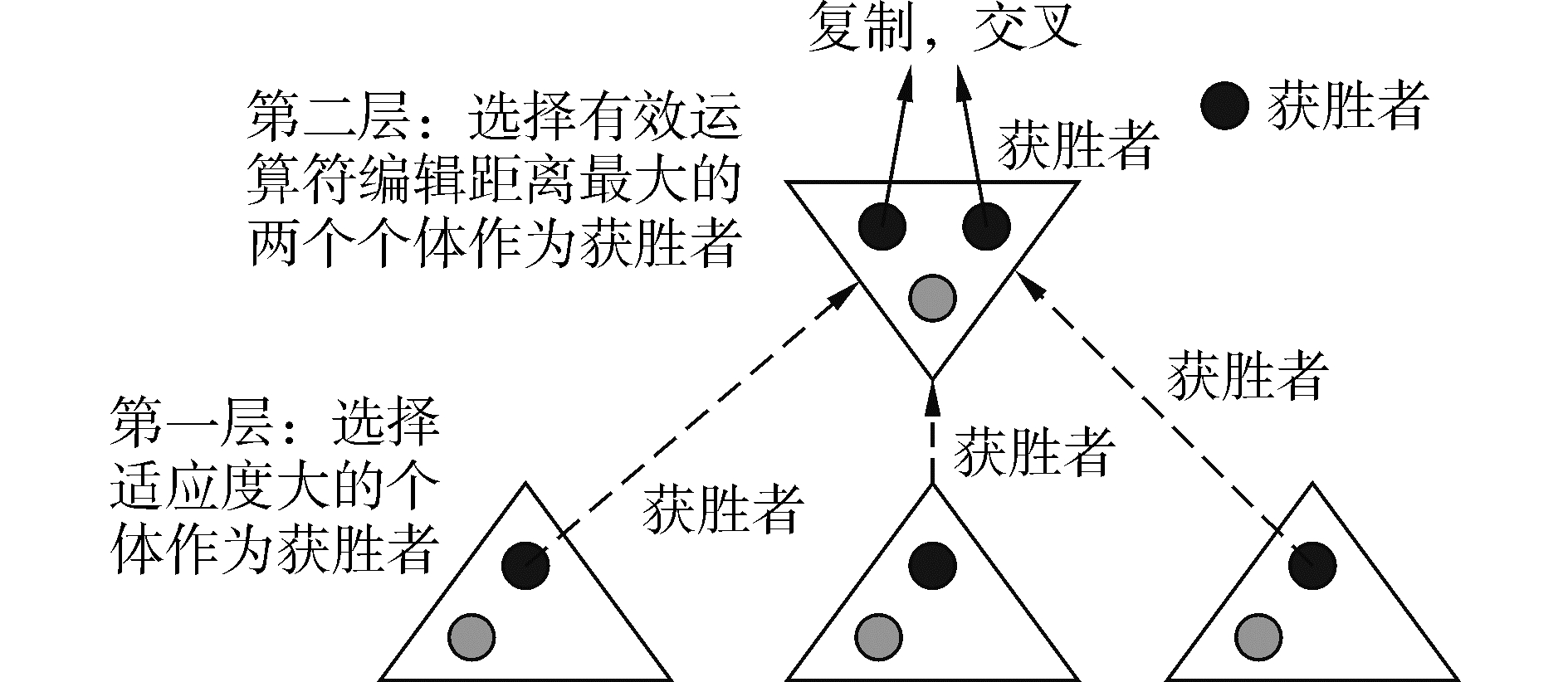
|
| 图1 双层锦标赛示意图 Figure 1 Two-layer tournament |
本文将种群年龄分层模型应用于线性遗传编程算法,用于提高该算法的种群多样性,同时控制种群的膨胀程度。对于种群的多样性,通过限制年龄相仿的个体在同一层竞争进化以提高种群整体多样性;通过双层锦标赛提高分层子种群的局部多样性,从而从整体和局部两个维度提高种群的多样性,减少早熟收敛的发生频率。对于种群膨胀程度的控制,通过将种群按照年龄进行分层,限制进化代数比较大 (年龄较大,长度一般比较长) 的个体的数量,并且在第AGEGAP×i代 (i≥0) 在L0层随机生成长度较短的新个体,新个体随着年龄的增长逐层升迁并替换高年龄层 (长度一般比较长) 中适应度低的个体,减轻种群的膨胀程度。
在基于种群年龄分层模型的线性遗传编程算法中,通过AGEGAP控制进化进程。第AGEGAP×i代 (i≥0),将每层中的超龄个体升迁至上一层,并在L0层随机生成新个体。第AGEGAP×(i-1) 代~第AGEGAP×i代 (i≥1),各分层的个体在层内执行传统的进化,并且在遗传算子中根据年龄增长规则增加个体的年龄。算法2是基于种群年龄分层模型的线性遗传编程算法。
算法2:
1) 设定算法参数,包括:
种群年龄分层模型的参数:分层层数Lmax,AGEGAP,分层元模式scheme,通过式 (1) 计算每层最大年龄限制AgeLimit;
线性遗传编程算法参数:最大进化代数GenMax,各分层子种群规模M,初始个体最大长度LenInitMax,个体最大长度LenIndMax,计算寄存器register个数,复制概率Pr,交叉概率Pc,变异概率Pm,函数集F,变量集T;
2) 种群在GenMax代内,执行以下进化过程:
① 如果generation%AGEGAP=0,执行以下操作:
a) 从Lmax-1层至L0层,将年龄超出最大年龄限制的个体升迁至上一层,并替换上一层中适应度比自己小的个体,如果该个体的适应度比上一层中所有个体的都小,则删除该个体;
b) 在L0层随机生成新个体,新生成的个体年龄设置为0,用于填补原L0层中的个体升迁到L1层留下的空缺位置。
② 如果generation%AGEGAP!=0,对每一层的子种群分别执行以下操作:
a) 计算每个个体的适应度;
b) 用下述遗传算子产生新个体:
复制:采用双层锦标赛,从父代种群中选择M′×Pr个优良个体进行复制,加入子代种群,并删除父代种群同等数量的劣质个体,复制算子选择的个体,如果该个体没有参与变异和交叉操作,年龄不变,否则年龄+1;
交叉:执行M′×Pc次交叉操作,每次交叉操作采用双层锦标赛选择个体,从父代种群中选取两个个体进行交叉,交叉所产生新个体加入子代种群中,交叉所产生新个体的年龄为父代个体年龄最大者的年龄加1;
变异:执行M′×Pm次变异操作,每次变异操作从父代种群中随机选取一个个体,随机改变该个体某一部分基因,将变异产生的新个体加入子代种群中,变异产生的新个体年龄为父代个体年龄加1。
3 实验及结果分析 3.1 测试问题及实验参数设置为了验证所提方法的有效性,本文选用符号回归问题作为测试问题,分别测试标准线性遗传编程算法 (linear genetic programming,LGP)、基于种群年龄分层模型的线性遗传编程算法 (age layered population structure-linear genetic programming,ALPS-LGP) 以及在分层子种群中用双层锦标赛选择策略的线性遗传编程算法Two Layer (tournament-age layered population structure-linear genetic programming,2LT-ALPS-LGP) 在提高种群多样性、控制种群膨胀程度以及在训练集和测试集的适应度情况。
LGP、ALPS-LGP以及2LT-ALPS-LGP共同的参数取值相同,3种算法共同的参数设置如表 2所示。LGP设置1 000个个体,ALPS-LGP和2LT-ALPS-LGP每层100个个体;ALPS-LGP与2LT-ALPS-LGP都分10层,AGEGAP取值10,分层元模式采用多项式。
| 参数 | 取值 |
| 函数集 | +,-,*,/ |
| 终端集 | 输入变量 |
| 进化代数 | 1 000 |
| 初始个体最大长度 | 10 |
| 个体最大长度 | 100 |
| 计算寄存器 | 4 |
| 复制比率 | 0.2 |
| 交叉比率 | 0.6 |
| 变异比率 | 0.2 |
测试函数为GP领域的基准函数,所选用的测试函数以及相应的训练集、测试集均采用文献[18-19]的建议,如表 3所示。
| 名称 | 目标函数 | 训练集 | 测试集 |
| Keijzer-6 | E[1, 50, 1] | E[1, 120, 1] | |
| Korns-12 | 2-2.1cos (9.8x) sin (1.3w) | U[-50, 50, 10000] | U[-50, 50, 10000] |
| Vladislavleva-4 | U[0.05,6.05,1024] | U[-0.25,6.35,5000] | |
| Nguyen-7 | U[0, 2, 20] | U[0, 2, 20] | |
| Pagie-1 | |
E[-5,5,0.4] | E[-5.4,4.6,0.4] |
| 注:U[a,b,c]表示在a与b之间的c个随机样本;E[a,b,c]表示从a开始直到b,每间隔c取一个样本;训练集和测试集相互独立。 | |||
设P(g)={X1,X2,…,XM}是规模为M的第g代种群,Xi为种群的第i个个体 (i=1,2,…,M),长度为Len (Xi);设edit (Xi,Xj) 为个体Xi和Xj有效运算符序列的编辑距离;具有n个样本的训练集为D={(X1,Y1),…,(Xn,Yn)},Xi(i=1,2,…,n) 为m(m≥1) 维向量,Yi(i=1,2,…,n) 为一维向量。种群多样性:第g代种群的多样性用M对随机选择的个体的平均编辑距离表示为
在实验中,LGP、ALPS-LGP以及2LT-ALPS-LGP 3种算法对每个测试函数均独立测试30次,种群多样性和种群膨胀程度的结果为所有测试结果的平均值。
图 2比较了3种算法控制种群膨胀的效果。在所测试的函数中,应用3种算法时,种群的膨胀程度均随着进化进程逐渐增大。对于测试函数Keijzer-6、Korns-12和Vladislavleva-4,应用LGP算法时,种群的膨胀程度接近个体最大长度,而应用ALPS-LGP以及2LT-ALPS-LGP两种算法时,种群的膨胀程度远小于应用LGP算法时种群的膨胀程度。对于测试函数Nguyen-7和Pagie-1,应用3种算法时种群的膨胀程度比较接近,并且远小于个体最大长度。可见,对于Keijzer-6、Korns-12和Vladislavleva-4这些复杂的测试函数,在搜索最优解过程中,种群倾向于进化得更加膨胀。此种情况下,应用ALPS-LGP以及2LT-ALPS-LGP两种算法能够有效控制种群的膨胀程度。对于Nguyen-7和Pagie-1这些简单的测试函数,应用3种算法时,种群只需进化少量的代数就可搜索到适应度较高的解,因此种群的膨胀程度较轻。
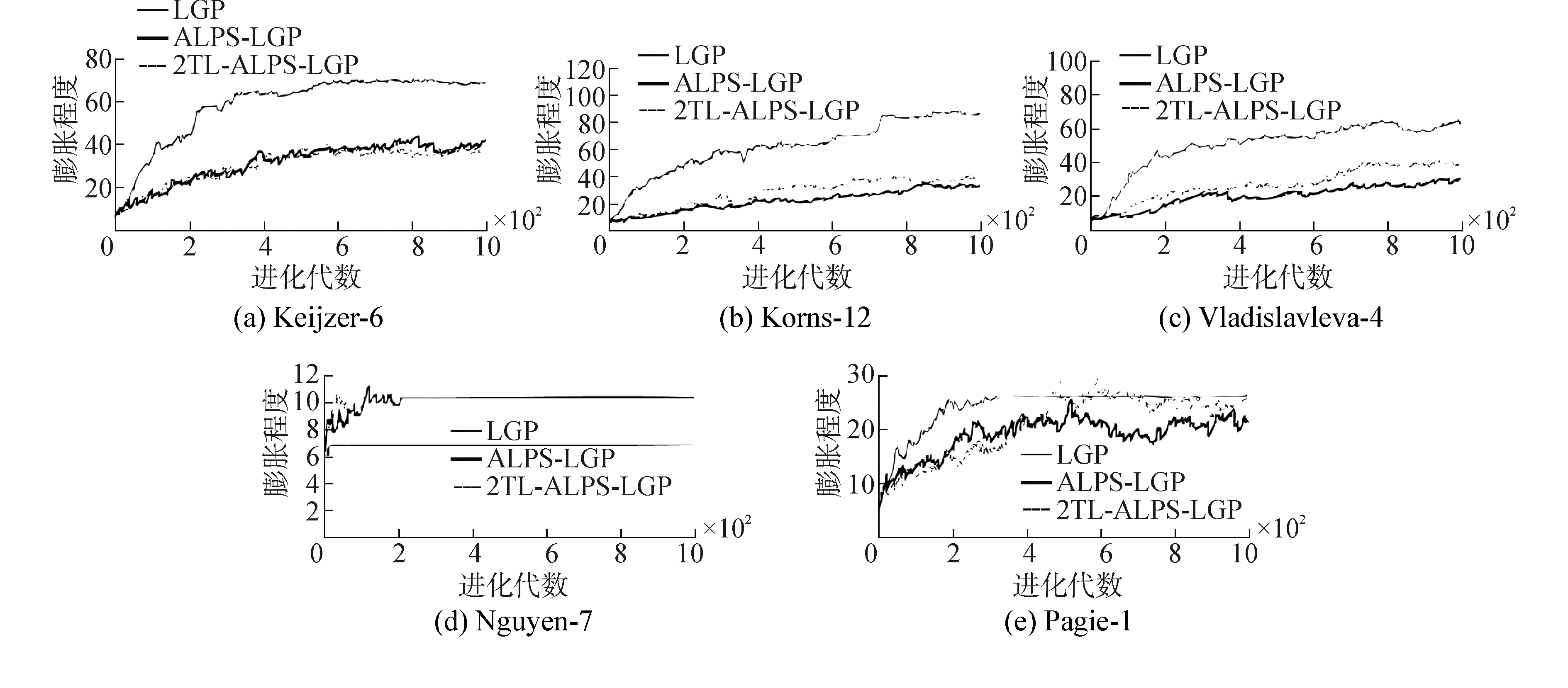
|
| 图2 种群膨胀程度控制效果 Figure 2 The effects of population bloat control |
图 3比较了3种算法控制种群多样性的效果。在用ALPS-LGP算法优于应用LGP算法。对于测试函数Keijzer-6、Korns-12和Vladislavleva-4,应用LGP算法时,种群的多样性在进化后期提高的幅度较小,而应用ALPS-LGP以及2LT-ALPS-LGP两种算法时,种群的多样性提高的幅度较大。对于测试函数Nguyen-7和Pagie-1,应用三种算法时种群的多样性进化少量的代数后就基本保持稳定。可见,对于Keijzer-6、Korns-12和Vladislavleva-4这些复杂的测试函数,应用ALPS-LGP以及2LT-ALPS-LGP两种算法能够有效提高种群的多样性。对于Nguyen-7和Pagie-1这些简单的测试函数,应用3种算法时,种群均只需进化比较少的代数就可以搜索到适应度较高的解,种群多样性均保持在比较低的水平。由上述结果可以看出,双层锦标赛选择策略和年龄分层的方法均有效提高了种群的多样性。

|
| 图3 种群多样性提升效果 Figure 3 The effects of population diversity improvement |
表 4描述3种算法在训练集和测试集的适应度情况 (函数名称和算法名称均进行缩写)。
| 函数 | 算法 | 训练集 | 测试集 | |||||
| 最小值 | 平均值 | 标准差 | 最小值 | 平均值 | 标准差 | |||
| Kei6 | LGP | 0.10 | 0.15 | 0.03 | 0.35 | 0.45 | 0.08 | |
| ALPS | 0.09 | 0.16 | 0.08 | 0.09 | 0.41 | 0.32 | ||
| 2TL | 0.08 | 0.10 | 0.01 | 0.09 | 0.27 | 0.18 | ||
| Kor12 | LGP | 0.89 | 1.00 | 0.07 | 1.07 | 1.03 | 0.90 | |
| ALPS | 1.03 | 1.04 | 0.02 | 1.15 | 1.10 | 0.95 | ||
| 2TL | 0.06 | 0.07 | 0.03 | 0.90 | 0.95 | 0.03 | ||
| Vla4 | LGP | 0.19 | 0.19 | 0.00 | 0.19 | 0.19 | 0.00 | |
| ALPS | 0.18 | 0.18 | 0.00 | 0.18 | 0.18 | 0.00 | ||
| 2TL | 0.17 | 0.18 | 0.01 | 0.17 | 0.18 | 0.01 | ||
| Ngu7 | LGP | 0.05 | 0.06 | 0.02 | 0.05 | 0.06 | 0.02 | |
| ALPS | 0.05 | 0.06 | 0.02 | 0.05 | 0.06 | 0.02 | ||
| 2TL | 0.04 | 0.06 | 0.01 | 0.04 | 0.06 | 0.01 | ||
| Pag1 | LGP | 0.09 | 0.10 | 0.00 | 0.09 | 0.10 | 0.00 | |
| ALPS | 0.07 | 0.08 | 0.01 | 0.07 | 0.08 | 0.01 | ||
| 2TL | 0.04 | 0.08 | 0.03 | 0.04 | 0.08 | 0.03 | ||
对所有测试函数,总体上,2LT-ALPS-LGP算法无论在训练集还是测试集上均表现最好,ALPS-LGP算法次之,LGP算法表现最差,说明种群年龄分层的方法以及双层锦标赛选择策略提高种群多样性有利于搜索全局最优解。对比3种算法在所有测试函数的训练集和测试集的表现情况,2LT-ALPS-LGP算法和ALPS-LGP算法并没有与LGP算法形成明显的优劣关系。可见同时提高种群的多样性和控制种群膨胀程度对线性遗传编程算法的泛化能力影响较小。
4 结论1) 对于复杂的测试函数,采用双层锦标赛选择策略的种群年龄分层模型能够明显提高种群多样性,同时控制种群的膨胀程度;
2) 而对于简单的测试函数虽有提高,但是不明显,主要是由于种群只需进化少量的代数就可以搜索到适应度较高的解造成的。
3) 训练集和测试集的适应度测试情况表明种群年龄分层的方法以及双层锦标赛选择策略提高种群多样性有利于搜索全局最优解,对算法的泛化能力影响较小。
| [1] | BRAMEIER M, BANZHAF W. Linear genetic programming[M]. New York Springer Science, Business Media, 2007:1-8. |
| [2] | KOZA J R. Genetic programming:on the programming of computers by means of natural selection[M]. Cambridge: MIT Press, 1992: 17-63. |
| [3] | GANDOMI A H, DANIAL M S, ALAVI A H, et al. Linear genetic programming for shear strength prediction of reinforced concrete beams without stirrups[J]. Applied soft computing, 2014, 19(2): 112–120. |
| [4] | MEHR A D, KAHYA E, YERDELEN C. Linear genetic programming application for successive-station monthly streamflow prediction[J]. Computers and geosciences, 2014, 70(9): 63–72. |
| [5] | TROIANO L, Birtolo C, ARMENISE R. Searching optimal menu layouts by linear genetic programming[J]. Journal of ambient intelligence and humanized computing, 2015: 1–18. |
| [6] |
吴昌友. 一种改进的人工鱼群优化算法[J].
智能系统学报, 2015, 10(3): 465–469.
WU Changyou. An improved artificial fish swarm optimization algorithm[J]. CAAI transactions on intelligent systems, 2015, 10(3): 465–469. |
| [7] | BRAMEIER M, BANZHAF W. Explicit control of diversity and effective variation distance in linear genetic programming[C]//5th European Conference on Genetic Programming. Kinsale, Ireland, 2002:3-5. |
| [8] | GAUDESI M, SQUILLERO G, TONDA A. An efficient distance metric for linear genetic programming[C]//15th Annual Conference on Genetic and Evolutionary Computation. Amsterdam, The Netherlands, 2013:6-10. |
| [9] | NGUYEN Q U, XUAN X H, O'NEILL M, et al. An investigation of fitness sharing with semantic and syntactic distance metrics[J]. Lecture notes in computer science, 2012, 7244: 109–120. DOI:10.1007/978-3-642-29139-5 |
| [10] | TOMASSINI M, VANNESCHI L, COLLARD P, et al. A study of fitness distance correlation as a difficulty measure in genetic programming[J]. Evolutionary computation, 2005, 13(2): 213–239. DOI:10.1162/1063656054088549 |
| [11] | BEADLE L, JOHNSON C G. Semantically driven crossover in genetic programming[C]//IEEE World Congress on Computational Intelligence, 2008:111-116. |
| [12] | BEADLE L, JOHNSON C G. Semantically driven mutation in genetic programming[C]//IEEE Congress on Evolutionary Computation, 2009:1336-1342. |
| [13] | ZHANG B T, HLENBEIN H. Balancing accuracy and parsimony in genetic programming[J]. Evolutionary computation, 1995, 3(1): 17–38. DOI:10.1162/evco.1995.3.1.17 |
| [14] | LUKE S, PANAIT L. A comparison of bloat control methods for genetic programming[J]. Evolutionary computation, 2006, 14(3): 309–344. DOI:10.1162/evco.2006.14.3.309 |
| [15] | SOTTO L F D P, MELO V V D. Studying bloat control and maintenance of effective code in linear genetic programming for symbolic regression[J]. Neurocomputing, 2015: 1–15. |
| [16] | HORNBY G S. ALPS:the age layered population structure for reducing the problem of premature convergence[C]//8th Annual Conference on Genetic and Evolutionary Computation, Washington, USA, 2006:815-822. |
| [17] | HORNBY G S. A steady-state version of the age-layered population structure EA[M].[S.l.]:Springer, 2010:87-102. |
| [18] | MCDERMOTT J, WHITE D R, LUKE S, et al. Genetic programming needs better benchmarks[C]//14th Annual Conference on Genetic and Evolutionary Computation. Pennsylvania, USA, 2012, 283(3):791-798. |
| [19] | WHITE D R, MCDERMOTT J, CASTELLI M, et al. Better GP benchmarks:community survey results and proposals[J]. Genetic programming and evolvable machines, 2013, 14(1): 3–29. DOI:10.1007/s10710-012-9177-2 |



