由于移动机器人在执行任务时需要行驶于不同的地面上,因此机器人需要具有安全穿越各种未知地面的能力。目前国内外许多学者使用视觉、激光传感器、超声波传感器、红外传感器等方法获取“感官”信号进行避障或路径规划研究。此类研究方法的主要目的是使移动机器人能顺利穿过各种“有形的”重重阻碍到达作业目的地。然而,当移动机器人行驶在平坦的沙地或者泥泞的土地时虽然前方没有任何障碍,机器人同样会有陷入的危险,称之为非几何危害[1]。此外,传统的感官避障方法容易受光照、尘埃、雾霾、地面覆盖物等的影响,而基于振动的方法可以感知地面承载层的信息,是一种良好的辅助手段。
Brooks等提出了自我监督的学习框架,给出了2个本体感受分类器,即基于振动的分类器与基于牵引力的分类器[2]。当机器人穿越不同地面时,本体感受分类器从轮地相互作用中获得地面特征并对地面分类,同时用于训练外感受分类器 (即视觉分类器)。这样机器人就能预测远方地面的机械性能。DuPont等应用微分测量单元 (differential measurement unit,DMU) 传感器采集无人地面车辆z轴的线加速度
本文利用奇异值分解 (singular value decomposition,SVD) 和功率谱密度估计两种方法对振动信号进行特征提取;给出改进的极限学习机算法,并在5种速度下基于2种特征以改进的极限学习机为分类器对5种地面进行分类;给出改进的模糊积分融合算法,采用改进的模糊积分算法对2个改进的极限学习机融合,并对地面进行分类。
1 地面分类算法使移动机器人以5种速度匀速在沙、碎石、草、土、沥青地面行驶,利用安装在左前轮轮臂上的三向加速度计和z向传声器,实时采集加速度信号和声压信号。机器人的振动来源于车轮与地面的相互作用,每种地面都产生特有的加速度和声压信号。考虑到x方向加速度信号对速度的变化比较敏感,影响分类泛化能力[3],故而选取y、z向加速度信号和z向声压信号作为分类数据。
1.1 特征提取 1.1.1 基于奇异值分解 (SVD) 的特征提取方法振动信号的时间序列为a1,a2,a3,…,重构一个m×n维矩阵:
| $ {{\mathit{\boldsymbol{D}}}_{m}}=\left[\begin{matrix} {{a}_{1}} & {{a}_{2}} & \cdots & {{a}_{n}} \\ {{a}_{2}} & {{a}_{3}} & \cdots & {{a}_{n+1}} \\ \vdots & \vdots & \ddots & \vdots \\ {{a}_{m}} & {{a}_{m+1}} & \cdots & {{a}_{m+n-1}} \\ \end{matrix} \right] $ | (1) |
式中:Dm称为重构的吸引子轨迹矩阵[7]。设A是一个m×n维实矩阵,它的奇异值分解是指存在矩阵U∈Rm×m、UUT=I和V∈Rn×n、VVT=I,以及矩阵Λ=[diag{λ1,λ2,…,λp}:0],使得
| $ \mathit{\boldsymbol{A}}=\mathit{\boldsymbol{U}}\mathit{\pmb{\Lambda }}{{\mathit{\boldsymbol{V}}}^{\rm{T}}} $ | (2) |
式中:λ1≥λ2≥,…,λp>0称为矩阵A的奇异值。矩阵A的秩为p,且p≤min (m,n)。
重构吸引子轨迹矩阵越接近于方阵 (或矩阵的奇异值越多) 效果越好,本文取m=257,n=256。因为有效信号对前几阶奇异值贡献最大,而噪声对各阶的贡献几乎相等,本文取前11阶奇异值作为特征值[8]。
y、z向加速度和z向声压数据在每一数据段内均得到11个特征,最后将3组数据的特征进行连接得到33维特征向量。
1.1.2 基于功率谱密度 (PSD) 的特征提取方法功率谱是指功率谱密度 (power spectrum density,PSD),功率谱估计是利用给定的一组样本数据估计平稳随机信号的功率谱密度。它能给出被分析对象的能量随频率的分布情况[9],因此在工程上应用十分广泛。本文采用经典的Welch法[10]对振动信号进行功率谱估计。
Welch法功率谱估计的主要步骤为:
1) 将长度为N的数据段分成L小段,每小段M个点,相邻小段交叠M/2个点,于是段数为
| $ L=\frac{N-M/2}{M/2} $ | (3) |
2) 对各小段加同样的平滑窗w(n) 后求傅里叶变换:
| $ {{X}_{i}}\left( {{e}^{\text{j}\omega }} \right)=\sum\limits_{n=0}^{M-1}{{{x}_{i}}\left( n \right)w\left( n \right){{\text{e}}^{-\text{j}\omega n}}}, i=1, 2, \cdots, L $ | (4) |
3) 求各小段功率谱的平均
| $ {{{\hat{S}}}_{x}}\left( {{\text{e}}^{\text{j}\omega }} \right)=\frac{1}{L}{{\sum\limits_{i=1}^{L}{\frac{1}{MU}\left| {{X}_{i}}\left( {{\text{e}}^{\text{j}\omega }} \right) \right|}}^{2}} $ | (5) |
式中:
对每一段的数据应用Welch法计算单边自功率谱密度并对其绝对值取自然对数,取自然对数的目的是为了避免较大数字范围的特征支配较小数字范围的特征,取感兴趣的频率范围为0~125 Hz。y、z向加速度和z向声压数据在每一个数据段内均得到129个特征,最后将3组数据的特征进行连接得到387维特征向量。
1.2 改进的极限学习机极限学习机[11](extreme learning machine,ELM) 是一种针对于单隐层前馈型神经网络的快速学习算法,根据ELM的学习规则,单隐层前馈型神经网络的输入权值和阈值可以随机选择。
隐含层节点数目的选择是影响分类效果和学习速度的一个重要参数,通常隐含层节点数目取训练样本数。当学习样本数过多时,隐含层节点数目会很大,这将导致该网络的学习速度大大降低。此外,分类准确率并非随着隐含层节点数目的增多而逐渐提高,而是呈不规则震荡[12]。这是因为隐含层节点存在冗余,这些节点不仅拖延了网络的训练速度,甚至节点之间相互掣肘反而降低了分类准确率,所以很难用试探的方法选择合适的隐含层节点数目。
为了消除冗余节点对极限学习机的训练速度和分类准确率的影响,需要对极限学习机的隐含层节点进行约减。
隐含层的输出矩阵H可以表示为
| $ \mathit{\boldsymbol{H}}=\left[{{\mathit{\boldsymbol{g}}}_{1}}\ \ {{\mathit{\boldsymbol{g}}}_{2}}\ \ {{\mathit{\boldsymbol{g}}}_{3}}\ \cdots {{{\mathit{\boldsymbol{\tilde{g}}}}}_{N}} \right] $ | (6) |
式中:gi为第i个隐层节点的输出,是N维列向量。
隐含层输出权值β,可以采用最小二乘法求解线性系统Ηβ=T获得,可以表示为
| $ \mathit{\pmb{\hat{\beta}}} ={{\mathit{\boldsymbol{H}}}^{\dagger }}\mathit{\boldsymbol{T}} $ | (7) |
式中:
用欧式距离来度量每个节点输出的相关性,任意两节点间的欧式距离表示为
| $ {{d}_{\left( i, j \right)}}=\sqrt{\sum\limits_{k=1}^{l}{{{\left( o_{i}^{k}-o_{j}^{k} \right)}^{2}}}} $ | (8) |
若任意两个隐含层节点的输出oi,oj(i≠j) 的欧氏距离的绝对值小于阈值ε,0 < ε < 1,则可以认为两个节点独立发挥作用,之间不存在冗余。否则认为两节点之间存在一个冗余,可以删减其一,约减过程是自适应的。阈值ε的取值按照对训练样本的分类精度最高为准则,取搜索步长为0.1,在区间[0, 1]内进行搜索。
ELM进行自适应约减的学习步骤如下:
1) 随机设定输入层权值W和节点阈值b;
2) 训练网络,求出隐含层输出矩阵H;
3) 根据H求出任意两个隐含层节点的输出oi,oj(i≠j) 的欧氏距离d(i,j),得到一个相关矩阵R;
4) 判断R中各元素的绝对值是否大于ε,并约减冗余节点,得到新的输入层权值W*和阈值b*;
5) 重新计算节点隐含层的输出矩阵H*;
6) 计算Moore-Penrose广义逆H†。
7) 用最小二乘法求解隐含层输出权值
基于SVD (或PSD) 特征采用约减后的极限学习机进行地面分类的算法原理如图 1所示。
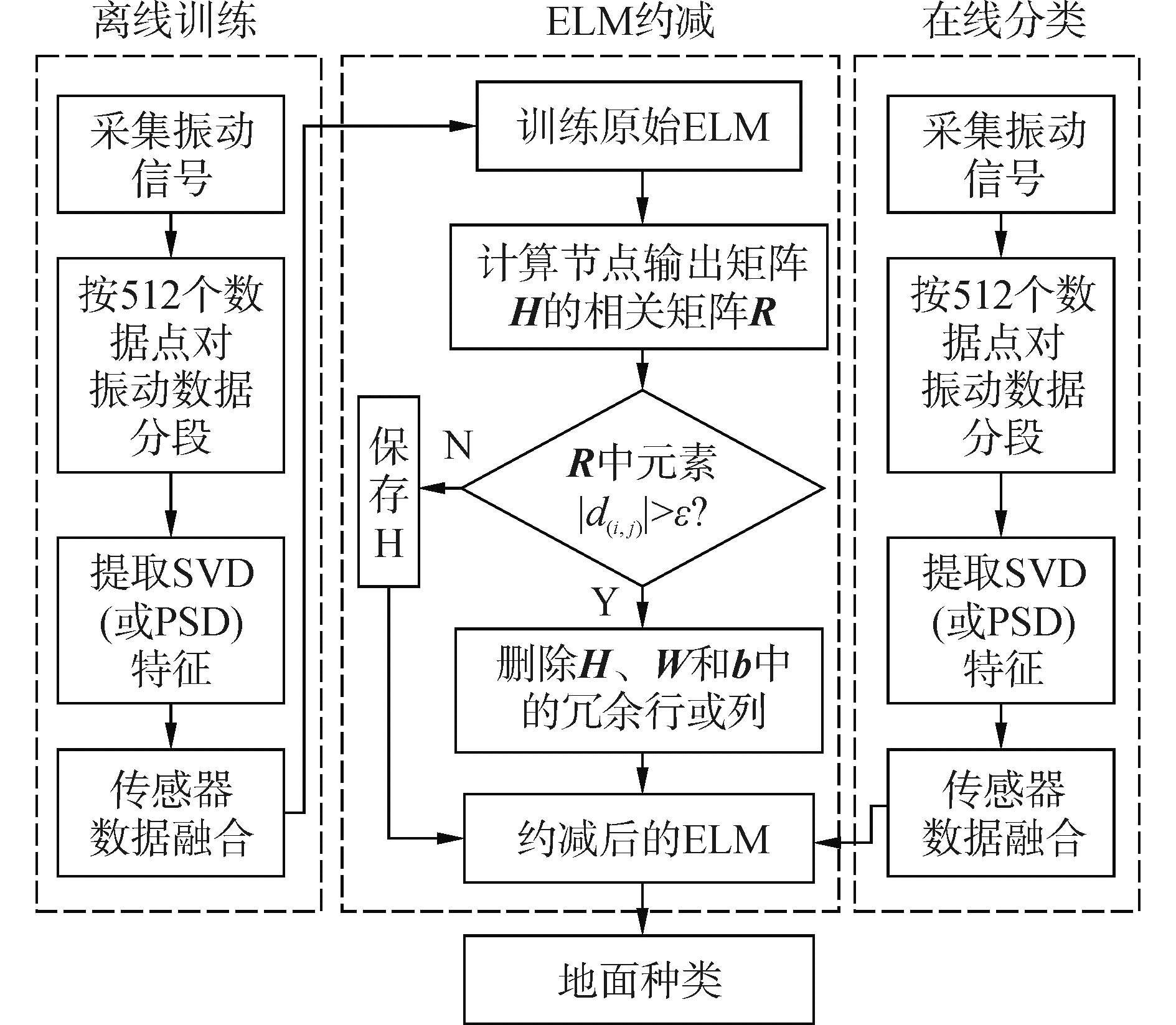
|
| 图1 基于SVD (或PSD) 特征和约减后ELM的地面分类流程图 Figure 1 Flowchart of terrain classification using subtracted ELM based on SVD (or PSD) feature |
基于模糊积分的分类器融合算法可以将各特征和分类器的贡献进行综合,能够遴选出贡献度大的特征和分类器的组合,获得更好的分类精度。基于模糊积分的分类器融合算法采用模糊测度来度量各单一分类器的重要程度,表达分类器之间的交互作用,抑制各单一分类器的不确定分类因素,因此模糊积分是一种有效的信息融合方法。本文采用Sugeno模糊积分[13]对改进的极限学习机进行融合。
模糊积分的概念建立在模糊测度[13]的基础上。设非空集合X={x1,x2,…,xn},h是定义在X上的非负可测函数,称为模糊积分函数,X中的元素根据函数值的大小按降序排列,使之满足单调条件h(x1)≥h(x2)≥…≥h(xn)。h在X上关于模糊测度g的Sugeno模糊积分为
| $ e = \int\limits_X {h\left( x \right)^\circ g\left( \cdot \right)} = \mathop {\max }\limits_{i = 1,2, \cdots ,n} {\mkern 1mu} \min \left[ {h\left( {{x_i}} \right),g\left( {{A_i}} \right)} \right] $ | (9) |
式中:e为Sugeno模糊积分,Ai={x1,x2,…,xi}为一个样本,xi为样本中的特征元素,模糊测度g(Ai) 可以由迭代公式求得
| $ \begin{align} &\ \ \ \ \ \ \ \ \ \ \ g\left( {{A}_{1}} \right)=g\left( \left\{ {{x}_{1}} \right\} \right)={{g}^{1}} \\ &g\left( {{A}_{i}} \right)={{g}^{i}}+g\left( {{A}_{i-1}} \right)+\lambda {{g}^{i}}g\left( {{A}_{i-1}} \right), 1 < i\le n \\ \end{align} $ | (10) |
式中:gi为模糊测度密度,参数λ在[-1,+∞]上具有唯一性,可以求得:
| $ \lambda +1=\prod\limits_{i=1}^{n}{\left( 1+\lambda {{g}^{i}} \right)} $ | (11) |
式中:n为样本的特征数,i为样本特征序号。
1.3.1 改进的模糊积分分类特征数目越多,按照式 (11) 计算参数λ时,需要计算的幂次越高,时间耗费急剧增加。当按式 (9) 求解模糊积分时,模糊积分函数形式不固定,而且不容易确定其参数。针对以上两个问题本文对模糊积分加以改进:一是给出λ的近似取值;二是给出适合本文地面分类算法的模糊积分函数。
1) λ的近似取值。
1.1节所述基于SVD和PSD的特征提取方法从每个样本提取的特征数分别为33和387,按式 (11) 求解λ时最多需要求解387次幂,因此计算量非常巨大,增加了算法的计算成本。式 (11) 中0≤gi≤1,当gi=1时,求解λ所消耗的时间如图 2所示。由图 2可看出,当幂次n接近400时求解λ的时间超过7 000 s,因此特征数目较大时,求解λ的计算成本是巨大的。式 (11) 中0≤gi≤1,当n的取值较大且等式的左边趋于零时,右边括号内的部分只需要在区间 (0,1) 内就可以使等式左右两边近似相等,且n越大,等式左右两边的误差越小。直接取λ=-1,当gi=0.5,n=33时,式 (11) 右边项与左边项的误差数量级达到了10-10,误差几乎可以忽略,使得等式近似成立。
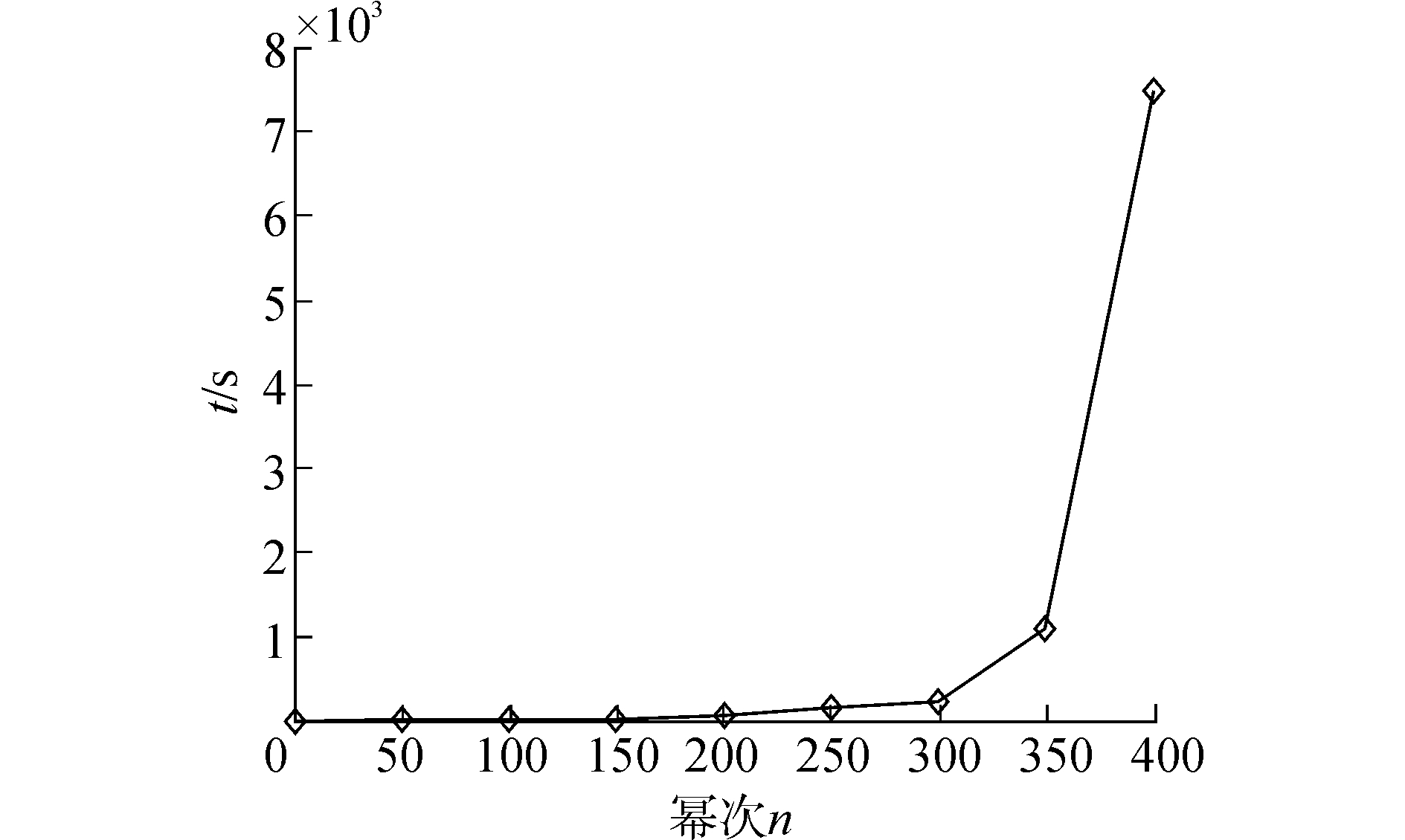
|
| 图2 求解λ时间耗费曲线图 Figure 2 Time consumption curve of solving λ |
针对传统方法计算λ的耗时问题,直接取λ=-1,避免了高次幂的运算,因此可以大幅降低模糊积分的计算成本。
2) 新的模糊积分函数。
针对本文的地面分类问题,确定模糊积分函数的形式为
| $ h(x)=\frac{1}{1+{{\text{e}}^{-\left( x-\alpha \right)\beta }}} $ | (12) |
式中:α表示矫正系数;β表示矫正后的放大倍数。对α和β在区间[0, 100]和[0, 10]内进行参数搜索。发现α在[7, 10]内取值,且β=3时,融合效果较好。本文取α=10,β=3。
1.3.2 基于改进模糊积分的ELM融合1) 模糊测度的确定。
测试样本经过极限学习机分类后得到的决策矩阵为
| $ {{\mathit{\boldsymbol{D}}}_{P}}={{\left[\begin{matrix} {{d}_{11}} & {{d}_{12}} & \cdots & {{d}_{1L}} \\ {{d}_{21}} & {{d}_{22}} & \cdots & {{d}_{2L}} \\ \vdots & \vdots & \ddots & \vdots \\ {{d}_{C1}} & {{d}_{C2}} & \cdots & {{d}_{CL}} \\ \end{matrix} \right]}_{C\times L}} $ | (13) |
式中:DP为决策矩阵,C为地面种类,L为分类器个数。因为基于模糊积分的分类器融合系统要求分类器的输出是非负实数,而决策矩阵DP的元素不是非负的,因此还不是直接的概率表达,需先将DP按列归一化到[0, 1],归一化公式为
| $ d{{'}_{mj}}=\frac{{{d}_{mj}}-{{d}_{j\min }}}{{{d}_{j\max }}-{{d}_{j\min }}} $ | (14) |
式中:m为DP的行号,j为DP的列号,即为ELM的序号,d′mj为DP中的元素按第j列归一化后的值,dmj为DP中的元素,djmin为DP中第j列元素的最小值,djmax为DP中第j列元素的最大值。
然后将决策矩阵DP进行概率表达转换:
| $ {{P}_{mj}}\frac{d{{'}_{mj}}}{\sum\limits_{m-1}^{C}{d{{'}_{mj}}}} $ | (15) |
式中:Pmj为第j个分类器将待识别样本分到第m类的概率。
本文选取各单一极限学习机对待识别样本的最大分类概率 (即转换成概率表达后的决策矩阵各列中的最大元素) 作为模糊测度密度,表示为
| $ g_j^i = \mathop {\max }\limits_{m \in \left[ {1,C} \right]} {\mkern 1mu} {P_{mj}} $ | (16) |
式中:i为待识别样本特征的序号,每个待识别样本的所有特征都取相同的模糊测度密度,j∈[1, 2]为极限学习机的序号。
2) 改进模糊积分的融合步骤。
当模糊测度和模糊积分函数都确定后,再计算模糊积分。模糊积分的计算步骤为:
① 分别将基于2种特征的待识别样本送入改进的ELM进行分类,获得决策矩阵DP;
② 将决策矩阵DP转换成概率表达形式,然后确定待识别样本的模糊测度密度gji,i为待识别样本特征的序号,j为ELM的序号;
③ 对λ取近似值-1,然后按式 (10) 确定待识别样本每个特征的模糊测度值gj(Ai);
④ 将模糊测度值gj(Ai) 和积分函数hj(xi) 代入式 (9) 得到每个待识别样本的模糊积分ej;
⑤ 对j个ELM对应的j个模糊积分ej取大,大者对应的ELM中的分类结果作为融合后的分类结果。基于改进模糊积分的ELM融合原理如图 3所示。
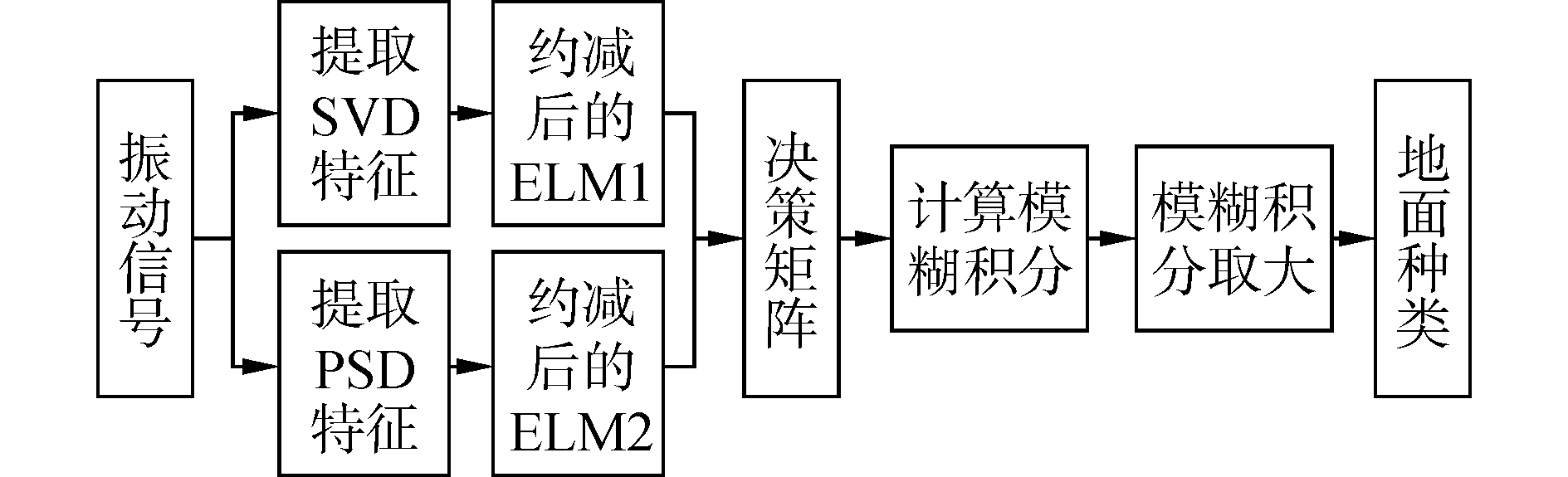
|
| 图3 基于改进模糊积分的ELM融合流程图 Figure 3 Flowchart of terrain classification using fused ELM based on improved fuzzy integral |
本实验系统包括四轮移动机器人、DH5922动态信号测试分析系统 (包括直流电压放大器、抗混滤波器和A/D转换器等)、三向加速度计、传声器、1394采集卡和台式电脑等。移动机器人如图 4所示,机器人总质量约为26 kg,关于移动机器人的更多信息可参看文献[14-15]。4个三向加速度计和4个垂直向下的传声器分别安装于机器人的4个轮臂上,左前轮轮臂上的加速度计和传声器如图 5所示。DH5922动态信号测试分析系统如图 6所示。

|
| 图4 四轮移动机器人 Figure 4 Four-wheeled mobile robot |

|
| 图5 左前轮轮臂上的加速度计和传声器 Figure 5 The accelerometer and microphone installed on the left-front wheel arm |

|
| 图6 DH5922动态信号测试分析系统 Figure 6 DH5922 dynamic signal test and analysis system |
选用的5种地面为:沙 (中粒干沙)、碎石 (外径2~4 cm)、草、土和沥青,其中沙、碎石和土在室内人工铺设,长为4.2 m,宽为0.8 m。在室外选取自然草地和铺设的沥青路面的局部作为实验地面。实验在9月中旬进行的,草仍然较为葱郁,草高约20 cm,草和沥青地面取长为4.2 m、宽为1.2 m。实验中的5种地面如图 7所示。

|
| 图7 实验中的5种地面 Figure 7 Five kinds of terrains in experiments 注:1.沙;2.碎石;3.草;4.土;5.沥青. |
使移动机器人分别以0.01、0.02、0.03、0.04、0.05 m/s五种速度在5种地面上匀速来回行驶,三向加速度计和传声器实时采集x向 (前进)、y向 (左右)、z向 (上下) 的加速度和z向的声压信号,采样频率为500 Hz。本文只采用左前轮的y、z向加速度和z向声压数据对地面进行分类。
2.2 实验结果对y、z向加速度信号和z向声压信号均按512个数据点进行分段,每段作为一个样本,得到306个样本;然后按1.1节中所描述的SVD和PSD特征提取方法分别进行特征提取;最后将加速度信号和声压信号简单连接,形成3个样本集,每个样本集均含有306个样本,在每个样本集中随机地选取其中一半作为训练集,选取另一半作为测试集。
为了验证改进极限学习机的性能,从分类准确率和实时性两个方面将该算法与BP神经网络进行对比。BP神经网络采用的学习函数为trainlm,输入和输出神经元的传递函数均选择线性传递函数purelin,隐层神经元的传递函数选择双曲正切S型传递函数tansig,目标误差为10-3,最大迭代次数为1 000[16]。本文所有算法程序均在Matlab 2011a环境下编写和运行,所用笔记本电脑的配置为:CPU:Core I3 CPU 2.20GHz;内存:2GB RAM;操作系统:Windows7。
在5种速度下采用改进的ELM和改进模糊积分融合的ELM实现了5种地面的分类。在0.02 m/s和0.04 m/s下基于SVD、PSD特征约减前后的ELM、BP神经网络和基于改进模糊积分融合的ELM对5种地面的分类结果和数据处理时间的比较如表 1和表 2所示。从表 1和表 2可以看出,在0.02 m/s和0.04 m/s下基于SVD特征的ELM节点分别约减了457个和610个,约减后的分类平均准确率分别提高了4.44%和9.54%,比BP神经网络分类平均准确率分别高3.56%和4.94%;基于PSD特征的ELM节点分别约减了637个和601个,约减后的分类平均准确率分别提高了4.97%和6.54%,比BP神经网络分类平均准确率分别高7.29%和12.81%。在0.02m /s和0.04 m/s下基于PSD特征未约减的ELM对碎石的分类准确率分别为65.36%、63.40%,通过约减ELM冗余节点,碎石地面的分类异常情况得到了较大的改善。
| 奇异值分解 (SVD) | 功率谱密度 (PSD) | SVD+PSD | ||||||||
| 未约减的ELM | 约减后的ELM | BP神经网络 | 未约减的ELM | 约减后的ELM | BP神经网络 | 2个约减后的ELM融合 | ||||
| ELM的节点数和阈值 | 765 | 308,ε=0.6 | — | 765 | 128,ε=0.6 | — | ELM1:308,ε=0.6 ELM2:128,ε=0.6 |
|||
| 地面种类/% | 沙 | 85.62 | 90.85 | 89.80 | 90.20 | 91.50 | 83.50 | 92.16 | ||
| 碎石 | 86.93 | 94.77 | 87.71 | 65.36 | 90.85 | 76.80 | 94.12 | |||
| 草 | 93.46 | 98.69 | 96.86 | 98.69 | 98.04 | 96.73 | 98.69 | |||
| 土 | 93.46 | 95.42 | 91.37 | 92.16 | 90.20 | 77.78 | 92.16 | |||
| 沥青 | 91.50 | 93.46 | 89.67 | 92.81 | 93.46 | 92.81 | 96.08 | |||
| 平均准确率/% | 90.20 | 94.64 | 91.08 | 87.84 | 92.81 | 85.52 | 94.64 | |||
| 765个样本的训练时间/s | 78.318 5 | 79.681 3 | 156.721 7 | 37.142 2 | 38.096 5 | 494.219 4 | 117.757 4 | |||
| 单个样本的测试时间/s | 0.099 7 | 0.099 6 | 0.099 5 | 0.037 5 | 0.037 4 | 0.037 5 | 0.199 | |||
| 奇异值分解 (SVD) | 功率谱密度 (PSD) | |||||||||
| 未约减的ELM | 约减后的ELM | BP神经网络 | 未约减的ELM | 约减后的ELM | BP神经网络 | |||||
| ELM的节点数和阈值 | 765 | 155,ε=0.4 | - | 765 | 164,ε=0.8 | - | ELM1:155,ε=0.4 ELM2:164,ε=0.8 |
|||
| 地面种类/% | 沙 | 87.58 | 89.54 | 87.19 | 83.01 | 83.01 | 78.30 | 92.81 | ||
| 碎石 | 84.97 | 96.08 | 84.58 | 63.40 | 91.50 | 73.85 | 95.42 | |||
| 草 | 72.55 | 97.39 | 94.25 | 99.35 | 99.35 | 91.11 | 98.04 | |||
| 土 | 86.93 | 90.20 | 87.06 | 86.27 | 85.62 | 63.27 | 90.85 | |||
| 沥青 | 84.97 | 91.50 | 86.93 | 88.89 | 94.12 | 83.01 | 90.85 | |||
| 平均准确率/% | 83.40 | 92.94 | 88.00 | 84.18 | 90.72 | 77.91 | 94.77 | |||
| 765个样本的训练时间/s | 78.216 2 | 79.516 0 | 189.453 0 | 37.359 4 | 38.771 5 | 464.121 1 | 118.287 2 | |||
| 单个样本的测试时间/s | 0.099 8 | 0.099 5 | 0.099 4 | 0.037 6 | 0.037 2 | 0.037 4 | 0.196 | |||
从表 1和表 2还可以看出数据处理时间的不同。1) 765个样本的训练时间。基于SVD特征约减前后的ELM时间相近,BP神经网络时间约是前两者的2倍,2个约减后的ELM融合的时间约是前两者的1.5倍;基于PSD特征约减前后的ELM时间相近,约是基于SVD特征约减前后的ELM时间的一半,BP神经网络时间约是前两者的13倍,2个约减后的ELM融合的时间约是前两者的3倍。2) 单个样本的测试时间。基于SVD特征约减前后的ELM与BP神经网络三者时间相近,2个约减后的ELM融合的时间约是前三者的2倍;基于PSD特征约减前后的ELM与BP神经网络三者时间相近,约是基于SVD特征约减前后的ELM与BP神经网络三者时间的三分之一,2个约减后的ELM融合的时间约是前三者的5倍。在0.01、0.03、和0.05 m/s下,以上各分类方法对765个样本的训练时间、单个样本的测试时间与在0.02、0.04 m/s下的结果在相同的数量级,也会得出如上相似的规律,这里不再赘述。综上所述,基于改进的ELM和改进模糊积分融合的ELM算法均能满足移动机器人地面分类的实时性要求。
在5种速度下基于SVD、PSD特征约减前后的ELM、BP神经网络和基于改进模糊积分融合的ELM对5种地面的分类结果如图 8所示。从图 8可以看出,在5种速度下基于SVD和PSD特征未约减的ELM对5种地面总的分类平均准确率 (即5种地面在5种速度下的平均准确率之和再除以5) 分别为85.76%和87.16%,BP神经网络对5种地面总的分类平均准确率分别为90.07%和79.85%,基于SVD和PSD特征约减后的ELM对5种地面总的分类平均准确率分别为93.90%和91.98%,两者均比未约减的ELM和BP神经网络对5种地面总的分类平均准确率有较大幅度提高。

|
| 图8 在5种速度下基于SVD和PSD特征约减前后的ELM、BP神经网络和基于改进模糊积分融合的ELM对5种地面分类结果的比较 Figure 8 Comparison of classification results using ELM, subtracted ELM, BP neural networks and fused ELM based on SVD and PSD features at five velocities |
在5种速度下基于SVD和PSD特征采用改进模糊积分融合的ELM对沙、碎石、草、土和沥青地面的分类平均准确率分别为93.07%、95.69%、98.30%、93.86%、95.16%,分别比单一改进的ELM的最高分类平均准确率分别提高了0.58%、1.31%、0.26%、0.52%、0.48%,平均提高了0.63%。采用改进的模糊积分对改进的ELM融合后5种地面总的分类平均准确率 (5种速度下的平均) 为95.22%,比基于SVD和PSD特征采用单一改进的ELM总的分类平均准确率分别提高了1.32%和3.24%。
3 结论本文针对移动机器人地面分类问题,给出了改进的极限学习机和改进的模糊积分融合的方法,并对地面进行分类;针对极限学习机隐含层节点存在冗余的问题,给出了基于节点输出相关性的约减方法,得出以下结论:
1) 在5种速度下基于SVD和PSD特征采用改进的极限学习机对5种地面总的分类平均准确率分别为93.90%和91.98%,比采用未约减的极限学习机总的分类平均准确率分别提高了8.15%和4.81%。
2) 针对模糊积分求解过程中存在的参数λ计算过于耗时的问题,直接取参数λ的简化值为-1。针对求解模糊积分时积分函数不容易确定的问题,给出了新的积分函数及参数α和β的取值。
3) 基于改进的模糊积分对改进的ELM融合可以发挥各分类器的长处,进一步提高分类准确率,在5种速度下5种地面总的分类平均准确率为95.22%,比基于SVD和PSD特征采用单一改进的极限学习机总的分类平均准确率分别提高了1.32%和3.24%。
4) 基于改进的ELM和改进模糊积分融合的ELM算法均能满足移动机器人地面分类的实时性要求。
| [1] | WILCOX B H. Non-geometric hazard detection for a mars microrover[C]//Proceedings of the Conference on Intelligent Robotics in Field, Factory, Service, and Space. Washington DC, USA, 1994:675-684. |
| [2] | BROOKS C A, IAGNEMMA K D. Self-supervised terrain classification for planetary surface exploration rovers[J]. Journal of field robotics, 2012, 29(3): 445–468. DOI:10.1002/rob.v29.3 |
| [3] | DUPONT E M, MOORE C A, COLLINS E G, et al. Frequency response method for terrain classification in autonomous ground vehicles[J]. Autonomous robots, 2008, 24(4): 337–347. DOI:10.1007/s10514-007-9077-0 |
| [4] | WEISS C, STARK M, ZELL A. SVMs for vibration-based terrain classification[C]//Autonome Mobile Systeme 2007. Heidelberg, Germany, 2007:1-7. |
| [5] | OJEDA L, BORENSTEIN J, WITUS G, et al. Terrain characterization and classification with a mobile robot[J]. Journal of field robotics, 2006, 23(2): 103–122. DOI:10.1002/(ISSN)1556-4967 |
| [6] | LIBBY J, STENTZ A J. Using sound to classify vehicle-terrain interactions in outdoor environments[C]//Proceedings of the IEEE International Conference on Robotics and Automation. Piscataway, USA, 2012:3559-3566. |
| [7] |
吕志民, 张武军, 徐金梧, 等. 基于奇异谱的降噪方法及其在故障诊断技术中的应用[J].
机械工程学报, 1999, 35(3): 85–88.
LYU Zhimin, ZHANG Wujun, XU Jinwu, et al. A noise reduction method based singular spectrum and its application in machine fault diagnosis[J]. Chinese journal of mechanical engineering, 1999, 35(3): 85–88. |
| [8] |
李强. 基于振动信号的轮式机器人地面分类方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2013: 75-80.
LI Qiang. Research on terrain classification methods for wheeled robots based on vibration signals[D]. Harbin:Harbin Engineering University, 2013:75-80. |
| [9] |
沈志远, 王黎明, 陈方林. 基于有限长序列分析的Welch法谱估计研究[J].
计算机仿真, 2010, 27(12): 391–395.
SHEN Zhiyuan, WANG Liming, CHEN Fanglin. Research on spectral estimation using welch method based on analysis of finite-length sequence[J]. Computer simulation, 2010, 27(12): 391–395. DOI:10.3969/j.issn.1006-9348.2010.12.095 |
| [10] | WELCH P D. The use of fast Fourier transform for the estimation of power spectra:A method based on time averaging over short, modified periodograms[J]. IEEE transactions on audio and electroacoustics, 1967, 15(2): 70–73. DOI:10.1109/TAU.1967.1161901 |
| [11] | HUANG G, ZHU Q, SIEW C. Extreme learning machine:a new learning scheme of feedforward neural networks[C]//Proceedings of 2004 IEEE International Joint Conference on Neural Networks. Piscataway, USA, 2004:489-501. |
| [12] |
申丰山, 王黎明, 张军英. 基于SVM技术的精简极速学习机[J].
华中科技大学学报:自然科学版, 2014, 42(6): 107–110.
SHEN Fengshan, WANG Liming, ZHANG Junying. Reduced extreme learning machine employing SVM technique[J]. Journal of Huazhong University of Science and Technology:natural science edition, 2014, 42(6): 107–110. |
| [13] | SUGENO M. Theory of fuzzy integrals and its applications[M]. Tokyo: Tokyo Institute of Technology, 1974: 7-29. |
| [14] | XU He, ZHANG Zhenyu, ALIPOUR K, et al. Prototypes selection by multi-objective optimal design:application to a reconfigurable robot in sandy terrain[J]. Industrial robot, 2011, 38(6): 599–613. DOI:10.1108/01439911111179110 |
| [15] | XU He, XU Yan, FU Hu, et al. Coordinated movement of biomimetic dual PTZ visual system and wheeled mobile robot[J]. Industrial Robot, 2014, 41(6): 557–566. DOI:10.1108/IR-05-2014-0345 |
| [16] |
时建峰, 程珩, 许征程, 等. 小波包与改进BP神经网络相结合的齿轮箱故障识别[J].
振动、测试与诊断, 2009, 29(3): 321–324.
SHI Jianfeng, CHENG Heng, XU Zhengcheng, et al. Fault diagnosis of gearbox using wavelet package and improved BP neural network[J]. Journal of vibration, measurement & diagnosis, 2009, 29(3): 321–324. |



