随着现代电子技术的迅速发展,电子设备在相关领域得到了广泛应用。模拟电路是电子设备的重要组成部分,据统计,电路模拟部分发生的故障占总故障的80%以上[1],而由于故障模型复杂,难以简单量化,同时存在容差、软故障和非线性等问题,模拟电路故障诊断方法相对发展缓慢,也一直是研究的热点[3-16]。此外,随着电路规模的增大和集成度的增高,实际测量时的可测节点越来越少,同时引脚间距的日益减小,增加了故障诊断信息的获取难度。这些都对模拟电路故障诊断技术提出了更高的要求。
故障字典法[2-4]是目前实用价值较高的一种方法,但该方法易受噪声和容差影响,多针对硬故障,尤其对于复杂模拟电路,诊断工作量较大。而采用模式识别[15-18]思想的故障诊断方法虽然在检测效果上有所提高,但也面临需要大量训练样本、训练时间长、故障种类数量和样本精度影响分类准确率、诊断过程复杂等问题。
传统的诊断方法往往将单一故障特征作为测试指标,进行故障定位,不足以反映电路的整体状态,容易造成故障模糊现象,影响诊断的准确性。为进一步提高故障诊断能力,在进行特征提取时应尽可能考虑到更多的电路信息,使选用的故障特征能更好的反应系统状态。
针对上述问题,提出电路特征信息矩阵的概念,依据电路在不同激励下各测点的响应特征向量组建立电路特征信息矩阵,以充分利用已知电路信息来全面描述电路状态。将马氏距离的概念进行相应加权处理后,引入诊断过程中,用于表征各故障特征向量之间的相似程度。通过Monte-Carlo分析构建各故障模式的马氏距离容差矩阵,描述元件容差特性对电路的影响。考虑到不同个体相似度对总体相似度的贡献差异,提出了离散度权重和模糊度权重的概念,对电路特征信息相似度矩阵进行相应的加权处理。最后,求取待测电路相对电路各故障模式的总体相似度矢量,并依据一定的判定准则实现故障诊断。
1 电路特征信息矩阵传统的故障诊断方法往往以一个特征信号作为测试指标(一般以电压作为测试信号)。不同故障模式的响应区间容易重叠,导致诊断结果出现模糊。针对这一问题,本文根据电路在不同激励下各测点的故障特征向量建立电路特征信息矩阵,以期全面反映电路的状态信息。设Yij=[xij1 xij2 …xijL](i=1, 2, …n, j=1, 2, , …m)为在测试激励信号i下,第j个测点的故障特征向量,其中n为采样激励数,m为电路测点数,L为选用故障特征的维数。则定义电路的特征信息矩阵Y:
| $\boldsymbol{Y} = \left[{\begin{array}{*{20}{c}} {{Y_{11}}}& \cdots &{{Y_{1m}}} \\ \vdots & \ddots & \vdots \\ {{Y_{n1}}}& \cdots &{{Y_{nm}}} \end{array}} \right]$ | (1) |
对于电路特征信号的选用,科研人员进行了大量研究,并提出了众多故障特征指标,包含时域瞬态特征,稳态波形特征、频域相关特征、小波系数特征、统计特征等众多类别。大多需要复杂的求解计算,获取过程较为困难。本文选用基本时域特征中的峰值电压、频率、相位和响应信号K个等时间间隔的电压采样,组成描述电路状态信息的故障特征向量。上述选用的各故障特征均可利用Pspice软件进行少数几次仿真获得,减小了数据获取难度,提高了诊断效率。
为使采样频率的选择更有针对性,从而以较少的频率数,尽可能充分的反应电路的状态信息,在进行采样频点选择时,首先通过计算、仿真求出电路网络函数或波特图,从而获得电路的转折频率,以转折频率为端点,划分频率子区间,最后在每个子区间内进行频率采样,获得采样频点。
实测诊断时,首先提取待测电路的电路特征信息矩阵,将其作为待诊断样本,通过对待测电路和不同电路故障模式下电路信息特征矩阵的关联、比较,求取其和各故障模式的总体相似程度,并按照一定的诊断规则,确定电路状态,实现对电路的综合诊断。
2 基于矩阵相似度的故障判定 2.1 改进马氏距离在进行数据分析处理时,距离概念通常被用做相似性的度量指标。马氏距离[12]是由印度统计学家马哈拉诺比斯(P·C·Mahalanobis)提出的一种样本间距离计算方法。通过计算目标样本与总体样本间的协方差距离,比较样本间的相似程度。马氏距离越小表示样本间相似程度越大。与传统的距离算法相比,马氏距离不受数据量纲影响,充分考虑到了特征参数之间的相互联系,有效避免不同变量间相关性干扰,适用于参数量纲种类较多的模拟电路故障诊断领域。因此,本文引入马氏距离相关概念,并将其作为求解矩阵相似度的辅助手段。
设有样本集x=(x1, x2, …, xn),协方差矩阵为记Σ,则样本向量y到样本集x之间的马氏距离定义为
| ${\boldsymbol{M}_d} = \sqrt {\left( {\boldsymbol{y-\bar x}} \right)\boldsymbol{\sum }{^{-1}\left( {\boldsymbol{y-\bar x}} \right)} } $ | (2) |
| $\bar x = \frac{1}{n}k\sum\limits_{i = 1}^n {{x_i}} $ | (3) |
虽然考虑了各样本指标间相关性和量纲的影响,但马氏距离的缺点在于它对各个特征指标的重要程度同等看待,忽略了各指标重要程度的差异,从而夸大了微小变量的作用,影响诊断结果的准确性。为减小这种影响,参考文献[13-14]中相关研究,为马氏距离加入权重矩阵,将式(2)、(3)改进为:
| ${\boldsymbol{M_d}} = \sqrt {\left( {\boldsymbol{y-\bar x}} \right)\boldsymbol{W\sum} {^{-1}\boldsymbol{W}\left( {\boldsymbol{y-\bar x}} \right)} } $ | (4) |
| $\boldsymbol{W} = {\text{diag}}\left( {{w_1}, {w_2}, \cdots, {w_n}} \right)$ | (5) |
针对本文具体情况,提出基于敏感度的加权平均法来确定权重矩阵。定义权值如下
| ${w_i} = {p_i}/\sum\limits_{i = 1}^n {{p_i}} $ | (6) |
| ${p_i} = \frac{1}{g}\sum\limits_{k = 1}^g {\frac{{\Delta {T_{ik}}}}{{{T_i}}}} $ | (7) |
式中:pi为第i个特征量的平均信息贡献率,其实质是对元件发生不同偏差时故障特征的增量灵敏度求均值,反应了特征量对故障的整体敏感程度,与传统的微分灵敏度和增量灵敏度相比,综合考虑了元件参数变化量的影响,提高了分析结果的准确度。权重矩阵的引入减小了微小变量对结果的影响,加强了主导变量的作用,且由式(6)可知:∑wi=1,wi∈[0, 1](i=1, 2, …, n),所以权重矩阵的引入并未破坏样本各向量间样本的相关性,是合理和可行的。
2.2 故障信息相似度加权矩阵考虑电路容差的影响,电路元件参数变为以其标称值为中心的一个小区间内变化的随机数,因而,电路在各状态下的故障特征不是一个确定值,而变成一个连续小区间。采用Mont-Carlo方法获取容差条件下电路数据,将电路特征信息矩阵中元素由单一的样本向量,变为容差条件下的样本向量组。计算各向量组的类间马氏距离,取最大值构建电路各故障模式的马氏距离容差矩阵如下:
| ${\boldsymbol{d}_k} = \left[{\begin{array}{*{20}{c}} {{d_{k11\max }}}& \cdots &{{d_{kqm\max }}} \\ \vdots & \ddots & \vdots \\ {{d_{kn1\max }}}& \cdots &{{d_{knm\max }}} \end{array}} \right]$ | (8) |
定义Si为在激励信号i下,测点j特征向量xij对故障模式k的相似度
| ${S_{kij}} = \left\{ \begin{gathered} 1, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < d < {d_{kij\max }} \hfill \\ \frac{{\exp \left( {10\left( {{d_{kij\max }}-d} \right)} \right)}}{{{d_{kij\max }}}}, \;\;d > {d_{kij\max }} \hfill \\ \end{gathered} \right.$ | (9) |
可得待测电路对故障模式k的电路故障信息相似度矩阵:
| ${S_k} = \left[{\begin{array}{*{20}{c}} {{S_{k11}}}& \cdots &{{S_{k1m}}} \\ \vdots & \ddots & \vdots \\ {{S_{kn1}}}& \cdots &{{S_{knm}}} \end{array}} \right]$ | (10) |
每种故障模式都有其相对应的故障信息相似度矩阵,通过对矩阵信息综合处理,可获得该故障模式的总体相似度。单纯的对各相似度进行累加求均值,忽略了不同个体相似度对总体相似度的贡献差异,所以需要考虑赋予其不同的权值。
本文采用Mont-Carlo分析法获样本数据,同一故障模式下由于激励信号和采样测点的不同,样本的离散程度也各不相同。离散程度越小,准确度越高,也就应赋予更大的权重。以样本的最大类间马氏距离dkijmax表示样本的离散程度,dkijmax越大,表示离散度越大。则在故障模式k下,测点j在激励i下的离散度权重系数可表示为
| ${t_{kij}} = \frac{{{{\left( {{d_{kij\max }}} \right)}^{-1}}}}{{\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{{\left( {{d_{kij\max }}} \right)}^{-1}}} } }}$ | (11) |
对于在某一激励下某个测点的各个故障特征个体相似度而言,如果其中一个的值明显高于其他相似度的值,则表明该判定结果的模糊程度越小,相对于其他判决结果也就应赋予更高的权重:
| ${\varphi _{ij}} = \frac{{\mathop {\max }\limits_{k = 1}^K \left( {{S_{kij}}} \right)}}{{\sum\limits_{k = 1}^K {{S_{kij}}} }}$ | (12) |
式中:φij代表在激励信号i下的测点j故障特征向量最大相似度在所有相似度之和中所占比例,φij越大,模糊度越小。定义模糊度权重系数如下
| ${g_{ij}} = \frac{{mn{\varphi _{ij}}}}{{\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{\varphi _{ij}}} } }}$ | (13) |
在考虑离散度和模糊性权重后,可得故障模式k下的电路特征信息加权相似度矩阵:
| ${{S'}_k} = \left[{\begin{array}{*{20}{c}} {{t_{k11}}{g_{11}}{S_{k11}}}& \cdots &{{t_{K1m}}{g_{1m}}{S_{K1m}}} \\ \vdots & \ddots & \vdots \\ {{t_{Kn1}}{g_{n1}}{S_{Kn1}}}& \cdots &{{t_{Knm}}{g_{nm}}{S_{Knm}}} \end{array}} \right]$ | (14) |
故障模式k的总体相似度可表示为
| ${v_k} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{t_{kij}}{S_{kij}}{g_{ij}}} } $ | (15) |
将各故障模式总体相似度按从大到小顺序重新排序,得向量v'=(v1', v2', …vK'),故障判定的基本准则如下:
1) 电路确诊条件:最大总体相似度大于某一阈值,且与其他总体相似度之差大于另一阈值。即,向量v'满足
| $\left\{ \begin{array}{l} {{v'}_1} > \eta \\ {{v'}_1}-{{v'}_2} > \gamma \end{array} \right.$ | (16) |
则电路状态判定为v1'所代表故障模式。式中,η,γ可根据实际需求自行选取。
2) 电路模糊状态条件:最大n个相似度均大于某个阈值,且其相似度之差的最大值小于某个阈值
| $\left\{ \begin{array}{l} {{v'}_i} > \eta '\\ \mathop {\max }\limits_{s, t = 1}^i \left| {{{v'}_s} - {{v'}_t}} \right| < \gamma ' \end{array} \right.$ | (17) |
则电路状态判定为可能为{v1', v2', …, vi'}中任一故障模式的模糊状态。
3) 其他情况下,判定电路处于无法诊断状态。
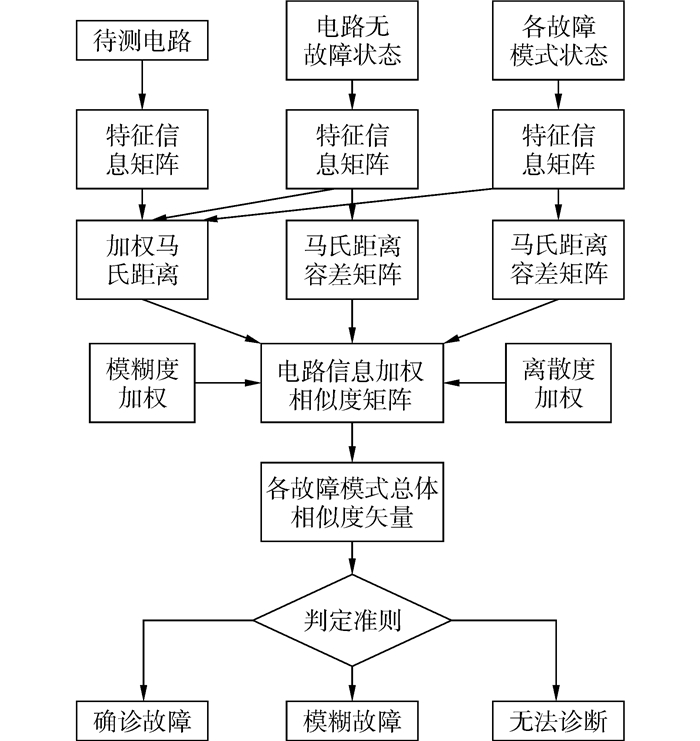
故障诊断的整体流程如图 1所示,下面将通过实验仿真进行分析验证。
|
| 图1 故障诊断流程图 Figure 1 Flowchart of fault diagnosis |
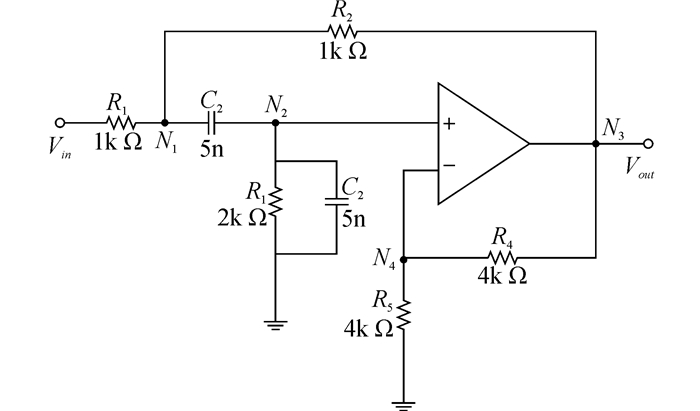
滤波电路在电子设备中有广泛的应用,也常被用作模拟电路故障诊断方法的验证电路,本文选用Sallen-Key带通滤波电路(如图 2所示)作为测试电路,进行方法验证。电路中各元件标称值为:R1=1 kΩ, R2=1 kΩ,R3=2 kΩ,R4=R5=4 kΩ,C1=C2=5 nF,其中电阻和电容的容差均设为5%。
|
| 图2 Sallen-Key带通滤波电路 Figure 2 Sallen-Key band-pass filter circuit |
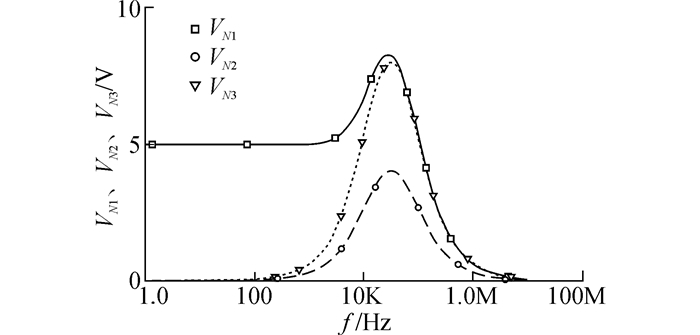
首先对容差条件下电路的硬故障进行方法验证,在PSPICE软件中搭建待测电路,选用N1、N2、N3为测试点,进行交流小信号分析,可得幅频特性曲线如图 3所示。采用第2节中所述方案,以转折频率为端点,划分频率子区间,在每个区间内进行频率采样,一共选用5个激励频率:1、10、20、50、100 kHz。选用时域特征中的峰值电压、相位、加上6个等间隔波形采样电压组成描述电路状态信息的故障特征向量。对电路的正常模式和各故障模式进行50次Monte-Carlo分析,获取测试数据,选用其中25组数据构建电路特征信息矩阵,剩余数据作为测试样本,对诊断结果进行分析验证。需要注意的是有些硬故障会导致电路无法正常工作,从而不能获取仿真数据,此时可用串联小电阻或大电阻来表示短路和断路状态。
|
| 图3 测试电路的幅频特性 Figure 3 Amplitude-frequency distribution of the circuit |
采用MATLAB进行数据处理,构建电路特征信息矩阵,通过计算,获得待测电路的各故障模式总体相似度矢量,选用判定阈值η=0.8,γ=0.2,η'=0.5,γ'=0.15,可得对容差电路硬故障的确诊率为97.1%,模糊率为2.6%,误诊拒诊率为0.3%。
再采用同样的方法对容差条件下电路的软故障进行方法验证,故障元件列表如表 1所示,按故障元件偏离标称值程度,分成3个诊断组,每组都包含12种故障模式,选用同样的判定阈值,诊断结果如表 2所示。
| 序号 | 故障元件 | 故障偏差度/% | ||
| 诊断组1 | 诊断组2 | 诊断组3 | ||
| 1 | R1↑ | +100 | +50 | +20 |
| 2 | R1↓ | -90 | -50 | -20 |
| 3 | R2↑ | +100 | +50 | +20 |
| 4 | R2↓ | -90 | -50 | -20 |
| 5 | R3↑ | +100 | +50 | +20 |
| 6 | R3↓ | -90 | -50 | -20 |
| 7 | R4↑ | +100 | +50 | +20 |
| 8 | R4↓ | -90 | -50 | -20 |
| 9 | C1↑ | +100 | +50 | +20 |
| 10 | C1↓ | -90 | -50 | -20 |
| 11 | C2↑ | +100 | +50 | +20 |
| 12 | C2↓ | -90 | -50 | -20 |
随着故障元件值偏离元件标称值程度的降低,故障确诊率相应的有所下降,模糊率、拒诊误诊率都有小幅度的增高,但总体来说,几种情况下,采用本文方法时电路的故障诊断率都保持了较高的水平,说明方法有较强的软故障诊断能力。
为验证电路特征信息相似度矩阵加权的必要性,选用诊断组2的故障设定和判定阈值,在MATLAB中进行数据分析处理时,不进行离散度和模糊度加权,可得电路的故障确诊率为85.1%,模糊率为10.8%,误诊拒诊率为4.9%。通过比较考虑权重和不考虑权重两种情况的诊断结果可知,进行权重加成后,能有效提高故障诊断能力。
为研究电路特征信息矩阵大小对故障诊断能力的影响,对矩阵进行降维处理,激励频率选用1 kHz和20 kHz,测点选用N3,特征向量为6个等间隔波形采样。选用诊断组2的故障设定和判定阈值,可得电路的故障确诊率为79.2%,模糊率为12.5%,误诊拒诊率为8.3%。结果说明特征信息矩阵包含信息量越多,诊断能力越强。但相应的诊断复杂度也会有所升高,在诊断时,可根据实际情况调整电路特征信息矩阵规模,以期以更小的代价获得更高的故障检测率。
传统的诊断方法往往从激励、测点、故障特征中的一个维度出发,进行故障定位。文献[15]提出了一种基于多测试点多特征信息构造原始样本集构造方法。文献[11]通过比较不同频率下样本与各故障模式的时域波形特征向量相似程度,实现故障定位。与上述方法相比,本文方法的特点在于:电路特征信息矩阵是围绕激励、测点、故障特征三个维度建立的,能更加系统全面的利用电路状态信息,具有更强的软故障诊断能力。
与文献[5-9]中方法相比,整个诊断过程均采用相关软件进行数据的采样分析和处理,数据获取难度低,同时避开了神经网络法需要的大样本训练和主成分分析、频谱分析、优化算法、D-S证据理论等复杂运算,操作更为简单。
4 结论本文提出了一种基于特征信息矩阵的容差电路故障诊断方法。其优点如下:1) 通过建立电路特征信息矩阵,期覆盖更多的故障信息,全面反映了电路状态特征。2) 采用加权马氏距离,消除了各样本指标间相关性和量纲的影响。3) 通过离散度和模糊度加权,加强敏感个体权重,提高信息矩阵的故障诊断能力。实验结果表明,该方法对容差条件下电路的软、硬故障均有较高的诊断正确率。
电路特征信息矩阵的建立提供了另一种样本集的构造思路。在实际诊断时,可根据电路具体情况和诊断需求对电路信息矩阵进行扩展、缩小或改进。本文选用时域特征和时域信号采样组建电路状态信息矩阵,但对于一些电路故障,单靠时域特征并不能将其完全敏化。可考虑对电路特征信息矩阵进一步改进,如在激励维度上加入阶跃响应、三角波、白噪声等信号,提取频谱特征等。
| [1] |
杨士元, 胡梅, 王红. 模拟电路软故障诊断的研究[J].
微电子学与计算机, 2008, 25(1): 1–8.
YANG Shiyuan, HU Mei, WANG Hong. Study on soft fault diagnosis of analog circuit[J]. Microelectronics & computer, 2008, 25(1): 1–8. |
| [2] | YANG Chenglin, TIAN Shulin, LONG Bing. Application of heuristic graph search to test-point selection for analog fault dictionary techniques[J]. IEEE transactions on instrumentation and measurement, 2009, 58(7): 2145–2158. DOI:10.1109/TIM.2008.2006725 |
| [3] | GOLONEK T, RUTKOWSKI J. Genetic-algorithm-based method for optimal analog test points selection[J]. IEEE Transactions on circuits and systems Ⅱ:express briefs, 2007, 54(2): 117–121. DOI:10.1109/TCSII.2006.884112 |
| [4] |
叶笠, 王厚军, 叶芃, 等. 容差模拟电路诊断中故障隔离的几何方法[J].
电子科技大学学报, 2011, 40(1): 53–57.
YE Li, WANG Houjun, YE Peng, et al. Geometric methods of faults isolation for analog diagnosis with tolerance[J]. Journal of university of electronic science and technology of China, 2011, 40(1): 53–57. |
| [5] |
祝文姬, 何怡刚. 一种新的模拟电路故障特征提取与诊断方法[J].
湖南大学学报:自然科学版, 2011, 38(4): 41–46.
ZHU Wenji, HE Yigang. A new fault feature extraction and diagnosis method of analog circuits[J]. Journal of Hunan university:natural sciences, 2011, 38(4): 41–46. |
| [6] |
唐圣学, 蔡红军, 李志刚. 基于小波与神经网络的模拟电路故障诊断融合方法[J].
中南大学学报:自然科学版, 2015, 46(1): 127–134.
TANG Shengxue, CAI Hongjun, LI Zhigang. Fault diagnosis fusion method for analog circuits based on wavelet and neural network[J]. Journal of central south university:science and technology, 2015, 46(1): 127–134. |
| [7] | LONG Bing, TIAN Shulin, WANG Houjun. Diagnostics of filtered analog circuits with tolerance based on LS-SVM using frequency features[J]. Journal of electronic testing, 2012, 28(3): 291–300. DOI:10.1007/s10836-011-5275-y |
| [8] |
徐宇亮, 孙际哲, 陈西宏, 等. 采用多目标粒子群算法的模拟电路故障诊断研究[J].
西安交通大学学报, 2012, 46(6): 92–97.
XU Yuliang, SUN Jizhe, CHEN Xihong, et al. Analog circuit fault diagnosis with multi-objective particle swarm optimization[J]. Journal of Xi'an jiaotong university, 2012, 46(6): 92–97. |
| [9] | ZHANG Yong, CHEN Xixiang, LIU Guanjun, et al. Optimal test points selection based on multi-objective genetic algorithm[C]//Proceedings of IEEE Circuits and Systems International Conference on Testing and Diagnosis. Chengdu, China:IEEE, 2009:1-4. |
| [10] | SPYRONASIOS A D, DIMOPOULOS M G, HATZOPOULOS A A. Wavelet analysis for the detection of parametric and catastrophic faults in mixed-signal circuits[J]. IEEE transactions on instrumentation and measurement, 2011, 60(6): 2025–2038. DOI:10.1109/TIM.2011.2115550 |
| [11] |
钟建林, 何友, 任献彬. 基于波形相似度的容差模拟电路软故障诊断[J].
电工技术学报, 2012, 27(8): 222–229.
ZHONG Jianlin, HE You, REN Xianbin. Soft fault diagnosis based on waveform similarity for tolerance analog circuit[J]. Transactions of China electro technical society, 2012, 27(8): 222–229. |
| [12] | DOGRUEL M, OZGUNZER U. Stability of hybrid systems[C]//Proceedings of the 1994 IEEE International Symposium on Intelligent Control. Columbus, OH, USA:IEEE, 1994:129-134. |
| [13] |
王晋, 李夕兵, 杨金林. 深部硬岩岩爆评判的加权马氏距离判别法[J].
采矿与安全工程学报, 2011, 28(3): 395–400.
WANG Jin, LI Xibing, YANG Jinlin. A weighted Mahalanobis distance discriminant analysis for predicting rock-burst in deep hard rocks[J]. Journal of mining & safety engineering, 2011, 28(3): 395–400. |
| [14] |
韩涵, 王厚军, 龙兵, 等. 基于改进马氏距离的模拟电路故障诊断方法[J].
控制与决策, 2013, 28(11): 1713–1717, 1722.
HAN Han, WANG Houjun, LONG Bing, et al. Method for analog circuit fault diagnosis based on improved Mahalanobis distance[J]. Control and decision, 2013, 28(11): 1713–1717, 1722. |
| [15] |
潘强, 杨超. 基于多测试点多特征信息的模拟电路故障诊断[J].
计算机测量与控制, 2013, 21(11): 2931–2934.
PAN Qiang, YANG Chao. Fault diagnosis of analog circuit based on multi-test points and multi-feature information[J]. Computer measurement & control, 2013, 21(11): 2931–2934. |



