Urea-SCR装置自欧Ⅳ阶段开始逐渐发展为降低柴油机NOx排放量的主流装备[1-5]。柴油机排放法规持续升级对NOx转化效率和排放量控制准确性的要求逐步提高[6-8],促使SCR装置控制系统成为重要的研究课题。
Urea-SCR系统为大时滞对象且具有扰动多样的特征,在解决其控制问题上,现有控制技术遇到瓶颈,而非线性自抗扰控制技术 (nonlinear active disturbance rejection control,NADRC) 表现出较好的综合控制品质。
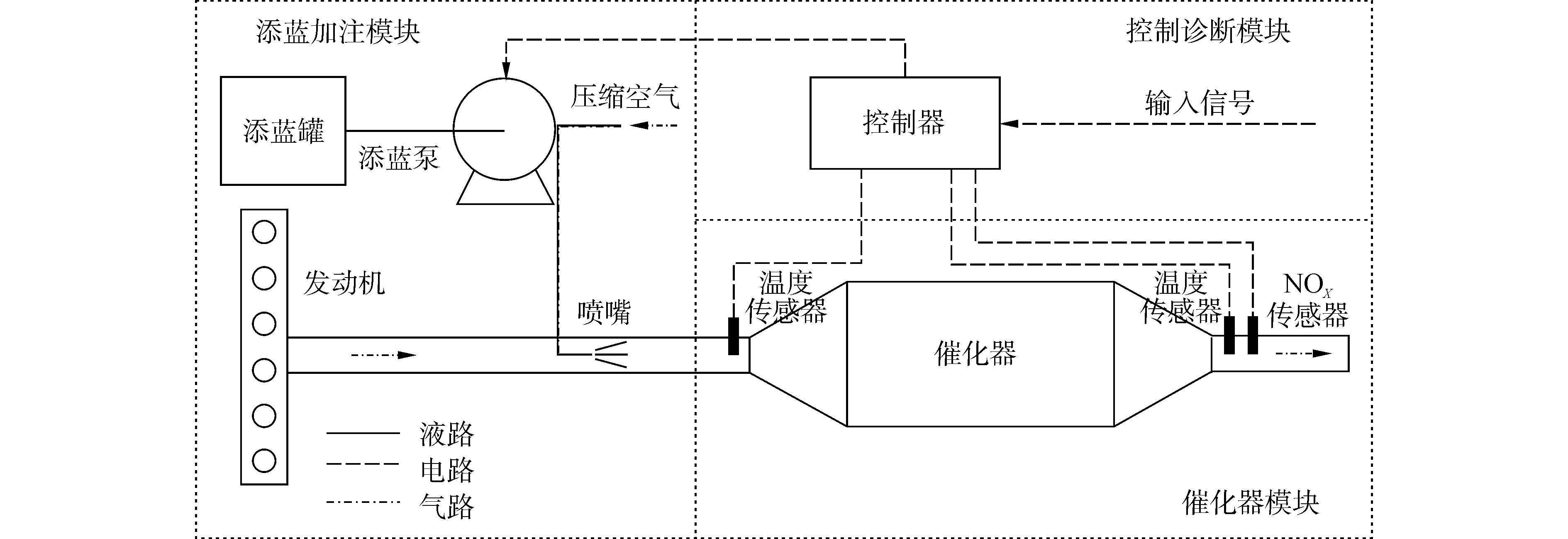
1 SCR装置控制系统的性能需求车用柴油机排放水平正处于国四阶段向国五阶段过渡的时期,国六排放标准也即将正式出台,匹配Urea-SCR装置将作为柴油机应对当前排放要求和排放升级的共用技术平台。典型的车载Urea-SCR装置主要由添蓝 (32.5%质量浓度的尿素水溶液,用于产生还原剂-NH3) 加注模块、催化器模块和控制诊断模块构成 (见图 1)。
|
| 图1 典型车载Urea-SCR装置工作原理示意 Figure 1 Schematic diagram of Urea-SCR devices on vehicles |
添蓝加注模块为控制量 (添蓝流量) 的执行机构,实现添蓝的计量、输送及加注;催化器模块为NH3与NOx的催化还原反应提供场所及催化作用;控制诊断模块为中央控制单元,集成了添蓝流量控制和故障诊断 (on board diagnostics,OBD) 功能。
1.1 车用柴油机排放标准动态GB17691-2005《车用压燃式、气体燃料点燃式发动机与汽车排气污染物排放限值及测量方法 (中国Ⅲ、Ⅳ、Ⅴ阶段)》规定,国五柴油机排放型式认证基于欧洲稳态测试循环 (European steady cycle,ESC) 和欧洲瞬态测试循环 (European transient cycle,ETC) 进行[6],相应的NOx排放限值示于表 1。车用柴油机国六排放标准虽然尚未正式出台,但将与欧Ⅵ(见表 1) 接近[7],测试循环也将采用世界统一稳态试验循环 (world harmonized steady-state cycle,WHSC) 代替ESC循环,采用世界统一瞬态试验循环 (world harmonized transient cycle,WHTC) 取代ETC循环,NOx排放许可限值预计设定在0.4~0.5 g/(kw·h)。
| 测试循环 | NOx排放限值 | |
| 国五阶段 | ESC ETC |
2.00 2.00 |
| 欧Ⅵ阶段 | WHSC WHTC |
0.40 0.46 |
目前,部分国五柴油机在实际应用中发生NOx排放超标的问题,激活扭矩限制器的行为严重地影响了车辆的正常使用[8]。本文研究发现,车辆运营期间时常存在多方面的扰动因素,SCR装置控制系统抑制扰动能力不足是造成NOx超标的主要原因[9]。
另一方面,根据柴油机传统燃烧技术的研究现状,难以通过燃烧优化使机内NOx排放降至3.5 g/(kw·h) 以下,意味着在国六阶段90%以上的NOx需要借助SCR装置来进行处理。此外,国六阶段排放认证循环将向低温区域偏移,催化还原反应的速率必将受到压制,因此SCR控制系统的动态响应能力面临新的需求。
综上,解决SCR装置在车用柴油机上的可靠应用问题,需要提高其控制系统抑制扰动的能力和动态响应性能。
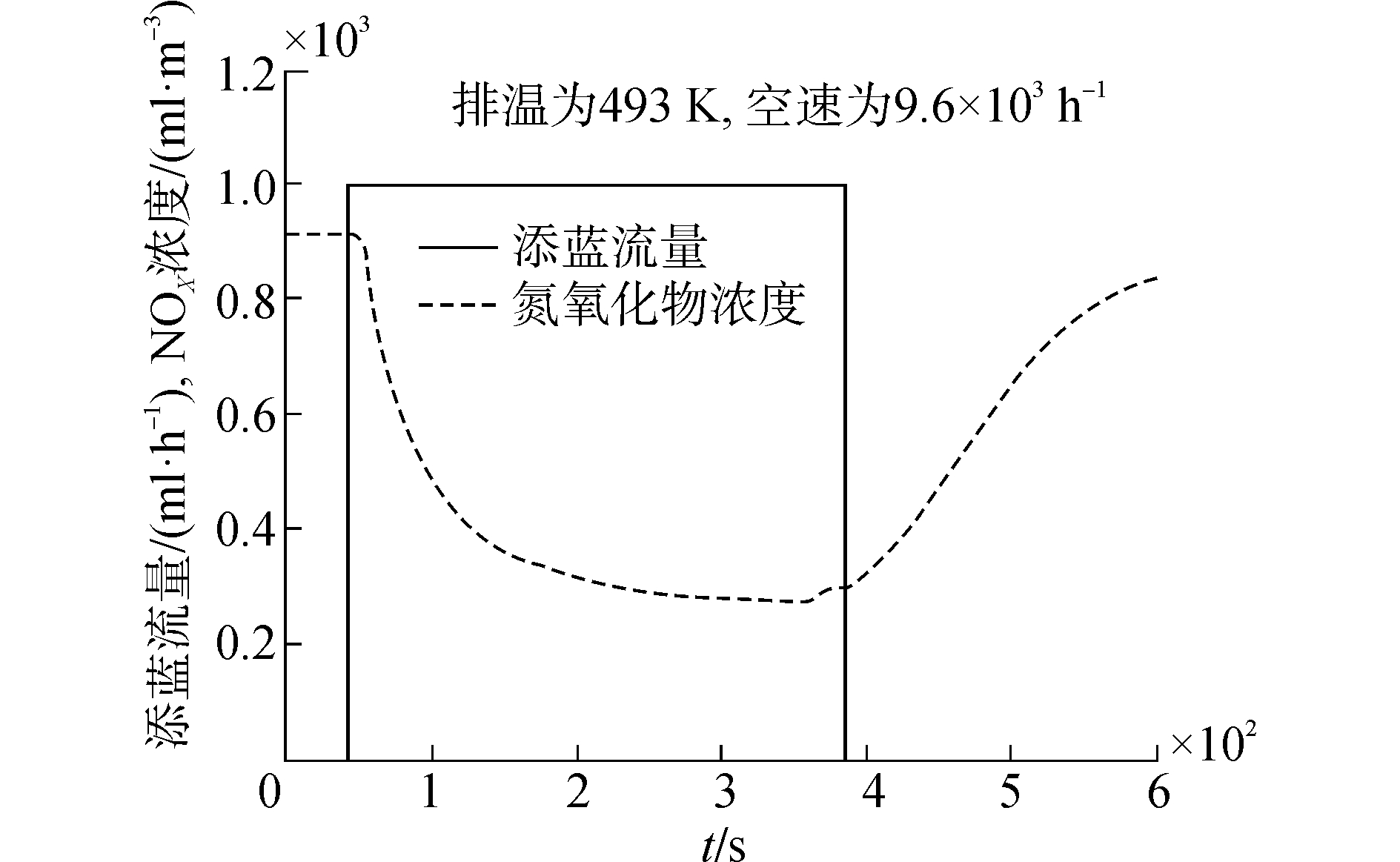
1.2 对象的多元可变阻容特性本文针对多套Urea-SCR装置进行应用研究发现,对象控制输入 (添蓝流量) 的改变与被控输出 (催化器下游的NOx浓度) 的变化之间存在典型特征。以某台4.7 L柴油机及其SCR装置为例,在柴油机工况充分稳定时,对象的被控输出随着控制输入的变化呈现出类似阻容特性曲线的特征 (见图 2),且被控输出的变化相对控制输入的改变存在明显的滞后 (图 2中约滞后6 s)。进一步研究表明,“阻”和“容”的大小与排气温度、空速和添蓝流量等因素有关,可见Urea-SCR装置的数学模型具有不确定性。
|
| 图2 SCR装置控制输入与被控输出的关系曲线 Figure 2 Control input vs. output for the SCR device |
根据上述类似阻容曲线的试验现象,可使用带纯时滞的一阶惯性环节作为Urea-SCR装置数学模型的一般形式。依据图 2数据进行模型参数辨识发现,时滞τ=6 s,而时间常数T=8.7 ms,即τ/T=689.7,可见Urea-SCR装置为大时滞对象[10]。
1.3 现有控制技术遇到的问题鉴于SCR装置的数学模型具有不确定性,自适应控制技术在该装置上得到应用尝试,然而模型参数的准确估计对发动机工况提出过于苛刻的要求,因此在实际应用中存在局限性[11]。经典PID控制虽然不依赖对象的精确模型,但由于信号处理简单和微分反馈难以发挥作用,在NOx高度转化和准确控制问题上出现矛盾[11]。开环控制可以针对已知扰动建立补偿机制,成为当前车用柴油机SCR装置主流的控制模式,但对未知扰动和不可建模因素带来的影响无能为力,在排放升级的驱使下,以复杂控制模型和繁琐标定程序为代价的开环控制模式正走入困境。
2 非线性自抗扰控制技术的可行性反馈控制是提高SCR装置NOx控制准确性和转化效率的重要途径。经典PID控制存在信号处理过于简单的问题,基于对象精确模型的技术舍弃了PID控制的最大优点。非线性自抗扰控制技术继承了“采用对象控制目标与被控输出之间的误差来决定控制策略”的过程控制思想,吸纳了现代数字信号处理技术,开发了状态误差反馈信号的非线性组合方式,克服了经典PID控制应用于时滞对象的缺陷。
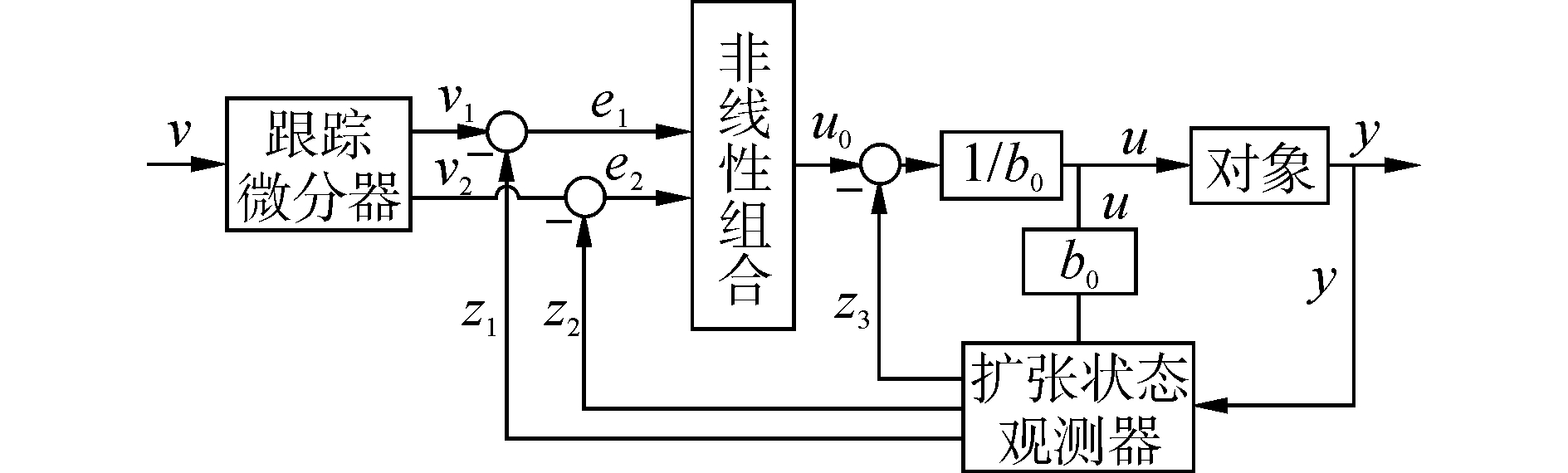
2.1 非线性自抗扰控制器的框架结构自抗扰控制技术考虑的外部扰动为影响被控输出且与系统状态无关的干扰因素,内部扰动则为影响系统被控输出且与系统状态有关的不确定性。自抗扰控制以积分器串联型线性系统为标准型,将被控对象中不同于标准型部分的影响扩张为新的状态变量,并构造扩张状态观测器予以实时地估计与补偿,从而将被控对象转化为标准结构,针对标准型设计误差反馈控制率。以二阶非线性对象为例,其非线性自抗扰控制器的基本框架结构示于图 3。
|
| 图3 二阶对象的非线性自抗扰控制器结构 Figure 3 Layout of NADRC for a second-order object |
非线性自抗扰控制器主要由对象控制目标的过渡过程、扩张状态观测器和状态误差反馈增益的非线性组合三个模块组成。通过为对象控制目标合理安排过渡过程 (v1) 解决时滞对象反馈控制中原始误差的产生问题,并给出过渡过程的微分信号 (v2);扩张状态观测器用于估计原系统的状态变量 (z1和z2) 以及扩张的状态变量 (z3),通过特定的反馈率对总和扰动作用进行补偿;误差反馈信号的非线性组合用于提高控制系统的灵敏性并降低超调的风险。
2.2 大时滞对象控制的处理方式在自抗扰控制技术应用于时滞对象的情况下,时滞环节存在四种近似处理方法,即无视时滞法、提高阶次法、输出预估法和输入预估法[12]。
本文在采用带纯时滞的一阶惯性环节作为SCR装置数学模型一般形式的基础上,采用提高阶次法将对象的时滞算子近似成一阶惯性环节,从而把时滞对象转化为二阶振荡对象,其近似误差作为一个扰动因素。
2.3 总和扰动作用的估计与补偿由于扰动形式的多样性,Urea-SCR装置控制系统成为非线性系统。自抗扰控制技术通过构造扩张状态观测器,可将SCR装置控制系统总和扰动的实时作用量扩充成新的状态变量。
扩张状态观测器是一个动态过程,只使用了原对象的输入-输出信息,而SCR装置控制系统满足能观性的条件,因此可根据系统输出提炼总和扰动的实时作用量。有了被扩张状态的估计值,在补偿因子b0已知的条件下可实现控制量的补偿,从而将SCR装置控制系统改造成积分器串联型线性系统。
3 SCR非线性自抗扰控制系统设计Urea-SCR装置控制系统具有大时滞、不确定性和非线性特征,自抗扰控制技术通过总和扰动作用的估计与补偿将其转化为积分器串联型线性系统。本节着重设计Urea-SCR装置的非线性自抗扰控制系统。
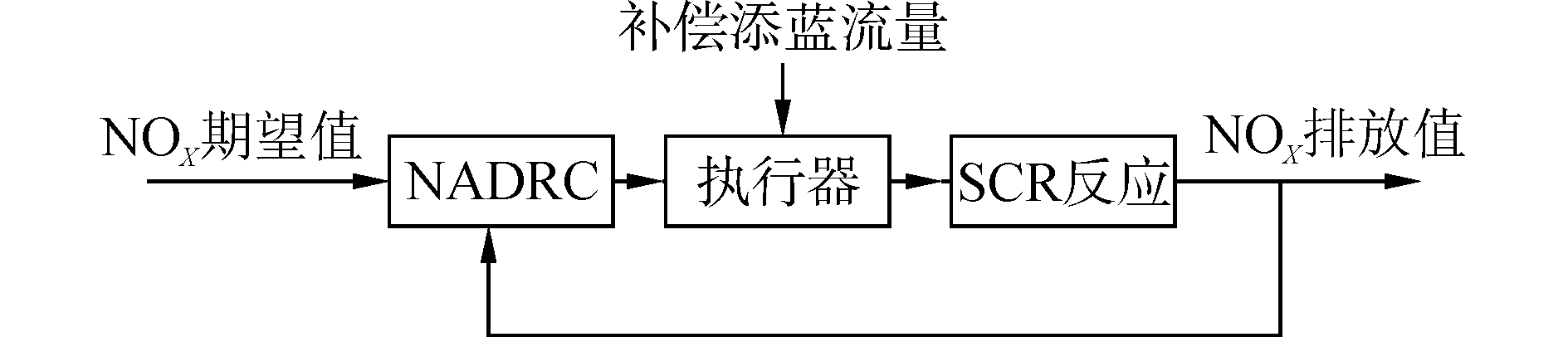
3.1 SCR装置控制系统总体结构根据Urea-SCR装置的工作原理 (见图 1),其基于二阶非线性自抗扰控制技术的控制系统总体结构可表示为图 4的形式。
|
| 图4 Urea-SCR装置控制系统的总体结构 Figure 4 Layout of the Urea-SCR control system |
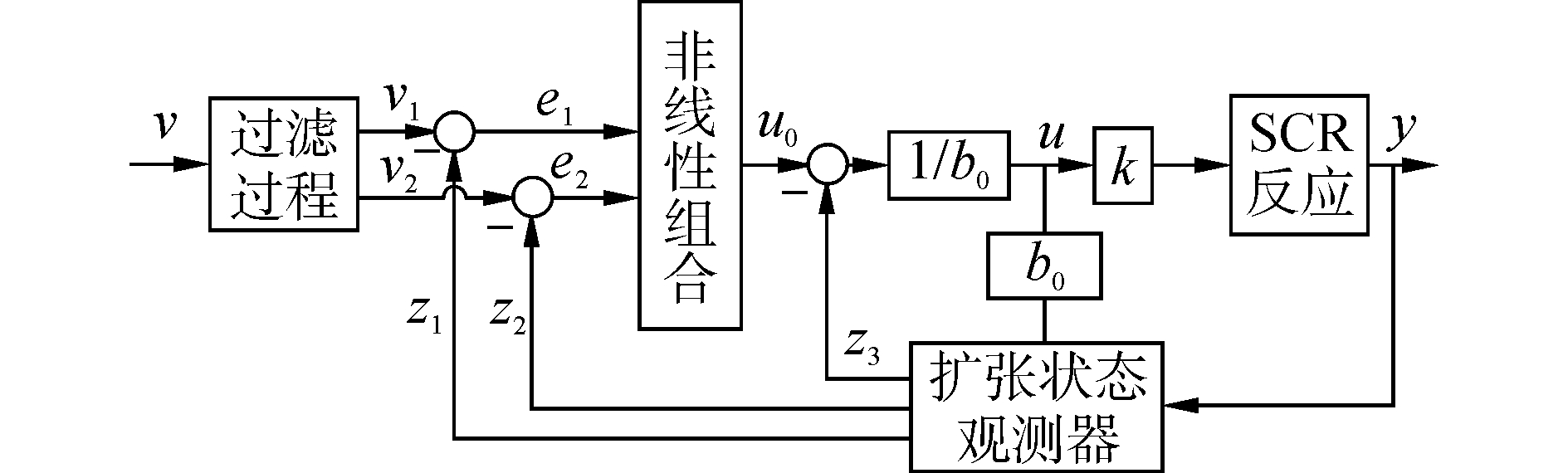
形式上,自抗扰控制器的扩张状态观测器和总和扰动估计与补偿相对固定,而被控目标的过渡过程和状态误差反馈增益的非线性组合存在多种。本文选择二阶最速跟踪微分器为NOx控制目标安排合理的过渡过程,实现对系统输入信号的快速无超调跟踪并给出良好的微分信号;选择幂次函数构造状态误差反馈增益的组合形式,利用其非线性效应提高NOx控制的灵敏性并抑制超调现象;使用三阶扩张状态观测器估计振荡环节的总和扰动作用,并采用特定的反馈律对其进行补偿。Urea-SCR装置二阶非线性自抗扰控制器的结构示于图 5。
|
| 图5 Urea-SCR装置非线性自抗扰控制器 Figure 5 NADRC of the Urea-SCR device |
图 5中,ν为NOx控制目标,ν1为针对NOx控制目标安排的过渡过程,ν2为过渡过程的微分信号;z1、z2为被控对象状态变量的估计值,z3为总和扰动作用的估计值;u0为所需降低的NOx体积浓度,由状态变量误差反馈增益非线性组合生成;b0为补偿因子,u为补偿之后所需降低的NOx体积浓度,k为NOx体积浓度向添蓝体积流量转换的系数,是发动机排气流量的函数;y为被控输出。
3.2.2 二阶非线性自抗扰控制器的离散算法1) 为NOx控制目标安排过渡过程。
二阶最速跟踪微分器的离散形式为
| $ \left\{ \begin{array}{l} {v_1}\left( {k + 1} \right) = {v_1}\left( k \right) + h{v_2}\left( k \right)\\ {v_2}\left( {k + 1} \right) = {v_2}\left( k \right) + h{\rm{fhan}}\left( {{v_1}\left( k \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {v\left( k \right),{v_2}\left( k \right),{r_0},{h_0}} \right) \end{array} \right. $ | (1) |
式中:h为采样步长;r0为快速因子;h0为滤波因子;fhan (x1, x2, r, h) 为离散系统的最速控制综合函数,其具体表达式为
| $ \left\{ \begin{array}{l} d = {r_0}{h_0}^2\\ {a_0} = {h_0}{x_2}\\ y = {x_1} + {a_0}\\ {a_1} = \sqrt {d\left( {d + 8\left| y \right|} \right)} \\ {a_2} = {a_0} + {\rm{sign}}\left( y \right)\left( {{a_1} - d} \right)/2\\ {s_y} = \left( {{\rm{sign}}\left( {y + d} \right) - {\rm{sign}}\left( {y - d} \right)} \right)/2\\ a = \left( {{a_0} + y - {a_2}} \right){s_y} + {a_2}\\ {s_a} = \left( {{\rm{sign}}\left( {a + d} \right) - {\rm{sign}}\left( {a - d} \right)} \right)/2\\ {\rm{fhan = }} - {r_0}\left( {a/d - {\rm{sign}}\left( a \right)} \right){s_a} - {r_0}{\rm{sign}}\left( a \right) \end{array} \right. $ |
2) 扩张状态观测器。
三阶扩张状态观测器的离散形式为
| $ \left\{ \begin{array}{l} e\left( k \right) = {z_1}\left( k \right) - y\left( k \right)\\ {z_1}\left( {k + 1} \right) = {z_1}\left( k \right) + h\left( {{z_2}\left( k \right) - {\beta _{01}}e\left( k \right)} \right)\\ {z_2}\left( {k + 1} \right) = {z_2}\left( k \right) + h\left( {{z_3}\left( k \right) - {\beta _{02}}{\rm{fal}}\left( {e\left( k \right)} \right.,} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {{\alpha _{01}},{\delta _{01}}} \right) + {b_0}u\left( k \right)} \right)\\ {z_3}\left( {k + 1} \right) = {z_3}\left( k \right) - h{\beta _{03}}{\rm{fal}}\left( {e\left( k \right),{a_{02}},{\delta _{02}}} \right) \end{array} \right. $ | (2) |
式中:β01、β02和β03为扩张状态观测器的增益;α01和α02为适当的常数;δ01和δ02为线性区间的长度;fal (e, a, d) 为幂次函数,其具体表达式为
| $ \begin{array}{*{20}{c}} {{\rm{fal}}\left( {{e_i},{a_i},{\delta _i}} \right) = \left\{ \begin{array}{l} \frac{{{e_i}}}{{{\delta _i}^{{\alpha _i} - 1}}},\;\;\;\left| {{e_i}} \right| \le {\delta _i}\\ {\left| {{e_i}} \right|^{{\alpha _i}}}{\rm{sign}}\left( {{e_i}} \right),\;\;\left| {{e_i}} \right| > {\delta _i} \end{array} \right.}\\ {\left( {i = 1,2} \right)} \end{array} $ |
3) 非线性组合。
针对Urea-SCR装置控制系统状态误差的反馈,引入幂次函数fal (e, α, δ) 构造了非线性组合,其离散形式表示为
| $ \left\{ \begin{array}{l} {e_1}\left( k \right) = {v_1}\left( k \right) - {z_1}\left( k \right)\\ {e_2}\left( k \right) = {v_2}\left( k \right) - {z_2}\left( k \right)\\ {u_0}\left( k \right) = {k_1}{\rm{fal}}\left( {{e_1}\left( k \right),{\alpha _1},{\delta _1}} \right) + {k_2}{\rm{fal}}\left( {{e_2}\left( k \right),{\alpha _2},{\delta _2}} \right)\\ u\left( k \right) = {u_0}\left( k \right) - {z_3}\left( k \right)/{b_0} \end{array} \right. $ | (3) |
式中:k1和k2为状态误差反馈增益,δ1和δ2为线性区间长度,α1和α2为适当的常数,b0为补偿因子。
3.3 非线性自抗扰控制器参数整定在选定非线性自抗扰控制器的算法之后,控制器的性能主要取决于跟踪微分器、扩张状态观测器和状态误差反馈非线性组合的参数值。研究发现,在SCR装置非线性自抗扰控制器的上述参数中,状态误差反馈增益k1、k2以及补偿因子b0为重点整定对象,鉴于非线性自抗扰控制器参数整定的理论尚不成熟,本文出于简化SCR装置控制系统开发的目的,结合经验试凑和指标寻优进行了控制器参数整定,其结果示于表 2。
| 参数 | 数值 | 参数 | 数值 | 参数 | 数值 |
| h | 0.05 | α2 | 0.25 | β01 | 20 |
| r0 | 50 | α02 | 0.25 | β02 | 52 |
| h0 | 0.05 | δ1 | 0.05 | β03 | 88 |
| b0 | 17.71 | δ01 | 0.05 | k1 | 15.10 |
| α1 | 0.5 | δ2 | 0.05 | k2 | 5.06 |
| α01 | 0.5 | δ02 | 0.05 |
为评价Urea-SCR装置非线性自抗扰控制系统的动态响应性能和扰动抑制能力,针对某台4.7 L车用柴油机及其Urea-SCR装置组织了台架试验。紧贴法规要求,采用测试循环NOx比排放作为控制系统动态响应性能的评价指标,采用NOx比排放控制的准确程度作为抑制扰动能力的评价指标。
该柴油机的压缩比为17.5:1,缸径为110 mm,额定功率为132 kW,额定功率转速为2 650±50 r/min,最低比油耗为200 g/(kw·h),燃油轨最高设计压力为160 MPa。本文使用了Groudfos公司生产的AAS Generic G2.5型添蓝加注装置和Continental AG公司生产的Uninox 5WK96614H型NOx传感器。SCR催化器采用筒式封装形式,催化剂载体为蜂窝陶瓷 (12.8 L),催化剂涂层为钒基。
4.1 试验条件与设备台架试验在标准大气环境下进行,发动机额定工况下的进气总管温度控制在47±2℃,燃油进油温度控制在40±2℃,冷却水出水温度控制在88±2℃,以保持试验条件的一致性。测功机为AVL DYNOSL型,排放分析仪为AMAi60型,氨气分析仪为LS25型。
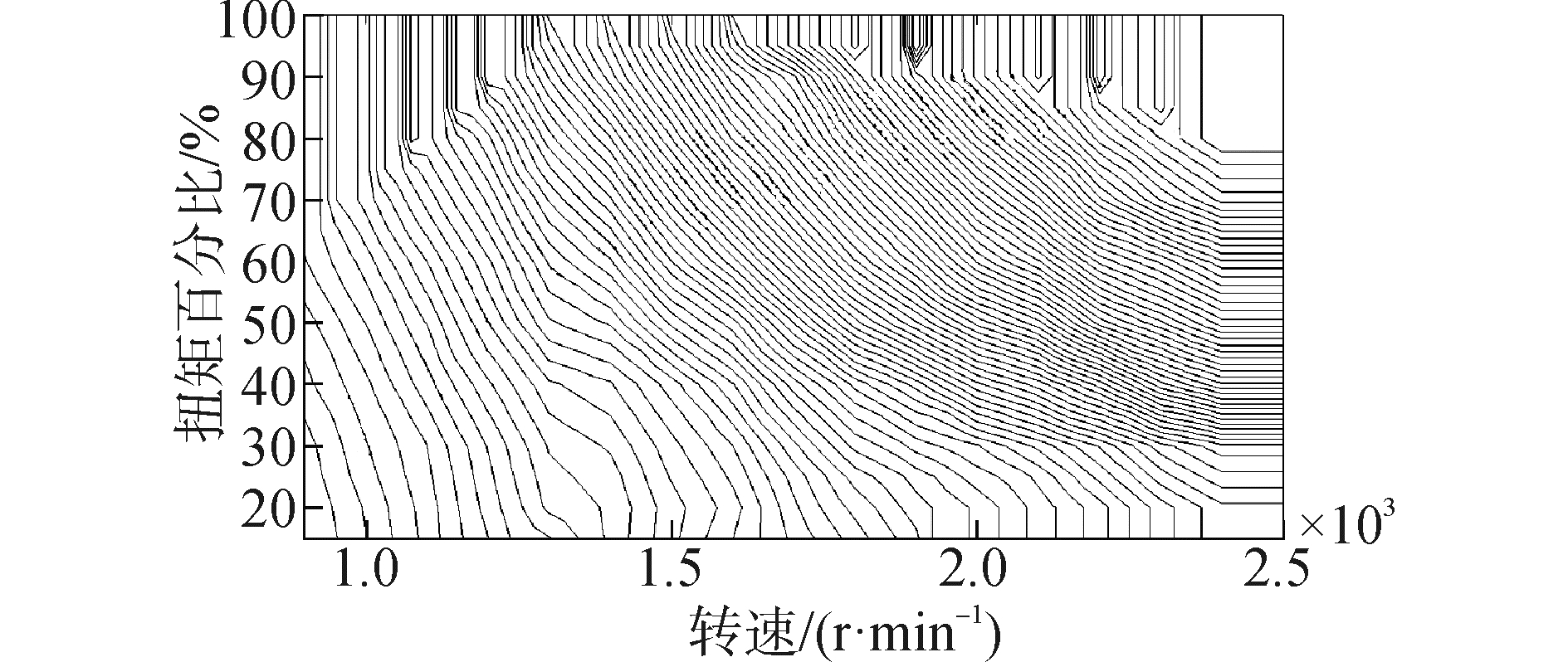
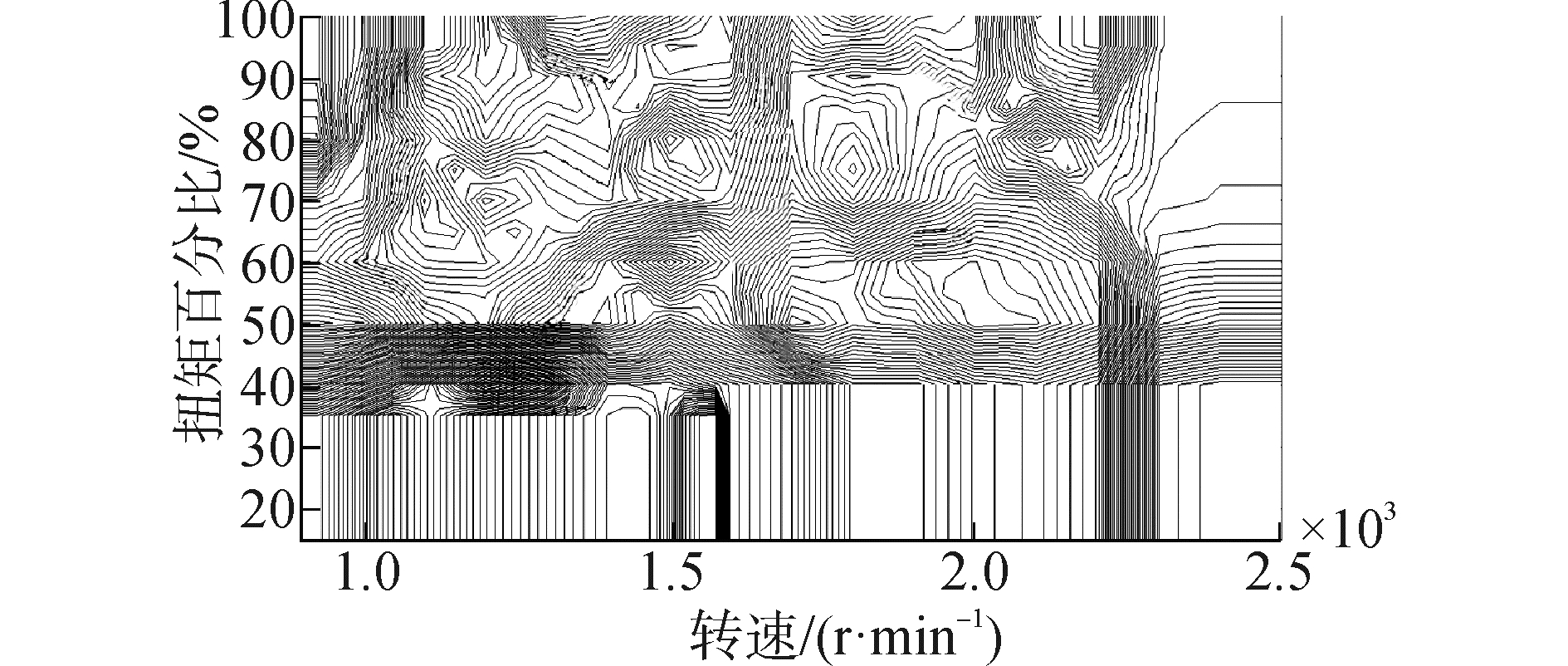
4.2 基础数据配置与系统状态变量初始值标定 4.2.1 控制系统基础数据配置SCR非线性自抗扰控制系统需要NOx控制目标脉谱和柴油机排气流量脉谱作为基础数据。本文通过万有特性试验获取了上述数据。柴油机排气流量脉谱示于图 6,NOx控制目标脉谱示于图 7。
|
| 图6 柴油机排气流量脉谱 Figure 6 Exhaust flow map for the diesel engine |
|
| 图7 柴油机NOx控制目标脉谱 Figure 7 NOx target map for the diesel engine |
在运行ETC期间发现,柴油机排气温度偏低且变化剧烈,以致控制量在“非零”和“为零”状态之间频繁切换。根据状态误差反馈增益的离散算法,在控制量向“非零”状态切换的时刻,控制作用的大小与系统状态变量的取值 (以下简称为“系统状态变量初始值”) 有关,在初始值取零的情况下控制作用将被严重地削弱,难以得到理想的NOx排放控制效果。因此,本文以适当提高初始控制作用为指导思想,对系统状态变量初始值进行试验标定并得到表 3所示的结果。
| 状态变量 | 初始值 |
| v1 | 150 |
| v2 | 0 |
| z1 | 150 |
| z2 | 0 |
| z3 | 17 500 |
| u0 | -1 160 |
通过基础数据配置和系统状态变量初始值标定,SCR装置非线性自抗扰控制系统被确定下来。进一步地,针对该系统分别开展了ESC和ETC试验来研究其综合控制品质。
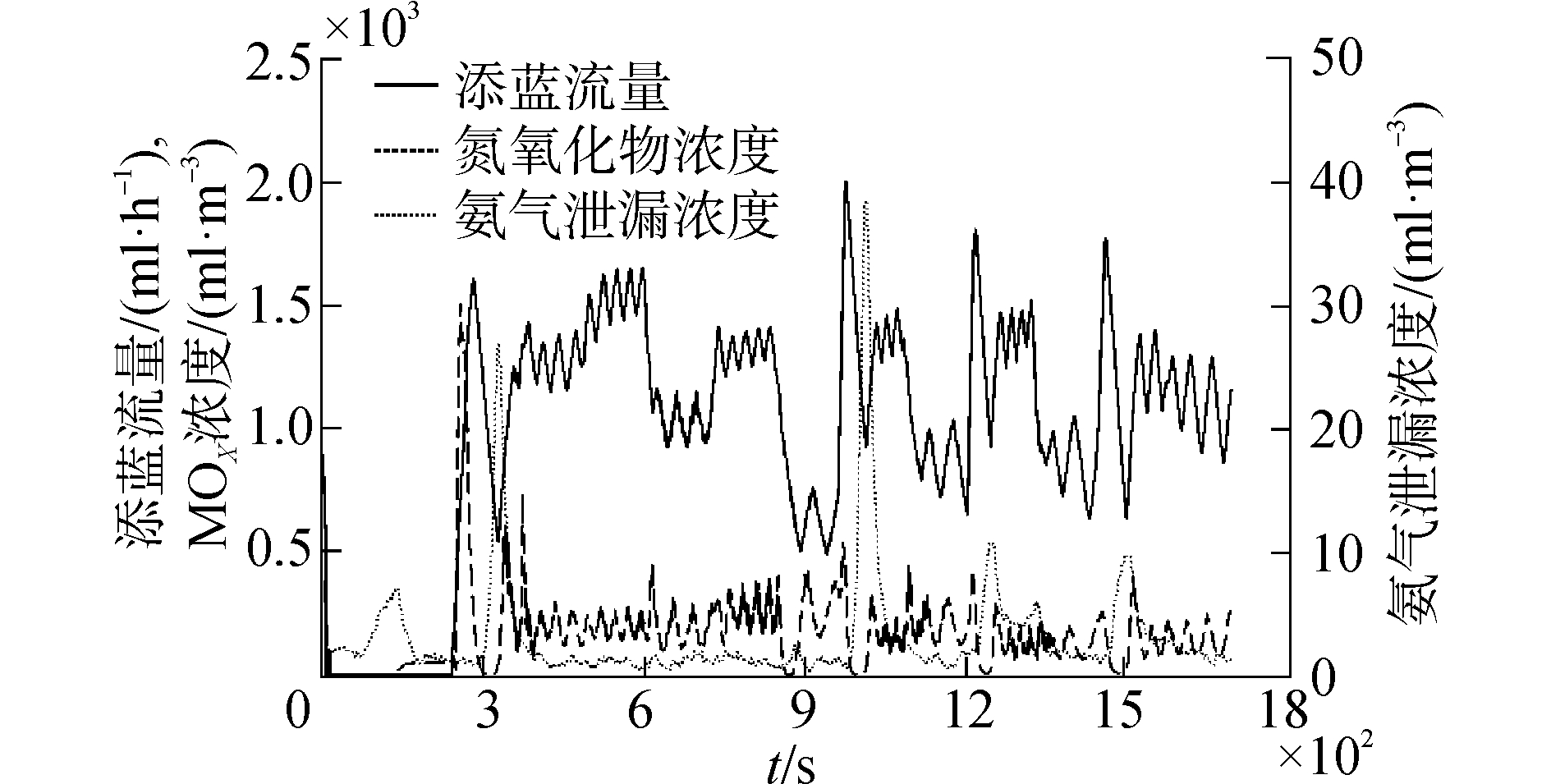
4.3.1 ESC试验结果与分析ESC试验表明,柴油机机内NOx比排放为10.1 g/(kw·h),被控输出为1.85 g/(kw·h),低于国五阶段的排放限值。循环期间添蓝流量、被控输出以及氨气泄漏浓度示于图 8,相关计算结果示于表 4。
|
| 图8 添蓝流量、被控输出和氨气泄漏浓度变化轨迹 (ESC) Figure 8 Tendencys of adblue rates, controlled NOx levels and NH3 slip concentrations (ESC) |
| 机内NOx/ (g·(kW·h)-1) |
被控输出/ (g·(kW·h)-1) |
氨泄漏/ (ml·m-3) |
转化效 率/% |
添蓝油 耗比 (v/v)/% |
|
| ESC | 10.10 | 1.85 | 3.10 | 81.70 | 6.20 |
| ETC | 11.68 | 1.66 | 8.55 | 85.80 | 6.40 |
| 抗扰 | 10.92 | 1.67 | 11.50 | 84.70 | 9.40 |
根据ESC试验结果,NOx转化效率达到81.7%,氨气泄漏平均值为3.1 ml/m3,添蓝消耗与燃油消耗的体积比处于正常范围。
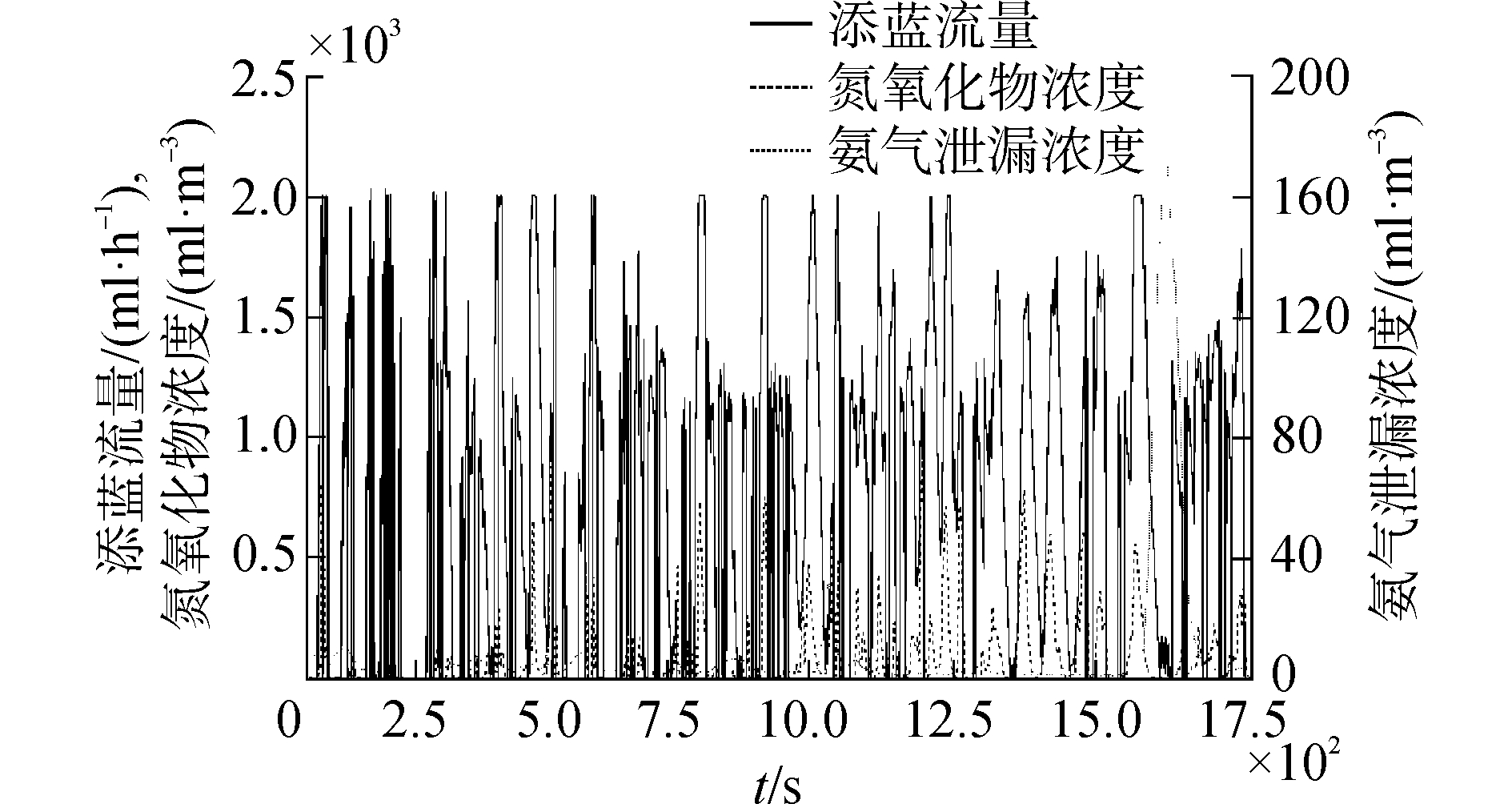
4.3.2 ETC试验结果与分析进行ETC试验发现,柴油机机内NOx比排放为11.68 g/(kW·h),被控输出为1.66 g/(kW·h),也低于国五限值。循环期间添蓝流量、被控输出以及氨气泄漏浓度示于图 9,相关计算结果示于表 4。
|
| 图9 添蓝流量、被控输出和氨气泄漏浓度变化轨迹 (ETC) Figure 9 Tendencys of Adblue rates, controlled NOx levels and NH3 slip concentrations (ETC) |
在ETC试验期间,发动机多次出现倒拖工况,催化器温度整体较低,偏离了SCR催化剂活性最佳的温度窗口 (350~450℃)。然而,应用同一策略对Urea-SCR装置进行控制,NOx转化效率依然能够达到85.8%,氨气泄漏平均值也远低于许可限值[8],能够符合柴油机国五阶段的排放要求。
4.4 抗扰能力试验改善动态响应特性和提高扰动抑制能力是本研究对Urea-SCR装置新型控制系统提出的两大核心需求。为此,进一步地引入扰动因素来评价该系统抑制扰动作用的能力。
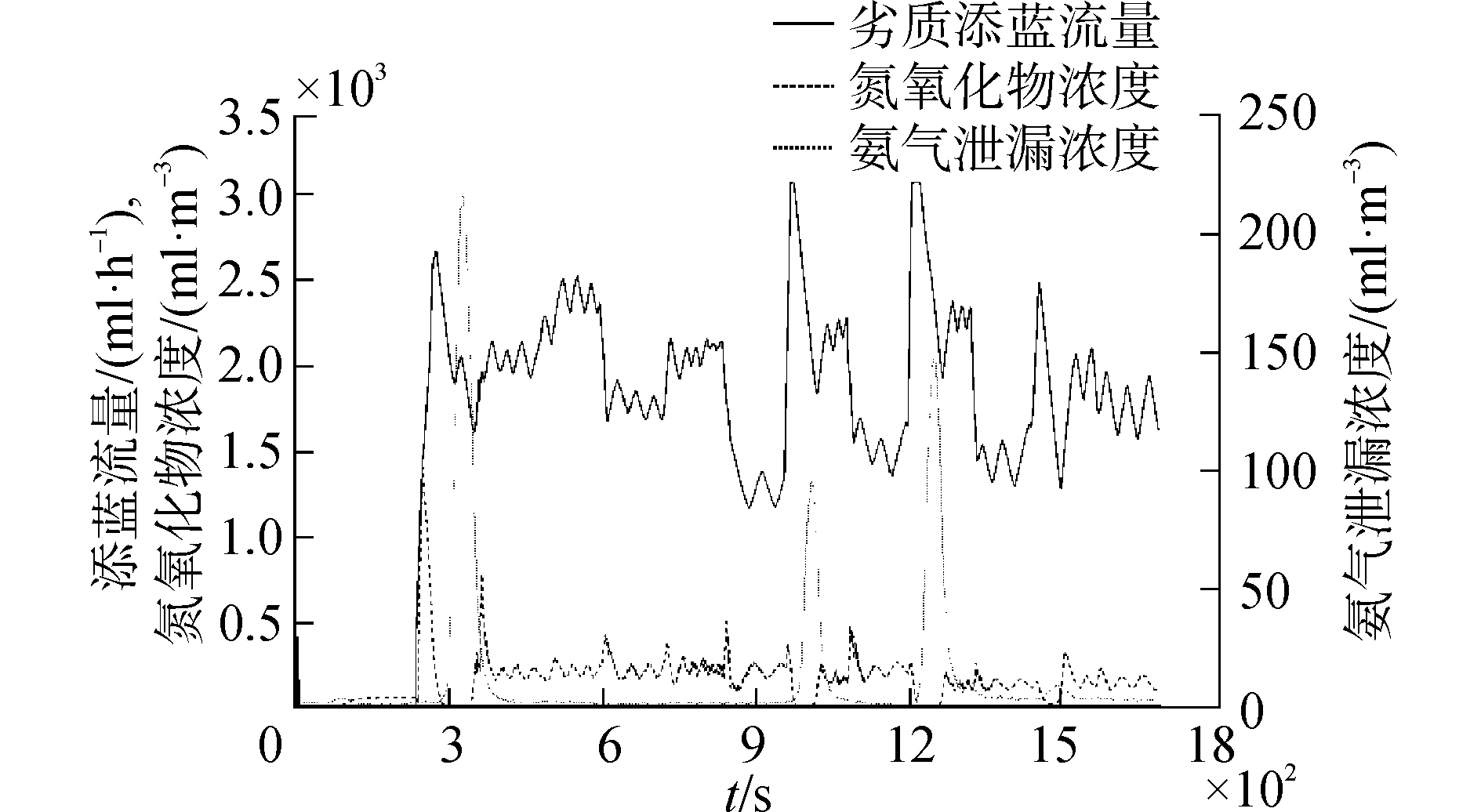
具体地,以21%质量浓度的尿素水溶液 (以下简称“劣质添蓝”) 取代添蓝作为还原剂,保持柴油机及其Urea-SCR系统的参数不变,再次进行ESC试验来考察NOx比排放和氨气泄漏情况。添蓝流量、被控输出以及氨气泄漏浓度示于图 10,相关计算结果示于表 4。
|
| 图10 添蓝流量、被控输出和氨气泄漏浓度变化轨迹 (抗扰) Figure 10 Tendencys of Adblue rates, controlled NOx levels and NH3 slip concentrations (disturbance rejection) |
分析ESC抗扰试验与ESC排放试验数据发现,两项试验期间发动机工况、排气流量以及进气温度的一致性较好,但受制于进气空调的能力,进气相对湿度出现显著的差异,以致机内NOx比排放发生了明显的变化[9]。另一方面,抗扰试验中使用劣质添蓝引起排气中水分增加,催化器温度相对排放试验也有所降低。因此,SCR控制系统实际上处于添蓝劣化、机内NOx浓度和排气温度变化等内外扰动作用之下。
抗扰试验结果表明,NOx比排放结果与排放循环试验结果较为接近,NOx排放控制的准确性得到保证,说明Urea-SCR装置非线性自抗扰控制系统有效地抑制了来自多方面的扰动作用。
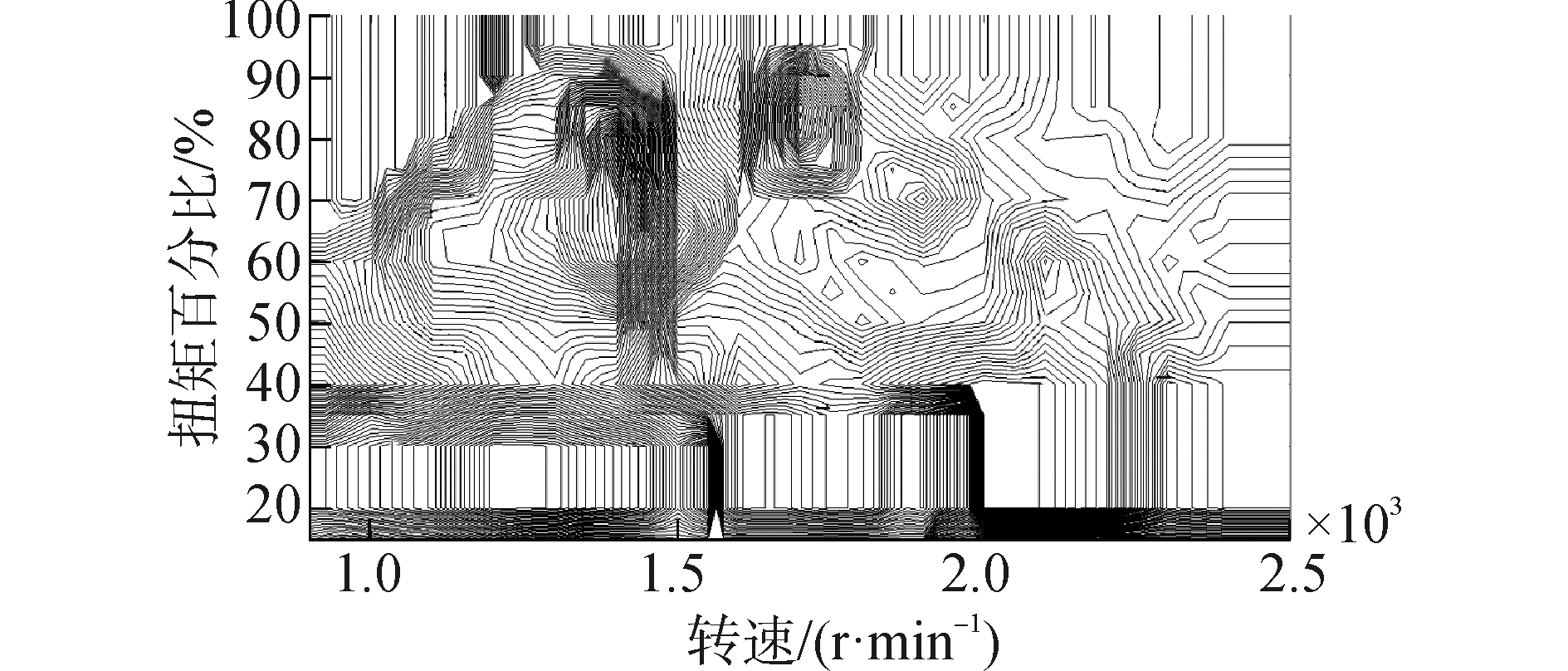
4.5 减排潜力试验国六阶段SCR装置对NOx转化效率的需求将达到90%左右。在上述试验中发现,氨气泄漏平均值低于OBD标准的限值,本文对NOx控制目标脉谱进行整体下调 (见图 11),再次进行ESC和ETC排放试验,初步地探索了SCR非线性自抗扰控制系统的减排潜力。相关试验结果示于表 5。
|
| 图11 减排潜力探索试验所用NOx控制目标脉谱 Figure 11 NOx target map for the reduction potential test |
| 测试 循环 |
机内NOx/ (g·(kw·h)-1) |
被控输出/ (g·(kw·h)-1) |
氨气泄漏/ (ml·m-3) |
转化 效率/% |
| ESC | 10.25 | 1.30 | 9.90 | 87.30 |
| ETC | 11.79 | 1.26 | 9.90 | 89.30 |
减排潜力试验结果表明,通过适当降低NOx控制目标,ESC和ETC的NOx转化效率分别达到87.30%和89.30%,而氨气泄漏值仍然远低于许可限值,表明该款发动机SCR装置非线性自抗扰控制系统尚存在可标定空间,通过深入开展精细标定工作,NOx转化效率有望逼近极限。
5 结论1) Urea-SCR装置非线性自抗扰控制系统具有良好的扰动抑制能力,柴油机NOx排放的准确控制可以得到保证。
2) SCR装置非线性自抗扰控制系统具有较好的动态响应性能,能够更好地提升排放测试循环中NOx的转化效率。
3) 非线性自抗扰控制技术能够作为SCR柴油机应对高等级排放要求的核心技术储备,对其控制器的设计开发具有重要的指导意义。
| [1] | SCHÄR C M, ONDER C H, GEERING H P, et al. Control of a urea SCR catalytic converter system for a mobile heavy duty diesel engine[R]. SAE Technical Paper 2003-01-0776, 2003. |
| [2] | SATO S, SATO S, HOSOYA M. Improvement of low-temperature performance of the NOX reduction efficiency on the urea-SCR catalysts[R]. SAE Technical Paper 2013-01-1076, 2013. |
| [3] | FROBERT A, RAUX S, CREFF Y, et al. About cross-sensitivities of NOx sensors in SCR operation[R]. SAE Technical Paper 2013-01-1512, 2013. |
| [4] | MENTINK P, WILLEMS F, KUPPER F. Experimental demonstration of a model-based control design and calibration method for cost optimal Euro-VI engine-aftertreatment operation[R]. SAE Technical Paper 2013-01-1061, 2013. |
| [5] | JOHANDEN K, BENTZER H, KUSTOV A. Integration of vanadium and zeolite type SCR functionality into DPF in exhaust aftertreatment systems-advantages and challenges[R]. SAE Technical Paper 2014-01-1523, 2014. |
| [6] | 中华人民共和国国家环境保护总局. GB 17691-2005, 车用压燃式、气体燃料点燃式发动机与汽车排气染物排放限值及测量方法 (中国Ⅲ、Ⅳ、Ⅴ阶段)[S]. 北京: 中国环境科学出版社, 2005. |
| [7] | MATTHEY J. Heavy duty diesel emissions guide Europe, USA and Japan[DB/MT]. Emission Control Technologies, 2012. |
| [8] | 中华人民共和国环境保护部. HJ 437-2008, 车用压燃式、气体燃料点燃式发动机与汽车车载诊断 (OBD) 系统技术要求[S]. 北京: 中国环境科学出版社, 2008. |
| [9] |
刘丙善, 吕林. 进气相对湿度诱使车用柴油机氮氧化物报警问题研究[J].
内燃机工程, 2015, 36(6): 27–31.
LIU Bingshan, LYU Lin. Research on NOx emission alarm caused by the intake-air relative humidity for truck diesel engines[J]. Chinese internal combustion engine engineering, 2015, 36(6): 27–31. |
| [10] | 诸静. 智能预测控制及其应用[M]. 杭州: 浙江大学出版社, 2002. |
| [11] | WILLEMS F, CLOUDT R, VAN DEN EIJNDEN E, et al. Is closed-loop SCR control required to meet future emission targets?[R]. SAE Technical Paper 2007-01-1574, 2007. |
| [12] |
韩京清.
自抗扰控制技术-估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008: 303-316.
HAN Jingqing. Active disturbance rejection control technique-the technique for estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press, 2008: 303-316. |



