2. School of Automation Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China
当今电子系统中80%的器件是数字的,但80%的故障发生在模拟器件上,而模拟电路的测试成本占总测试成本的80%[1],所以模拟电路故障诊断的重要性日益突出。除故障定位外,在电路系统剩余寿命估计、故障辨识、元件失效机理分析等环节中,还需要对故障元件参数进行在线辨识以提供更丰富的信息。目前,高质量的模拟电路参数辨识方法鲜有报道。
早期的故障诊断方法可分为测前仿真法 (simulation before test,SBT) 和测后仿真法 (simulation after test,SAT)[2]。近年来,人工智能算法和数字信号处理 (digital signal processor,DSP) 算法广泛应用到故障诊断上,出现了既不属于SBT,也不属于SAT的智能算法,如:小波分析法具有良好的时频分辨率,但计算复杂[3-4]。人工神经网络法利用计算机强大的运算能力快速简单地完成诊断过程,但需要充足的训练样本[5]。支持向量机的学习策略灵活,但在选择典型特征进行训练分类上存在困难[6]。遗传算法收敛性好,鲁棒性高,计算时间少,但计算过程中的参数选择依靠经验确定,容易影响诊断效果[7]。模糊算法计算量小,缺点是依靠经验获得的算子和判断准则会降低故障诊断准确率[8]。专家系统法能快速获得最佳诊断结果,但依赖于知识的获得和累积过程,需要较强的专家系统的学习能力和自适应能力[9]。这些方法在模拟电路的故障检测和故障定位方面取得了较好效果,但对模拟电路进行参数辨识的效果有待进一步提高。
代数学具有理论推导严密的特点,在实际工程问题的解决中得到广泛应用,为了获得较好的模拟电路故障定位和参数辨识效果,本文从代数角度提出了模拟电路故障诊断与参数辨识的新方法。
1 诊断和参数辨识的代数方法原理若Y(t) 为被测电路的输出电压响应,以Ts为周期对的Y(t) 采样,获得采样序列Y(nTs) 中的k×k个元素可以表示成一个k阶方阵如下:
| $ \left[{\begin{array}{*{20}{c}} {Y\left( {{T_s}} \right)}&{Y\left( {\left( {k + 1} \right){T_s}} \right)}& \cdots &{Y\left( {k \times k-k + 1} \right){T_s})}\\ {Y\left( {2{T_s}} \right)}&{Y\left( {\left( {k + 2} \right){T_s}} \right)}& \cdots &{Y\left( {k \times k-k + 2} \right){T_s})}\\ \vdots & \vdots & \ddots & \vdots \\ {Y\left( {k{T_s}} \right)}&{Y\left( {2k{T_s}} \right)}& \cdots &{Y\left( {k \times k} \right){T_s})} \end{array}} \right] $ |
后面称这个方阵为响应矩阵A,它的行元素代表k倍下抽样频率的采样值,列元素代表一个时间段内的连续采样值。因此,响应矩阵的元素能体现输出响应的变化,随器件参数的变化而变化。记ΔY(nTs) 为响应矩阵A的元素的扰动,矩阵扰动理论中的Rouché′s理论[10]表明:矩阵的本征值是矩阵元素的连续函数。若矩阵A=(aij)∈Cn×n,定义变量
| $ \begin{align} & \mathit{\boldsymbol{a}}_{i}^{'}={{\left( {{a}_{i1}}, \cdots, {{a}_{i, i-1}}, {{a}_{i, i+1}},\cdots, {{a}_{in}} \right)}^{\rm{T}}}, \\ & {{G}_{i}}\left( \mathit{\boldsymbol{A}} \right)=\left\{ z\in \bf{C} \right.:\left| z-{{a}_{ii}} \right|\le \left. {{\left\| a_{i}^{'} \right\|}_{1}} \right\}, \\ & \ \ \ \ \ \ \ \ \ \ i=1, 2, \cdots, n, \\ \end{align} $ |
那么,盖尔圆盘定理[10]证明了矩阵A的所有本征值λ(A) 满足:
| $ \lambda \left( \mathit{\boldsymbol{A}} \right) \subset \mathop \cup \limits_{i = 1}^n {G_i}\left( \mathit{\boldsymbol{A}} \right) $ | (1) |
式 (1) 表明矩阵本征值的变化范围由矩阵的元素决定,矩阵元素变化会引起矩阵本征值随之变化。Ostrowski定理[10]给出了矩阵本征值扰动的上界与矩阵元素扰动量之间的关系,即
| $ \left| {{\lambda }^{'}}-\lambda \right|<\left( n+2 \right)\ {{\left( {{n}^{2}}\varepsilon \right)}^{\frac{1}{n}}} $ | (2) |
式中:λ′是矩阵 (A+εB) 的本征值,λ是矩阵A的本征值,ε是任意大于0的常数, n是矩阵的阶。
式 (1) 和 (2) 表明:矩阵元素的变化量与矩阵本征值变化量之间存在一一对应关系。因为被测电路的响应矩阵元素受器件参数影响,所以器件参数与响应矩阵的本征值之间具有一定的对应关系。那么,利用通过测前仿真获得响应矩阵本征值随故障器件参数变化而变化的对应关系的数学模型后,根据实际电路输出响应矩阵的本征值,可算出实际电路的器件参数值,从而实现故障诊断和参数辨识的一体化处理。
n阶方阵有n个本征值,把所有本征值都纳入计算,会增加计算成本。如果只用一部分本征值进行计算,又会丢失部分信息,降低故障诊断准确率和参数辨识精度。另外,因为测试误差的影响和被测信号的多样性,即使响应矩阵的元素全为实数,也可能存在非实数本征值而难以建立故障模型。如果直接用相应矩阵本征值进行故障诊断和参数辨识理论上可行,但实际效果不佳。
因为响应矩阵A的元素随被测电路中可诊断器件参数的变化而变化,为了解决响应矩阵的本征值多而且本征值可能有虚部的问题,本文把响应矩阵的主本征值和Frobenius范数联合,进行故障诊断与参数辨识。
量子力学理论表明可观测物理量可以用一个厄密尔算符表示,并且该算符的主本征值是实数本征值[11]。另外,主本征值随矩阵元素变化而变化的灵敏度较大。所以,用主本征值作为故障特征能获得较好的参数辨识灵敏度,也能解决响应矩阵的本征值存在虚部的问题。
矩阵的Frobenius范数‖A‖F(下文简称F范数) 可表示为
| $ {\left\| \mathit{\boldsymbol{A}} \right\|_{\rm{F}}} = \sqrt {\sum\limits_{i = 1}^m {{{\sum\limits_{j = 1}^n {\left| {{a_{i, j}}} \right|} }^2}} }, $ |
即F范数的大小由矩阵的所有元素ai,j共同决定,而ai,j随器件参数变化而变化,所以,F范数随器件参数的变化而变化,用F范数作为故障特征既能体现输出响应的变化,又能在一定程度上减少随机误差的影响。
可观测物理量的响应矩阵的F范数和主本征值都是实数,被测电路的故障响应矩阵的F范数和主本征值均以被无故障响应矩阵的F范数和主本征值为中心上下偏移。被测电路的器件参数改变时,F范数和主本征值同时进行相同变化的概率比其中只有一个量变化相同的概率小。所以,联合响应矩阵的F范数和主本征值进行故障诊断和参数辨识能获得的故障诊断性能,比只用本征值或F范数作为故障特征获得的故障诊断性能更好。
2 故障诊断和参数辨识的数学模型把被测电路中n个待诊断的器件参数用n个向量x1,x2,…,xn组成的向量系X表示。设器件的标称值为 (x1,0,x2,0,…,xn,0),电路在j时刻的n个器件的实际参数状态记为x1,j,x2,j,…,xn,j,那么电路在第j时刻对应的m个输出响应观测量表示为Yi,j,(i=1,2,…,m),这里的m个输出响应观测量既可以是一个测试点上的多个输出响应 (如电压、相位或频率等),又可以是多个测试点上的输出响应。被测电路在输入激励信号u=(u1,u2,…,ur) 的作用下,输出响应矢量Yi,j可以表示为
| $ {Y_{i, j}} = {f_{i, j}}\left( {{\mathit{\boldsymbol{x}}_{1, j}}, {\mathit{\boldsymbol{x}}_{2, j}}, \cdots, {\mathit{\boldsymbol{x}}_{n, j}}, {u_1}, {u_2}, \cdots, {u_r}} \right) $ | (3) |
从式 (3) 求解x1,j,x2,j,…,xn,j后,若发现其中某一xi,j偏离其标称值xi,0的范围大于容差值上限,则该元件故障,故障参数为xi,j。当电路的测试点或测试观测量较少时,即当m < n时,式 (3) 为一亚定方程式,它有无穷多个解。实际模拟电路规模大,器件数量多,要用式 (3) 直接实现故障诊断需要较多的观测量,实际电路的测试点有限,该方法不满足实际电路需求。
考虑到实际电路发生故障往往是先从单个器件或单独模块开始,假设电路中的第i个器件的参数xi偏离标称值大于容差范围,其余各元件的参数都在标称值的容差允许范围内,激励信号u保持不变,则式 (3) 可近似表示为
| $ {Y_{i, j}} = {f_i}\left( {{x_{1, 0}}, {x_{2, 0}}, \cdots, {x_i}, \cdots, {x_{n, 0}}} \right) $ | (4) |
式 (4) 中只有一个未知参数xi,可以降低计算复杂程度。但实现参数辨识还存在三个问题:1) 实测电路中xi的位置信息是未知的,这需要进行更复杂的计算才有可能实现故障定位;2) 受器件容差的影响,即使只有一个器件xi发生故障,器件参数实际值不等于 (x1,0,x2,0,…,xi,…,xn,0);3) 函数fi(·) 由电路结构和元件特性确定,获得准确的fi(·) 比较困难。
器件xi在j时刻的故障参数值记为xi,j,式 (4) 中的Yi为实际电路响应矩阵的主本征值和F范数,分别记为Li,j、L′i,j。因为响应矩阵的F范数L′i,j和主本征值Li,j都随器件参数xi,j变化而变化,所以可以把Li,j和L′i,j用泛函表示为
| $ {L_{i, j}} = V\left[{{x_{i, j}}} \right] $ | (5) |
| $ \begin{align} &L{{'}_{i, j}}=V'\left[{{x}_{i, j}} \right] \\ \end{align} $ | (6) |
由级数的性质可知Li,j和L′i,j可以分别用多项式表示。因为器件参数变化超过容差允许的范围,就认为电路发生参数型故障,所以器件参数能正常变化的范围比较小,响应矩阵的F范数和主本征值变化随器件参数变化而变化的趋势线可以看成是一段抛物线,因此式 (5) 和 (6) 分别表示的Li,j和L′i,j可以近似表示为
| $ {L_{i, j}} = {a_i}x_{i, j}^2 + {b_i}{x_{i, j}} + {c_i} $ | (7) |
| $ L{{'}_{i, j}}=a{{'}_{i}}x_{i, j}^{2}+b{{'}_{i}}{{x}_{i, j}}+c{{'}_{i}} $ | (8) |
式中:ai、bi、ci和a′i、b′i、c′i是方程系数,可以通过测前仿真获得。方程 (7) 和 (8) 建立了故障特征和器件参数之间的数学模型。
3 减少容差影响的措施 3.1 减少容差对主本征值的影响模拟器件的实际参数与标称值之间存在容差。要确保故障诊断方法的有效性,必须考虑容差的影响。
响应矩阵A由被测电路输出响应决定,设故障参数集为X,则A可以看是有限维实欧几里得空间X上的实对称线性映射。对X的任意j维线性子空间S(满足dimS=j),X满足以下j-1个线性条件:
| $ \left( {x, {f_i}} \right) = o, \;\;\;i = 1, \cdots, j-1, $ | (9) |
式中:fi是A的第i个本征值所对应的本征向量。根据:X的子空间在线性映射T下的像是U的子空间,如果dimU < dimX,则存在x≠0,使得Tx=0。每个j维子空间S都包含满足式 (9) 中j-1个线性条件的非零向量x。因此,在x按A的本征向量展开的公式中的前j-1个本征向量的系数为零, X中的任意向量都可以表示成本征向量fi的线性组合。即
| $ \frac{{\left( {x, \mathit{\boldsymbol{A}}x} \right)}}{{\left( {x, x} \right)}} = \frac{{\sum {{\lambda _i}f_i^2} }}{{\sum {f_i^2} }}, $ |
式中:x∈X,标量积 (x,Ax) 和 (x,x) 是双线性映射函数,取A的本征值从小到大依次为λ1,λ2,…,λn,则满足
| $ \mathop {\max }\limits_{x \in S} \frac{{\left( {x, \mathit{\boldsymbol{A}}x} \right)}}{{\left( {x, x} \right)}} \ge {\lambda _j} $ | (10) |
因为对任意i≤j,都有λi≤λj,故由式 (10) 可得
| $ {\lambda _j} \ge \frac{{\left( {x, \mathit{\boldsymbol{A}}x} \right)}}{{\left( {x, x} \right)}} $ | (11) |
根据式 (10) 和 (11) 得
| $ {\lambda _j} \ge \mathop {\min }\limits_{\dim S = j} \mathop {\max }\limits_{x \in S, x \ne 0} \frac{{\left( {x, \mathit{\boldsymbol{A}}x} \right)}}{{\left( {x, x} \right)}} $ | (12) |
不等式 (12) 说明响应矩阵本征值的变化与器件参数x的变化之间具有较好的线性对应关系,所以可以通过线性校正,减少容差对主本征值的影响。
3.2 减少容差对F范数的影响因为容差直接影响矩阵元素的变化,而F范数是矩阵元素绝对值的平方和再开平方,容差的实质是器件实际参数与标称值之间有较小偏离,容差引起F范数的变化量ΔL′i,j可以用式 (8) 对xi,j求导数获得,求导结果为xi,j的一次多项式,所以ΔL′i,j与器件参数的容差之间具有线性对应关系,通过线性校正,可以减少容差对F范数的影响。
仿真获得被测电路的标称值参数状态对应的响应矩阵主本征值和F范数分别记为y和y0。测量有容差影响的被测电路无故障响应,计算实际电路正常状态下的响应矩阵主本征值和F范数分别记为y′和y′0。由方程 (7) 和 (8) 得到减少容差影响的故障诊断和参数辨识的模型为
| $ {L_{i, j}} = {a_i}x_{i, j}^2 + {b_i}{x_{i, j}} + {d_i} $ | (13) |
| $ L{{'}_{i, j}}=a{{'}_{i}}x_{i, j}^{2}+b{{'}_{i}}{{x}_{i, j}}+d{{'}_{i}} $ | (14) |
式中:di=ci-y+y′,d′i=c′i-y0+y′0。
4 故障诊断与参数辨识过程为了便于理解,首先根据故障模型方程 (13) 和 (14),对被测电路中仅有两个待诊断器件 (分别记为器件1和器件2) 的情况进行介绍。
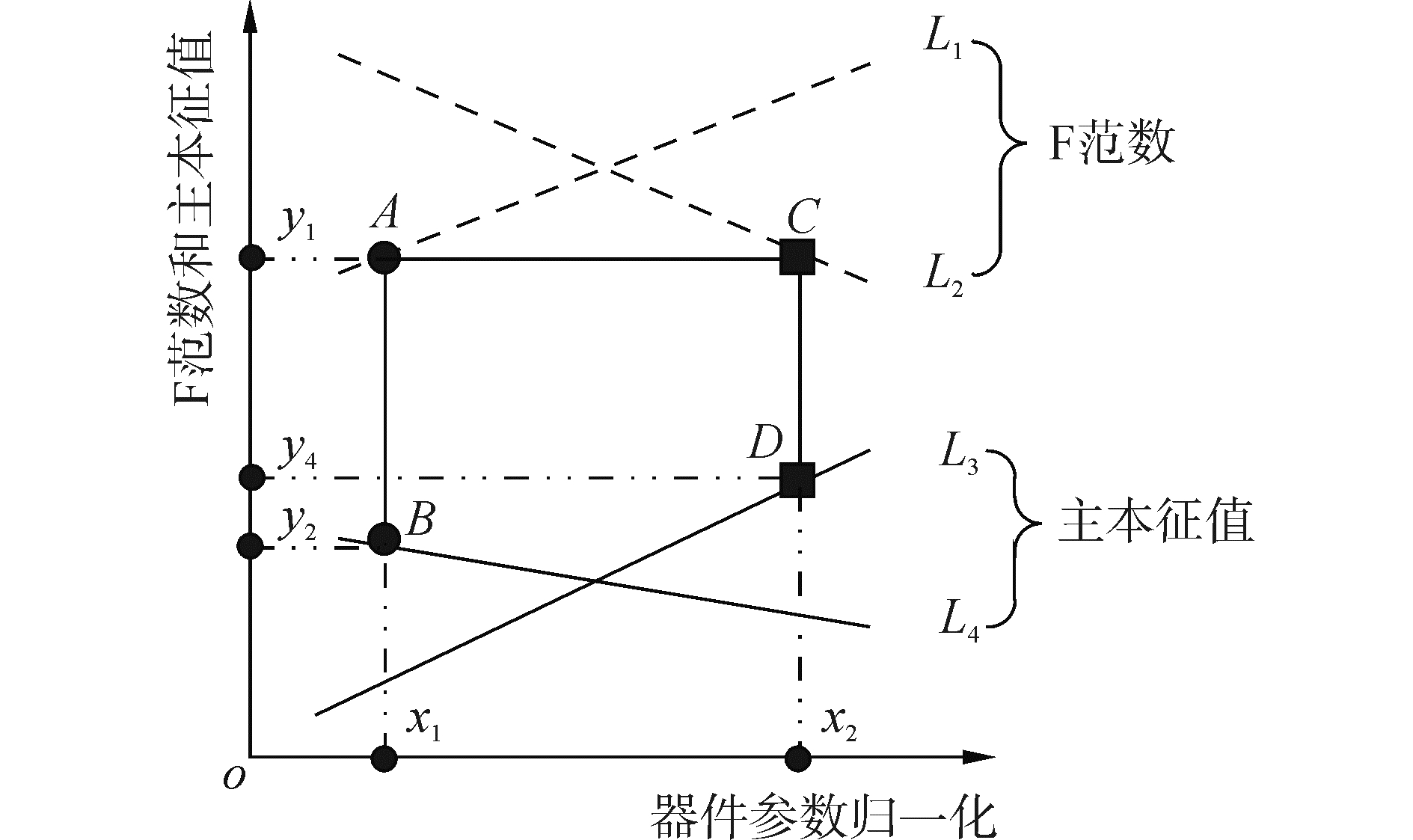
诊断原理如图 1所示 (图中虚线L1和L2表示与方程 (13) 对应的F范数随被诊断器件参数的变化而变化的两条趋势线。实线L3和L4表示与方程 (14) 对应的主本征值随被诊断器件参数的变化而变化的两条趋势线)。其中L1和L4是器件1的参数变化时响应矩阵的一对F范数和主本征值曲线,L2和L3是器件2的参数变化时的另一对F范数和主本征值的变化曲线。L1~L4均通过仿真和线性校正获得。图中横坐标为器件参数归一化值,所以没有单位。采用归一化值可把实际电路中不同类型的器件统一到一个模型上处理。纵坐标为F范数和主本征值,也没有单位。通过在如图 1所示的多对曲线上找到与被诊断电路输出响应矩阵的F范数和主本征值最匹配的一对曲线来实现故障诊断和参数辨识的过程包括三个步骤。
|
| 图1 诊断和辨识原理图 Figure 1 Diagnosis and identification diagram |
1) 通过仿真和线性校正获得故障诊断模型对应的系数ai、bi、di和a′i、b′i、d′i。
2) 找最可能发生故障的器件。首先,测量被测电路的输出响应,算出输出响应矩阵的F范数y1和主本征值y2。y1和y2分别对应方程 (13) 和 (14) 中的L′i,j和Li,j。接着,由y1和曲线L1对应的方程 (14) 求出器件1的参数归一化值x1(A点的横坐标),由x1和L4对应的方程 (13)) 求出对应的主本征值y3(B点的纵坐标)。同理,由y1和L2对应的方程可求出器件2的参数归一化值x2(C点的横坐标),由x2和L3对应的方程可求出对应的主本征值y4(D点的纵坐标)。然后,利用最小误差判据,找出y3和y4中与y2最接近的数。图 1中,与器件1参数变化对应的y3和y2最接近,说明器件1最可能发生故障。
3) 故障定位和参数辨识。如果最可能发生故障的器件1的参数在其容差允许范围内,则电路无故障,否则,电路发生故障,故障定位结果为器件1故障,故障参数辨识结果为步骤2),由y1和曲线L1对应的方程 (14) 求出器件1的参数x1。
如果被测电路有P个待诊断的器件,则从1到p对待诊断的器件进行编号,即方程 (13) 和 (14) 中的i=1,2,…,p。通过仿真和计算获得系数ai、bi、di和a′i、b′i、d′i后,测试被测电路,算出响应矩阵A的主本征值L0,T和F范数L′0,T;用L0,T代替二次方程 (13) 中的Li,j后,代入P组系数ai、bi、di算得P组解,记为xi,T(1)和xi,T(2);对i=1,2,…,p中的每个i值,把xi,T(1)和xi,T(2)分别作为xi,j,把a′i、b′i、d′i代入式 (14),算出对应的P组Li,j(1)和Li,j(2),把每组Li,j(1)和Li,j(2)中与L′0,T最接近的那个数记为L′i,T,xi,T(1)和xi,T(2)中与L′i,T对应的那个数记为xi,T;用ΔLi=|L′0,T-L′i,T|算出i个ΔLi;找出ΔLi中最小的元素ΔLq,与下标q对应的xi,T记为xq,T;如果xq,T超出器件q的容差范围,电路的器件q发生故障,故障参数辨识结果为xq,T;如果xq,T在器件q的容差范围内,则电路无故障。
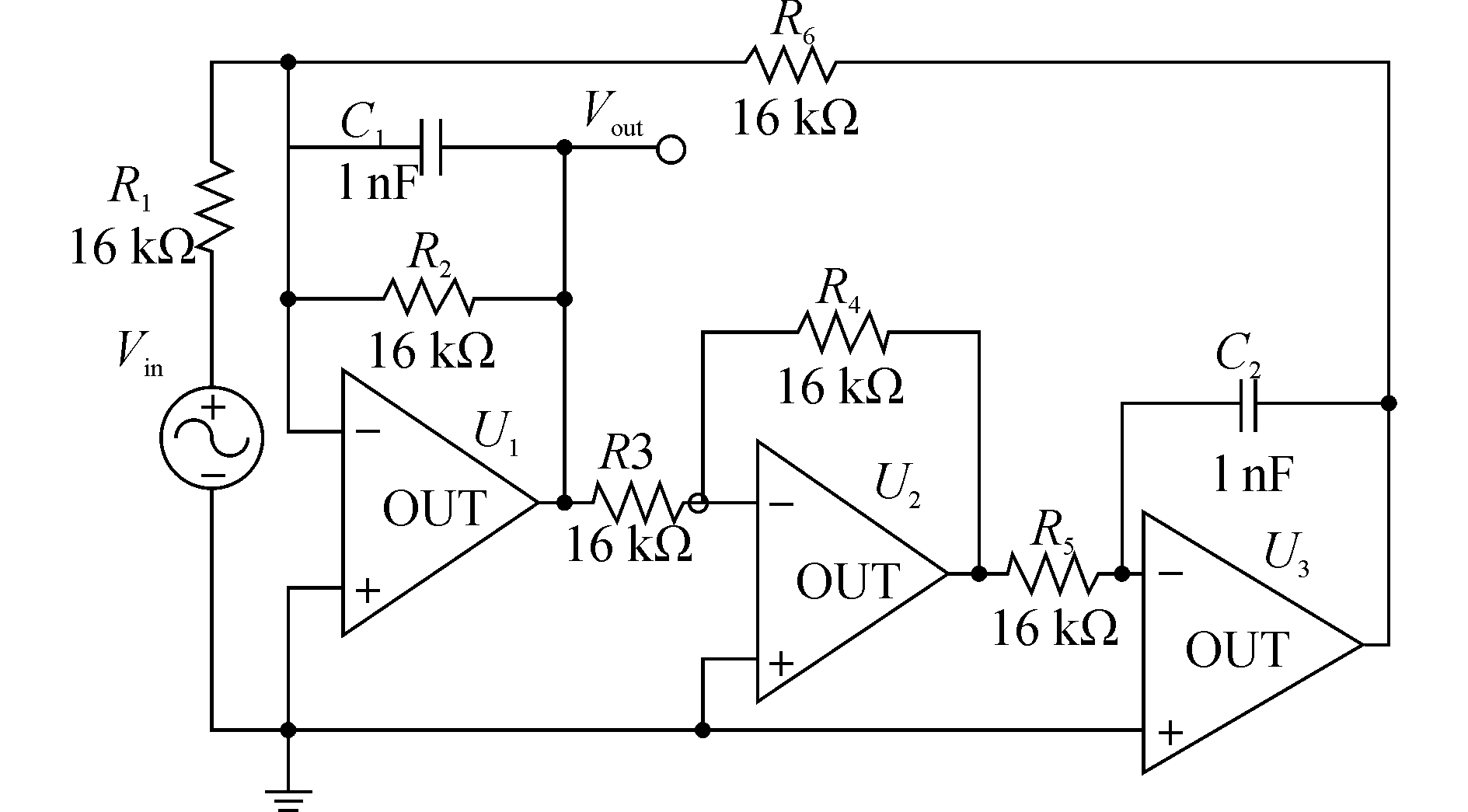
5 实验结果分析 5.1 仿真实验结果采用国际标准电路Tow-Thomas带通滤波器[12]作为被仿真电路。该滤波器的原理电路和器件参数标称值如图 2所示。激励信号是幅度为5 V,频率为5 kHz的正弦电压信号。无源器件的最大允许容差是标称参数的±5%,C1、R4和R5组成待诊断的故障集,选节点Vout为输出响应测试点,在3 GHz处理器、1GB随机存取器的电脑上用Matlab工具软件中进行响应信号处理。
|
| 图2 Tow-Thomas带通滤波器标准电路 Figure 2 Tow-Thomas band-pass filter |
把器件C1、 R4和R5从1~3依次进行编号。依次对每个器件的参数在标称值的70%~130%以3%的步进改变的21个状态进行仿真,算出对应的21组主本征值和F范数,对21个主本征值进行最小二乘拟合,得到方程 (7) 的系数 ai、bi、ci。对21个F范数进行最小二乘拟合,得到方程 (8) 的系数a′i、b′i、c′i。
从仿真标称值状态对应的响应矩阵计算出主本征值y和F范数y0。在容差范围内改变器件标称值来模拟实测电路存在的容差,具体的模拟方式是把C1加大3%,R5减少2%,R4加大2%作为无故障电路,算出对应的响应矩阵主本征值y′和F范数y′0。取di=ci-y+y′和d′i=c′i-y0+y′0得到方程 (13) 和 (14) 的系数ai、bi、di和a′i、b′i、d′i,表 1给出了上述相应参数的具体数值。
| 参数 | 器件1 (C1) |
器件2 (R4) |
器件3 (R5) |
| ai | -0.002 9 | -0.318 4 | -1.483 6 |
| bi | 0.370 7 | -0.688 3 | 4.394 6 |
| ci | 2.025 0 | 3.402 0 | -0.518 5 |
| a′i | 0.377 8 | 5.850 7 | -2.432 1 |
| b′i | 1.430 5 | -20.377 5 | 13.352 5 |
| c′i | 7.238 4 | 23.576 2 | -1.874 1 |
| y | 2.392 5 | 2.392 5 | 2.392 5 |
| y0 | 9.045 6 | 9.045 6 | 9.045 6 |
| y′ | 2.414 3 | 2.414 2 | 2.414 1 |
| y′0 | 9.317 8 | 9.317 6 | 9.317 7 |
| di | 2.046 8 | 3.423 7 | -0.496 8 |
| d′i | 7.510 6 | 23.848 2 | -1.602 1 |
保持C1参数加大3%,R5减少2%,其他器件参数不变,仿真获得R4增大到标称值的118%(归一化值为1.18) 的输出响应,计算得到对应的主本征值L0,T=2.161 8,F范数L′0,T=7.963 9;用L0,T代替 (13) 式中的Li,j,把下标i从1~3取值的3组本征值函数曲线系数ai、bi、di依次代入式 (13),算出x1,T=0.310 9,x2,T=1.184 4,x3,T=0.847 3。把xi,T作为xi,j和对应下标的a′i、b′i、d′i代入式 (14),算出L′1,T=7.975 6,L′2,T=7.964 2,L′3,T=7.985 6。根据ΔLi=|L′0,T-L′i,T|算出ΔLi中最小的元素是ΔL2,对应的x2,T=1.184 4,超出器件2(R4) 的容差范围,所以诊断结果为电路发生故障,故障器件为器件2(R4),故障参数辨识结果的归一化值为x2,T=1.184 4,辨识结果与实际值1.18的绝对误差为0.44%。
为了验证所提出方法的有效性,保持激励信号和采样频率125 kHz不变,对3个被诊断的器件分别以8%的步进从器件标称值的76%~124%改变的诊断结果如表 2所示,表中↑表示器件故障类型为参数比标称值大,↓表示器件故障类型为参数比标称值小。诊断结果表明:21个参数状态的故障定位全部正确,参数辨识的最大误差为0.68%。
| 故障 类型 |
归一 化参数 |
故障 定位 |
辨识 结果 |
辨识 误差/% |
| C1↑ | 1.24 | C1(√) | 1.243 6 | 0.36 |
| 1.16 | C1(√) | 1.166 8 | 0.68 | |
| 1.08 | C1(√) | 1.078 1 | -0.19 | |
| C1 | 1.00 | 正常 (√) | 1.002 1 | 0.21 |
| C1↓ | 0.92 | C1(√) | 0.918 8 | -0.12 |
| 0.84 | C1(√) | 0.843 1 | 0.31 | |
| 0.76 | C1(√) | 0.762 5 | 0.25 | |
| R4↑ | 1.24 | R4(√) | 1.236 6 | -0.34 |
| 1.16 | R4(√) | 1.165 3 | 0.53 | |
| 1.08 | R4(√) | 1.082 5 | 0.25 | |
| R4 | 1.00 | 正常 (√) | 0.998 8 | -0.12 |
| R4↓ | 0.92 | R4(√) | 0.924 5 | 0.45 |
| 0.84 | R4(√) | 0.843 9 | 0.39 | |
| 0.76 | R4(√) | 0.757 4 | -0.26 | |
| R5↑ | 1.24 | R5(√) | 1.245 1 | 0.51 |
| 1.16 | R5(√) | 1.155 4 | -0.46 | |
| 1.08 | R5(√) | 1.083 7 | 0.37 | |
| R5 | 1.00 | 正常 (√) | 1.001 1 | 0.11 |
| R5↓ | 0.92 | R5(√) | 0.922 7 | 0.27 |
| 0.84 | R5(√) | 0.837 5 | -0.25 | |
| 0.76 | R5(√) | 0.764 4 | 0.44 |
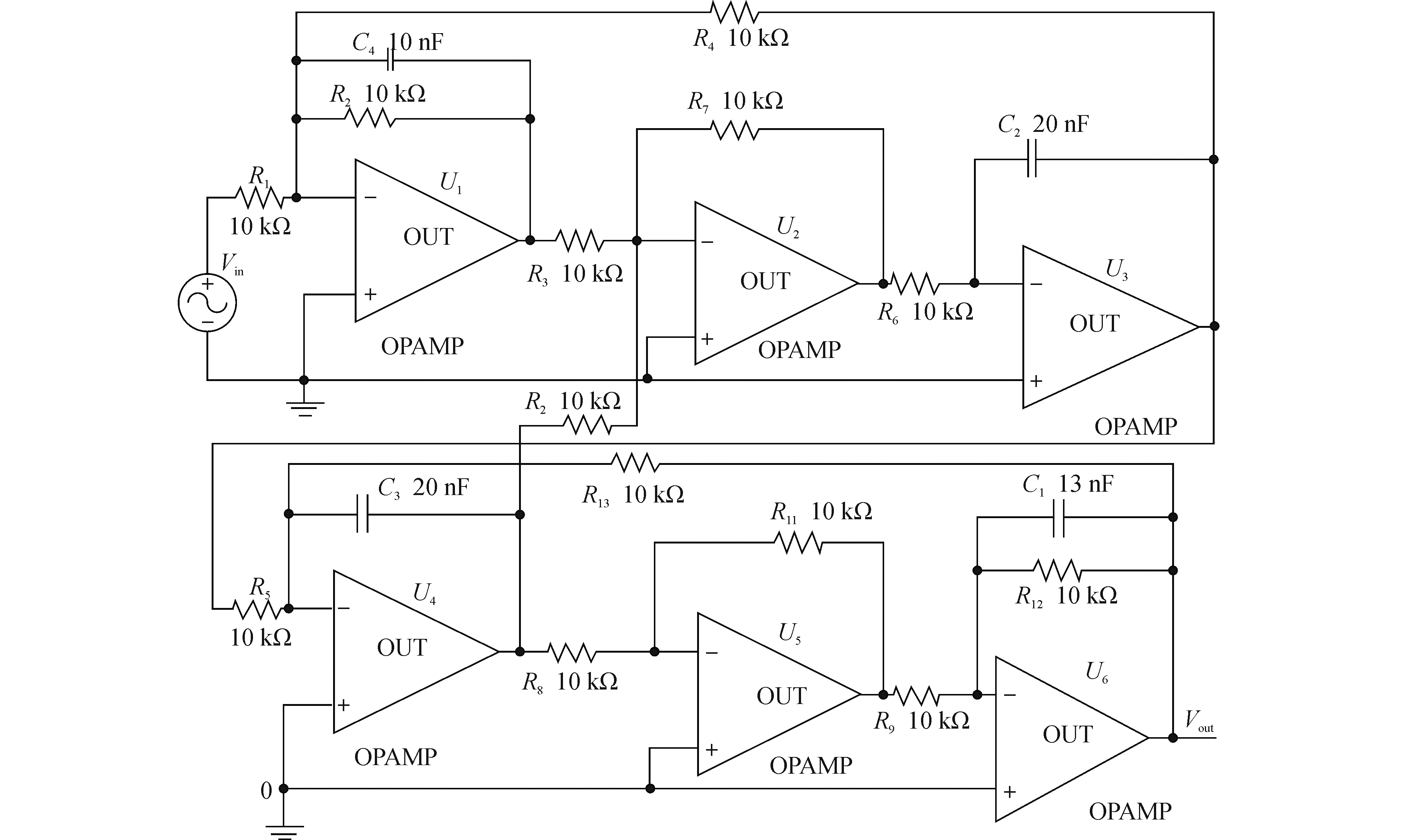
选取国际标准电路中的跳蛙低通滤波器电路作为实测电路[12]。电路中器件的标称值和电路结构如图 3所示。滤波器的截止频率是1.4 kHz。用信号源YB1603产生的正弦激励信号频率为1 kHz,幅度为6 V。Vout为响应测试端,用NI公司USB-9201数据采集器获取输出响应信号采样值。
|
| 图3 跳蛙低通滤波器标准电路 Figure 3 Leapfrog low-pass filter |
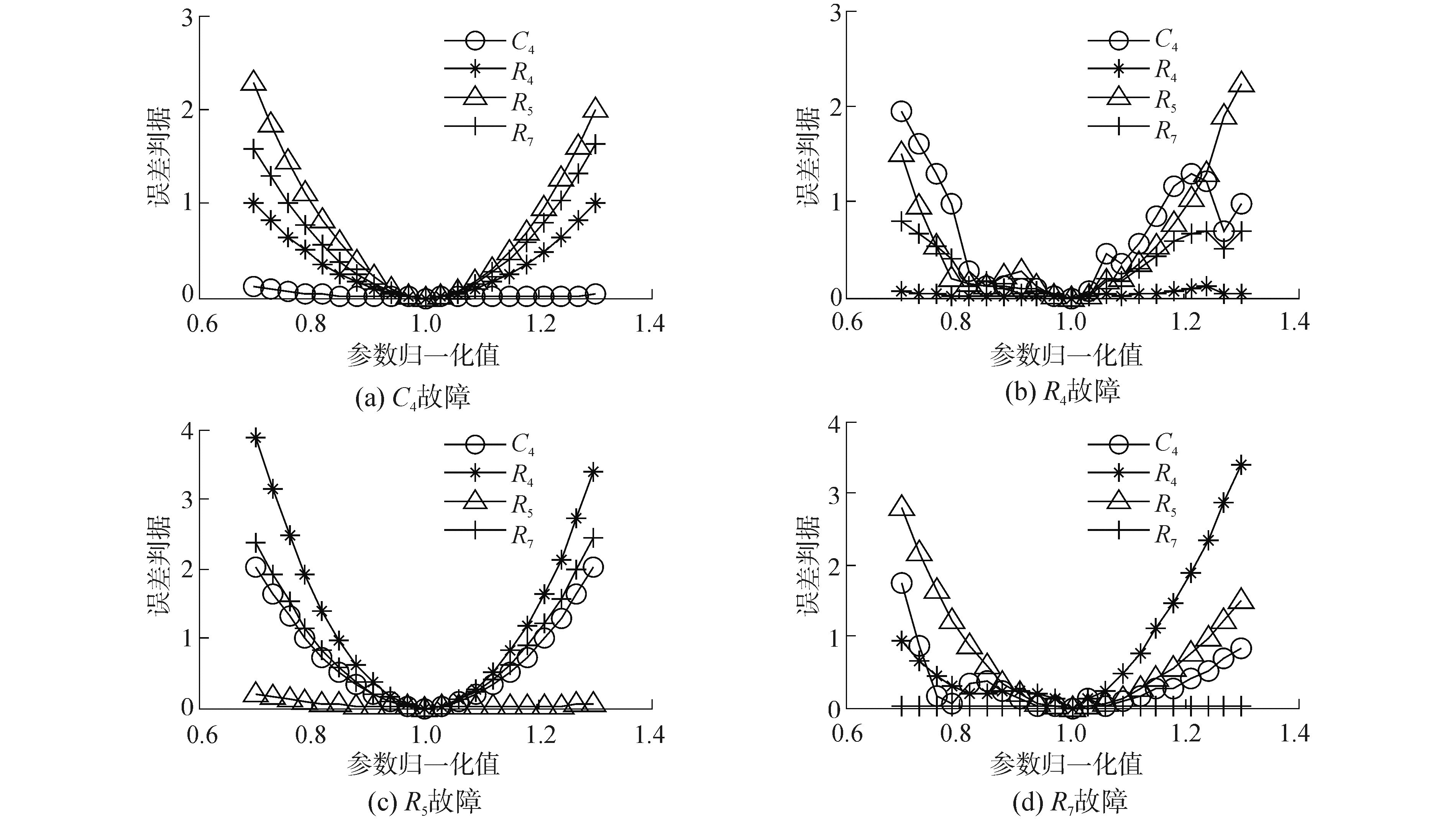
把器件C4、R4、R5和R7的参数分别在其标称值的70%~130%内以3%的步进变化的84种参数状态作为故障集。计算得到的误差判据ΔLi的结果如图 4所示。图 4表明:当电路发生故障时,ΔLi中的最小元素与故障器件对应,用ΔLi中的最小元素能准确地进行故障定位。故障定位结果和故障参数辨识结果如表 3所示,84个故障集的故障定位全部正确,参数辨识结果最大误差为1.21%。结果表明,所提出的方法的故障定位和故障参数辨识精度高。
|
| 图4 误差判据ΔLi的取值情况 Figure 4 The results of error criterion ΔLi |
| 器件实 际值 |
参数辨识结果 | 定位结果 | |||
| C1 | R4 | R5 | R7 | (√) | |
| 0.700 0 | 0.708 0 | 0.711 2 | 0.710 9 | 0.710 4 | (√) |
| 0.730 0 | 0.728 8 | 0.739 0 | 0.732 9 | 0.728 5 | (√) |
| 0.760 0 | 0.768 4 | 0.770 3 | 0.764 6 | 0.768 2 | (√) |
| 0.790 0 | 0.784 8 | 0.796 3 | 0.799 4 | 0.797 7 | (√) |
| 0.820 0 | 0.830 6 | 0.831 1 | 0.829 9 | 0.830 8 | (√) |
| 0.850 0 | 0.843 5 | 0.847 6 | 0.855 5 | 0.857 8 | (√) |
| 0.880 0 | 0.874 6 | 0.889 9 | 0.890 1 | 0.891 0 | (√) |
| 0.910 0 | 0.904 7 | 0.920 1 | 0.900 4 | 0.915 6 | (√) |
| 0.940 0 | 0.932 2 | 0.947 6 | 0.930 6 | 0.934 4 | (√) |
| 0.970 0 | 0.963 2 | 0.998 9 | 0.962 3 | 0.964 5 | (√) |
| 1.000 0 | 0.990 2 | 1.004 5 | 0.991 4 | 0.996 6 | (√) |
| 1.030 0 | 1.039 9 | 1.035 4 | 1.020 9 | 1.037 5 | (√) |
| 1.060 0 | 1.068 6 | 1.071 2 | 1.054 8 | 1.067 8 | (√) |
| 1.090 0 | 1.099 4 | 1.080 5 | 1.082 4 | 1.098 6 | (√) |
| 1.120 0 | 1.131 1 | 1.130 1 | 1.127 4 | 1.114 5 | (√) |
| 1.150 0 | 1.157 8 | 1.162 0 | 1.159 8 | 1.155 7 | (√) |
| 1.180 0 | 1.171 2 | 1.189 6 | 1.188 4 | 1.187 9 | (√) |
| 1.210 0 | 1.220 9 | 1.232 1 | 1.207 8 | 1.218 9 | (√) |
| 1.240 0 | 1.247 8 | 1.244 7 | 1.234 7 | 1.249 9 | (√) |
| 1.270 0 | 1.280 1 | 1.278 9 | 1.261 2 | 1.268 8 | (√) |
| 1.300 0 | 1.290 4 | 1.310 5 | 1.309 7 | 1.238 5 | (√) |
| 比较内容 | 小波算法 | 遗传算法 | 神经网络 | 本方法 |
| 计算时间/ms | 197 | 421 | 308 | 281 |
| 故障定位/% | 99.5 | 99.7 | 99.8 | 99.8 |
| 参数辨识 | 不能 | 能 | 不能 | 能 |
| 测试点数 | 6 | 7 | 7 | 5 |
将本方法与近年提出的几种方法进行比较的结果如表 5所示,比较结果表明本方法的计算时间少、参数辨识能力强。
6 结论本文提出一种模拟电路故障诊断和参数辨识代数方法。仿真结果和实测数据得出以下结论:
1) 利用响应矩阵的F范数和主本征值随器件参数变化而变化的关系建立故障模型,可用线性补偿的方法减少容差影响,实现故障定位和参数辨识的一体化处理,能够减少参数辨识的计算时间,降低测试成本。
2) 联合响应矩阵的F范数和主本征值进行故障诊断的准确率和参数辨识精度较高。
3) 由于满足单故障诊断的方法可以推广到多故障诊断上,所以本方法可以通过增加测试点或划分模糊故障集等方式进行多故障诊断。
| [1] | LI F, WOO P Y. Fault detection for linear analog IC-the method of short-circuits admittance parameters[J]. IEEE transactions on CASI:fundamental theory and applications, 2002, 49(1): 105–108. |
| [2] | 唐人亨. 模拟电子系统的自动故障诊断[M]. 北京: 高等教育出版社, 1991: 17-19. |
| [3] | XIAO F, FENG L. A novel linear ridgelet network approach for analog fault diagnosis using wavelet-based fractal analysis and kernel PCA as preprocessors[J]. Measurement, 2012, 45(3): 297–310. DOI:10.1016/j.measurement.2011.11.018 |
| [4] | SPYRONASIOS A D, DIMOIPOULOS M G. Wavelet analysis for the detection of parametric and catastrophic faults in mixed-signal circuits[J]. IEEE transactions on instrumentation & measurement, 2011, 60(6): 2025–2038. |
| [5] |
谢涛, 何怡刚, 姚建刚. 基于高阶累积量和改进BP神经网络的模拟电路故障诊断[J].
电路与系统学报, 2012, 17(4): 18–22.
XIE Tao, HE Yigang, YAO Jiangang. The analog circuit fault diagnose based on higher order cumulant and improved BP neural network[J]. Journal of circuits and systems, 2012, 17(4): 18–22. |
| [6] | LUO H, WANG Y, LIN H, et al. Module level fault diagnosis for analog circuits based on system identification and genetic algorithm[J]. Measurement, 2012, 45(4): 769–777. DOI:10.1016/j.measurement.2011.12.010 |
| [7] | PRASAD V, PINJALA S, MURTY K. Mixed integer programming method for fault diagnosis of linear analogue circuits[J]. Electronics letters, 1992, 28(13): 1184–1185. DOI:10.1049/el:19920748 |
| [8] |
王佩丽, 彭敏放, 杨易旻, 等. 应用模糊最优小波包和LS-SVM的模拟电路诊断[J].
仪器仪表学报, 2010, 31(6): 1282–1288.
WANG Peili, PENG Meifang, YANG Yimin, et al. Analog circuit diagnosis using fuzzy-rule based optimalwavelet packet and LS-SVM[J]. Chinese journal of scientific instrument, 2010, 31(6): 1282–1288. |
| [9] | SATY T, SATY G, RAO R. Implementing an expert system for fault diagnosis of electronic equipment[J]. Engineering applications of artificial intelligence, 1995, 8(3): 355–364. DOI:10.1016/0952-1976(95)00012-P |
| [10] | WILKINSON J H. The algebraic eigenvalue problem[M]. Oxford, Clarendon, 1988:62-64. |
| [11] | GRIFFITHS D J. Introduction to quantum mechanics[M]. New Jersey, the United States, Addison Wesley, 2004:96-98. |
| [12] | KAM B, ARABI K, BELL I. Analog and mixed-signal benchmark circuits-First release[C]//ITC, Washington DC, USA, 1997:183-190. |



