2. National Engineering Research Center of Shipbuilding, Dalian University of Technology, Dalian 116023, China;
3. China FAW Group Cooperation R & D Center, Changchun 130011, China
气缸套是内燃机的主要受热部件之一,其工作条件非常恶劣。在工作过程中,气缸套内壁接触冷热交变的气态工质以及活塞组件,而外壁又被冷却介质所包围,其受热极不均匀。气缸套作为薄壁筒类零件,由于较大的温度梯度有可能造成过大的热变形,致使与活塞组的正常间隙被破坏,磨损增大;如果气缸套内壁温度过高将使润滑情况恶化,导致活塞、气缸套擦伤。掌握气缸套温度场分布状态是准确分析气缸套热负荷和热变形情况的基础,对于保证高性能内燃机的可靠性是非常重要的[1]。气缸套温度场分析还是气缸套故障分析的必要环节之一[2]。气缸套温度对于柴油机的NOx排放也有重要影响[3]。可见气缸套温度场的准确预测对于柴油机研究与开发至关重要。
对气缸套进行热负荷分析时,准确获得气缸套的受热边界条件是分析的关键。在内燃机的一个工作循环中,工质温度变化剧烈。另外,由于活塞的往复运动,气缸套内表面与燃气的接触面积也在周期性变化。高温燃气时间上和空间上的高频率双瞬态变化在气缸套壁面薄层内产生周期性的高频温度波动,这种波动时导致零件失效的一个重要因素[4]。
受到计算软硬件条件的限制,以往的研究大多以稳态传热方法求解气缸套温度场。俞小莉等[5]在实验的基础上,利用数学方法反求得到了气缸体内表面稳态传热边界条件的经验公式。基于此经验公式,王希珍等[6-7]分别对稳态工况下气缸套的稳态温度场进行了有限元分析。冯立岩等将活塞、活塞环、气缸套以接触对方式建立耦合模型进行传热过程分析[8]。董洪全在研究气缸套传热问题时以气缸套固定分区方式进行稳态传热计算[9]。高兴义等[10]以稳定温度场为初始条件,施加变化的缸套与燃气接触边界条件进行有限元计算,给出缸套表面层的温度波动情况,但其边界条件求取时未考虑边界空间变化。肖金生等[11]推导了瞬态边界条件加载方法,但其分析采用一维简化模型且只针对与燃气直接接触区域,不能得到气缸套整体温度波动的分布情况。随着技术的发展,目前的高性能计算工作站足以胜任复杂的三维瞬时有限元分析。对燃烧室部件活塞、气缸盖的流固耦合方法分析开始普及。流固耦合计算的热边界条件中,缸外换热边界条件可采用三维CFD计算,缸内换热边界条件可采用一维工作循环计算[11],或者采用三维CFD计算[12-14]。但该方法适用于燃气接触表面无变化的部件,而气缸套与燃气接触表面随着活塞的往复运动呈周期变化,因此气缸套的瞬态边界条件加载需要根据活塞瞬时位移建立移动边界。本文以某型号中速柴油机气缸套为研究对象,通过发动机工作过程数值模拟得到缸内工质的瞬时温度和换热系数;结合活塞瞬时位置,对缸套内表面进行区域划分求得其瞬时热边界条件;进而应用ANSYS软件对气缸套温度场进行有限元计算,得到稳定工况下循环瞬态温度场分布情况,为缸套的设计和分析提供参考。
1 传热分析基本理论在缸套温度场分析中,可以把缸套看成是无内热源、各向同性的三维实体。在直角坐标系下,其满足的瞬态导热微分方程[15]为
| $ \rho c\frac{{\partial T}}{{\partial t}} - \lambda \left( {\frac{{{\partial ^2}T}}{{\partial {x^2}}} + \frac{{{\partial ^2}T}}{{\partial {y^2}}} + \frac{{{\partial ^2}T}}{{\partial {z^2}}}} \right) = 0 $ | (1) |
式中:ρ、c、λ分别为材料的密度、比热和导热系数,t为时间,T为气缸套温度。
导热微分方程为数学形式,对于特定的气缸套导热现象,求解时必须给出反映其特点的单值条件。其中包括:
1) 几何条件:气缸套的几何形状,尺寸及相对位置;
2) 物理条件:气缸套的物理特征,如材料物性参数,内热源分布情况等;
3) 初始条件:t=0时刻,气缸套内稳步分布状态:T|t=0=T0(x, y, z),对稳态导热,不需此条件;
4) 边界条件:给定气缸套各边界上的热状态,常见有三类:温度、热流密度、表面介质温度和对流换热系数。气缸套导热计算采用第三类边界条件。
2 气缸套有限元模型建立本文的研究对象为某型号涡轮增压中冷中速柴油机,气缸数为16缸,呈50°V型夹角布置。柴油机标定功率为2 800 kW,标定转速为1 000 r/min,标定工况时的最大爆发压力为13.5 MPa,冷却方式为压力水冷循环。
柴油机气缸套为钻孔冷却气缸套,考虑到其为轴对称结构,利用ProE建立1/2气缸套几何模型。建模过程进行适当的简化,模型中不考虑小的倒角和圆角等细节结构,保留内部冷却孔道。利用ICEM软件进行网格划分,为保证计算精度,对气缸套内表面进行棱柱层加密。最后划分132 686个单元,25 822个节点。网格划分如图 1所示。

|
| 图1 气缸套有限元模型 Figure 1 The finite element model of the liner |
气缸套材料为铬钼铜合金铸铁,材料密度为7 300 kg/m3,比热容和导热系数随温度变化如表 2所示。
| 温度/℃ | 导热系数/ (W·(m·℃)-1) |
比热容/ (W·(kg·℃)-1) |
| 100 | 47.0 | 523 |
| 200 | 46.6 | 536 |
| 300 | 43.6 | 565 |
| 400 | 41.2 | 578 |
合理的换热边界条件和初始条件对温度场计算至关重要。气缸套温度场模拟中采用第三类边界条件,即换热表面介质的换热系数和相应的介质温度。缸套换热情况复杂,主要换热表面有缸套内表面,冷却水套及冷却水孔,气缸套与机架接触面等。
3.1 初始条件确定为了得到初始条件,先进行稳态传热计算。发动机一个工作循环中,缸内气体经过进气、压缩、燃烧、排气等过程,压力和温度变化很大,这导致燃烧室壁面的换热情况非常复杂。要准确获得燃气的温度和换热系数,应对特定机型和工况进行缸内气体工作过程模拟。本文利用GT-POWER建立柴油机的工作过程模型,模拟得到额定工况下缸内工质平均温度和气缸壁平均换热系数的瞬时变化曲线,如图 2所示。

|
| 图2 气缸壁平均换热系数和缸内工质平均温度瞬时变化曲线 Figure 2 Heat transfer coefficient near cylinder wall and mean temperature vs. crank angle |
根据以上结果可以求得燃气平均换热系数αm和燃气综合平均温度Tres分别为
| $ {\alpha _m} = \frac{1}{{{\tau _0}}}\int_0^{{\tau _0}} {{\alpha _g}{\rm{d}}\tau } $ | (2) |
| $ {T_{res}} = \int_0^{{\tau _0}} {{\alpha _g}{T_g}{\rm{d}}\tau /\int_0^{{\tau _0}} {{\alpha _g}{\rm{d}}\tau } } $ | (3) |
式中:αg、Tg分别为燃气瞬时换热系数和瞬时温度。计算得到αm为630 W/(m2·℃),Tres为695℃。
按文献[3]推荐,柴油机气缸套内表面稳态传热边界条件在轴向高度上有如下分布规律:
| $ {\alpha _m}\left( h \right) = {\alpha _m}\left( {1 + {k_1}\beta } \right){{\rm{e}}^{ - {\beta ^{1/3}}}} $ | (4) |
| $ {T_{res}}\left( h \right) = {T_{res}}\left( {1 + {k_2}\beta } \right){{\rm{e}}^{ - {\beta ^{0.5}}}} $ | (5) |
式中:
实际情况中,由于进排气门、喷孔位置的影响,轴向的换热系数也应有所不同,本文在计算中忽略换热系数的周向差别。
冷却水侧的对流换热系数按文献[10]计算:
| $ {h_w} = B\frac{{{{\left( {{\rho _w}{v_w}} \right)}^{0.8}}}}{{{d_d}^{0.2}}} $ | (6) |
式中:vw为冷却水流速;dd为决定尺寸;ρw为冷却水密度;B为系数,按冷却水温选取。
缸套与机体间换热系数由接触热阻决定,其值取决于材料的性质、接触面光洁度和表面压力等参数。本文按照经验值选取。
3.2 瞬态传热边界条件确定缸内燃烧放热是缸套热负荷的主要来源。在工作过程中工质温度和换热系数波动剧烈;而且随着曲轴转角的改变,缸套与工质的接触面积也不断变化。
3.2.1 气缸套和活塞相对位置关系确定燃气与缸套接触面积的变化需要确定缸套和活塞的相对位置的变化规律。假设活塞沿缸套内壁只做上下往复运动,忽略其摆动。气缸套和活塞的相对位置关系可用图 3所示几何关系来表示。

|
| 图3 活塞-缸套位置关系示意图 Figure 3 The relative position of piston and cylinder liner |
活塞移动距离与曲轴转角之间的关系式为
| $ s = r\left( {1 - \cos \varphi } \right) + l - \sqrt {{l^2} - {r^2}{{\sin }^2}\varphi } $ | (7) |
式中:l为连杆长度,r为曲柄半径。
由活塞和缸套的相对位置关系,可计算出工作循环内缸套与缸内工质接触长度的变化曲线,如图 4所示。

|
| 图4 工质接触区长度变化曲线 Figure 4 The length of contact region of working fluid with liner |
气缸套内表面区域划分示意图如图 5所示,对于一个工作循环内的任一瞬时,气缸套内表面从上到下可以依次分为三部分:工质接触区、活塞接触区和曲轴箱空气对流换热区域。

|
| 图5 气缸套内表面区域划分示意图 Figure 5 The division of cylinder liner inner face |
1) 工质接触区分为两部分:对应燃烧室区域和对应火力岸区域;缸套内表面对应于燃烧室区域的温度和换热系数从燃气瞬时温度和换热系数曲线上直接获取。对应火力岸区域,由文献[1]得该区域放热系数约为燃烧室内放热系数的0.3倍。
2) 活塞组接触区分为两部分:活塞环区和活塞裙部;活塞组和气缸套之间通过润滑油膜连接,将润滑油膜的传热简化成沿径向的一维导热热阻,只考虑导热作用[6]。由以上假设,活塞和缸套间的换热可写为
| $ {q_{p - l}} = \frac{{{\lambda _{{\rm{oil}}}}}}{{{\delta _{{\rm{oil}}}}}}\left( {{T_p} - {T_l}} \right) $ | (8) |
式中:λoil为润滑油导热系数,δoil为润滑油厚度,Tp为活塞温度,Tl为缸套温度。关于润滑油膜厚度,环区选取10~20 μm,裙部选取0.5 mm。
3) 曲轴箱空气对流区域;参考经验数值,选取曲轴箱换热系数为200 W/(m2·℃),曲轴箱温度选取80℃。
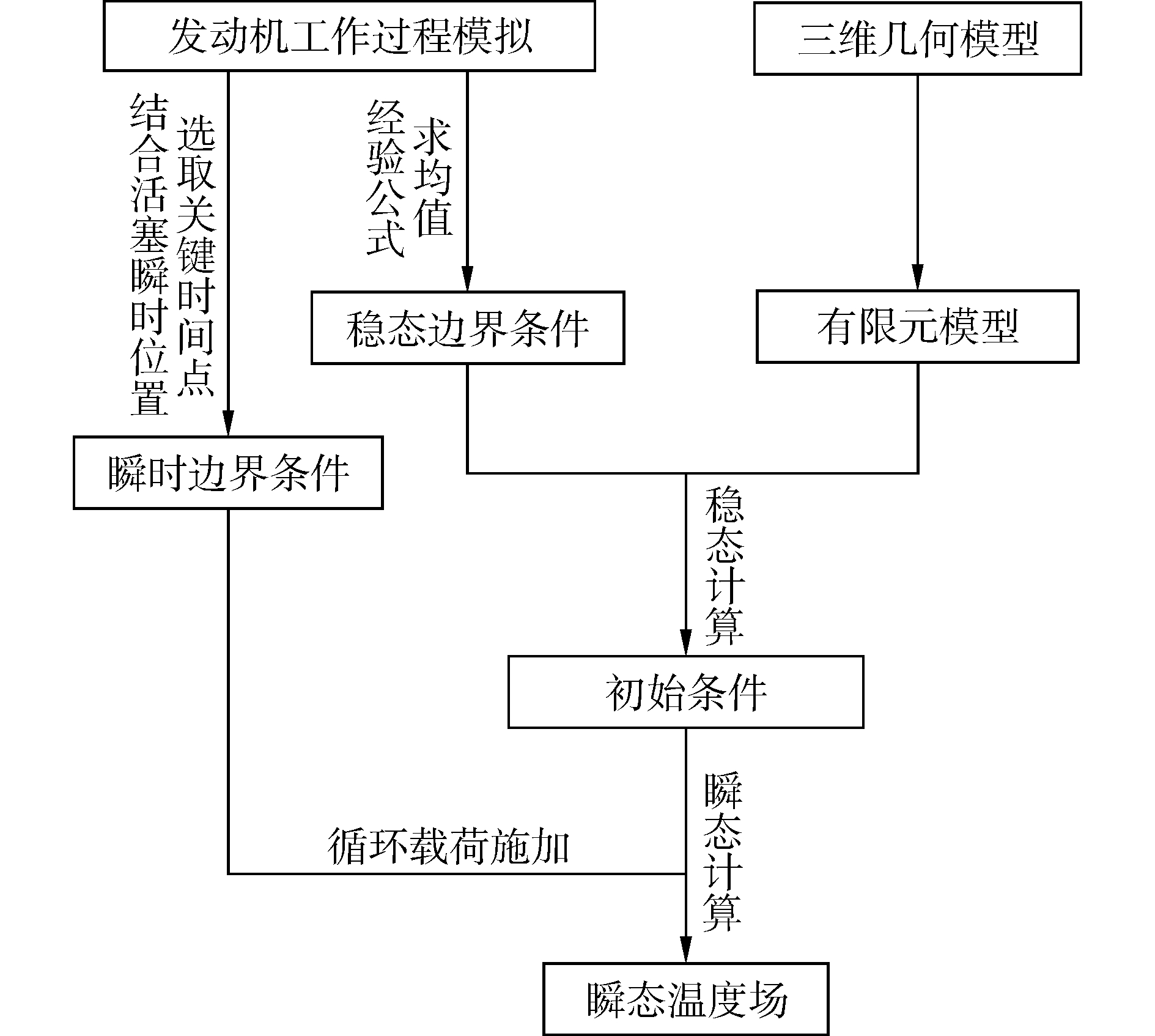
4 温度场计算与结果分析及验证 4.1 温度场计算瞬态计算时,考虑到计算机的计算能力,选择缸内工质数据变化关键点。一个工作循环内,共选取18个关键点。压缩和燃烧阶段,由于工质温度和换热系数变化剧烈,关键点选取较为密集,进排气阶段选点较为稀疏。对于每一个关键点,以此时刻活塞位置为基准将内表面分为不同区域,并分别求得各自的热边界条件,进而以缸套内表面轴向长度为横坐标,对应的温度和换热系数为纵坐标,生成一组表格文件作为此时刻内表面的瞬态热边界条件。将所有时刻的热边界条件输入ANSYS,以时间为坐标,选择坡道加载的方式以拟合燃气曲线。最后利用循环语句进行周期性载荷施加。开始计算一段时间后计算稳定,得到气缸套循环瞬态温度场结果。
4.2 结果分析图 7显示了400℃A时刻气缸套整体温度场云图。图 8显示了270℃A (工作循环内温度最低) 和400℃A (工作循环内温度最高) 时刻气缸套局部温度场对比图。图 9显示了循环结束时即720℃A时刻内壁沿轴向温度变化图。
|
| 图6 温度场计算流程示意图 Figure 6 The schematic of temperature field calculation |

|
| 图7 270℃A时刻气缸套整体温度云图 Figure 7 The temperature field distribution of cylinder liner at the time of 270℃A |

|
| 图8 270℃A和400℃A时刻局部气缸套温度场云图对比图 Figure 8 The temperature field distribution of cylinder liner at the times of 270℃A and 400℃A |

|
| 图9 缸套内表面轴向温度变化图 Figure 9 The axial temperature of cylinder liner inner face |
总体看来,缸套整体温度分布沿轴向有较大差异,从上到下温度逐渐降低,温度最高的区域为气缸套内壁上部对应燃烧室余隙容积的部分。
为了体现气缸套内表面的温度波动情况,选取不同位置的几个点做出其工作循环内温度变化曲线,如图 10所示。从图中可以看出,不同位置处温度变化趋势总体一致。缸套上部对应燃烧室余隙容积区域温度波动最为剧烈,幅值为24℃。随着轴向距离的增加,温度波动幅值逐渐减小,至距缸套顶面150 mm处几乎没有明显温度波动。

|
| 图10 气缸套内表面不同位置循环温度波动曲线 Figure 10 The variation of transient temperature of the cylinder liner inner face |
为了体现气缸套温度波动在缸套厚度方向的变化情况,选取相同轴向距离 (距顶面10 mm) 但距内表面不同深度的几个点,做出其工作循环温度变化曲线,如图 11所示。从图中可以看出,温度波动在深度方向衰减剧烈,随着深度增加,波动幅值迅速减小,距内表面1.4 mm处波动幅值已经很小,3 mm处温度已经平稳。

|
| 图11 气缸套距内表面不同深度温度波动曲线 Figure 11 The variation of transient temperature at different depth of the liner |
为保证计算结果的准确性,与厂家给出的气缸套温度测点测试结果进行对比验证。温度测试中选择热电偶测量温度。在气缸套上钻直径为3 mm的盲孔,热电偶热节点焊在接近气缸套内壁面的孔底。温度测点有3个,沿气缸套周向每隔22.5°依次布置,测点距缸套顶面68 mm,在柴油机标定负荷条件下,三个测点①、②、③的温度测量值依次为148.6℃、152.3℃、147.0℃(如图 12)。

|
| 图12 气缸套温度测点布置图 Figure 12 The liner temperature measurement locations |
选取测点对应位置的节点,计算结果显示工作循环内温度值为149.1℃~151.1℃,三个温度测点的平均值为149.3℃,与测量值相差1.2%,误差在可接受范围内。
5 结论1) 传统的气缸套分析视气缸套导热为稳态导热,与实际情况不符。本文考虑气缸套内表面受高温燃气时间和空间上的瞬态变化的影响,得到气缸套循环瞬态温度场分布情况,有助于提高分析的准确性和合理性。
2) 柴油机在稳定工况运行时,气缸套内表面温度处于稳定波动状态,温度波动值最大为24℃,处于气缸套上部,且温度波动幅值沿气缸轴线向下止点方向不断减小,气缸套内部温度波动沿径向方向迅速衰减。热负荷集中在缸套上部,需要进行热应力分析及疲劳分析,并进行强度校核。
3) 考虑到喷孔位置及进排气影响,气缸套温度在周向也有一定差异。对缸套温度场进一步研究需要利用三维数值模拟软件对燃气换热边界条件的空间分布进行模拟。
| [1] |
肖永宁, 潘克煜, 韩国埏.
内燃机热负荷和热强度[M]. 北京: 机械工业出版社, 1988.
XIAO Yongning, PAN Keyu, HAN Guoyan. Internal combustion engine thermal load and thermal strength[M]. Beijing: China Machine Press, 1988. |
| [2] | ESPADAFOR F J, VILLANUEVA J B, GARCÍA M T, et al. Analysis of a diesel generator cylinder failure[J]. Engineering failure analysis, 2010, 17(4): 913–925. DOI:10.1016/j.engfailanal.2009.11.003 |
| [3] | MALOUF T C, MOSKWA J J. How cylinder cooling and liner temperature profiles affect NO emissions:a device for R&D:SAE technical paper 2016-01-0983[R].[S.l.]:SAE, 2016. |
| [4] |
杨万里, 陈国华, 叶晓明, 等. 内燃机燃烧室零件表面薄层瞬态传热研究[J].
小型内燃机与摩托车, 2001, 30(6): 1–3.
YANG Wanli, CHEN Guohua, YE Xiaoming, et al. Study of instantaneous heat transfer within chamber for internal combustion engine components[J]. Small internal combustion engine, 2001, 30(6): 1–3. |
| [5] |
俞小莉, 郑飞, 严兆大. 内燃机气缸体内表面稳态传热边界条件的研究[J].
内燃机学报, 1987, 5(4): 324–332.
YU Xiaoli, ZHENG Fei, YAN Zhaoda. The research of the boundary conditions of steady thermal conduction on the inner surface of cylinder in internal combustion engines[J]. Transactions of CSICE, 1987, 5(4): 324–332. |
| [6] |
王希珍, 严兆大, 周军. 柴油机缸套热负荷评估的分析及实验研究方法[J].
内燃机工程, 2001, 22(4): 62–65.
WANG Xizhen, YAN Zhaoda, ZHOU Jun. Analytical and experimental method of thermal load estimation for diesel engine cylinder liner[J]. Chinese internal combustion engine engineering, 2001, 22(4): 62–65. |
| [7] |
冯国增, 马哲树. 柴油机气缸套三维温度场数值计算与分析[J].
机械设计与制造, 2008(9): 1–3.
FENG Guozeng, MA Zheshu. 3-Dimension temperature field numerical simulation and analysis research on cylinder liner of diesel engine[J]. Machinery design & manufacture, 2008(9): 1–3. |
| [8] |
冯立岩, 范立云, 隆武强, 等. 柴油机活塞组耦合模型有限元分析[J].
汽车工程, 2004, 26(2): 153–156.
FENG Liyan, FAN Liyun, LONG Wuqiang, et al. Finite element analysis on a coupled model for piston assembly of a diesel engine[J]. Automotive engineering, 2004, 26(2): 153–156. |
| [9] |
董洪全, 冯慧华, 王艳霞, 等. 气缸套变形多场耦合建模与分析技术[J].
内燃机学报, 2014(3): 276–282.
DONG Hongquan, FENG Huihua, WANG Yanxia, et al. Multi-field coupling modeling and analysis of cylinderLiner deformation[J]. Transactions of CSICE, 2014(3): 276–282. |
| [10] |
高世义, 李东成, 陈庆敏, 等. 缸套瞬态温度场的有限元分析[J].
内燃机学报, 1992, 10(3): 262–266.
GAO Shiyi, LI Dongcheng, CHEN Qingming, et al. Finite element analysis of transient temperature field in cylinder liner[J]. Transactions of CSICE, 1992, 10(3): 262–266. |
| [11] |
肖金生, 曾宪友, 杨俊岭, 等. 内燃机气缸套温度波及波动热应力的有限差分分析[J].
武汉交通科技大学学报, 1998, 22(3): 227–230.
XIAO Jinsheng, ZENG Xianyou, YANG Junling, et al. Temperature fluctuation and thermal stress fluctuation analysis of I. C. engine cylinder liner[J]. Journal of Wuhan transportation university, 1998, 22(3): 227–230. |
| [12] |
骆清国, 刘红彬, 龚正波, 等. 柴油机气缸盖流固耦合传热分析研究[J].
兵工学报, 2008(7): 769–773.
LUO Qingguo, LIU Hongbin, GONG Zhengbo, et al. Study on the fluid-solid coupled heat transfer of the diesel engine cylinder head[J]. Acta armamentaii, 2008(7): 769–773. |
| [13] |
邓邦林, 刘敬平, 杨靖, 等. 基于流固耦合的缸盖温度场分析[J].
汽车工程, 2012(3): 203–206.
Deng Banglin, Liu Jingping, Yang Jing, et al. An Analysis on the Temperature Field of CylinderHead Based on Fluid-Solid Coupling[J]. Automotive Engineering, 2012(3): 203–206. |
| [14] | DONG Zhelin, CHEN Guohua, JIANG Yankun, et al. Modeling of transient heat transfer for the 3-D coupling components in an internal-combustion engine:SAE technical paper 2012-01-1759[R].[S.l.]:SAE, 2012. |
| [15] |
杨世铭, 陶文铨.
传热学[M]. 4版. 北京: 高等教育出版社, 2006: 41-47.
YANG Shiming, TAO Wenquan. Heat transfer[M]. 4th ed. Beijing: Higher Education Press, 2006: 41-47. |



