2. College of Aerospace and civil Engineering, Harbin Engineering University, Harbin 150001, China
空间交会技术是航天领域一项非常复杂、难度很大的工作。随着航天技术尤其载人航天技术的发展,空间交会技术也得到了迅速发展和广泛应用。未来几十年,世界范围内的航天活动将包括建立轨道空间站,载人登月并建立月球基地,载人行星或小行星探测等任务。从这些航天活动的特点来看,均需要实现航天器在地球轨道或星际间的交会。
交会过程中的一个重要影响因素是追踪航天器的推力约束问题。推力约束包含两个方面,即幅值约束和方向约束。由于航天器的承载能力有限,发动机本身能产生的推力也有限。国内外已对小推力交会问题进行了大量的研究,一般将追踪航天器推力视为常值小推力[1-6]。文献[7]将控制输入约束的交会问题转化为具有线性矩阵不等式的凸优化问题。Yamakawa使用C-W方程提出了常值径向小推力作用下周期轨道的半解析方法[8]。Paul采用分段多项式的方法解决了常值推力下的轨道优化问题[9]。Pardis研究了航天器推力饱和时交会的优化问题[10-11]。文献[12]研究了针对卫星星座重组机动时小推力优化问题,考虑了推力约束和过程约束。Lantoine考虑了交会中的推力幅值限制和避免碰撞约束等条件,采用有约束的线性二次调节器完成了交会过程的优化设计[13]。
此外,考虑到在交会过程中,敏感器视域、光学测量器对光照条件的要求[14]以及避免在对接时发动机火焰对目标器的影响等因素,有必要考虑推力方向约束下的制导策略。Sukhanov对考虑推力方向约束的小推力轨道转移作了研究,得出了一些必要的优化条件[15-16]。Bertrand采用平滑策略解决了bang-bang优化控制问题,之后Mitani将平滑策略应用到具有幅值和方向约束的连续推力的轨道转移问题上[17-18]。Willard Curtis等研究了一种新的非线性控制方法[19],Mitani将此方法应用到交会过程,并引入推力约束,成功实现了有约束交会对接的控制律设计[20-21]。
模型预测控制不但在普通工业领域获得了广泛的应用[22],而且正逐渐应用到航空航天领域。模型预测控制既可以应用到小推力航天器星际转移问题[23],又被应用到航天器交会和逼近操作过程的制导领域[24]。Sheared将约束模型预测控制应用到F-16模型中[25]。朱彦伟等研究了航天器近距离相对运动的模型预测控制[26]。Singh将模型预测控制应用到航天器逼近过程中,解决了多种限制下的航天飞机与ISS之间的交会对接问题[27]。
在对国内外研究现状进行相关调研后,发现国内对推力方向受限的轨道控制问题上的研究目前文献不多,多数研究集中在常值径向推力方向。同时将模型预测控制应用到航天器交会过程的研究相对缺乏或者对推力约束问题的讨论不深。因此,可以将模型预测控制应用到航天器交会中,并用来处理推力约束问题。
1 航天器交会动力学模型当目标星轨道为圆轨道时的C-W方程如下[28]
| $ \left\{ \begin{gathered} \ddot x-2\omega \dot y-3{\omega ^2}x = {u_x} \hfill \\ \ddot y + 2\omega \dot x = {u_y} \hfill \\ \ddot z + {\omega ^2}z = {u_z} \hfill \\ \end{gathered} \right. $ | (1) |
式中:
进行如下变换:
| $ \sigma = R_0^2{\alpha _{{\text{max}}}}/\mu \left[\begin{gathered} {\bar x} \hfill \\ {\bar y} \hfill \\ \end{gathered} \right] = \frac{1}{{\sigma {R_0}}}\left[\begin{gathered} x \hfill \\ y \hfill \\ \end{gathered} \right] $ | (2) |
式中:αmax为最大推力加速度。
设
| $ \left\{ \begin{gathered} \dot {\boldsymbol{x}} = \boldsymbol{Ax} + \boldsymbol{Bu} \hfill \\ \boldsymbol{y} = \boldsymbol{Cx} \hfill \\ \end{gathered} \right. $ | (3) |
其中
| $ \begin{gathered} \boldsymbol{A} = \left[\begin{gathered} 0\;\;0\;\;\;\;1\;\;\;0 \hfill \\ 0\;\;0\;\;\;\;0\;\;\;1 \hfill \\ 3\;\;0\;\;\;\;0\;\;\;2 \hfill \\ 0\;\;0\;\;-2\;\;0 \hfill \\ \end{gathered} \right], \boldsymbol{B} = \left[\begin{gathered} 0\;\;\;0 \hfill \\ 0\;\;\;0 \hfill \\ 1\;\;\;\;0 \hfill \\ 0\;\;\;\;1 \hfill \\ \end{gathered} \right], \hfill \\ \boldsymbol{C} = \left[\begin{gathered} 1\;\;0\;\;0\;\;0 \hfill \\ 0\;\;1\;\;0\;\;0 \hfill \\ \end{gathered} \right] 。\hfill \\ \end{gathered} $ |
航天器在交会中会受到推力约束,推力约束分为幅值约束和方向约束两部分。这里取航天器的最大推力加速度为αmax=0.02 m/s2;定义推力方向角为y与-u之间的夹角,见图 1,这里取约束角为γ。下面给出推力约束条件如下:
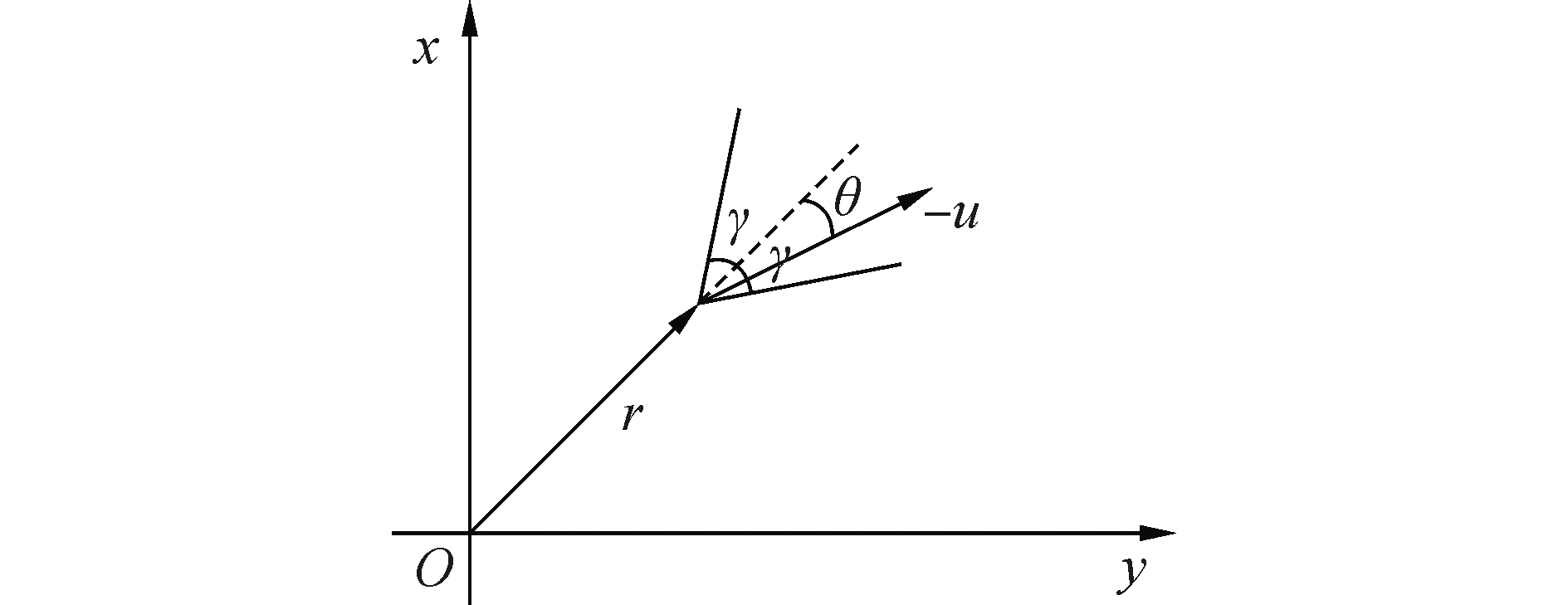
|
| 图1 推力方向角 Figure 1 The thrust direction angle |
幅值约束条件:
| $ \left\| \boldsymbol{u} \right\| \leqslant {\alpha _{\max }} $ | (4) |
方向约束条件:
| $ \cos \theta = \frac{{-{\boldsymbol{y}^{\text{T}}} \cdot \boldsymbol{u}}}{{\left\| \boldsymbol{y} \right\|\left\| \boldsymbol{u} \right\|}} \geqslant \cos \gamma $ | (5) |
式中:θ为推力方向角,
模型预测控制理论能够很好地处理约束问题,因此本节将模型预测控制算法应用到航天器交会中。首先对式(3) 做离散化处理,设采样时间为T,变换为
| $ \left\{ \begin{gathered} {\boldsymbol{{\tilde x}}_{k + 1}} = \boldsymbol{\tilde A}{{\boldsymbol{\tilde x}}_k} + \boldsymbol{\tilde B}{{\boldsymbol{\tilde u}}_k} \hfill \\ {\boldsymbol{{\tilde y}}_k} = \boldsymbol{C}{{\boldsymbol{\tilde x}}_{k + 1}} \hfill \\ \end{gathered} \right. $ | (6) |
假设预测时域和控制时域均为p,在预测时域内的迭代如下
| $ \begin{gathered} k\;\;\;\;\;\;\;\;{\boldsymbol{{\tilde x}}_k} = {\boldsymbol{{\tilde x}}_k} \hfill \\ k + 1\;\;\;\;{\boldsymbol{{\tilde x}}_{k + 1}} = \boldsymbol{\tilde A}{{\boldsymbol{\tilde x}}_k} + \boldsymbol{\tilde B}{{\boldsymbol{\tilde u}}_k} \hfill \\ k + 2\;\;\;\;{{\boldsymbol{\tilde x}}_{k + 2}} = \boldsymbol{\tilde A}{{\boldsymbol{\tilde x}}_{k + 1}} + \boldsymbol{\tilde B}{\boldsymbol{{\tilde u}}_{k + 1}} = {\boldsymbol{{\tilde A}}^2}{\boldsymbol{{\tilde x}}_k} + \boldsymbol{\tilde A\tilde B{{\tilde u}}_k} + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\boldsymbol{\tilde B}{\boldsymbol{{\tilde u}}_{k + 1}} \hfill \\ k + 3\;\;\;\;{{\boldsymbol{\tilde x}}_{k + 3}} = \boldsymbol{\tilde A}{\boldsymbol{{\tilde x}}_{k + 2}} + \boldsymbol{\tilde B}{\boldsymbol{{\tilde u}}_{k + 2}} = {\boldsymbol{{\tilde A}}^3}{{\boldsymbol{\tilde x}}_k} + {\boldsymbol{{\tilde A}}^2}\boldsymbol{\tilde B}{{\boldsymbol{\tilde u}}_k} + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\boldsymbol{\tilde A\tilde B{{\tilde u}}_{k + 1}} + \boldsymbol{\tilde B}{\boldsymbol{{\tilde u}}_{k + 2}} \hfill \\ \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \hfill \\ k + p\;\;\;{\boldsymbol{{\tilde x}}_{k + p}} = \boldsymbol{\tilde A}{\boldsymbol{{\tilde x}}_{k + p-1}} + \boldsymbol{\tilde B{{\tilde u}}_{k + p-1}} = {\boldsymbol{{\tilde A}}^p}{\boldsymbol{{\tilde x}}_k} + {\boldsymbol{{\tilde A}}^{p-1}}\boldsymbol{\tilde B}{\boldsymbol{{\tilde u}}_k} + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \ldots + \boldsymbol{\tilde A\tilde B{{\tilde u}}_{k + p - 2}} + \boldsymbol{\tilde B{{\tilde u}}_{k + p - 1}} \hfill \\ \end{gathered} $ | (7) |
将式(7) 简化为
| $ {\tilde X_{k + 1}} = \boldsymbol{M}{\boldsymbol{\tilde X}_k} + \boldsymbol{N}{\boldsymbol{\tilde U}_k} $ | (8) |
其中
离散二次型指标函数选为
| $ {\boldsymbol{J}_k} = \sum\limits_{i = 0}^{p-1} {\left( {\boldsymbol{\tilde x}_{k + i}^{\text{T}}\boldsymbol{Q}{\boldsymbol{{\tilde x}}_{k + i}} + \boldsymbol{\tilde u}_{k + i}^{\text{T}}{\boldsymbol{R}_1}{{\boldsymbol{\tilde u}}_{k + i}}} \right) + \boldsymbol{\tilde x}_{k + p}^{\text{T}}} \boldsymbol{S}{\boldsymbol{\tilde x}_{k + p}} $ | (9) |
式中:Q=diag(q,q,q,q),q>0;R1=I2×2,S> 0。
将式(8) 代入式(9) 中,可得
| $ {\boldsymbol{J}_k} = \boldsymbol{\tilde U}_k^{\text{T}}\boldsymbol{H}{\boldsymbol{{\tilde U}}_k} + 2\boldsymbol{\tilde x}_k^{\text{T}}\boldsymbol{G}{{\boldsymbol{\tilde U}}_k} + \boldsymbol{\tilde x}_k^{\text{T}}\boldsymbol{F}{\boldsymbol{{\tilde x}}_k} $ | (10) |
其中
| $ \begin{gathered} \left\{ \begin{gathered} \boldsymbol{H} = \sum\limits_{i = 1}^p {\boldsymbol{N}_i^{\text{T}}} \boldsymbol{Q}{\boldsymbol{N}_i} + \boldsymbol{N}_p^{\text{T}}\boldsymbol{S}{\boldsymbol{N}_p} + \boldsymbol{R} \hfill \\ \boldsymbol{G} = \sum\limits_{i = 1}^p {\boldsymbol{N}_i^{\text{T}}} \boldsymbol{Q}{\boldsymbol{M}_i} + \boldsymbol{N}_p^{\text{T}}\boldsymbol{S}{\boldsymbol{M}_p} \hfill \\ \boldsymbol{F} = \sum\limits_{i = 1}^p {\boldsymbol{M}_i^{\text{T}}} \boldsymbol{Q}{\boldsymbol{M}_i} + \boldsymbol{M}_p^{\text{T}}\boldsymbol{S}{\boldsymbol{M}_p} \hfill \\ \end{gathered} \right. \hfill \\ \boldsymbol{R} = \left[\begin{gathered} {\boldsymbol{R}_1}\;\;0\;\; \ldots \;\;0 \hfill \\ 0\;\;\;{\boldsymbol{R}_1}\; \ldots \;\;0 \hfill \\ \vdots \;\;\;\;\; \vdots \;\;\;\; \vdots \;\;\;\; \vdots \hfill \\ 0\;\;\;0\;\; \ldots \;\;{\boldsymbol{R}_1} \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} $ |
最优化求解过程是确定使得指标函数值最小的最优输入序列:
| $ \boldsymbol{\tilde U}_k^* = \arg \;\mathop {\min }\limits_{{U_k}} \left( {\boldsymbol{\tilde U}_k^{\text{T}}\boldsymbol{H}{{\boldsymbol{\tilde U}}_k} + 2\boldsymbol{\tilde x}_k^{\text{T}}{\boldsymbol{G}^{\text{T}}}{{\boldsymbol{\tilde U}}_k}} \right) $ | (11) |
指标函数关于
| $ \frac{{\partial {\boldsymbol{J}_k}}}{{\partial {{\boldsymbol{\tilde U}}_k}}} = 2\boldsymbol{H}{\boldsymbol{\tilde U}_k} + 2\boldsymbol{G}{\boldsymbol{\tilde x}_k} $ | (12) |
当
| $ {\boldsymbol{\tilde U}}_k^* = - {{\boldsymbol{H}}^{ - 1}}{\boldsymbol{G}}{\widetilde {\boldsymbol{x}}_k} $ | (13) |
预测控制将最优控制序列的第一个元素作用于被控对象,即有
| $ \begin{gathered} {\boldsymbol{{\tilde u}}_k} =- \boldsymbol{\kappa} {\boldsymbol{{\tilde x}}_k} = \hfill \\ \;\;\;\;- \left[{{\boldsymbol{I}_{{n_u}}}\;\;0\;\;\; \cdots \;\;0} \right]{\boldsymbol{H}^{ -1}}\boldsymbol{G}{\boldsymbol{{\tilde x}}_k} = \hfill \\ \;\;\;\; -\lambda {\boldsymbol{H}^{ -1}}\boldsymbol{G}{\boldsymbol{{\tilde x}}_k} \hfill \\ \end{gathered} $ | (14) |
影响系统稳定性的主要因素为局部镇定器K(
1) 0∈XT;
2)
3) K(
4) ψ(0)=0,ψ(
5)
选择局部镇定器
假设局部镇定器为
| $ {\left( {\boldsymbol{\tilde A}-\boldsymbol{\tilde B\kappa} } \right)^{\text{T}}}\boldsymbol{S}\left( {\boldsymbol{\tilde A}-\boldsymbol{\tilde B\kappa} } \right)-\boldsymbol{S} + \boldsymbol{Q} + {\boldsymbol{\kappa} ^{\text{T}}}\boldsymbol{R\kappa} \leqslant 0 $ | (15) |
由于反馈矩阵
| $ \boldsymbol{\kappa} = \left[\begin{gathered} 7.947{\text{ }}1\;\;\;\;\;\;\;-1.661{\text{ }}0\;\;\;\;\;\;6.621{\text{ }}1\;\;\;\;\;\;-0.255{\text{ }}4 \hfill \\ 1.796{\text{ }}6\;\;\;\;\;\;\;\;5.559{\text{ }}8\;\;\;\;\;\;\;\;0.321{\text{ }}7\;\;\;\;\;\;\;6.413{\text{ }}4 \hfill \\ \end{gathered} \right] $ |
| $ \begin{gathered} \boldsymbol{S} = \hfill \\ \left[\begin{gathered} 1{\text{ }}370.43\;\;\;\;\;\;-66.306{\text{ }}6\;\;\;\;\;\;212.215\;\;\;\;\;\;\;\;46.148{\text{ }}8 \hfill \\ -66.306{\text{ }}6\;\;\;\;1{\text{ }}194.28\;\;\;\;\;\;\;\;-41.513{\text{ }}8\;\;\;\;\;137.500 \hfill \\ 212.215\;\;\;\;\;\;\; - 41.513{\text{ }}8\;\;\;\;\;197.534\;\;\;\;\;\;\;\;1.569{\text{ }}55 \hfill \\ 46.148{\text{ }}8\;\;\;\;\;\;137.500\;\;\;\;\;\;\;\;1.5695{\text{ }}5\;\;\;\;\;\;\;\;\;188.909 \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} $ |
对上述给定的仿真条件的合理性进行分析。影响反馈矩阵
在终端约束集XT内,选择局部镇定器
| $ {\boldsymbol{\tilde x}_{k + 1}} = \left( {\boldsymbol{\tilde A}-\boldsymbol{\tilde B\kappa} } \right){\boldsymbol{\tilde x}_k} $ | (16) |
当系统(16) 稳定时,
| T | q | ||||
| 0.1 | 1 | 10 | 50 | 100 | |
| 0.001 | + | + | + | + | + |
| 0.01 | + | + | + | + | + |
| 0.05 | + |  |
 |
 |
 |
| 0.1 |  |
 |
 |
 |
 |
| 0.5 |  |
 |
— | — | — |
注:其中+代表收敛性弱, 代表收敛性中, 代表收敛性中, 代表收敛性强;—代表无解。 代表收敛性强;—代表无解。 |
|||||
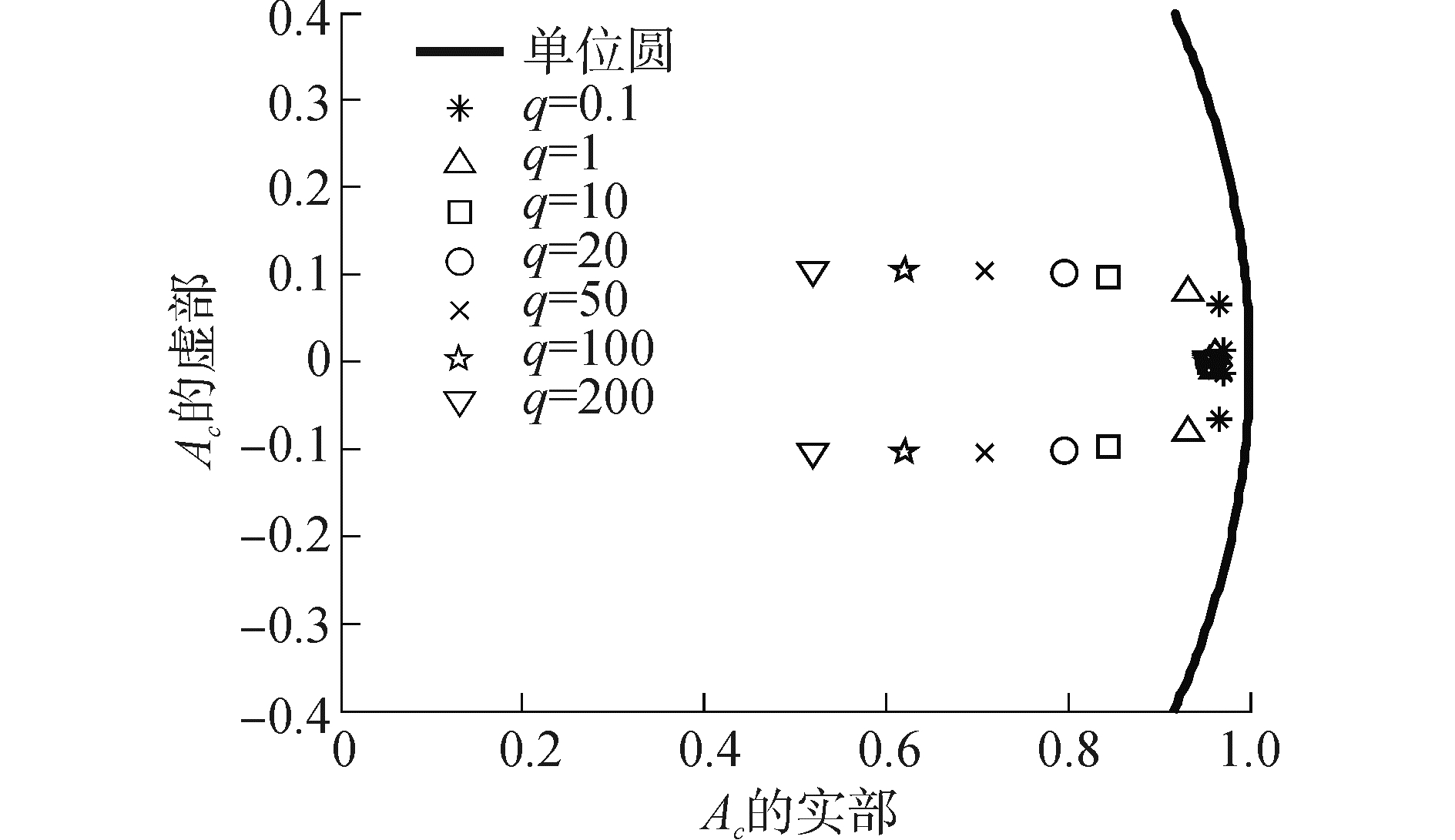
图 2表示了Ac的闭环极点随q的变化情况。从图中可以看出,在T=0.05时,对应q闭环极点均在单位圆内,说明了在该条件下式(16) 是收敛的。随着q的增大,可以看出闭环极值点到原点的距离在变小,即系统的收敛性变强。
|
| 图2 Ac的闭环极点随q的变化 Figure 2 Poles of Ac influenced by q |
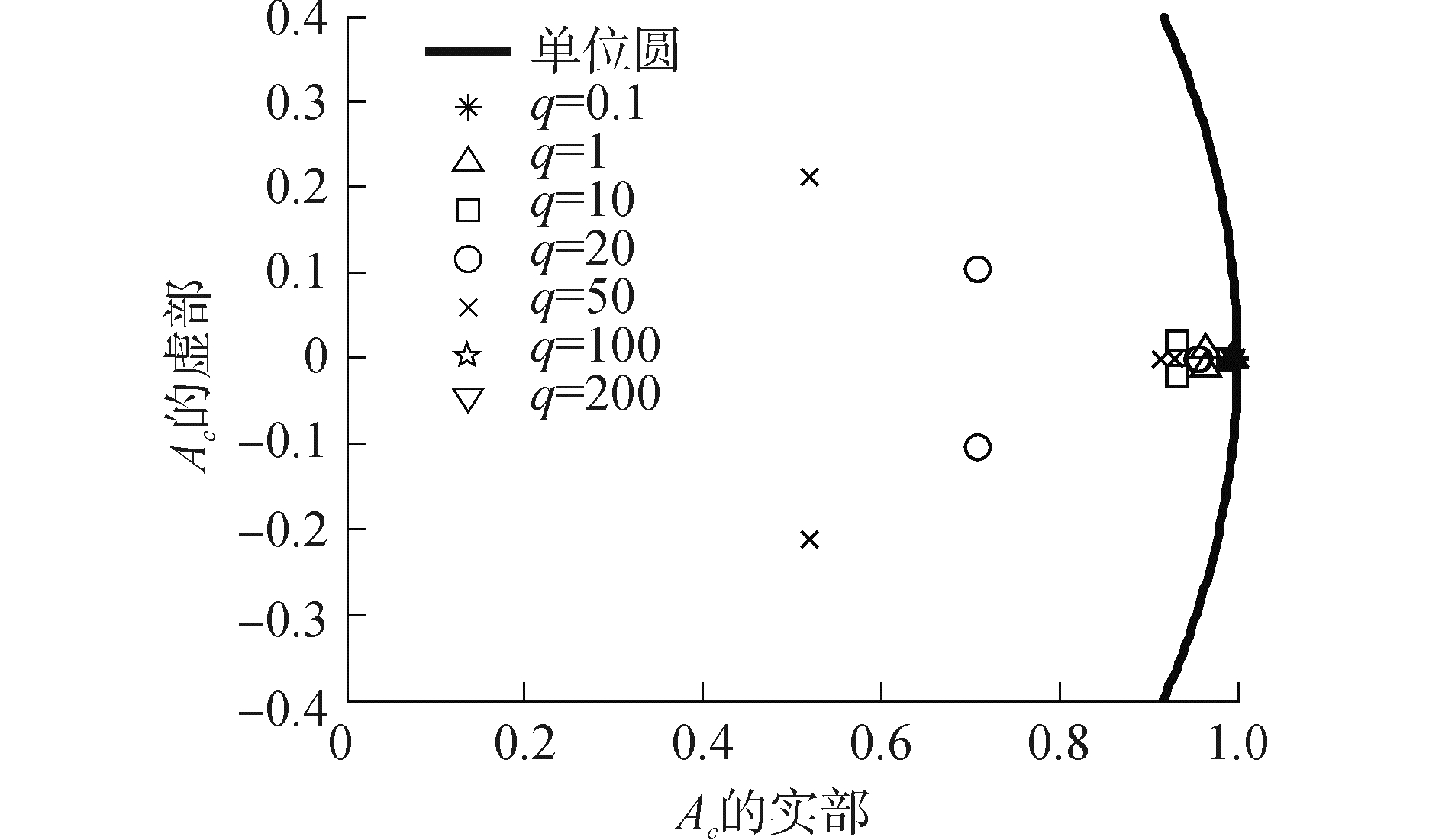
图 3表示了Ac的闭环极点随T的变化情况。从图中可以看出,在q =50时,对应T闭环极点均在单位圆内,说明了在该条件下式(16) 是收敛的。随着T的增大,可以看出闭环极值点到原点的距离在变小,即系统的收敛性变强。
|
| 图3 Ac的闭环极点随T的变化 Figure 3 Poles of Ac influenced by T |
系统终端状态与闭环极点的特征值和特征向量具有一定的关系。通过不同的q和T值得收敛值和理论值之间的关系,见表 2,从表中可以看出,在|θ|∞能够收敛的情况下,理论值和仿真的收敛值基本相等;不收敛情形时,|θ|∞呈现一定的周期性变化,变化范围较大。在q、T较大时,收敛值可以在30°以内。
| q | T | ||||
| 0.05 | 0.1 | ||||
| 数值 | 理论 | 数值 | 理论 | ||
| 0.1 | — | 144 | — | 141 | |
| 1 | — | 129 | — | 124 | |
| 10 | 104 | 96.4 | 65 | 65 | |
| 50 | 23.4 | 23.0 | 21.3 | 21.3 | |
| 100 | — | 21.1 | 14.7 | 14.7 | |
综上所述,在计算局部镇定器的反馈矩阵
下面求解系统的终端约束集。如果系统状态变量满足
| $ E\left( \boldsymbol{P} \right) = \left\{ {\boldsymbol{\tilde x} \in {{\boldsymbol{\text{R}}}^n}:{{\boldsymbol{\tilde x}}^{\text{T}}}\boldsymbol{P}\boldsymbol{\tilde x} \leqslant 1} \right\} $ | (17) |
且存在线性反馈控制律
| $ {\left( {\boldsymbol{\tilde A}-\boldsymbol{\tilde B\kappa} } \right)^{\text{T}}}\boldsymbol{P}\left( {\boldsymbol{\tilde A}-\boldsymbol{\tilde B\kappa} } \right) \leqslant \boldsymbol{P} $ | (18) |
令W=P-1,上式根据Schur补定理,变为
| $ \left[\begin{gathered} \;\;\;\;\;\boldsymbol{W}\;\;\;\;\;\;\;\;\;\;\;\boldsymbol{W}{\left( {\boldsymbol{\tilde A}-\boldsymbol{\tilde B\kappa} } \right)^{\text{T}}} \hfill \\ \left( {\boldsymbol{\tilde A}-\boldsymbol{\tilde B\kappa} } \right)\boldsymbol{W}\;\;\;\;\;\;\;\;\boldsymbol{W} \hfill \\ \end{gathered} \right] \geqslant 0 $ | (19) |
那么E(P)为系统关于
终端约束集除了满足式(18) 外,还应该满足推力约束,在这里只考虑幅值约束,即有
| $ \left\| {\boldsymbol{\kappa} {{\boldsymbol{\tilde x}}_k}} \right\| \leqslant 1 $ | (20) |
由于
| $ \left[\begin{gathered} \;\boldsymbol{I}\;\;\;\;\;\;\boldsymbol{\kappa W}{\boldsymbol{\kappa} ^{\text{T}}} \hfill \\ \boldsymbol{\kappa W}{\boldsymbol{\kappa} ^{\text{T}}}\;\;\;\boldsymbol{I} \hfill \\ \end{gathered} \right] \geqslant 0 $ | (21) |
通过求解下面的MAXDET问题:
| $ \left\{ \begin{gathered} \mathop {\min }\limits_W-\log \left( {{\text{det}}W} \right) \hfill \\ {\text{subject}}\;{\text{to}}\left( {19} \right)\left( {21} \right) \hfill \\ \end{gathered} \right. $ | (22) |
可得到终端约束集的P的形式,结果如下
| $ \boldsymbol{P} = \left[\begin{gathered} 69.043{\text{ }}9\;\;\;-4.497{\text{ }}8\;\;\;\;57.094{\text{ }}1\;\;\;\;6.652{\text{ }}0 \hfill \\ -4.497{\text{ }}8\;\;\;46.598{\text{ }}4\;\;\;-5.211{\text{ }}3\;\;\;\;46.168{\text{ }}9 \hfill \\ 57.094{\text{ }}1\;\;\; - 5.211{\text{ }}3\;\;\;52.468{\text{ }}2\;\;\;\;\;0.373{\text{ }}6 \hfill \\ 6.652{\text{ }}0\;\;\;\;46.168{\text{ }}9\;\;\;\;0.373{\text{ }}6\;\;\;\;\;\;50.401{\text{ }}7 \hfill \\ \end{gathered} \right] $ |
根据上述所述,在线优化的算法即在每个采样时刻的预测时域内求解如下最优化问题:
| $ \left\{ \begin{gathered} \mathop {\min }\limits_{{u_k}} {\boldsymbol{J}_k} = \boldsymbol{\tilde U}_k^{\text{T}}\boldsymbol{H}{{\boldsymbol{\tilde U}}_k} + 2\boldsymbol{\tilde x}_k^{\text{T}}\boldsymbol{G\tilde U}_k + \boldsymbol{\tilde x}_k^{\text{T}}\boldsymbol{F}{\boldsymbol{{\tilde x}}_k} \hfill \\ {\text{s}}{\text{.t}}. \hfill \\ {\left\| {{{\boldsymbol{\tilde u}}_k}} \right\|_2} \leqslant 1, \frac{{-{\boldsymbol{{\tilde y}}_k}^{\text{T}} \cdot {\boldsymbol{{\tilde u}}_k}}}{{\left\| {{{\boldsymbol{\tilde y}}_k}} \right\|\;\left\| {{\boldsymbol{{\tilde u}}_k}} \right\|}} \geqslant \cos \;\gamma \hfill \\ {{\boldsymbol{\tilde x}}_{k + p}} \in E\left( \boldsymbol{P} \right) \hfill \\ \end{gathered} \right. $ | (23) |
在上述优化问题中,存在一个非线性约束
| $ \boldsymbol{\hat B} = \left[{{\boldsymbol{{\tilde A}}^{p-1}}\boldsymbol{\tilde B}\;\;\;{\boldsymbol{{\tilde A}}^{p-2}}\boldsymbol{\tilde B}\;\; \cdots \;\;\;\boldsymbol{\tilde B}} \right] $ | (24) |
那么
| $ {\boldsymbol{\tilde x}_{k + p}} = {\boldsymbol{\tilde A}^p}{\tilde x_k} + \boldsymbol{\hat B}{\boldsymbol{\tilde U}_k} $ | (25) |
则
| $ {\left\| {{\boldsymbol{P}^{1/2}}\left( {{\boldsymbol{{\tilde A}}^p}{\boldsymbol{{\tilde x}}_k} + \boldsymbol{\hat B}{\boldsymbol{{\tilde U}}_k}} \right)} \right\|_2} \leqslant 1 $ | (26) |
将Jk进行变换,得到如下形式
| $ \begin{gathered} {J_k} = \boldsymbol{\tilde U}_k^{\text{T}}\boldsymbol{H}{\boldsymbol{{\tilde U}}_k} + 2\tilde x_k^{\text{T}}\boldsymbol{G}{\boldsymbol{{\tilde U}}_k} + \boldsymbol{\tilde x}_k^{\text{T}}\boldsymbol{F}{{\boldsymbol{\tilde x}}_k} \hfill \\ = {({\boldsymbol{H}^{\frac{1}{2}}}{{\boldsymbol{\tilde U}}_k} + {\boldsymbol{H}^{-\frac{1}{2}}}{\boldsymbol{G}^T}{{\boldsymbol{\tilde x}}_k})^{\text{T}}}({\boldsymbol{H}^{\frac{1}{2}}}{{\boldsymbol{\tilde U}}_k} + {\text{ }}{\boldsymbol{H}^{-\frac{1}{2}}}{\boldsymbol{G}^{\text{T}}}{{\boldsymbol{\tilde x}}_k}) + \hfill \\ {\boldsymbol{{\tilde x}}^{\text{T}}}_k\boldsymbol{F}{\boldsymbol{{\tilde x}}_k}-{\boldsymbol{{\tilde x}}^{\text{T}}}_k\boldsymbol{G}{\boldsymbol{H}^{ - 1}}\boldsymbol{G}{\boldsymbol{{\tilde x}}_k} \hfill \\ \end{gathered} $ | (27) |
上式等式右边的后两项与优化变量
| $ {\left\| {{\boldsymbol{H}^{1/2}}{{\boldsymbol{\tilde U}}_k} + {\boldsymbol{H}^{-1/2}}{\boldsymbol{G}^{\text{T}}}{{\boldsymbol{\tilde x}}_k}} \right\|_2} \leqslant \xi $ | (28) |
式中:ξ为新引进的优化指标,这样优化问题(23) 转化为二阶锥规划形式:
| $ \left\{ \begin{gathered} \mathop {\min }\limits_{{u_k}} \xi \hfill \\ {\text{s}}{\text{.t}}. \hfill \\ {\left\| {{{{\boldsymbol{\tilde u}}}_k}} \right\|_2} \leqslant 1,\frac{{ - {{{\boldsymbol{\tilde y}}}_k}^{\text{T}} \cdot {{{\boldsymbol{\tilde u}}}_k}}}{{\left\| {{{{\boldsymbol{\tilde y}}}_k}} \right\|\;\left\| {{{{\boldsymbol{\tilde u}}}_k}} \right\|}} \geqslant \cos \;\gamma \hfill \\ {\left\| {{{\boldsymbol{H}}^{1/2}}{{{\boldsymbol{\tilde U}}}_k} + {{\boldsymbol{H}}^{ - 1/2}}{{\boldsymbol{G}}^{\text{T}}}{{{\boldsymbol{\tilde x}}}_k}} \right\|_2} \leqslant \xi \hfill \\ {\left\| {{{\boldsymbol{P}}^{1/2}}{{\boldsymbol{A}}^p}{{{\boldsymbol{\tilde x}}}_k} + {\boldsymbol{\hat{B}}}{{{\boldsymbol{\tilde U}}}_k}} \right\|_2} \leqslant 1 \hfill \\ \end{gathered} \right. $ | (29) |
综上所述,上述系统是一个混杂系统,受控对象是连续模型,控制算法需要在线滚动优化,因而是离散的。图 4表示了混杂系统的控制框图。
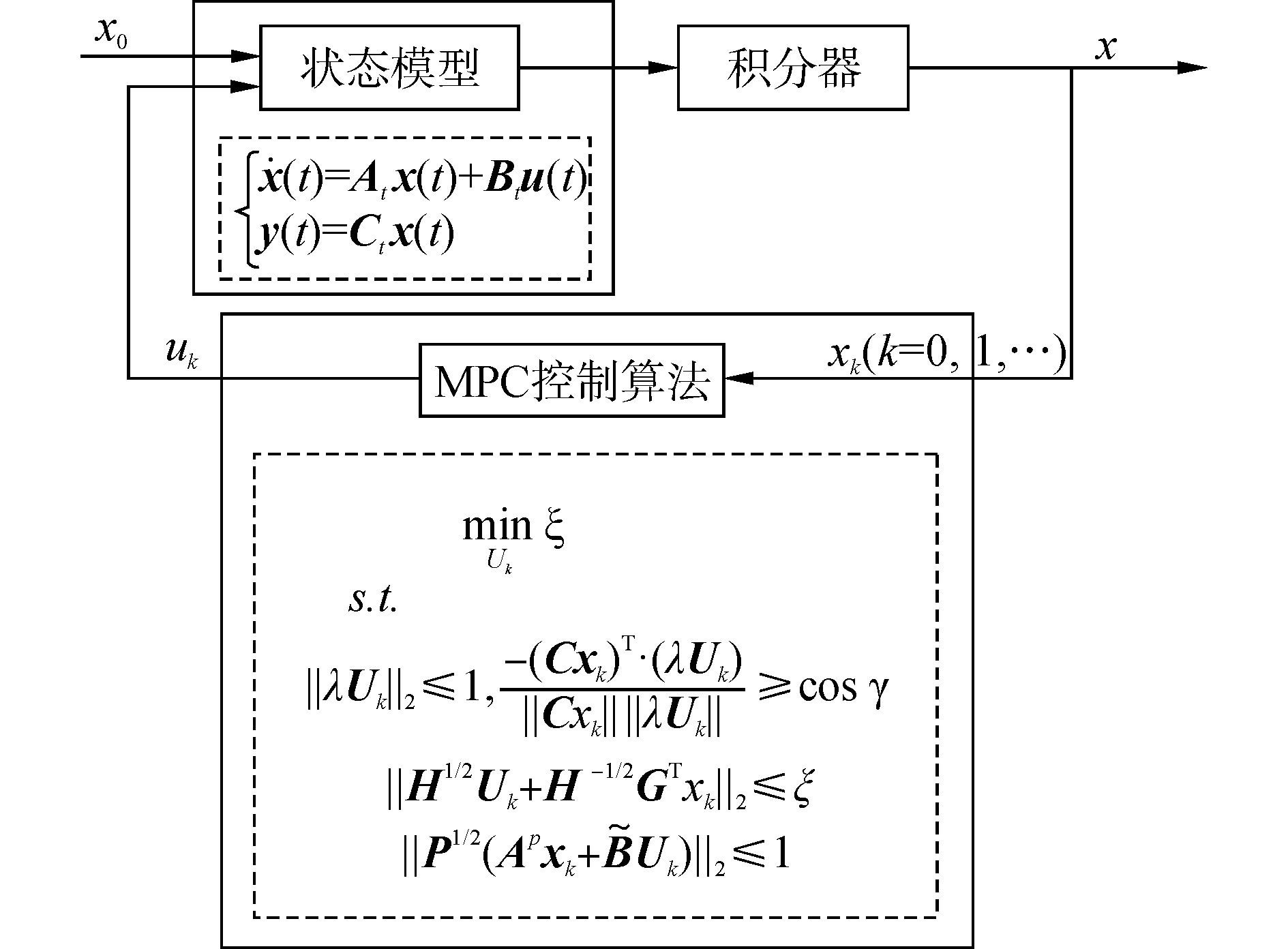
|
| 图4 混杂系统的控制框图 Figure 4 Control block diagram of mixed system |
为验证本文提出的算法,建立以下仿真条件:设r0 =10 km,θ0 =0°,那么初始位置和速度满足[x0y0vx0vy0]T=r0[cos φ0-2sin φ0-sin φ0-2cos φ0]T。下面以初始相位角取φ0 =150°时来进行仿真。地球引力常数μ =3.986×1014 m3s-2,地球半径Re=6 378.136 km,目标航天器轨道高度h =500 km,最大约束加速度αmax=0.02 m/s2,模型预测控制下的推力约束角γ =60°,预测时域p=50,T=0.05,q=50,状态模型的递推步长为ΔT=0.005。仿真结束条件设为追踪航天器与目标航天器距离r≤1 m和v≤5.5×10-4 m/s。仿真结果见图 5~7。
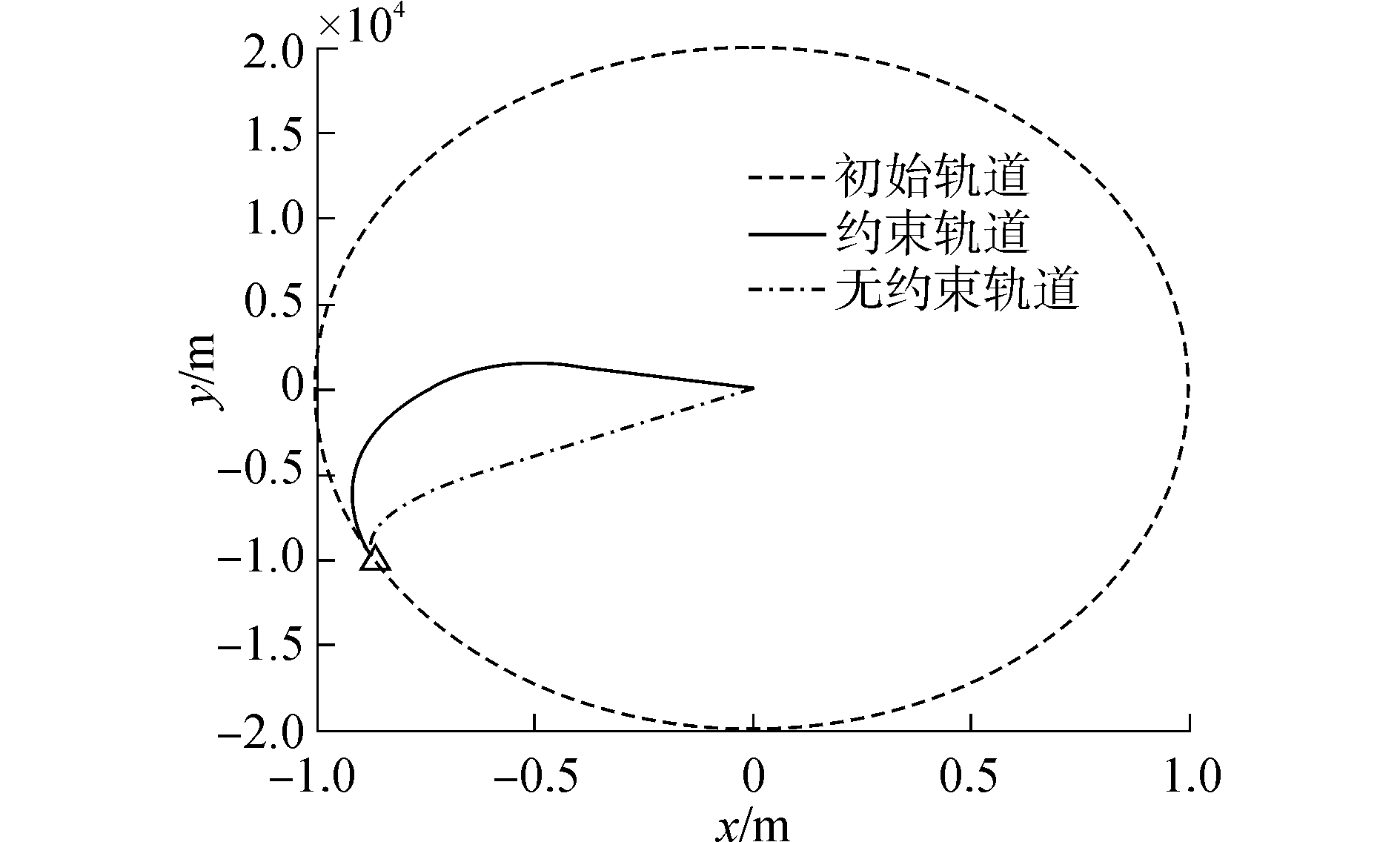
|
| 图5 轨道曲线 Figure 5 Rendezvous orbit trajectory |
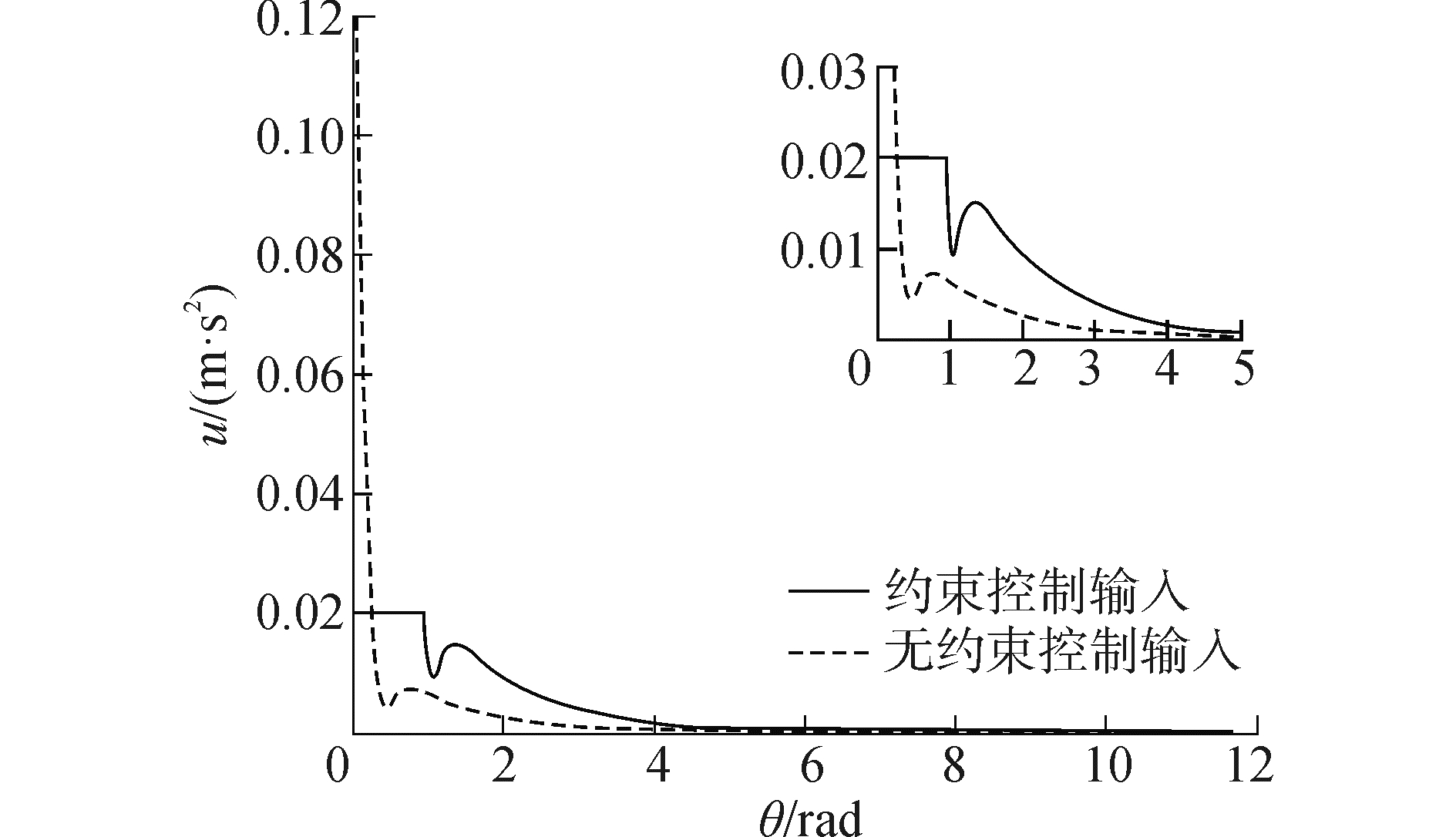
|
| 图6 控制输入曲线 Figure 6 Rendezvous control input |
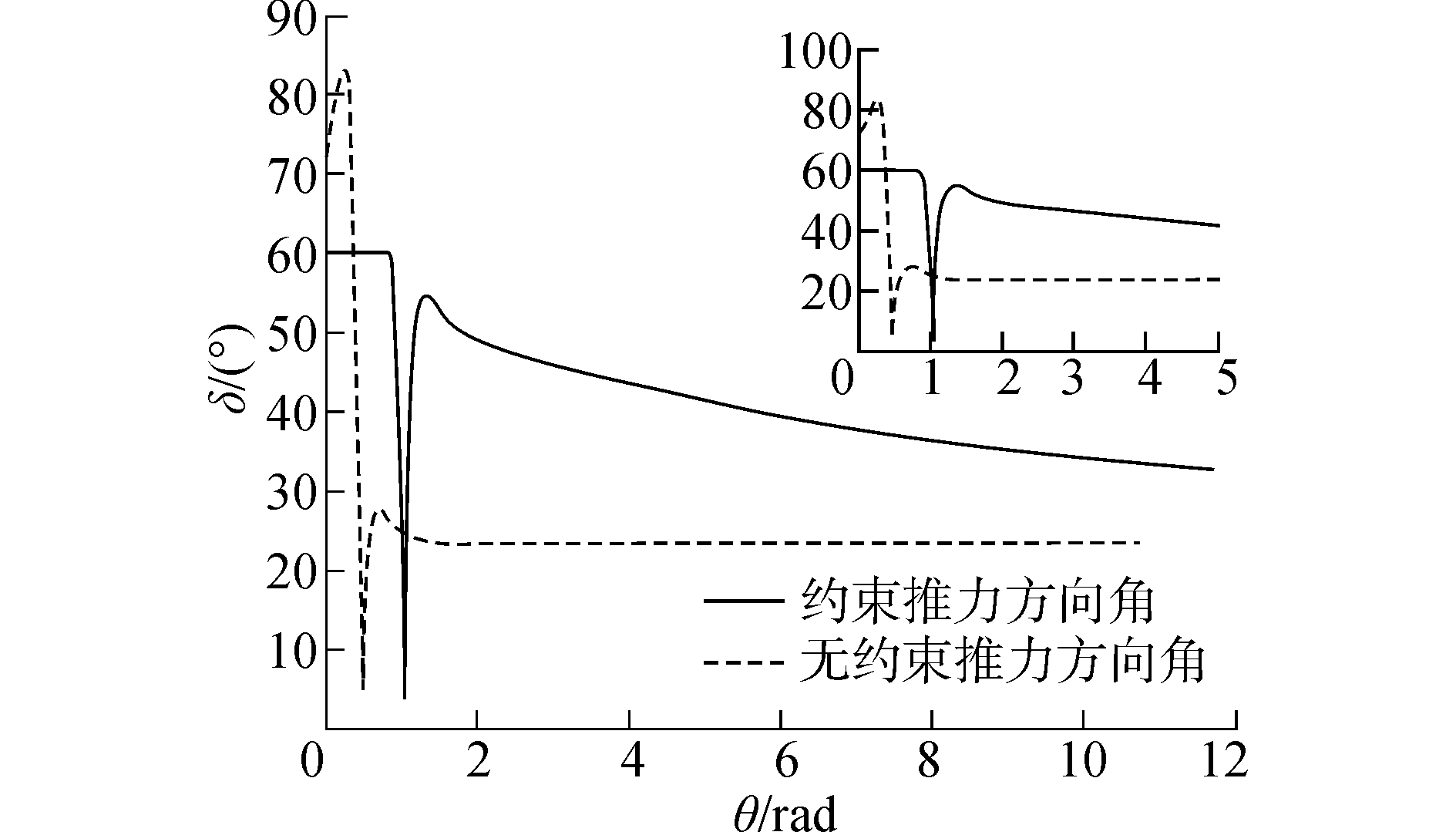
|
| 图7 推力方向角曲线 Figure 7 Rendezvous thrust direction |
从图 5看出,从给定的初始点位置,轨道曲线收敛到原点,即追踪航天器能够实现与目标航天器的交会。但无约束时,轨道曲线相对平直,目标航天器到达结束条件所需要的时间较短。在考虑约束情况时,由于对推力幅值和方向的限制,目标航天器需要在可行域内运动,这样产生的轨道曲线相对弯曲,而且目标航天器到达结束条件时花费的时间更长。从图 6和图 7看出,在不考虑约束时,控制输入和推力方向角在一定时间内会比较大;有约束时控制输入和推力方向角能被限制在约束条件内。
4 结论1) 模型预测控制算法能够很好地控制追踪航天器实现与目标航天器之间的交会;
2) 从仿真结果来看,设计的制导策略能够满足系统约束的要求;
3) 相对于无约束情形,有约束交会需要花费更长的时间,轨道曲线更弯曲。
本文提出的算法基于目标星为圆轨道的情况并忽略了扰动,具有一定的局限性,因此实际应用受到一定限制,后续需要研究更复杂的情形。本文的策略将推力幅值约束和推力方向约束均考虑到交会过程中,具有一定的新颖性,为后续研究提供一定的借鉴意义。
| [1] |
李亮, 和兴锁, 张娟, 等. 考虑地球扁率影响的任意椭圆轨道小推力最优交会控制[J].
西北工业大学学报, 2005, 3(23): 401–405.
LI Liang, HE Xingsuo, ZHANG Juan, et al. Optimum low-thrust power rendezvous between neighboring elliptic orbits considering the oblateness of earth[J]. Journal of North Western Polytechnical University, 2005, 3(23): 401–405. |
| [2] |
任远, 崔平远, 栾恩杰. 基于退火遗传算法的小推力轨道优化问题研究[J].
宇航学报, 2007, 1(28): 162–166.
REN Yuan, CUI Pingyuan, LUAN Enjie. Low-thrust trajectory optimization based on annealing-genetic algorithm[J]. Journal of astronautics, 2007, 1(28): 162–166. |
| [3] |
张亚锋, 和兴锁. 椭圆轨道小推力最短时间交会研究[G]//第九届全国振动理论及应用学术会议论文摘要集. 杭州, 2007: 222-228.
ZHANG Yafeng, HE Xingsuo.Optimum low-trust rendezvous between elliptical orbits with the general orbital elements[G]//The Proceedings of the Ninth National Symposium on Vibration Theory and Application. Hangzhou, 2007:222-228. |
| [4] |
陈伟跃, 荆武兴, 程博. 小推力速度闭环交会制导律设计[J].
宇航学报, 2009, 3(30): 1031–1038.
CHEN Weiyue, JING Wuxing, CHENG Bo. Fast closed-loop guidance law with finite thrust amplitude jets for rendezvous[J]. Journal of astronautics, 2009, 3(30): 1031–1038. |
| [5] |
祝开艳, 龚胜平. 利用小推力实现与多颗小行星交会[J].
信息技术, 2010, 11: 1–4.
ZHU Kaiyan, GONG Shengping. Rendezvous with multiple asteroids using low-thrust[J]. Information technology, 2010, 11: 1–4. DOI:10.3969/j.issn.1674-7461.2010.01.001 |
| [6] |
张万里, 王常虹, 夏宏伟, 等. 连续小推力航天器轨道交会问题的制导律设计[J].
哈尔滨工业大学学报, 2012, 1(44): 36–42.
ZHANG Wanli, WANG Changhong, XIA Hongwei. Guidance law of spacecraft for continuous low-thrusts orbital rendezvous problem[J]. Journal of Harbin Institute of Technology, 2012, 1(44): 36–42. |
| [7] |
高会军, 杨学博, 王常虹. 一种有限推力航天器交会轨道的鲁棒设计方法[J].
空间控制技术与应用, 2009, 2(35): 3–36.
GAO Huijun, YANG Xuebo, WANG Changhong. A robust orbit design method for thrust-limited spacecraft rendezvous[J]. Aerospace contrd and application, 2009, 2(35): 3–36. |
| [8] | YAMAKAWA H, FUNAKI I. Radially accelerated periodic orbits in the clohessy-wilthire frame[J]. Journal of astronautical sciences, 2008, 1(56): 1–16. |
| [9] | PAUL J E, BRUCE A C. Optimal finite-thrust spacecraft trajectories using collocation and nonlinear programming[J]. Journal of guidance, control, and dynamics, 1991, 5(14): 981–985. |
| [10] | PARDIS J C, CARTER E T. Optimal power-limited rendezvous with thrust saturation[J]. Journal of guidance, control, and dynamics, 1995, 5(18): 1145–1150. |
| [11] | CARTER E T, PARDIS J C. Optimal power-limited rendezvous with upper and lower bounds on thrust[J]. Journal of guidance, control, and dynamics, 1995, 5(18): 1145–1150. |
| [12] | MASSARI M, ZAZZERA B F. Optimization of low-thrust reconfiguration maneuvers for spacecraft flying in formation[J]. Journal of guidance, control, and dynamics, 2009, 5(32): 1629–1637. |
| [13] | LANTOINE G, EPENOY R. Quadratically constrained linear-quadratic regulator approach for finite-thrust orbital rendezvous[J]. Journal of guidance, control, and dynamics, 2012, 6(35): 1787–1797. |
| [14] |
潘刚, 任萱. 空间交会对接中太阳光照窗口的研究[J].
飞行力学, 2002, 20(2): 62–66.
PAN Gang, REN Xuan. Study on sun illumination window during a space interconnection[J]. Flight dynamics, 2002, 20(2): 62–66. |
| [15] | SUKHANOV A A, PRADO A F B, DE A. Optimization of transfers under constraints on the thrust direction: Ⅰ[J]. Cosmic research, 2007, 5(45): 417–423. |
| [16] | SUKHANOV A A, PRADO A F B, DE A. Optimization of transfers under constraints on the thrust direction: Ⅱ[J]. Cosmic Research, 2008, 1(46): 49–59. |
| [17] | BERTRAND R, EPENOY R. New Smoothing techniques for solving bang-bang optimal control problems-numerical results and statistical interpretation[J]. Optimal control applications and methods, 2002, 4(23): 171–197. |
| [18] | MITANI S, YAMAKAWA H. Continuous-thrust with control magnitude and direction constraints using smoothing techniques[J]. Journal of guidance, control, and dynamics, 2013, 1(36): 163–174. |
| [19] | WILLARD C, RANDAL W B. Satisficing: a new approach to constructive nonlinear control[J]. IEEE transactions on automatic control, 2004, 7(49): 1090–1102. |
| [20] | MITANI S, YAMAKAWA H. Novel nonlinear rendezvous guidance scheme under constraints on thrust direction[J]. Journal of guidance, control, and dynamics, 2011, 6(34): 1656–1669. |
| [21] | MITANI S, YAMAKAWA H. Satisficing nonlinear rendezvous approach under control magnitude and direction constraints[J]. Journal of guidance, control, and dynamics, 2014, 2(37): 497–512. |
| [22] |
张秀玲, 陈丽杰, 逄宗朋, 等. RBF神经网络的板形预测控制[J].
智能系统学报, 2010, 5(1): 70–73.
ZHANG Xiuling, CHEN Lijie, PANG Zongpeng, et al. Apredictive system for process control of flatnessinrollingmills usingaradialbasis function net work[J]. CAAI transactionson intelligent systems, 2010, 5(1): 70–73. |
| [23] | STAREK J A, KOLMANOVSKY I V. Nonlinear model predictive control strategy for low thrust spacecraft missions[J]. Optimal control applications and methods, 2014, 35(1): 1–20. DOI:10.1002/oca.v35.1 |
| [24] | DI C S, PARK H, KOLMANOVSKY I. Model predictive control approach for guidance of spacecraft rendezvous and proximity maneuvering[J]. International journal of robust and nonlinear control, 2012, 22(12): 1398–1427. DOI:10.1002/rnc.2827 |
| [25] | SHEARER C, HEISE S. Constrained model predictive control of a nonlinear aerospace system[G]//Guidance, Navigation, and Control Conference and Exhibit, 1998: 4235. |
| [26] |
朱彦伟, 杨乐平. 航天器近距离相对运动的鲁棒约束预测模型控制[J].
控制理论与应用, 2009, 26(11): 1273–1281.
ZHU Yanwei, YANG Leping. Spacecraft proximity relative motion under robust constrained model predictive control[J]. Control theory & applications, 2009, 26(11): 1273–1281. |
| [27] | SINGH L, BORTOLAMI S, PAGE L. Optimal guidance and thruster control in orbital approach and rendezvous for docking using model predictive control[G]//AIAA Guidance, Navigation, and Control Conference, 2010: 7754. |
| [28] |
赵钧.
航天器轨道动力学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2011: 20-36.
ZHAO Jun. Spacecraft orbital dynamics[M]. Harbin: Harbin institute of techndogy press, 2011: 20-36. |
| [29] |
郑大钟.
线性系统理论[M]. 第2版. 北京: 清华大学出版社, 2008: 76-89.
ZHENG Dazhong. Linear system thery[M]. Second Edition. Beijing: Tsinghua University Press, 2008: 76-89. |



