2. School of Civil Engineering, Tianjin University, Tianjin 300072, China
随着经济和社会的持续快速发展,中国已成为全球最大的能源消费国。我国陆地及近海油气资源开发增长已较困难,石油开采从陆地走向海洋,从浅海走向深海已经成为必然趋势。
作为海洋油气开发系统的组成部分之一,水下油气输送系统包括深海管道、立管、管汇中心、管道终端等,长期承受极端载荷作用,包括来自系统外部的环境载荷,如高水压、内波、海流及海水腐蚀的联合作用,与来自系统内部的油气输送载荷,如高油温、高油压及油气腐蚀的作用,极易发生结构失效,甚至引发泄漏事故,造成巨额的经济损失和灾难性的环境污染[1]。
为了保障流动,避免原油中的石蜡在管壁上沉积及水合物的形成,必须提高原油输送温度和输送压力,而高温和高压产生的轴向压力是导致管道整体屈曲[2]的最主要原因。
目前的研究多针对于原油温度场,Jian Su[3-6]对某多层管道在流动开启和关闭过程中的瞬时热传导进行了分析,给出了开启和关闭过程中流体沿程温度变化曲线,M. Carr[7]和H. Rong[8]在相关研究中直接给出了管道在流动开启和关闭过程中沿程温度时变曲线;盛磊祥[9]、张园园[10]和孙伟栋[11]等对管道停输后原油径向温降进行了研究,忽略了停输过程中管道轴向温度梯度,将三维不稳定传热问题简化为横截面上的二维不稳定传热问题。此外,国内的研究主要针对埋地管道[10-11],而对于深海管道来说,埋置或者挖槽并不经济,也不现实,故多是直接铺设于海床之上,其边界条件不同于埋地管道。
综上,目前缺乏对管道温度场的研究,因此对管道温度效应的研究也是考虑恒温作用,而实际上在原油输送过程中,原油不断向周围介质散热,原油沿程温度会有所降低,由于原油与管道之间的对流换热,管道的沿程温度也随之降低。因此,有必要对裸铺管道在稳态流动时的非均匀温度场进行研究。
本文利用GAMBIT建立了单层管道几何模型并划分网格,利用FLUENT软件对管道在稳态流动时的非均匀温度场进行了数值模拟,对网格独立性进行了分析,得到了管道沿程温度曲线,并对FLUENT模型进行了验证,最后进行了管道温度场参数化分析。
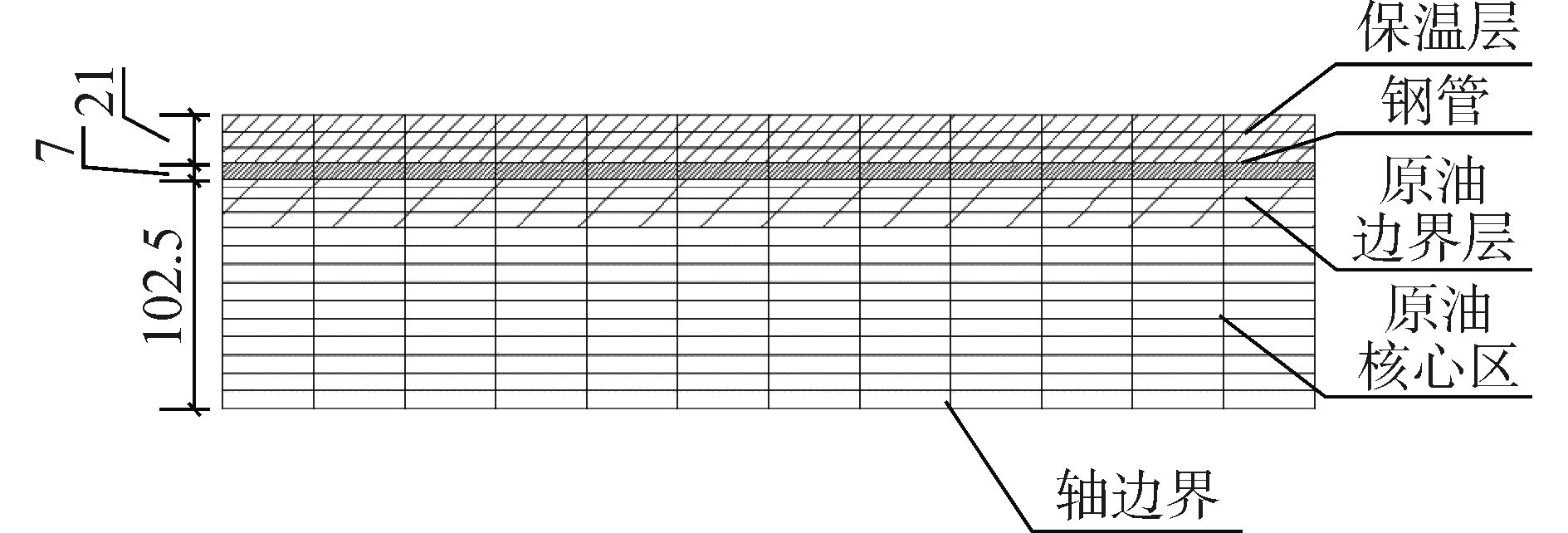
1 单层管道模型建立参考某单层管道工程,管道尺寸取为219 mm×7 mm,长度取1 000 m,保温层厚度20 mm,原油入口流速0.5 m/s,入口温度80℃。深海水温保持在4℃。由于管道直接铺设于海床之上,与海床接触面积相比与海水接触面积很小,为简化计算并节约计算成本,假设与管道接触的海床温度与周围海水温度相同,因此可根据对称性,利用轴边界条件将实际三维模型简化为二维模型,仅取旋转面计算。采用GAMBIT建立几何模型并划分网格,管道中间任意一段的GAMBIT模型如图 1所示,模型中包括原油、管道和保温层三部分,其物性参数选取见表 1。鉴于管道和原油之间存在热交换,为了获得管道准确的温度场,需要划分边界层网格。
|
| 图1 管道GAMBIT 模型 Figure 1 The GAMBIT model of the pipeline |
| 材料 | 密度/(kg·m-3) | 比热容/(J·(K·kg)-1) | 导热系数/(W·(m·K)-1) | 动力粘度系数/(kg·(m·s)-1) |
| 原油 | 855 | 2 100 | 0.14 | 0.04 |
| 钢管 | 7 850 | 500 | 48 | — |
| 保温层 | 60 | 700 | 0.04 | — |
本模型共选用四种不同的边界条件,其中水平对称轴选用轴边界条件,原油进口选用速度进口边界条件,原油出口选用出流边界条件,其余边界条件均为壁面边界条件。由于钢管内壁(钢管与原油的接触面)和外壁(钢管与保温层的接触面)属于双侧壁面(壁面两侧均为计算域),可将其设为耦合壁面,而无需定义其他热力学参数,求解器可以直接利用邻近网格的流场变量计算壁面上的热交换,本文即是将钢管内壁和外壁均设置成了耦合壁面。
考虑到深海管道直接裸铺在海床上,深海水温保持在4℃,而管道最外层与海水之间的换热系数较大,使得两者的温度基本相等,因此,将管道保温层的外壁定义为温度边界条件。
2 单层管道网格独立性分析 2.1 网格划分原油和钢管之间发生对流换热,在钢管和保温层中仅存在热传导,经计算发现,钢管和保温层的网格划分方式对管道温度场无影响,故本节仅讨论原油的不同网格划分方式对管道温度场的影响。
网格质量对计算精度和稳定性有很大的影响,好的网格质量能够提高收敛性和计算精度,减少计算时间。考虑到几何模型简单且规则,而且将网格布置得与流动方向正交,可以最小化数值扩散的影响,故使用结构化网格—四边形网格。
一般情况下,在流动核心区(远离壁面的区域)网格纵横比不超过5∶1,对于边界层内的四边形网格,纵横比不超过10∶1。
综合考虑计算精度与计算成本,钢管和保温层的径向网格数分别取1和3,轴向网格尺寸分别取25 mm和40 mm。对于边界层网格,需要定义首层网格高度、增长系数以及边界层层数,不同网格划分方式如表 2所示。
| 网格划分方式 | 轴向网格尺寸 | 首层网格高度 | 增长系数 | 边界层层数 | 核心区径向网格数 | 网格数量 |
| 1 | 25 | 2.5 | 1.2 | 6 | 11 | 840 000 |
| 2 | 25 | 3 | 1.2 | 5 | 12 | 840 000 |
| 3 | 25 | 4 | 1.1 | 5 | 12 | 840 000 |
| 4 | 25 | 4 | 1.2 | 4 | 10 | 720 000 |
| 5 | 40 | 4 | 1.1 | 5 | 12 | 525 000 |
| 6 | 40 | 4 | 1.2 | 4 | 10 | 450 000 |
| $\mathsf{Re}=\frac{ud}{v}=\frac{ud}{\mu /\rho }=\frac{0.5\times 0.205}{0.04/855}=2\ 191<2\ 200$ |
故计算模型选用粘性模型中的层流模型。由于需要求解温度,故激活能量方程。
考虑到流动的不可压缩性,故采用基于压力的求解器,压力—速度耦合算法选用SIMPLE,压力插值格式选用Standard,进行稳态求解。
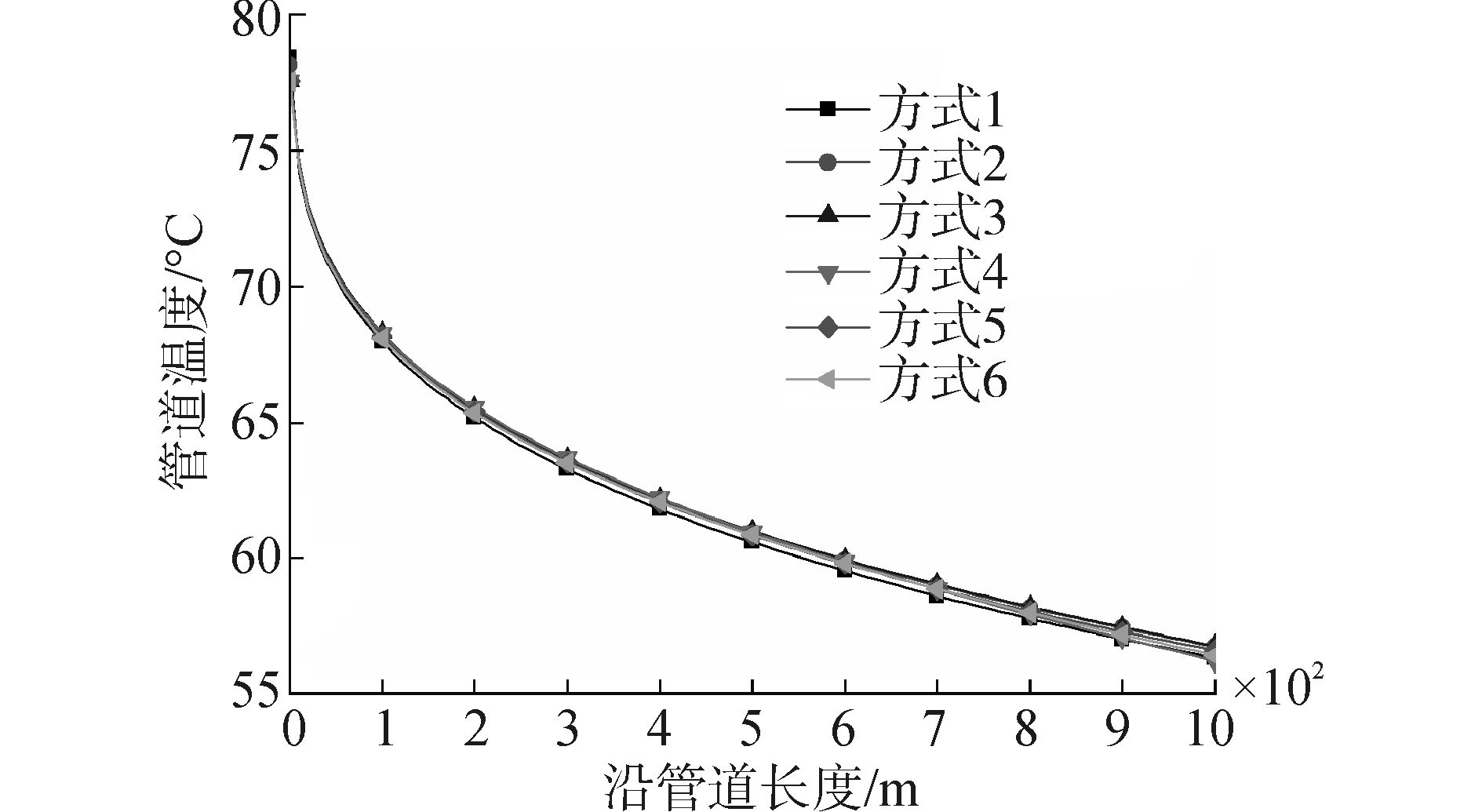
2.3 计算结果采用FLUENT对管道的非均匀温度场进行了数值模拟,提取管道各网格节点温度数据,绘制管道沿程温度曲线,六种不同网格计算模型的管道沿程温度计算结果如图 2所示。
|
| 图2 不同网格划分方式的计算结果 Figure 2 The calculation results of different mesh genera⁃tion methods |
从图 2中可以看出,不同网格划分方式,管道沿程温度的变化趋势基本一致,管道各处的温度梯度不同,管道入口附近,温度梯度较大,温降较快,曲线较陡,随着流动进行,温度梯度减小,温降变慢,温度曲线变缓。
分别计算了各网格划分方式计算结果相比网格划分方式6的误差,最大相对误差如表 3所示。
| 网格划分方式 | 1 | 2 | 3 | 4 | 5 | 6 |
| 最大相对误差/% | 1.13 | 0.76 | 0.63 | 0.43 | 0.33 | 0.00 |
从表 3可以看出,最大相对误差仅1.13%,说明各网格划分方式对计算结果的影响较小,综合考虑计算成本与精度,故选择网格划分方式6。
3 模型验证本节通过对比理论公式计算与FLUENT数值模拟得到的原油沿程温度,来验证FLUENT模型的正确性,并对比了原油沿程温度与管道沿程温度,其中FLUENT数值模拟的原油沿程温度取截面平均温度。
3.1 原油与管道之间的换热系数不考虑原油粘度随温度的变化,管内层流换热Sieder-Tate准则关系式为[12]
| $Nu=1.86{{(Re\cdot Pr\frac{d}{l})}^{^{1/3}}}$ | (1) |
式中:Nu为努塞尔数;Re为雷诺数;Pr为普朗特数;d为管道内径,m;l为管道长度,m;
经计算,可知:
| $\begin{align} & \ \ \ \mathit{Re}=\frac{ud}{v}=\frac{ud}{\mu /\rho }=\frac{0.5\times 0.205}{0.04/855}=2\ 191<2\ 200 \\ & Pr=\frac{v}{a}=\frac{v}{\lambda /(\rho c)}=\frac{uc}{\lambda }=\frac{0.04\times 2\ 100}{0.14}=600>0.6 \\ & \ \ \ \mathit{Re}\cdot Pr\frac{d}{l}=2\ 191\times 600\times \frac{0.205}{1\ 000}=269.5>10 \\ \end{align}$ |
故满足该准则关系式的使用范围。
将计算结果代入,有
| $h=1.86{{(\mathsf{Re}\cdot Pr\frac{d}{l})}^{^{1/3}}}(\frac{\lambda }{d})=8.2\text{W/}{{\text{m}}^{\text{2}}}\cdot \text{k}$ |
| $U=\frac{1}{\frac{1}{h}+\frac{{{r}_{1}}}{{{\lambda }_{1}}}\ln \frac{{{r}_{2}}}{{{r}_{1}}}+\frac{{{r}_{1}}}{{{\lambda }_{2}}}\ln \frac{{{r}_{3}}}{{{r}_{2}}}}$ | (2) |
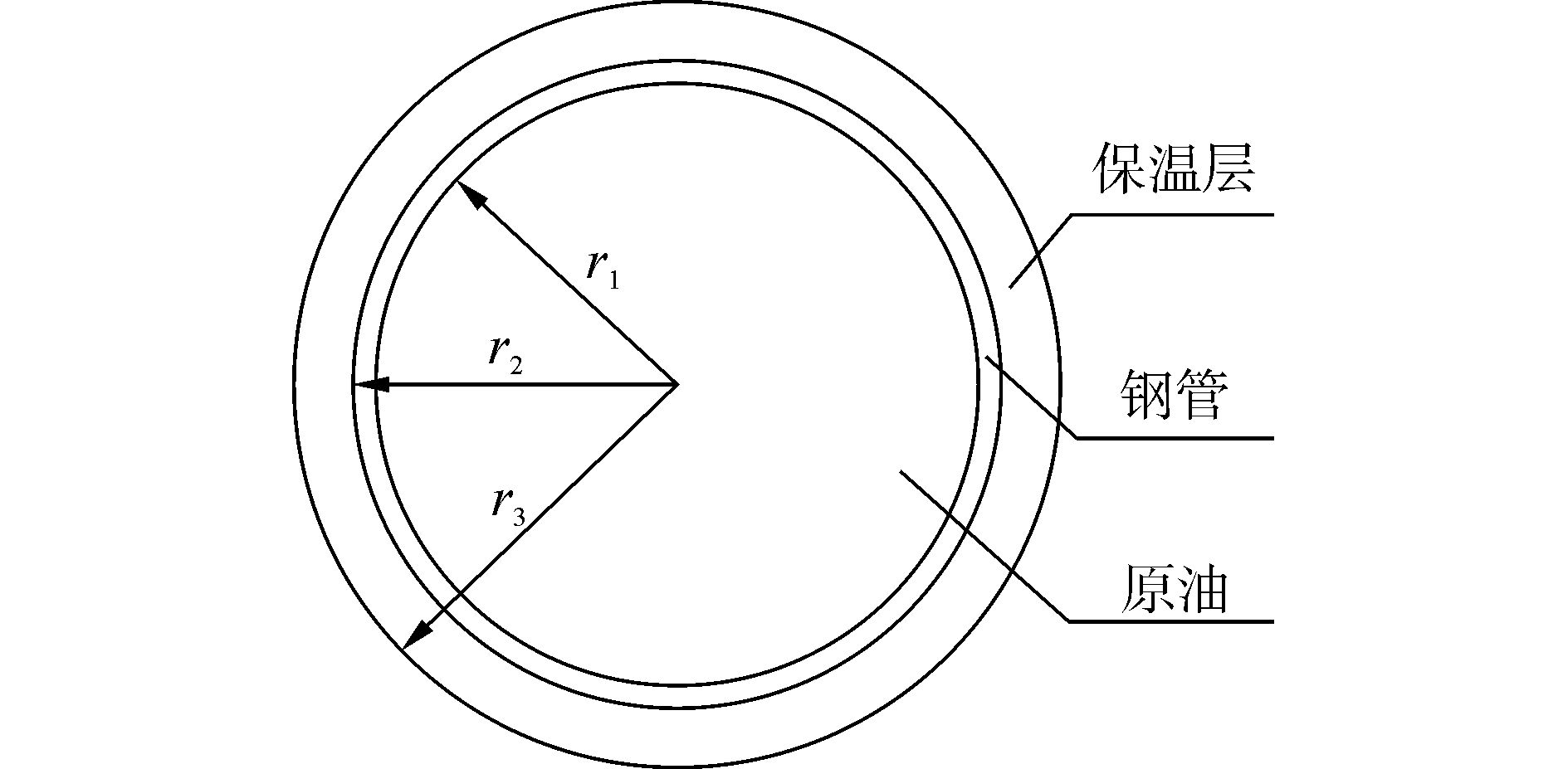
式中:h为原油与管道之间的换热系数,W/(m2·K);λ1为钢管的导热系数,W/(m·K);λ2为保温层的导热系数,W/(m·K);ri(i=1,2,3)为管道半径,m,如图 3所示。将各参数取值代入,得U=1.81W/(m2·K)。
|
| 图3 管道横截面 Figure 3 The cross section of the pipeline |
管道入口油温为TR,℃;距离管道入口L的油温为TL,℃;管道周围介质温度为T0,℃;原油与管道周围介质之间的总传热系数为U,W/(m2·K);管道直径为D,m;原油质量流量为G,kg/s;原油比热容为c,J/(K·kg);L为距管道入口长度,m。原油沿程温降计算如下所述。
设在距离管道入口l(l<L)处取一长度为dl的微管段,当管内原油流动至此处时温度降为T,经过dl这一微段距离后原油温度又降低了dT。原油温度与周围介质温差为T-T0 ,因此,长度为dl的微段单位时间内向周围介质散失的热量为 UπDdl(T-T0)。在稳态传热过程中,若忽略原油的摩擦热,则原油释放的热量为GcdT,根据dl微段内的热平衡关系有:
| $U\text{ }\!\!\pi\!\!\text{ }D\text{d}l(T-{{T}_{0}})=-Gc\text{d}T$ | (3) |
将式(3)采用分离变量法积分,可得管道内原油沿程温降关系式为
| $\left\{ \begin{align} & \int_{0}^{L}{U}\text{ }\!\!\pi\!\!\text{ }D\text{d}l=\int_{{{T}_{R}}}^{{{T}_{L}}}{-}Gc\frac{\text{d}T}{T-{{T}_{0}}} \\ & U\text{ }\!\!\pi\!\!\text{ }Dl=Gc\ln \frac{{{T}_{L}}-{{T}_{0}}}{{{T}_{R}}-{{T}_{0}}} \\ & {{T}_{L}}={{T}_{0}}+({{T}_{R}}-{{T}_{0}})e\frac{U\text{ }\!\!\pi\!\!\text{ }D}{Gc}L \\ \end{align} \right.$ | (4) |
式(4)即为管道内原油沿程温降计算公式,又称苏霍夫公式。该公式没有考虑管内油流摩擦生热对温降的影响。
3.4 FLUENT数值模拟与苏霍夫公式计算结果对比通过FLUENT数值模拟得到的原油沿程温度与通过苏霍夫公式计算得到的原油沿程温度结果如表 4所示,最大相对误差0.07%,满足精度要求,从而验证了FLUENT模型的正确性。
| 距管道入口长度/m | 油温/℃ | 相对误差/% | |
| FLUENT | 苏霍夫公式 | ||
| 0 | 80.00 | 80.00 | 0.00 |
| 100 | 79.66 | 79.70 | 0.05 |
| 200 | 79.35 | 79.40 | 0.07 |
| 300 | 79.05 | 79.11 | 0.07 |
| 400 | 78.76 | 78.81 | 0.07 |
| 500 | 78.47 | 78.52 | 0.06 |
| 600 | 78.19 | 78.23 | 0.05 |
| 700 | 77.91 | 77.94 | 0.03 |
| 800 | 77.64 | 77.65 | 0.01 |
| 900 | 77.37 | 77.36 | 0.02 |
| 1000 | 77.11 | 77.07 | 0.05 |
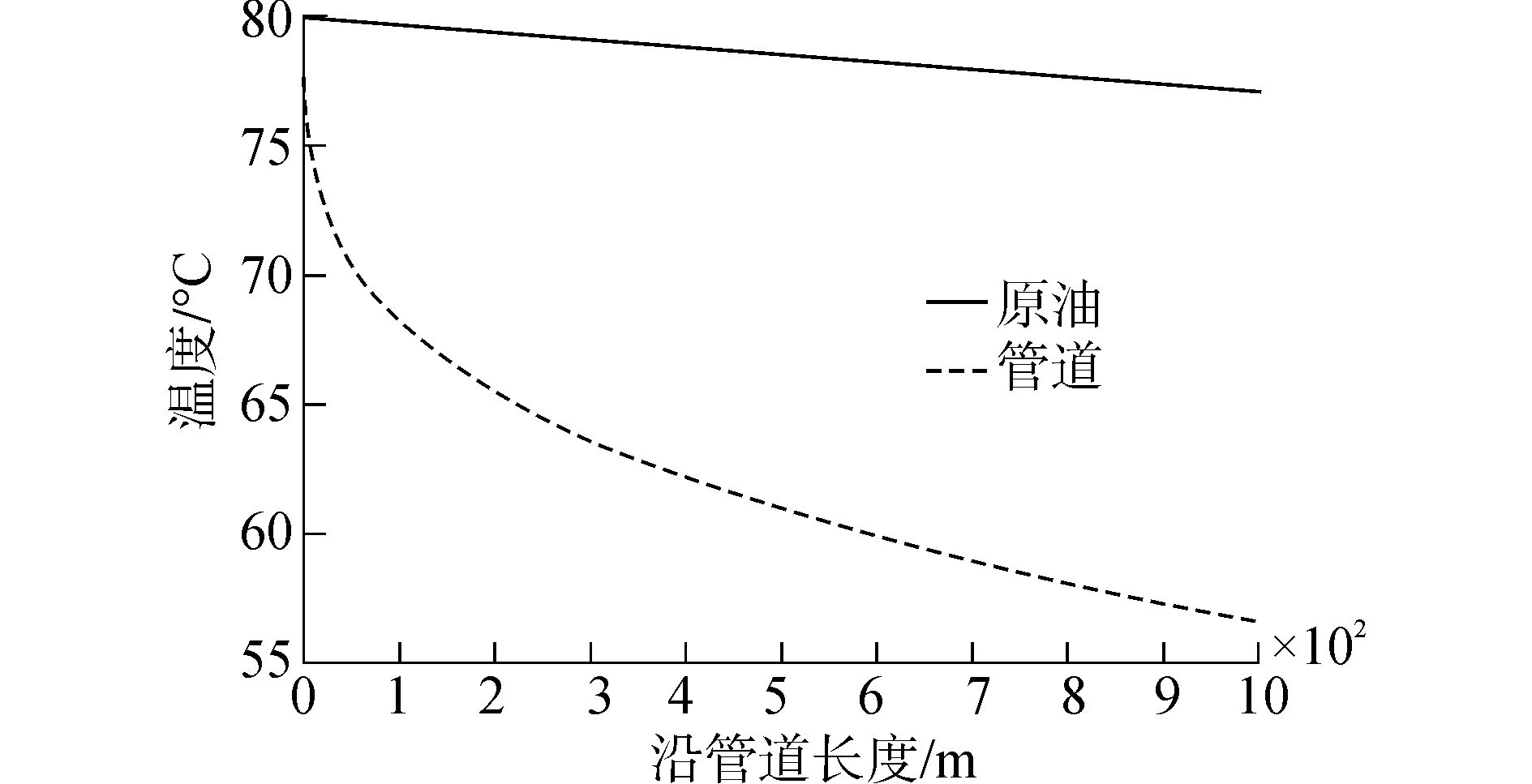
通过FLUENT数值模拟得到的原油沿程温度与管道沿程温度如图 4所示,从图中可以看出,管道沿程温度低于原油沿程温度,二者差值随着沿管道长度增大而增大,最大相差27%。
|
| 图4 原油沿程温度与管道沿程温度 Figure 4 The temperature of thecrude oil and pipe along the pipeline |
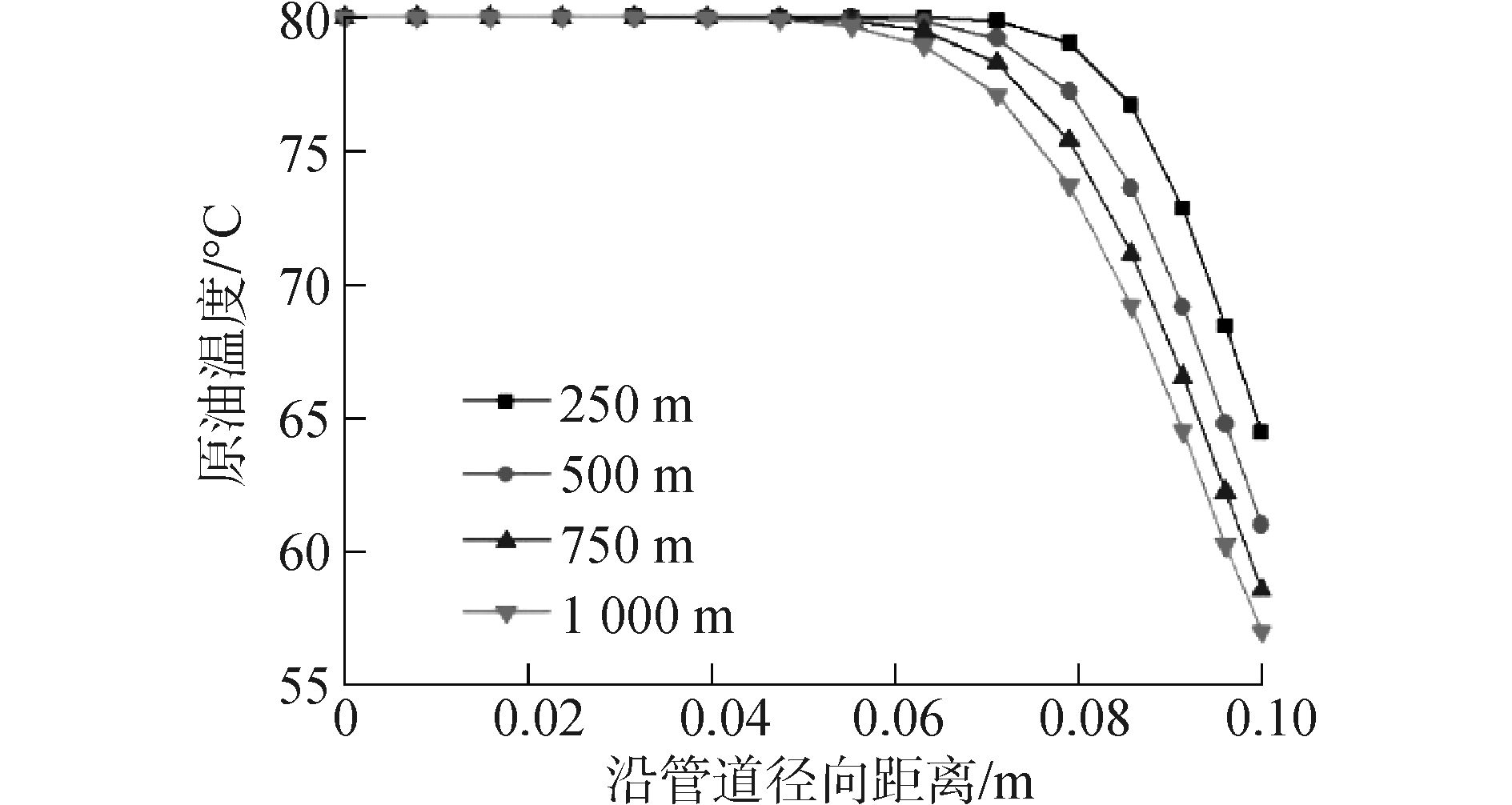
提取距入口250、500、750和1 000 m的原油径向温度数值并绘制成曲线,如图 5所示。
|
| 图5 原油径向温度 Figure 5 The radial temperature of the crude oil |
从图中可见,距离管道壁面一定厚度范围内,原油温度显著降低,该温度发生显著变化的薄层称为温度边界层,随着沿管道长度的增大,温度边界层的厚度也逐渐增大。温度边界层的存在导致了管道沿程温度与原油沿程温度之间的较大差异。
4 稳态流动管道温度场参数化分析为了进一步研究稳态流动管道温度场,本节选取了原油入口温度、原油入口流速和保温层厚度三个参数,对其进行参数化分析。
4.1 原油入口温度原油入口温度分别取80℃、70℃和60℃,原油入口流速为0.5 m/s,保温层厚度为20 mm。不同油温下的管道沿程温度曲线如图 6所示,管道温降如表 5所示。

|
| 图6 不同油温下的管道沿程温度曲线 Figure 6 The curve of the pipe temperature along the pipeline with different crude oil inlet temperature |
| 原油入口温度/℃ | 60 | 70 | 80 |
| 管道温降/℃ | 15 | 18 | 21 |
从图 6和表 5可以看出,对于不同原油入口温度,管道温度梯度均逐渐减小。随着原油入口温度的增大,管道沿程温度升高,而管道温降也有所增加,这是因为在其他条件相同的情况下,原油入口温度越高,原油散热越多,原油沿程温降越大,因此管道温降也越大。
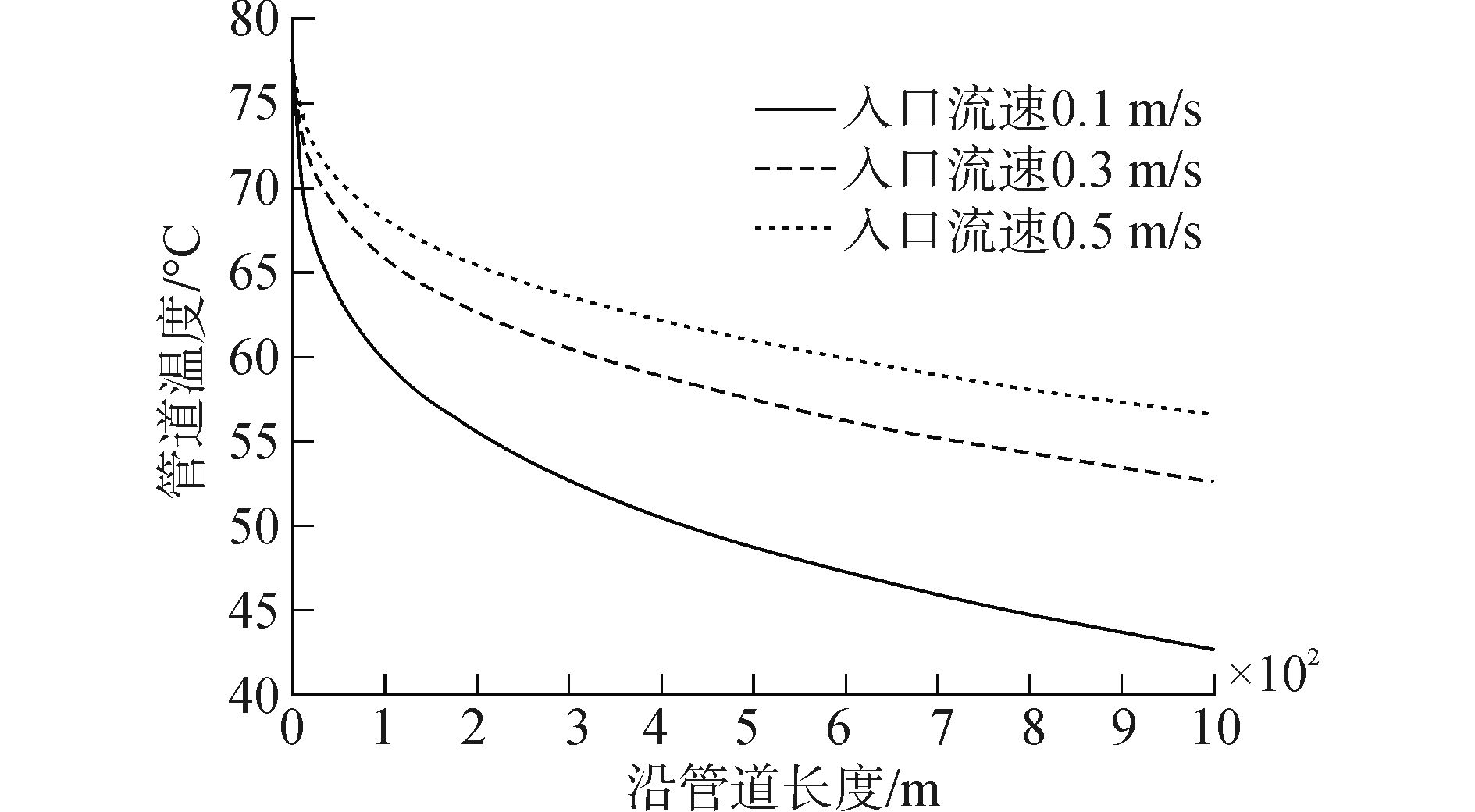
4.2 原油入口流速原油入口流速分别取0.1、0.3和0.5 m/s,原油入口温度为80℃,保温层厚度为20 mm。不同原油入口流速下的管道沿程温度曲线如图 7所示,管道温降如表 6所示。
|
| 图7 不同原油入口流速管道沿程温度曲线 Figure 7 The curve ofthe pipe temperaturealong the pipeline with different crude oil inlet velocity |
| 原油入口流速/(m·s-1) | 0.1 | 0.3 | 0.5 |
| 管道温降/℃ | 35 | 25 | 21 |
从图 7和表 6可以看出,对于不同原油入口流速,管道温度梯度均逐渐减小。随着原油入口流速的增大,管道沿程温度升高,管道温降也有所减小,这是因为原油入口流速的增大导致原油与管道的换热系数减小,原油对管道的散热减小,因此管道沿程温度升高。
4.3 保温层厚度保温层厚度分别取20、25和30 mm,原油入口温度为80℃,入口流速为0.5 m/s。不同保温层厚度下的管道沿程温度曲线如图 8所示,管道温降如表 7所示。

|
| 图8 不同保温层厚度管道沿程温度曲线 Figure 8 The curves of the temperaturealong the pipeline with different thermal insulation layerthickness |
| 保温层厚度/mm | 20 | 25 | 30 |
| 管道温降/℃ | 21 | 18 | 16 |
从图 8和表 7可以看出,对于不同保温层厚度,管道温度梯度均逐渐减小。随着保温层厚度的增大,管道沿程温度升高,管道温降减小,这是因为保温层厚度增大使得保温层的热阻增大,总传热系数减小,原油散失的热量减小,因此管道沿程温度升高。
4.4 保温层外壁与海水换热系数上述分析均是将管道保温层的外壁定义为恒温的温度边界条件,实际上海水与管道之间存在对流换热,本节探索表面传热系数(换热系数)对管道温度场的影响。
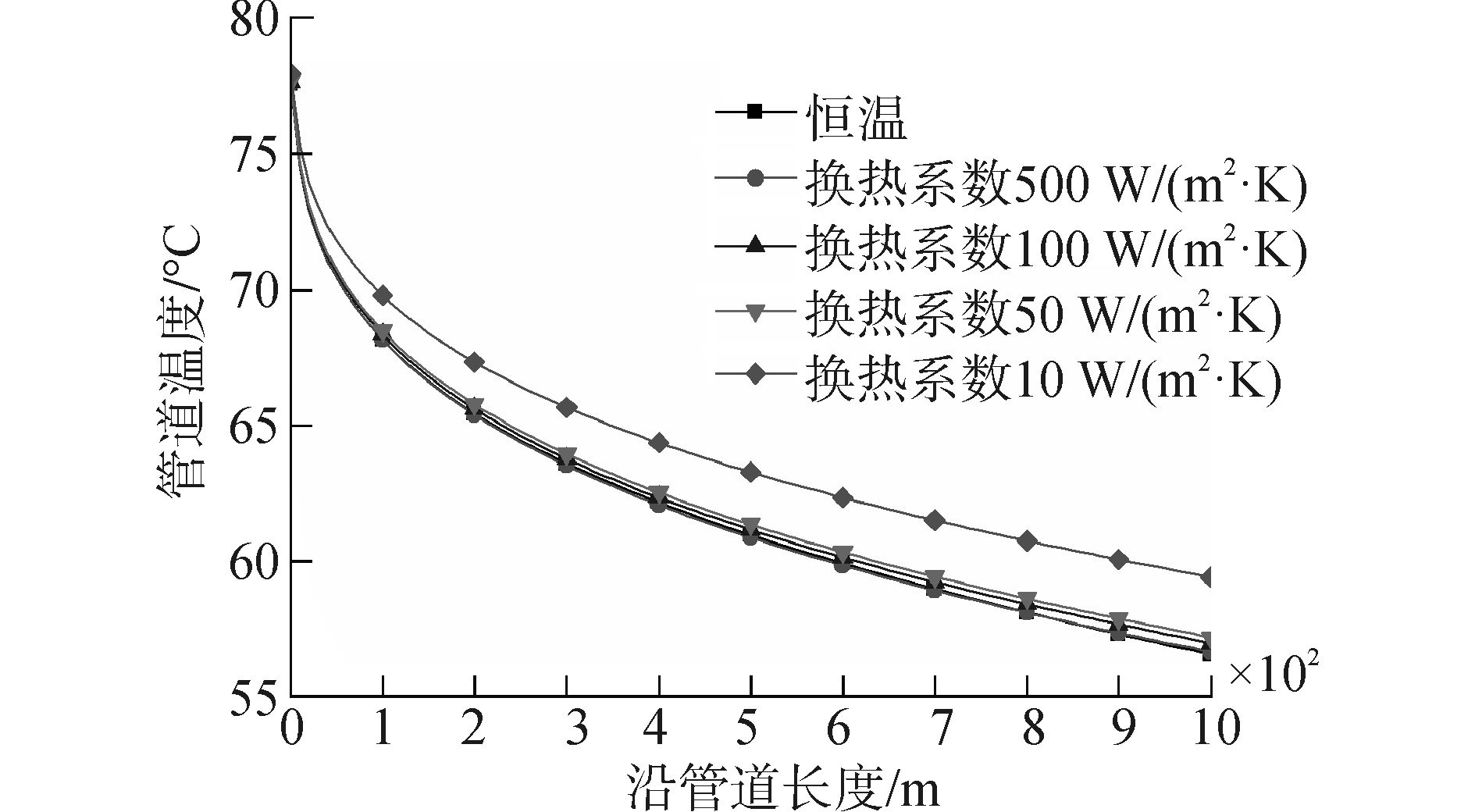
换热系数分别取500、100、50和10 W/(m2·K),海水温度取4℃,原油入口温度为80℃,保温层厚度为20 mm,入口流速取0.5 m/s。不同换热系数(恒温边界条件相当于换热系数无穷大)下的管道沿程温度曲线如图 9所示,管道温降如表 8所示。
|
| 图9 不同换热系数层流管道沿程温度曲线 Figure 9 The curve of the temperaturealong the pipeline with different heat transfer coefficient |
| 换热系数/(W·(m2·K)-1) | 恒温 | 500 | 100 | 50 | 10 |
| 层流管道温降/℃ | 21.0 | 20.9 | 20.6 | 20.5 | 18.5 |
| 注:恒温相当于换热系数无穷大 | |||||
从图 9可以看出,对于不同换热系数,层流时管道温度梯度均逐渐减小。随着换热系数减小,管道温度升高,管道温度梯度减小,管道温降减小,这是因为换热系数减小使得海水与管道保温层之间的热交换减弱,海水与原油之间的总传热系数减小,原油散失的热量减小,因此管道沿程温度升高。
经计算可知,换热系数为500 W/(m2·K)时的管道沿程温度与恒温时管道沿程温度的最大相对误差仅为0.18%,换热系数为100 W/(m2·K)时的管道沿程温度的最大相对误差也仅为0.75%,而水自然对流的换热系数一般大于100 W/(m2·K),因此将管道保温层的外壁定义为恒温的温度边界条件满足计算精度要求。
5 结论本文利用FLUENT软件对管道在稳态流动时的非均匀温度场进行了数值模拟,得到了管道沿程温度曲线,并对管道温度场进行了参数化分析,可得出以下结论:
1) 稳态流动时管道沿程温度逐渐减小,温度梯度也逐渐减小;原油径向温度分布不均匀,管道沿程温度低于原油沿程温度。
2) 管道沿程温度随着原油入口温度的升高而升高,随着原油入口流速的增大而升高,随着保温层厚度的增大而升高。
3)管道温降随着原油入口温度的升高而增大,随着原油入口流速的增大而减小,随着保温层厚度的增大而减小。
4) 保温层外壁与海水之间换热系数变化时,管道沿程温度与恒温边界条件管道沿程温度十分接近,满足计算精度要求。因此对于管道非均匀温度场研究,可以将管道保温层的外壁简化为恒温的温度边界条件。
5) 对管道温度效应的研究应考虑管道实际温度场,本文所得到的管道沿程温度曲线可为管道非均匀温度效应研究提供参考。
| [1] | WANG Zhe, YU Jianxing, LIU Hongbo, et al. Study of failure mechanisms of deep-sea oil and gas transport systems under extreme conditions[J]. Science, 2014, 346: 58–62. |
| [2] |
王哲, 马克俭, 陈志华, 等. 深海管道整体屈曲研究综述[J].
天津大学学报:自然科学与工程技术版, 2014, 47(S): 17–23.
WANG Zhe, MA Kejian, CHEN Zhihua, et al. Overview of global buckling of deep-sea pipeline[J]. Journal of Tianjin university:science and technology, 2014, 47(S): 17–23. |
| [3] | SU Jian, CERQUEIRA D R. Simulation of transient heat transfer in multilayered composite pipeline[C]//Proceeding of OMAE01, 20th International Conference on Offshore Mechanics and Arctic Engineering. Rio de Janeiro, Brazil:American Society of Mechanical Engineers, 2001:299-304. |
| [4] | SU Jian, CERQUEIRA D R, ESTEFEN S F. Simulation of transient heat transfer of sandwich pipes with active electrical heating[J]. Journal of offshore mechanics and arctic engineering, 2005, 127(4): 366–370. DOI:10.1115/1.2073090 |
| [5] | SU Jian, REGIS C R, BOTTO A. Thermal analysis of combined active heating and passive insulation of deepwater pipelines[C]//ASME 200221st International Conference on Offshore Mechanics and Arctic Engineering. Oslo, Norway:American Society of Mechanical Engineers, 2002:185-190. http://proceedings.asmedigitalcollection.asme.org/volume.aspx?volumeid=14996 |
| [6] | SU Jian, CERQUEIRA D R, ESTEFEN S F. Thermal analysis of sandwich pipes with active electrical heating[C]//ASME 200322nd International Conference on Offshore Mechanics and Arctic Engineering. Cancun, Mexico:American Society of Mechanical Engineers, 2003:809-814. http://proceedings.asmedigitalcollection.asme.org/volume.aspx?volumeid=15567 |
| [7] | CARR M, SINCLAIR F, BRUTON D. Pipeline Walking-understanding the field layout challenges and analytical solutions developed for the SAFEBUCK JIP[C]//Proceedings of the 2006 Offshore Technology Conference. Houston, Texas, USA:Offshore Technology Conference, 2006. |
| [8] | RONG Haicheng, INGLIS R, BELL G, et al. Evaluation and Mitigation of axial walking with a focus on deep water flowlines[C]//Proceedings of the 2009 Offshore Technology Conference. Houston, Texas:Offshore Technology Conference, 2009. |
| [9] |
盛磊祥, 许亮斌, 蒋世全, 等. 基于Fluent的海管内停输管内原油温度变化过程分析[J].
中国造船, 2009, 50(S): 333–337.
SHENG Leixiang, XU Liangbin, JIANG Shiquan, et al. Analysis of oil temperature decreasing trend in shut down submarine delivery pipe based on fluent[J]. Shipbuilding of China, 2009, 50(S): 333–337. |
| [10] |
张园园. 热油管道停输降温过程的数值计算[D]. 青岛:中国石油大学(华东), 2007.
ZHANG Yuanyuan. Numerical calculation of hot oil pipeline temperature drop process after shutdown[D]. Qingdao:China University of Petroleum (East China), 2007. http://cdmd.cnki.com.cn/Article/CDMD-10425-2007227503.htm |
| [11] |
孙伟栋. 海底输油管道传热模拟计算[D]. 大庆:大庆石油学院, 2007.
SUN Weidong. The heat transfer calculation and analysis of submarine oil pipeline[D]. Daqing:Daqing Petroleum Institute, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10220-2007070353.htm |
| [12] | 许国良, 王晓墨, 邬田华, 等. 工程传热学[M]. 北京: 中国电力出版社, 2005. |



