2. School of Electronic and Information Engineering, Heilongjiang Institute of Technology, Harbin 150050, China
合成孔径雷达是一种全天候、全天时的主动式微波遥感器,在军用和民用方面发挥着重要作用。但由于相干斑噪声的影响,增加了解译SAR图像的复杂性[1-2]。抑制相干斑噪声是SAR图像去噪的主要任务。抑制方法主要分两大类,即成像前的多视平滑处理技术和成像后的滤波处理技术。后者是研究的重点,经典的方法包括Lee滤波方法[3]、数学形态学方法、小波变换方法、偏微分方程方法、均值滤波、经验模态分解方法、稀疏分解方法等[4-8]。Lee滤波器对于相干斑噪声发育不完全的区域效果不好。数学形态方法的局限性在于除去噪声的同时会使目标和背景之间的边界发生变形。偏微分方程方法在图像细节保持方面有一定的缺陷。小波变换方法由于窗口大小固定、分解层数和小波基的事先选取,都对去噪结果影响较大。经验模态分解方法在一定程度上克服了小波变换的不足, 是一种完全数据驱动的自适应分解算法,但在处理过程中模态分量的选择、阈值的选择等问题都直接影响去噪效果。稀疏表示方法利用图像元素间的某种联系与噪声分布的孤立、随机性的区别,达到去噪的目的,但逼近误差的设定与噪声的大小有着直接的关系,在预先无法得到信噪比的情况下,去噪效果会受到影响。为了减少上述不确定性,提出了一种经验模态分解和稀疏表示相结合的去噪方法,该方法利用经验模态分解数据驱动这一特点,把含噪图像分解,再利用稀疏表示对噪声的抑制性,实现去噪。
1 经验模态分解和稀疏表示 1.1 经验模态分解下面给出二维经验模态分解的具体过程:
1) 对图像进行预处理,设待处理图像f(x, y)。
2) 计算出f(x, y)的极大值和极小值点。
3) 根据极大值emax(x, y)和极小值emin(x, y)点构造插值曲面,分别记为上包络面和下包络面。
4) 计算包络面的均值曲面:
| $ {\text{mean}}\left( {x,y} \right) = \frac{{{e_{\max }}\left( {x,y} \right) + {e_{\min }}\left( {x,y} \right)}}{2} $ | (1) |
5) 用图像f(x, y)减去均值曲线面mean(x, y)得到h(x, y)
| $ h\left( {x,y} \right) = f\left( {x,y} \right) - mean\left( {x,y} \right) $ | (2) |
6) 令h1, 1(x, y)=h(x, y),hl, k(x, y)中表示图像中第l个IMF分量,表示图像经过了k次筛分。判断是否满足IMF的约束条件,若满足则说明此时的h1, 1(x, y)是一个IMF;不满足则以此时的h1, 1(x, y)为待处理图像f(x, y),再重复上述的步骤,直到筛选出hl, k(x, y)满足IMF的约束条件为止[9]。约束条件定义为:
| $ \sum {_{x = 0}^{x = m}} \sum {_{y = 0}^{y = n}} \frac{{{{\left| {{h_{l,k - 1}}\left( {x,y} \right) - {h_{l,k}}\left( {x,y} \right)} \right|}^2}}}{{h_{l,k}^2\left( {x,y} \right)}} < \varepsilon $ | (3) |
7) 计算残余量:
| $ r\left( {x,y} \right) = f\left( {x,y} \right) - {h_{l,k}}\left( {x,y} \right) $ | (4) |
8)如果残余量r(x, y)中有不少于两个的极值点,则将r(x, y)作为新的待处理图像f(x, y)重复上述分解过程,直到最终的残余量r(x, y)中没有极值点,记做rL(x, y),终止二维经验模态分解过程。此时原信号可以表示为
| $ f\left( {x,y} \right) = \sum {_{l = 1}^L{h_l}} \left( {x,y} \right) + {r_L}\left( {x,y} \right) $ | (5) |
式中:hl(x, y)表示图像中第l个IMF分量。
1.2 稀疏表示每个图像y都可以表示成列向量x,x∈Rn。对于稀疏模型,首先要定义一个冗余字典D∈Rn×k,k > n,D即是冗余的。建立基于已知D的稀疏表示:
| $ \mathop \alpha \limits^ \wedge = \arg \;\mathop {\min }\limits_\alpha \;{\left\| \alpha \right\|_0}{\text{s}}{\text{.t}}D\alpha = x $ | (6) |
即:x能被字典D稀疏地表示,且||$\mathop \alpha \limits^ \wedge $||0$ \ll $n代表$\mathop \alpha \limits^ \wedge $的原子数非常少。
为了使上述模型更加有利于计算,将采用误差约束项‖Dα-x‖22≤ε代替Dα=x。定义稀疏度L,满足‖$\mathop \alpha \limits^ \wedge $‖≤L≤n,即要求用于表示向量的字典原子个数不超过L。
2 经验模态分解和稀疏表示的去噪模型稀疏表示在去噪的时候,要预先估算噪声的程度,以改变逼近的误差,但大多数情况下是无法准确估计噪声程度的。为了减小由于估计噪声误差引起的不确定性,结合经验模态分解的特点,对图像采取先进行经验模态分解,分解后对前2个模态分量进行噪声强度估计,根据噪声强度对前两个模态分量进行稀疏分解及重构,以此减小噪声误差估计不准引起的偏差。
设含相干斑噪声SAR图像y,无噪声图像SAR图像x,相干斑噪声n,则
| $ y = x \cdot n $ | (7) |
在去噪过程中,通常将乘性噪声转换为加性噪声再进行处理,采用对数转换方式会使SAR图像的统计特性发生完全改变,同时相干斑噪声的统计特性也会发生改变[10]。所以采用如下加性噪声模型:
| $ y = x \cdot n = x + x \cdot \left( {n - 1} \right) = x + f $ | (8) |
这里认为f是加性噪声,近似于高斯分布[11]。
由于经验模态分解是一种非常有效的自适应分解方法,对含信号y进行经验模态分解,得到若干固有模态分量IMF[12],即
| $ y = \sum\limits_{l = 1}^L {\left( {x,y} \right) + {r_{L + 1}}} \left( {x,y} \right) $ | (9) |
利用EMD的去噪算法中,一般认为第一层固有模态分量,即h1(x, y)是由大部分噪声能量构成,在处理过程中经常忽略其中的信号细节,这样处理是不准确的,通过对含噪图像的分解结果可以看出第一个固有模态分量中含有少量的细节信息,若将其完全滤除会导致信号细节信息丢失。所以通过EMD有效地去噪方法,关键是提取出固有模态分量中的信号信息,抑制噪声信息。这也成为处理固有模态分量的难度所在。
Zhaohua Wu等通过研究发现,高斯噪声经EMD分解后,各个固有模态分量都服从正态分布。h1(x, y)、h2(x, y)主要是由噪声构成,只有少部分细节信息,而且其所含的噪声服从正态分布。由于图像细节信息元素间有内在联系,即结构特性,该特性与原子特性相吻合,具有稀疏性,而噪声是随机的、不相关的、孤立的、离散的,没有结构特性,不具有稀疏性。故采用稀疏表示方法,对h1(x, y)、h2(x, y)进行稀疏分解,在重构过程中利用h1(x, y)、h2(x, y)的方差确定重构参数S,对h1(x, y)、h2(x, y)进行重构:
| $ {S_i} = \frac{{\operatorname{var} \left( {{h_i}\left( {x,y} \right)} \right)}}{{67.42}} $ | (10) |
式中:67.42是由经验模态分解后,对第1模态分量及第2模态分量做了大量实验确定的,与原始信号类型有关。由于h1(x, y)、h2(x, y)中噪声服从零均值正态分布,以h1(x, y)为例,设计去噪过程。
设H1(x, y)为h1(x, y)的无噪声部分:
| $ {H_1}\left( {x,y} \right) = D \cdot \alpha $ | (11) |
D是字典α是稀疏表示系数。则
| $ \begin{array}{1} \hat \alpha = \mathop {\arg \min }\limits_\alpha {\left\| \alpha \right\|_0} \hfill \\ 满足\left\| {D \cdot \alpha - {h_1}\left( {x,y} \right)} \right\|_2^2 \leqslant T \hfill \\ \end{array} $ | (12) |
T与重构参数S有关,选择合适的μ,上式可等效为
| $ \hat \alpha = \mathop {\arg \min }\limits_\alpha \left\| {D \cdot \alpha - {h_1}\left( {x,y} \right)} \right\|_2^2 + \mu \cdot {\left\| \alpha \right\|_0} $ | (13) |
| $ {{\hat H}_1}\left( {x,y} \right) = D \cdot \hat \alpha $ | (14) |
$\hat H$1(x, y)是对H1(x, y)的估计值,即去噪后值。
同理,求出h2(x, y)去噪后的估计值$\hat H$2(x, y)。
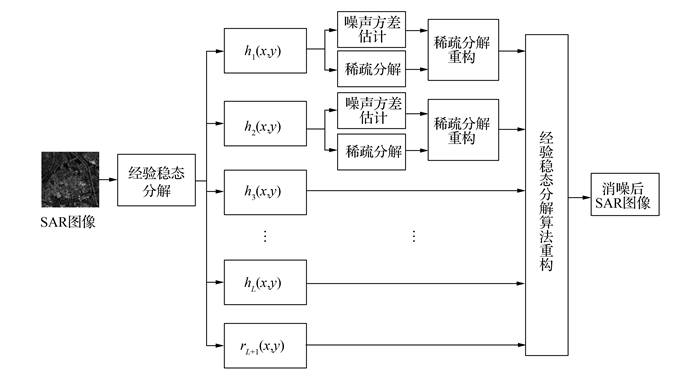
|
| 图1 SAR图像去噪整体框架 Figure 1 The framework of SAR image denoising |
实验选用一幅相干斑噪声较强,区域较平坦的SAR图像,如图 2所示。为了对比本文方法的优劣,实验方面选择了与Lee、EMD、稀疏表示3种去噪方法进行对比。客观评价标准采用几种适合SAR图像去噪的评价指标:图像均值、图像方差、等效视数[13]、边缘保持指数。

|
| 图2 含噪SAR图像 Figure 2 The speckled SAR image |
首先,对含噪SAR图像作经验模态分解,分解结果如图 3所示,可以看出经过分解后的5个固有模态分量中,前两个固有模态分量含有的噪声成分较多,故后续处理以前两个固有模态分量为主。

|
| 图3 含噪SAR图像经验模态分解结果 Figure 3 The results of EMD for SAR image |
对前两个固有模态分量进行稀疏分解,在重构过程中通过计算其方差,确定重构参数S,利用该参数对两个固有模态分量进行重构,结果如图 4。
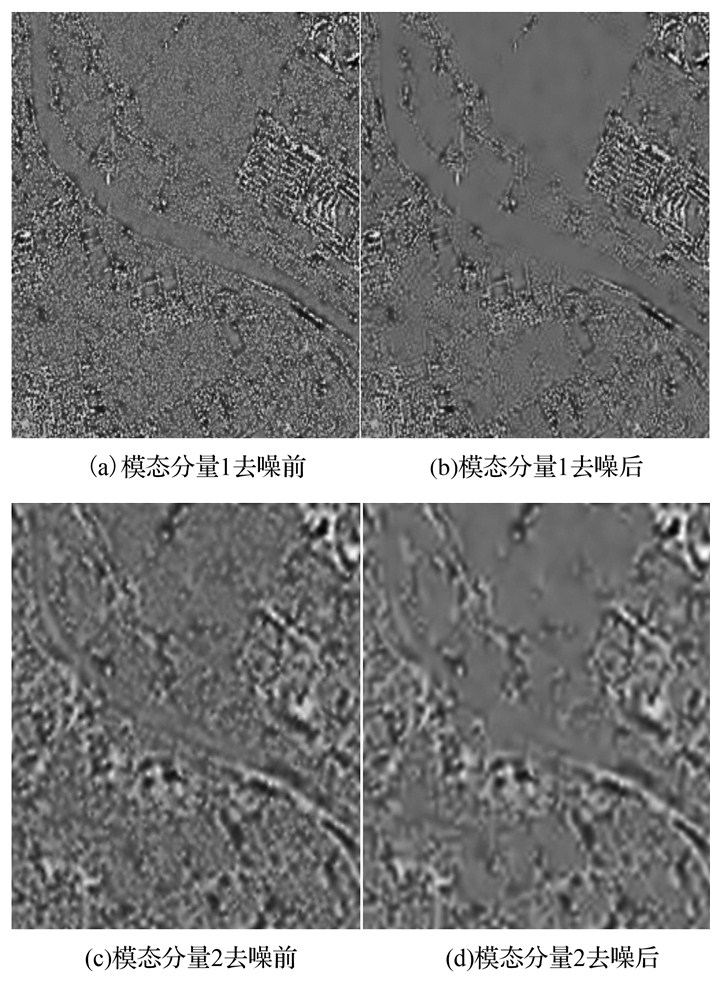
|
| 图4 前两个固有模态分量及其稀疏分解去噪结果 Figure 4 The results of first IMF and second IMF de-nosing |
最后,将去噪后的固有模态分量与未处理的各固有模态分量进行重构,得到去噪后的SAR图像。

|
| 图5 图像的去噪结果对比 Figure 5 Comparison of image denoising results |
| 去噪方法 | 图像均值 | 图像方差/×103 | 等效视数 | 边缘保持指数 |
| 原图 | 69.399 4 | 2.47 | 1.948 1 | - |
| Lee | 69.222 8 | 1.40 | 3.414 4 | 0.329 8 |
| EMD | 82.060 4 | 1.13 | 5.956 5 | 0.413 4 |
| 稀疏表示 | 78.002 0 | 1.05 | 5.763 7 | 0.426 2 |
| 本文方法 | 80.170 1 | 1.19 | 5.359 9 | 0.580 1 |
从实验结果可以看出,Lee滤波器从主观评价角度,虽然滤除了部分噪声,但其边缘信息保留得不够好。客观上看,图像均值变化不大,保持了图像的平均强度;图像的方差较原始图像下降很多,体现了滤波能力较强这一特点;通过等效视数可以看出滤波器相干斑抑制能力一般;边缘保持指数显示出滤波后图像水平与垂直方向边缘的保持能力一般。
EMD滤波器从主观评价角度,滤除了部分噪声,但剩余噪声依旧很多,根据图像的不同,需要人工干预滤波程度。客观上看,图像均值有所提高,增强了图像的平均强度;图像的方差较原始图像下降很多,滤波能力较Lee滤波器强;通过等效视数可以看出滤波器相干斑抑制能力较Lee滤波器提升;边缘保持指数显示出滤波后图像水平与垂直方向边缘的保持能力较Lee滤波器提升。
稀疏表示方法从主观评价角度,平坦区域滤波效果较好,滤除了大部分噪声,这个方面较前两种方法都强;客观上看,图像均值较EMD方法低,但也保持了图像的平均强度;图像的方差较原始图像下降很多,体现了滤波能力较强这一特点;通过等效视数较大可以看出滤波器相干斑抑制能力较强;边缘保持指数显示出滤波后图像水平与垂直方向边缘的保持能力较强。
本文从主观评价角度,明显优于Lee滤波器和EMD方法,比稀疏表示方法略好。客观上看,图像均值提高,增强了图像的平均强度;图像的方差较原始图像下降很多,体现了滤波能力较强这一特点;通过等效视数可以看出Lee滤波器相干斑抑制能力在几种方法中不是最好的;边缘保持指数显示出滤波后图像水平与垂直方向边缘的保持能力最强。
4 结论本章提出了一种针对SAR图像的去噪的新方法,该方法具有良好的点源保持特性。
1) 该方法即利用了经验模态分解的多分辨率特点,实现了频域的划分;
2) 利用了稀疏表示的原子特性,将图像的结构保持;
3) 同时利用噪声是随机的、不相关的、孤立的、离散的,没有结构特性,不具有稀疏性这一特点,实现了多分辨率的滤波。
最后给出了实验对比,从主观及客观角度证明了本文提出方法的有效性。
| [1] |
高博, 王俊, 原慧. 一种参数自适应的SAR图像去噪方法[J].
西安电子科技大学学报:自然科学版, 2015, 42(5): 63–67.
GAO Bo, WANG Jun, YUAN Hui. Parameter adaptive SAR image denoising method[J]. Journal of Xidian university, 2015, 42(5): 63–67. |
| [2] |
袁湛, 何友, 蔡复青. SAR图像伪加性相干斑噪声统计特性[J].
宇航学报, 2012, 33(6): 754–760.
YUAN Zhan, HE You, CAI Fuqing. Statistics of pseudo additive speckle noise in SAR image[J]. Journal of astronautics, 2012, 33(6): 754–760. |
| [3] | LEE J S. Digital image enhancement and noise filtering by use of local statistics[J]. IEEE transactions on pattern analysis and machine intelligence, 1980, 2(2): 165–168. |
| [4] | ELAD M, AHARON M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE transactions on image processing, 2006, 15(12): 3736–3745. DOI:10.1109/TIP.2006.881969 |
| [5] |
郭德全, 杨红雨, 刘东权, 等. 基于稀疏性的图像去噪综述[J].
计算机应用研究, 2012, 29(2): 406–413.
GUO Dequan, YANG Hongyu, LIU Dongquan, et al. Overview on sparse image denoising[J]. Application research of computers, 2012, 29(2): 406–413. |
| [6] | NUNES J C, BOUAOUNE Y, DELECHELLE E, et al. Image analysis by bidimensional empirical mode decomposition[J]. Image and vision computing, 2003, 21(12): 1019–1026. DOI:10.1016/S0262-8856(03)00094-5 |
| [7] |
易子麟, 尹东, 胡安洲, 等. 基于非局部均值滤波的SAR图像去噪[J].
电子与信息学报, 2012, 34(4): 950–955.
YI Zilin, YIN Dong, HU Anzhou, et al. SAR image despeckling based on non-local means filter[J]. Journal of electronics & information technology, 2012, 34(4): 950–955. |
| [8] |
刘帅奇, 胡绍海, 肖扬. 基于稀疏表示的Shearlet域SAR图像去噪[J].
电子与信息学报, 2012, 34(9): 2110–2115.
LIU Shuaiqi, HU Shaohai, XIAO Yang. Shearlet domain SAR image de-noising via sparse representation[J]. Journal of electronics & information technology, 2012, 34(9): 2110–2115. |
| [9] |
王立国, 宛宇美, 路婷婷, 等. 结合经验模态分解和Gabor滤波的高光谱图像分类[J].
哈尔滨工程大学学报, 2016, 37(2): 284–290.
WANG Liguo, WAN Yumei, LU Tingting, et al. Hyperspectral image classification by combining empirical mode decomposition with Gabor filtering[J]. Journal of Harbin engineering university, 2016, 37(2): 284–290. |
| [10] | XIE Hua, PIERCE L E, ULABY F T. Statistical properties of logarithmically transformed speckle[J]. IEEE transactions on geoscience and remote sensing, 2002, 40(3): 721–727. DOI:10.1109/TGRS.2002.1000333 |
| [11] | FOUCHER S, FARAGE G, BENIE G. SAR image filtering based on the stationary contourlet transform[C]//Proceedings of the IEEE International Conference on Geoscience and Remote Sensing Symposium. Denver, USA:IEEE, 2006:4021-4024. |
| [12] |
邵欣, 尹清波, 鲁明羽. 基于EMD和模极大值的造影图像血管提取[J].
智能系统学报, 2015, 10(6): 851–857.
SHAO Xin, YIN Qingbo, LU Mingyu. Vessels extraction in coronary angiogram based on empirical mode decomposition[J]. CAAI transactions on intelligent systems, 2015, 10(6): 851–857. |
| [13] |
崔瑞, 薛磊, 汪波. 基于等效视数的ISAR干扰效果评估方法[J].
系统工程与电子技术, 2008, 30(5): 887–888.
CUI Rui, XUE Lei, WANG Bo. Evaluation method of jamming effect on ISAR based on equivalent number of looks[J]. Systems engineering and electronics, 2008, 30(5): 887–888. |



