2. Research Office, State Grid Corporation of China, Beijing 100031, China
为使压气机叶片的几何进口角适应来流方向,动叶片通常设计成根部安装角大、尖部安装角小的扭转叶片,处于工作状态下的扭转叶片会因气动力和离心力的综合作用而发生扭转变形[1]。由于扭转变形直接改变了叶片的结构外形,使得叶片的叶顶间隙和来流冲角发生变化,进而对压气机的流量、效率及稳定裕度等重要性能参数产生显著影响[2]。同时,现代压气机的设计追求更高的功重比,叶片负荷不断上升而质量比却在下降,这种设计理念导致柔性叶片不得不在高应力状态下工作[3],叶片的扭转变形问题变得更为严重。因此,在压气机设计阶段必须计入叶片弹性变形的影响。
文献[4]考察了叶片变形对风扇气动性能的影响,研究发现:叶片的变形造成风扇压比提高约2.5%,而流量和效率下降约5%,可见风扇性能下降明显。李绍斌[5]的研究表明,90%的叶片总变形量与惯性载荷有关,10%的叶片总变形量与气动力有关。已有的研究表明[6-8],叶片的最大变形位置靠近叶片顶部,且越接近叶顶前缘,形变量越大。有关压气机叶顶流动的研究指出[9-12],无论对于气体压力的有效提升还是压气机能否维持稳定的运行状态,叶顶区域的流场状态都发挥着至关重要的作用。为能实现压气机的设计性能指标,应确保叶片由冷态 (加工状态) 转变为热态 (工作状态) 后,其形状与设计外形相近或吻合[13-14]。因此,提供准确的叶型加工数据就成为设计过程中的重要环节。
Ohtsuka等[15]首次从理论和实验角度探索了叶片的扭转变形问题,但他的研究只考虑了离心力而忽略了气动载荷对叶片变形的影响。Liu[16]分析指出,气动力对叶片扭转变形有显著作用,即便气动力较离心力低一个数量级,仍然不可忽略其对叶片变形的作用。郑赟等[17]提出了一种适用于跨声速风扇叶片的预变形设计方法。但该方法中需要采用非定常流固耦合计算,增加了预变形计算的复杂程度,不便于工程实际运用。
本文从工程实用角度出发,采用现有的成熟商业软件,在同时考虑气动力与离心力的前提下,给出一种基于弱耦合迭代的预变形计算方法,对某单级跨声速压气机的转子叶片进行了预变形设计。结果表明,本文采用的方法可以在20个迭代步内达到收敛状态,残差量级在10-5 mm以下,能够满足工程应用中高效、高精度的要求。
1 计算方法压气机叶片在离心载荷和气动载荷作用下的变形属于流固耦合问题,考虑到应用强耦合方法的客观困难[18],以及收敛难度和耗时严重等问题,从工程实用角度出发,本文基于商业软件ANSYS与CFX,采用弱耦合方法完成气动力与叶片结构的耦合计算。弱耦合方法中结构和流体的求解相互独立,仅在耦合界面上交换数据,通过联合现有的通用结构和流体分析软件即可实现,能够充分发挥各自领域的优势,有效保证了计算精度和效率。
流体计算的任务是为结构计算提供叶片表面的压力分布。由于静气动弹性仅关注最终变形结果,对叶片的变形过程不关心,因此气动力通过求解三维定常雷诺平均方程获得。
结构计算的任务是在给定气动力和离心力条件下计算出叶片结构的变形量。叶片的有限元基本方程如下
| $ \mathit{\boldsymbol{KU}} = \mathit{\boldsymbol{F}} $ |
式中:K为叶片刚度矩阵,U为位移矢量,F为载荷矢量。
2 预变形方法叶片设计点的热态叶型是冷态叶型在设计点离心力和气动力作用下变形后的状态,由此可知,叶片受力为变形后状态的离心力和气动力。因此,本文ANSYS结构分析所采用的载荷条件均为设计点热态叶型的压力和离心力,且对应节点的载荷数据在迭代过程中保持不变。
整个预变形计算过程围绕下式展开:
| $ X_{{\rm{cold}}}^i = {X_{{\rm{hot}}}} - U_{{\rm{cold}}}^{i - 1} $ |
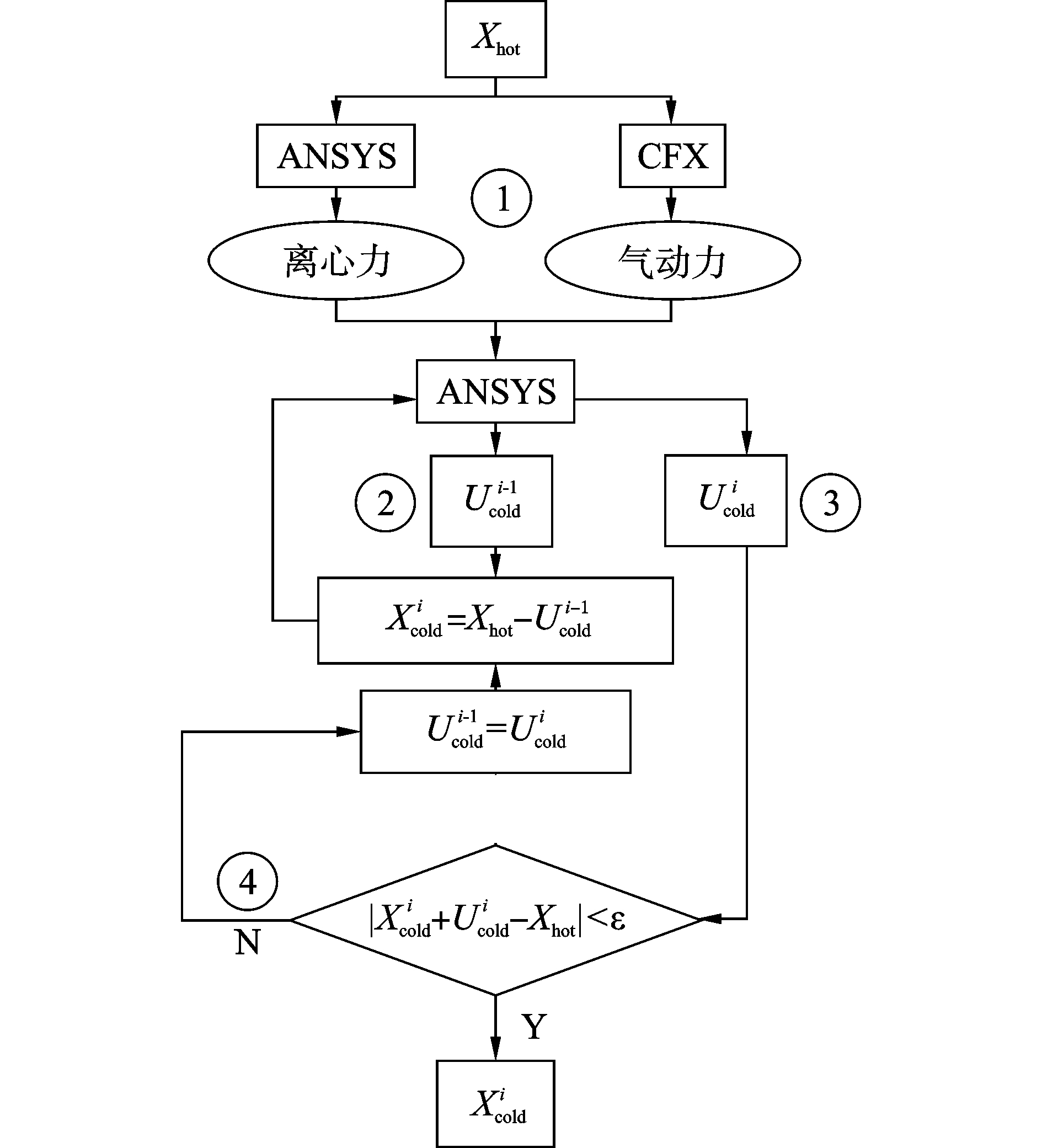
式中:i为循环次数,Xcoldi为第i次循环的冷态叶型坐标,Xhot为设计点的热态叶型坐标,Ucoldi-1为第i-1次循环中冷态叶型Xcoldi-1在气动载荷和离心载荷作用下产生的节点位移。图 1给出了叶片预变形算法的流程图,其总体思路是,对上次循环确定的冷态叶型Xcoldi-1施加载荷求得节点位移Ucoldi-1,进而得出本次循环的冷态叶型Xcoldi,然后对叶型Xcoldi施加载荷,判断其变形后状态是否与热态叶型Xhot相符或接近,若满足要求,则输出冷态叶型Xcoldi,否则继续执行循环。
|
| 图1 叶片预变形算法流程图 Figure 1 Process of blade untwist design |
具体步骤如下:
1) 首先提取热态叶型Xhot的载荷条件,应用ANSYS进行结构分析获得叶片在旋转角速度下各节点所受的离心力,应用CFX进行流体分析获得叶片表面各节点所受的气动力。
2) 对冷态叶型Xcoldi-1施加步骤1中提取的气动载荷和离心载荷,计算出节点位移Ucoldi-1,进而可得Xcoldi=Xhot-Ucoldi-1(首次迭代以热态叶型Xhot作为冷态叶型Xcold0)。
3) 对修正后的冷态叶型Xcoldi施加步骤1中提取的载荷条件,计算出节点位移Ucoldi。
4) 判断Xcoldi加载后的变形状态是否与Xhot相符或接近,即是否满足|Xcoldi+Uoldi-Xhot| < ε(ε为指定的残差值),若满足,则输出加工叶型Xcoldi,否则,重复步骤2、3、4。
3 压气机转子叶片预变形计算以某单级跨声速压气机为研究对象,在设计点工况,针对其转子叶片进行预变形设计。压气机基本参数如表 1所示。
| 结构参数 | 性能参数 | 叶片材料属性 | |||||
| 参数 | 值 | 参数 | 值 | 参数 | 值 | ||
| 转子叶片数 | 36 | 转速/(r·min-1) | 24 566.8 | 弹性模量/Pa | 2.06×1011 | ||
| 静子叶片数 | 46 | 总压比 | 1.97 | 泊松比 | 0.3 | ||
| 叶顶间隙/mm | 0.4 | 流量/(kg·s-1) | 10.1 | 密度/(kg·m-3) | 7 850 | ||
| 叶尖切线速度/(m·s-1) | 452 | 绝热效率 | 0.828 | ||||
本文流体域数值模拟采用CFX求解N-S方程,高分辨率格式求解能量、动量和连续方程,湍流模型选取兼顾计算效率与精度的k-ε高雷诺数湍流模型。边界条件给定为:进口总压101 325 Pa,总温288.15 K,出口静压151 000 Pa,转子转速设定为24 566.8 r/min,动、静域交界采用掺混平面法。转子叶片固体域计算采用ANSYS求解结构动力学方程,认为轮毂具有足够刚性,所以将叶片根部设定为固定约束,同时,对叶片体各个节点施加离心载荷,对叶片表面施加气动载荷。
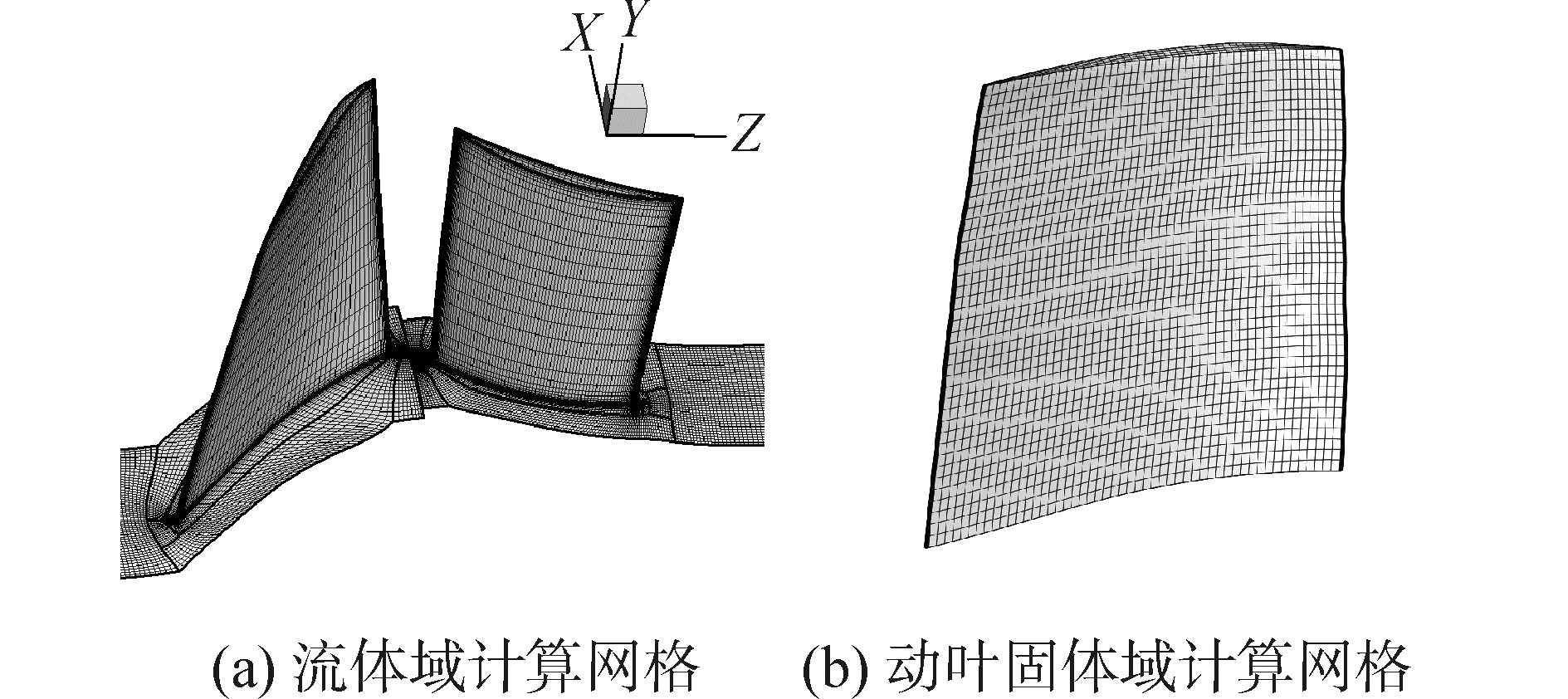
图 2为本文计算采用的网格,其中图 2(a)为压气机级流体域网格,图 2(b)为转子叶片固体域网格。级流体域网格 (图 2(a)) 采用IGG/Autogrid划分,为减弱进出口边界压力波的非正常反射,将转子上游和静子下游流道分别延长了2.5倍弦长。转子与静子通道均采用O4H型网格拓扑,转子叶顶间隙区域采用蝶形网格拓扑结构 (O型内嵌H型),网格正交性良好。对近壁面网格进行加密处理,使壁面第一层网格的y+维持在30左右,以满足湍流模型的求解要求。转子流道和静子流道的网格总数分别为60万和40万。转子叶片的固体域网格 (图 2(b)) 使用六面体实体单元对有限元模型进行离散,弦长方向、叶高方向和叶宽方向的节点数为66×42×5,六面体单元总数为10 496。
|
| 图2 流场和结构计算网格 Figure 2 Mesh for fluid and solid domain |
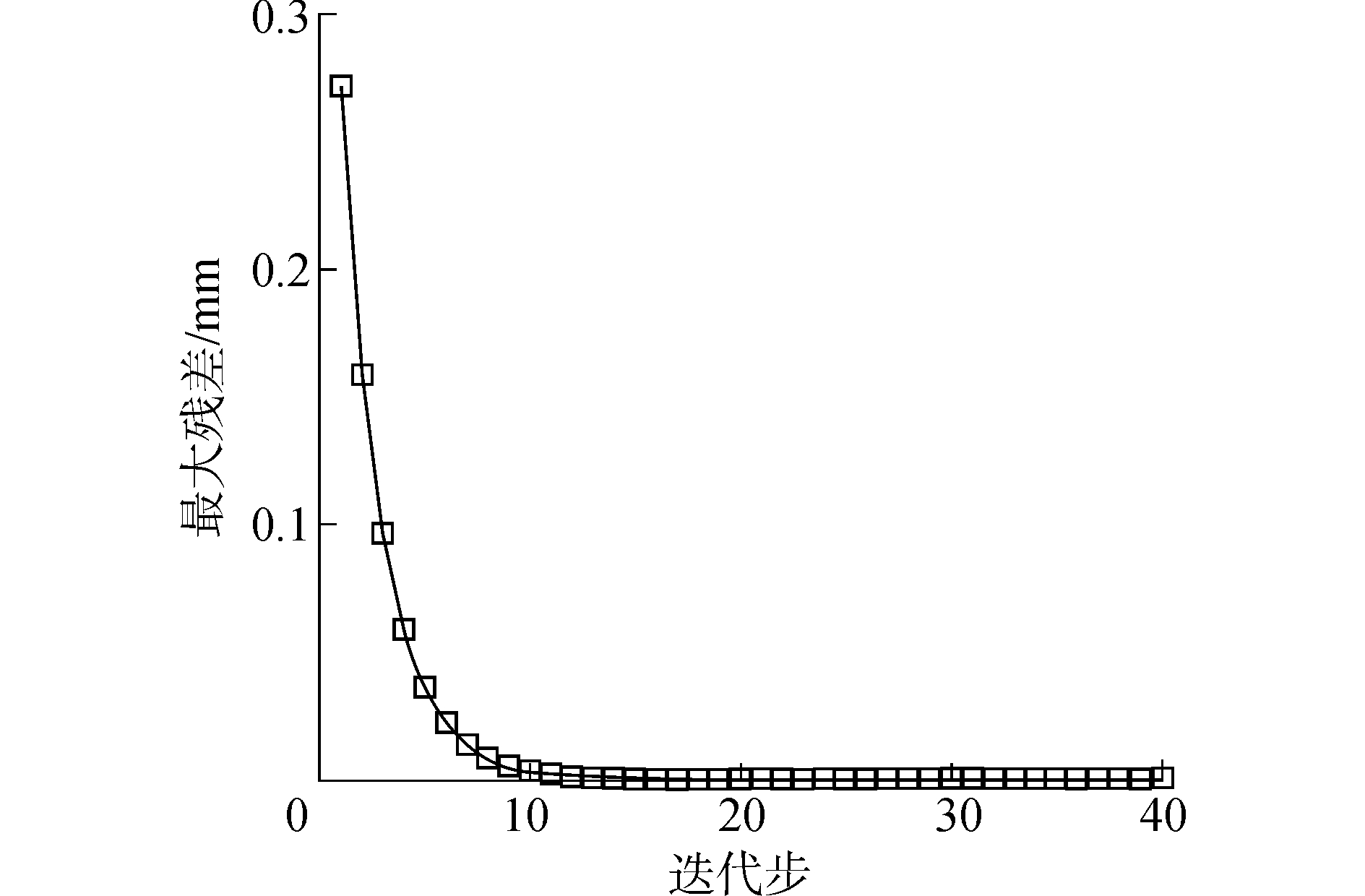
为获得足够精度的预变形叶型,在求解图 1中步骤4) 中的残差ε时,计算了叶片固体计算域所有网格节点的残差值,并取其中的最大值作为参考值。图 3给出了最大残差随迭代步的变化曲线,由图可知,本文采用的迭代方法具有较高的计算效率,经过10个迭代步残差即可下降到10-3 mm,当计算到第20步时,残差降至10-5 mm,此后残差维持在这一量级,达到收敛状态。因此,认为第20步计算得到的冷态叶型数据有效,可作为加工叶型数据使用。
|
| 图3 最大残差曲线 Figure 3 Maximum residual curve |
图 4给出了三组冷、热态及设计叶型的对比,由图可以看出,冷、热态叶型的差别主要集中在叶顶前缘位置。由于迭代计算开始时并没有对应的冷态叶型,因而以设计叶型为初始的冷态叶型 (如图 4(a))。在对该冷态叶型施加载荷后,得到的热态叶型偏离了设计叶型,该热态叶型朝向使叶顶来流冲角增大的方向变形,叶顶的气动负荷随之上升,而气动稳定性会随之下降,图 4(a)再次说明了考虑叶片预变形的必要性。图 4(b)为第2步迭代后的叶型对比,可见,迭代计算使得热态叶型更接近设计叶型,但由于迭代不充分,冷态叶型预变形不足,对应的热态叶型仍与设计叶型存在较大偏差。图 4(c)为第20步迭代结果的对比,此时残差以下降至10-5 mm量级,得出的热态叶型与设计叶型基本重合,对应的冷态叶型数据可输出作为加工数据使用。

|
| 图4 冷态叶型与热态叶型的对比 Figure 4 Comparison of cold and hot blade profile |
本文综合考虑了气动力和离心力对叶片变形的作用,采用基于弱耦合迭代的叶片预变形设计方法,对某跨声速压气机转子叶片进行了预变形设计,获得了该压气机在设计点工况对应的冷态叶型,研究得出以下结论:
1) 对于本文所采用的预变形计算方法,无需编写复杂的程序代码,利用现有的成熟商业软件即可完成,适合于工程应用和推广。
2) 本文在预变形计算过程中同时考虑了气动载荷和离心载荷,并对所有冷态叶型施加相同的气动和离心载荷,该气动和离心载荷由设计叶型求得,即认为在每次迭代中冷态叶型的受力与预期热态叶型受力相同,这样的前提条件更符合物理实际。
3) 本文的预变形设计方法兼具高效与高精度的特点,仅需20个迭代步即可得到残差小于10-5 mm量级的预变形叶型数据。
| [1] |
曲文浩. 航空发动机压气机叶片的静力学及模态分析[D]. 沈阳: 东北大学, 2012: 5-6.
QU Wenhao. Statics and modal analysis of aero-engine compressor blades[D]. Shenyang:Northeastern University, 2012:5-6. |
| [2] | LIU Gaolian. A new generation of inverse shape design problem in aerodynamics and aerothermoelasticity:concepts, theory and methods[J]. Aircraft engineering and aerospace technology, 2000, 72(4): 334–344. DOI:10.1108/00022660010340141 |
| [3] | MIKRUT P L. Vibration of axial turbomachinery blades:measurement and fluid-structure interactions[D]. Notre Dame:University of Notre Dame, 2012. |
| [4] |
郑赟, 田晓, 杨慧. 跨声速风扇叶片变形对气动性能的影响[J].
航空动力学报, 2011, 26(7): 1621–1627.
ZHENG Yun, TIAN Xiao, YANG Hui. Impact of blade deflection on aerodynamic performance of a transonic fan[J]. Journal of aerospace power, 2011, 26(7): 1621–1627. |
| [5] |
李绍斌. 跨音速压气机高负荷弯扭静叶设计及其级的气动性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2007: 85-136.
LI Shaobin. Design of highly loaded dihedral stator and investigation on the aerodynamic stage performance in an axial transonic compressor[D]. Harbin:Harbin Institute of Technology, 2007:85-136. |
| [6] | KALLESØE B S, HANSEN M H. Some effects of large blade deflections on aeroelastic stability[C]//47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando, Florida:AIAA, 2009. |
| [7] |
李鑫. 考虑流固耦合效应的压气机内部流动模拟[D]. 哈尔滨: 哈尔滨工业大学, 2010.
LI Xin. The flow simulation in the compressor with the effect of fluid-solid interaction[D]. Harbin:Harbin Institute of Technology, 2010. |
| [8] |
胡丹梅, 张志超, 孙凯, 等. 风力机叶片流固耦合计算分析[J].
中国电机工程学报, 2013, 33(17): 98–104.
HU Danmei, ZHANG Zhichao, SUN Kai, et al. Computational analysis of wind turbine blades based on fluid-structure interaction[J]. Proceedings of the CSEE, 2013, 33(17): 98–104. |
| [9] | PUTERBAUGH S L, BRENDEL M. Tip clearance flow-shock interaction in a transonic compressor rotor[J]. Journal of propulsion and power, 1997, 13(1): 24–30. DOI:10.2514/2.5146 |
| [10] | DU Juan, LIN Feng, CHEN Jingyi, et al. Flow structures in the tip region for a transonic compressor rotor[J]. Journal of turbomachinery, 2013, 135(3): 031012. DOI:10.1115/1.4006779 |
| [11] | SAKULKAEW S, TAN C S, DONAHOO E, et al. Compressor efficiency variation with rotor tip gap from vanishing to large clearance[J]. Journal of turbomachinery, 2013, 135(3): 031030. DOI:10.1115/1.4007547 |
| [12] |
胡书珍, 张燕峰, 卢新根, 等. 跨声速轴流压气机间隙泄漏流触发旋转失速[J].
推进技术, 2010, 31(1): 47–51.
HU Shuzhen, ZHANG Yanfeng, LU Xingen, et al. Tip leakage flow trigger rotating stall in a transonic axial-flow compressor[J]. Journal of propulsion technology, 2010, 31(1): 47–51. |
| [13] |
郑赟, 王彪, 杨慧. 跨声速风扇叶片的静态气动弹性问题[J].
航空动力学报, 2013, 28(11): 2475–2482.
ZHENG Yun, WANG Biao, YANG Hui. Static aeroelastic problems of transonic fan blades[J]. Journal of aerospace power, 2013, 28(11): 2475–2482. |
| [14] | MAHAJAN A J, STEFKO G L. An iterative multidisciplinary analysis for rotor blade shape determination[C]//29th Joint Propulsion Conference and Exhibit. Monterey, CA:AIAA, 1993. |
| [15] | OHTSUKA M. Untwist of rotating blades[J]. Journal of engineering for power, 1975, 97(2): 180–187. DOI:10.1115/1.3445954 |
| [16] | LIU Gaolian. The generalized untwist problem of rotating blades:a coupled aeroelastic formulation[C]//ASME 1994 International Gas Turbine and Aeroengine Congress and Exposition. The Hague, Netherlands:ASME, 1994. |
| [17] |
郑赟, 王彪, 杨慧. 跨声速风扇叶片的反扭设计研究[J].
机械工程学报, 2013, 49(5): 147–153.
ZHENG Yun, WANG Biao, YANG Hui. Numerical study on blade un-running design of a transonic fan[J]. Journal of mechanical engineering, 2013, 49(5): 147–153. DOI:10.3901/JME.2013.05.147 |
| [18] |
陶海亮, 朱阳历, 郭宝亭, 等. 压气机叶片流固耦合数值计算[J].
航空动力学报, 2012, 27(5): 1054–1060.
TAO Hailiang, ZHU Yangli, GUO Baoting, et al. Numerical simulation of aeroelastic response in compressor based on fluid-structure coupling[J]. Journal of aerospace power, 2012, 27(5): 1054–1060. |



