无人水下航行器(unmanned underwater vehicle, UUV) 由于其优秀的隐蔽性和机动性,在水下侦察预警领域具有很高的战术价值和军事应用前景。近年来基于UUV载体的声呐设备对水下目标的探测跟踪方法是水声学领域的热门研究课题之一。在UUV无人干预的工作环境下,如何让声呐对未知目标进行自动检测,具有很高的研究意义和应用价值。
常规的目标检测跟踪算法是一种检测后跟踪方法(track after detection, TAD)。通过对声呐设备采集到的阵列数据进行实时分析,获取对目标方位的估计。基于前序数据中的目标方位信息,完成对目标的跟踪。在实际的水下声场环境中,由于水下杂波、噪声、载体自噪声等诸多干扰因素的影响,会出现目标信噪比低、航迹不连续的现象。在这种情况下上述方法存在如下缺点:1) 难以从干扰峰值中筛选出有效目标峰值,2) 对于航迹连续性差的目标,无法有效检测。
针对上述情况,基于检测前跟踪(track before detection, TBD) 思想[1],将多帧数据统筹分析,把目标检测问题转化为方位历程图中线条识别问题,从而克服噪声干扰、航迹断续的影响。同时,为了改善算法性能,提出了对方位历程图的两个预处理算法:基于信息融合的二值化处理,有效抑制载体自噪声干扰;基于自适应区域生长理论[2]的航迹增强算法,提升非连贯航迹的检测效果。
1 信号模型以N元均匀线形传感器阵列为例。阵列接收的远场窄带信号y的数学模型如下
| $ y=A\left(\mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right)\cdots+n $ | (1) |
式中:y∈CN×M表示N元阵列的接收信号,M为采样点数; Θ=[θ1 θ2 … θK]表示K个信源信号入射传感器阵列的方向; s∈CK×M为目标信号,n∈CN×M为传感器加性噪声; 阵列导向矩阵A(Θ)∈CN×K,A=a(θ1) a(θ2) … a(θK)。
| $ \begin{array}{*{20}{c}} {\boldsymbol{a}\left({{\theta _i}} \right)={{\left[{a\left({{\theta _i}, 1} \right)\;\;\;a\left({{\theta _i}, 2} \right)\;\ldots \;a\left({{\theta _i}, N} \right)} \right]}^{\rm{T}}}}\\ {\boldsymbol{a}\left({{\theta _i}, n} \right)={\rm{exp}}(-{\rm{j}}2{\rm{\pi }}f\left({n -1} \right)d{\rm{sin}}{\theta _i}/c)}\\ {i=1, 2, \ldots, K;n=1, 2, \ldots, N} \end{array} $ | (2) |
式中:d为等间距线型水听器阵列的间距,水听器数目为N,f为信号中心频率,c为声速。
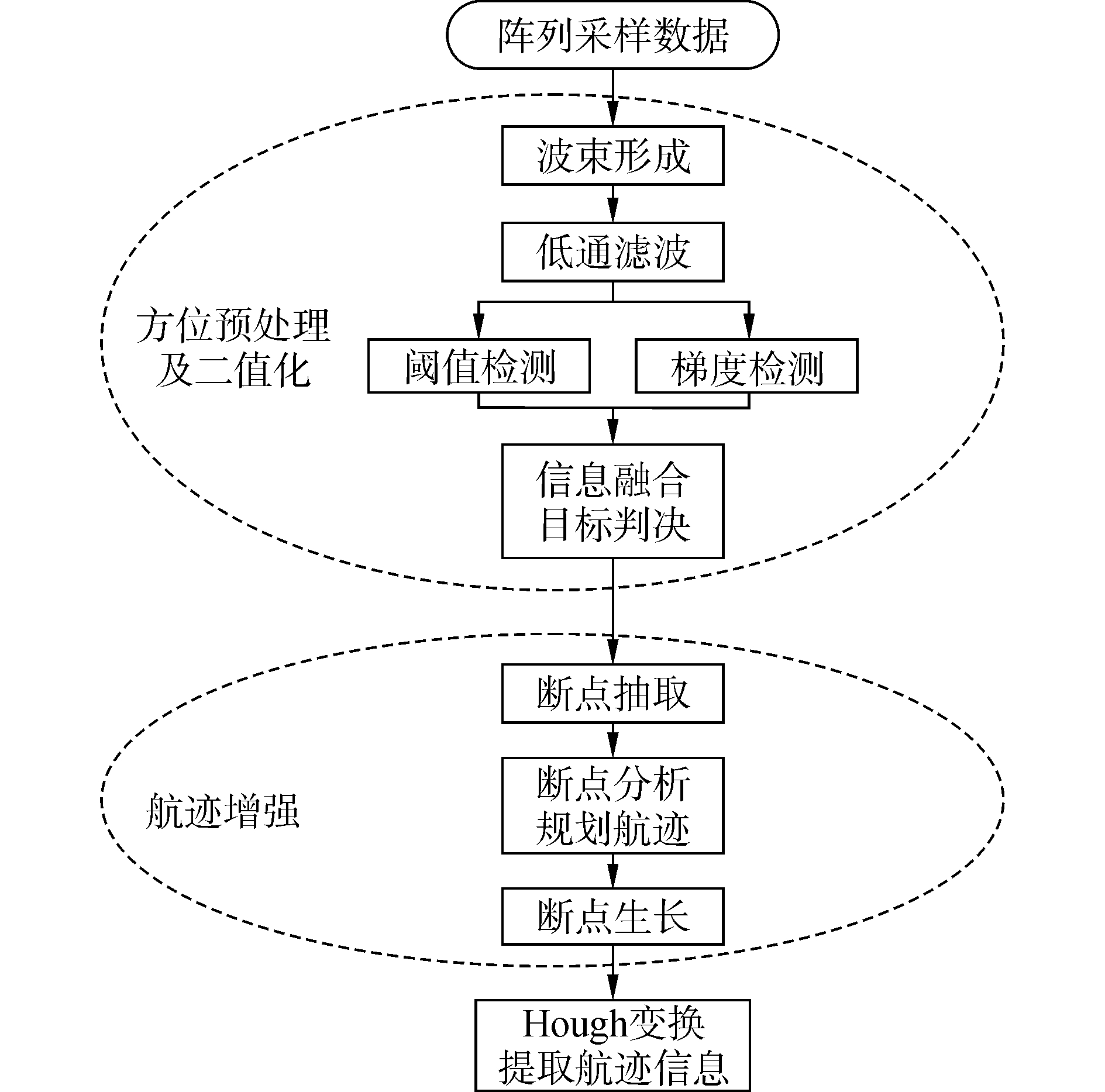
2 自动目标检测算法 2.1 方位预处理及二值化目标检测算法流程图如图 1所示,观察图可知,算法的第一步称为方位预处理及二值化。在这个阶段,原始阵列采样数据经波束形成器生成方位历程图,并通过一系列处理,由灰度图像转变为二值化图像。本阶段包含三部分处理:1) 波束形成,2) 低通滤波,3) 基于信息融合的峰值判定。
|
| 图1 目标检测算法流程图 Figure 1 Target detection framework |
检测与跟踪的基础,是基于波束形成方法得到的目标方位估计。水下目标噪声往往呈现为宽带信号,而针对宽带信号的高精度波束形成算法,具有很大的计算量,对于在功耗和计算能力上有限的水下航行器信号处理系统并不适用。常规波束形成算法[3]对于宽带信号具有计算量小和鲁棒性高的优点,能够满足本文需求。
常规波束形成(conventional beamforming, CBF),或称为时延-相加系统,波束形成输出BFt(θ)=
由于多波束系统对0°~180°范围内的波束曲线离散采样,因此在方位谱中存在高频突变成分。此外,波束曲线中偶尔也会出现噪点、野值。为避免这些成分对目标检测构成干扰,采用低通滤波对方位历程图进行预处理,流程如下:1) 将方位历程图像变换至傅里叶空间; 2) 设计低通滤波器进行频域滤波; 3) 经傅里叶逆变换回图像空间。
2.1.3 信息融合峰值检测在拖曳阵的工作环境中,距离较近的载体辐射噪声相对于远场目标是一个非常强的干扰源。实验结果显示,在浅海环境下载体匀速直线运动时,载体自噪声呈现为多途干扰[4],辐射能量在方位10°~30°之间平缓分布。针对以上特征,设计了一种结合峰值信息与梯度信息的二值化方法,在检测出远场目标峰值的同时,屏蔽平台自噪声的干扰峰值。本方法包含三个步骤:峰值检测,梯度分析,融合判定。
1) 峰值阈值检测
阈值处理的关键在于识别系数DT和检测门限γ的选取。记声场环境噪声均值为M,噪声起伏为σ2。当波束曲线中出现目标峰值时,记为LP(θ)。检测指数定义为DT=20lg[(LP(θ)-M)/σ]。基于奈曼-皮尔逊准则的接收机工作特性(ROC) 曲线,在水下声场环境中,识别系数阈值取经验值γ=6 dB,此时正确检测概率Pd≈96%[5]。
综上,峰值检测准则为
| $ peaks\left({p, \theta } \right)=\left\{ \begin{array}{l} 1, \;\;\;\;\;\;\;\;DT \ge 6\;\;{\rm{dB}}\\ 0, \;\;\;\;\;\;\;DT <6\;\;{\rm{dB}} \end{array} \right. $ | (3) |
2) 梯度分析
根据分布特征的区别,选取适当的梯度阈值来区分拖体自噪声与目标峰值。阈值门限设定为R=λ·mean(G(p, θ)),其中,mean(G(p, θ)) 为波束曲线梯度均值,λ为经验门限系数,取值2.0。判决准则如下:
| $ grad\left({r, \theta } \right)=\left\{ \begin{array}{l} 1, \;\;\;\;\;\;\;\;G\left({r, \theta } \right)\ge R\\ 0, \;\;\;\;\;\;\;G\left({r, \theta } \right)<R \end{array} \right. $ | (4) |
3) 融合判定
综合峰值特征与梯度信息,提出如下目标检测方案:扫描所有检测出的峰值点,其对应的角度邻域中,是否存在梯度非零值,如果存在,则该峰值点被判定为有效目标峰值,否则,视为干扰并置零。
2.2 基于TBD思想的航迹提取方法检测前跟踪(TBD) 是一种基于时间融合思想,对目标进行跟踪和检测的技术[6-7]。与传统检测后跟踪方法不同之处在于,TBD技术不会针对单次采样数据给出处理结果,而是通过对多帧累积数据统一处理,统筹目标峰值在各帧数据之间的连续性,从而得到目标的特征估计。
Hough变换是一种常见的TBD算法,常应用于图像处理中边缘检测[8]。一些学者将Hough变换应用于雷达、声呐目标信号检测领域[9],研究结果证明了该方法的适用性。基于Hough变换的目标航迹检测具有以下的特点与优势。
1) 检测方法简单。通过将图像空间中的直线转换为参数空间中的峰值点,Hough变换将复杂的整体特征检测问题转化为相对容易解决的局部峰值检测问题。
2) 对于不连续航迹的容忍度高,抗干扰能力强。对于顺序检测算法难以有效跟踪的不连贯航迹,Hough变换通过累加同一航迹上的峰值点,突出航迹信息,忽略航迹局部中断,以及一些噪点野值对检测结果的影响。
3) 计算量小。普通灰度图像的Hough变换计算量往往较大,但是经过上文所述的二值化处理之后,方位历程图中有效值数量大幅减小,大大减小Hough变换的计算量。
基于以上特点,在无人工干预的工作环境,为了有效跟踪不连续的目标航迹,选取Hough变换来进行目标航迹检测。具体的算法流程如下:
1) 将预处理所得二值化方位历程图经Hough变换至参数空间。采用Duda于1972年提出的改进Hough变换方法[10],以避免产生过大的运算量。
2) 将参数空间等分为离散的区块。对数据空间映射过来的曲线所经过的区块进行累积,统计累加量超过设定阈值的有效区块。
3) 获取有效区块中的局部峰值,运用质心法[11]计算峰值邻域U内的等效重心,作为该邻域等效峰值的估计。重心计算公式如下:
| $ rh{o_G}=\frac{{\sum\limits_{rho}^U {\sum\limits_{theta}^U {rho} } \cdot \left({rho, theta} \right)}}{{\sum\limits_{rho}^U {\sum\limits_{theta}^U {f\left({rho, theta} \right)} } }} $ | (5) |
| $ thet{a_G}=\frac{{\sum\limits_{rho}^U {\sum\limits_{theta}^U {theta} } \cdot \left({rho, theta} \right)}}{{\sum\limits_{rho}^U {\sum\limits_{theta}^U {f\left({rho, theta} \right)} } }} $ | (6) |
其中,f(rho, theta) 为参数空间对应区块的累积量。
4) 通过逆Hough变换,将重心反映射至图像空间,得到对应航迹的估计。对应关系如下:
| $ k=-\frac{1}{{\tan \left({thet{a_G}} \right)}}, b=-\frac{{rh{o_G} \cdot k}}{{\cos \left({thet{a_G}} \right)}} $ | (7) |
上节介绍了基于Hough变换的航迹提取、目标检测算法,该方法具有检测方式简单,对干扰和非连贯航迹宽容度高的特点。但是在实际工作中,目标航迹往往存在断点且断点间隔较大的情况,如图 2中目标B所示。由于航迹峰值点太少,该目标在Hough参数域的对应峰值很低,难以被有效检测。图 2为根据某次实验数据计算所得方位历程图。

|
| 图2 方位历程图 Figure 2 Bearing-time image |
针对上述目标的特点,提出的一种航迹增强算法,其核心思想是将属于相同航迹的断点互连,达到修补缺失航迹、增强目标特征的目的。
形态学中常用的断点互联算法是膨胀腐蚀算法[12]。但是由于该算法实质上是对断点进行无差别互连,存在计算量过大、航迹变形以及不同航迹峰值点误连等缺点。采用的断点连接算法称为自适应区域生长[13],常应用于图像分割等领域。其原理是选取图像中一个或多个像素点作为生长点,依据一定的生长准则逐步增长连接区域,直至没有可以归并的像素点为止。基于自适应区域生长的工作机制,提出如下航迹增强算法,分为生成断点分布、建立生长准则和航迹生长三步。
2.3.1 生成断点分布在航迹生长之前,需要先将方位历程图中所有断点坐标标注出来,方法如下:
1) 由上至下扫描binspec(p, θ),找到值为“1”的点后,将其置为“0”;
2) 考察该点八邻域,若邻域内全部为“0”,则判定该点为断点,将其值重置为“1”;若八邻域中有非零值点,则该点非断点,保持“0”值;
3) 扫描结束,即得到正向断点子集Df;
4) 由下至上,以相同方式扫描,得到逆向断点子集Dr;
5) 计算两次扫描所得谱图的并集D=Df∪Dr,即二值方位历程图断点集合。
断点集D记录了方位历程图中各航迹段的起点与终点,以及独立的噪点、野值的坐标。
2.3.2 建立生长准则断点生长准则(相似性准则) 是对航迹进行有效划分的关键,选取符合逻辑、宽容度合适的生长准则,能得到更好的生长效果。根据目标方位航迹的特点,提出如下相似性准则:
1) 同一快拍中不同方位的断点,一定属于不同航迹;
2) 快拍间隔Δp:确立最大容忍快拍间隔Pmax,凡两断点间快拍间隔Δp>Pmax,则判定两者不属于同一航迹;
3) 方位变化量Δθ:远场目标的方位角应该是一个时间缓变函数,限定其方位角随时间的变化率Ra(Rate of azimuth change),则相同航迹的断点之间方位角差异不可超过Ra·Δp;
4) 能量差异Δe:同一目标的辐射量级在短时间内不会剧烈变化,因此航迹两相邻断点的能量差异应该在一定范围内:
| $ \begin{array}{l} \Delta e=\left| {pBeam({p_{i+1}}, {\theta _{i+1}})-pBeam({p_i}, {\theta _i})} \right|\\ <={R_e} \cdot pBeam({p_i}, {\theta _i}) \end{array} $ |
Re表征阈值占目标能量的比例。
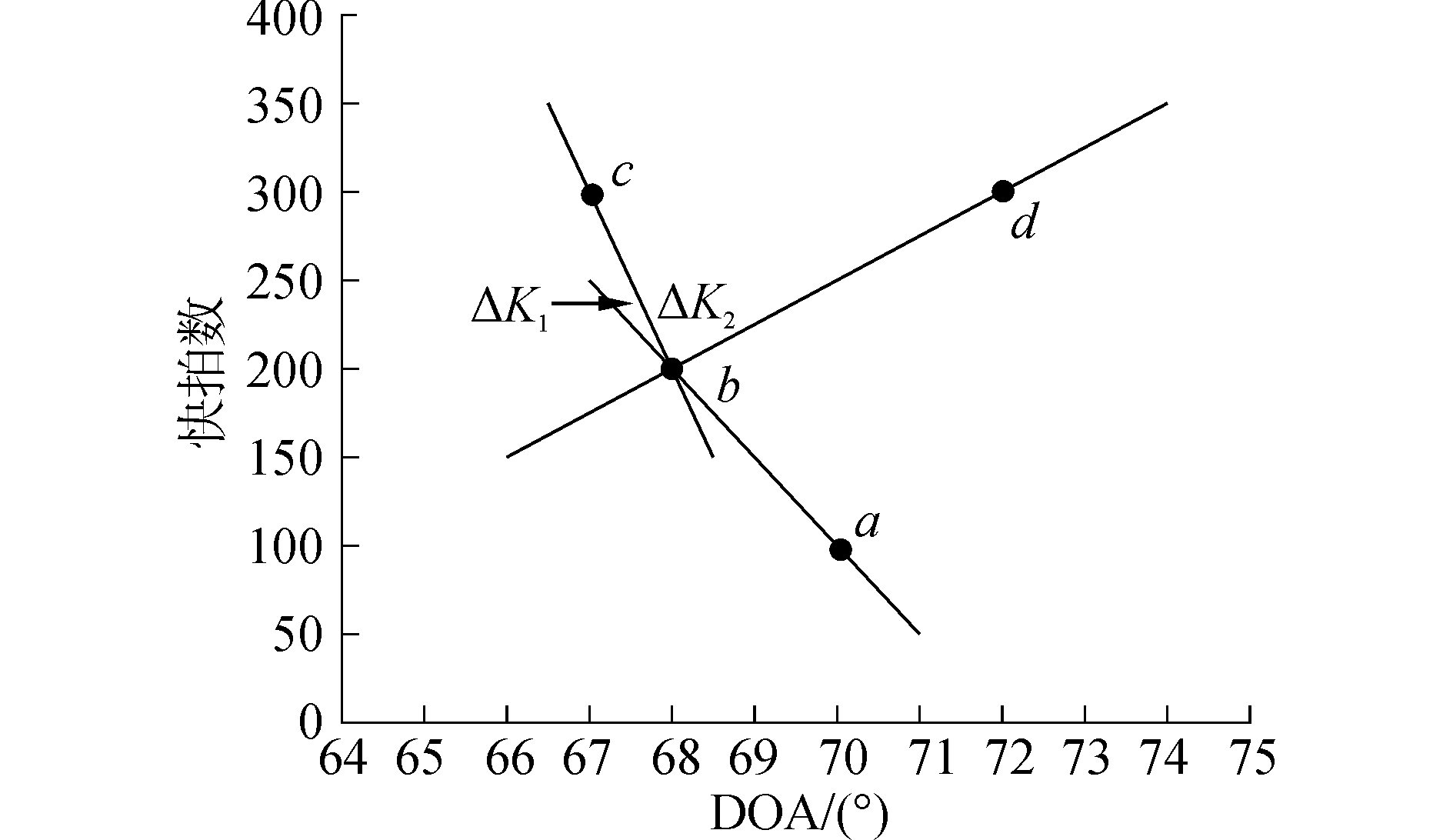
5) 斜率变化Δk:考虑到目标航迹的前后一致性,为避免将噪点和野值纳入航迹,生长准则中引入基于斜率控制[14]的判定准则。如图 3所示,a、b为已知属于同一航迹的两断点,c、d为待判定断点。记ab之间斜率kab,bc之间斜率kbc,则ab与bc的夹角
| $ \Delta {k_1}={\rm{arctan}}\left| {({k_{bc}}-{k_{ab}})/(1+{k_{ab}}\cdot{k_{bc}})} \right| $ | (8) |
|
| 图3 斜率控制示意图 Figure 3 Slope control |
同理,可计算bd夹角Δk2。设定阈值Φ,凡Δk>Φ,则判定当前断点不属于前序航迹。如示意图 4所示,相比峰值d、c更符合航迹ab的后续断点。
|
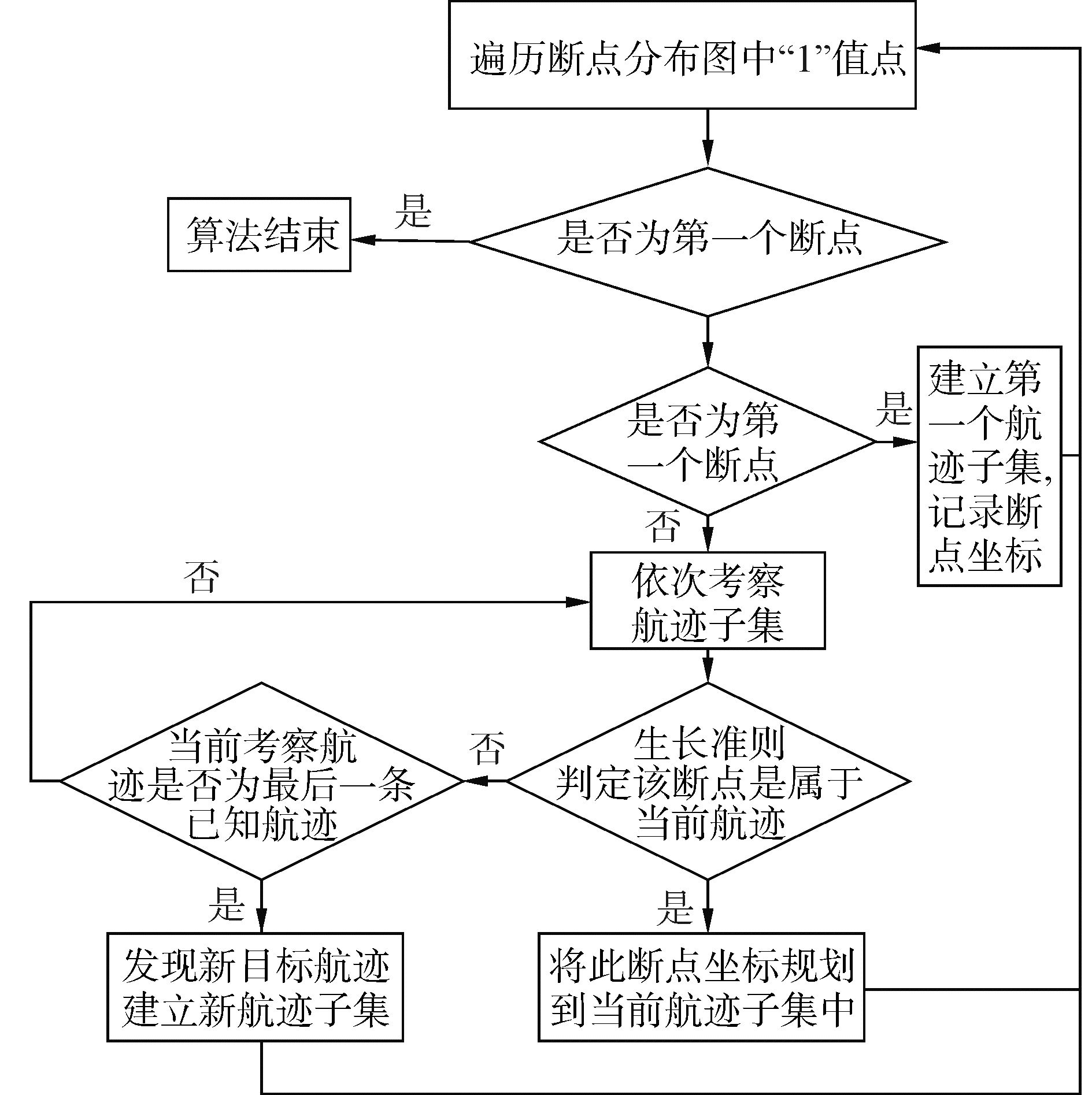
| 图4 航迹规划流程图 Figure 4 Target track growing framework |
基于上文所给出的生长准则,可以从方位历程图断点中规划出属于不同航迹的断点子集。基于得到的航迹断点子集,在方位历程图中将相同航迹的相邻断点以单像素线条相连,从而完成航迹的自适应生长。具体的规划流程如图 4所示。
3 实验数据分析 3.1 实验环境截取某次海试数据进行算法验证。接收阵的形式为拖曳线列阵,拖船航速6 kn,保持匀速直线运动。水听器阵列距拖船150 m,入水深度10~15 m,从而模拟以水下无人平台为载体的声场环境。信号入射角定义为:接收阵行进方向为0°,阵尾方向为180°。拖曳阵围绕声源机动,目标方位角在45°~135°间缓变。声源发射间歇性宽带信号,从而形成非连贯航迹的目标特征。
3.2 数据处理结果及分析本次试验中,线列阵数据采样率为10 kHz,每96 ms产生一帧方位曲线。选取625次快拍(96 ms×625=60 s) 作为TBD算法的检测时间窗,即假定在1 min内,目标航迹近似直线段,从而满足Hough变换的检测前提。
对图 3中的数据进行二值化处理,相关结果在图 5(a)、(b)、(c)中给出。可以看出,图 5(a)中峰值检测结果中包含了65°附近的非连续的目标方位峰值、路过船只在正横方向附近的航迹峰值,以及30°附近的载体自噪声峰值。图 5(b)所示梯度分析结果印证了上文对载体自噪声分布特征的预测,自噪声谱在梯度谱中被大量滤除。在图 5(c)所示的信息融合检测结果中,在保留绝大部分目标峰值的前提下,剔除了大部分载体自噪声的干扰峰值。

|
| 图5 方位历程图二值化结果 Figure 5 Binaryzation result |
航迹增强结果在图 6中给出。图 6(a)显示了二值化方位历程图的断点分布结果,图 6(b)给出经过自适应生长后航迹的增强效果。可以看出在保持原始方位历程图中航迹不变的前提下,对属于同一目标航迹的断点进行了连接,增强了目标B航迹的连续性, 并且通过选取合适的生长准则,避免了不同目标之间的误连现象。

|
| 图6 航迹自适应生长 Figure 6 Adaptive growing of target tracks |
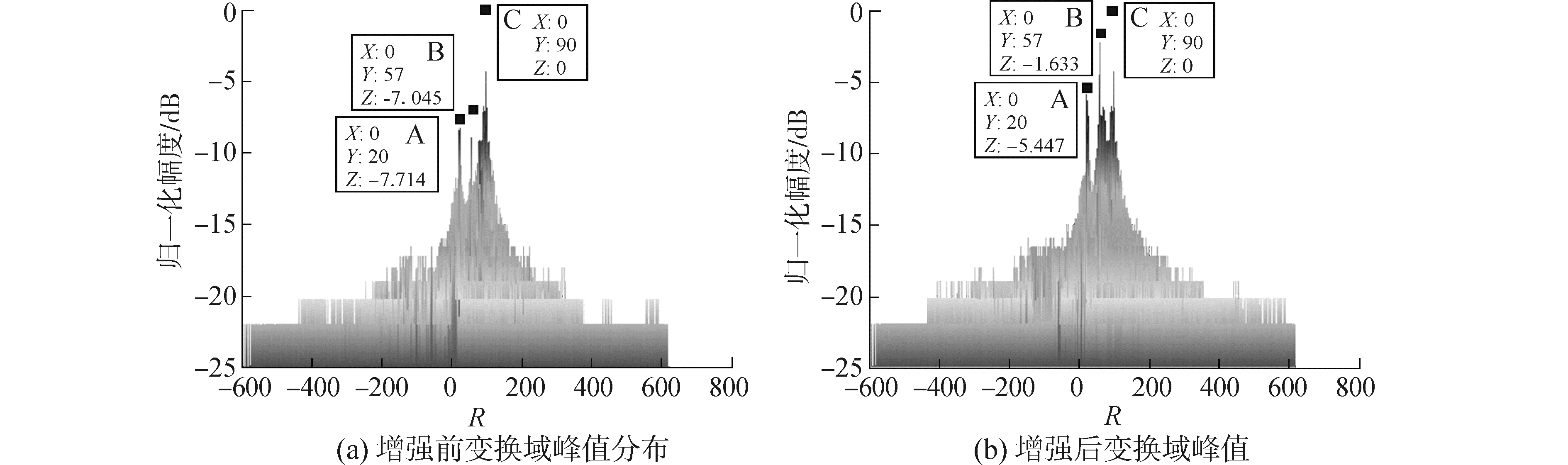
方位历程图的Hough变换域结果在图 7、8中给出。图 7对比了航迹增强前后Hough变换域中峰值分布。可以看出,对于原始的方位历程图,变换域中目标B对应峰值较低,与载体自噪声相近,从峰值能量上难以区分。通过对航迹增强,目标B峰值由图 7(a)中的-7 dB增至图 7(b)中的-1.633 dB。采用全局最大值的0.3倍(-5 dB) 作为检测阈值,经测试能够正确检测目标峰值的同时屏蔽载体噪声干扰峰值A。
|
| 图7 增强效果对比 Figure 7 Comparison between the original peaks and enhanced peaks in hough domain |

|
| 图8 航迹特征提取 Figure 8 Target track extraction |
根据上文分析,完整的航迹信息分布于峰值邻域内。基于质心法求取邻域等效重心作为相应航迹的参数估计,再由Hough反变换得到方位历程图中的航迹估计,结果如图 8所示。图 8(a)显示了质心法得到的等效重心分布,图 8(b)绘出根据重心坐标参数得到的航迹估计。可看出上述方法较准确地跟踪了目标航迹,同时屏蔽了自噪声航迹的干扰。
考查时间窗长度对检测结果的影响,对一段10 min的采样数据分别以625次快拍和312次快拍为时间窗进行处理,得到对目标航迹的连续处理结果,如图 9所示。结果显示采用较小的时间窗具有更好的跟踪效果,航迹的细节更丰富。

|
| 图9 连续处理结果 Figure 9 Continuous process result with different lengths of TBD window |
依据TBD思想,针对基于无人平台的拖曳线列阵声呐的工作模式提出了一种基于纯方位分析的自动目标检测算法。实验结果表明,该算法对载体自噪声、环境噪声以及杂波具有比较好的抗干扰能力,对航迹不连贯目标宽容度好,检测率高,可有效识别并提取不连续目标的方位轨迹,在无人工干预条件下能够满足水声目标自动检测的需求。
| [1] | KEMPER Jr P J, DIMARCO J S. Imaging infrared seeker signal processing overview:image processing, adaptive thresholding, and track processing[C]//Proceedings of the SPIE Conference on Infrared Imaging Systems:Design, Analysis, Modeling, and Testing. Orlando, Florida, USA, 1999:266-273. |
| [2] | CHANG Y L, LI Xiaobo. Adaptive image region-growing[J]. IEEE transactions on image processing, 1994, 3(6): 868–872. DOI:10.1109/83.336259 |
| [3] | 李启虎. 声呐信号处理引论[M]. 北京: 海洋出版社, 2000. |
| [4] | HUI J, ZHAO A B, SUN K P, et al. The simulation of tow ship noise on towed linear array[J]. Advanced materials research, 2012, 433-440: 2706–2711. DOI:10.4028/www.scientific.net/AMR.433-440 |
| [5] | BOUVET M, SCHWARTZ S C. Comparison of adaptive and robust receivers for signal detection in ambient underwater noise[J]. IEEE transactions on acoustics, speech, and signal processing, 1989, 37(5): 621–626. DOI:10.1109/29.17553 |
| [6] | DAVEY S, RUTTEN M, GORDON N. Track-before-detect techniques[M]. New Jersey: Wiley, 2012: 311-362. |
| [7] | GROSSI E, LOPS M, VENTURINO L. Track-before-detect for multiframe detection with censored observations[J]. IEEE transactions on aerospace and electronic systems, 2014, 50(3): 2032–2046. DOI:10.1109/TAES.2013.130148 |
| [8] | RAO Bin, ZONG Zhiwei, NIE Yuanping. Track-before-detect of weak ballistic target using elliptical Hough transform[C]//Proceedings of IET International Radar Conference. Xi'an:IEEE, 2013. |
| [9] | CARLSON B D, EVANS E D, WILSON S L. Search radar detection and track with the Hough transform. Ⅰ. System concept[J]. IEEE transactions on aerospace and electronic systems, 1994, 30(1): 102–108. DOI:10.1109/7.250410 |
| [10] | DUDA R O, HART P E. Use of the Hough transformation to detect lines and curves in pictures[J]. Communications of the ACM, 1972, 15(1): 11–15. DOI:10.1145/361237.361242 |
| [11] |
张爱华, 王亮. 基于时变图像序列的脉搏信息提取[J].
仪器仪表学报, 2007, 28(5): 820–825.
ZHANG Aihua, WANG Liang. Information detection of pulse wave base on time-varying images[J]. Chinese journal of scientific instrument, 2007, 28(5): 820–825. |
| [12] | GONZALEZ R C, WOODS R E. Digital image processing[M]. 3rd ed. India: Pearson Education, 2007. |
| [13] | HOLZ D, BEHNKE S. Fast range image segmentation and smoothing using approximate surface reconstruction and region growing[C]//Intelligent Autonomous Systems 12. Berlin Heidelberg:Springer, 2013:61-73. |
| [14] |
于广婷, 朱聪, 李柏林, 等. 光学图像中一种新的边界断点连接方法[J].
计算机应用研究, 2014, 31(4): 1264–1266, 1280.
YU Guangting, ZHU Cong, LI Bailin, et al. New connecting method for border breakpoints in optical image[J]. Application research of computers, 2014, 31(4): 1264–1266, 1280. |



