金属橡胶是一种新型的干摩擦阻尼材料[1],具有承载能力强、耐高低温、易制成各种形状及刚度可调节等优点,在工程机械隔振领域中得到广泛应用[1-3]。金属丝网橡胶材料是一种全新工艺制备的新型干摩擦隔振材料,与以往金属橡胶材料相比,成型工艺有了改进。传统加工方法先将金属丝制备成螺线卷,再由螺线卷缠绕制成毛坯压制成型。中间存在大量手工加工过程,难以控制环节较多,如缠绕的金属丝螺旋径,在单位长度上很难保证完全相同,在编织过程中,也很难保证金属丝编排分布的均匀性,制备的金属橡胶构件力学性能稳定性较差[4]。金属丝网橡胶材料的加工是先将金属丝按规则编织成金属丝网,再对金属丝网进行纹路压制处理,最后通过模具冲压成型。经实验研究发现,使用这种工艺制备的金属丝网橡胶材料隔振性优越,力学性能更加稳定[5],且能够机械化批量生产。目前大多数对金属橡胶材料的研究集中在其隔振力学性能,主要是在简谐激励下进行动态试验及理论分析[6-8], 而在实际工程中,隔振元件经常会受到冲击载荷,冲击载荷在系统中消失很快,但是所引起的响应却具有极其严重的破坏性,若设备冲击瞬时响应力或位移幅值超过了设备本身的结构强度所允许的响应时,将导致设备损坏,严重影响设备的可靠性和使用寿命,目前金属橡胶材料抗冲击性能的研究还相对较少,且仍然以试验研究为主[9-10],因此有必要对金属橡胶材料的抗冲击性能及耗能缓冲机理开展进一步研究。
基于上述原因,本文通过对金属丝网橡胶隔振器进行冲击试验,研究了冲击载荷、相对密度及负载质量对金属丝网橡胶隔振系统抗冲击力学性能的影响,在线性系统冲击响应理论基础上,结合金属丝网橡胶材料干摩擦特性,推导了金属丝网橡胶隔振系统冲击加速度响应最大值的近似计算公式,研究了公式的适用范围。
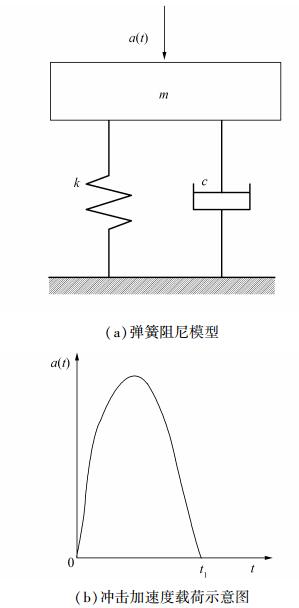
1 冲击加速度响应图 1所示为粘性阻尼线性系统动力学模型,其中m、k和c分别为系统的负载质量、刚度和阻尼系数,受到加速度冲击载荷a(t) 作用。
|
| 图1 线性系统动力学模型 Figure 1 The kinetic model of linear system |
根据振动理论,线性系统受到冲击载荷时的运动方程为
| $ m\ddot{x}+c\dot{x}+kx=0 $ | (1) |
当初始位移为x0=0时,由初速度v0所引起的振动为
| $ x\left( t \right)=\frac{{{v}_{0}}}{{{\omega }_{d}}}{{\text{e}}^{-\xi {{\omega }_{n}}t}}\text{sin}({{\omega }_{d}}t) $ | (2) |
式中:ξ为阻尼比,其值为c/2mωn;ωn是圆频率,
由式(2) 求二阶导可得系统加速度响应
| $ \begin{align} & \ \ \ \ \ \ \ \ \ \ \ \ \ {{a}_{sr}}\left( t \right)=\ddot{x}\left( t \right)= \\ & \frac{{{v}_{0}}{{\omega }_{n}}}{\sqrt{1-{{\xi }^{2}}}}{{\text{e}}^{-\xi {{\omega }_{n}}t}}\text{sin}({{\omega }_{d}}t-2\text{arctan}\frac{\sqrt{1-{{\xi }^{2}}}}{\xi }) \\ \end{align} $ | (3) |
冲击试验中,以响应发生时刻作为时间零点开始记录试验数据,可略去相位,则式(3) 简化为
| $ {{a}_{sr}}\left( t \right)=\frac{{{v}_{0}}{{\omega }_{n}}}{1-{{\xi }^{2}}}{{\text{e}}^{-\xi {{\omega }_{n}}t}}\text{sin}~({{\omega }_{d}}t) $ | (4) |
金属丝网橡胶属于干摩擦阻尼材料,与粘性阻尼系统相比,阻尼和刚度都取决于金属丝网橡胶的位移变形量,即金属丝网橡胶隔振器的预紧量,当预紧量较大时,阻尼比可以由能量耗散系数近似代替[8],能量耗散系数等于一个循环耗散的能量与最大变形势能的比值,则阻尼比
| $ \xi \approx \psi =\frac{\Delta W}{W} $ | (5) |
式中:ψ是能量耗散系数,ΔW是一个循环损耗的能量,W是最大变形势能。
将式(5) 代入式(4),隔振系统加速度响应为
| $ \begin{align} & a{{\left( t \right)}_{sr}}=\frac{{{v}_{0}}{{\omega }_{n}}W}{\sqrt{{{W}^{2}}-\Delta {{W}^{2}}}}{{\text{e}}^{-\frac{\Delta W}{W}{{\omega }_{n}}t}} \\ & \ \ \ \ \text{sin}({{\omega }_{n}}\sqrt{1-{{(\frac{\Delta W}{W})}^{2}}}t) \\ \end{align} $ | (6) |
考虑金属丝网橡胶的刚度非线性,刚度为金属丝网橡胶位移变形量的函数
| $ k=k\left( s \right) $ | (7) |
式中:s为金属丝网橡胶位移变形量,k(s) 为金属丝网橡胶非线性刚度函数。
金属丝网橡胶对外显示刚度为其非线性刚度和内部摩擦力的合力,金属丝网橡胶在受压变形过程中,非线性刚度产生的弹性势能和金属丝摩擦损耗能量的差值为W-ΔW,利用能量比例对系统刚度进行修正,则有
| $ k=\frac{W-\Delta W}{W}k\left( s \right) $ | (8) |
令χ=
则减振系统固有频率
| $ {{\omega }_{n}}=\sqrt{\frac{k}{m}}=\sqrt{\frac{\chi k\left( s \right)}{m}} $ | (9) |
将式(9) 代入式(6),得到金属丝网橡胶减振系统冲击加速度响应:
| $ {{a}_{sr}}\left( t \right)=\frac{p{{v}_{0}}}{\sqrt{m}}{{\text{e}}^{-\frac{\Delta W}{W}\sqrt{\frac{\chi k\left( s \right)}{m}}\cdot t}}\text{sin}\left( \frac{\chi k\left( s \right)}{p\sqrt{m}}t \right) $ | (10) |
其中,
式(10) 为金属丝网橡胶减振系统受到速度冲击载荷时的冲击加速度响应,当受如图 1所示加速度冲击载荷时初速度:
| $ {{v}_{0}}=\int_{0}^{{{t}_{1}}}{a\left( t \right)\text{d}t} $ | (11) |
将式(11) 代入式(10),得到加速度冲击载荷作用下系统冲击加速度响应
| $ {{a}_{sr}}\left( t \right)=\frac{p\int_{0}^{{{t}_{1}}}{a\left( t \right)\text{d}t}}{\sqrt{m}}{{\text{e}}^{-\frac{\Delta W}{W}\sqrt{\frac{\chi k\left( s \right)}{m}}t}}\text{sin}\left( \frac{\chi k\left( s \right)}{p\sqrt{m}}t \right) $ | (12) |
由式(12) 可得金属丝网橡胶减振系统冲击加速度响应最大值为
| $ {{a}_{sr}}{{\left( t \right)}_{\text{max}}}=\frac{p\int_{0}^{{{t}_{1}}}{a\left( t \right)\text{d}t}}{\sqrt{m}}{{\text{e}}^{-\frac{\text{ }\!\!\pi\!\!\text{ }\Delta W}{2\sqrt{{{W}^{2}}-\Delta {{W}^{2}}}}}} $ | (13) |
上式为单个金属丝网橡胶试件的冲击加速度响应最大值的近似计算公式,对于图 2的金属丝网橡胶减振系统,上下两个金属丝网橡胶试件并联,刚度为原来2倍,此时隔振系统的刚度k=2χk(s),系统冲击加速度响应最大值为
| $ {{a}_{sr}}{{\left( t \right)}_{\text{max}}}=\frac{\sqrt{2}p\int_{0}^{{{t}_{1}}}{a\left( t \right)\text{d}t}}{\sqrt{m}}{{\text{e}}^{-\frac{\text{ }\!\!\pi\!\!\text{ }\Delta W}{2\sqrt{{{W}^{2}}-\Delta {{W}^{2}}}}}} $ | (14) |

|
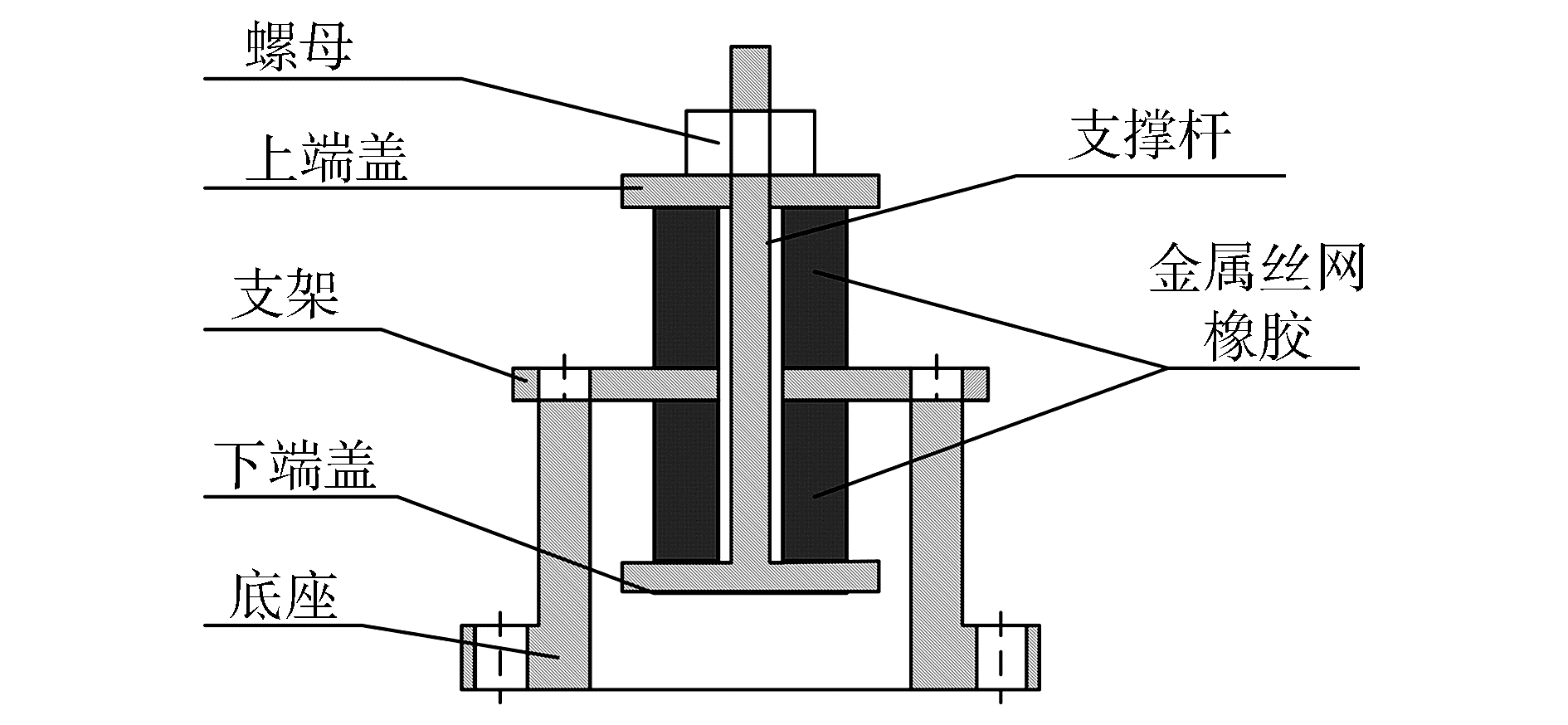
| 图2 金属丝网橡胶隔振器结构示意图 Figure 2 Structure schematic diagram of metal-net rubber isolator |
图 3所示为试验用金属丝网橡胶试件,试件外形结构为圆环形,相对密度ρ分别为0.16、0.20和0.25,金属丝丝径0.2 mm,试件外径40 mm,内径11.6 mm,高度20 mm。图 2为金属丝网橡胶隔振器结构示意图,金属丝网橡胶隔振器由底座、支架、紧固螺母、上下端盖、支撑杆和两个金属丝网橡胶试件组成,在振动过程中,通过上下端盖和支撑杆可以将振动过程中产生的上下拉压受力转化成金属丝网橡胶试件所能承受的压力,且可以通过调节紧固螺母控制预紧量。
|
| 图3 金属丝网橡胶 Figure 3 Metal-net rubber |
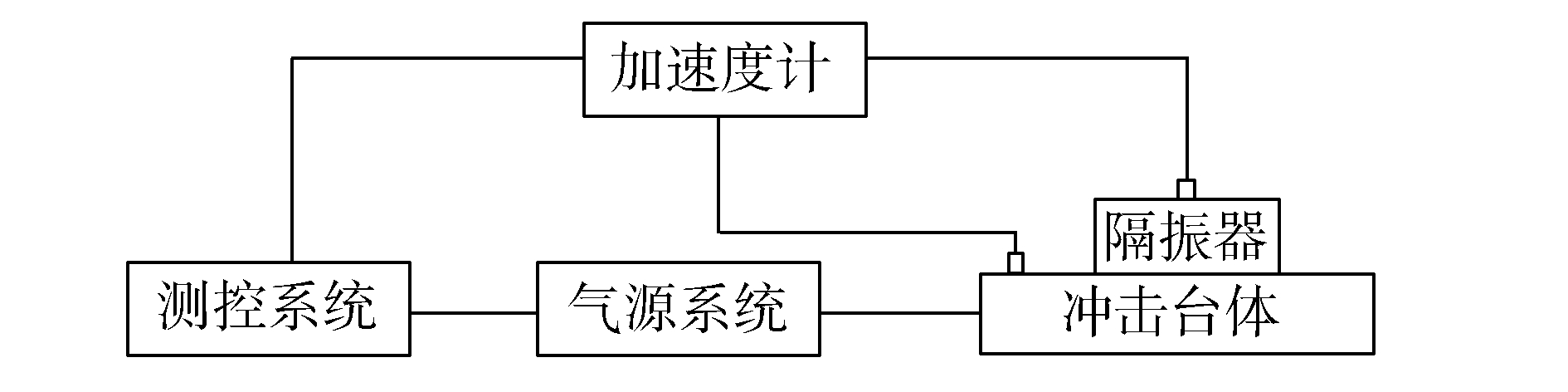
试验使用的冲击试验装置是江苏东菱振动SY11-600垂直冲击/碰撞试验机,如图 4所示,该装置由冲击台体、气源系统、测控系统和波形发生器四部分组成。图 5所示为冲击测试原理图,试验时,先在计算机上的冲击测试软件中设置试验的相关参数,测控系统将信号传输给气源系统,通过气压驱动使冲击台面上升到设定高度,释放气压,台面自由下落,与安装在底座上的波形发生器碰撞,产生一个冲击波形,通过波形发生器和冲击高度调节冲击脉冲持续时间和冲击强度,在冲击台面上和隔振器质量块上各放一个加速度传感器,用来测量输入冲击加速度和冲击加速度响应。

|
| 图4 冲击试验装置 Figure 4 Shock testing machine |
|
| 图5 冲击测试原理图 Figure 5 Schematic diagram of shock experiment |
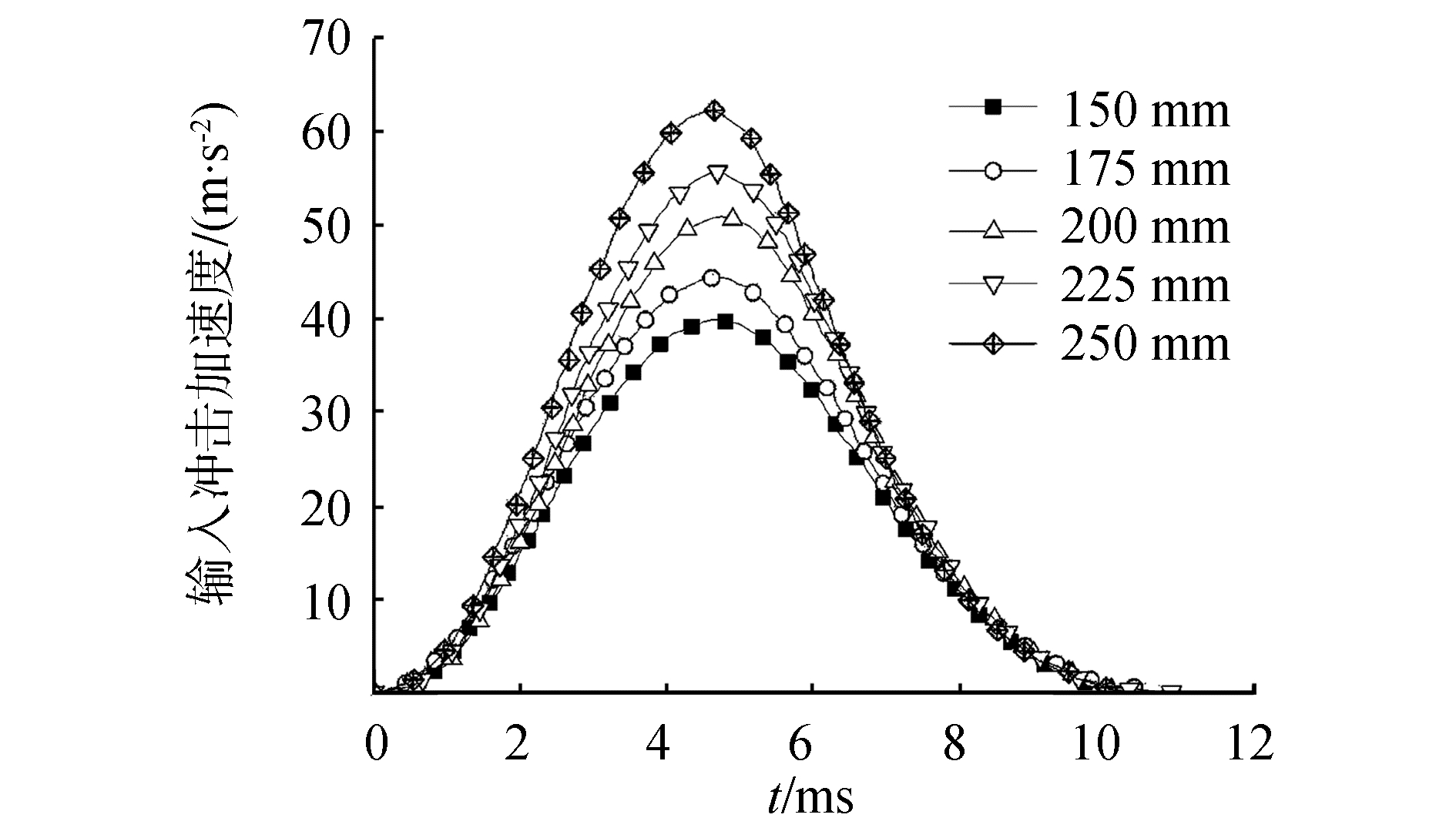
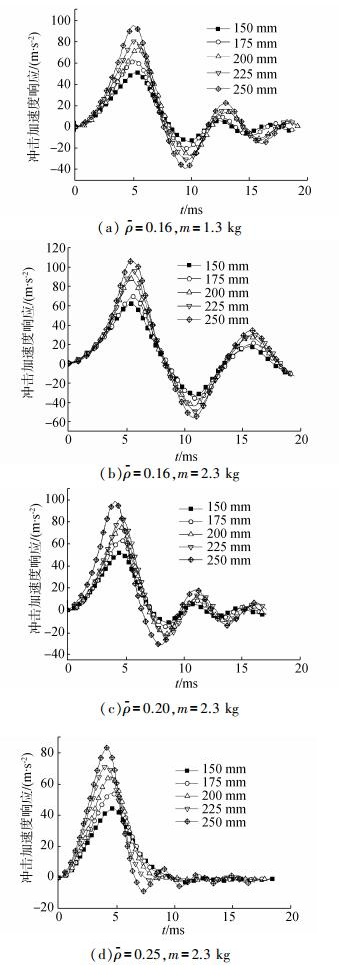
对相对密度ρ=0.16, 0.20, 0.25金属丝网橡胶试件组成的隔振器进行不同高度冲击试验,金属丝网橡胶预紧量为4 mm (试件高度20%),负载质量m为1.3 kg和2.3 kg。冲击高度h (冲击台面上升高度)150~250 mm产生的冲击加速度脉冲如图 6所示,脉冲波形为半正弦波,脉冲持续时间为10 ms。图 7所示为金属丝网橡胶隔振器冲击试验结果,由图可知,在冲击加速度脉冲载荷作用下,金属丝网橡胶隔振系统冲击加速度响应为一系列近似正弦脉冲波,且随着时间推移,冲击加速度响应脉冲波幅值和脉冲波持续时间不断减小,这是因为金属丝网橡胶属于干摩擦阻尼材料,在隔振系统受冲击载荷自由振动时,通过内部金属丝之间的摩擦耗散大量振动中的能量,导致系统动能迅速减小,并且随着冲击加速度载荷的增大,第一个冲击加速度响应脉冲波的持续时间不断减小,这是由于金属丝网橡胶材料的刚度取决于自身的位移变形量[6],随着冲击加速度载荷的增加,金属丝网橡胶自由振动中的幅值增大,刚度随之增大,从而导致隔振系统固有频率增大,振动周期变短;在ρ=0.16时,随着负载质量m的增加,系统惯性增大,固有频率减小,受冲击后的振动幅值增大,金属丝网橡胶的刚度增大,硬特性增强,阻尼减小,冲击加速度响应的衰减速度降低,第一个冲击加速度响应脉冲波的持续时间增大,冲击加速度响应曲线向右移动;当负载质量固定时,随着试件相对密度由0.16增加到0.20,隔振系统刚度增大,固有频率增大,冲击加速度响应曲线向左移动,当ρ=0.25时,由于相对密度过大,隔振系统刚度过大,在冲击载荷较小时,第一个冲击加速度响应脉冲波持续时间时间变长,与输入冲击加速度脉冲接近,当载荷足够大时,恢复上述变化规律。
|
| 图6 冲击加速度脉冲 Figure 6 Shock acceleration pulse |
|
| 图7 冲击试验结果 Figure 7 Shock experimental results |
在冲击试验中,采用冲击隔离系数作为隔振器的抗冲击特性表征[10]。冲击隔离系数η定义为
| $ \eta =\frac{{{a}_{sr}}{{\left( t \right)}_{\text{max}}}}{a{{\left( t \right)}_{\text{max}}}} $ | (15) |
式中:a(t)max为冲击加速度载荷的最大值,asr(t)max为冲击加速度响应的最大值。
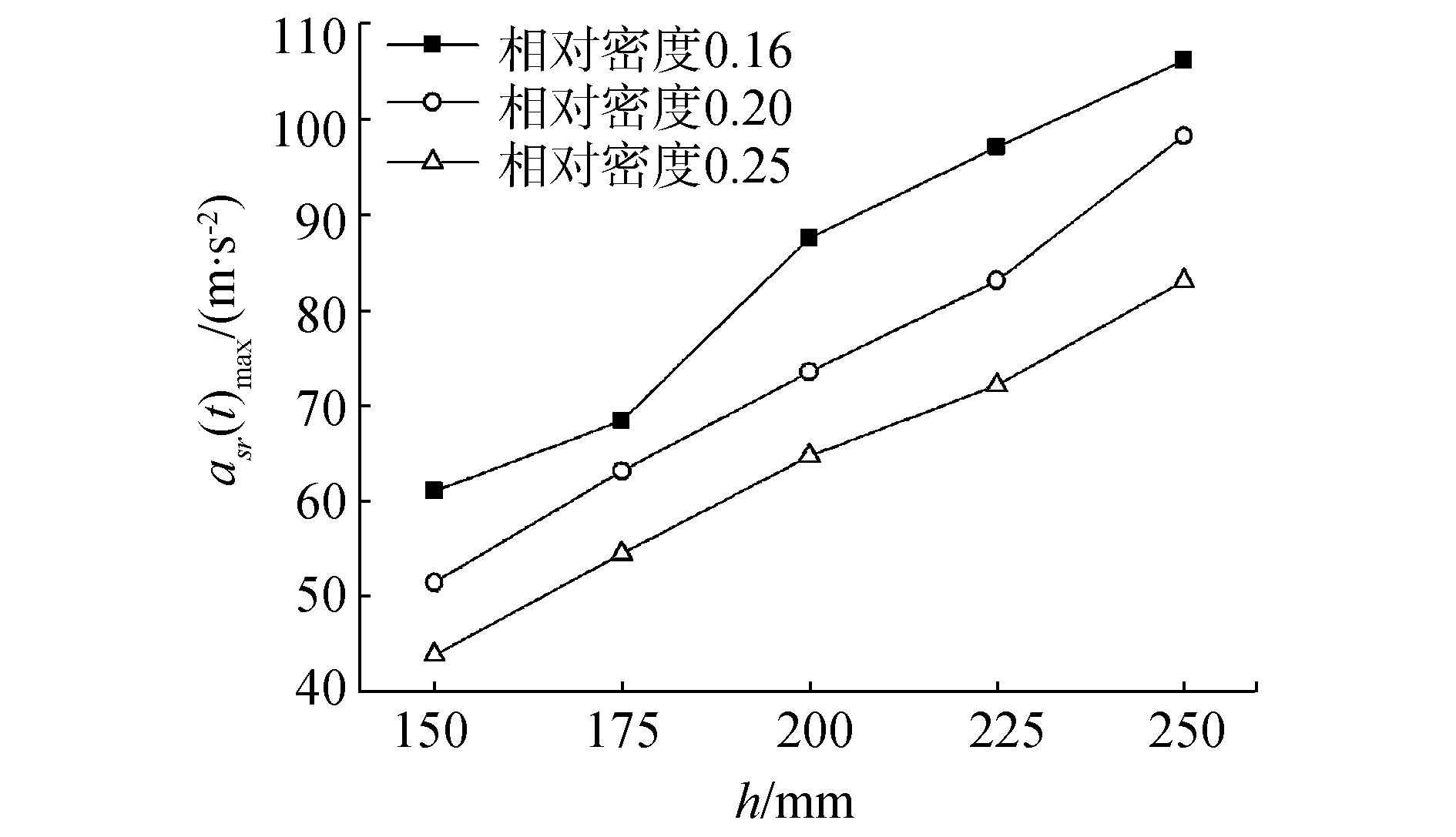
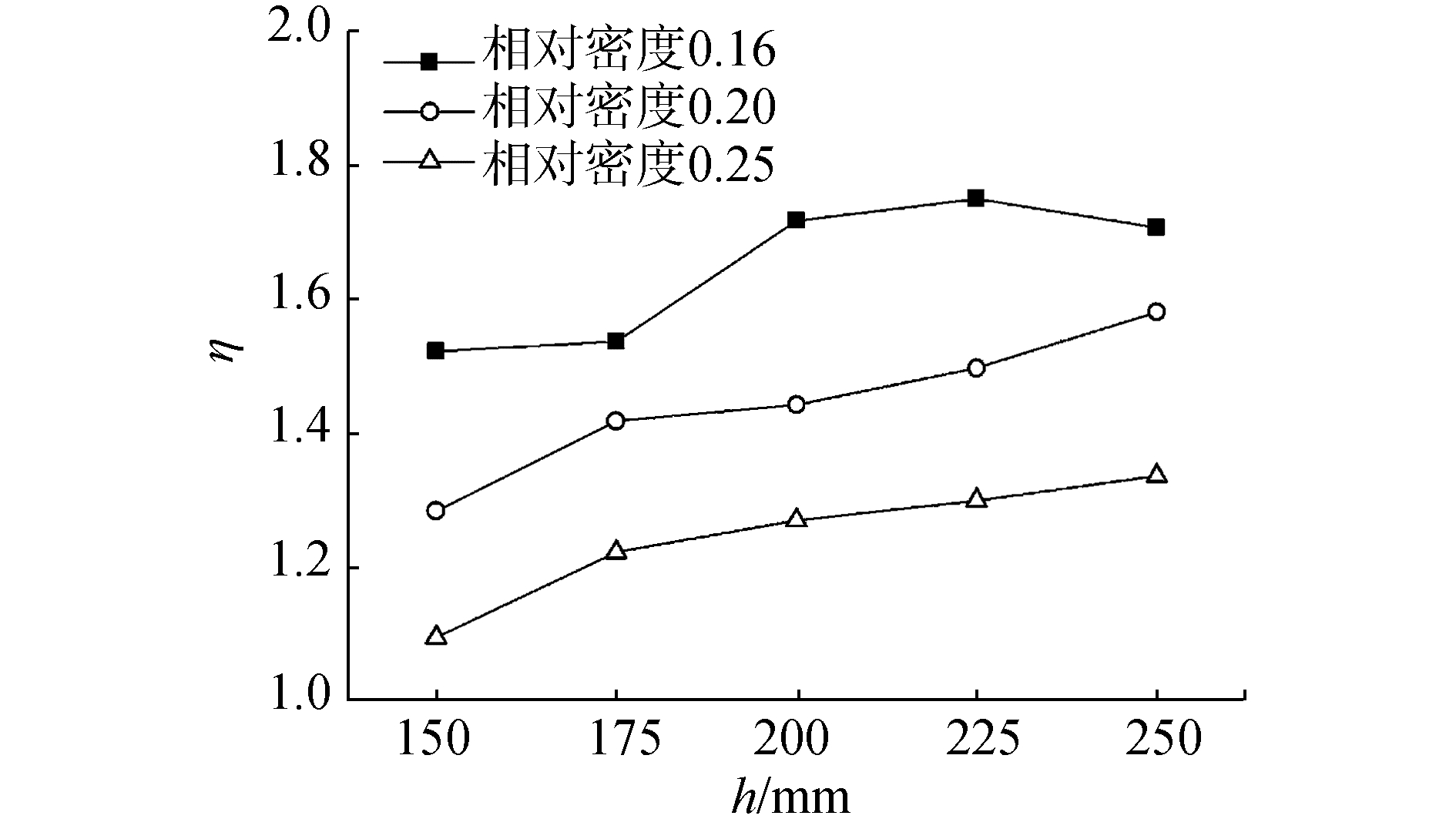
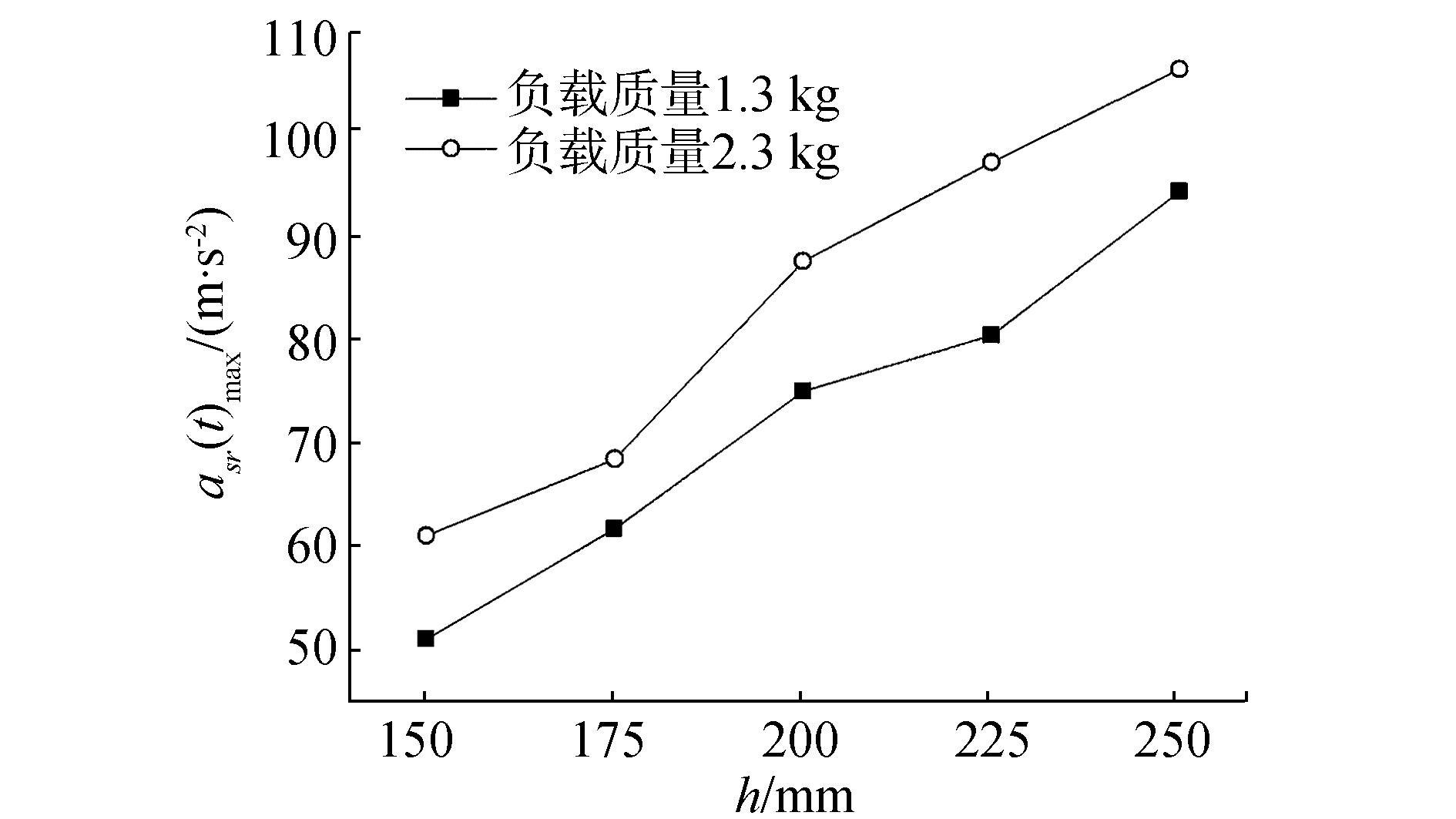
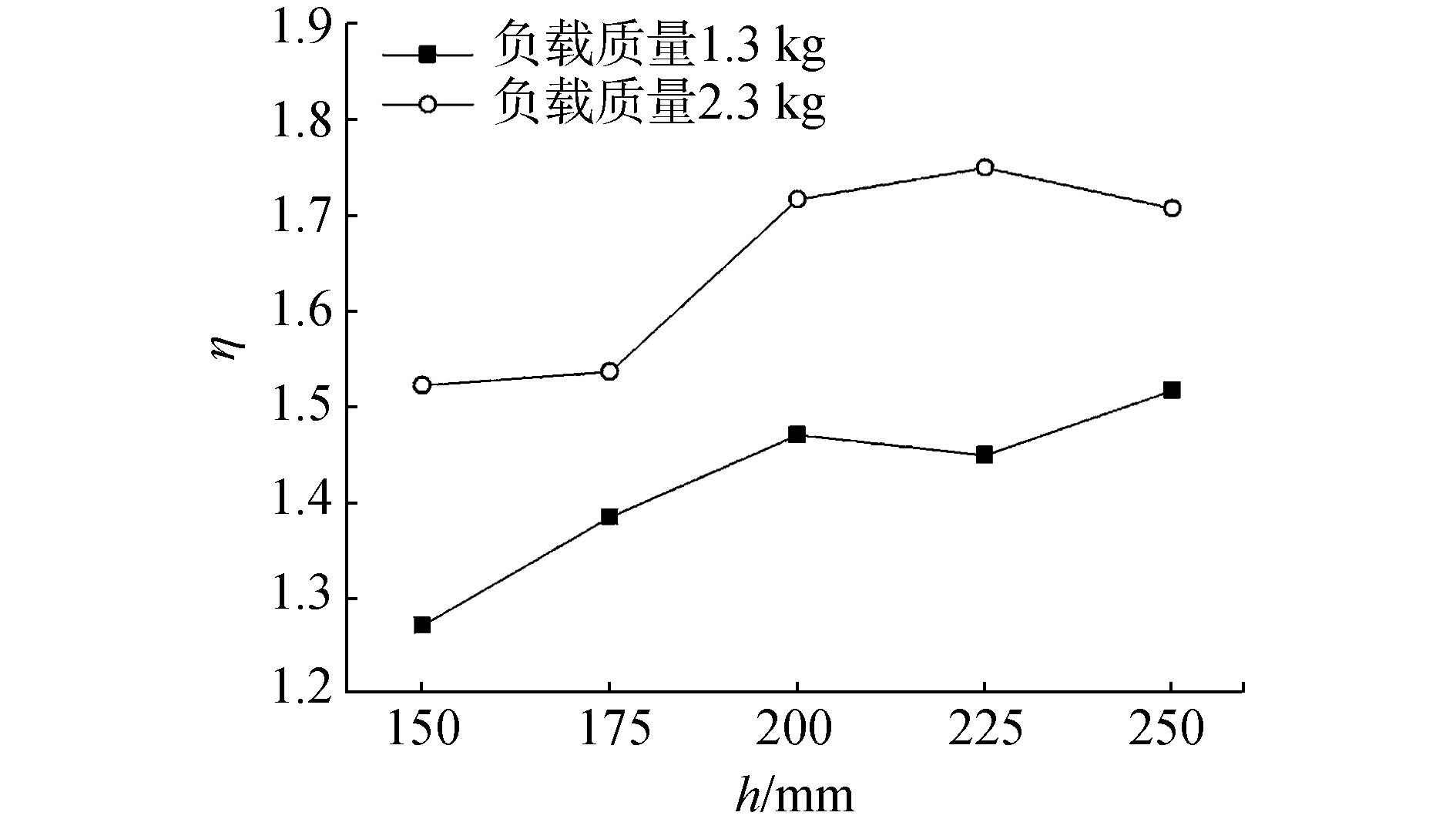
图 8为不同相对密度的冲击加速度响应最大值-冲击高度关系曲线,由图可知,相同冲击高度下,随着试件相对密度的增加,冲击加速度响应最大值逐渐减小。图 9为不同相对密度的冲击隔离系数-冲击高度关系曲线。从图中可知,冲击隔离系数也随相对密度的增加而降低,上述变化规律是由金属丝网橡胶材料的刚度非线性特性造成的,当ρ=0.16, m=2.3 kg时,相对于负载质量所产生的惯性载荷,隔振系统刚度过小,系统冲击加速度响应最大值和冲击隔离系数均较大;当ρ增至0.20时,系统刚度增大,此时系统刚度可以承担起负载质量所产生的惯性载荷,系统冲击加速度响应最大值和冲击隔离系数均减小;当ρ=0.25时,系统刚度过大,由前面分析知,系统响应与输入接近。此时负载质量相对系统刚度过小。此规律同样可由图 10和图 11进一步确定,在ρ=0.16,m=1.3 kg时,负载质量较小,系统刚度可以承担起负载质量所产生的惯性载荷,系统冲击响应的asr(t)max和冲击隔离系数η均减小。
|
| 图8 不同相对密度的冲击加速度响应最大值-冲击高度关系曲线 Figure 8 Relationship between maximum shock acceleration response and shock height under different relative densities |
|
| 图9 不同相对密度的冲击隔离系数-冲击高度关系曲线 Figure 9 Relationship between shock isolation coefficient and shock height under different relative densities |
|
| 图10 不同负载质量的冲击加速度响应最大值-冲击高度关系曲线 Figure 10 Relationship between maximum shock acceleration response and shock height under different load mass |
|
| 图11 不同负载质量的冲击隔离系数-冲击高度关系曲线 Figure 11 Relationship between shock isolation coefficient and shock height under different load mass |
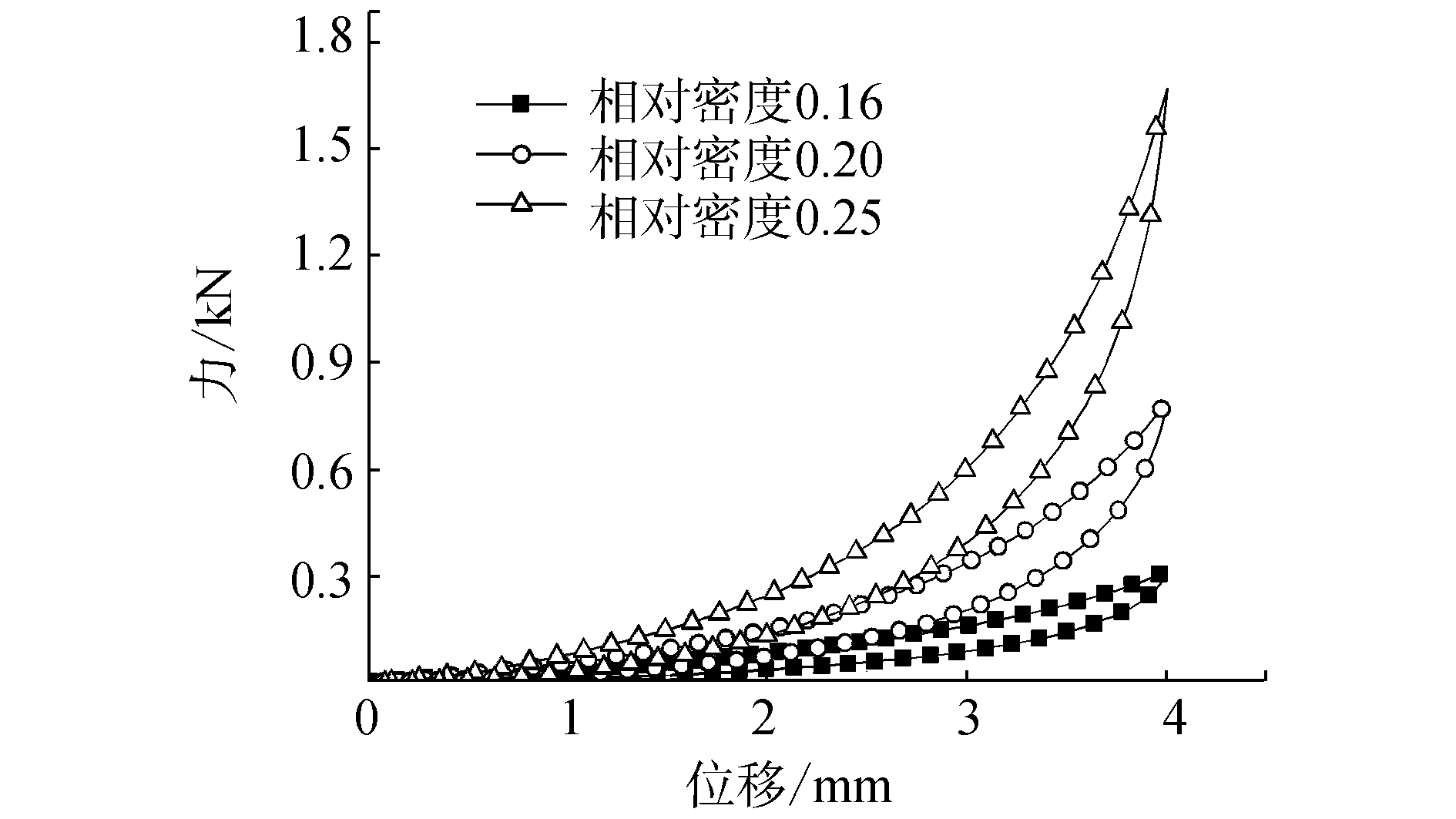
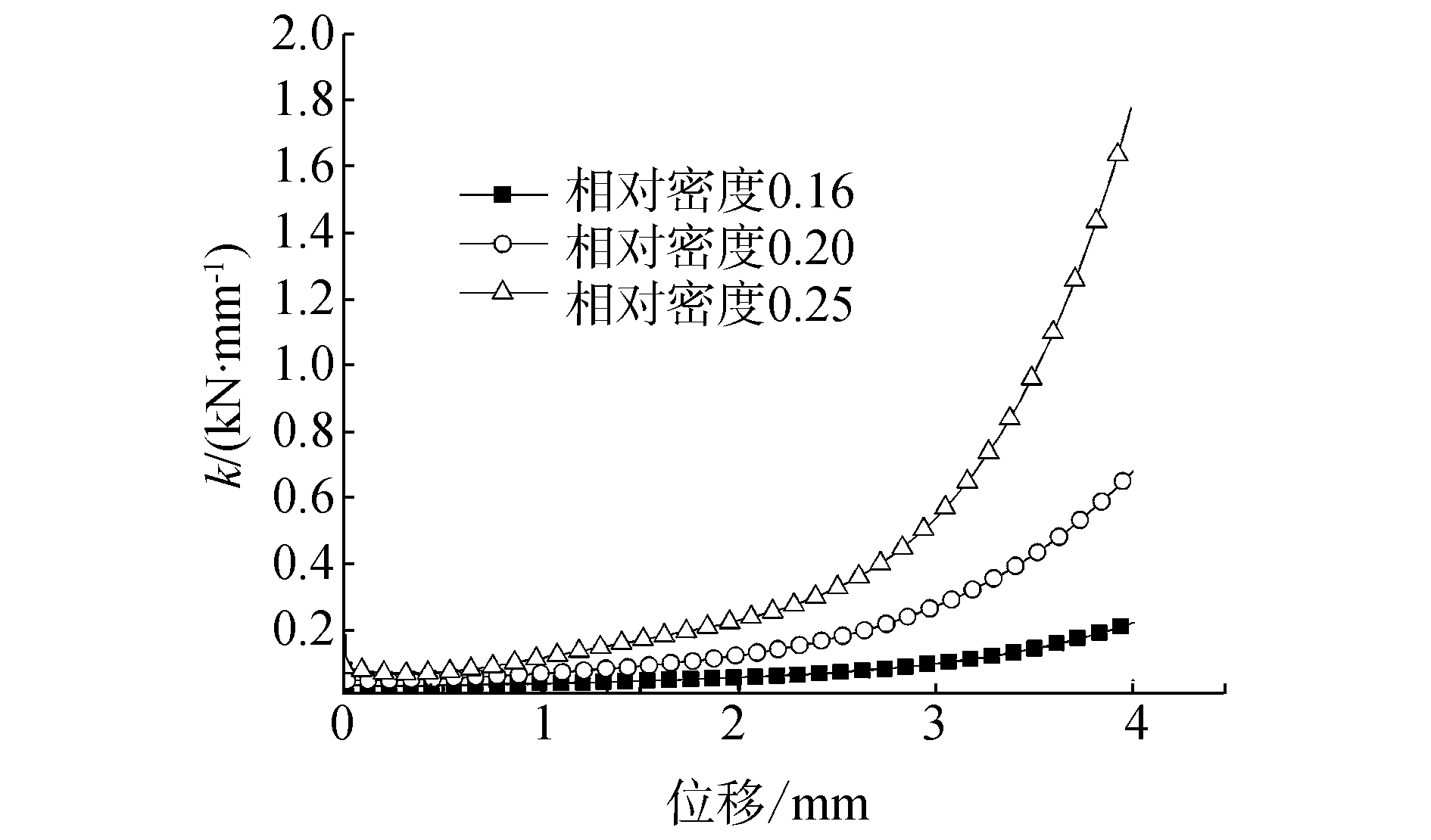
图 12为位移变形量与预紧量相同的金属丝网橡胶静态力-位移曲线,图 13为金属丝网橡胶的非线性刚度曲线,表 1为计算所得的相关理论计算参数,通过式(14) 对金属丝网橡胶隔振系统冲击加速度响应最大值进行理论计算,并与试验结果比较分析。由前面隔振器冲击试验结果分析可知,系统刚度和负载质量产生的惯性载荷对金属丝网橡胶隔振系统抗冲击力学性能具有重要影响,因此定义惯性载荷与系统刚度比值:
| $ \lambda =\frac{ma{{\left( t \right)}_{\text{max}}}}{k\left( s \right)\cdot i} $ | (16) |
|
| 图12 金属丝网橡胶力-位移曲线 Figure 12 Force-displacement curve of metal-net rubber |
|
| 图13 金属丝网橡胶非线性刚度 Figure 13 Nonlinear stiffness of metal-net rubber |
| ρ | W/J | ΔW/J | k/(N·mm-1) |
| 0.16 | 0.44 | 0.17 | 234 |
| 0.20 | 0.89 | 0.31 | 680 |
| 0.25 | 1.62 | 0.50 | 1775 |
式中,i为单位1 mm,λ为无量纲比值。
表 2为冲击加速度响应最大值的理论值和试验值,由表中数据可知,当ρ=0.16, m=1.3 kg,冲击加速度响应最大值的理论值与试验值比较接近,在比值λ=0.19,冲击载荷较小时,冲击加速度响应最大值误差较小,随着冲击载荷增大,误差逐渐增大;当m增至2.3 kg时,λ≥0.34,理论计算误差增大,由前面分析知,此时隔振系统刚度相对负载质量所产生的惯性载荷过小,金属丝网橡胶在缓冲过程中的位移变形较大,由位移变形量和预紧量相同的迟滞回线近似计算的刚度明显小于系统实际刚度,计算的能量耗散系数大于系统实际能量耗散系数,误差较大;当ρ增至0.20时,0.10≤λ≤0.16,系统刚度增大,在冲击载荷较小时,λ≤0.12,负载质量所产生的惯性载荷较小,误差较大,随着冲击载荷增大,系统惯性载荷逐渐增大,误差逐渐减小;ρ=0.25时,λ < 0.06,此时系统刚度过大,近似计算的粘性阻尼系统与实际金属丝网橡胶干摩擦阻尼系统相差过大,误差急剧增大。
| h/mm | ρ=0.16,m=1.3 kg | ρ=0.16,m=2.3 kg | ρ=0.20,m=2.3 kg | ρ=0.25,m=2.3 kg | |||||||||||||||
| 试验值/(m·s-2) | 理论值/(m·s-2) | 误差/% | λ | 试验值/(m·s-2) | 理论值/(m·s-2) | 误差/% | λ | 试验值/(m·s-2) | 理论值/(m·s-2) | 误差/% | λ | 试验值/(m·s-2) | 理论值/(m·s-2) | 误差/% | λ | ||||
| 150 | 51.00 | 52.70 | 3.33 | 0.19 | 61.04 | 39.34 | 35.56 | 0.34 | 51.50 | 74.74 | 45.13 | 0.10 | 43.94 | 126.16 | 187.12 | 0.038 | |||
| 175 | 61.69 | 58.24 | 5.59 | 0.21 | 68.46 | 44.10 | 35.58 | 0.38 | 63.21 | 82.61 | 30.72 | 0.12 | 54.50 | 139.44 | 155.85 | 0.042 | |||
| 200 | 75.01 | 64.72 | 13.70 | 0.24 | 87.56 | 48.32 | 44.82 | 0.43 | 73.57 | 90.48 | 22.98 | 0.13 | 64.77 | 152.73 | 135.80 | 0.048 | |||
| 225 | 80.43 | 69.92 | 13.06 | 0.27 | 97.11 | 52.14 | 46.31 | 0.47 | 83.12 | 98.35 | 18.35 | 0.14 | 72.14 | 166.01 | 130.12 | 0.052 | |||
| 250 | 94.27 | 76.39 | 18.97 | 0.30 | 106.10 | 57.02 | 46.26 | 0.53 | 98.25 | 108.18 | 10.11 | 0.16 | 83.08 | 179.29 | 115.80 | 0.058 | |||
本文通过对金属丝网橡胶隔振系统冲击响应研究,推导出金属丝网橡胶隔振系统冲击加速度响应最大值的近似计算公式,并进行了金属丝网橡胶隔振器冲击试验,研究结果表明:
1) 金属丝网橡胶相对密度、系统负载质量及冲击载荷对隔振系统冲击加速度响应具有显著影响。冲击载荷的增加会导致隔振系统固有频率增大,振动周期变短;负载质量的增加,则导致系统固有频率减小;在相同冲击高度下,随着金属丝网橡胶相对密度的增加,冲击加速度响应最大值逐渐减小,但冲击隔离系数随相对密度的增加而降低。
2) 在系统负载质量所产生惯性载荷与系统刚度比值λ=0.19时,冲击加速度响应最大值的理论计算结果与试验结果进行比较误差最小,冲击加速度响应最大幅值误差小于5%,当0.14 < λ < 0.30时,理论计算结果与试验结果比较接近,冲击加速度响应最大值的误差可控制在20%以内。
| [1] |
赵程, 贺跃进, 张恒. 金属橡胶的应用研究[J].
噪声与振动控制, 2006, 26(5): 45–47.
ZHAO Cheng, HE Yuejin, ZHANG He. Application research of metal-rubber[J]. Noise and vibration control, 2006, 26(5): 45–47. |
| [2] |
王平, 张国玉, 高玉军, 等. 金属橡胶减振器在机载光电吊舱复合减振系统中的应用[J].
振动与冲击, 2014, 33(5): 193–199.
WANG Ping, ZHANG Guoyu, GAO Yujun, et al. Application of metal-rubber dampers in vibration reduction system of an airborne electro-optical pod[J]. Journal of vibration and shock, 2014, 33(5): 193–199. |
| [3] |
杨广双, 陈忠明. 金属橡胶减振器在发动机安装时的减振设计研究[J].
飞机设计, 2007, 27(3): 7–10.
YANG Guangshuang, CHEN Zhongming. Research of steel wire-gauze pad dampers for vibration isolation of engine installation[J]. Aircraft design, 2007, 27(3): 7–10. |
| [4] | 董秀萍, 张力. 新型材料-金属橡胶建模及应用[M]. 北京: 化学工业出版社, 2010. |
| [5] |
邹广平, 刘泽, 唱忠良, 等. 金属丝网橡胶压缩力学性能研究[J].
实验力学, 2014, 29(6): 676–682.
ZOU Guangping, LIU Ze, CHANG Zhongliang, et al. On the compression properties of metal wire mesh rubber[J]. Journal of experimental mechanics, 2014, 29(6): 676–682. |
| [6] |
许建东, 郭宝亭, 朱梓根, 等. 金属橡胶材料的振动特性[J].
航空动力学报, 2004, 19(5): 619–622.
XU Jiandong, GUO Baoting, ZHU Zigen, et al. The vibration performance of metal-rubber material[J]. Journal of aerospace power, 2004, 19(5): 619–622. |
| [7] |
杨春香, 周易, 张虎. 金属橡胶动态隔振性能的实验研究[J].
航空学报, 2006, 27(3): 536–539.
YANG Chunxiang, ZHOU Yi, ZHANG Hu. Research on dynamic performance of metal rubber damper[J]. Acta aeronautica et astronautica sinica, 2006, 27(3): 536–539. |
| [8] | MA Yanhong, LIANG Zhichao, WANG Hong, et al. Theoretical and experimental steady-state rotordynamics of an adaptive air film damper with metal rubber[J]. Journal of sound and vibration, 2013, 332(22): 5710–5726. DOI:10.1016/j.jsv.2013.06.002 |
| [9] |
夏宇宏, 姜洪源, 魏浩东, 等. 金属橡胶隔振器抗冲击性能研究[J].
振动与冲击, 2009, 28(1): 72–75.
XIA Yuhong, JIANG Hongyuan, WEI Haodong, et al. Shock protection characteristics of metal rubber isolators[J]. Journal of vibration and shock, 2009, 28(1): 72–75. |
| [10] |
金鸣, 薛前光, 田立强, 等. 金属橡胶减振器振动及冲击特性实验研究[J].
电子产品可靠性与环境试验, 2012, 30(2): 20–23.
JIN Ming, XUE Qianguang, TIAN Liqiang, et al. Experimental study on vibration and shock characteristics of metal rubber damper[J]. Electronic product reliability and environmental testing, 2012, 30(2): 20–23. |



